( 1)2.6. Емкость и сопротивление перехода.
Модуляция решетки ПЭЗ перехода естественным образом должна отразиться на его емкости. Но прежде, чем перейти к определению этой емкости, необходимо рассмотреть способы ее нахождения. Общепринятый способ вычисления через диэлектрическую проницаемость
( 1)
неприемлем, поскольку величина 
определялаясь в предположении, что электроны движутся со скоростью света [7]. Кроме того, для структуры с переменными свойствами невозможно указать конкретное значение
( 2).
Следовательно, при этом соседние заряды образуют конденсатор емкостью 
По сечению
S полупроводник образует S/z2 конденсаторов, включенных параллельно, а по длине l/z - последовательных. Несмещенный полупроводник будет обладать бесконечной емкостью, а емкость смещенного полупроводника равна
( 3).
Рис. 1 Вольт-фарадная характеристика условного диода (справа – начало кривой).
При обратном смещении перехода он образует зону минимальной емкости и оставшиеся зоны можно не учитывать. На рис.11 приведена диаграмма изменения емкости перехода на прямой ветви диода. Из нее видно, что обратная ветвь дает возможность получать управляемую емкость до единиц нанофарад.
Глубоко ошибочным следует признать то, что полупроводники характеризуют сопротивлением [8]. Это типичные источники тока, которые в последовательном включении переходят из управляющего режима в подчиненный.
Рис. 2. Изменение модуля ПЭЗ вблизи пятки диода.
В подчиненный режим переходит участок полупроводника с меньшим модулем
z`, изменение которого происходит в десятки тысяч раз (рис. 12). Динамическое сопротивление диода равно
( 4).
Подчиненная структура (в данном случае –почти все тело полупроводника) вынуждена принять значение тока управляющей структуры и воздействие всего внешнего напряжения. Динамическое сопротивление перехода при том же токе обусловлено очень малым напряжением на переходе
( 5).
Рис. 3. Динамическое сопротивление диода (слева) и перехода в функции напряжения.
Поэтому и его динамическое сопротивление много меньше
( 6).
Графики этих функций даны на рис. 13.
Представляет практический интерес постоянная времени
t открытого диода. Сопоставляя рисунки (12 и 13), можно отметить существование экстремума t на прямой ветви. Отметим также, что принятое в современной теории выражение “омическое сопротивление” перехода или диода в целом, не вполне корректно.
2.7. Поверхностные и объемные эффекты в полупроводниках
Этот раздел крайне важен не только для объяснения протекающих электрических процессов. Он дает ключ к пониманию причин тех или иных нетривиальных эффектов в полупроводниках. В основе подобных эффектов лежит дискретность атомной структуры полупроводника и структуры ПЭЗ. Последняя подвержена существенным изменениям как в функции объемной плотности r основного и примесного материалов, так и в функции действующей напряженности НЕ. Взаимодействие этих структур протекает по-разному.
Привычное изображение атомной структуры полупроводников в виде прямоугольной сетки - это условность, необходимая для плоского отображения
объемной структуры полупроводников (тетрагональной). Точно так же и мы представили структуру ПЭЗ условно кубической, что позволяет нам корректно проводить лишь относительный анализ происходящих изменений. Однако, существуют пределы корректности и для относительных сравнений.
Выясним порядок межатомного расстояния в основном материале полупроводниковой техники – кремнии. Справочные данные [9] атомного радиуса кремния 
и межатомного расстояния 
не очень позволяют оценить свободу движения ПЭЗ в теле полупроводника. Для массы атома кремния 
(кг) можно указать объем, приходящийся на один атом
(м3).
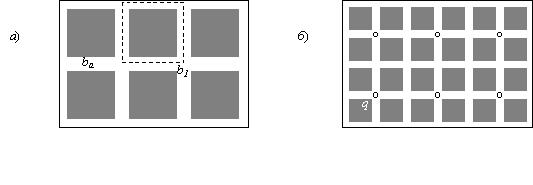
Рис. 4. Плоское масштабное изображение структуры атомов (а) полупроводника и расположение в ней пространственных электронов (б).
Собственный же объем атома кремния равен 1,00787E-29 (м
3). Теперь плоское изображение структуры кремния можно представить в масштабе квадратами (рис.14а), стороны b которых соответственно равны 2,726E-10 и 2,167E-10(м).Черные квадраты символизируют объем атомов. Свободные электроны (рис. 14б) размещаются в промежутках между атомами так, что в объеме куба ПЭЗ размещается
n3 атомов. Здесь n=z/b –целое число и, если вычислить модуль ПЭЗ для кремния
(м), можно найти значение
.
То есть, на один свободный электрон приходится 9261 атом, что подтверждает невозможность атомного происхождения ПЭЗ.
Вынужденное округление вверх говорит, что куб структуры ПЭЗ несколько растянут, то есть, свободные электроны немного “сжимают” охватываемую группу атомов. Значит, для того, чтобы занять энергетически выгодную позицию свободные электроны вынуждены потерять часть энергии. Эти потери исчезают при легировании кремния материалом с более высокой плотностью. Правда, для этого потребуется очень высокий процент примеси. Однако сам факт асимметричной чувствительности к примесям различной
плотности в какой-то мере объясняет различия подвижности дырок и электронов в существующей теории.Совершенно неизвестное ранее явление наблюдается в полупроводниках при действии внешней электрической напряженности. Рассмотрим поведение кубической ячейки ПЭЗ при таком воздействии (рис. 15).
Рис. 5. Деформация ячейки ПЭЗ.
На элементарный заряд
q ПЭЗ действует сила
, которая добавляет к исходному давлению Р добавочную величину
( 7).
Очевидно, что деформация куба решетки ПЭЗ (на рисунке справа) прекратится при равенстве 
, однако давление само является функцией неизвестной энергии электрона
( 8).
Поэтому желательно перейти к относительной деформации ячейки ПЭЗ, модуль
z которой соответствует нормальным условиям, в том числе действующей гравитационной напряженности. То есть, необходимо найти отклик
решетки ПЭЗ на действие относительной напряженности 
. Поскольку в направлении, перпендикулярном линии напряженности, модуль z не меняется (рис.16),
Рис. 6. К изменению объемной плотности ПЭЗ.
то при этом растет объемная плотность зарядов 
. Одновременное возрастание давления в сжимаемой ячейке и величины 
уравновешивает внешнюю электрическую напряженность за счет разности потенциалов соседних электронов
( 9).
Таким образом, независимо от величины давления в ячейке ПЭЗ увеличение напряженности в некоторое число раз
k вызывает рост числителя (39) в
раз и уменьшение знаменателя в раз (см. формулы 20 и 21).
Движению электронов слева направо (рис. 15, 16) соответствует полярность приложенного напряжения, показанная на рис. 17.
Рис. 7. Формирование волны давления в полупроводнике.
В такой полярности электроны правого конца полупроводника уносятся в металлический проводник. Поэтому с этого конца полупроводника формируется и движется влево волна отрицательного давления, обусловленная очередностью сжатия ячеек ПЭЗ. Образующийся разрыв между электронами вакуумирует близлежащие
ячейки, чем ускоряет их и заставляет “догнать” сжатые ячейки.Указанный выше рост объемной плотности зарядов требует набрать дополнительный электрический заряд в теле полупроводника 
. В результате, происходит интереснейшее явление: пока полупроводник набирает требуемый заряд, ток
Время, необходимое для заполнения полупроводника дополнительным зарядом весьма значительное и зависит от объема полупроводника, а также величины скачка электрической напряженности. В этом отрезке времени наблюдается рост тока в полупроводнике. При достаточно большой напряженности рост тока в цепи
( 10)
продолжается долго и почти линейно. Вероятно, этот факт был истолкован как тепловой процесс, отчего и была синтезирована искусственная зависимость (5) тока диода от температуры.
В то же время, влияние температуры на ток в полупроводнике, безусловно, есть. Оно обусловлено температурной зависимостью энергии электрона 
, которая определяет давление в ячейке ПЭЗ. С ростом давления числитель в формуле (39)
начинает расти быстрее, чем в раз и наступает возможность саморазогрева полупроводника.
На рис. 18 показаны временные диаграммы относительного нарастания тока в полупроводнике (брусок 7х7х23мм) при различных значениях электрической напряженности и рассеиваемой мощности. Отчетливо видно, что при малых мощностях рассеивания ток стабилизируется в течение 1,5-2 минут. С увеличением рассеиваемой мощности ток не стабилизируется (кривая 4).
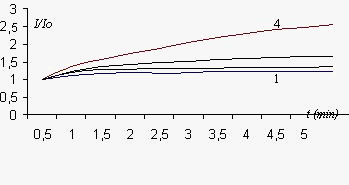
Рис. 8. Относительное изменение тока в полупроводнике во времени.
Кривая 1-напряженность 130 (В/м);Начальная мощность 0,002 Вт. Кривая 2- напряженность 260 (В/м); Начальная мощность 0,02 Вт. Кривая 3- напряженность 520 (В/м); Начальная мощность 0,25 Вт. Кривая 4- напряженность 870 (В/м); Начальная мощность 0,8 Вт.
Теоретически влияние температуры на ток в полупроводнике возможно только при наличии напряженности (формула 39). В противном случае, ток насыщения при Н
Е=0 должен бы быть также равным нулю.Эксперименты подтверждают отсутствие токов термогенерации и независимость обратного тока (тока насыщения) диодов от температуры при малых мощностях рассеивания.
Скорость ПЭЗ – это среднее значение ускоренного движения электронов в интервалах времени между столкновениями с атомами полупроводника. При естественной напряженности 
электроны получают ускорение 
. Для некоторой вероятности р<1 столкновения с атомами можно определить длину свободного пробега электронов
( 11).
Функция пути вида (
at2/2) при малых интервалах времени почти не отличается от функции (a1 t/2). Среднее значение скорости
становится линейной функцией модуля ПЭЗ, т.е. обратной функцией плотности вещества. В практических целях не требуется точного определения скорости ПЭЗ, поэтому данное приближение приемлемо для широкого диапазона плотностей материалов.
Тетраэдрическая форма кристаллов полупроводника делает почти невозможным получение ровной поверхности пластин. -По крайней мере, настолько ровной, чтобы
поверхность пластины принадлежала одному слою ПЭЗ. Мы впервые можем научно обосновать допустимую шороховатость пластин 
Практически достичь этого на большой площади пластины невозможно. А малейшие послабления в требованиях и вовсе приводят к появлению на поверхности кратеров, не заметных для глаза. Их называют ловушками и не зря.
Появление поверхностной разноплотности способно создать поверхностный диод, совершенно аналогичный нормальному объемному диоду. Поверхностный дефект, действительно, является ловушкой для электронов, создающей локальное градиентное электрическое поле.
Подобные явления возможны и внутри тела полупроводника. Каждое нарушение структуры может создавать виртуальный переход. Примечательное свойство полупроводников в том, что электроны движутся по линии напряженности и не могут двигаться перпендикулярно ей. Значит, дифракция в полупроводниках маловероятна. Поэтому дефекты структуры могут образовать два встречных перехода и эта часть поперечного сечения уже не участвует в проводимости. Вероятность этого тем выше, чем длиннее тело проводника по линии напряженности.
Наконец, последнее из замечательных свойств полупроводников, проявляющееся при наличии в них примеси. Мы несколько идеализировали перестройку структуры ПЭЗ (рис. 14б) в легированном полупроводнике. В действительности, резкой грани для округления отношения
n=z/b нет, поскольку отдельные атомы примеси располагаются неравномерно. Тем более, они не могут быть симметрично расположены относительно ячейки ПЭЗ, которая, к тому же, в процессе работы меняет свои размеры. Факторы случайности усиливаются технологической неравномерностью границ переходов, а также возможностью изменения геометрической фигуры ячеек ПЭЗ. В результате, линии границ перехода могут флуктуировать на
в рабочем цикле полупроводника.