( 1).Поскольку основное уравнение полупроводников представлено в виде тока, будем в дальнейшем ток считать основным параметром. Всякий отклик основного параметра на приложенную электрическую напряженность (или напряжение) мы называем функциональным. Это значит, что в отсутствии воздействий не должно быть никаких изменений тока в полупроводнике. Однако существует два вида самопроизвольных вариаций тока, называемых шумами или дрейфом. Шумом называют такие вариации тока, среднее значение которых во времени равно нулю. Соответственно, дрейфом называют изменения тока, имеющие монотонный характер.
Шумы. Различают два основных вида шумов в полупроводниках: дробовый шум и фликкер-шум. Дробовый шум понимается как неравномерное движение дискретных носителей электрического тока. Он статистически распределен во времени равномерно и потому его спектр зависит от величины тока. Но эта зависимость почти функциональная, сдвигающая частоту моды спектра пропорционально току. В полупроводниках этого не наблюдается, поэтому часто данный вид шума называют шумом рекомбинации электронов и дырок.
Мы уже доказали отсутствие всяких “дырок” в полупроводниках, следовательно, причину таких шумов надо искать в реальных процессах. Тем более, что вышеизложенный принцип создания тока в полупроводнике реально использует неравномерный способ движения электронов.
Для понимания сущности дробового шума достаточно забыть трактовку тока, как количество электричества, прошедшее через поперечное сечение проводника. Ведь, сечение не определено, значит, для каждого конкретного электрона, участвующего в создании тока, существует свое физическое событие, создающее ток. Именно таким событием является преодоление расстояния z, когда свободные электроны восстанавливают предшествующее взаимное расположение. Неравномерное движение электронов, вызванное любой из ранее рассмотренных причин, создает асинхронность событий – шум. Величина тока определяется скоростью движения электронов, то есть, частотой этих событий, что и определяет примущественный спектр шума.
Механизм появления фликкер-шумов связан с зарядовой структурой пространства [10]. В открытом космосе на радиусе орбиты Земли скорость ПЭЗ можно оценить величиной ~900 (км/с), а в нижних атмосферных слоях ее вычисленное значение равно 9,6Ч 10-6 (м/с).
Очевидно, что на границе резкого перепада скорости ПЭЗ произойдет накопление пространственных зарядов – резкое возрастание объемной плотности зарядов, простирающееся на многие десятки километров. Нижние слои атмосферы также различаются по плотности, но самое главное – они подвижны и появляются на пути ПЭЗ случайным образом. Именно поэтому, как отмечалось выше, нам не удалось определить фактическую плотность ПЭЗ.
Облака имеют различные размеры и скорость. Они пересекают путь ПЭЗ за различное время (размеры облачности, значение скорости) и имеют различную степень влияния на интенсивность потока ПЭЗ (толщина облака, его плотность). Все это отражается в виде модуляции параметра В, что создает на поверхности Земли и любом теле с площадью
S, модуляцию гравитационного потока
( 1).
Амплитудные флуктуации тока (42) являются шумами. Они могут быть выражены также в виде вариаций потенциала или заряда. Это позволяет нам ввести отвлеченный безразмерный показатель относительных флуктуаций.
Допустим, что разноплотность облаков проявляется во времени гармонически.
( 2).
Положим также, что амплитуда А вариаций и их период пропорциональны плотности облачностей. Тогда с учетом приближенного выражения для плотности воздуха в функции высоты над землей
(кг/м3) ( 3)
самый нижний слой атмосферы создает максимальные вариации обобщенного параметра
( 4).
Каждый последующий (при движении вверх) элементарный слой 
вносит дополнительное воздействие, пропорциональное текущей плотности
( 5).
Фазовый сдвиг 
представляет собой отношение времени 
прохождения ПЭЗ разности высот
. На рис. 19 приведены диаграммы суммарного сигнала, синтезированного для частот от w до 7w (при Ао=1).
|
|
|
Рис. 1. Суммарный сигнал относительных амплитуд с частотами от
w до 7w .а
)- фазы сигналов случайные; б)- сигналы синхронизированы. Справа экспериментально регистрируемые фликкер-шумы.Видно, что данный график воспроизводит типичный мерцательный характер фликкер-шума [11]. Мало что меняется в нем при увеличении числа зон – сказывается преобладающее действие случайности сдвига фаз. Сигнал на рис. 19б в точности воспроизводит сигналы щипковых инструментов.
Интересно отметить, что нижняя граница частот не ограничена вплоть до нуля, ибо кроме облачностей на плотность атмосферы влияют и другие процессы, среди которых могут быть и очень медленные (изменения температуры, влажности).
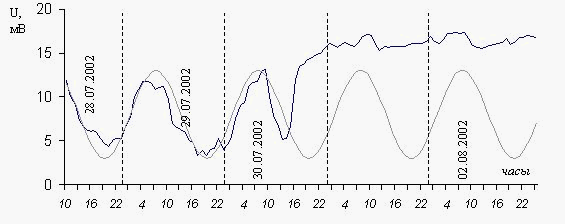
Рис. 2. Экспериментальная кривая изменения интенсивности потока ПЭЗ.
Совершенно случайно нами было зарегистрировано задымление Москвы (рис. 20) 30-го июля 2002г. Регистрировались самые низкие частоты, поэтому интервалы между измерениями составляли 10 минут. Гармоническая кривая – это аппроксимация реальных значений регистрируемого параметра. Более высокочастотные изменения сигнала вносятся нижними слоями атмосферы. Задымление происходит в непосредственной близости от поверхности Земли и оно практически блокирует низкочастотную составляющую.
Не случайно также то, что в разных источниках верхняя граница фликкер-шумов указывается не одинаковой (от 200 до 400 Гц) [12]. Это всего лишь означает нестабильность размеров облачностей и скоростей их движения. Абсолютно логично также, что меньшим размерам облачностей соответствует меньшая амплитуда влияния. Она оказывается обратно пропорциональной частоте, отчего и родилось второе название “1/
F -шум”.Относительные значения вариаций параметра
BG в полупроводнике в значительной мере ослаблены, поскольку объемная плотность зарядов в полупроводнике выше, чем в воздухе в
раз.
