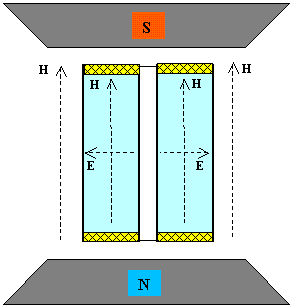
Рассмотрим цилиндрический конденсатор, помещённый в однородное магнитное поле H, параллельное его оси (см. рис.). В пространстве между обкладками конденсатора, помимо магнитного, существует также и радиальное электрическое поле напряжённости , где e - заряд на внутренней обкладке конденсатора, численно равный, но противоположный заряду на его внутренней обкладке, l - длина конденсатора, а r - векторное расстояние точки поля от оси конденсатора.

65

        Мы предполагаем, что длина конденсатора настолько больше его диаметра, что краевыми эффектами можно пренебречь, т. е. можно пользоваться формулой, строго справедливой лишь для бесконечно длинного конденсатора. Далее, для простоты полагаем, что в полости конденсатора находится газ, отличием диэлектрической проницаемости которого от единицы можно пренебречь. В пространстве между обкладками конденсатора вектор Пойнтинга отличен от нуля и равен

        Таким образом, мы приходим к представлению о непрерывной циркуляции энергии по замкнутым путям в статическом электромагнитном поле. Представление это не приводит к каким либо следствиям, могущим быть непосредственно проверенным на опыте, а потому лишено непосредственного физического смысла.

        Примем, однако, во внимание, что плотность электромагнитного количества движения g пропорциональна вектору Пойнтинга S ¹). Утверждение, что в рассматриваемом статическом поле локализовано количество движения с объёмной плотностью

66

,                                                                                             (1)

        Правда, общее количество всего статического поля в целом по необходимости равно нулю. Однако, зная пространственное распределение электромагнитного количества движения, мы можем определить момент этого движения K относительно центра инерции конденсатора по формуле

,                                                                                                   (2)

,

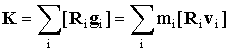определяющей момент механического количества движения системы материальных точек массы m_i и скорости v_i. Если мы разрядим конденсатор, то исчезнет как электрическое поле E, так и электромагнитный момент количества движения K. На основании закона сохранения момента количества движения мы должны заключить, что система конденсатор + магнит, возбуждающий поле H, приобретает в процессе разряда равный K момент механического количества движения. Если, например, магнит закреплён неподвижно, а конденсатор может свободно вращаться вокруг своей оси, то в процессе разряда он должен приобрести угловую скорость вращения , где I - момент инерции конденсатора относительно его оси.

        Этот доступный опытной проверке вывод, вытекающий из предположения о локализации в электромагнитном поле количества движения с плотностью g, может быть подтверждён непосредственным расчётом, к которому мы теперь и перейдём.

к нему радиоактивного вещества, вызывающую ионизацию газа между обкладками конденсатора. Если плотность разрядного тока в газе равна j, то каждый элемент объёма газа dV будет во время разряда испытывать силу (1/c)[jH]dV, момент же всех сил, испытываемых газом, будет равен

,                                                                                                 (3)

        Введём цилиндрическую систему координат z, r, a , ось z которой совпадает с осью конденсатора. Если бы магнитного поля не было, то вектор плотности тока был бы радиальным (j = |j_r|). В магнитном поле H линии тока, благодаря эффекту Холла, приобретут спиралевидную форму, и слагающая будет отличной от нуля, слагающая же j_z ввиду аксиальной симметрии поля останется равной нулю: j_z = 0.

Далее, ввиду той же симметрии момент N приложенных к газу сил будет направлен вдоль оси z (N_x = N_y = 0).

.

        Приняв во внимание, что поле H однородно, что j_z = 0 и что поэтому Rj = rj = rj_r, получаем

.

        Ток, протекающий в момент времени t через коаксиальную с конденсатором цилиндрическую поверхность радиуса r, равен

,

причём ток считается положительным, если он направлен от оси конденсатора наружу. Сила тока J(t) не зависит от радиуса r цилиндрической поверхности (мы пренебрегаем возможностью накопления 

68

объёмных зарядов в полости конденсатора) ²). Поэтому

,

где V - объём полости конденсатора. Наконец, сила тока J(t), протекающего через конденсатор от его внутренней обкладки к внешней, равна быстроте убыли заряда e на внутреннеё обкладке конденсатора:

.

        Так как N и H направлены по оси z, то окончательно

.

        Механический момент количества движения конденсатора K_M будет под воздействием момента сил N изменяться по закону

.                                                                                                 (4)

.

.

        Так как из соображений симметрии явствует, что слагающие по осям x и y вектора K равны нулю, то, сравнивая последнее уравнение с (4), получаем:

69

,

.                                                                                                      (5)

        Таким образом, мы подтвердили непосредственным подсчётом, что сумма электромагнитного и механического моментов количества движения остаётся постоянной во времени, так что при разряде конденсатора в магнитном поле он должен приобрести равный K механический момент количества движения K_M.

        Правда, в области макроскопических явлений экспериментальное измерение электромагнитного количества движения и его момента представляет очень трудную задачу ввиду ничтожной величины связанных с ними эффектов ³). Так, например, излучение света возбуждённым атомом, вообще говоря, связано с изменением момента количества движения электронов в атоме, причём это изменение по порядку величины сравнимо с абсолютной величиной момента атома.