 (1)
(1)ПРИЛОЖЕНИЕ 1в
G. M. Graham & D. G. Lahoz
Department of Physics, University of Toronto,
Toronto, Canada MSS 1A7
Nature Vol. 285 15 May 1980
Наблюдение статического электромагнитного количества движения в вакууме
Подробное изложение
журнальной статьи. Известные канадские
физики впервые в мире успешно осуществили
ряд искусных трудных для выполнения
экспериментов из области фундаментальной
классической электродинамики, касающихся
самой сути основополагающих физических
знаний. Это, прежде всего, измерения (во
второй половине 1970-ых годов) момента
количества движения в замкнутой системе,
содержащей источник постоянного
магнитного поля и меняющегося в
квазистационарном режиме электрического
поля. Ознакомление с их работами (этой и
другими) способствует более глубокому
пониманию сокровенных основ классической
электродинамики и будет полезным для тех
лиц, чья деятельность (работа или учёба) так
или иначе соприкасается с областью
современной фундаментальной физики (научно-технических
работников, студентов и т. д.) Это, по сути,
первый практический шаг в физику будущего.
"Наша программа измерения сил, связанных с
электромагнитным количеством движения на низких
частотах в веществе достигает кульминации в
первом прямом наблюдении свободного
электромагнитного момента количества движения,
создаваемого квазистатическими (неволновыми)
независимыми полями E
и B в пространстве
между пластинами цилиндрического конденсатора.
Чтобы зарегистрировать его движение
использовалась резонансная подвеска.
Наблюдаемые изменения момента импульса
согласуются с классической теорией в пределах
ошибки ~ 20%. Это наводит на мысль, что вакуум есть
место, где что-то движется, при наличии
статических полей, обладающих ненулевым
вектором Пойнтинга, как и предвидели Максвелл и
Пойнтинг. "
71
При установлении электромагнитной природы света, Максвелл противопоставил дальнодействию Вебера свою динамическую модель вакуума со скрытой материей в движении. Его идеи были объяснены Пойнтингом с помощью теоремы о потоке энергии, но позднее подверглись противодействию со стороны теории относительности. Однако в настоящее время есть сомнения относительно Максвелловской среды. В соответствии с релятивистской теорией Минковский установил, как чистое следствие уравнений Максвелла, что плотность сил Лоренца может быть точно выражена как дивергенция Максвеловского тензора в вакууме,
Tvac, за вычетом скорости изменения вектора Пойнтинга: (1)
(1)
В соответствии с идеями Максвелла-Пойнтинга,
последний член (Минковского) в уравнении (1) может
быть интерпретирован как локальная реакция сил,
действующих на заряды и токи, если окружающий их
вакуум несёт в себе электромагнитный импульс.
Эйнштейн и Лауб заметили, что при интегрировании
уравнения (1) по всему пространству, член ![]() создаёт
обращающийся в нуль поверхностный интеграл и,
поэтому, система сил Лоренца во Вселенной должна
быть дополнена величиной
создаёт
обращающийся в нуль поверхностный интеграл и,
поэтому, система сил Лоренца во Вселенной должна
быть дополнена величиной
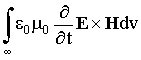 ,
,
чтобы не нарушался третий закон Ньютона. Вектор, противоположный последнему, в (1), обычно интерпретируется как нелокальная реакция зарядов и токов на волновые поля, но, согласно классическому примеру, он представляет действительную реакцию сил даже в случае индуцированных (неволновых) полей.
"Мы дополнили наше знание первым прямым наблюдением составляющей Минковского для неволновых полей
E и B, заключённых в малом объёме, так что локальная природа слагаемого, описывающего реакцию вакуума, также была продемонстрирована." Эксперимент состоит в измерении аксиального (осевого) момента72
силы, действующей на цилиндрический конденсатор, вместе с проводами для подачи переменного напряжения на его пластины, помещённого в соосно-направленное магнитное поле. Таким образом, ExH имеет азимутальное направление внутри вакуумного объёма конденсатора. Детали конденсатора, смонтированного на торсионно-осцилляторной подвеске, изображены на рисунке.
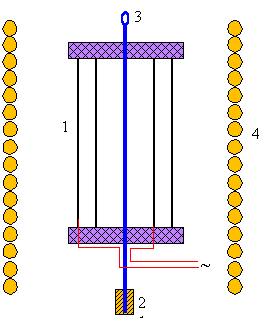
1 - цилиндрический конденсатор, 2 -
торсионно-осцилляторная подвеска, 3 - зеркальце,
4 - радиально расположенные провода для подачи
переменного напряжения на пластины,
5 - сверхпроводящий соленоид.
Конденсатор, вместе с проводами, образует жесткую электрически замкнутую цепь. Добротность механической системы Q превышала 10
5. Момент силы определяли по отклонению светового зайчика, отражённого от укреплённого на оси конденсатора зеркальца.Измеренные моменты сил в таблице сравниваются с действующими в подвеске расчётными, полностью определяемыми
73
суммарной силой Лоренца, приложенных к радиальным проводам, по которым течёт ток
I, переносящий заряды на обкладки подвешенного конденсатора.Расчётные и наблюдаемые амплитуды моментов сил для типичных амплитуд полей (электрическое поле подается на внутренний электрод) |
|||
E0 MVm-1 |
B0 T |
T0,calc pNm |
T0,obs pNm |
0.58 0.64 1.3 1.7 2.3 |
0.13 0.22 0.22 0.19 0.22 |
2.0 3.5 7.1 7.9 12.4 |
1.8 4.4 8.5 8.7 17.0 |
Таким образом, момент силы равен ![]() , где
, где
Несмотря на то, что результат объясняется классическим электромагнетизмом, он неуклонно ведёт к признанию физической реальности вектора Пойнтинга, даже если
E и H возникают из независимых источников. Это можно видеть при рассматривании системы, в которой действует реакция по отношению к моменту силы (где тот фактор, который создаёт противодействие наблюдаемому моменту силы?). Это не может быть ни внешняя электрическая цепь, так как токовая петля, с очевидностью, замкнута в пределах подвески, ни магнит, который, как круговая катушка, не может получить аксиальный момент силы (сила параллельна его собственному току).74
По отношению к закону сохранения момента количества движения, петля (включающая в себя конденсатор, вместе с подводящими напряжение проводами) есть замкнутая система и реакцию момента силы можно мыслить себе как изменение электромагнитного количества движения, которое несут в себе сами поля в области их сосуществования, внутри вакуумного пространства конденсатора. Так как I = C0dV/dt, то расчётный момент силы, в точности, равен объёмному интегралу от rxд(ExH)/дtc2, так что полная реакция момента силы определяется при значении реальной плотности момента количества движения rx(ExH)/c2.
"Примечательно, что неизвестные "частицы" могут быть идентифицированы как причина наблюдаемого электромагнитного количества движения регистрируемого механическим детектором. Однако это не подразумевает введения нового содержания, потому что концепция энергии-импульса, создаваемых макроскопическими квазистатическими электромагнитными полями уже содержится в уравнениях Максвелла. В соответствии с этим и с нашими экспериментальными результатами, постоянные магниты и электреты могут быть использованы для создания маховика электромагнитной энергии непрерывно циркулирующей в вакуумном пространстве конденсатора, как, если бы Максвелловская среда обладала свойством сверхтекучести. Определённо новое содержание заключается в том, что квазистатические поля Максвелла есть не просто ненаблюдаемая среда во взаимодействии между веществом и веществом: она имеет в действительности механические свойства, постулированные Максвеллом в противовес теории "действия на расстоянии".
Эти эксперименты продолжаются, и полное сообщение будет опубликовано в другом месте."
75