
ПРИЛОЖЕНИЕ 1г
О законах сохранения импульса-энергии
при наличии
квазистационарных электрических и магнитных
полей.
Обоснованные теоретически и подтверждённые экспериментально явления, о которых идёт речь в приложениях 1а, 1б, 1в, не находят объяснения в свете знаний всей современной физики и свидетельствуют о её глубоком кризисе.
Рассмотрим то общее, что объединяет работы, приведённые в ПРИЛОЖЕНИЯХ 1а, 1б, 1г.
Предметом анализа каждой из них является замкнутая система, содержащая два вида материальных компонентов - вещественные и полевые. К первому относятся источники магнитного поля и электрические заряды (связанные с такими элементами как диски, обкладки конденсатора, провода и т. д.), ко второму - электрические и магнитные поля. Напомним, что электрическое поле, по современным представлениям, является самостоятельным,
отличным от вещества видом материи (см., например, соответствующие статьи пятитомной физ. энциклопедии под ред. Прохорова). Одна из двух полевых компонент (электрическая или магнитная) предполагается постоянной, другая может изменяться в квазистационарном режиме (сколь угодно медленно), что позволяет полностью пренебречь влиянием электромагнитного излучения. Такие поля иногда называют неволновыми (nonradiating fields).В каждой работе приводится обоснование (нашедшее у Грэхема и Лахоза экспериментальное подтверждение), согласно которому вся совокупность вещественных (механических) компонентов под действием силы Лоренца (Ампера) изменяет состояние движения, т. е. приобретает момент количества движения или, говоря по-другому, момент импульса. Но где противодействие? Образно говоря, если в замкнутой системе что-то вдруг завращалось, то что-то другое должно завращаться в противоположную сторону или остановиться (если вращалось до этого). Найти такой противодействующий фактор в механике не проблема, часто он очевиден. Ненамного труднее разобраться при наличии (в дополнение к механическим компонентам) электромагнитных волновых полей (типа световой парус в солнечной системе). Но как быть в случае стационарных полей,
76
например, как у Фейнмана? Где то, что завращалось (или прекратило вращение) в противовес диску? Не видно! Обратим внимание, что и у Тамма и у Грэхема и Лахоза точно такая же картина, потому что магнит не может испытывать момент силы вдоль линий токов, создающих магнитное поле и, следовательно, приобретать момент количества движения, противодействующий конденсатору. В обеих работах подчёркивается, что тот момент количества движения который получает конденсатор распространяется на всю совокупность вещественных элементов системы (конденсатор + магнит). В этом и состоит уникальность динамики квазистационарных полей, не имеющая аналогий в других областях физики. Может быть, выручает представление о применимости вектора Пойнтинга и плотности импульса к стационарным, независимым (неволновым) полям, как это сделано в каждой из рассмотренных работ (Фейнмана, Тамма, Грэхема и Лахоза).
Рассмотрим вопрос подробнее. Приведённая Грэхемом и Лахозом формула

известна всем студентам физических специальностей (обозначения, как в источнике). Её вывод содержится в той же книге Тамма (параграф 105) или (в несущественно изменённом виде) в "Электродинамике сплошных сред, Л. Д. Ландау, Е. М. Лифшица, М., 1957". Левая часть есть плотность силы Лоренца
fL (часто силой Лоренца называют только её магнитную часть - второй член слева). После интегрирования по всему пространству второй член справа исчезает (см. Грэхем иЛахоз) и получается соотношение (см. Тамм)![]()
где ![]() -
плотность импульса волнового
электромагнитного поля.
-
плотность импульса волнового
электромагнитного поля.
Следует подчеркнуть, что полученные формулы выведены именно для волновых электромагнитных полей (для лучистой энергии). Вопрос состоит в том, правомерно ли применять их к статическим (независимым) полям. Сразу же скажем, что единого мнения
77
нет, есть несколько основных категорий мнений.
Таким образам, понятие об импульсе статических полей является далеко не всеми разделяемой гипотезой, по разному понимаемой теми, кто её принимает. Вместе с тем следует отметить очевидный факт: авторы обсуждаемых работ теоретически и экспериментально обосновали существование сил, действующих в замкнутых,
78
по общепринятым
критериям, системах и не имеющих реакции противодействия со стороны вещественных компонентов этих систем. Авторы пытаются найти эту реакцию со стороны полевой компоненты, привлекая гипотезу, согласно которой электромагнитная энергия статических полей циркулирует в вакууме, перенося необходимый "скрытый" импульс. Попробуем оценить насколько успешно это представление "работает", в свете закона сохранения энергии.Известно, что электромагнитное поле, имеющее вектор Пойнтинга
S обладает плотностью энергии W, причём S = cWn, где n - единичный вектор вдоль направления S (см. Л. Д. Ландау, Е. М. Лифшиц. Теория поля. Изд-во "Наука", М.. 1973, с.148). Переходя к проекциям S и n на направление n, получим S = cW, отсюда W = EH/c.Это значит, что между пластинами конденсатора в опыте Грэхема и Лахоза заключалась не только энергия электрического поля wE = CU2/2, где C - ёмкость конденсатора, U - напряжение на его пластинах, но и дополнительная энергия wEH, зависящая от величины магнитного поля в которое этот конденсатор помещён (энергию магнитного поля, в силу постоянства последнего, не учитываем).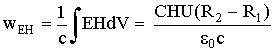
Отсюда отношение дополнительной (электромагнитной) энергии к электрической будет равным
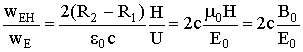
где ![]() -
величина эффективного электрического поля между
пластинами конденсатора. В опыте Грэхема и
Лахоза
-
величина эффективного электрического поля между
пластинами конденсатора. В опыте Грэхема и
Лахоза
79
питания. Так как напряжение определялось источником питания, то ток заряда конденсатора должен, примерно, во столько же раз превосходить расчетный (соответствующий только электрической компоненте), Во столько же раз возрос бы заряд на его обкладках и, следовательно, многократно увеличилась бы эффективная ёмкость. Действительно, полная энергия поля в конденсаторе wEH + wE была бы равной, C*U2/2, где C* = C(2cB0/E0 + 1) - эффективная ёмкость; I* = I(2cB0/E0 + 1) - эффективный ток. Легко видеть, что при отсутствии магнитного поля (B0 = 0) эффективный ток совпадает с нормальным током зарядки конденсатора I. Увеличение тока привело бы, в свою очередь, к увеличению силы Лоренца и, как следствие, момента этой силы. Последовавшее за этим, в среднем, более чем стократное увеличение отклонения светового зайчика немедленно было бы зарегистрировано экспериментаторами, которые наблюдали эффект, отвечающий нулевому вкладу электромагнитной компоненты. Отсюда, с необходимостью следует вывод, что плотность энергии, и, следовательно, импульса стационарного (квазистационарного) электромагнитного поля всегда равны нулю. Этот вывод можно было сделать и, не дожидаясь опытов Грэхема и Лахоза. Если бы ёмкость конденсаторов зависела от магнитного поля, в котором они находятся, то это уже давно дало бы о себе знать при настройке входных контуров радиоаппаратуры; в сотни и тысячи раз изменялись бы резонансные частоты. Мало того, в соответствии с прямыми точными вычислениями (см. "Академический вариант" сайта) изменение магнитного поля при постоянном электрическом (как в опыте Фейнмана) ведёт к нарушению равенства между величиной, названной (как оказалось неправильно) импульсом статических полей и механическим количеством движения (если бы был импульс, то равенство сохранялось бы всегда). Вместе с тем, ключевая роль эксперимента Грэхема и Лахоза неоспорима, так как не оставляет никакой возможности отрицать само существование обсуждаемого явления. Таким образом, сторонники третьей категории, несомненно, правы в том, что стационарные электромагнитные поля не переносят никакого импульса и энергии.
На основании вышеизложенного можно константировать очевидный факт. Вся современная физическая наука не может объяснить причину теоретически обоснованного и экспериментально наблюдаемого явления приобретения под действием сил Лоренца (в частности, силы Ампера) механического количества движения (момента количества движения) замкнутой, по современным представлениям, системой, содержащей электрические заряды и магнитные элементы. Проще говоря, физика нашего времени не знает и принципиально не может объяснить откуда берётся момент количества движения в классическом эксперименте Грэхема и Лахоза.
80
Каждый осознавший вышесказанное, одновременно осознает и состояние кризиса, современной физики, по существу, не менее глубокого чем вызванного в конце XIX века отрицательным результатом опыта Майкельсона или другого известного в начале XX века как "ультрафиолетовая катастрофа". Новая послекризисная физика так же разительно и революционно будет отличаться от современной, как релятивистская от Ньютоновской или как квантовая от классической (см. настоящий сайт). Она не отменит достигнутых знаний, но даст возможность видеть их в новом объединяющем свете.
81