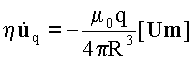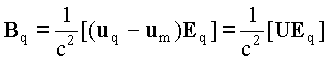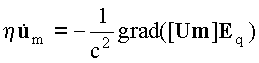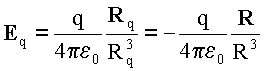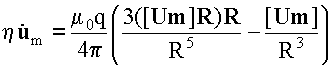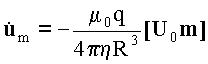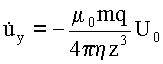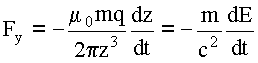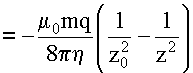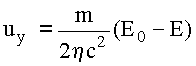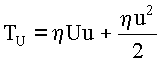ГЛАВА
2. Движение замкнутой, по традиционным
критериям, системы,
содержащей электрический заряд и
токовый магнитный диполь -
неизвестный современной науке вид
поступательного движения
- Уравнения
движения для системы точечный заряд -
точечный магнитный диполь.
- Решение
при одинаковых массах частиц. Понятие
импульсного потенциала.
- Вывод о
существовании сил, не имеющих
противодействия со стороны вещественной
и полевой компонент.
- Теорема
о кинетической энергии. Вывод о не
замкнутости системы.
Очевидно, характер движения системы,
содержащей электрические и магнитные элементы,
независимо от того есть или нет в ней полевые
компоненты, будет определяться силами,
приложенными к её вещественным составляющим или,
иными словами, уравнениями движения для
вещественных элементов и, как следствие, для
центра инерции (ЦИ) системы. Одна из простейших,
удобных для анализа систем, содержит точечный
электрический заряд и точечный магнитный диполь.
В связи с этим можно сформулировать следующую
задачу.
Две частицы (тела) одинаковой массы
h , одна из которых
имеет электрический заряд q, а другая постоянный
токовый магнитный момент - m (магнитный диполь) свободно движутся со скоростями,
малыми по сравнению со скоростью света. Размеры
частиц малы по сравнению с расстоянием между
ними (точечное приближение). В начальный момент
времени заряд находится на расстоянии R0 от магнитного диполя и удаляется от
него (приближается к нему) со скоростью U0 в направлении вектора R0. Определить ускорения и скорости
каждой из частиц как функции времени и на
основании этого сделать вывод о состоянии
движения (или покоя) центра инерции (ЦИ) частиц.
Начальные импульсы частиц предполагаются
достаточно большими, чтобы пренебречь
квантовыми эффектами (в частности, для ионов и
атомов с элементарным зарядом и
35
магнитным
моментом, соизмеримым с магнетоном Бора
кинетическая энергия должна превышать десятые
доли электроно-вольта, иначе пришлось бы
использовать квантовые уравнения).
Уравнения движения частиц имеют вид:
|
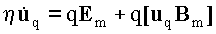 |
1) (см.
примеч. в конце части 2) |
(1) |
|
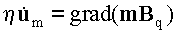 |
|
(2) |
где: |
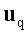 , ,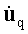
|
скорость и
ускорение заряда |
|
|
Em
|
напряжённость
электрического поля, индуцированная движением
магнитного диполя |
|
|
Bm |
- индукция
магнитного поля магнитного диполя |
|
|
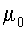
|
магнитная
постоянная |
|
|
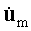
|
ускорение
магнитного диполя |
|
|
Bq |
индукция
магнитного поля, создаваемого движущимся
зарядом |
|
Левые части (1), (2) представляют собой скорости
изменения импульсов частиц, правые - приложенные
к ним активные силы. Формально, следовало бы
добавить уравнение для моментов сил, что привело
бы к проявлению в правых частях (1), (2)
дополнительных членов. Мы этого не делаем
(авансом), т. к. найденное ниже решение
удовлетворяет условию, согласно которому
моменты сил, проложенных к компонентам системы,
равны нулю, в связи с чем вектор
m будет сохранять начальное
направление, исключая возможность
магнитно-дипольного излучения. Эффекты,
обусловленные влиянием электромагнитного
излучения, вследствие ускорения получаемого
частицами при их взаимодействии, так же
предполагаются пренебрежимо малыми (что, в
частности, выполняется для любых заряженных и
имеющих магнитный момент элементарных частиц,
ионов, атомов и т. д., удовлетворяющих условиям
задачи и движущихся на расстояниях друг от друга,
более чем характерные атомные размеры - 10-10 м и для любых макроскопических
заряженных и намагниченных тел.)
Подставляя в (1) 
Em = -[umBm]
и, учитывая, что скорость заряда по отношению к
магнитному диполю
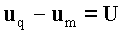
36
(
um -
скорость магнитного диполя), получим:
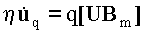
Так как
m ^ R, то
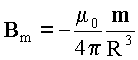 ,
,
где
R -
абсолютная величина расстояния заряда от
магнитного диполя 2) (см.
примеч. в конце части 2). Отсюда следует, что
|
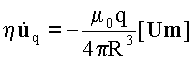
|
(3) |
Входящее в уравнение (2) индуцированное
движущимся зарядом магнитное поле
Bq можно представить в
виде двух слагаемых Bq = Bq1 + Bq2; где Bq1 = [uqEq]/c2 ( с - скорость света) создаётся
электрическим полем Eq движущегося заряда, а Bq2
= -[umEq]/c2 обусловлено движением магнитного
диполя в электрическом поле заряда. Поэтому
|
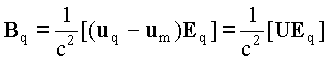
|
(4) |
После подстановки (4) и алгебраических
преобразований (2) примет вид:
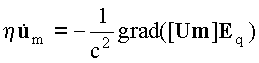
Подставляя
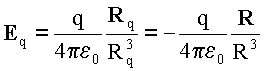
где
Rq-
расстояние, отсчитываемое от заряда и,
дифференцируя по координатам (также
отсчитываемым от заряда), получим:
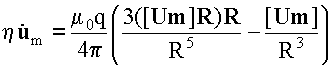
|
(5) |
Уравнения движения (3) и (5) имеют
решение, удовлетворяющее начальному условию
если
U=U0.
Так как векторы
U0 и R коллинеарные, то первый член в
скобках в (5) обратится в 0:

|
(6) |
37
Таким образом уравнения движения приобретают
непосредственно интегрируемый вид и позволяют
получить ускорения обеих частиц, выраженные
через их электрические характеристики и
скорость относительного движения:

|
(7) |
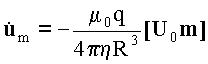
|
(8) |
Отсюда следует, что
 ..............
..............
где  -
ускорение ЦИ системы, в связи с чем обе
рассматриваемые частицы и их ЦИ будут двигаться
с одинаковым ускорением
-
ускорение ЦИ системы, в связи с чем обе
рассматриваемые частицы и их ЦИ будут двигаться
с одинаковым ускорением
 вдоль
направления, перпендикулярного U0 и m, в соответствии с уравнением:
вдоль
направления, перпендикулярного U0 и m, в соответствии с уравнением:

|
(9) |
Из (7) и (8) следует равенство нулю моментов
активных сил, относительно середины расстояния
между частицами
(R/2). Отсюда, принимая во внимание, что в
точке нахождения магнитного диполя Bq = 0 (значит момент силы не действует на
магнитный диполь), следует равенство нулю суммы
моментов сил в системе, т. е. исключение уравнения
для моментов сил оправдано.
Уравнение (9) интересно тем, что связывает
ускорение ЦИ замкнутой, по общепринятым
критериям, системы с относительным движением
составляющих её частиц.
Выберем правую Декартову систему координат
так, чтобы вектор
m был направлен по оси x, u - по y, U0 и R по z (см. Рис 6).
Тогда
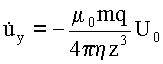
|
(10) |
Учитывая, что величина равнодействующей силы
Fy=2h (duy/dt) и что U0=dz/dt, получим:
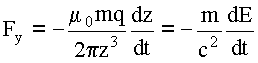
|
(11) |
38
где -
E=-q/4pe0z2- величина
напряжённости электрического поля, создаваемого
зарядом в точке нахождения магнитного диполя.
Подставляя
z = z0 + U0t, где: z0 = R0, t - время, и интегрируя (10), получим:

|
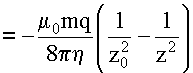 |
(12) |
Уравнение (12), описывает неординарную ситуацию:
две частицы удаляются друг от друга с постоянной
скоростью
U0,
свободно, не теряя кинетическую энергию
относительного движения. В то же время они
движутся с одинаковыми ускорениями и скоростями
в поперечном направлении (относительно
лабораторной системы координат).
Согласно Рис.6, двигаясь равномерно по инерции
со скоростями
U0/2 вверх и вниз относительно ЦИ,
одновременно они, вместе со своим ЦИ, будут
двигаться влево с одинаковыми ускорениями и
скоростями, причём, скорость, а значит и импульс
зависят только от относительного расстояния
между частицами.

Рис.6.
m - магнитный
момент; um - скорость
магнитного диполя; u - скорость центра инерции; ЦИ - центр
инерции; R - расстояние
от магнитного диполя до заряда; uq
- скорость заряда; q -
величина заряда; U0 - скорость заряда относительно
магнитного диполя; x, y, z - оси Декартовых
координат.
39
Согласно Рис.6, двигаясь равномерно по инерции
со скоростями U0/2 вверх и вниз
относительно ЦИ, одновременно они,
вместе со своим ЦИ, будут
двигаться влево
с одинаковыми ускорениями
и скоростями, причём, скорость, а значит и
импульс зависят только от относительного
расстояния между частицами.
Можно заметить, что поле заряда в точке
нахождения диполя по величине равно:
E=q/4pe0R2 , поэтому (12)
принимает вид:
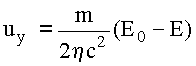
где
E0-
электрическое поле в точке z0. Соответственно величина импульса (p = py) будет:
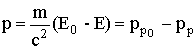
|
(13) |
где
pp=mE/c2 = -m0mq/4p R2, pp0 -
начальное значение. Напрашивается
интересная аналогия. Связь между импульсом
приобретаемым системой двух частиц: заряд -
магнитный диполь при перемещении заряда из точки
R0 в R, формально совпадает со
связью между кинетической Т и потенциальной П энергиями
двух зарядов: Т=П0-П
при аналогичном перемещении
одного из них.. По этой причине величину pp в дальнейшем
можно называть механическим потенциальным
импульсом или, просто потенциальным импульсом
либо импульсным потенциалом системы
(векторное обобщение дано в третьей части
работы). Очевидно, импульсный потенциал как и
энергетический определён с точностью до
произвольной константы (скалярной или
векторной). Как можно видеть (см. часть 1),
импульсный потенциал совпадает с “импульсом
статических полей”: G=pp=mE/c2. Обе
эти величины показывают какой импульс
приобретёт система при относительном
перемещении заряда из одной точки в другую.
Отметим, что импульсный потенциал обычной
замкнутой системы всегда равен нулю, поэтому
данное понятие неизвестно современной науке.
Из (12) следует, что в связи с возрастанием
uy, также будет
возрастать и кинетическая энергия системы T=h(uy2+U02/2)=Tc
+ T0, где Tc - кинетическая энергия системы
вследствие движения её ЦИ, T0- начальная кинетическая энергия. Но
за счёт чего? Ведь начальная кинетическая
энергия, определяемая относительным движением
частиц (T0 =h U02/2) сохраняется. Может быть, на этот раз
помогут пресловутые статические поля (см. Часть1)?
Предположим, что это так. Тогда в силу закона
сохранения энергии: cG+p2/4h = const или после
дифференцирования cdG + pdp/2h = 0. Так как, в силу закона сохранения
импульса должно выполняться dp = -dG, то получим: p
= 2hc (частицы должны превратиться в
кванты света и улететь), что ещё раз подтверждает
неприменимость концепции статических полей.
Таким образом ни вещественные ни полевые
компоненты не обеспечивают
40
выполнение законов
сохранения импульса и энергии и не создают
ответные силы реакции, противодействующие
активным силам, приложенным к частицам,
образующим данную систему.
Можно показать справедливость следующего
утверждения.
Любое устройство (типа чёрный ящик), ускоренно
движущееся под действием силы, не имеющей
ответной реакции противодействия со стороны
вещественных и полевых компонентов
(безреактивной силы), не может получить
приращение кинетической энергии за счёт убыли
энергии своего собственного источника питания.
Пусть какое-либо устройство движется под
действием безреактивной силы и приобретает
скорость
u - в
лабораторной системе отсчёта. Его кинетическая
энергия будет T0=h u2/2 (h - масса устройства). С точки зрения
наблюдателя, движущегося со скоростью U в направлении,
обратном u
приобретённая кинетическая энергия составит
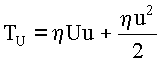
т.е. станет больше на
h Uu. Так как
все инерциальные системы отсчёта равноправны, то
Tu не может
иметь определённую предпочтительную величину. В
то же время источник питания должен тратить на
приобретение Tu определённую энергию, которую можно
было бы проконтролировать соответствующими
измерительными приборами и тем самым выделить из
всех инерциальных систем отсчёта одну
привилегированную, что явно не увязывается с
принципом относительности. Налицо явное
противоречие. Это значит, что принцип
относительности (даже в области малых скоростей)
запрещает приобретать энергию на движение под
действием силы смещения за счёт собственного
источника питания системы. Что и требовалось
доказать.
Вышеизложенный материал даёт основание
сформулировать следующее заключение. Тот факт,
что силы, действующие на вещественные элементы,
не уравновешиваются силами реакции, указывает на
то, что они являются не внутренними, а внешними по
отношению к системе, которая, вопреки
первоначальным посылкам, фактически оказывается
не замкнутой, т. к. взаимодействует с отличными от
вещества и поля материальными структурами, от
которых получает импульс и кинетическую энергию.
41
Это свидетельствует о неполноте современных
критериев замкнутости (не замкнутости) систем в
классической электродинамике.
ВЫВОДЫ:
- Решение уравнений движения для системы,
состоящей из двух свободно движущихся частиц,
электрического заряда и магнитного диполя,
показывает, что при удалении друг от друга
(сближении друг с другом) с равномерной
относительной скоростью обе частицы вместе с их
центром инерции движутся с одинаковыми по
величине и направлению ускорениями
перпендикулярно прямой, их соединяющей, в
результате чего, вся замкнутая по общепринятым
критериям система приобретает импульс и
кинетическую энергию.
- Величина импульса по п. 1 определяется только
разностью начального и конечного расстояний
между частицами, в связи с чем вводится понятие
об “импульсным потенциале”, который для
“обычных” замкнутых систем всегда равен нулю,
поэтому не используется в современной науке.
- Приложенные к частицам активные силы не имеют
противодействующих им сил реакции со стороны
вещественных и полевых компонентов системы,
следовательно являются не внутренними, а
внешними по отношению к ней. Таким образом
рассматриваемая система, вопреки первоначальным
представлениям, фактически не является
замкнутой.
- С привлечением принципа относительности
доказана теорема, согласно которой любое
устройство (типа чёрный ящик), ускоренно
движущееся под действием сил, не имеющих
ответной реакции противодействия со стороны
вещественных и полевых компонентов
(безреактивных сил), не может получить приращение
кинетической энергии за счёт убыли энергии
своего собственного источника питания.
- Рассматриваемая не замкнутая (в соответствии с
выводами по п. п. 3, 4), система , взаимодействует с
отличными от вещества и поля материальными
структурами, от которых получает импульс и
кинетическую энергию.
- Выводы по п. п. 3, 4, 5 свидетельствуют о
неполноте современных критериев замкнутости (не
замкнутости) систем в классической
электродинамике.
42
Примечания к Части 2:
1
) -
Вывод уравнения (1) приводится в [6]. При учёте
торможения излучением в его правой части должен
появится член m0q2u"/6pc [6],
(u" - вторая
производная скорости заряда по времени) который
становится достаточно большим лишь в магнитных
полях, соизмеримых с 4p (he)2c/m0e3, где me и e -
масса и заряд электрона, что составляет 1012 Тл и
достигается лишь на расстоянии порядка
классического радиуса электрона 10-13 см. Такое поле на 11 порядков
превышает практически достижимое в магнитных
материалах - до 10 Тл, поэтому приведённый член не
рассматривается. Иными словами, уравнение (1)
рассматривается в той области значений
магнитного поля, в которой торможением за счёт
излучения можно полностью пренебречь.
2
) - При учёте
запаздывания R следует
заменить на R+uR/c, что
приведёт к появлению в разложении напряжённости
полей дополнительных слагаемых, которые по
условию задачи (u<<c) пренебрежимо малы.
43
ПЕРЕЙТИ К СЛЕДУЮЩЕЙ
СТРАНИЦЕ
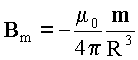 ,
,