chast3

ГЛАВА 3. Основные характеристики и области применения
новых форм движения, энергии и материи

Вывод основной формулы для результирующей силы.
Область применения.
Свойства импульсного потенциала.
Инфинитное движение.
Понятие об электровакууме.
Оценки величин сил размыкания.
Выводы.

В более общем случае электрический заряд и магнитный диполь имеют произвольную ориентацию и относительную скорость (малую, по сравнению со скоростью света), а магнитный момент может изменять свою величину и направление. В этих условиях весьма проблематично найти решение уравнений движения, в чем, однако, нет ни нужды, ни смысла, т. к. представляет интерес не вид траекторий, по которым движутся компоненты системы, а характер действия результирующей силы. Её мгновенное значение можно найти суммированием правых частей уравнений движения:

Сохраняя обозначения, принятые в Части 2 и, учитывая (1), (2), можно записать:

....................	(14)
	(15)

где F_q и F_m - силы, приложенные к заряду и магнитному диполю соответственно; F_i - вызванная изменением магнитного момента сила индукции; F_e - так называемая, магнитодинамическая сила, действующая на меняющийся магнитный диполь, находящийся в электрическом поле.

где A- векторный потенциал магнитного диполя (см. [7]),

Отсюда видно, что F_iи F_e равны по величине и противоположны по направлению

Подставляя в правой части (14),

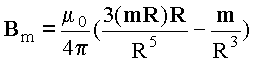
а в правой части (15)

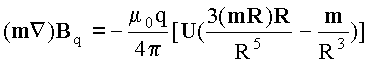
и, складывая уравнения (14), (15) получим:

где - F - равнодействующая сил системы.

Согласно уравнению Максвелла

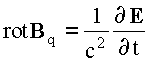
где - E = E_q - электрическое поле заряда в точке нахождения магнитного диполя.

Так как электрическое поле изменяется за счёт движения заряда, то частную производную по времени можно заменить на полную. Таким образом получим:

(16)

Применительно к задаче, рассмотренной во второй части, полученная формула даёт результат, совпадающий с выражением (11).

Формула (16) есть главная цель настоящей работы. Она определяет мгновенное значение равнодействующей силы в системе двух частиц: точечного магнитного диполя и произвольно движущегося по отношению к нему точечного электрического заряда. По традиционным представлениям о законе сохранения импульса в замкнутых системах она не имеет право на существование т. к. должна давать нулевой результат. Однако, формула (16) описывает новый закон природы, такой же фундаментальный, как сами уравнения Максвелла, послужившие исходной базой её вывода (правильность которого может подтвердить любой эксперт, разбирающийся в классической электродинамике).

Сила F (16), приложенная к частицам (вещественным элементам), составляющим систему, по причинам, рассмотренным выше (см. Часть 2), не имеет противодействующей силы реакции как со

стороны других вещественных элементов (которых нет), так и со стороны полевых элементов т. е. статических полей, не имеющих импульса (см. Часть 1, 2 и Часть 3, ниже), в связи с чем рассматриваемая система, первоначально считавшаяся замкнутой, фактически не является таковой. Поэтому силу F целесообразно назвать размыкающей силой или силой размыкания, а соответствующую систему разомкнутой системой (в отличие от не замкнутой системы).

Так как скорость изменения электрического поля определяется током смещения j_s, то (16) можно переписать в виде:

(17)

Таким образом, ток смещения, протекающий через пространство, занятое частицей, обладающей магнитным моментом, является причиной появления размыкающей силы F.

Обратим внимание на то, что ток смещения, входит в формулы (16), (17) как следствие уравнения Максвелла

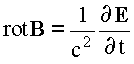
имеющего универсальную природу. Поэтому размыкающие силы могут создаваться не только при движении зарядов, но и при воздействии на магнитные материалы переменных электрических полей любого типа (индукционное, волновое, вращательное, см. "Аспекты" (Возбуждение безреактивных сил вращением), и др.). Магнитные моменты также могут создаваться не только магнитными материалами, но и токами (см. Часть 1, пример с вращающейся заряженной сферой). Таким образом, получают право на жизнь другие разновидности разомкнутых систем, например, включающие в себя только магнитные элементы (без электрических зарядов и токов проводимости) или только движущиеся электрические заряды (без магнитных диполей) и т. д.

При синхронном (синфазном) изменении магнитного момента и тока смещения, согласно (16), (17), получается знакопостоянная равнодействующая, что открывает возможность инфинитного ускоренного движения.

Рассмотрим представляющиеся наиболее важными частные случаи применения формул (16), (17).

Пусть магнитный диполь будет практически неподвижным (т. е., настолько инертным, что перемещение за время наблюдения мало по сравнению с расстоянием между частицами), его магнитный

момент стационарным по величине и направлению, а электрический заряд, способным перемещаться по произвольно заданной траектории. Это значит на систему налагаются геометрические голономные связи, к тому же идеальные (поскольку силы Лоренца не производят работу над зарядами), не влияющие на равнодействующую сил.

Интегрируя по времени (16), получим импульс p_r, приобретаемый системой при перемещении заряда из точки R₀ в точку R

(18)

......................

(19)

где: - E₀, E - электрическое поле, действующее на магнитный диполь со стороны заряда, удалённого от него на расстояние R₀, R соответственно;

(20)

Как видно, формулы (18), (19), (20) являются векторным обобщением (11), (12), что свидетельствует о расширении сферы применимости представления о введённом выше (Часть 2) импульсном потенциале, который определяется формулой (20) с точностью до произвольной векторной константы, не влияющей на результат вычисления импульса системы при относительном перемещении заряда из одной точки в другую (см. формулу (19)).

Согласно вышеприведённому, будут иметь место следующие заключения о свойствах импульсного потенциала:

Импульс разомкнутой системы определяется начальным и конечным расстоянием заряда от магнитного диполя и не зависит от траектории и скорости его перемещения.

Импульс, приобретаемый разомкнутой системой при перемещении заряда по замкнутому контуру равен 0.

Импульс, приобретаемый разомкнутой системой при перемещении заряда из начального положения в бесконечно удаленную точку равен

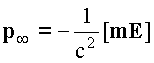
где E- электрическое поле в точке

нахождения магнитного диполя в начальном положении. (Импульсный потенциал бесконечно удалённой точки принимается равным нулю.)

Как и в частном случае (см. Часть 2), импульсный потенциал, определяемый формулой (20) совпадает с величиной, называемой Таммом “импульсом всего статического поля в целом” (G = p_p) и, по его мнению (как было установлено выше - ошибочному), всегда равен нулю (см. Часть 1). Согласно настоящему материалу, обе эти величины неотождествимы с реальным импульсом. Они служат, своего рода, индикаторами, показывающими какой импульс приобретёт система при относительном перемещении заряда из одной точки в другую. В связи с тем, что импульсный потенциал обычной замкнутой системы (как говорилось выше) всегда равен нулю, его ненулевое значение является достаточным условием или признаком разомкнутости системы:

где M- вектор намагниченности. Это локальная форма импульсного потенциала, удобная для вычисления в системах, содержащих, магнитные материалы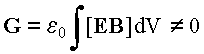

нелокальная форма, пригодная к использованию во всех случаях.

Отметим также, что изменение магнитного момента магнитного диполя повлекло бы за собой изменение G (вплоть до полного обнуления или изменения знака на противоположный), без какого-либо нарушения постоянства механического импульса системы (p_r), что особенно ярко высвечивает полную несостоятельность этого понятия, как средства объяснения импульсного равновесия и явно указывает (уже в который раз) на не замкнутость (разомкнутость) системы.

В случае U = 0 (R = const), в правых частях уравнений (14), (15) останутся только равные по величине противоположные по направлению силы F_iи F_e (пара сил). Момент импульса, приобретаемый под действием этой пары, будет равен K = q[R(A₀ - A)], где A - векторный потенциал, откуда следует, что величина K_p = q[RA] играет роль потенциала для момента импульса при постоянном R, вследствие чего, имеет место закон сохранения: K + K_p= const. Если вектора m и R взаимно перпендикулярны, то,

переходя к величинам, получим: K = m₀q(m₀-m)/4pR, где m₀ и m - величины магнитных моментов в начальном и конечном состояниях системы. Теперь вернёмся к эксперименту Фейнмана (Рис. 3). В начальном состоянии магнитный момент равен m₀. До тех пор, пока ничего не происходит конечное состояние совпадает с начальным (m₀ = m ), что соответствует К=0. При выключении соленоида m становится равным нулю, вследствие чего система приобретает момент импульса K = m₀qm₀/4pR. Однако, по мнению Фейнмана, механический момент импульса приобретается за счёт исчезновения момента импульса статических полей

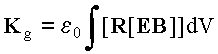
(область интегрирования - всё пространство), прямые вычисления которого, как упоминалось в Части 1, дают в два раза меньший результат, свидетельствующий о неверности традиционного подхода.

Данный выше частный закон сохранения K + K_p= const утверждает, что если в системе рассматриваемого типа возникает магнитный момент, то непременно должен появляться попутный момент импульса. Применим это правило к элементарным частицам, в частности к электрону. Предположим , что электрон имеет конструкцию, напоминающую рис.3. Пусть на расстоянии, известном как классический радиус электрона r_e=m₀e²/4p от магнитного диполя равного магнетону Бора (m_Б) находится заряд e. Тогда (см. выше) K=m₀em_Б/4pr_e. Вычисления дают правильный результат: , где - постоянная Планка (m_e - масса электрона). Как ни удивительно, а формула “работает” даже на уровне элементарных частиц. В таком случае постоянная Планка не есть независимая мировая константа, а определяется через параметры электрона. Конечно, приведённый “классический” подход к микромиру является весьма условным, однако можно ожидать, что различные элементарные частицы и

атомные ядра обладают присущими им импульсными потенциалами, которые должны проявлять себя в различных реакциях.

Формулы (16), (18) путём интегрирования легко распространить на системы, содержащие протяжённые намагниченные и заряженные тела. При этом:

где: M- вектор намагниченности; V - занятый намагниченным веществом объём интегрирования.

Из последней формулы следует, что, если, например, (см. Рис. 7) взять намагниченную пластину с прикреплёнными к ней электродами, а затем подать потенциал, то возникнет размыкающая сила, под действием которой всё устройство (пластина вместе с источником напряжения и соединительными проводами, общей массой h ) приобретёт импульс [ME]V/c² и придёт в движение в направлении, перпендикулярном плоскости, в которой лежат вектора M и E со скоростью u = [ME]V/h c²

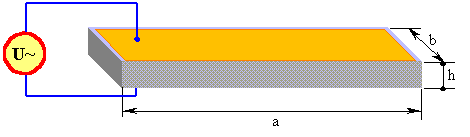
Рис. 7. Простейший "безреактивный" элемент

Очевидно, что, если, к примеру, пластина намагничена вдоль ребра b, то при подаче переменного напряжения, она будет совершать механические колебательные движения вдоль ребра a.

Кинетическая энергия этих механических колебаний, в соответствии с теоремой, установленной выше (см. Часть 2) приобретается не за счёт источника питания U~ , а извне, от материальных структур, отличных от вещества и поля.

Особенно интересен случай синхронного изменения намагниченности и тока смещения, связанный как отмечалось выше с возможностью ускоренного инфинитного (безреактивного) движения. Если на электроды рассмотренного выше устройства (Рис. 7) подавать синусоидальное напряжение, так, чтобы электрическое поле внутри пластины, менялось по закону E = E₀sinw t, в сочетании с перемагничиванием пластины по закону M = M₀cosw t, то размыкающая сила станет знакопостоянной со средним значением F_ср = w M₀ E₀V/2c², в результате чего, устройство сможет ускоренно

двигаться в свободном пространстве (в направлении, перпендикулярном векторам E и H) или совершать работу при наличии сил противодействия. Подобным образом поведёт себя и устройство, изображённое на Рис.8.

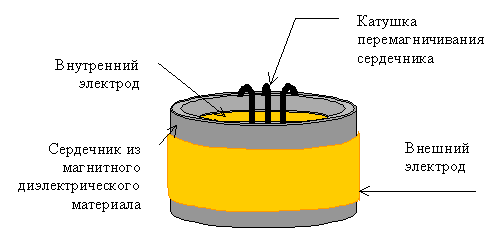
Рис. 8. Схема устройства для получения безреактивной тяги.

При подаче на его металлические электроды переменного напряжения, а на катушку перемагничивания тока, так, чтобы внутри цилиндрического сердечника, сделанного из магнитного диэлектрического материала, электрическое поле и намагниченность менялись по тем же законам, появится размыкающая сила с таким же средним значением, которая так же вызовет поступательное ускоренное движение вдоль оси цилиндрического сердечника. Что касается вращающих моментов, то они практически отсутствуют в данных системах: во-первых, благодаря форме магнитных сердечников (прямоугольной (Рис. 7) или, особенно, цилиндрической (Рис. 8)) в них очень малы магнитные поля, создаваемые токами проводимости при перезарядке электродов, во-вторых из-за взаимной компенсации моментов сил. Целенаправленное использование этих факторов позволяет избавляться от нежелательных вращающих моментов, даже, если они есть, что оправдывает их исключение из рассмотрения, при изучении вопросов поступательного движения.

Рис.7 и рис.8 иллюстрируют запатентованный способ реализации безреактивного движения [8].

Отметим интересную особенность, связанную с отсутствием относительного движения макроскопических элементов (деталей) устройств в обоих случаях. Так как проводники не пересекают “силовых линий” магнитного поля, то нет и сил индукции, против которых источник питания не совершает никакой работы, не тратя свою энергию, на ускорение системы или на преодоление ею сил сопротивления, что ещё раз наглядно подтверждает справедливость теоремы об энергии разомкнутой системы (Часть 2, Выводы, п.4). Источник питания нужен только для создания и поддержания полей. Остальная энергия, как упоминалось выше, поступает в систему от внешних структур, связанных с видом материи не вещественной и не полевой природы. Примем, по определению, что это есть электродинамический или электрический вакуум или, просто, электровакуум, который мы не будем в данной работе априорно отождествлять с такими известными понятиями, как физический вакуум или эфир. Можно лишь сказать, что электровакуум - это качественно своеобразная, отличная от вещества и поля, форма материи, существование которой обосновано законами классической электродинамики и механики. Она заполняет собой всё физическое пространство и способна вступать в импульсное (силовое) и энергетическое взаимодействие с разомкнутыми системами.

Оценки показывают, что, используя доступные магнитные материалы и величины полей (магнитная индукция до 0,1 Тл, электрическая напряжённость - до 10⁵В/м, частота до Гц), можно получить плотность силы до нескольких мГ/см³, что достаточно для её экспериментального обнаружения. С уменьшением размеров и увеличением частоты плотность силы возрастает - в сантиметровом и миллиметровом диапазоне длин волн можно ожидать от 1до 10 Г/см³, что достаточно для технических применений в энергетике, на транспорте и пр. На микроскопическом уровне (в масштабах молекул и атомов) магнитные и, особенно, электрические поля могут достигать громадных величин, поэтому в диапазоне инфракрасных и оптических частот плотность сил смещения может достигать многих килограммов на см³. Конечно на этих уровнях следует пользоваться уже не классическими, а квантовыми представлениями.

Существование сил, не имеющих обратной реакции со стороны вещественных и полевых материальных структур (названных размыкающими а, в техническом аспекте, безреактивными силами), составляет содержание нового универсального закона природы, обоснованного принципами классической электродинамики и механики, достоверность и фундаментальность которого соответствует исходным наукам. Результаты опыта Грехема и Лахоза [2] следует рассматривать как экспериментальное подтверждение частного случая, касающегося эффекта действия момента силы, о которой идёт речь. Привлечение законов сохранения импульса и энергии диктует необходимость признания существования вида материи (электровакуума или фохата), отличного от вещества и поля, заполняющего собой всё физическое пространство и способного вступать в импульсное (силовое) и энергетическое взаимодействие с веществом, открывая возможность инфинитного безреактивного движения в свободном пространстве и получения энергии от невещественных и не полевых, но материальных структур. Оценки величин эффектов вселяют уверенность в неограниченные перспективы, которые откроются перед Земной цивилизацией при использовании новых сил природы во всех областях человеческой деятельности (безреактивный наземный и космический транспорт, безтопливная энергетика, градостроительство в трёх измерениях и пр.). Теоретические и экспериментальные исследования в этом направлении представляются

очень актуальными задачами сегодняшнего дня.

В методологическом плане, представление о классической электродинамике, как о законченной науке становится несостоятельным, что, видимо, можно распространить на любую фундаментальную науку

ВЫВОДЫ:

На основании законов классической электродинамики получена формула, дающая, вопреки современным представлениям о законе сохранения импульса, ненулевую величину, для равнодействующей силы в замкнутой, по традиционным понятиям, системе двух взаимодействующих частиц: точечного электрического заряда и точечного магнитного диполя (слово “точечный” означает малость размеров частиц, по сравнению с расстоянием между ними), имеющих произвольную ориентацию и произвольную относительную скорость. Выводы, полученные для точечных частиц путём интегрирования распространяются на сложные системы, содержащие протяжённые электрические и магнитные элементы.

Сила по п.1 может сообщать системе ускоренное движение (включая инфинитное), импульс и кинетическую энергию. Она так же, как и, приложенные к частицам активные силы, не имеет противодействующей силы реакции со стороны вещественных и полевых компонентов системы, следовательно является не внутренней, а внешней, по отношению к данной системе. Таким образом рассматриваемая система, вопреки первоначальным представлениям, фактически не является замкнутой, что снимает противоречие с законом сохранения импульса (сила названа, по определению, размыкающей силой, а система - разомкнутой системой).

При постоянстве магнитного момента, импульс по п. 2, приобретается системой вследствие перемещении заряда из одной точки в другую и определяется только координатами данных точек, независимо от скорости и траектории перемещения. По этой причине вводится величина, связанная с электрическими параметрами компонентов (потенциальный импульс), неравенство которой нулю является достаточным признаком разомкнутости системы. Существуют импульсные потенциалы и других типов, а так же потенциалы моментов импульсов, с каждым из которых связан свой закон сохранения. ................................................................................... ................................. ..................................................................................................................................................................... ............................... ...............................................................................................................................................................................................................................54

Импульсные и моменто-импульсные потенциалы могут быть присущими различным элементарным частицам и атомным ядрам, проявляя себя в различных реакциях с их участием, в частности частица, обладающая магнитным моментом, должна иметь так же и сопутствующий момент количества движения (что показано на примере электрона).

Согласно теореме об энергии (см. Часть 2, Выводы, п. 4), кинетическая энергия разомкнутой системы приобретается ею не за счёт собственного источника питания, а в процессе взаимодействия с отличным от вещественного и полевого видом материи, названным, по определению, электровакуумом, заполняющем собой всё пространство, однако, априори не отождествляемым ни с физическим вакуумом, ни с эфиром. Электровакуум обладает способностью вступать в процессы импульсного (силового) и энергетического взаимодействия с веществом.

Эффекты взаимодействия по п. 4, при определённых условиях, могут быть весьма значительными, что создаёт неограниченные перспективы их применения во всех областях человеческой деятельности, связанных с естественными науками и техническими приложениями. (прежде всего универсальный безреактивный транспорт, безтопливная энергетика и т. п.).

Выводы по п. п. 1 - 4, представляют собой содержание нового универсального закона природы, обоснованного принципами классической электродинамики и механики, вследствие чего обладающего такой же фундаментальностью и достоверностью (частный случай имеет экспериментальное подтверждение в опыте Грехема и Лахоза), характер которого, отвечает актуальным проблемам, стоящим перед наукой и практикой, в связи с чем теоретические и экспериментальные исследования в области разомкнутых систем являются приоритетными задачами сегодняшнего дня.

ЗАКЛЮЧЕНИЕ

Установленные в работе законы природы получены путём решения обычных, ничем не примечательных для классической электродинамики задач обычными методами, известными всем, имеющим техническое образование и, следовательно, обладают такой же незыблемостью и предсказательной силой, как и сама классическая электродинамика в области её применимости.

Каждый, кто ещё помнит основы векторного анализа, может самостоятельно придти к выводам, изложенным в работе. В частях I и II продемонстрированы различные пути, ведущие к одним и тем же результатам.

Несмотря на то, что выводы построены на традиционной фундаментальной базе они настолько необычны и непривычны для сложившейся парадигмы, что, будучи, в сущности, ортодоксальными, с трудом воспринимаются представителями ортодоксальной науки (хотя и не всеми). Благодаря своей процедуре получения, они, по существу, имеют статус новых законов природы, кардинально изменяющих наши представления о пространстве, подобно тому, как, в не столь отдалённом прошлом, изменила представления о времени специальная теория относительности (СТО).

Коснёмся их подробнее. Основываясь только на законах классической электродинамики доказана теорема о существовании равнодействующей силы для систем, считающихся замкнутыми, т. к. они не взаимодействуют с не содержащимися в них вещественными или полевыми элементами. Как оказалось, испытываемые движущимися зарядами силы Лоренца и силы, действующие на магнитные диполи, не подчиняются правилу, справедливому для всех замкнутых механических систем, равнодействующая которых всегда равна нулю, что противоречит общепринятой парадигме, согласно которой исключений не может быть никогда. Доказанная теорема наглядно и очевидно (см. Часть I) и вместе с тем строго и убедительно (см. Часть II) опровергает это ложное ни на чём не основанное мнение. Равнодействующая, названная размыкающей силой или безреактивной силой есть. Она может достигать значительных величин, вполне достаточных для полётов космических кораблей нового типа. Перелёты, для которых в настоящее время нужны месяцы и годы, смогут совершаться за часы и дни. В конце Части I более подробно приведены и другие аспекты практического применения установленных сил.

Вопрос откуда берётся энергия, требующаяся для совершения безрективными силами работы (например, для тех же космических полётов) выходит за рамки чистой классической электродинамики. Необходимо привлечь ещё принцип относительности и проанализировать безреактивное движение в различных инерциальных системах отсчёта, при этом, не снижая общности, вполне можно ограничиться малыми скоростями (намного меньшими скорости света), при которых релятивистский (эйнштейновский) принцип относительности переходит в известный каждому галилеевский. Оказывается, что справедлива теорема, согласно которой работа, совершаемая силами, названными выше размыкающими или безреактивными, не может осуществляться за счёт убыли внутренней энергии системы (т. е. полной энергии входящих в систему зарядов, магнитных диполей и создаваемых ими полей, включая энергию источников электропитания).

Выходит так, что свободное пространство не только позволяет совершать движение, отталкиваясь от него (как при ходьбе по земле), но и обеспечивает необходимой для этого энергией. И пусть в это с трудом верится, но так утверждают две строго и неопровержимо доказанные теоремы, основанные на самых фундаментальных из известных законах природы. Этих теорем вполне достаточно для развития различных прагматических приложений. Однако остаются без ответа некоторые важные в научном плане вопросы, от чего именно происходит "отталкивание" при безреактивном движении, откуда все-таки берётся энергия? Как быть с законами сохранения количества движения (импульса) и энергии?

Всё становится на свои места, если принять существование новой разновидности материи, в дополнение к двум известным - веществу и полю. Электровакуум является структурной составляющей (может быть не единственной) более общей формы материи - физического вакуума. Он заполняет собой все пространство и взаимодействует с веществом (электрически заряженными и обладающими магнитным моментом частицами и макроскопическими телами), обеспечивая выполнение основных законов сохранения: закона сохранения количества движения (импульса), закона сохранения момента количества движения (момента импульса) и закона сохранения энергии. Существование электровакуума не противоречит никаким общепринятым в настоящее время теориям, а может служить основой для их

лучшего понимания и дальнейшего развития.

Установленные законы природы и наиболее важные следствия из них составляют основы теории электродинамического вакуума (электровакуума), которая, в отличие от несметного множества спекулятивных (построенных на разного рода предположениях и гипотезах) разработок по соответствующей тематике, является единственной и уникальной конструктивной теорией, не только устанавливающей существование новых законов природы, но и дающей практическое руководство по их использованию.

В наше время, во всём мире тратятся огромные интеллектуальные и материальные ресурсы на создание универсальных теорий мироздания, таких как различные единые теории полей. Однако изложенные выше материалы дают полное основание утверждать, что это напрасные потери сил и времени, потому что подобные теории не могут быть полными, а значит и верными, если они не используют те представления о свойствах пространства, которые заложены в электродинамике, включая вновь установленные законы, или если аналогичные выводы не получаются как следствие. Иными словами, установленные законы природы являются индикатором правильности любых претендующих на всеобщность или касающихся характера пространства-времени теорий.

В заключение коснёмся некоторых особенностей практического воплощения изложенных знаний. Рабочая частота должна быть как можно более высокой, поближе к верхней границе радиодиапазона т. е. где-то в области миллиметровых волн. Размеры рабочей ячейки (подобной, изображённой на Рис 2, Часть I) должны быть на порядок меньше длины волны, т.е. менее 1 мм, а толщина ещё меньше. Это значит, что элементы двигательных установок следует изготовлять по технологии производства микросхем, содержащих тысячи и миллионы таких ячеек. На такие модули следует подавать постоянное напряжение питания, которое внутри преобразуется в рабочее, соответствующей частоты. Подъёмная сила подобных устройств может до 1000 раз превышать их вес. Из них монтируются двигательные установки. Предварительно надо будет найти или создать подходящие материалы, способные эффективно работать в условиях одновременного воздействия сильных магнитных и электрических полей СВЧ диапазона.

Всё это потребует предварительного развёртывания достаточно

масштабных и напряжённых экспериментальных исследований. Чтобы получить какое-то представление о трудоёмкости таких экспериментов достаточно привести слова одного из первопроходцев Д. Лахоза (автора вошедшего в физическую энциклопедию под ред. А. М. Прохорова эксперимента по измерению силы Абрахама и автора единственного эксперимента подтверждающего теорию, изложенную в настоящей работе [2]) о том, что эти эксперименты выполнены вопреки мнению скептиков, утверждающих о невозможности их постановки на современном технологическом уровне. Однако не знакомые этим скептикам изложенные здесь теоретические разработки открывают новые возможности.

СПИСОК ЛИТЕРАТУРЫ

1. И.Е.Тамм. Основы теории электричества. Издательство технико-теоретической литературы, М.,”НАУКА”, 1989, с. 404-408, 411, 241

2. G.M.Graham, D.G.Lahoz. Nature, 285, 154, 1980.

3. Фейнман, Лейтон, Сэндс. Фейнмановские лекции по физике, т.6, изд-во “Мир”, 1977, стр. 59, 304.

4. Costa de Beauregard Olivier. C. r. Acad. Sci. 263, No23, B1279, 1966. (РЖФ, 1967, 5Б85).

5. Costa de Beauregard Olivier. C. r. Acad. Sci. 260, No25, 6546-6549, 1965. (РЖФ, 1965, 8Б141).

6. Л Д. Ландау, Е. М. Лифшиц. Теория поля. Изд-во “Наука”, М., 1973, с. 70, 265-266.

7. D.G.Lahoz, G.M.Graham. Can. J. Phys., 57, No5, 1979, p.667-676.

8. Г. П. Иванов, Ю. Г. Иванов. Способ получения тяги. Патент РФ № 2172865, М., 2001 г.

ПЕРЕЙТИ К СЛЕДУЮЩЕЙ СТРАНИЦЕ