Операции с матрицами на C++. Класс DMatrix
Коды Фибоначчи для синхронизации управления *
William H. Kautz
( Оригинал статьи на английском:
Fibonacci Codes for Synchronization Control )
Аннотация
Описывается
новое семейство кодов для представления последовательных двоичных данных, при
условии, что максимальное расстояние между последовательными изменениями
значений (0→1, 1→0 или обоих типов), или между рядом стоящими цифрами (0-ми, 1-ми
или обоими) ограничено. Эти коды могут применяться для записи или передачи
цифровых данных без сопровождающего тактового сигнала. В таких случаях тактовый
сигнал должен быть восстановлен в процессе чтения (приема, декодирования) и за
точность его восстановления отвечают сами данные.
Показано,
что коды, разработанные для такого типа синхронизации, являются оптимальными, а
требование к степени их избыточности очень низкое. Кодеры и декодеры для этих
кодов имеют вполне разумную сложность и могут быть легко приспособлены для
обнаружения или исправления ошибок почти с теми же дополнительными затратами,
которые требуются для произвольных данных.
I.
Введение
Всякий
раз, когда двоичная последовательность записывается на носитель с
последовательным доступом при чтении, должны существовать некоторые
средства для восстановления тактовых
сигналов, которые разделяют и распознают рядом стоящие цифры. Известны
несколько методов такой синхронизации, но все они относительно дороги,
поскольку требуют для правильного тактирования большую степень избыточности, а
именно:
1) Отдельный канал
тактовых импульсов может быть использован для синхронизации одного или
нескольких параллельных каналов данных. (В той же мере дополнительный канал
может быть каналом для проверки на нечетность.)
2) Трехуровневые
сигналы могут быть использованы для того чтобы отличать единицу («уровень+») и
ноль («уровень–») сигнала от его отсутствия («уровень 0»). Таким образом, при
использовании троичной системы счисления каждая двоичная цифра
самосинхронизируется.
3) Чтение может
выполняться с приблизительно равномерной скоростью, так что может быть
использован локальный тактовый сигнал постоянной частоты. В этом случае
фиктивный блок из одной или нескольких синхронизирующих цифр обычно
располагается в конце каждого блока
данных, так что скорость
локального тактового сигнала может периодически подстраиваться под скорость
чтения.
В
данной работе мы предлагаем придерживаться пункта 3), за исключением того, что синхронизирующая
информация будет теперь распределена по всему блоку данных с помощью
специального способа кодирования. Мы покажем, что такой метод синхронизации
требует намного меньше избыточности, чем обычная блочная синхронизация в пункте
3). Для того диапазона длины слов и интервалов синхронизации, который
встречается на практике, сложность схем кодирования и декодирования вполне
разумна, даже когда код немного усложнен с целью обнаружения ошибок.
Предлагаемые
коды связаны, хотя и не эквивалентны некоторым префиксным кодам Гилберта [I], которые предназначены для других
задач синхронизации.
II.
Поставка
задачи кодирования
Независимо
от того, сосредоточена ли избыточная информация в блоке, в конце кодового слова
или распределена по всему слову, синхронизация управления основывается на
повторяющихся измерениях интервалов времени, за которые сигнал чтения меняется с 0 на 1 или 1 на 0. Считывание
последовательности двоичных цифр выдвигает требование, чтобы все
последовательные переходы в двоичном значении сигнала в каждом разрешенном кодовом
слове были отделены друг от друга не
более чем на заданное число позиций m. В терминах того, что мы будем
называть «строка» – последовательность рядом стоящих цифр ограниченной длины в
кодовом слове – это условие означает:
|
каждое кодовое слово из n
цифр не содержит строк из нулей или единиц длиной более m. |
(1) |
Мы
будем искать для произвольных чисел m и n (m ≤
n)
код C1(m, n), представляющий собой список
кодовых слов из n
цифр,
удовлетворяющий условию (1).
Сформулируем
постановку задачи в следующей эквивалентной форме. Для каждого кодового слова
из n
цифр
a
= (anan-1
… a2a1),
принадлежащего коду C1(m, n), мы можем сформировать
дополнительное слово b
из
(n-1)
цифр, b
= (bn-1bn-2
… b2b1),
используя правило bj
= aj
![]() aj+1, j
= 1, 2, … , n
– 1, где
aj+1, j
= 1, 2, … , n
– 1, где ![]() означает исключающее ИЛИ
(сумма по модулю 2). Таким образом, каждое слово b является,
в некотором смысле, двоичной производной для соответствующего слова a. Каждой строке a, состоящей из одних нулей или из
одних единиц, это преобразование приводит в соответствие строку b из одних нулей (но на 1 цифру
короче, чем a).
Кроме того, преобразование обратимо с точностью до выбора a1,
что согласуется с утверждением: «если слово a принадлежит
коду C1,
то a’
= (a’na’n-1
… a’2a’1) (инверсия слова a) также принадлежит этому коду».
Далее, каждой паре слов (a,
a’),
принадлежащих коду C1(m, n), соответствует слово b, принадлежащее коду C2(m-1, n-1), каждое из слов которого имеет
длину n-1
и не содержит строк из нулей длиной более, чем m-1. То есть код C2(m, n) мы определяем как код, удовлетворяющий
условию:
означает исключающее ИЛИ
(сумма по модулю 2). Таким образом, каждое слово b является,
в некотором смысле, двоичной производной для соответствующего слова a. Каждой строке a, состоящей из одних нулей или из
одних единиц, это преобразование приводит в соответствие строку b из одних нулей (но на 1 цифру
короче, чем a).
Кроме того, преобразование обратимо с точностью до выбора a1,
что согласуется с утверждением: «если слово a принадлежит
коду C1,
то a’
= (a’na’n-1
… a’2a’1) (инверсия слова a) также принадлежит этому коду».
Далее, каждой паре слов (a,
a’),
принадлежащих коду C1(m, n), соответствует слово b, принадлежащее коду C2(m-1, n-1), каждое из слов которого имеет
длину n-1
и не содержит строк из нулей длиной более, чем m-1. То есть код C2(m, n) мы определяем как код, удовлетворяющий
условию:
|
каждое кодовое слово из n
цифр не содержит строк из нулей длиной более m. |
(2) |
Так
же просто можно определить код C3(m, n), состоящий из слов c = (cncn-1
… c2c1),
полученных путем инверсии слов b
= (bnbn-1
… b2b1)
из кода C2(m, n), то есть c = b’.
Условие для C3(m, n) – следующее:
|
каждое кодовое слово из n
цифр не содержит строк из единиц длиной более m. |
(3) |
Пусть
Ni(m, n) – количество слов в коде Ci(m, n), i ![]() (1, 2, 3). Тогда
справедливы формулы:
(1, 2, 3). Тогда
справедливы формулы:
N1(m, n) = 2 N2(m-1, n-1),
N2(m, n) = N3(m, n).
Однозначная
зависимость между кодовыми словами в этих трех кодах позволяет утверждать
следующее. Если известно, что один из этих трех кодов является максимальным, то и два других также
являются максимальными. Под максимальным мы понимаем код, содержащий
максимально возможное количество кодовых слов, удовлетворяющих условиям (1),
(2) или (3).
Заметим
также, что эти коды (если их можно построить) позволят скорее решить задачу уровня или эффективности механизма чтения, чем задачу синхронизации. В этом
случае мы будем требовать, чтобы в каждом слове каждая пара нулей (код C3(m, n)) или каждая пара единиц (код C2(m, n)) или каждая пара, состоящая из
цифр 0 и 1 (код C1(m, n)) была разбита вставкой не менее
чем m
цифр
противоположного значения. Наши коды не только отвечают этим трем требованиям,
но и имеют минимальную избыточность в том случае, если они являются
максимальными в смысле нашего определения.
III.
Конструирование кодов
Семейство
кодов C3(m, n) для любых положительных целых m и
n,
m
≤
n,
может быть создано следующим образом. Вспомним, что обычное двоичное число –
это последовательность не более чем k цифр, если нам нужно
представлять числа от 0 до 2k
– 1. То есть
x = ![]() dj 2j-1 ,
dj 2j-1 ,
где
dj
–
цифры двоичного числа x
= (dkdk-1
… d2d1).
Веса 2j-1 - это степени базиса двоичной системы (j = 1, 2, …, k).
Рассмотрим
теперь применение множества уменьшенных весов w1,
w2,
…, wn
для
n-цифрового
представления x
= (ckck-1
… c2c1),
x = ![]() cj wj
. (4)
cj wj
. (4)
Для
каждого положительного целого порядка s (s ≤
n)
определим веса wj(s) =
wj
:
|
wj = 2j-1, 1 ≤
j ≤ s , |
(5) |
|
wj = wj-1 + wj-2 +
… + wj-s , s < j . |
Таким
образом, первые s
весов – такие же, как и в обычной двоичной системе, а каждый из следующих весов
есть сумма предыдущих s
весов.
Например,
при s
= 2 получаются такие веса:
w1
= 1, w2
= 2, w3
= 3, w4
= 5, w5
= 8, w6
= 13 и т.д.
Это
– хорошо известная последовательность чисел Фибоначчи [2]. Таким образом, для
любого s>0
можно построить последовательность обобщенных весов Фибоначчи порядка s по формуле (5).
В
таблице I
приведены значения таких весов для некоторого диапазона значений j и
s.
Способ расчета весов приведен в Приложении. Заметим, что последовательность wj – строго возрастающая,
wj
> wj-1 (6)
при
любом фиксированном s.
|
j= |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
s=1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
s=2 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
144 |
233 |
|
s=3 |
1 |
2 |
4 |
7 |
13 |
24 |
44 |
81 |
149 |
274 |
504 |
927 |
|
s=4 |
1 |
2 |
4 |
8 |
15 |
29 |
56 |
108 |
208 |
401 |
773 |
1490 |
|
s=5 |
1 |
2 |
4 |
8 |
16 |
31 |
61 |
120 |
236 |
464 |
912 |
1793 |
|
s=6 |
1 |
2 |
4 |
8 |
16 |
32 |
63 |
125 |
248 |
492 |
976 |
1936 |
|
s=7 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
127 |
253 |
504 |
1004 |
2000 |
|
s=8 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
255 |
509 |
1016 |
2028 |
|
s=9 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
511 |
1021 |
2040 |
|
s=10 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1023 |
2045 |
|
s=11 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2047 |
|
s=12 |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
|
N1(m, n) = 2wn(m) |
N2(m, n) = N3(m, n) = wn+1(m+1) |
|||||||||||
Теперь,
выполняя процесс кодирования, покажем, что для
фиксированного s
и для любого целого x от 0 до wn+1 – 1 существует единственное n-разрядное двоичное представление с
весами Фибоначчи x = (cncn-1 … c2c1), удовлетворяющее условию 3) для
кода C3(s-1, n).
Этот
процесс – индуктивный (то есть – итеративный), он создает представление для x, начиная с цифры старшего разряда,
следующим образом.
Пусть
yn
= x;
вычислим yn-1,
yn-2, … , yi, … , y1
по формуле:
yj-1 = yj - cj wj , (7)
где
cj
= 1, если wj ≤
yj
≤
wj+1
.
Таким
образом, число x
уменьшается
с помощью весов из последовательности wj , не приводя к отрицательному
результату. Если вес wj
участвует во взятии разностей, то cj = 1, иначе – cj = 0. Например, для s = 2, n
= 6 и
x
= 19, берем весовую последовательность:
13, 8, 5, 3, 2, 1 (см. Табл. I) и
получаем, что 19 = (101001):
|
19 – 13 = 6 |
c6 = 1, |
|
6 – 8 < 0 |
c5 = 0, |
|
6 – 5 = 1 |
c4 = 1, |
|
1 – 3 < 0 |
c3 = 0, |
|
1 – 2 < 0 |
c2 = 0, |
|
1 – 1 = 0 |
c1 = 1. |
Этот
же способ аналогичен способу, с помощью которого мы обычно преобразуем
десятичную запись числа в обычную двоичную:
19 = (10011),
|
19 – 16 = 3 |
c5 = 1, |
|
3 – 8 < 0 |
c4 = 0, |
|
3 – 4 < 0 |
c3 = 0, |
|
3 – 2 = 1 |
c2 = 1, |
|
1 – 1 = 0 |
c1 = 1. |
Единственность
представления обеспечивается конструкцией (7), следующей непосредственно из
(4), если мы покажем, что процесс всегда
заканчивается нулевым остатком. Предположим, что это верно для любого x из
интервала 0 ≤ x
< wj
(очевидно для j
=
1). Для каждого x
из
интервала wj
≤
x
< wj+1
конструкция (7) дает нам cn
= cn-1
= … = cj+1
= 0 и
cj
=
1, так как все разности: x
– wn,
x
– wn-1,
… , x
– wj+1,
x
– wj
,
кроме последней – отрицательные, т.к. wj >
wj-1.
Теперь рассмотрим разность x
– wj. Формула (5), определяющая веса wj
,
может быть преобразована к следующему виду (путем замены j на
j+1
и почленного вычитания):
|
wj+1 = 2wj , 1 ≤
j ≤ s , |
(8) |
|
wj+1 = 2wj - wj-s
, s < j , |
поэтому wj+1
≤ 2wj.
Таким образом, разность x
– wj
ограничена неравенством:
x – wj
<
wj+1
– wj
≤
wj
;
следовательно, по
индуктивному предположению, кодирование разности x – wj с помощью конструкции (7) приведет к
завершению с нулевым остатком.
Индукция
верна для j = n,
поэтому можно утверждать, что для любого целого x,
0 ≤ x
< wn+1
, существует уникальное представление x = (cncn-1
… c2c1).
Осталось
доказать, что не более чем s-1
последовательно расположенных cj
могут
иметь значение 1. В соответствии с (4),
каждая последовательность из s
c-цифр, ci = ci-1
= … = ci-s+1
= 1, приводит к добавлению следующей
суммы весов:
wi +
wi-1
+ … + wi-s+1
,
которая, в соответствии
с (5), равна следующему весу wi+1
. Рассмотрим самую левую такую строку.
Если i < n, то ci+1 = 0,
и
строка
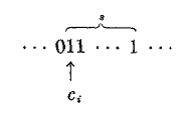
может быть переписана
как
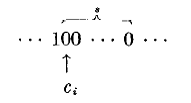
без изменения суммы (4).
Подобная подстановка может быть сделана для всех остальных строк из единиц,
находящихся справа. Так как применение конструкции (7) формирует разряды слева
направо, все s-последовательности
единиц заменяются на нули, и последовательность из s единиц не может появиться. Если же
i
= n,
мы получаем x
≥
wn+1
, что невозможно, так как для x было
задано ограничение 0 ≤ x
< wn+1. Данное представление числа с весами
Фибоначчи, созданное с помощью (7), удовлетворяет, таким образом, условию (3)
для кода C3(m, n), где m = s – 1, следовательно, утверждение
последнего пункта доказано.
I.
Максимальность
кодов с весами Фибоначчи
Из
единственности представления для каждого целого значения x,
0 ≤ x
<
wn+1
, для кода C3(m, n), доказанной в предыдущем
параграфе, следует, что код содержит, по крайней мере,
N3(m, n) = wn+1(m+1)
кодовых
слов. Теперь нам нужно показать, что код C3(m, n), содержащий большее количество
кодовых слов, не существует, то есть наш код с весами Фибоначчи является
максимальным.
В
соответствии с равенствами, полученными в пункте II, связанные между собой коды C2(m, n) и C1(m, n), выведенные из кода C3(m, n), являются максимальными тогда и
только тогда, когда C3(m, n) – максимальный. Несложно доказать
наше утверждение для C1(m, n). Для этого надо показать, что для
данных m и n число N1(m, n) возможных n-цифровых двоичных
слов, не содержащих строк из нулей или единиц длиной более m, не превышает 2wn(m).
Для этого обратим внимание, что каждая пара дополняющих друг друга кодовых
слов, например, 0100101000 и
1011010111 может быть представлена
единственным образом в виде упорядоченного разложения числа n в сумму длин
строк из нулей или единиц.
Riordan [3] показал, что
количество таких упорядоченных разбиений числа n (которые он назвал композициями n), не содержащих
слагаемых, больших, чем m, равно числу, которое мы обозначили в (5) как wn(m).
Таким образом,
N1(m, n) ≤ 2wn(m)
Следовательно,
все такие коды максимальны.
В
дальнейшем мы будем использовать обозначения C1(m, n), C2(m, n) и C3(m, n) для кодов, заданных конструкцией
(7).
II.
Кодирование и декодирование
Основные
приемы кодирования и декодирования могут обсуждаться в терминах кода C3(m, n), т.к. преобразование слов из
данного кода в соответствующие слова кодов C2(m, n) и C1(m, n) довольно просто, как
концептуально, так и практически.
Задачи
кодирования и декодирования, по существу, идентичны; базовый процесс в обоих
случаях представляет собой конверсию двоичных чисел, представленных с помощью одного
множества весов, в двоичные числа, представленные с помощью другого множества
весов:
|
|
|
|
веса
– степени 2 |
веса
Фибоначчи |
Тем
не менее, такие конверсии требуют проведения некоторого количества
арифметических вычислений, которые в одной системе счисления могут быть
произведены более просто, чем в другой. Следовательно, наилучшие кодер и
декодер могут использовать совершенно разные конверсионные алгоритмы.
Если
арифметические операции проводятся в обычной двоичной системе, кодирование
нужно производить с помощью процесса (7), а декодирование – с помощью (4). В
обоих случаях надо представить каждый вес Фибоначчи в k-цифровом двоичном виде.
Для x = 19 и s =
2 процесс имеет вид:
Кодирование:
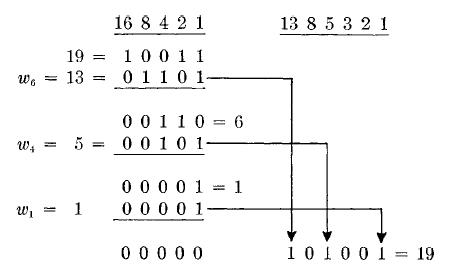
Декодирование:
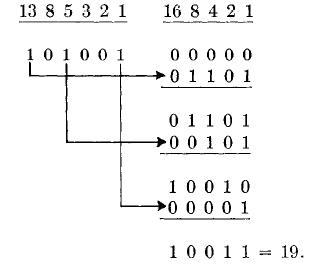
В
случае, если арифметические операции выполняются в системе с весами Фибоначчи, назначение
наших двух равенств меняется на противоположное: (4) используется для
кодирования, а (7) – для декодирования. Однако выполнение операции сложения в
Фибоначчи–системе не столь тривиально. В обычной двоичной системе переполнение
позиции j (с весом – 2j-1) добавляет к сумме 2 * 2j-1 = 2j
; это переполнение добавляется к цифре
переноса позиции j+1
(с весом – 2j). В системе с весами Фибоначчи тождество (8), которое
можно записать в виде:
|
2wj = 2wj+1 ,
1 ≤ j ≤ s , |
|
|
2wj = wj+1 - wj-s , s < j , |
говорит нам о том, что
итог 2wj
,
приводящий к переполнению позиции j, может привести не только к переносу влево,
на позицию j+1, но и вправо, на позицию (j-s) , если таковая имеется в представлении.
Это
вдвойне усложняет схему параллельного сумматора, двунаправленность делает
переход сумматора от параллельной к простой последовательной форме практически
невозможным. Более того, результат такого Фибоначчи-суммирования может быть, в
общем случае, в дальнейшем удален слева в результате образования строки из 1-ц
длиной более (s-1).
Следовательно, применение арифметики, базирующейся на обычных двоичных числах,
является предпочтительным.
Интересно
было бы понять, существуют ли процедуры кодирования или декодирования, при
которых можно было бы получать цифры закодированного слова синхронно с
поступлением цифр исходного слова. При внимательном взгляде на простые двоичные
эквиваленты весов Фибоначчи и веса Фибоначчи, эквивалентные простым двоичным
весам становится очевидным, что, в общем случае, ни старшие, ни младшие разряды
результата не могут стать известными до тех пор, пока все цифры источника не
получены и не преобразованы. Таким образом, схема, выполняющая преобразование,
должна содержать «сигнальную линию» распространения вправо и влево на всю длину
слова. Работа кодера в режиме последовательного выполнения операций, как в
случае сумматора обычных двоичных чисел, таким образом, в целом невозможна.
( Перевод статьи сделан
не до конца. )