Другие статьи
А.В.Никитин
( andvnikitin@yandex.ru , andrejnikitin.narod.ru)
Логическая система Само…
Вообще-то,
это должна была сделать кибернетика. Полвека назад. На заре своей юности. Когда
идея Логической Машины еще была основной. Возможно, что-то и было. Мир большой.
Но мне не удалось найти материалов, хоть как-то систематизирующих уровни
решений логических задач. Если такая система существует, то тогда мне
совершенно непонятно, почему математическая логика не начинается с этой
систематики.
Ведь
очевидно же, что логические задачи, как и уровни их решений, совершенно
различны. И тем не менее, математическая логика начинается с тривиальных
булевых функций.
Меня
всегда интересовал вопрос: Как мы думаем? Как это происходит. Где рождаются все
эти думы и мыслишки. Они где-то начинаются и где-то заканчиваются.
Этот
процесс организует мозг. Он каким-то непостижимым образом умудряется из
простенькой формы «вопрос – ответ» раздуть огромную задачу, требующую решения
на самом высоком уровне понимания. Ведь не было же никакой задачи, и вдруг, …
есть. И, оказывается, сложная задача.
Мозг
– центр управления самостоятельной логической системы, которая сама находит
себе проблемы и сама же их решает. Так функционируют все живые логические
системы, которые плавают, летают, бегают и ползают вокруг нас. Но, мозг
появился не сам по себе. Это продукт эволюции клеточных структур, организованных
в единый организм.
Значит
весь логический аппарат, которым владеет мозг, каким-то образом использует и
клетка.
Я
взял за основу клетку. Хочет же она есть, ей надо размножаться, она воюет с
соседями и защищается, значит, какие-то логические действия её логический
аппарат делает. Какие?
Да,
это биологический автомат, но, это же … целый завод, автоматический. По
функциям.
Он
как-то и чем-то управляется. Сбоев в работе очень мало. Значит, логика в
действиях есть и очень жесткая. Какая?
Завод
требует организации мышления. А клетка – очень большой завод. С очень
разветвленной структурой. И все это надо синхронизировать.
Само
по себе ничего не появляется. Вся автоматика процессов сложена из систем
контроля и управления. Тут ускорить, тут притормозить, тут приостановить, там
запустить, время пришло. Пищу принять, включить переработку, запустить конвейер
стандартной обработки, … остановить, отходы собрать, провести очистку рабочей
зоны, отходы отвести в пункт общего сбора, и наконец – сбросить. И это только
одна линия. А таких производственных линий в клетке – десятки.
Такая автоматика требует думок…
И
логическая система клетки, она, скорее всего в ядре, сложная и многоплановая.
Она основана на химии, но это не важно, логика там есть и математика – тоже.
И
мы думаем так, а не иначе, потому, что так … думает клетка.
Чтобы
понять отличия, надо понять сходства.
Тут
вопрос не в уровне, или в технической основе, у нее химические элементы и
связи, у нас электрические импульсы, мы думаем об одном, а она - о
другом, вопрос в сходствах, родстве, основах этих способов – думать. В логике и
математике. В механизме образования информационных связей, способах хранения и
обработки информации, на самом низком уровне. На уровне элементарных
автоматических операций с 0 и 1.
В
этом различие нас и компьютера, и родство нас с клетками.
Где-то
там…, а совсем не в общих философских осмыслениях.
Кстати,
вопрос различия структур из клеток мы не рассматриваем. Это один порядок Живого.
Рыбы, ящеры, млекопитающие, с точки зрения идеи, заложенной в клетку, это один
порядок размерности её реализации, и один механизм.
Вот
с этих позиций я стал систематизировать возможные уровни решений
логических задач на основе возможностей таких самостоятельных саморазвивающихся
логических систем. Оказалось, что задача не может появиться сама по себе. Она
должна быть развернута и сформулирована. Формирование задачи и её решение
оказались взаимосвязаны.
Основой
системы стала все же математическая логика. Хоть и далеко не в полной мере.
Логика,
логика… А что, вообще, такое – логика. Вроде бы, наука. О чем?
Наверное,
о правильности и стройности рассуждений…, о системности …
Вот
Аристотель учил, что любой вопрос может иметь только два варианта ответа – ДА и
НЕТ. А с ним спорили: Не так. Может быть три ответа - ДА, НЕТ, НЕ ЗНАЮ.
Кто
прав, непонятно до сих пор. Тысячи лет прошло, а все спорят…
С
логикой связаны понятия: событие, условие, причина, следствие, доказательство,
… сравнение, выбор …
Логика
сравнения эквивалентов.
Вот, наверное, о чем надо говорить…
Все
вариации на тему логических рассуждений, так или иначе приводят … к выбору
нужного образца. Для решения, для выбора ответа, для сравнения, для определения
того или иного признака. Для всего…
Нам
нужен образец, эталон, эквивалент. Того, что мы подвергаем сомнению или,
наоборот, пытаемся найти среди множества, может быть и похожих, но … не тех, не
совсем тех, и совсем не тех…
Вот
этот, примерно похож, а вот этот почти…, вот, вот, … этот. Точно, этот. Нашли.
Ответ. Решение. Образец для подражания…
Вот
оказывается, главная проблема. Если есть «что-то», непонятное, и надо сделать
это «что-то» - понятным, то нужен образец, хотя бы примерный, для первичного
сравнения, и формирования первого определения этого «чего-то»…
Это
было похоже,… на…, вот это. Да, на вот это.
На
дворе льет дождь. Насколько сильный дождь? Да, льет, как из ведра!
Вот
и нашелся образец, мера сравнения. Но ведро же, маленькое, а туча… огромная, и,
тем не менее, если вас окатить всем содержимым ведра сразу, … вот, это и будет
– дождь, как из ведра. Ливень. Льет так, что в миг сухого места не оставит. Это
вам не моросящий дождик, который оставит капельки только поверху, пока вы зонт
достаете и раскрываете.
Первичным
источником информации для логических систем является реакция регистраторов
реальности, т.е. наших органов слуха, зрения, вкуса, обоняния и осязания.
Реальность воспроизвести нельзя. Она слишком многогранна, и потому –
невоспризводима. Регистраторы реальности, у нас всех –
разные, а значит, и запоминают они реальность в разных форматах. У
каждого – своя реальность. И воспринимаемая, и запоминаемая. И тем более –
воспроизводимая. Чем точнее копируется реальность нашими регистраторами, тем
больше информации мы извлекаем из реальности вокруг нас.
Важнее
получить не простую копию, а её обработанный эквивалент, применимый для наших
нужд. Вот она наша запомненная реальность. То, что мы поняли. А
остальное – зачем…, отбросить, и всё.
Запомненная
нами реальность, она для нас, все равно – реальность, самая настоящая. Других у
нас нет, и быть не может. Только эту реальность мы ощущаем, понимаем, и
подвергаем анализу. Один большой эквивалент большой реальности дробим на малые
части, но все равно – эквиваленты. Образцы, образы, примитивы, эталоны…, для
собственных нужд. Кусочки большой реальности.
Мы
потом эти кусочки будем прикладывать к реальности, сравнивать, и на их основе
снова находить сходства и различия. С реальностью…
Для
определения своего отношения к объекту рассмотрения нам нужен его понятный
эквивалент сравнения. Если не с чем сравнить, то … объекта просто – нет. Он
невоспроизводим нашими органами чувств. А то, что хоть как-то прямо или
косвенно воспроизводится, всё имеет хоть какие-то эквиваленты, пусть тех
же ощущений.
Вот
где нужна система. Система определения в применении того или иного эквивалента.
Какой образец нам нужен для решения этой задачи, определители этого образца,
главные свойства и качества. Если образец найден, то задача – решена.
Для
этой цели, сравнения образцов, нам и нужна … логика.
Математическое
описание эквивалентности абстрактно, и может быть приложено к любому понятию и
пониманию эквивалентов. Принцип один. Говорим ли мы о звуках, зрительных образах,
и не только зрительных, понятие образа значительно шире, или о типах логических
задач, мы все равно говорим и об их эквивалентах.
О
них мы будем говорить постоянно. Постепенно раскрывая смысл понятия
эквивалентов.
Начнем
мы с математического определения эквивалентности. Специалисты найдут в этом
определении массу недостатков и неточностей, но все же…
Другого
у меня нет.
Если написать вот такое равенство:
|
а + в + с
= в + а + с = с + а + в = D |
(1) |
То, с точки зрения математики оно
верно. Знак равенства (=) означает равносильность всех приведенных выражений.
Если любое из этих выражений равно D, то все они равносильны. Так они и
записаны. Но, допустим:
|
а + в + с = D |
(2) |
это:
|
Выражение = Сумма = D |
(3) |
Непонятно, откуда взялась «сумма»,
или в полученном равенстве лишнее D?
Давайте разберемся.
а + в + с — «выражение», одно из
многих…
D — результат, элемент сравнения.
Чтобы к нему приравнять все остальные
выражения их надо вычислить. Таким образом:
Выражение = Сумма — процедура
вычисления
сумма = D
—определение эквивалента.
Сумма — эквивалент сравнения.
Полная запись будет выглядеть:
|
Выражение = эквивалент = Результат |
(4) |
К этой формуле можно привести любое
математическое равенство.
И мы пришли к равенству
эквивалентов.
Равенство эквивалентов может
существовать только при условии однородности эквивалентов.
Это логическое понимание
эквивалентности.
Но, мы же кубометры делим на рабочих
и получаем…, ну, что-то получаем, и это считается нормальным.
Это верно и с математической точки
зрения, потому, что во всех случаях вычислений мы имеем дело только с одним
эквивалентом – числом. Что бы оно не обозначало. И этим сохраняем логическое
равенство эквивалентов в решении.
Обратимый и необратимый эквивалент.
Но существуют и другие варианты
установления эквивалентности. Чтобы использовать и разнородные эквиваленты мы
введем знаки операции — ![]() ,
для двухсторонней эквивалентности, и —
,
для двухсторонней эквивалентности, и — ![]() ,
для односторонней.
,
для односторонней.
|
|
(5) |
Или:
|
|
(6) |
Выражение ![]() —
взаимное присвоение, оно не равносильно А=В, это обратимый переход от одних
эквивалентов к другим. От леса к деревьям этого леса, и обратно.
—
взаимное присвоение, оно не равносильно А=В, это обратимый переход от одних
эквивалентов к другим. От леса к деревьям этого леса, и обратно.
Выражение ![]()
![]() приводит
к операции присвоения (а в логике – импликации), но оба выражения отражают один
процесс.
приводит
к операции присвоения (а в логике – импликации), но оба выражения отражают один
процесс.
Процесс преобразования эквивалентов.
Эквивалент В получает значение эквивалента А (или и эквивалент А получает значение
эквивалента В), если это возможность выражена знаком операции.
Вот теперь попробуем разобраться с
эквивалентностью и эквивалентами …
Возьмем две палочки и сложим в
кучку…
Мы произвели операцию сложения и
сравнения в соответствии с формулами (3), (5) и (6):
|
(1+1) = 2 |
(7) |
Что у нас получилось? Из двух
палочек получилась одна кучка, эквивалентная этим палочкам и из них же
состоящая. Но все же – кучка.
Теперь возьмем две капли воды и
сложим:
|
(1+1) = 2 |
(8) |
Сольем две капли и получим одну
большую каплю, эквивалентную двум первоначальным, но одну.
В чем принципиальная разница между
этими примерами? Палочки можно обратно забрать из кучи в их первоначальном
виде, а капли, если сложение в большую каплю уже произведено – нет. Т.е. в
одном случае, когда-нибудь можно сделать обратную операцию присвоения 1 кучка ![]() 2
палочки, для следующей задачи, а в другом уже нельзя, т.к. те же первоначальные
капли (до последней молекулы) получить невозможно, даже теоретически…
2
палочки, для следующей задачи, а в другом уже нельзя, т.к. те же первоначальные
капли (до последней молекулы) получить невозможно, даже теоретически…
Но, с формальной точки зрения, оба
полученных эквивалента в примерах необратимы, с той лишь разницей, что первый
необратим в пределах этой задачи, а второй и потенциально необратим.
Результат операции эквивалентного
одностороннего преобразования, неоднородный с исходными элементами, является
односторонним и необратимым.
В нашем случае полученный Результат
прекращает действие его недавнего эквивалента — Суммы.
Необратимость полученного
эквивалента предполагает невозможность одновременного использования разных
эквивалентов.
Если, в результате сложения палочек
мы получили одну кучку, то принятый единичный эквивалент – кучка будет обладать
свойством необратимости. Если необходимо от кучки перейти обратно к сумме
палочек, то снова, через операцию присвоения: 1кучка ![]() 2
палочки, и тогда сумма 2 палочки будет эквивалентом для одной палочки и еще
одной…, но кучки уже не будет.
2
палочки, и тогда сумма 2 палочки будет эквивалентом для одной палочки и еще
одной…, но кучки уже не будет.
Если использовать приведенные выше
примеры, то, это пример одностороннего преобразования:
|
2 палочки |
(9) |
И двухстороннего
преобразования:
|
2 палочки |
(10) |
Таким образом, кучка, после
проведения операции присвоения, не равносильна палочкам, а одна «большая» капля
не равносильна двум «маленьким».
Выражение: 1 кучка + 2 палочки,
будет некорректным.
Капля – это определение множества.
Можно сказать, что это единичное множество, состоящее из одной капли,… или
множество молекул в капле, или множество мелких капелек в одной, или… мы не
будем определять состав множества и оставим его неопределяемым. Само
множество определено – капля, кучка и этого достаточно.
Сумма однородных необратимых
неопределяемых множеств – необратимый неопределяемый эквивалент – одно
необратимое множество.
Конечно, в данном случае,
несчетность, не обязательная характеристика эквивалента. Посчитать, может быть
и можно. Но, с одной стороны — ну кто бы и как это считал?
Это же — куча, капля, лысина,
удивление, ужас и т.д.
А, с другой — множество
неопределяемого состава несчетно по определению. Из нескольких куч в сумме
можно получить только одну большую кучу…
Возникает вопрос, можно ли
сравнивать кучки?
Если единицы измерения одинаковы –
можно.
1 кучка палочек = 1 кучка палочек,
независимо от их прошлой эквивалентности разному количеству палочек. Ту эквивалентность
они уже потеряли.
Системы логического определения.
Тут,
как мне кажется, и не все просто, и не все так понятно, как это представляется.
Наверное,
у системы логического определения давно есть какое-нибудь научное название.
Наверное…
Как
мне кажется, в процесс определения логической системы входит не только, и
не сколько, система логических состояний, взаимосвязанная с принятыми
логическими ответами, но и … способ их формирования.
А
это интересная цепочка логических ходов и поворотов…
Что
из чего получилось, почему это так, а не иначе…
Эти
вопросы возникли, когда я начал для себя определять, что такое … логическая
задача.
Что
такое простая задача и сложная, почему одна задача требует односложного ответа
ДА или НЕТ, а другая… как раз в этих ответах и не нуждается.
С
задачами я пока так и не разобрался, сложно это оказалось. Но, кое-какие выводы
получились…
Правильно
поставленный вопрос, это … - половина ответа. Совершенно справедливо замечено.
В вопросе или задаче должны быть заложены и возможные ответы. Пусть косвенно…,
но они должны быть. Система задача – ответ, это единый логический
комплекс. Одно без другого не может существовать.
И
наоборот, если есть система логических ответов, то она способна ответить только
на определенный круг логических задач. Каков вопрос - таков и ответ.
Таким
образом, система логических ответов определяет круг решаемых системой задач.
Но,
жизнь сложна, задачи появляются самые разные…, значит, под них должны иметься в
запасе и соответствующие системы ответов.
Вот
и получается, что система определений для логики должна включать
как систему ответов, так и систему решаемых задач. И, видимо, соответствующие
логические пространства для решения разных задач, допускающих различные системы
ответов. Или логическое пространство должно подходить для всех задач. А может
быть, задача видоизменяется, до … подходящего уровня? Или все типы
решаемых логикой задач должны быть увязаны в единую цепь стандартных решений по
имеющимся у системы стандартным схемам. От самой простой, до самой сложной…, по
стандартным схемам,… со стандартными ответами…, если «вопрос – ответ», это
единое целое?
Тогда
надо внимательно разобраться с логическими ответами…, сделать стандартные
обоснованные схемы логических ответов. Эти же схемы и будут применяться к
задачам, связанным с этой схемой ответов…
Если
взять просто, ДА и НЕТ, или ДА, НЕ ЗНАЮ, НЕТ, то это ничего не дает. Система
ответов начинает быть воспроизводимой и понятной только по отношению к Я. Это объект
- владелец логической системы.
Начнем
мы со схемы абсолютного определения. Это самая простая схема. Она содержит
только один возможный ответ. Но, система логики подразумевает и наличие
противоположности. Как в ответах, так и в схемах их получения. В данном случае,
в качестве альтернативы логическому ответу здесь выступает сам объект Я.
Он
определяется в абсолютном понимании: Я – есть, или меня – НЕТ.

Рис. 1. Однозначное определение.
Но,
выбор тут сильно ограничен. Одним возможным вариантом. Альтернативы, как это
может показаться, тут нет. Потому и показаны две схемы. Это или Жизнь,
или Смерть. Для объекта Я выбора нет. По отношению к нему - только что-то
одно. Без вариантов.
Но,
если единственное свойство этой схемы – безальтернативность выбора,
относительно объекта Я, то это и достоинство,… и недостаток. Недостаток в
абсолютности и безальтернативности. А достоинство – в
относительности этой безальтернативности. Парадокс? Напротив. Это две
стороны одной медали. Это главный стимул для развития логики. Абсолютную
сторону мы выяснили, а какая – относительная?
Я
– хочу…, и все. Без вариантов.
И
второй вариант безальтернативной относительности:
Я
– не хочу, … и хоть режьте…
Но,
оба эти, вроде бы противоположных ответа означают одно и то же - определение
цели. Того самого безальтенативного выбора. Я ИМЕЮ, или Я НЕ ИМЕЮ…
И
эти ответы не связаны между собой. Никак. Это разные системы определения.
Потому и ХОЧУ я одного, а НЕ ХОЧУ - совершенно другого.
Вот
эта первичность однозначного определения сразу поставила логику в целевое
русло. Вне зависимости от всех остальных систем логических ответов.
Усложнение системы вызвано только сложностями существования. Мир сложен, и с
простыми мерками к нему не подойдешь. Надо соответствовать…
Объект
Я находится внутри системы определения, но себя он учитывает, только как объект,
координирующий пространство. Вот Я, и мне надо выбрать: или то, что - справа,
или то, что – слева. От меня.
Я
– центр системы отсчета. Вот так:

Рис.2. Система определений двоичной логики.
С
другой стороны, то, что справа, противоположно тому, что слева. На границе
противоположностей – Я. Я могу и в сторону отойти, а граница –
останется. Это еще и ось симметрии между равнозначными для меня, но такими
разными ответами.
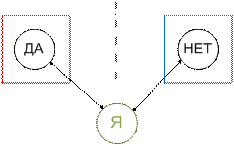
Рис.3. Логические ответы на уровне противоположности.
Объект
Я сделал очень важный для логики шаг. Он вышел из системы определений. И тем самым
перевел систему из конкретной, в которой Я принимает любую, но одну сторону в
решении задачи, в абстрактную. В этой новой системе определения он уже со
стороны оценивает возможность принятия решения, не делая этого конкретного
шага. Он решает задачу абстрактно. Для себя, для соседа….
Но,
даже после ухода объекта Я из системы определения двухзначная логика осталась
логикой абсолютного выбора. На уровне противоположности. Даже в абстрактном
варианте.
Такое
определение логических ответов на уровне противоположности становится первой и
самой устойчивой системой. Она присутствует практически во всех более сложных
схемах уже с несколькими уровнями определения. Это видно при рассмотрении схем.
Тут
всё несколько сложнее. Объект Я находится вне системы. И потому может заменить
себя в системе на еще один уровень определения. Например, на - НЕ ЗНАЮ.
Как
мы видим, конечные ответы в этой системе, в общем случае, имеют не только абстрактный,
но и относительный характер по отношению к объекту Я. Он - вне системы.

Рис. 4. Система определения троичной логики.
Только
куда же денешься от конкретики выбора, сначала - своего. В этой системе
определения появился второй уровень. Сначала объект Я должен только для себя
выбрать, будет он вообще выбирать, или - нет. На уровне абсолютности. А
уж потом относительно – за себя, за соседа…
В
этом, как мне кажется, скрыто главное противоречие между двоичной и троичной
логикой. Троичная логика, в принципе, абстрактна и относительна, двоичная –
абсолютно конкретна. По отношению к объекту принятия решения. Это
позволяет троичной логике участвовать в относительных системах определения,
чего двоичная логика лишена, в принципе.
Система
ответов троичной логики составлена из пары относительных
противоположностей. Относительно НЕ ЗНАЮ.
Потому
здесь, на месте НЕ ЗНАЮ, всегда может быть другой эквивалент –
противоположный неопределенности. Абсолютная определенность выбора. По
отношению к объекту Я, естественно. При сохранении относительной
противоположности к ответам. Например: ответ – ВЫБОР СДЕЛАН.
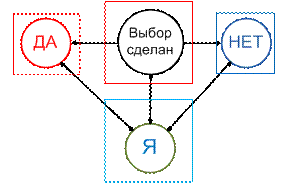
Рис.5. Абсолютность и относительность логических ответов
И
уже все равно, что было в системе ответов для выбора. Объект Я, сначала
решая задачу относительного выбора в системе ответов троичной логики,
потом решил задачу и абсолютного определения. Для себя. Он переставил
порядок действий в системе определения. Это отражено и в системе
логических ответов. Троичная логика стала работать в другой системе
определения. Но, пока осталась … троичной.
Вот
этот переход к выбору порядка следования абсолютности или относительности
- главное качество троичной логики.
Но,
практически это – … почти переход уже к четверичной логике…
Но,
если можно сделать шаг назад и выйти из логической системы определения один
раз, то почему бы не сделать это и еще раз? Объект Я вышел. И вот
что получилось:
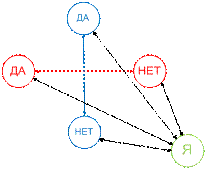
Рис. 6. Четвертичная система относительного определения.
Но,
все почему-то сразу усложнилось…
Теперь,
что бы определиться с ответом, надо было сначала определить ось симметрии для
определения, а потом уж выбирать ответ. И получалось, что, хоть система и
разрешает широкий выбор логических ответов, выбирать приходится уже в три
этапа,… и только между ДА и НЕТ. И сложно, и трудновыполнимо. Но, система
осталась, как память.
Несимметричная четверичная система.
Объект
Я понял, что … далеко шагнул, надо возвращаться. В систему определения. Чтобы
сразу исключить один этап – выбор оси симметрии. Вот туда и был сделан шаг – на
ось симметрии.
Но
в центр нельзя, опять запутаешься с выбором, и потому – немного в сторону…

Рис.7. Несимметричная четвертичная система определения.
Вот
теперь всё оказалось и просто и понятно. Относительно. Есть простая система
первичного определения на уровне ДА и НЕТ. И вторичная. Она определяет уже
относительное определение внутри выбранного варианта. Вот оно развитие троичной
логики на новом этапе.
Такой
вариант оказался очень привлекательным. И выбор ответов есть, и определение
однозначно. Вот на этом варианте ответов логической системы остановка была
долгой.
Многозначная логика.
Но…
предел понимания еще не достигнут. Можно, все же, еще сделать один шаг – в
центр.
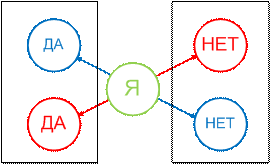
Рис. 8. Симметричная четвертичная система определения.
При
этом шаге объекта Я в центр системы определения всё изменилось
кардинально. Система обрела симметричность, но надо было сохранить и различие
определений в осях симметрии. Теперь логические ответы различных направлений
должны обозначать нечто одно, но … разное. Потому, что выбора в осях симметрии
не стало. Их оказалось слишком много…
И
потому, снова первичное определение по абсолютному признаку ДА или НЕТ, а уж в
группе – снова выбор…, между ДА и снова, каким-то ДА…, относительно чего-то …
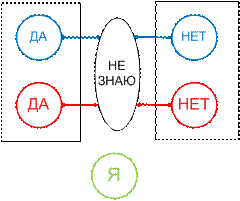
Рис. 9. Пятеричная система определения.
Что-то
получилось. Но уж очень сложное. Надо что-то менять. Осей симметрии много, а
толку от них…, вот с них и начнем. Оставим только … правую и левую…

Рис.10. Многозначная система определения.
Что
хотели, то и … получили. Многозначную систему логического определения.
Расширенную троичную…, в сторону усиления свойств определенного
логического ответа. Такую систему можно еще расширять, возможности есть,
но вот … необходимость…
Получилась
система трехступенчатого определения. Для логической системы такой уровень
вложений – уже очень сложен. Сначала нужно определиться на уровне абсолютной
необходимости: Принимать решение, или – нет.
Затем
выбрать группу определителей: Да, Нет, Не знаю.
И
выбрать нужный эквивалент ответа…
И
хоть порядок определения может быть любой, но…
Это
уже сложно.
Совместимость систем логических
ответов.
Все
работающие сегодня логические схемы имеют одну и ту же простейшую систему
определения логического состояния: есть импульс или сигнал, или – нет. И
соответствующую техническую интерпретацию этого: наличие – 1, отсутствие - 0.
Троичная
логика добавила знак к единице: +1 или -1, и 0. И это в корне изменило
всё. Тогда, полвека назад, двоичная и троичная системы оказались практически
несовместимы, даже на уровне электронных схем. Сегодня ситуация
изменилась. Созданы триггеры на любое количество логических состояний…, но,
тогда, троичная логика явно опередила свое время. Хотя, как знать,… возможно,
шанс еще есть…
Но
пока противостояние продолжается, и это не в пользу троичной логики. Потому,
что двоичная , тем временем бурно развивается.
И
все же, можно ли совместить в одном логическом пространстве разные системы?
Частично, конечно. А полностью адаптировать?
Давайте
подумаем…
Если
система ответов имеет четное число пар противоположностей, без
неопределенностей, то такая логическая система может как-то быть адаптирована в
электронные схемы двоичной логики. Но вход и выход должны иметь полную систему
определителей. В какой системе задан вопрос, в такой же должен быть получен и
ответ. А как внутри решена эта проблема, так ли это важно. Это важно, и
вот почему…
Совместимость
систем логических ответов зависит не только от математики, заложенной в ту или
иную схему, но и от философской платформы, определяющей её применение.
Система
двоичной логики не имеет пространственной ориентации. Тот или иной логический
ответ в электронных элементах фиксируется в одной точке. На выходе логического
элемента. Троичная логика пошла по тому же пути.
Так
же можно организовать и четверичную систему,… и восьмеричную…, что и было
реализовано. При таком пути решающее значение имеют фиксирующие элементы
- триггеры. Для любой системы счисления с четным основанием, достаточно …
двоичных триггеров. Но только для систем счисления, а не систем
логических ответов. Это разные вещи. Правда, мы их все время путаем…
Все
системы логического определения имеют четкую пространственную ориентацию. И это
в корне отличает их от систем счисления.
При
введении пространственной ориентации в троичную систему счисления мы
переводим её в систему логического определения. Что изменилось?
Простейшее
решение:
ДА,
НЕТ, НЕ ЗНАЮ, мы разделяем на пары логических противоположностей, как ДА – НЕ
ЗНАЮ, и НЕ ЗНАЮ – НЕТ. В той и другой системе противоположностей применимы
двоичные фиксаторы состояний 0 и 1. Теперь необходимо связать ячейки НЕ
ЗНАЮ в обеих парах линией связи. Состояние обеих ячеек теперь будет всегда
одинаковым: или 1 или 0. Логическая система при таком соединении будет
работоспособной, а как система счисления – нет. Почему? Потому, что теперь
логические состояния в техническом выражении везде одинаковы: 0 и 1. И надо
лишь договориться, что правая часть это ДА, левая – НЕТ, а в центре – НЕ ЗНАЮ.
И выполнять эту договоренность на всех участках логических цепей. И логика
будет работать, а для вычислительных сетей это реализовать невозможно. Хоть, мы
во всех случаях и считали до трех…
Специалисты
по логическим схемам это знают.
Так
что, вопрос применения троичной логики уперся не в техническую реализацию, а в
соединение логики и вычислений. Разные логические уровни сигнала в одном
проводнике нужны только для вычислений. Там без уровней -1, +1, 0,
проходящих в одном проводнике, не обойдешься.
Вот,
оказывается, в чем загвоздочка …, в ориентации противоположностей. На уровне
логических цепей. При наличии пространственной ориентации в логических
цепях одновременное применение разных систем логического определения
имеет и смысл и решение. На логических элементах двоичной логики.
Задача
оказалась вполне решаемой… теоретически. Для практического решения надо еще
множество вопросов … задать … и решить.
Здесь
пока я включил только часть материала. О типовых схемах модальной логики. Но,
эти же принципы представления схем типовых задач логики можно распространить и
далее. Типизация схем задач вполне предсказуема.
Здесь
мы попробуем сопоставить схемы задач со схемами логических ответов. Для тех же
задач. И посмотрим…, что получится.
«Стремление обогатить
язык логики и расширить ее выразительные возможности привело к возникновению
модальной логики. Ее задача — анализ рассуждений, в которых встречаются
модальные понятия, служащие для конкретизации устанавливаемых нами связей, их
оценки с той или иной точки зрения.» [1]
«Все модальные понятия
можно разделить на абсолютные и сравнительные. Первые представляют собой
характеристики, приложимые к отдельным объектам, вторые относятся к парам
объектов, первые являются свойствами объектов, вторые — отношениями между
объектами. Абсолютными модальными понятиями являются, например, понятия
“хорошо” и “плохо”, сравнительными — понятия “лучше” и “хуже”.»[1]
Модальных
логик много. Логика предпочтений, эпистемическая логика, паранепротиворечивая
логика, логика этики, логика изменения, но и это еще не все:
«В логике времени
к абсолютным модальностям относятся понятия “было” (“всегда было”), “есть” и
“будет” (“всегда будет”). Сравнительными модальными понятиями являются
“раньше”, “позже” и “одновременно”.
В логике оценок наряду с
абсолютными оценочными понятиями “хорошо”, “(оценочно) безразлично” и “плохо” исследуются
также сравнительные оценочные понятия “лучше”, “равноценно” и “хуже”.
В логике причинности
изучаются отношения “...есть причина...” и “...есть следствие...”, которые
можно рассматривать как сравнительные каузальные модальности. Им соответствует
абсолютная каузальная модальность “детерминировано (предопределено)”.»[1]
Таким
же образом, например, можно создать и логику… расстояний. Для этого необходимо
ввести абсолютные понятия «близко», «далеко», «точно» и что-то неопределенное,
например «безразлично где », а потом ввести относительные понятия «ближе»,
«дальше», «одинаково» … и тоже что-то неопределенное…
Далее
включаем аппарат математической логики, и получаем вполне самостоятельную
модальную логику. А что, можно…
Принцип
известен, результат почти предсказуем.
Но,
вопрос не в этом, модальные логики понятны и их количество может расти
неограниченно.
Видимо
это одна логика с приложениями по направлениям. Так, по крайней мере,
получается по [1]. Модальные логики создали почти классический набор
стандартных схем решений. Понимаемых и математически, и интуитивно.
И
все же, давайте, подумаем. Что задают модальные понятия во всех логиках?
Они
задают эквиваленты. Абсолютные и относительные. Эквиваленты отбора. Контрольные
образцы для абсолютного сравнения. И их относительные соотношения с измеряемым
логическим понятием.
Для
полного комплекта между противовесами не хватает только нейтральности или
неопределенности. Её всегда можно установить по краевым противоположностям. И
она устанавливается.
Модальные
логики решили главную задачу. Они дополнили абсолютные эквиваленты логических
состояний относительными эквивалентами сравнения.
Типовые схемы модальных логик.
Модальные
логики разрабатывают системы абсолютных и относительных отношений эквивалентов
определения. Мы это уже увидели. Осталось построить эти схемы.
Но,
оказывается, все многообразие логических отношений можно свести к одной
схеме. В цифровом отображении. Она предельно точно отражает
взаимоотношение определителей.
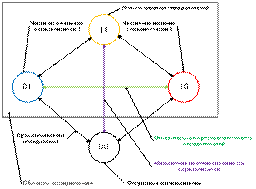
Рис.11. Схема взаимодействия логических определителей.
Так
как система определения включает в себя абсолютные и относительные
противоположности определителей, то и сама схема становится системой и абсолютного
определения и относительного. В таких видах эти системы и включены в модальные
логики. Как мы видим, схема только частично симметрична. На уровне абсолютной
противоположности в схеме симметрии нет. Отсутствие определителей однозначно
лишает выбора в путях достижения результата. Только наличие хоть
какого-то определения позволяет начать путь к достижению цели.
Вернемся
к примеру построения логики расстояний. Вот так может выглядеть её система
абсолютного определения:
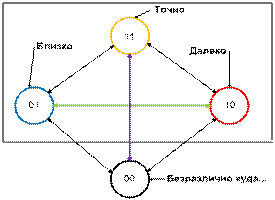
Рис.12. Абсолютная система определителей логики расстояний.
Когда
может быть применена такая схема достижения результата? При определении самого
наличия цели. Пока нет цели, и говорить о чем-то…, странно.
В
качестве цели мы должны найти ориентир, эквивалентный набору наших
определителей. Мы же что-то хотели найти…, раз, в путь собираемся?
Но
вот, цель сформирована, и начинается глобальное определение подходов, где-то
там… даже в абсолютном выражении. Куда точно нам надо попасть, где мы и где
цель? Далеко до неё, или вот она – рукой подать…, два пальца по карте.
С
абсолютными определителями на карте мы разобрались. И теперь включается в
работу схема относительных определений.
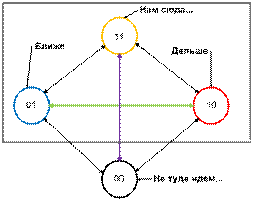
Рис.13. Схема относительного определения.
Мы
знаем, где находится цель, … на карте, а в реальности путь к ней надо еще
искать…
Сначала
глобальное определение на уровне абсолютных противоположностей. А мы вообще, туда
идем? Вот цель, а вот – мы…
Цель
где-то … там. Нам туда. Вот так, по карте, будет ближе, но … болотом, а так
будет дальше, но по дороге. Путь лишний намотаем…, но без проблем. Так куда
пойдем?
И
мы начинаем определяться с относительными противоположностями «ближе – дальше»,
но уже в привязке к известной цели. В том и относительность определения…
И
наконец, в путь…
Логическую
задачу движения мы вроде бы решили, но, все равно, на каждой развилке будем
строить схемы абсолютного и относительного определения. Куда нам: направо,
налево или прямо, а не двинуть ли нам чуть левее, далеко от траверза
отклонились…
Вопросы
разные, а схема решений одна и та же.
Кажется,
мы немного увлеклись одной логикой расстояний. Перейдем к другим системам
определения. К системам ответов многозначной логики.
Вот
как будет выглядеть система логических ответов относительно «НЕТ» и «ДА»:

Рис.14. Система логических ответов относительно «НЕТ» и
«ДА».
Схемы
оказались одинаковыми, что и предполагалось. Их можно попробовать даже
объединить…
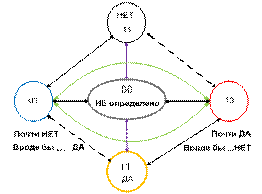
Рис. 15. Совмещение логических ответов.
Непонятно
получилось…, но если пойти по черным стрелочкам, отбросив пунктиры, то … мы
получим что-то очень знакомое:
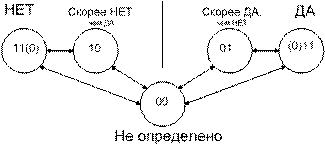
Рис. 16. Разворот схемы определений в систему ответов
многозначной логики.
Мы
получили один из вариантов системы логических ответов многозначной логики. И он
получился вполне логичным. В нем присутствуют и абсолютные, и относительные
противоположности. Насколько такая система логична…, посмотрим.
Для
такой системы очень просто подобрать весовые эквиваленты логических ответов.
Допустим, так:
(0)11
– ф-2 =0,382
01
– Ф-1 = 0,618
00
– 1= 1
10
– Ф = 1,618
11(0)
– Ф2 = 2,618
При
этом, сумма (0)11 + 01 = 1, и разность 11(0) – 10 =1, произведение
противоположностей (0)11 ![]() 11(0)
= 1 и 01
11(0)
= 1 и 01 ![]() 10
=1.
10
=1.
Вполне
применимая система получилась…, она допускает и неограниченное
симметричное увеличение количества логических ответов системы. Интересно, что в
весовых эквивалентах ни один ответ системы не является отрицательным, а
операция инверсии возможна….
Для
получения наглядности ответы этой системы лучше кодировать как: …001, 01, 00,
10, 100,…, но, тут как кому нравится…
Код
11 для данной логической системы видимо должен утверждать только то, что ответ
противоположен абсолютной неопределенности 00, а какой он, ДА или НЕТ, так ли
это важно…
Мы
понимаем это, например, когда надо ответить на простой вопрос:
-Я
надеюсь, завтра Вы не опоздаете?
Ответить
однозначно, ДА или НЕТ, как-то не получается…
Вот
интересная цитата:
«Речь идет, прежде всего, о
трансформации базовой геноматрицы Р в матрицу Адамара [1 1; -1 1] при учете важного
отличия буквы Т (или U в РНК) от остальных трех букв: молекулы последних
наделены функционально важной аминогруппой NH2, а буква T/U лишена
ее. Кроме того, только буква Т заменяется на другую букву U при переходе от ДНК
к РНК. Соответственно обозначение букв С, А, G через «+1», а буквы T/U – через
«-1» обращает базовую матрицу Р в матрицу Адамара. При этом все матрицы
кронекерова семейства Р(К) становятся матрицами Адамара.» [29]
Понятно,
что речь идет о системе кодирования ДНК. Далее идет сплошная математика,
но, главное для нас, уже сказано…
В
ДНК просматривается та же схема взаимодействия логических определителей,
что и в модальных логиках. Четыре основания ДНК составляют две пары
противоположностей А-Т и Ц –Г. Приведенное выше отличие основания Т от
всех остальных, почти автоматически определяет пару А-Т, как абсолютные
противоположности, а пару Ц-Г переводит в относительные. Вместе эти
основания составляют систему из четырех логических состояний, которая лучше
всего кодируется двухзначным бинарным кодом:
00,
01, 10, 11.
Это,
как мне кажется, уже не может быть простым совпадением…
Приведенные
примеры показывают состоятельность наличия в логической системе единого
комплекса «вопрос – ответ», имеющего типовую схему, как решения, так и ответов.
Это
одна и та же схема.
Таким
образом, для начала решения задачи необходимо выбрать систему ответов. Она
определяет порядок решения задачи. Но, это и типовая схема самой задачи.
Типизация
решений приводит к одному вопросу, с которого начинается любое решение: Что мы
хотим выяснить, решая задачу?
Необходимо
установить цель. И относительно неё уже примерять различные схемы типовых
решений и типовых ответов. И то и другое нам известно до начала решения задачи.
Мы лишь делаем примерку схем под цель задачи. А наличие цели - без
альтернатив, это мы уже выяснили. Иначе нет смысла решать задачу…
Вот
мы и подошли к логическому определению. Что же это такое?
Видимо,
логическим определением надо считать выбор схемы для решения той или иной
задачи. В этом случае вместе с задачей мы имеем и схему применимых к ней
логических ответов, типовой алгоритм решения, и связь с другими
возможными схемами.
Не
так уж мало.
И
все было бы хорошо, если бы разные логические задачи могли быть решены в одном
и том же логическом пространстве. Но, мы же сами вывели схемы ответов Булевой
логики, троичной, и т.д. Каждая логика работает в своем пространстве,
организованном только под неё. Как же быть?
Вот
здесь и возникает вопрос математики и логики.
Первые эквиваленты логической
системы.
Эквивалент безальтернативного
логического определения.
Собственно,
мы с ними уже немного познакомились. Давайте теперь по порядку…
Простая
схема, принятая за эквивалент логической системой – однозначный выбор.
Схема простая, а обозначает она для логической системы очень много. Прежде
всего это понятия безальтернативных чувств. Мы их хорошо знаем. Это чувства:
голода, жажды, страха, самосохранения, а также любопытство, влечение, …
ну и т.д.
Тут
надо бы уточнить кое-что.
Безальтернативное
понятие ХОЧУ, это – образование ЦЕЛИ. И объект стремится решить задачу
ХОЧУ, достигнуть заветную ЦЕЛЬ. Получить ОБЪЕКТ его ЦЕЛИ. Приближение к
ЦЕЛИ в этом случае рассматривается как достижение РЕЗУЛЬТАТА в целевой задаче.
Безальтернативное
понятие НЕ ХОЧУ, это тоже – образование какой-то ЦЕЛИ, но вот задача в этом
случае решается противоположная – никогда не достигать этой ЦЕЛИ. Вот такую
цель, от которой объект стремится удалиться, мы и назовем ПРОТИВОЦЕЛЬ. Понятно,
что ЦЕЛЬ и ПРОТИВОЦЕЛЬ – логические противоположности. Они формируют в
логической системе задачи противоположной направленности. В абсолютном
выражении мы эти задачи уже знаем, Это задача Я – ЕСТЬ, и задача Я – НЕТ.
Вот эти схемы задач и являются эквивалентами основ всех целевых задач
любой направленности.
Вот,
оказывается как, схема безальтернативного логического определения лежит
в основе всех наших первичных чувств и инстинктов, со времен образования
клетки.
И
понятие ЦЕЛЬ в этом списке – одно из первых…
Появление
противоположностей в цели заставило перейти на двоичную логику. Куда ж
денешься, жизнь заставляет…
Схемы
альтернативного логического определения, это двоичная и троичная логика. Начнем
с двоичной. Появились противоположности логических ответов в одной
задаче, это - ДА и НЕТ.
Это
сразу усложнило решение простых безальтернативных задач. Надо соблюдать
наличие противоположностей. И теперь задача Я – ЕСТЬ, и задача Я – НЕТ
появляются, обе сразу. Как одна задача с применением противоположностей.
Формируется два направления рассмотрения задачи. Мы их хорошо знаем. И
получается альтернатива, между «хочется» и « можется»…, реальная оценка и наших
сил, и необходимости выполнения поставленной целевой задачи.
Таким
образом, конкуренция целей является уравновешиванием не
только для логических систем высокого уровня, она заложена в логику Живого
изначально. Как схема типового решения. На
уровне противоположностей. А вот их баланс – у каждого свой….
Причем,
как в абсолютном понимании, так и в относительном. Трудно найти границу между
«хочется» и «колется», но находим же, … ограничение безальтернативного
желания и такого же - инстинкта самосохранения. Границу между «можно» и
«нельзя». Но, так как понятия ДА и НЕТ имеет только абсолютный характер, то и
граничные условия на уровне противоположностей мы каждый раз
устанавливаем как в первый раз. Заново определяем этот самый неуловимый баланс
равновесия наших чувств. У них отсутствует понятие – норма. К сожалению…
Появление
двухзначной логики позволило решить еще одну задачу. Задача появилась, когда
клетка сдвинулась с места. Звучит это немного сложно: Альтернативное
исполнение безальтернативных задач. А переводится это на разговорный
язык очень просто.
Например,
так: Поехали … и … Стоп.
Команда
активизации и команда на торможение. Само действие имеет
безальтернативный характер. Только исполнять. Или только… остановиться.
Но выполнять их надо … в нужный момент. По команде. Команда, как и положено,
имеет абсолютное понимание: Только так.
У
логической системы появился внутренний кнут для безусловного исполнения.
И когда мы говорим, что выполняемое сегодня решение принято на основе сложного
выбора, то не очень в это верится. Очень часто этот кнут щелкает еще до
взвешивания аргументов, по каким-то внутренним соображениям нашей
логической системы, далеким от аргументов именно этого выбора…, и мы начинаем
исполнять то, что только потом, может быть, как-то сумеем
аргументировать. Говорят, интуиция…
Возможно.
Но
вот этот командный безальтернативный переход «от слов к делу» мы запомним. Как
приказ к действию. Всё – выбор сделан. Пора…
Появление
схем двухзначной логики сразу определило путь дальнейшего
развития системы логического определения. Создание противоположностей
и их баланса. Просто и эффективно. Почти все логические определения у нас и
идут на уровне – или, … или. Да – Нет. И мы к этому привыкли.
И почти все логические задачи имеют такие ответы. Противоположность заложена… в
самой задаче, и в ответах. Тут надо выбирать… в абсолюте. Или … или…, третьего
не дано. Аристотель не ошибся с логическими ответами. Они
составляют основу логического определения. Все четные системы с большим количеством
логических ответов всегда можно привести к этой, двоичной, на уровень – ДА и
НЕТ. Да и нечетные – тоже, в основном.
Теперь
мы можем подвести маленький итог. С появлением системы двоичного логического
определения в логической системе появилось сразу несколько типовых схем
задач и их решений. Первая и главная – задача альтернативного выбора с
безальтернативным исполнением. Мы уже о ней говорили. Кнут. Если
решение принято – действуй. Но такому переходу от слов к делу постепенно стало
предшествовать еще и стандартное решение типовой задачи выбора. Иногда и
многоступенчатого. Когда трудно сразу решиться, надо подобрать аргументы,
взвесить…
Задача
создания логической противоположности
быстро переросла в техническую задачу копирования, теперь копии
создаются не только логические, но и реальные. Кстати, что тут было первым, а
что потом…, так ли это важно, но задача определения противоположности в
этом списке точно – первая. Находить научились тогда, когда стало понятно, чем
они должны отличаться. А потом уж – создавать…
Ну
и конечно задача создания баланса противоположностей. Уравновешивать
одну крайность другой, до этого надо было еще додуматься…
В
техническом исполнении это - задача управления на балансе антагонистов.
Один вправо, другой влево, а вместе – на месте. Кстати, тогда появилась и задача
прямого управления на основе линии связи. А вместе с ней и центр
управления, и управляемый объект.
Тогда
же появились и первые математические понятия: 0, 1, много. Ими логика
оперирует до сих пор. И конечно – ось симметрии. Как граница
между одним и … другим. И конечно, Я – посередине…
И
все же…
Не
хватило двоичной системы определителей, когда потребовалось решить новую задачу
– координацию действий. Безальтернативную однозначную систему вообще
нельзя использовать, двоичная логика имеет только абсолютное значение
определителей. А координация требует относительного определения. Движения
должны быть точными и быстрыми.
Вот
когда пришло время троичной логики. Время относительного определения. Чуть
больше (чем было), чуть меньше…, вот, точно … в цель.
Троичная
логика, безусловно, логичнее двоичной. И по форме, и по содержанию.
Это
уже логика нашего логического определения.
Наш
самый распространенный ответ, не –ДА, не – НЕТ, а – м-м-м, НЕ ЗНАЮ… надо
подумать. Или что-то в этом роде…
Вот
когда появились схемы типовых задач широкого спектра. На основе относительных
соотношений. Основных типов – два.
Техническая
задача управления по отклонениям, уточняющая и возвращающая
систему в нужное положение каждый раз, после появления возмущающих отклонений.
Это стало возможным после появления и решения сходной, но уже логической задачи
сравнения, с выявлением сходств и различий. На этой основе появились точные
определения границ и ограничений, постоянного действия. Если
нельзя, то… вот отсюда, а там – уже можно. Вот она – граница. Тут. И
сегодня, и завтра…
И
наконец, выдающееся изобретение – петля обратной связи.
Связи,
соединяющей управляемый объект с центром управления, в которой идут сигналы
от управляемого объекта. Прямое управление было организовано еще в
системе двоичного управления, введение обратной связи замкнуло кольцо
управления, появилась и задача пропорционального управления. Вот
теперь понятия – больше, дальше, быстрее …, обрели смысл. Вместе с их
противоположностями.
На
основе петли обратной связи стало возможным создание сложных логических систем
управления. Этот же принцип управления заложен и в нас.
Мы
говорили о двух типах задач. Какой же второй? Второй тип задач основан на
введении понятия ОЖИДАНИЕ. В логической системе появилось логическое состояние
-НЕ ЗНАЮ. Появилось время … остановиться и подумать. Как отдельное
действие.
Решить
сложную многоуровневую логическую задачу, наконец-то, принять аргументированное
решение, а система управления …. Пока пусть подождет.
Правда,
логическое состояние НЕ ЗНАЮ, тут же получило свою противоположность – ОТВЕТ
ЕСТЬ. Определенность в ответ на неопределенность. Двоичная логика не дремлет…
На
этом этапе появилась очень важная задача – прогнозирование. Прогноз, это
еще не окончательно, это только вариант, но вдруг… так и окажется. Прогнозирование
заглянуло в будущее. Что там, за горизонтом настоящего, лучше бы заранее…,
а то вдруг – чего, … и не успеем. Эта задача стала постоянной целью
логической системы, и стимулом её развития.
ОЖИДАНИЕ
тоже получило свою противоположность – РЕЗУЛЬТАТ.
И
потому, наличие ОТВЕТА в решении, это еще не повод…, а вот получение
РЕЗУЛЬТАТА, это уже…
Получение
результата прекращает ожидание, пора…, есть баланс противоположностей. Задача
решена.
Всё
дальнейшее развитие логической системы пошло на основе троичной логики.
Типовые схемы троичной логики оказались универсальным средством для решения
многих различных по смыслу и классу задач. Но в основе всех решений – типовая
схема.
С
возможными типовыми ответами. Они известны заранее, надо только выбрать…
Когда
у нас уже имеется такой внушительный арсенал средств для решения любых
логических задач, то надо бы понять, как ими пользоваться. Как ими пользовались
до нас?
Вот
задача. Надо её решить. Что будем делать?
Можно
попробовать решить её методом «научного тыка», т.е. пробовать все подряд,
авось получится…
Можно,
но … времени нет на эти эксперименты.
Можно…
начать решение … с начала. Вот берем первое условие и начинаем искать решение
для него. Потом второе…, ну и …
Можно,
но тоже – долго. Так можно решать, когда времени – вагон, а тут надо – быстро.
А
что у нас там – в арсенале? Посмотрим, пыль смахнем, приложим, вдруг подойдет.
Тут из подходящего и перебирать-то особо нечего, вот, вот, и … вот.
А
вот это уже – вариант…
Так
примерно и начинается решение, пусть и совсем незнакомой задачи. С поиска
подходящих моделей, схем, шаблонов, … - типовых эквивалентов
решения.
Исходная
задача каждый раз получает новое понимание вместе с прикладываемым к ней
очередным эквивалентом. Задача меняется под эквивалент. И хоть мы помним
и исходное определение задачи, но и получаемые из неё типовые варианты тоже
имеем ввиду….
Так
прикинули, теперь с этой стороны, теперь так попробуем…., так, так и так…
И
получили комплекс типовых задач и их решений. Из одной.
Запутаемся
же…, нет, найдем основные признаки и состав шаблонов для решения. Задача,
оказывается, состоит из этого типового шаблона, из вот этого, и этого…., и
вроде – всё.
Ну,
эти задачи мы решать умеем, тут – так, тут – вот так, и … есть решение.
И
неважно, что задача была незнакомой и новой, мы её … поняли, на основе
эквивалентов, составили новый эквивалент решения, и … получили ответ.
НЕ
решая задачи. Быстро… и со вкусом.
В
таком решении есть существенный недостаток. Получаемый ответ не всегда
обоснован. Мы же ничего не вычисляли и не проверяли. Мы взяли типовые схемы,
наложили их на задачу, и вывели ответ… по схемам, а не как результат
решения этой задачи.
Насколько
эти ответы совпадают?
Если
задачу решать, то, конечно…, хотя, шаблонное решение, вероятно,…
будет верным в большинстве случаев.
Ошибки
при таком решении, безусловно, есть, и будут, но… время, сколько мы потратим
времени на вычисление обоснованного ответа? Нас за это время раза три съесть
успеют…
Уж
лучше с ошибками, но … быстро. Решить … и смыться.
Фактор
времени стал основным в обосновании принципа нахождения решения задачи в логике
Само…
Но
не отменил обоснованное решение задачи, если в этом есть суровая необходимость.
Задачи решаются. Если время есть…
Тоже
с применением всего арсенала средств, а как же…
Потому
что, задачи, почти все, появляются у нас в неявной, такой простенькой
форме «вопрос – ответ», или и того нет, а копнешь, там – такое…
Вот
и копаем. Отсюда и …до конца географии…
В
этот раздел включены логические решения самого низкого уровня. Но,… эти решения
применяются во всех дальнейших более высоких уровнях решений. Они являются основой
логики Само…
Тут
надо бы определиться с иерархией уровней логических решений.
1.
Функция.
2.
Операция – должна иметь ответ.
3.
Действие – должно иметь результат.
Вот
примерно так. Из этого и будем исходить…
Логическое
действие, это маленькая задача. Логическое
действие имеет Результат. Решение в логическом действии имеет
односторонний и необратимый характер. Логическое действие нацелено на результат.
Решение есть, если получен результат. В рамках одного логического
действия может быть проведено множество логических операций и получено
множество логических ответов. Действие не закончено, пока нет заключения о
результате. Но, как только получен результат, действие считается
законченным. Единственным эквивалентом проведенного логического действия
остается результат. И потому, никакие преобразования в математических
выражениях между двумя действиями невозможны. Можно работать только с
результатами этих действий.
Логическая
операция получает ответ. Пока ответ не
получен, операция не закончена. От проведенной операции значимым итогом
остается ответ.
При
этом совершенно не важно, сколько времени занимает та или иная операция, что при
этом происходит. Нам важен факт проведения операции … и ответ.
Мы
находим варианты ответов, ищем путь в нужному эквиваленту, можно вернуться,
изменить входные величины и снова произвести решение. Ответ еще не результат,
только ответ…
Логическая
операция состоит из логических и математических функций.
Логическая
функция, это как раз то, с чем сегодня
работает алгебра логики. Конъюнкция, дизъюнкция…
Логические функции.
Если
понимать логические функции, так, как они сегодня трактуются в математической
логике, то функция, это взаимодействие аргументов. Сам факт этого.
Например,
вот такое простейшее выражение, как 1+1=2 имеет два взаимодействия -
(+) и (=). Это функция сложения и функция равносильности, или равенства.
В
этом случае в логику автоматически попадают все функции математики.
Но,
выделены, как логические функции только несколько. Конъюнкция, дизъюнкция,
инверсия…
Хотя,
при этом никуда не делись и сравнительные функции: (>), (<), ( ![]() )….
)….
Они,
точно так же, просто обязаны входить в состав логических функций.
Надо
бы добавить в логические функции ещё две группы функций – создание
и присвоение статуса эквивалента.
Функция создания противоположности.
Создание
противоположности по заданному элементу. Это функция целевая.
Пока
у нас только одна такая функция. Хотя и имеет два варианта записи.
Вот
первый:
|
Ц
( |
(11) |
Но
есть и второй вариант. Это функция получения противоположности от логической
противоположности. Вот этот варианта записи:
|
Ц
( |
(12) |
Понятно,
что применение этой функции позволяет реализовать операцию копирования. В том
числе, и получение копии с заданного образца по заданному признаку.
Функции присвоения.
Формально,
запись этой функции выражается двумя знаками: ( ![]() )
и (
)
и ( ![]() ).
Видимо, это формально две разные функции. Рассмотрим их…
).
Видимо, это формально две разные функции. Рассмотрим их…
Одностороннее присвоение.
Знак
( ![]() )
устанавливает одностороннее действие функции. Функция одностороннего
присвоения, это:
)
устанавливает одностороннее действие функции. Функция одностороннего
присвоения, это:
|
а
|
(13) |
Если
а ![]() в,
то а больше нет, есть только в. И все,
что раньше соответствовало понятию а, теперь должно
соответствовать понятию в. Путь даже объект а и
остался, но он уже стал объектом в.
в,
то а больше нет, есть только в. И все,
что раньше соответствовало понятию а, теперь должно
соответствовать понятию в. Путь даже объект а и
остался, но он уже стал объектом в.
С
другой стороны, это знак, указывающий движение решения в сторону результата.
Это ограничение действий по возврату решения назад, к исходным выражениям. Это
знак перехода из одной части решения в другую, без возможности простого
возврата. Всё, та часть решения уже сделана, мы уже в других условиях, теперь
мы тут, и должны действовать только в этих условиях. Если все же
появляется необходимость возврата к исходным данным, то следует сделать новую
операцию присвоения и перейти к исходному эквиваленту. И только тогда
переходить к дальнейшим преобразованиям.
Это
и знак следствия. То, что понимает под ним функция импликации. Если а,
то в. Из а следует в. Так его и
следует понимать.
С
введенными формальностями.
Переход к исполнительной команде.
Важным
следствием из функции одностороннего присвоения является функция перехода к
исполнительной команде. Запишем её так:
|
а |
(14) |
У
нас появилось еще одно базовое понятие – исполнительная команда. Она обозначена
как d. Подчеркивание и присваивает статус команды исполнения
какого-то действия. Вот тут одностороннее присвоение и работает так, как это и
заложено в исходной функции. Начало выполнения команды прекращает
действие всех предыдущих преобразований аргументов. Началось
безусловное выполнение команды, и что там было до этого…, уже не важно.
Видимо,
более точная запись этой функции должна выглядеть так:
|
а |
(15) |
Должно
быть уточнение, какая команда начинает исполняться…
Наверное,
будет и условный переход к исполнению команды, но это уже позже…
Переход к финальному эквиваленту.
Эта
функция имеет более жесткие условия перехода от одного эквивалента к другому,
чем функция одностороннего присвоения. Она запрещает возможность
обратного преобразования. Общая форма записи этой функции :
|
a| |
(16) |
Введенная
в запись вертикальная черта показывает невозможность возврата к исходному эквиваленту.
Всё, дело сделано, возврата нет. Теперь можно использовать только этот
эквивалент.
Взаимное присвоение.
Знак
( ![]() )
устанавливает двухстороннее действие функции. Выражение функции взаимного
присвоения можно записать так:
)
устанавливает двухстороннее действие функции. Выражение функции взаимного
присвоения можно записать так:
|
а
|
(17) |
Если
а ![]() в,
то они стали эквивалентами друг друга. И пусть это совершенно разные понятия
или объекты, они стали равносильны в применении с логической точки
зрения.
в,
то они стали эквивалентами друг друга. И пусть это совершенно разные понятия
или объекты, они стали равносильны в применении с логической точки
зрения.
После
этого можно поставить между ними и другой знак функции: а = в.
Но,
только – после…
Теперь
это будет уже правомерно. И логически обоснованно. Теперь мы можем говорить а,
и при этом подразумевать в, и наоборот…, что является нормальным
явлением, с точки зрения логики.
Определение цели.
Частным,
но очень важным следствием функции присвоения становится функция присвоения
статуса – Цели. Запишем его так:
|
а
|
(18) |
Выделим
из выражения функцию:
|
(
|
(19) |
Это
функция определения цели. Понятие цели, это базовое понятие логики. Цель у
логической системы появилась еще на стадии однозначной логики, когда даже не
было понятия противоположности. Мы о цели уже говорили.
С
развитием логической системы развилось и понятие цели. Оно изменилось, и …
появилась необходимость к возврату от цели к конкретности объекта:
|
а |
(20) |
Эта
функция позволяет уточнить понятие цели по мере изменения свойств объекта а.
Выражение
функции стало иным:
|
( |
(21) |
Цель
получила возможность изменения, вместе с изменением объекта цели.
И
вместе с этим, цель стала самостоятельным понятием логики. К нему применима и
функция инверсии, без изменения объекта цели. Это смена направления действия.
Если
Ц(а) – достигнуть а, то противоположность действий относительно
объекта цели ![]()
![]() (а) – никогда не достигать а.
(а) – никогда не достигать а.
Обобщение и детализация.
Это,
как раз, переход «от штучек к кучке» и обратно. По направлению действия они
противоположны:
|
а,а,а,…
А(а)
|
(22) |
Функция
минимизирует применение математики в логических операциях. В математическом смысле
это взаимный переход от суммы элементов массива к массиву, как новой единице
измерения. А в логическом смысле, например, от деревьев к лесу, и обратно. Для
логической системы применение этой функции обусловлено несчетностью понятия много.
Все, что выходит за рамки определяемой счетности логическая система почти
автоматически переводит в единичность нового эквивалента. Переход назад
осуществляется в случае необходимости обращения к конкретному элементу
множества.
Множественность
переходов из одной системы эквивалентов в другую, и назад, привел к обратимости
этого процесса и на уровне функции:
|
а,а,а,…
|
(23) |
Правда,
эта функция требует организации хранения, как первичной информации, так и
получаемого эквивалента.
Еще немного о функциях.
Как
мне кажется, в понятие функция сегодня вмешалась и вычислительная техника. Дело
в том, что за каждым знаком математического действия скрывается … набор
микрокоманд его выполнения. Взять данные из ячеек с номерами…., записать в
регистр,… взять данные из ячеек… и записать в регистр,… провести разрядное
суммирование, с записью результата в ячейки…, обнулить регистры и ячейки
данных…
Для
каждой функции свой набор. И потому, введение в функции и исполнение команды
никак не отражается на изменении понятия функции. В отношении вычислительной
техники, по крайней мере. Мы лишь зафиксировали на уровне логики то, что там
уже заложено.
Мы
ввели логическое понятие – Цель. Тут, как мне кажется, надо еще формализовать
понятие цели. Потому, что хотим мы этого или нет, а с целями начнут работать и
на уровне функций, как с логическими объектами. Но, не все функции могут быть
применены к целям.
Я
пока не знаю решения. Надо думать.
Логические операции
Опять,
если следовать математической логике, то логическая операция отличается от функции
наличием эквивалента её выполнения, в каких-то единицах измерения. Это может
быть и логический ответ системы. Но это может быть и иной эквивалент, например,
исполнительная команда, или цель, или действительно, эквивалент, заменяющий эти
выражения функций.
В этом случае, выражение 1+1 =2, это операция вычисления суммы (1+1), которая и
зафиксирована в ответе: =2.
Будем
придерживаться этого понимания.
После
введения функций присвоения изменилась и возможная форма логической операции.
Теперь она не ограничивается только математическим соотношением эквивалентов
ответа и исходного выражения. У нас добавились функции
одностороннего и взаимного присвоения статуса эквивалентов. Появились
понятия цели и исполнительной команды.
Функции
присвоения частично ограничивают взаимные преобразования частей и выражений
операции. Появилась односторонняя направленность действий.
Ну,
так, потому это и не математика, а логика…
В
связи с этим можно выделить две формы логических операций. Промежуточная и
финальная операция.
Финальная операция.
Понятно,
что, например, признаком финальной операции является безусловный переход к
исполнительной команде. На этом все преобразования внутри операции
автоматически прекращаются, и сама операция – тоже. Остается только исполнительная
команда. И её исполнение.
|
а
|
(24) |
Таким
образом, появление любого из аргументов выражения дизъюнкции автоматически
ведет к началу исполнения команды d(c). Без вариантов.
Логическим
ответом такой операции является только один ответ по отношении к исполнительной
команде – ДА.
Но
применение финальной операции этим не исчерпывается.
Конечная операция.
Это
операция конечного преобразования. Она фиксирует логический ответ операции.
Если необходимо вернуться к преобразованиям, то теперь это можно сделать только
операцией обратного присвоения. От кучки перейти обратно к штучкам. Мы это уже
видели. И тогда можно продолжить…
Статусом
конечной обладает, например, операция одностороннего присвоения статуса
цели:
|
(а+в)
|
(25) |
Если
цель появилась, то операция – закончилась. Теперь мы можем работать только с
целью.
Дополнение.
На
этой операции мы акцентируем внимание. Формальная запись может выглядеть так:
|
а+
|
(26) |
Мы
дополняем элемент а его противоположностью ![]() и
фиксируем его как новый блок информации, возможно, и новый счетный элемент
системы.
и
фиксируем его как новый блок информации, возможно, и новый счетный элемент
системы.
Разделение
Эта
операция логически обратная дополнению. Она позволяет разделить единый блок
информации на составляющие:
|
а |
(27) |
Мы
получаем отдельно элемент а и его противоположность ![]() .
.
Создание противоположности.
Операция
создания логической противоположности фиксирует наличие противоположности по
признаку а:
|
Ц ( |
(28) |
В
таком виде это только математическое определение противоположности. Это операция
поиска противоположности в имеющихся образцах. По действию эта операция
эквивалентна операции инверсии булевой логики.
Но
есть и другая возможность:
|
Ц ( |
(29) |
Это
уже целенаправленное создание противоположности. Созидательная операция.
Понятно,
что в итоге операции пока записан только планируемый ответ. Потому он и
заключен в скобки. Выполнение этой операции не всегда возможно. Выполнение
может быть гарантированно обеспечено на другом уровне – логического действия.
Промежуточная операция.
Логические
операции, не имеющие признаков финальной или конечной операции можно
считать промежуточными. К ним относятся все операции современной математической
логики.
Логические действия.
Ну
вот, наконец, добрались и до логических действий. Чем они отличаются от задач?
Тем,
что имеют четкий РЕЗУЛЬТАТ. Было так, а стало – так. И цель стала ближе.
Конечно,
в основе вывода результата лежит функция перехода к финальному эквиваленту. Это
и есть отличительный признак логического действия.
Таким
образом, мы можем записать общую формулу логического действия, например, с
помощью функции одностороннего присвоения, примерно так:
|
Д=(a,b,c) |
(30) |
Выражение
Д=(a,b,c), это
какие-то функциональные логические преобразования. Они заканчиваются функцией
присвоения эквивалента. Теперь это уже операция, так как мы вывели логический
ответ. Вот теперь, применением функции перехода к финальному эквиваленту, мы
присваиваем этому ответу статус результата. Этот переход и означает
окончание логического действия. Действие закончено. Получен его результат, как
единственный эквивалент. Результатом действия, как мы видим в данном случае,
стал не логический ответ, а его новый эквивалент.
Математические
и логические действия алгебры логики никто не отменял. Нам нужен результат этих
действий. Вот его мы должны фиксировать. Но необходимо расширить список
логических действий.
Какие
же логические действия мы вводим?
Дополнение
Сравнение.
Выбор
Нахождение
противоположности.
Создание
противоположности.
Копирование
Вот,
примерно в таком порядке мы их и рассмотрим.
Но,
сначала…
Дополнение.
Вот
теперь мы закончим операцию дополнения получением результата:
|
Д=а+
Д=а+
Д=а+
|
(31) |
У
нас несколько вариантов фиксирования результата.
Мы
можем зафиксировать само наличие блока информации, состоящего из элемента и его
противоположности.
Мы
можем присвоить блоку информации а ![]() и
два логически противоположных эквивалента результата. Пока мы только
зафиксируем такую возможность, а оценим это действие чуть позже…
и
два логически противоположных эквивалента результата. Пока мы только
зафиксируем такую возможность, а оценим это действие чуть позже…
Кстати,
такая запись логического действия является самым простым вариантом записи.
Она
может служить образцом для формирования логического действия из любой операции,
если вопрос касается только фиксации результата операции в виде конечного
эквивалента.
Сравнение
Логическое
действие сравнения не могло появиться на стадии логической операции в связи с
изначальной относительностью результата. Такой возможностью изначально обладает
только троичная логика. Компромиссные решения мы пока не рассматриваем.
Сравнение
может происходить в различных вариантах. Некоторые виды сравнения мы
рассмотрим…
Сравнение по эталону.
Рассмотрим
сначала вариант сравнения, когда заданы только эталон и множество для
сравнения. В этом случае результат будет выведен в оценочных показателях
относительно эталона.
Возможные
результаты для элемента в из множества элементов сравнения этого
логического действия сведены в таблицу 1.
Таблица
1.
|
Сравнение |
Критерий оценки |
Результат |
(32) |
|
?(а)=( в,c)\а| |
а>в |
а больше в |
|
|
а<в |
а меньше в |
||
|
а
|
а эквивалентно в |
||
|
а
|
а не равно в |
||
|
а=в |
а равно в |
Выбор
в этой операции мы не проводим. Нас интересуют соотношение с эталоном
определяемого признака в сравниваемых образцах, а не сами образцы. Это мы
и фиксируем в результате действия сравнения.
Далее
полученный при сравнении результат может быть использован в выборе,
например, в качестве критерия отбора или условия для проведения какой-то из
последующих операций.
Сравнение по заданному отношению к признаку эталона.
И
еще один вид сравнения. Сравнение производится по заданному критерию оценки
относительно а. И необходимо сделать заключение по
проведенному сравнению. Получить результат.
Здесь
нам придется ввести абсолютные критерии для характеристики сравнения.
Вот
они условия, по которым идет отбор:
![]() - всё, что больше эталона сравнения.
- всё, что больше эталона сравнения.
![]() - всё, что меньше эталона сравнения.
- всё, что меньше эталона сравнения.
![]() - предельные значения относительно эталона.
- предельные значения относительно эталона.
![]() - сравнимо по эквивалентности с эталоном.
- сравнимо по эквивалентности с эталоном.
Пока
достаточно…
Само
логическое действие сравнения для такого вида сравнения в общем виде может быть
записано так:
|
?(а)=(в,c,d,e,)\( |
(33) |
Действие
сравнения включает в себя набор функций и операций в каком-то порядке
следования. Это уже вполне определенная программа логических вычислений с
применением исполнительных команд.
Правила
сравнения и отбора мы задали. Вот теперь работают математические действия
сравнения. Всё, что отвечает критериям отбора, будет выведено в результат.
Эквивалентность.
Это
особый случай сравнения. Здесь необходимо вывести заключение о примерном
сходстве объектов сравнения. Видимо, по какому-то признаку. И в
логической системе должен быть заложен принцип выведения такой эквивалентности.
Полная
запись этого действия выглядит примерно так:
|
?(а)=
(А,В,С,)\( |
(34) |
Главным
в этом действии является введение знака взаимного присвоения эквивалентов
объектам А(а) и С(а) по признаку а. Это означает введение
связи между этими эквивалентами. В данном случае, это ассоциативная связь. Вот
она и является результатом действия.
Критерии
эквивалентности элементов можно найти в нечеткой логике. В её первичном
понимании и применении для относительных эквивалентов. Потому, что метод
экспертной оценки в этой логике неприменим. Не умеет логика вычислять результат
сложными математическими методами. К нечеткой логике мы еще вернемся…
Выбор.
Теперь
покажем выбор. Из двух возможных вариантов надо выбрать, ну конечно,
пока, только один:
|
В=(а,в)| |
(35) |
По
этой причине в результате стоят скобки. Сделайте выбор и поставьте нужный
ответ, уже без скобок.
Создание противоположности.
Вот
теперь мы вернемся к функции создания противоположности. Полная запись действия
создания противоположности теперь имеет примерно такой вид:
|
П(а)=а+Ц
( |
(36) |
В
состав действия включен и механизм исполнения. По эталону а мы создаем
противоположность методом дополнения. Затем проводим разделение блока на
составные части и исключаем из результата исходный эталон. Запись можно
формализовать и дальше:
|
П(а)=а+Ц
( |
(37) |
Определение противоположности.
Наверное,
мы можем сравнить имеющиеся эквиваленты по признаку противоположности
нашего оригинала:
|
?( |
(38) |
И
определить наиболее подходящий. Если у нас есть определяемые признаки
сравнения. Хотя бы математические. Но, все равно, в конечном итоге, это еще и
выбор:
|
В( |
(39) |
И
определение противоположности переходит на уровень исполнительной задачи.
Копирование.
Копирование
формально состоит из двух законченных логических действий:
|
П(а)=
а+Ц ( П(
|
(40) |
Первым
действием создается противоположность к исходному элементу а методом
дополнения и последующего разделения составляющих. В результате этого действия
мы получаем ![]() . Теперь уже с этим элементом
проводим ту же операцию получения противоположности, в результате которой
получается логическая копия исходного элемента.
. Теперь уже с этим элементом
проводим ту же операцию получения противоположности, в результате которой
получается логическая копия исходного элемента.
Логика
исполнительных решений.
Это
логика автоматических действий. Задачи, попадающие на этот уровень логики,
должны иметь отработанные решения. Выполнение решения идет в автоматическом
режиме. На этом уровне идет достижение цели, запланированной высшими уровнями
логики. И под их контролем. По этой причине иногда и нужны остановки в
выполнении задачи. Остановки запланированы. На точках окончания очередного
действия. При получении результата. Только на этом этапе можно остановить общий
ход решения и изменить алгоритм задачи. Возврат назад невозможен, но изменить
что-то еще можно.
Исполнительные задачи логики.
Это
уже решения, имеющие результат в виде достижения поставленной для задачи цели.
С
цели всё начинается, и ей же заканчивается. Исполнительные задачи логики имеют
четкий отличительный признак. Решением задачи должен стать результат достижения
цели. Достигли цели, есть результат.
И
главное: Исполнительные задачи решаются по готовому алгоритму решения. Набор
алгоритмов для решения исполнительных задач является одним из определителей
степени развития логической системы.
Исполнительные
задачи выросли из логических действий. И потому в какой-то степени повторяют
их. Но, на другом уровне. Условия функционирования логических систем
усложнились, а вместе с ними выросли до задач и вначале достаточно простые
логические действия.
Исполнительных
задач, видимо, много. Это и задачи логической системы. И задачи управления. И
задачи обработки и хранения информации. Весь тот комплекс задач, который
требует конкретного результата проведенных действий. Результат должен
соответствовать цели логической системы.
Пока
мы выберем только некоторые основные задачи, обеспечивающие работу логической
системы.
Выбор
Вот
теперь выбор идет по целевой характеристике. По достижению цели. Ориентация на
цель определяет и стратегию возможного выбора.
Задача
с применением одного из вариантов выбора:
|
Ц(а)
=[ В=(в, с,d)\(Ц(a))]| |
(41) |
Кстати,
в этой задаче, видимо, количество выбранных элементов может быть больше
одного. Мы же выбираем варианты и, отсекая невыполнимый. Это тоже
выбор, но по другим критериям. Выбор по противоположности. Но это уже другая
задача…
Создание противоположности.
Если
ввести целевую характеристику в логическое действие создания противоположности,
то мы получим уже задачу:
|
Ц(
|
(42) |
Это
запись исполнительной задачи создания противоположности. В математических
эквивалентах. И давайте посмотрим, что получилось. Мы ввели цель
получения противоположности а, и реализовали её с фиксацией результата.
Логическое действие стало решением исполнительной задачи.
Но,
это только математический эквивалент решения. За ним стоит и полный комплекс
задач управления по реальному созданию противоположности, как в логическом, так
и в физическом её понимании. И потому полная запись действий логической системы
по созданию противоположности может занять не один десяток страниц….
Определение противоположности.
Понятно,
что выбор производится и на основе сравнения элементов какого-то множества по
признаку противоположности к исходному:
|
Ц( |
(43) |
Мы
вводим целевую характеристику сравнения, критерии, в виде примерной эквивалентности,
находим наиболее подходящий. И присваиваем ему статус противоположности.
Критерий отбора предполагает проведение операции дополнения исходного элемента
элементом сравнения. Если при проведении дополнения достигается
эквивалентность, то сравнение переходит в финальную стадию - фиксации
полученного результата. Примерно подобным образом клетка создает
противоположность полученной молекуле неизвестной структуры. По кусочкам
собирает противоположности и дополняет ими открытые связи молекулы, блокируя
тем самым её возможно опасную химическую активность.
Это
выбор элемента массива по заданному целевому признаку и присвоение ему статуса
противоположности объекта целевой функции:
|
Ц( |
(44) |
Такое
действие производится, если критерий оценки не имеет определяемой
счетности, например, выбор маршрута или ограничения. По логическим факторам
отбора. Здесь определяющим фактором служит уже целевая характеристика
элемента.
Конкуренция целей.
Любая
цель системы имеет самый высокий статус и необходимость её достижения. Цели
системы не могут конкурировать между собой, потому что все цели системы –
разные. Они не компенсируются одна другой. Каждая цель сама по себе.
И
все же. Есть и баланс и конкуренция целей.
В
этом случае разговор идет не о самих целях, а о силе их влияния на логическую
систему. Вот функциональное влияние (fЦ ) любой цели на логическую систему
имеет общий характер.
И
потому, мы вправе записать, например, как баланс целей, такое выражение:
|
fЦ(А)
= fЦ(В); |
(45) |
Выражение
конкуренции целей выражает неравенство:
|
fЦ(А)
|
(46) |
И
его частные случаи:
|
fЦ(А)>fЦ(В); fЦ(А)
<fЦ(В); |
(47) |
И
вычислить характер и знак отклонения:
|
fЦ(А)
-fЦ(В)= |
(48) |
Цель,
имеющая самое большое функциональное влияние на логическую систему, становится
приоритетной целью системы. И тогда появляется возможность выбрать главную цель
по наибольшему влиянию. Задача выглядит так:
|
Ц(
|
(49) |
В
данном случае мы применили сравнение функции влияния разных целей. Нашли максимальный
показатель и по нему вывели соответствующую цель, как главную цель.
Но,
это не единственный вариант решения. Это математический путь.
Есть
еще логический. Когда сравниваются логические эквиваленты, не имеющие четкого
математического определения. Эту задачу я пока для себя не решил…
Решение исполнительных задач.
Как
я уже говорил, решение исполнительных задач идет по отработанному алгоритму
решения. С одной оговоркой. По действиям. Далее все зависит от уровня сложности
решаемой задачи. Если решение хорошо отработано и не зависит от изменения
внешних факторов, то переход от одного действия к другому происходит быстро.
Если
решение зависит от внешнего влияния, то после выполнения каждого или
почти каждого действия происходит останов решения. Почему?
Происходит
коррекция алгоритма решения и результатов. Там где это возможно, идет возврат к
уже проведенным действиям, изменение исходных данных, и новое решение. Только
после уточнения условий идет продолжение общего решения задачи.
По
этой причине вся промежуточная информация по решению задачи должна
сохраняться до окончания общего решения. Да и потом – тоже. Есть повод
для анализа и уточнения алгоритма решения…
Это
уже другой уровень логики. Логика прогнозирования. Она потребовала и других
ориентиров. До этого мы рассматривали ответы, результаты, цели, исполнительные
команды. Все это осталось. Но … в исполнительных задачах. Там, где
требовалось только одно – решать задачи и действовать в соответствии с
результатами.
Новый
уровень логики потребовал введения новых универсальных средств ориентации в
пространстве представления. Новый ориентир должен объединить все старые
ориентиры в один универсальный. С него все должно начинаться и им же заканчиваться.
Такой ориентир нашелся. Это – событие.
У
понятия событие много толкований. Мы пока ограничимся только одним.
Событие,
это зафиксированное изменение состояния.
Если
логическая система фиксирует любое изменение состояния, это – событие. И не важно,
изменение чего именно. Реальности, решения логической задачи, информации, цели
или состояния. Это всё – события. И все они имеют одинаковый начальный статус в
логике представления. Правда, потом все начинает изменяться. С события ми
происходит то же самое, что и с целями. Одни становятся главными и
определяющими, вторые уходят в тень. До поры, до времени. Третьи становятся
контрольными точками теперь уже новых логических связей, причинно-
следственных. Оказывается, что бы произошло событие А, обязательно
должно произойти событие В. И наоборот, если произошло событие В, то
произойдет и событие А. Или может произойти. События А и В оказались
связанными.
Событие
В оказалось условием для осуществления события А.
Возник
новый вид логической связи событий – условная связь. Условия, как определяющие
факторы осуществления событий быстро стали самостоятельными логическими
понятиями.
И
теперь, для любого события должны быть определены условия его совершения.
Условность
событий распространилась и на решение задачи. Это оказалось очень удобно. Здесь
сработал переход от сравнительной характеристики условий к абсолютной. Если
условие это то, что должно предшествовать или произойти одновременно, то
условность, это предполагаемый вариант решения, предшествующий реальному. Условное
решение не предполагает совершения каких-то реальных действия, это лишь прогноз
решения. Один из возможных вариантов.
Переход
от реальности решений к условности резко расширил возможности логической
системы в поиске решений по достижению поставленных целей. Но, одновременно и
заставил перейти на качественно новые виды решения логических задач. И не
только решения, но и представления этих задач. Чтобы начать решение
задачи, необходимо четко представлять саму задачу. Что это такое, есть ли
аналоги, как это понимать?
Задача
должна быть узнаваемой. Определяемой. Представляемой.
На
этом уровне решения логических задач, как мне кажется, заканчивается логика …
клетки. Переход на следующий уровень логики для клетки невозможен по
причине отсутствия у неё развитых регистраторов реальности.
А,
например, у человека, на этом уровне появилась речь, и её формальное системное
средство общения и понимание – язык, в фонетическом и лингвистическом
понимании. Только на этом уровне логики можно управлять мышцами, связками,
дыханием, мимикой.
На
этом уровне из букв складываются и пишутся слова. Тут надо просто брать,… и
делать. Формальный язык общения, это, прежде всего, набор абстрактных понятий и
правил. Для образного мышления эта задача невыполнима. Все остальные
понятия и смыслы, вкладываемые в слова и мысли, это уже потом, на уровне
образов.
Условный переход.
Обычно,
кажется, из химии мы впервые узнаем, что можно записать, например, ход
химической реакции через условие. Примерно так:
|
(Sn2 + O2 ) |
(50) |
И,
странное дело, оказывается интуитивно понятным и логичным появление значка ![]() .
Все, почти сразу понимают, что реакция идет при … нагревании.
.
Все, почти сразу понимают, что реакция идет при … нагревании.
Такая
форма записи условного перехода оказалась очень удачной и быстро стала
применяться повсеместно. Везде, кроме … логики.
Видимо,
специалисты по логике скептически оценивают логическую справедливость такой
формы записи.
И
для этого есть основания.
Ну,
действительно, возьмем и запишем условный переход от события А к событию В в
зависимости от исхода события С:
|
А
|
(51) |
С
логической точки зрения это абсурд. В качестве предполагаемого условия у нас
стоит событие. Тогда уж лучше:
|
А
|
(52) |
Что
переводится, как: Если произойдут событие А и С, то произойдет и событие В. Логическое
действие конъюнкции здесь совершенно обосновано. И логически, … и
математически, что очень немаловажно. Действие производится с одинаковыми
величинами, и ответ мы получаем … в этой же размерности – событии. Все четко и
понятно.
А
как же интуитивная логичность химической реакции?
Отметим,
что в качестве условия в этой форме записи стоит логический объект, несравнимый
с начальными объектами и конечным ответом. Нагрев. И тогда условный
переход становится логичным и понимаемым.
Но,
в логике событий, кроме событий, других логических объектов – нет.
Взяли
исходные компоненты Sn (событие) и О(событие) , произвели
их нагревание ( событие), и получили новый компонент SnO (событие).
При таком понимании запись химической реакции с нагревом в виде условного
перехода, с логической точки зрения, теряет смысл.
Математики
это уловили. И условный переход в математическом понимании выглядит примерно
так:
|
f(x2+b) |
(53) |
В
этом логическом переходе нам сообщается, что при b=0 функция y=x2+b
становится функцией y=x2. Только
при этом условии. Во всех остальных случаях первоначальная функция сохраняется.
С
точки зрения логики, как и математики, условность перехода здесь обоснована. В
условии стоит не событие, а логический ответ.
Первый
выход из логического тупика есть.
Я
могу предложить еще один.
Для
этого введем понятие – шаблон решения логической задачи.
Закодируем
схемы решений, как шаблоны с номером соответствующего рисунка. И запишем, что
схема рис. 13 у нас получает код – Ш13.
А
теперь обратимся к рис.4. Оказывается, задачу можно решать по одному шаблону,
но с разной направленностью, относительно объекта.
Понятно.
Обозначим их, как Ш14 и ![]() .
.
И
все эти шаблоны мы должны применить к решению какой-то задачи. Мы работаем в
логике событий. И задача в основе имеет – событие. Решением задачи будет получение
какого-то события с каким-то исходом, в виде логического ответа. Так мы это и
запишем:
|
Ш14(С)=ДА; |
(54) |
Таким
образом, для решения задачи, относительно события С применена схема
шаблона Ш4. Необходимый нам ответ – ДА. Но, понятно, задача может быть
решена с любым исходом…, какой получится. Нам бы надо – ДА.
Мы
получаем выражение условного логического перехода:
|
А
|
(55) |
Это
выражение говорит, что для перехода от события А к событию В надо
решить задачу относительно события С по шаблону Ш14 с получением
логического ответа ДА. Только при этом условии такой переход возможен.
Условность перехода логически и математически обоснована. И в качестве условия
стоит … событие С.
И
нам оказывается уже совершенно не важно, в системе какой логики, двоичной или
троичной, будет решаться задача и будет получен ответ. Нам важно, чтобы событие
С произошло. И тогда мы доберемся до В.
Никакой
конъюнкцией этот условный переход не записать. И величины несравнимы, и
результат … пока неизвестен.
Мы
лишь подтвердили интуитивную логичность условного перехода. А вместе с ним и
то, что логика событий имеет значительные отличия от формальной математической
логики логических ответов. От Булевой логики.
Условный
переход в логике событий занимает центральное место.
Он
объединяет условия и события.
Условия.
Пока
сформулируем это понятие примерно так: Условие – это внешний или внутренний
фактор, косвенно влияющий на ход решения логической задачи.
И
иногда, самым радикальным образом, к сожалению…
А
для логической системы, условие - это задача, требующая решения параллельно
с основной, в заданный момент времени.
Хорошо,
если условие задано простым логическим ответом, но все же, его необходимо
получить в нужное время в нужном месте.
Как
мы уже выяснили, условие в логике условных решений может быть задано или
шаблоном решения для получения заданного состояния события, или логическим
ответом, при котором задача имеет решение.
Возможно,
есть и другие виды записи условий, посмотрим.
Шаблоны.
Мы
ввели новые понятия – шаблоны. Это схемы решения задач, но за схемами реальные
решения исполнительных задач или логических действий. Выбора, сравнения,
нахождения противоположности…
С
другой стороны, это всего лишь простейшая схема, определяющая тип задачи и логику
ответов, а так же и один вид примитивов, применяемых в логике условных
решений.
В
какой-то мере, шаблоны имеют сходство с целями. Сами по себе они мало что
значат. Но в соединении с основными единицами измерения той или иной логики они
составляют значительную часть аппарата решений.
Видимо,
как и цели, шаблоны представляют собой логические объекты. И это значит, что с
ними можно так и обращаться. Они участвуют в логических функциях, операциях и
действиях, как все другие объекты. Вот, например:
|
|
(56) |
Конъюнкцией
шаблонов мы получили новый шаблон. Я не смог для себя решить, какая запись
более справедлива. Конъюнкция справедлива по соображениям логики, а сложение -
по математическим. Мы используем два простых шаблона и получаем … третий. Но,
он все так же состоит из двух шаблонов. Они могут использоваться в решении в
любом порядке, но обязательно – оба. Да, собственно, так у нас и получается.
Даже если мы выбираем оптимальный путь до цели, то все равно, у нас есть еще
одна нерешенная задачка. А мы вообще-то пойдем в путь, или так, размышляем…, из
спортивного интереса?
Этот
вопрос входит в общее решение, как обязательная часть.
Тот
самый шаблон Ш2…, и без него задача не имеет решения.
Примерно
так, из простых шаблонов и набирается сложное решение.
Мне
даже кажется, что самый распространенный в применении шаблон решений закреплен
в ДНК. Я уже говорил об этом. Основание Т отличается всех остальных оснований,
но служит логической противоположностью основанию А. Есть и вторая пара
логических противоположностей: Г – Ц. Вместе они составляют готовый
шаблон рис.7. По нему работают все модальные логики, и не только…
Действительно,
самый массовый в применении.
Да,
шаблон, это первый вид примитивов. Он так и используется. В качестве составной
части сложных конструкций.
Модели и примитивы.
От
того, что мы нашли какие-то шаблоны и сложили их в одну кучу, в общем случае,
почти ничего не изменится. Да, мы нашли простые способы представления и
объяснений того, что хотим применить. И что?
Вот
теперь начинается работа. Надо увязать простые шаблоны в единое решения. Что
это будет потом, логическое действие или сразу задача, это пока не важно.
У нас пока только голые схемы. Как в примере (55 ). Надо поставить им в
соответствие решаемые по ним задачи. Где у нас относительные сравнения, а где
абсолютные ответы. Вариантов не так много. Можно перебрать все.
Полученные
варианты, это уже не просто сумма шаблонов, это уже - модели.
Логическая
модель – типовое решение для типовых задач. Пока
мы ограничимся таким определением. Моделью можно считать решение, уже прошедшее
неоднократную проверку. Работа с моделями – отдельная часть деятельности
логической системы. Они требуют систематизации и отдельного постоянного
внимания.
И
моделирование – строительство и закрепление новых моделей, важная
часть этой работы.
Модель,
это почти всегда – задача. Потому, что она строится под конкретную цель. А
целью служит определяющий признак модели:
|
Ц
(а) = [ В=(Ш2 |
(57) |
Это
только примерное выражение выбора модели. Выбор идет по определяющему признаку а,
например, по относительному сравнению. Этим признаком обладает только
шаблон Ш4. В нем есть две оси определения. Если относительное сравнение
находится на основной оси шаблона, тогда выпадает шаблон Ш2, абсолютного
определения. Остается применить схему относительного определения на другой оси.
Так и построено большинство задач модальных логик.
А
вот если определяющим признаком станет величина объекта сравнения, то схема,
хоть и останется той же, но её применение в другой задаче закрепится как новая
модель. И только потом может объединиться с моделью относительного определения.
Если логическая система установит, что это – одно и то же…
Потому
у нас и десятки модальных логик, это те самые модели под конкретную логику,
каждая сама по себе, хоть основа модели везде одна и та же. Задачи у логик – разные.
Под
задачу и модель.
Полученная
модель снова может получить статус примитива для конструирования
других задач, более сложных, где эти логики работают одновременно.
Это
потребует новой увязки примитивов уже на этом уровне. Произошло укрупнение модели.
Возможно, что она получит и статус шаблона, если её применение станет очень
частым. Это и понятно. Функция обобщения работает на всех уровнях.
Задачи логики условных решений.
Задача условного перехода.
Выражение
условного логического перехода с условием в виде шаблона задачи и логических
ответов привела к созданию нового класса логических задач. Мы не будем
показывать знак условного перехода в виде стрелки с условием, теперь на него у
нас просто не будет места.
Вот
простейшая форма задачи:
|
|
(58) |
Конечно,
в основе задачи – цель, достижения события В. Но, это выбор шаблонов решений
для достижений событий С, D,… и т.д.
Это необходимо для решения задачи перехода от события А к событию В, при
условии, что шаблоны решений в условиях будут иметь соответствующие логические
ответы.
И
задача превращается в головоломку. Надо учесть множество влияющих факторов на
одном условном переходе. От пункта А в пункт В.
Есть
выход. Надо разбить одну задачу на кучу маленьких и решать их по отдельности…
Или
вообще не решать. Выбрать наиболее влияющие, и ограничить задачу только этими
факторами. И тогда уже выбирать приемлемый вариант.
Только
развитие органов чувств позволило логической системе сделать следующий переход.
Конечно, это развитие логики условностей. За пределы логики клетки.
На
этом уровне восприятия реальность может быть зарегистрирована в значительно больших
объемах информации, и с разных сторон. Появилось изображение, как отражение
реальности органами зрения, появились звуки, к тактильному «чувству локтя»
добавилось осязание, химический контакт стал вкусом и запахом. Все эти
виды отражения действительности необходимо было, понятно, с логической точки
зрения, привести к одному эквиваленту. Только в этом случае логическая система
получает доступ к обработке всей этой информации на общих основаниях логики. С
применением всего арсенала накопленных логических функций и решений. В одном
логическом пространстве. В нейронных сетях мозга, универсальным и скоростным
средством отображения информации – электрическим импульсом. Химическая логика
окончательно осталась на нижнем уровне, условных и исполнительных решений.
Если там еще соблюдался баланс химической и электрической логики, то на этом
уровне осталась только одна технически возможная реализация логики –
электрическая.
Логика
мозга перешагнула порог хоть и условных, но вполне конкретных моделей и
прогнозов. На уровне конкретности логических объектов. Нужен был новый
уровень решений. Отражение реальности стало многогранным, конкретность объектов
исчезла. Нет ни четкого врага, ни понятной пищи…
Все
стало отдельным. Звук врага, его запах, вид…, надо было снова связывать всё в
одно понятие. Это враг. По звуку, по виду, по запаху…
Вот
она жестокая необходимость появления логики образных решений. И такая логика
появилась. В качестве логических эквивалентов – образы. В качестве
логических ответов – эмоции или ощущения.
Образ.
Образ
– логический объект этого уровня логических решений. Все решения всех задач
идут на уровне этих эквивалентов.
Образ
одновременно сложный и простой логический объект. На этом уровне логики
логическая функция обобщения а,а,а,… ![]() А(а) была доведена до
предельного логического понимания. Образ состоит из примитивов, но и сам
становится примитивом в составе более сложного образа.
А(а) была доведена до
предельного логического понимания. Образ состоит из примитивов, но и сам
становится примитивом в составе более сложного образа.
Бесконечное
дробление образа, в котором каждый осколок – образ, привело логику к пониманию
абсолюту относительности в своей перспективе, и относительности любого
абсолюта. Сложно? А скажите, что такое – близко? Это где-то рядом, … в
миллиметрах, метрах, парсеках? Но, рядом, туточки…
Абсолютное
понятие в относительном измерении.
Переход
на относительность понятия образа позволил сравнивать несравнимое. Атом и
галактику, черное и белое…
И
мы спокойно это делаем, потому, что мы работаем с образами, а не с реальными
объектами нашего мира.
И
тем не менее, образ как объект, состоит из примитивов, которые можно собрать в
образ, а можно разобрать, и тогда каждый примитив снова станет – образом.
Каждый
штрих в рисунке, взятый отдельно – образ, но это и малая часть большого. И
потому в образе нет мелочей. Но и его сложность не бесконечна.
Если
мы говорим о зрительных образах, то, это - картинка в крупных
мазках. Только главное. Это, то главное, что выбрано из виденного в
реальности. Другого быть не может. Если дерево, то … ствол, крона, … и
всё. Как будто издалека. В общих чертах. Много таких деревьев
– лес, и теперь лес уходит в перспективу. Мы собираем образ.
А
если наоборот. Дерево. А ближе? Появляются ветви,… но пропадает цельность.
Кусок ствола в коре, ветки листья…, еще ближе, …остались только ветки и
листья, или только ствол с корой, которая уже стала морщинистой…
Это
детализация образа, но от этого он не стал фрагментарным, он оброс новыми
деталями. Мы незаметно перешли на другой образ, потом на третий,…
Образ
сохраняет постоянную видимую сложность. Логическое пространство образа требует
заполнения, для сохранения логической структуры образа. Это мозг подсмотрел у
природы. Там не бывает пустоты. При любой детализации или любой степени
обобщения.
Ту
же самую степень сложности сохраняют и образы других органов чувств. Звуковые,
вкусовые, обонятельные, тактильные…
И
все вместе, они – образ. Многогранный образ, главные свойства конкретного
физического объекта. Неповторяемый, но бесконечный в своей сложности….
Логические действия с образами.
Образ
неуничтожим, пока он представим логической системой. Пока она может
поддерживать постоянную структуру образа. И потому, все логические и многие
математические операции можно выполнять и с образами. Например:
|
О1
О1
О1/О2=О5; |
(59) |
Ну,
и т.д. …
С
другой стороны, представимость образа ограничена абсолютом. Возьмем понятие
«много», и … у каждого будет свой образ, но, ни один не будет соответствовать
действительному «много». Потому, что много – непредставимо. Как и
бесконечность, абсолютно большое и абсолютно малое, да мало ли у нас абсолютных
понятий.
На
эти случаи есть образы, которые только примерно соответствуют абсолютам, но это
– выход. Хотя, мы не понимаем этой подмены и спрашиваем: Вот если это –
бесконечность, то, что … за ней? Вопрос в вечность…
Постоянная
структура сложности образов поддерживается логической системой для очень важных
логических действий – сравнения и получения противоположности. Они
производятся в понятном для системы виде – по частям целого. По фрагментам –
примитивам. Для данного образа это примитивы, и всё, по ним можно определиться.
В этом конкретном случае. А то, что здесь - примитивы, то, где-то это - образы,
вот где-то и будем разбираться. А пока, белое на черном и черное на белом –
противоположности, хоть изображают они одно и то же. Позитив и негатив.
Вонь и аромат – образные противоположности, но и то, и другое – запахи.
Эмоции.
А
вот это – логические ответы логики образных решений. Это результат в виде
логического ответа. На уровне операций и логических действий. По этой причине
наше эмоциональное состояние так изменчиво.
Видимо
определение идет в системе нечеткой логики. Отсюда и такая богатая палитра
эмоций. Ответ ДА, видимо, означает возможность достижения поставленной цели в
задаче, а выражается в эмоциональном чувстве согласия с конечным образом
решения. Мы получаем внутреннее удовлетворение.
Ответ
НЕТ, это внутреннее несогласие, выплескивание эмоций, чувство опустошенности.
Ответ
НЕ ЗНАЮ, скорее всего, это – чувство тревоги, ожидания чего-то …
Но,
задач у логики образных решений много, они не всегда заметны, они, в
большинстве своем, в сознании не отражаются. А вот их логические ответы …
появляются, вроде бы ниоткуда, или вдруг исчезают в никуда…
Задачи логики образных решений.
Решение
задач этого уровня идет в образах. И конечный результат решения, тоже – образ.
С
математической точки зрения, любой образ, это массив информации. Для начала,
хотя бы на уровне логических объектов – фрагментов, примитивов, из которых
собран образ. С ними и можно работать. Для образа примитивы – отдельные
признаки определения. Вполне подходящий материал для работы. Для сравнения, для
получения противоположности.
И
цель – образ. Задача достижения цели выглядит вполне понятной.
Но,
логика образов еще очень мало изучена с логической точки зрения. Я могу
написать выражение целевой задачи, но …
Я
совсем не уверен в необходимости этого. Тут надо еще много понять и сделать…
Мозг,
как новый логический аппарат взаимодействия с реальностью, просто обязан был
использовать весь арсенал логических решений клетки. Как основу для
собственного развития. Мозг создан клеточной структурой по великой
необходимости. Для обеспечения и улучшения собственной жизни.
Но
улучшение общего уровня жизни всегда идет за счет … деградации функций
отдельных индивидуумов. Далее идет специализация клеток под конкретные функции
с потерей самостоятельности.
Ну,
все как у нас, хочешь жить лучше, не выделяйся и займись своим делом. Пироги –
пирожник, а сапоги – сапожник.
Новый
орган логического управления, имея в своем распоряжении весь логический арсенал
клетки, вместе с ним получил и способ управления. Через Центр. Централизованное
управление было реализовано клеткой.
Где
находится центр управления клеткой понятно. В ядре – органе логического
управления. А вот логического названия у него пока нет. Место расположения в
ядре, кажется определено, это – ядрышко. Центральное образование в относительно
большом ядре.
Мозг
тоже имеет центр управления. Но с ним картина обратная. Точное место пока не
совсем определено, а вот его логическое проявление мы все знаем точно. Это
сознание.
Центр
управления мы ассоциируем со своим Я. Если Я в сознании, то я - функционирую и
способен решать логические задачи. Я живу.
Сознание
– логическая необходимость для обеспечения решений на уровне образов. Если
образ – копия реальности, пусть и смоделированная, но …, то необходимо как-то
отличать копии от самой реальности.
Реальность,
это то, что – сейчас. В настоящий момент. Но была и вчерашняя реальность и
будет завтрашняя.
Сознание
– зона Настоящего. То, что воспринимается сознанием, это – Сейчас.
И
в этом Сейчас производятся логические решения на уровне образов. Центр
управления мозга, наше Я, все время устанавливает различные соотношения между
реальностью и логическими решениями по контролю за работой всего организма.
Понятно, задач много, надо успевать везде…
То,
что мы регистрируем в сознании, только отблески той логической деятельности и
тех решений, что проводит мозг. Если ничего существенного не происходит.
Но,
вот появилась настоящая проблема, требующая срочного решения. И тут проявляется
вся сила централизованного управления…
И
оказывается, что есть центры управления исполнительными решениями, условными и,
конечно, образными. И есть четко налаженный обмен информацией между уровнями, и
система управляющих исполнительных команд.
Не
важно, на каком уровне логических решений возникла проблема. Она тут же
оказывается на высшем уровне. В решение включается весь арсенал самостоятельной
логической системы. На всех уровнях.
И
теперь уже мы одинаково остро понимаем, что такое - Да и НЕТ, на всех уровнях
логического понимания, они быстро обретают эмоциональное и образное выражение,
и прогнозируемое продолжение…
Теперь
можно точно сказать, что любая самостоятельная логическая система начинает
решение логической задачи на самом высоком уровне решений. Это
позволяет полнее понять суть задачи. Это важно.
Потому
что, мы чаще всего получаем не задачу, а только часть данных, составляющих
задачу. Перед решением надо осознать саму задачу.
Установить
цели, понять условия решения. И сроки, отпущенные на это…
Сразу
решает задачу только логика исполнительных решений. И то, … при условии, что
задача уже точно сформулирована. Но и тут, решение идет под контролем центра
логики условных решений. Уже есть модель решения, есть и прогноз исполнения,
осталось только решать. Хотя, решать задачи практически – трудное дело. Потому,
на это и целый уровень логики выделен. Как на уровне клетки, так и на уровне
мозга.
Но
и формулирование задачи совсем не просто. И даже очень не просто. Потому в этом
и участвуют сразу два самых высоких уровня.
Формирование
задачи идет одновременно со строительством её модели. Образы и эмоции формируют
образную модель. Она сразу раскладывается на условные модели и их
компоненты.
Образ
значительно информативнее любой условной модели. И потому на один образ
появляются несколько возможных условных моделей решений. И все они начинают
проверяться на пригодность, прогнозированием. Результаты прогнозирования снова
формируются в образ. Вот что будет, если…
И
снова работает логика образов. На образ прогноза вырабатывается свой логический
ответ в виде эмоций. Да, вот этот подойдет, а вот это…, да никогда в жизни…
Но
слов еще нет, одни эмоции. Слова подберутся позже, если это необходимо…
Вот,
наконец, задача обретает вполне понимаемый образ. Это значит, что образ уже
обработан логикой условных решений, сформирована модель, есть схема решения и
прогнозируемые результаты.
Можно
считать, что задача решена. Логически.
Остался
последний этап решения – практическая реализация, на уровне исполнительных
решений. Сделать то, что мы решили.
Ну,
что же…, надо подводить итоги:
1.САМОстоятельная
и САМОразвивающаяся логическая система не имеет одной определенной
математической логики с устойчивой системой логических ответов. Это
эволюционный процесс наложения каждой новой системы логического определения на
уже имеющиеся в арсенале логической системы. В любой саморазвивающейся
логической системе представлены все виды типовых математических логик.
Переходы, от однозначной к двоичной, от двоичной к троичной, и далее, к
многозначной логике, хорошо определяются. Необходимость применения для
решения задачи соответствующей математической логики определяется применяемой
схемой.
Однозначная
логика дала ЦЕЛЬ.
Двоичная
логика установила ПРОТИВОПОЛОЖНОСТИ и предложила ВЫБОР.
Троичная
логика решила задачу СРАВНЕНИЯ. С определением СХОДСТВА и РАЗЛИЧИЙ.
Все
математические логики существуют в логической системе и определяют ход решения
любой логической задачи.
2.
Все задачи, решаемые системой логического определения, изначально ЦЕЛЕВЫЕ, и
направлены на РЕЗУЛЬТАТ. На достижение поставленной цели.
3.
Решение задачи производится на основе МОДЕЛИРОВАНИЯ ЛОГИЧЕСКОЙ КОПИИ ЗАДАЧИ по,
пусть и неполному ОРИГИНАЛУ.
3.
Логическая копия задачи формируется в виде составной схемы ЗАДАЧА –
ОТВЕТЫ. Применяемая к задаче схема определяет систему логических ответов.
Как для всей задачи, так и для её составных частей. Схема задачи строится
на основе ТИПОВЫХ схем с известными РЕЗУЛЬТАТАМИ в виде логических
ответов.
4.
Основными составляющими решения становятся: метод нахождения или создания
ЛОГИЧЕСКИХ ПРОТИВОПОЛОЖНОСТЕЙ, метод многократного применения
эквивалентности на уровне ОБОБЩЕНИЕ – ДЕТАЛИЗАЦИЯ, метод нахождения
УЗЛОВЫХ ТОЧЕК решения, и СОГЛАСОВАНИЕ ГРАНИЧНЫХ ПЕРЕХОДОВ.
5.
Результатом моделирования логической копии задачи является ОБРАЗ -
ПРОГНОЗИРУЕМАЯ МОДЕЛЬ задачи. В ней заложен и ПРОГНОЗИРУЕМЫЙ РЕЗУЛЬТАТ.
6.
ПРОГНОЗ становится РЕШЕНИЕМ, если в нем отсутствует вариационная часть. Переход
прогноза в решение является целью задачи МОДЕЛИРОВАНИЯ.
Честно
сказать, в этих выводах нет ничего, неизвестного специалистам. Может быть,
вызовет недоумение только первый пункт. А остальное…
Есть
же у нас классическая, неклассическая, формальная, математическая и нечеткая
логика, теория управления, теория автоматических систем, теория автоматов,
теория моделирования и прогнозирования, теория СИМО, теория однородных
вычислительных систем, да и кибернетика еще жива…
Всё
это есть. И все мои выводы находятся где-то в основах этих наук, может быть
даже в предисловиях к ним. Но, любая из них быстро – в ширь и глубь, каждая в
свою сторону, и ответов на свои вопросы я там так и не нашел.
Не
знаю, может быть, вопросы не те…
Заключение.
Пока
мы разбирались с логикой самостоятельных и саморазвивающихся логических систем,
коими являются все живые организмы на Земле, как-то сама собой сложилась и
систематика уровней логических решений, о которой я упоминал в начале.
Теперь
мы можем выставить логические решения по уровням сложности:
1. Базовый уровень логики. Он включает функции, операции и
логические действия.
2. Исполнительные решения. Логика типовых объектов и признаков.
3. Условные решения. Логика событий и условий.
4. Образные решения. Логика образов и эмоций.
Не
так уж сложно все это теперь выглядит. Хотя, если продолжить уточнение
систематизации уровней сложности, то картина будет уже совсем другой.
Поразительно,
что клетка довела уровень своих решений до условного, а мозг, со всеми его
преимуществами, смог подняться от клетки только на один уровень. Видимо,
сложная это дело - многогранное и полное представление сложности задач, и
нужны огромные усилия, чтобы подняться над тем, что есть, и понять, как можно
рассмотреть проблему с другой, еще неизвестной высоты.
Самостоятельная
логическая система пока даже в принципе не способна применять сложные
математические методы вычислений. Она вынуждена использовать только
отработанные простейшие типовые схемы задач и логических ответов весьма
ограниченного набора. Можно предположить, что обработка информации от наших
органов восприятия реальности идет на высочайшем уровне однородности типовых
логических схем. Только такой технический подход обеспечивает полную
однородность логического пространства мозга. Базовые приемы логики работают на
всех уровнях.
Становится
совершенно понятным, что вся информация хранится в клетках, большая часть - в
нейронах. И тогда 20-80 млрд. нейронов, каждый из которых является и
хранилищем какого-то массива информации, вот он уровень технических достижений
Природы. Можно сравнить с нашими компьютерами…
Но,
мне пока непонятно, как в эту систему укладывается саморазвитие этих
самостоятельных логических систем. На каких принципах идет рост связей и самой
системы. Тут какая-то другая математика. На других принципах и других единицах.
Надо
думать…
г.
Екатеринбург
май 2009г.
1.
Ивин А.А. Логика. http://www.vusnet.ru/biblio/archive/ivin_logik/ec3.aspx
2.
Николай Паклин. Нечеткая логика – математические
основы. BaseGroup
Labs http://www.basegroup.ru/fuzzylogic/math.htm
3.
Андрей Зубинский. Четко о нечетком. http://itc.kiev.ua/article.phtml?ID=19514&IDw=29
4.
Введение в теорию нечетких множеств.
http://fuzzyfly.chat.ru/vvedenie.htm
5.
А.Хомич.Ассоциативная машина. Представление
знаний. Целенаправленное поведение. http://neural.narod.ru/Assoc.htm
6.
Д.А.Поспелов. Десять
"горячих точек" в исследованиях по искусственному интеллекту http://www.raai.org/library/getauthor.php?author=Поспелов%20Д.А.
7.
Д.А.Поспелов, Г.С.Осипов Прикладная
семиотика http://www.raai.org/library/getauthor.php?author=Поспелов%20Д.А.
8.
А.П. Стахов КОМПЬЮТЕРЫ ФИБОНАЧЧИ И
НОВАЯ ТЕОРИЯ КОДИРОВАНИЯ: ИСТОРИЯ, ТЕОРИЯ, ПЕРСПЕКТИВЫ. 2003г. admin@goldenmuseum.com
9.
Стахов А.П. Новый тип элементарной
математики и компьютерной науки, основанных на «золотом сечении». 2003 г
10.
Стахов А.П. Коды Фибоначчи. Сайт
«Музей Гармонии и Золотого Сечения» http://www.goldenmuseum.com
11.
А.М. Хазен. О термине
действие-энтропия-информация http://www.bazaluk.com/texts/library/hazen.htm
12.
Н.П. Брусенцов Блуждание в трех
соснах (Приключения диалектики в информатике) Москва, SvR — Аргус, 2000. – 16
с. и в сборнике: «Программные системы и инструменты»,Труды ф-та ВМиК МГУ, №1,
Москва: МАКС Пресс, 2000, с.13-23
13.
Н.П.Брусенцов Заметки о троичной
цифровой технике — часть 1 http://www.computer-museum.ru/histussr/12-1.htm
14.
Н.П.БРУСЕНЦОВ ЗАМЕТКИ О ТРОИЧНОЙ
ЦИФРОВОЙ ТЕХНИКЕ — ЧАСТЬ 2. Сборник «Архитектура и программное оснащение
цифровых систем. МГУ, 1984 г. http://www.computer-museum.ru/histussr/12-2.htm
15.
Л.Керолл и троичная машина http://www.computery.ru/upgrade/numbers/2004/153/history_153.htm
16.
А. Кушнеров. Троичная цифровая
техника. Ретроспектива и современность. Университет им. Бен-Гуриона, Беэр
– Шева , Израиль. 2005г. http://314159.ru/kushnerov/kushnerov1.pdf
17.
М. Я. Эйнгорин. МАТРИЧНЫЕ
ПОСТРОЕНИЯ В Кi - ЗНАЧНОЙ ЛОГИКЕ. 2000 г. Нижний Новгород. Институт Прикладной
Физики РАН. УДК 510.644, 519.143, 519.716.32 http://www.uic.nnov.ru/~emy/mnogolog.html
18.
И.А.Палий. Введение в теорию
вероятностей: Учебное пособие. -М. :Высшая Школа, 2005. – 175 стр.
19.
Целкова Н.В., Напалков А.В. Теория
СИМО (единая многоуровневая система средств формального описания)
// «Академия Тринитаризма», М., Эл № 77-6567, публ.10554, 22.07.2003
20.
Никитин А.В. На пути к машинному
разуму. Круг третий. // «Академия Тринитаризма», М., Эл № 77-6567,
публ.12962, 14.02.2006
21.
Никитин А.В.Эволюционный путь
саморазвития искусственного интеллекта http://trinitas.ru/rus/doc/0016/001c/00161450.htm
22.
Никитин А.В., Математика счетной
логики // «Академия Тринитаризма», М., Эл № 77-6567, публ.13584,
21.07.2006 Адрес документа:
http://www.trinitas.ru/rus/doc/0016/001b/00161278.htm#_Toc140482292
23.
Никитин А.В. Математика природы. http://andrejnikitin.narod.ru/math_nature.htm
24.
В.Г.Редько Курс лекций «Эволюционная
кибернетика»: http://www.keldysh.ru/pages/BioCyber/Lectures.html
25.
Э.В. Евреинов, Ю.Г. Косарев.
Однородные универсальные вычислительные системы высокой производительности. //
Новосибирск: Наука, 1966.
26.
Алгебра логики. Справочник. http://psi-logic.narod.ru/bool/bool3.htm
27.
З. Фрейд Психология
бессознательного. М. Просвещение, 1990 г.
28.
Винер Н. Кибернетика, или управление
и связь в животном и машине. – 2-е издание. М.:Наука; Главная редакция изданий
для зарубежных стран,1983. 344 с.
29.
С.В. Петухов, Элементы матричной
генетики, натуральной генетической музыки и матрионного анализа
// «Академия Тринитаризма», М., Эл № 77-6567, публ.14719, 19.02.2008
http://trinitas.ru/rus/doc/0232/004a/02321076.htm
30.
Станимир Илиев Философские
истоки целевой логики http://www.orientalia.org/article280.html
31.
А. М. Анисов Логика
неопределенности и неопределенности во времени
http://khazarzar.skeptik.org/books/anisov03.htm#prim0
32.
Копылов Михаил Теория вероятностей
(«белые» пятна) http://physmatica.narod.ru/Articles/Mathematics/TherVer.htm
33.
Вероятностная логика. БСЭ http://bse.sci-lib.com/article004247.html
34.
Я.Я. Голота О ДВУХ “ВЫЧИСЛИТЕЛЬНЫХ
ВОЛЬНОСТЯХ”, ОГОРЧАЮЩИХ ЛОГИКА
http://www.inftech.webservis.ru/it/ii/logic/index.html
35.
Логические элементы на основе ДНК http://www.vechnayamolodost.ru/menutop/strarazfon/logicheskie_elementi_na_osnove_dnk.html