ГЛАВНАЯ СТРАНИЦА

Практика

Для начала потренируемся на простейшем примере. Научим нейросеть определять дисперсию шума. Вообще, конечно, это называется «почесать левой рукой правое ухо», потому что расчет выборочной дисперсии делается с помощью простейшей формулы. Но мы не ищем легких путей, поэтому сделаем это с помощью дифференциального уравнения и нейросети.

А заодно изучим функционал программы.

Генерация сигналов

Начнем с простого, с создания сигналов. Прежде, чем решать практические задачи, то есть работать с записями сигналов от датчиков, надо потренироваться на сигналах, созданных искусственно.

Нажмите кнопку Генерация сигналов. Откроется форма генерации.

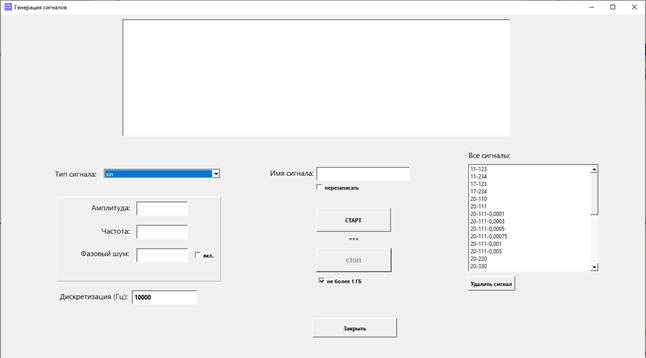
В нижней части справа – список Все сигналы. Это перечень сигналов, находящихся в папке signals. В эту папку попадают сигналы, сгенерированные программой; также можно положить туда файл с записью сигнала, полученной от внешнего источника, например, запись с датчика.

Слева находится выпадающий список Тип сигнала. Можно выбрать следующие типы:

1. sin

Это, как не трудно догадаться, синус. При его выборе открываются для заполнения поля:

– Амплитуда

– Частота

– Фазовый шум

Под фазовым шумом понимается нестабильность начальной фазы w₀ сигнала sin(w * t + w₀). Фаза w₀ ведет себя как случайный процесс с гауссовскими приращениями с дисперсией, значение которой и вводится в поле «Фазовый шум». Чтобы задействовать такой шум, нужно поставить галку «вкл.».

Введите значения 100 (амплитуда), 100 (частоота), 0.5 (фазовый шум) и поставьте галку «вкл.».

Если в настройках вашей системы Windows разделитель целой и дробной части числа – не точка, а, например, запятая – вводите запятую или поменяйте эту настройку.

Внимание! Здесь и везде, в случае, если вы введете в поле для числа недопустимые символы, значение числа будет воспринято и сохранено как число 0.

Введите имя сигнала и нажмите СТАРТ. На графике будет отображаться генерируемый сигнал, под кнопкой СТАРТ – количество сгенерированных значений и длительность в секундах; длительность рассчитывается, исходя из значения частоты дискретизации (левый нижний угол).

Нажмите СТОП. Процесс завершится, сигнал будет добавлен в список Все сигналы.

Если нужно перезаписать сигнал под таким же именем, поставьте галку «перезаписать».

Галка «не более 1 ГБ» служит для того, чтобы случайно не забить диск компьютера генерацией слишком длинного сигнала. Если она установлена, процесс завершится при достижении этого значения.

Для начала рекомендуется генерировать сигналы длиной около 10 тыс. значений – этого обычно достаточно для работы алгоритма.

Уберите галку «вкл.» и снова запусите процесс. На графике будет отображаться чистая синусоида.

2. pow(sin)

Этот сигнал вычисляется по формуле A * B ^{sin(w * t)}.

При его выборе для заполнения доступны поля:

Множитель – это A,

Основание – это B,

Частота – это w / (2 * pi).

3. Равномерный шум

Это шум с равномерным распределением на интервале, необходимо задать его мат. ожидание и дисперсию.

4. Гауссовский шум

Это шум с гауссовским распределением. Задаем мат. ожидание и дисперсию. Шум генерируется методом Бокса-Мюллера.

5. Экспоненциальный шум

Это шум с экспоненциальным распределением. Задаем параметр Лямбда.

После того, как мы поупражнялись с генерацией, можем удалить созданные вами сигналы (ставим курсор на сигнал в списке и жмем Удалить сигнал).

Сигналы, созданные разработчиком, пока не удаляйте, будем на них тренироваться.

В нашем первом обучающем примере будем использовать для обучения сигналы под именами: «гаусс. 10-10», «гаусс. 10-30»; здесь первая цифра – мат. ожидание (среднее значение) шума, вторая – его дисперсия. Для проверки будем использовать еще и сигналы с другими дисперсиями: «гаусс. 10-3» - «гаусс. 10-40».

Внимание! Если вы скачали с этого сайта облегченный архив с программой, без сигналов-примеров, для разбора первого примера нужно сгенерировать два сигнала, с именами «гаусс. 10-10», «гаусс. 10-30» (именно с такими именами, так как эти имена прописаны в «наборе для обучения» из этого примера). Это гауссовские шумы с мат. ожиданием = 10 и дисперсиями 10 и 30.

Обучающие наборы

Для обучения нейросети недостаточно одного сигнала, ведь мы хотим научить сеть различать сигналы разного типа. Поэтому необходимо создать обучающий набор.

Жмем на кнопку Наборы для обучения.

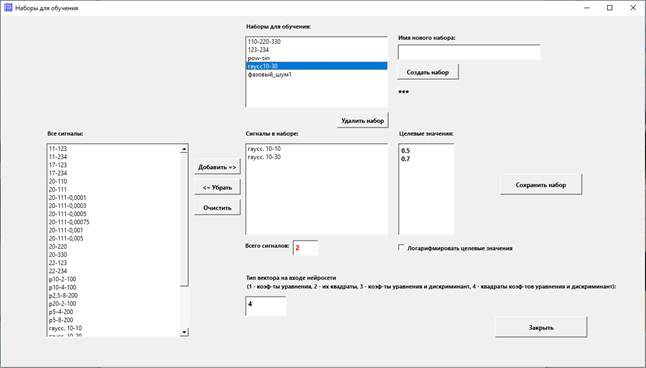
Видим на открывшейся форме:

1. Список «Наборы для обучения». Здесь перечислены ранее созданные наборы. Ставим курсор на какой-либо набор и видим в списках и полях ниже параметры этого набора.

2. «Сигналы в наборе» – список сигналов, поочередно (случайным образом) подаваемых на вход нейросети.

3. «Целевые значения». Мы будем учить сеть выдавать на выходе эти значения для соответствующих им обучающих сигналов. В этом и будет заключаться работа нейросети после обучения: подаем на вход интересующий нас сигнал, а нейросеть отвечает, например, «0.5». И мы таким образом узнаем, что сеть думает об этом сигнале. Например, она считает распознаваемый сигнал похожим на соответствующий этому значению обучающий сигнал.

4. Список «Все сигналы». Отсюда будем добавлять сигналы в наш набор.

5. Галка «Логарифмировать целевые значения».

На каждой итерации процесса обучения нейросеть сравнивает рассчитанное ею значение с целевым и рассчитывает ошибку. При установленной галке сравниваться будут не сами значения, а числа, полученные по формуле log(1 + x). Иногда так удобнее.

6. Поле «Тип вектора на входе нейросети».

Вспомним, что вектор на входе сети формируется из подогнанных на данном шаге коэффициентов уравнения, имеющего вид:

C₀ * X'' + (C₁ + C₂ * t + ... + C_n+1 * tⁿ) * X = 0.

В простейшем случае можно подать на вход вектор (C₀, C₁, ..., C_n+1), имеющий длину n + 2, где n – степень многочлена. Если мы хотим так сделать, ставим в поле цифру 1.

Часто лучший результат получается, если вместо к-тов C_i подавать их квадраты. В этом случае ставим в поле цифру 2.

Важной характеристикой многочлена является его дискриминант. Как известно, при формировании обучающего вектора важно использовать максимально информативные характеристики исследуемого объекта. Практика показывает, что дискриминант является такой характеристикой.

Мало кто знает (кроме профессиональных математиков), что дискриминант можно посчитать не только для второй степени, но и для других. Известны формулы для 2-й, 3-й и 4-й степеней. Для более высоких степеней есть формулы для дискриминанта, использующие корни (а их мы не знаем). Поэтому, внимание: если мы будем использовать многочлены выше 4-й степени, дискриминант будет считаться по формуле для 4-й степени; в этом есть смысл только тогда, когда к-ты при степенях > 4 очень малы.

Итак, для использования вектора типа (C₀, C₁, ..., C_n+1, дискриминант) ставим цифру 3, для использования вектора типа «квадраты C_i и дискриминант» – ставим цифру 4.

Примечание: на самом деле, длина вектора может быть установлена больше или меньше, чем мы только что описали, разберемся с этим, когда будем работать с установками под кнопкой Нейросеть.

Но, как бы то ни было, здесь (в описании набора) мы заказываем использование коэффициентов или их квадратов, а также указываем, будет ли обязательно использоваться дискриминант.

Создание нового набора

1. Введите имя нового набора в одноименное поле. Нажмите Создать набор.

2. Добавьте сигналы из списка Все сигналы в список Сигналы в наборе (выделяем сигнал и жмем кнопку).

3. Напротив каждого из задействованных сигналов в поле Целевые значения введите такое значение. Мы будем обучать нейросеть выдавать такие значения в качестве реакции на сигналы, похожие на сигналы в обучающем наборе.

Рекомендуем ставить небольшие целевые значения, лучше – доли единицы.

Галку «Логарифмировать целевые значения» пока лучше не трогать – это «на любителя».

4. Заполните поле Тип вектора на входе нейросети.

5. Нажмите кнопку Сохранить набор.

Внимание! Максимальное количество сигналов в наборе – 10 штук!

Корректировка имеющегося набора

1. Поставьте курсор в списке на один из имеющихся наборов для обучения.

2. Измените параметры набора.

3. Нажмите кнопку Сохранить набор.

Примечание: здесь и в других формах поля с красным шрифтом недоступны для корректирования.

Для нашего обучающего примера создан набор под именем «гаусс10-30», содержащий сигналы «гаусс. 10-10» и «гаусс. 10-30» и соответствующие им целевые значения 0.5 и 0.7.

Задание параметров алгоритма происходит под кнопками Подготовка, Уравнение и Нейросеть на правой панели главной формы.

Установите курсор на настройку «set_», будем корректировать ее параметры.

Предварительная обработка данных («Подготовка»)

Нажмите на кнопку Подготовка.

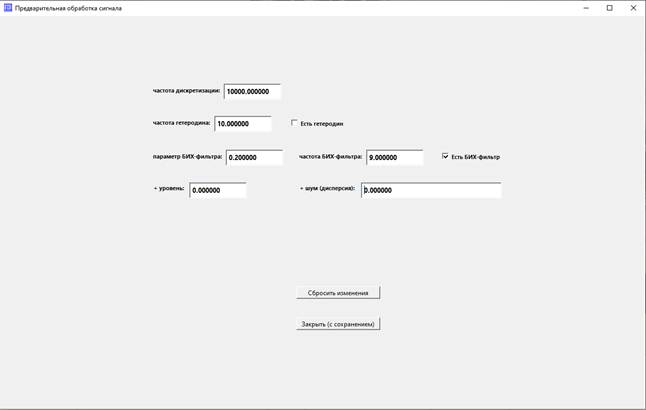
Первое, что нужно отметить – это необходимость задать частоту дискретизации сигналов из обучающего набора. Имеется в виду, что все эти сигналы должны иметь одинаковую частоту дискретизации.

Если сигналы генерировались из данной программы, значит, мы задавали эту частоту при генерации и должны ее помнить. Если это сигналы «со стороны», значит, мы должны ее знать, или хотя бы знать, что все такие сигналы регистрировались с одинаковой частотой.

Про гетеродин и узкополосный фильтр (здесь – БИХ-фильтр) я говорил в разделе «Описание нейросети». Чтобы задействовать гетеродин или фильтр, поставьте соответствующую галку.

Поле «+ уровень»: к значениям сигналов прибавляется введенное в поле число.

Поле «+ шум (дисперсия)»: к значениям сигналов добавляется гауссовский шум с нулевым средним и дисперсией, введенной в это поле.

Добавление шума на этапе предварительной обработки часто помогает в борьбе с переобучением сети. Особенно, если наш обучающий набор не отличается разнообразием.

Закрытие формы (кнопкой или крестиком) приводит к сохранению введенных данных. Если вы ввели что-то не то и хотите вернуться к предыдущему варианту, нажмите кнопку «Сбросить изменения».

Установим значения:

частота дискретизации = 10000 (т.к. все сигналы были сгенерированы с такой частотой),

частота гетеродина – любая, галку не ставим,

параметр БИХ-фильтра = 0.2, частота БИХ-фильтра = 9.0, ставим галку,

уровень и шум делаем нулевые.

Параметры уравнения

Нажмите кнопку Уравнение.

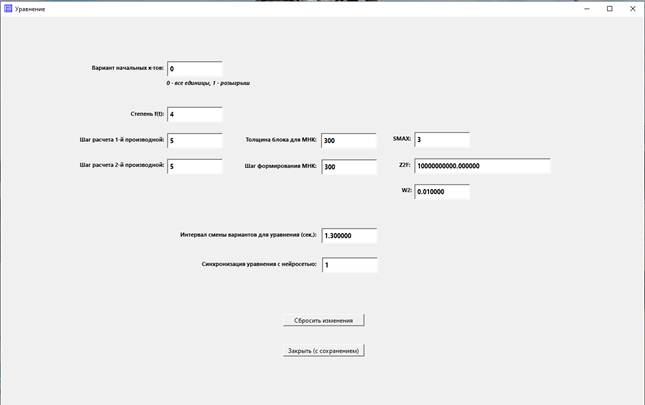
Поле «Вариант начальных к-тов»

Подгонка коэффициентов уравнения происходит путем их последовательной корректировки. Предлагается два варианта: все единицы и случайное присвоение начальным коэффициентам значений 1 или 2. Со вторым вариантом лучше не экспериментировать раньше времени, так как в этом случае возникает слишком много вариантов результата подгонки, нейросеть будет обучаться слишком долго.

Для 1-го варианта в это поле вводится число 0, для второго – число 1.

Введем значение 0.

Поле «Степень f(t)»

Это степень многочлена, входящего в наше уравнение. То есть, если задать степень 4, то будут подгоняться коэффициенты уравнения:

C₀ * X'' + (C₁ + C₂ * t + C₃ * t² + C₄ * t³ + C₅ * t⁴) * X = 0, где X – сигнал.

Введем в это поле значение 4.

Поля «Шаг расчета 1-й производной» и «Шаг расчета 2-й производной»

В уравнении присутствует 2-я производная сигнала (X''). При чтобы ее рассчитать, сначала нужно рассчитать 1-ю производную. Можно считать эти производные с шагом 1, то есть делить разность двух соседних отсчетов сигнала на период дискретизации; но обычно это неразумно, так как присутствующий в сигнале шум будет портить производную.

Поэтому введем в эти поля значения 5.

Поле «Толщина блока для МНК»

Первая стадия алгоритма подгонки коэффициентов состоит в преобразовании прямоугольной матрицы системы уравнений в квадратную методом МНК.

Наша система уравнений на очередном шаге выглядит следующим образом. После получения N значений сигнала имеем N уравнений, каждое из которых содержит 6 переменных: C₀ ... C₅ . После преобразования МНК получаем матрицу размером 6x6. Число, которое надо ввести в поле – это и есть N.

Введем значение 300.

Поле «Шаг формирования МНК»

Формировать нашу систему уравнений можно с любым шагом. Например, можно строить ее сначала для моментов времени t₀, ..., t₂₉₉, затем – для моментов t₁, ..., t₃₀₀ (шаг = 1), то есть в следующую систему попадут почти те же данные, что и в предыдущую.

Введем в поле значение 300. То есть каждая следующая матрица будет содержать только новые данные. Это не всегда лучший вариант, но пока сделаем так.

Поле «SMAX»

Этот параметр (натуральное число) предназначен для настройки проекционного алгоритма, с помощью которого находятся приближенные значения системы линейных уравнений, то есть к-ты C_i.

Если это число велико (>3), решение нестабильно. Это хорошо, если процесс нестабилен и требуется нащупать потенциальную яму в пространстве решений. Но, как правило, это плохо, так как не удается нащупать лучшее решение.

Поэтому рекомендуется задавать значения SMAX = 2 или SMAX = 3.

Введем значение SMAX = 3.

Поле «Z2F»

Этот параметр (положительное действительное число) имеет то же предназначение. В отличие от SMAX, для поиска стабильного решения вводим значение побольше, и наоборот.

Здесь уже больше простор для творчества, параметр можно варьировать на порядки.

Введем значение Z2F = 10000000000.0.

Поле «W2»

Этот параметр имеет следующий смысл. Мы построили систему уравнений, например, из 300 строк. Преобразовали ее методом МНК (то есть домножили на транспонированную матрицу системы), нашли приближенные решения.

Получили еще 300 строк. Опять домножили на транспонированную матрицу. Но наш алгоритм снабжен усреднением: проекционный алгоритм будет применен не к новой системе МНК, а к усредненной между новой и предыдущей с помощью к-та W2.

Чем больше значение W2, тем сильнее усреднение.

Введем значение W2 = 0.01.

Поле «Интервал смены вариантов для уравнения (сек.)»

Вспомним, что на вход алгоритма случайным образом подаются отрезки разных сигналов. После подачи несколько отрезков одного сигнала (то есть одного варианта) надо переключиться на другой сигнал. Данный параметр указывает, через какой промежуток времени надо делать переключение. Имеется в виду, конечно, физическое время сигнала, а не время расчета.

Введем в поле значение 1.3.

Поле «Синхронизация уравнения с нейросетью»

Если мы считаем, что для подгонки коэффициентов С_i требуется несколько итераций, можно отправлять решения на нейросеть не каждый раз. Целое положительное число в данном поле указывает, сколько раз нужно уточнять коэффициенты уравнения перед их отправкой на вход сети.

Как правило, для более качественной подгонки выгоднее увеличивать количество уравнений.

Введем в поле значение 1.

Параметры нейросети

Нажмите кнопку Нейросеть.

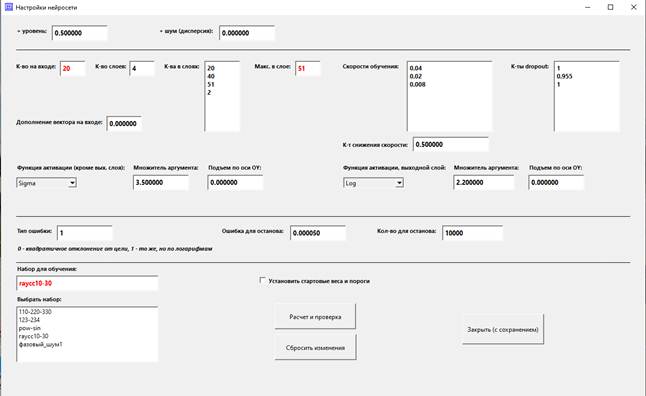
Поля «+ уровень» и «+ шум (дисперсия)»

Эти поля не следует путать с такими же в предварительной подготовке данных. В настройках нейросети добавление уровня и гауссовский шум применяются уже к вектору на входе нейросети. То есть видоизменяются составляющие вектора: в зависимости от того, какой выбран тип вектора на входе нейросети, составляющими могут быть рассчитанные коэффициенты уравнения или их квадраты, а также дискриминант.

Причем в поле «+ шум (дисперсия)» вводится не дисперсия этого шума, а множитель для ее вычисления. Сама дисперсия вычисляется по формуле [множитель] * [i-я составляющая вектора]. Так сделано потому, что, как правило, составляющие вектора различаются на порядки.

Значение уровня применяется и при обучении, и при распознавании. Шум накладывается только при обучении, так как его смысл – в том, чтобы разнообразить обучающую выборку; при распознавании он будет только портить результат.

Введем значения:

уровень = 0.5,

шум = 0.0

и выберем, чтобы не забыть, обучающий набор (слева внизу): «гаусс10-30» (кликнуть на него в списке).

Теперь – самый интересны блок, архитектура сети.

Поле «Кол-во слоев»

Мы решаем простую задачу и вряд ли здесь требуется много слоев. Но мы не ищем легких путей и введем значение 4.

Список «Кол-ва в слоях»

Здесь надо ввести 4 числа – количества нейронов в каждом из слоев. Порядок ввода: удаляем старые значения, вводим первое на первой строке, жмем Enter, вводим следующее и т.д.

После ввода имеет смысл нажать на кнопку Расчет и проверка. Если сделана ошибка, в середине формы появится сообщение об ошибке, например, «Ошибка в количествах узлов».

Если ошибки нет, появится сообщение «OK!» и будут рассчитаны значения в полях «К-во на входе» и «Макс. в слое».

Введем значения:

20

40

51

2

и нажмем на кнопку.

Следует объяснить, почему для входного слоя выбрано значение 20.

Выше была задана степень уравнения = 4. Это значит, что в уравнении 6 слагаемых: вторая производная X'' и 5 членов с X (0-я, 1-я, ..., 4-я степени t). Кроме того, в установках нашего Набора мы указали, что будет использоваться дискриминант – это еще один член вектора на входе. Значит, логично установить значение 7. Но можно выбрать и другое число. Я подобрал число 20, хотя при 7-ке на входе тоже работает, но хуже.

Что будет, если задать меньшее (чем 7) количества нейронов на входном слое? В этом случае к-тах при членах со старшими степенями не будут использоваться нейросетью. Вряд ли в этом есть смысл, хотя – кто знает, может быть, есть задачи, когда такой вариант хорошо работает.

И противоположный случай: можно задать большее к-во входных нейронов, чем имеется чисел для формирования обучающего вектора. Тогда «лишние» члены вектора будут заполнены некоторой константой. Для ее задания есть поле:

Дополнение вектора на входе

Введем в это поле 0.0.

Список «Скорости обучения»

На разных слоях можно задавать разные скорости обучения. Это действительные положительные числа из интервала (0, 1].

С помощью этих коэффициентов корректируются веса и пороги сети на связях между слоями, поэтому их на 1 шт. меньше, чем число слоев.

Введем значения:

0.04

0.02

0.008

Разделитель целой и дробной части должен быть таким, как установлено в настройках Windows; обычно это точка.

Обычно имеет смысл делать разные значения скорости обучения на разных слоях.

Поле «К-т снижения скорости»

Процесс обучения завершается, когда значение функционала ошибки E определенное количество раз оказывается меньше наперед заданного значения Em.

Предположим, ошибка в первый раз оказалась меньше заданной. Вполне возможно, что сеть уже хорошо обучена, но на следующих шагах продолжается коррекция весов и порогов, что может не улучшить, а испортить правильную настройку сети.

Поэтому при достижении значения Em делаются 2 вещи:

1. Выключается алгоритм Dropout;

2. Снижается скорость обучения.

Для реализации 2-го пункта введен коэффициент снижения скорости. При E < Em скорости обучения каждом слое умножается на этот коэффициент. Если ошибка на одном из следующих шагов опять становится большой (E >= Em), значение скорости обучения восстанавливается (и включается алгоритм Dropout).

Введем в это поле значение 0.5.

Задание функций активации

Реализован распространенный подход: на всех слоях, кроме выходного, задается одна функция активации, на выходном есть возможность применить другую функцию.

Функции параметризованы. После выбора функции в поле «Множитель аргумента» вводится коэффициент, на который умножается аргумент функции, в поле «Подъем по оси OY» – аддитивный коэфффициент.

В результате стандартная функция активации f(x) превращается в f(a*x)+b.

Выберем функции и параметры для них:

Функция активации (кроме вых. слоя) = Sigma

Множитель аргумента = 3.5

Подъем по оси OY = 0.0

Функция активации, выходной слой = Log

Множитель аргумента = 2.2

Подъем по оси OY = 0.0

Поле «Тип ошибки»

Здесь задается функционал ошибки, вычисляемой на каждой итерации обучения сети. Величина ошибки влияет на результат, когда E < Em и алгоритм отсчитывает число итераций с таким исходом.

Введем в это поле число 1, то есть признак квадратов логарифмированных отклонений.

Поле «Ошибка для останова»

Это пороговое значение ошибки (Em), при достижении которого (E < Em) определенное количество раз процесс обучения заканчивается.

Введем в это поле число 0.000050.

Поле «Кол-во для останова»

Это количество итераций обучения с ошибкой E < Em, после которого обучение завершается.

Введем в это поле число 10000.

Галка «Установить стартовые веса и пороги»

Напомним, что прежде, чем задавать параметры алгоритма на формах Подготовка, Уравнение и Нейросеть, мы установили курсор на одну из настроек (то есть нейросетей) в окне «Настройки сети». То есть мы создаем новую нейросеть на базе существующей.

Все введенные параметры хранятся в файлах этой настройки. Там же хранятся и результаты обучения: веса и пороги нейросети.

Если не устанавливать галку «Установить стартовые веса и пороги», там останутся веса и пороги, унаследованные от нейросети, принятой за базовую. Это может привести к плохому результату, и вот почему. Предположим, мы не удовлетворены предыдущим результатом обучения и решили немного поменять один из параметров. Если не сбрасывать рассчитанные веса/пороги, при старте обучения начнется их коррекция, и она может оказаться недостаточно сильной, чтобы «перескочить» на правильное решение.

Поэтому, если мы только приступаем к обучению, надо сбросить рассчитанные значения (поставить галку). Если же мы хотим дообучить нейросеть, надо убрать галку.

При изменении значений в списке «К-ва в слоях» галка устанавливается принудительно и убрать ее нельзя, т.к. количество весов и порогов изменяется и предыдущие веса и пороги теряют смысл.

Поставим галку «Установить стартовые веса и пороги».

Обучение

Проверим, что в окне Настройки сети выбрана настройка, параметры которой мы только что задавали ("set_"). В окно Настройка-результат введем имя новой настройки, которая образуется в результате обучения на базе настройки "set_". Например "set_gauss_1". Поставим галку Сохранить результат – при остановке процесса обучения результат будет сохранен в "set_gauss_1".

Запускаем процесс нажатием на кнопку Старт. Начнется чтение из файлов, перечисленных в Наборе для обучения. Будут отображаться графики участков записей, выхваченных таймером.

Так как установлена галка Уравнение (внизу экрана, под словом Включить), на основе загружаемых данных будут составляться и решаться уравнения. Подождем секунд 10 или больше, чтобы алгоритм нащупал более-менее приемлемые решения. Затем поставим галку Нейросеть.

Теперь решения уравнений начали использоваться для формирования обучающих наборов, нейросеть начала обучаться.

Ошибка (первое число в окне с цифрами) при удачном ходе обучения снижается. В настройках мы задавали ошибку и количество для останова. Как только этот критерий сработает, обучение остановится, внизу формы появится сообщение "OK".

Если остановка долго не происходит, а значение ошибки «гуляет» (то падает, то опять растет) – значит, испытание оказалось неудачным. Долго ждать завершения нет смысла, так как долгое обучение нейросети обычно приводит к ее переобучению. Поэтому надо нажать кнопку Сброс. После этого еще раз повторить запуск процесса. Если все попытки обучения оказываются неудачными, надо изменять настройки.

Если мы задали слишком жесткий критерий останова (ошибка/количество), но видим, что в процессе обучения ошибка стала маленькой и держится на этом уровне, можно нажать кнопку Стоп. При таком завершении процесса результат будет сохранен. Кнопка Стоп бывает активной в процессе обучения, если установлены галки Нейросеть и Сохранить результат.

При наших настройках завершение обучения, скорее всего, произойдет с первой или второй попытки.

Анализ результата обучения

Итак, мы обучили нейросеть, теперь надо проверить, как она работает.

Выбираем в Настройках сети появившуюся там настройку "set_gauss_1" (ставим на нее курсор).

Чтобы оценить качество распознавания, надо подавать на нейросеть разные сигналы. Для этого нажимаем на кнопку Установки.

На открывшейся форме в списке слева выбираем курсором сигнал для идентификации, «гаусс. 10-10». Это один из двух сигналов, участвовавших в обучении, следовательно, он должен хорошо распознаваться.

Снимаем галку «Выбрать сигнал для идентификации/модельный», чтобы выбрать модельный сигнал; выбираем курсором тоже «гаусс. 10-10». Это нужно для того, чтобы видеть, каково целевое значение.

Закрываем форму.

Нажимаем кнопку Распознать и ставим галку Нейросеть.

В окне слева видим следующее:

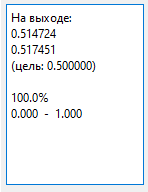
(Внимание! Скорее всего, у вас с первого захода не получится такой хороший результат. Что делать в случае менее качественного результата, разберем далее, в теме Дообучение. А пока можно поставить курсор на получившуюся у меня настройку "set_gauss" и нажать Распознать + галка Нейросеть)

Итак, мы видим результат, как на картинке выше.

Это означает, что нейросеть, читая сигнал «гаусс. 10-10», распознает его как 0.514724/0.517451 (у меня получились такие значения, у вас будут немного другие).

Почему их два? Потому что на выходном слое у нас 2 нейрона. Целевое значение для каждого вектора – одно, поэтому целевой вектор – двумерный, состоящий из двух одинаковых чисел, в данном случае это 0.5.

Такая схема непривычна для знакомых с нейросетями, но сделано так. Эта идеология является компромиссной между нейросетями со скалярным выходом и с векторным выходом.

В общем, оба числа должны быть близки к целевому значению.

Нажмем кнопку Стоп.

Информация «100% / 0.000 – 1.000» показывает долю попаданий всех членов выходного вектора (здесь – двух) в заданный интервал (0.000, 1.000).

Под кнопкой Установки можно задать несколько интервалов для сбора статистики. Иногда такая статистика помогает. В нашем случае можно задать, например, интервалы (0.4, 0.6) и (0.6, 0.8):

Протестируем распознавание другого сигнала из набора. В Установках выберем в качестве сигнала для идентификации и модельного сигнала «гаусс. 10-30».

Закроем форму и запустим распознавание: Распознать + галка Нейросеть.

У меня получилось так:

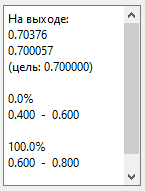
То есть второй сигнал тоже распознается. Нажмем Стоп.

Теперь мы можем выбрать любой сигнал и спросить нейросеть, на что он больше похож, на сигнал с дисперсией 10 или на сигнал с дисперсией 30? Если ответ будет близок к 0.5, это означает ответ «похоже на дисперсию 10», если близок к 0.7 - «похоже на дисперсию 30».

Выберем в Установках сигнал «гаусс. 10-3» (сгенерированный с мат. ожиданием 10 и дисперсией 3) и распознаем его.

У меня получилось так:

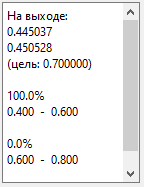
То есть нейросеть говорит: «больше похоже на дисперсию 10, но, наверное, дисперсия меньше».

Для сигнала «гаусс. 10-20» (дисп. = 20):

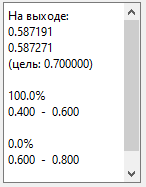
То есть нейросеть говорит: «возможно, дисперсия где-то в интервале между 10 и 30», так как 0.587 лежит между 0.5 и 0.7.

Для сигнала «гаусс. 10-40» (дисп. = 40):

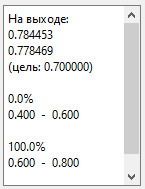
То есть нейросеть говорит: «возможно, дисперсия более 30» (т.к. числа 0.784 и 0.778 > 0.7).

Надо заметить, что нейросеть «не обязана» давать хороший результат на сигналах, далеких от использованных при обучении. Сеть можно считать обученной, если она распознает хотя бы сигналы, близкие к обучающим.

Тот факт, что сеть правильно анализирует сигналы с дисперсиями 3, 20 и 40 – это «приятный бонус», который иногда случается. Из этого можно сделать вывод, что мы подобрали подходящую архитектуру сети.

Посмотрим теперь, какова будет реакция на сигналы с шумами с равномерным и экспоненциальным распределением, с дисперсией 10, как у одного из обучающих сигналов.

Выберем для распознавания «равн. 10-10». Для порядка в качестве модельного выберем "гаусс. 10-10".

Результат:

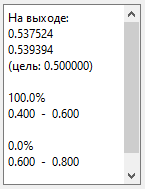
То есть нейросеть говорит: «дисперсия близка к 10». То есть ей оказалось все равно, равномерное это распределение или гауссовское.

Теперь выберем для распознавания «эксп. 0.316 (10)». Это экспоненциальный шум с параметром лямбда = 0.316, при котором дисперсия равна 10.014.

Результат:

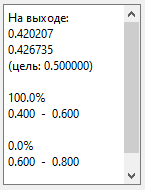
Как видим, с экспоненциальным шумом сеть, обученная на шуме гауссовском, работает хуже. То есть если перед нами стоит задача определять дисперсию сигналов с экспоненциальным шумом, то и обучать сеть лучше на таких сигналах.

Дообучение

С большой вероятностью у вас результаты обучения оказались хуже. Значит, надо заняться дообучением получившейся у вас настройки "set_gauss_1".

Выберем ее курсором.

Ужесточим критерий останова под кнопкой Нейросеть: сделаем Ошибка для останова = 0.000001, Кол-во для останова = 100000.

Уменьшим до минимума снижение скорости обучения. Это значит, что при первом достижении значения ошибки 0.000001 будет сделано 100000 итераций с минимальной коррекцией весов и порогов. Дело в том, что часто сильная коррекция на последних итерациях приводит к ухудшению результата, а мы хотим получить стойкий результат.

Итак, поставим К-т снижения скорости = 0.000001.

Введем в поле Настройка-результат новое имя, например, "set_gauss_2". Поставим галку Сохранить результат.

Нажмем Старт, сосчитаем до десяти и включим галку Нейросеть.

Далее – как всегда: либо дождемся автоматической остановки обучения, либо, увидев стабильно маленькую ошибку, нажмем Стоп.

Испытаем получившийся результат: ставим курсор в списке настроек на "set_gauss_2" и работаем с панелью Распознавание.

Если результаты дообучения не удовлетворяют, начинаем все с начала: работаем с настройкой "set_", сохраняя результат в "set_gauss_1", потом дообучаем "set_gauss_1" в "set_gauss_2".

Еще рекомендации по дообучению.

1. Часто помогает изменение целевых значений. Идем в Наборы для обучения, выбираем наш набор ("гаусс10-30") и меняем, например, 0.7 на 0.8 или еще на какое-то число.

2. Если один из векторов распознается плохо, можно его задвоить:

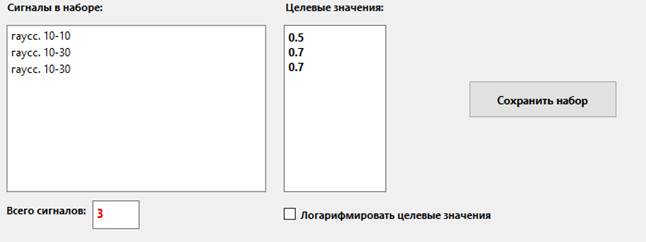
(не забывайте нажимать кнопку Сохранить набор)

Таким образом, сигнал "гаусс. 10-30" будет подаваться в 2 раза чаще, чем "гаусс. 10-10". Вообще, любой любой сигнал подается на вход сети во столько раз чаще другого, во сколько раз чаще он упоминается в наборе.

3. Ну и, конечно, можно корректировать архитектуру сети и любые другие настройки под кнопками Подготовка, Уравнение и Нейросеть.