Д.С.Клещев

О формально разрешимой системе скрытых аксиом

Principia Mathematica

A savage Python lives in the Forest

Резюме статьи

Математики-пифагорейцы допустили логическую ошибку в доказательстве теоремы о несоизмеримости стороны и диагонали квадрата. В современной математике эта ошибка привела к появлению противоречивых теорий и концептуальному кризису математической науки. В статье «О формально разрешимой системе скрытых аксиом Principia Mathematica» содержится решение данной проблемы.

Ключевые слова: история математики, аксиоматическая теория, теория чисел, теорема Г.Кантора и возражение А.Зенкина, конструктивная математика.

A summary of paper

The antique thinkers have allowed a logical mistake in the theorem of incommensurability between the sides and the diagonal of a Mono-square. Having moved for the modern mathematics, this mistake has led to multiple contradictions in the foundations of the mathematical science. The paper "On Formally Decidable System of The Latent Axioms Principia Mathematica" contains the decision given problems.

Keywords: axiomatic theory, theory of numbers, G.Cantor's theorem and A.Zenkin's protest, constructive mathematics.

100_7889 Информация об авторе

Образование: Уральский госуниверситет им. А.М.Горького, исторический факультет. Адрес: 624603, Свердловская обл., г.Алапаевск, ул.Революции, 4. E-mail: nirvansky@mail.ru

About the author

Education: Ural State University (in 2002). Address: RUSSIA,

624603, Sverdlovsk area, Alapaevsk, street of Revolution, 4. E-mail: nirvansky@mail.ru

ipse dixit

По легенде открытие иррациональных чисел связано с именем Пифагора или с одним из его учеников, который, рассматривая квадрат со стороной, равной единице, обнаружил явление несоизмеримости стороны и диагонали квадрата. Если мы взглянем на современную теорему, доказывающую иррациональность √2, то обнаружим, что в ее основе лежит все та же теорема несоизмеримости, появившаяся более двух тысяч лет назад благодаря Пифагорейской школе. Рассмотрим доказательство этой теоремы методом «четных и нечетных», которое с небольшими изменениями публикуется во всех учебных пособиях.

(I) Теорема: не существует рационального числа, квадрат которого равен 2.

Доказательство. Предположим, что существует рациональное число m/n, квадрат которого равен 2: (m/n)² = 2. Если целые числа m и n имеют общие множители, то дробь m/n можно сократить, поэтому мы в праве сразу предположить, что данная дробь несократима. Из условия (m/n)² = 2 следует, что m² = 2n².

Поскольку число 2n² четно, то и число m² тоже должно быть четным. Тогда четным будет и число m. Таким образом, число m=2k, где k – целое число. Подставляя 2k в формулу m² = 2n², получаем: 4k² =2n², откуда n² = 2k². В таком случае число n² будет четным; но тогда будет четным и число n. Выходит, что числа m и n четные, что противоречит тому, что дробь m/n несократима. Следовательно, исходное предположение о существовании дроби m/n, удовлетворяющей условию (m/n)² = 2, неверно. Таким образом, среди всех рациональных чисел нет такого, квадрат которого был бы равен 2. Поэтому решением уравнения (m/n)² = 2 является непериодическая десятичная дробь…

Очевидно, такое доказательство не удовлетворяет элементарным правилам логики, поскольку число n в теореме равно стороне квадрата, то есть единице, числу нечетному (!), а число m в теореме равно бесконечной десятичной дроби 1,4142…, которая, как и любая другая дробь, не может быть ни четным, ни нечетным числом. Сама постановка вопроса о поиске некоего отношения целых чисел m/n методом «четных и нечетных» является в данном случае некорректной манипуляцией или argumentum ad ignorantiam (с лат. «аргумент к незнанию»). Для того, чтобы искать отношение m/n, необходимо воспользоваться правилами перевода десятичных дробей в обыкновенные, о которых пифагорейцы не знали и знать не могли.

Ссылаясь на непререкаемый авторитет имени Пифагора, математики-пифагорейцы Феодор, Теэтет и Архит создали в IV веке до н.э. теорию несоизмеримости нецелых корней. Любая критика их трудов жестко подавлялась. Платон, как известно, за отрицание атомистами теории несоизмеримости сжигал труды Демокрита.[1] По той же причине, судя по всему, был изгнан из Южной Италии, а затем из Афин, Евдокс Книдский, создатель теории пропорций (от греч. άνάλογος, «соизмеримый», «согласный»). Так почему же теорема (I), несмотря на всю абсурдность своего «доказательства», признавалась пифагорейцами истинной? Прежде всего, потому, что античным математикам не были известны десятичные дроби, которые получили широкое распространение только в XVI веке н.э. Кроме того, в пифагорейской арифметике вообще не использовались дроби так, как мы их себе представляем. Поскольку важнейшей из всех пифагорейских аксиом являлась Аксиома Неделимости Единицы. Другой характерной для пифагорейцев аксиомой, имевшей математическое и религиозно-философское значение, была Аксиома Четно-Нечетности Единицы.[2]

В рамках такой Пифагорейской Системы Аксиом доказательство теоремы (I), в самом деле, могло быть признано непротиворечивым. Однако сомнения в справедливости теории несоизмеримости возникали. Многими античными философами утверждалась возможность бесконечной делимости величин и свободно становящейся потенциальной бесконечности (τό άπειρον). Из учения Евдокса (V книга «Элементов» Евклида)[3] следовало, что величины будут находиться в некотором отношении между собой, даже если они окажутся меньше единицы (например, 1 > √2 / 2). Поэтому в III веке до н.э. античная математика переживала серьезный методологический раскол.

Примирить традиции пифагорейцев с представлениями Евдокса удалось Аристотелю, который, признавал пифагорейскую Аксиому Неделимости Единицы и, в то же время, был первым, кто на основании определений Евдокса изрек знаменитое infinitum actu non datur (лат. «бесконечность не задана актуально). Совмещение противоречащих друг другу концепций было достигнуто путем введения в основания математики фундаментальной Аксиомы Разделения Геометрии и Арифметики: «Для числа имеется предел в направлении к наименьшему, а в направлении к большему оно всегда превосходит любое множество, для величин же наоборот: в направлении к меньшему оно превосходит все своей малостью, а в направлении к большему бесконечной величины не бывает. Причина та, что единица неделима».[4]

Именно на основании Аксиомы Разделения Геометрии и Арифметики была построена вся Евклидова геометрия, включившая в качестве своих приложений и пифагорейскую теорию несоизмеримости, и Евдоксову теорию пропорций. Таким образом, в основаниях математики изначально сложилась следующая Аристотеле-Евклидова Система Аксиом:

1. Аристотелева Аксиома Разделения Геометрии и Арифметики.

2. Пифагорейская Система Аксиом:

a) Аксиома Неделимости Единицы;

b) Аксиома Четно-Нечетности Единицы.

3. Аксиома Евдокса-Архимеда: для любых двух отрезков А и В можно указать такое натуральное число n, что n B >A.

4. Евклидова Система Аксиом Геометрии.

de omnibus dubitandum

Для математиков периода античности все пифагорейские аксиомы имели религиозно-философский, теоретический и практический смысл. Однако вскоре античная наука пришла в упадок. Прагматичная арабская математика вобрала в себя только самые полезные знания древних греков и заимствовала брахманическую десятичную систему счисления. Поэтому новоевропейская наука, которая стала формироваться после крестовых походов, не являлась непосредственным продолжением античной математики. Многие пифагорейские правила и аксиомы утратили в ней прежнюю значимость.

В самом деле, если средневековые схоласты еще штудировали Аристотеля, повторяя, в том числе, пифагорейское положение о неделимости единицы, то после Джордано Бруно, Николая Коперника, Галилео Галилея, Иоганна Кеплера, Франсуа Виета, Пьера Ферма, Рене Декарта и многих других ученых XV-XVII вв. наследие античной науки стало подвергаться критическому переосмыслению. Рене Декарт, один из основателей математического анализа, был первым, кто поднял эпистемологическую проблему разделения геометрии и арифметики.

Картезианский метод координат позволял говорить о единой природе геометрии и арифметики, опровергая Аристотелеву аксиому их разделения на основании того, что объекты исследования выражались в них через общее понятие числа. Теория измерения интервалов, разработанная Рене Декартом в соответствии с Аксиомой Евдокса-Архимеда, привела его к мысли о том, что общая мера (или единица соизмерения) должна существовать для любых отрезков.[5] Тем самым философская система Декарта противопоставила себя античной теории несоизмеримости. Хотя изучение иррациональных чисел не привело Декарта к результатам, подтверждающим его гипотезу «простой природы» несоизмеримых отрезков, он продолжал с недоверием относиться ко всем традициям и авторитетам античной математики.

В эпоху Исаака Ньютона и Готфрида Лейбница пифагорейская Аксиома Неделимости Единицы окончательно перестала восприниматься как sine qua non арифметики и перешла в разряд метафизических проблем, не представлявших особого интереса для точной науки. По сути дела, в XVII-XVIII вв. можно было вполне обоснованно утверждать, что существует две арифметики: пифагорейская арифметика, включавшая в себя Аксиому Неделимости Единицы, и аналитическая арифметика, из которой Аксиома Неделимости Единицы была исключена.

Трансформация Аристотеле-Евклидовой Системы Аксиом, произошедшая в результате становления новоевропейской науки, создала предпосылки для тщательного изучения аксиом геометрии и арифметики, которое началось в XIX веке в работах Г.Ф.Гаусса, Н.Лобачевского и Я.Бояи. Р.Дедекинд, сопоставляя аксиомы геометрии с теорией чисел, обратил внимание на явную нестыковку V книги «Элементов» Евклида, где подразумевалось, что все геометрические величины соизмеримы, с другими разделами Евклидовой геометрии, где появлялись задачи с использованием несоизмеримых отрезков длины. Таким образом, получалось, что все точки, соответствующие иррациональным числам, никак не учитывались в определениях Евклидовой геометрии; с формальной точки зрения на Евклидовой прямой они выпадали, поэтому нельзя было сказать, что такая числовая прямая является непрерывной.

В математическом трактате «Непрерывность и иррациональные числа» Р.Дедекинд писал: «Принятое до сих пор введение иррациональных чисел связывается именно с понятием о протяженных величинах – которое само нигде не определено – и определяет число как результат измерения такой величины другою такого же рода. Вместо этого я требую, чтобы (…) иррациональные числа были вполне определены через посредство рациональных. Но как это сделать – вот в чем вопрос».[6] Ответ был найден Р.Дедекиндом в том, чтобы вместо соизмеримых и несоизмеримых отрезков взять два класса P и Q, таких что каждая точка первого класса лежит влево от каждой точки второго, при этом существует одна и только одна точка, которая производит сечение прямой на два класса. Весьма существенным было то, что точка сечения относилась к первому или ко второму классу произвольно, за счет чего в Аксиоме Дедекинда и достигалась непрерывность.

Принципиально иного представления о непрерывности придерживался Г.Кантор. Если для Р.Дедекинда непрерывность состояла в наделении одним и тем же свойством классов соизмеримых и несоизмеримых величин, то Г.Кантор считал все целые числа «прототипом разрывности», а непрерывность, по его мнению, следовала из свойства несчетности всех действительных чисел. Различные представления о непрерывности послужили поводом к возникновению между Р.Дедекиндом и Г.Кантором научной дискуссии.[7] Аксиома Кантора о Стягивающихся Отрезках, несмотря на сходство с Аксиомой Дедекинда, предполагала существование непрерывного перехода от вложенных друг в друга отрезков (одномерных объектов) к одной общей для них точке (нульмерному объекту). Благодаря своей аксиоме о стягивающихся отрезках Г.Кантор восстановил в современной математике представление об актуальной бесконечности (уже применявшееся в апориях Зенона, а также в средневековой математике Николая Кузанского) и заложил основы теории бесконечных множеств.

Р.Дедекинд согласился поддержать теорию Г.Кантора с условием, что тот приведет строгое доказательство своей гипотезы континуума, согласно которой вся числовая прямая равномощна несчетному множеству. Но многочисленные попытки доказать эту гипотезу потерпели неудачу и выявили в теории множеств неразрешимые парадоксы, подобные тому, который обнаружил сам Г.Кантор (бесконечное множество, составленное из всех трансфинитных чисел, должно выражаться трансфинитным числом Ω, а значит, включать само себя и оказаться больше самого себя).

falsa in uno, falsa in omnibus

После обнаружения парадоксов в теории бесконечных множеств Г.Кантора, многие математики выразили свою озабоченность по поводу дальнейшей судьбы математической науки. Даже Д.Гильберт, поддерживавший теорию бесконечных множеств, был вынужден согласиться, что «состояние, в котором мы находимся сейчас в отношении парадоксов, на продолжительное время невыносимо. Подумайте: в математике – в этом образце достоверности и истинности – образование понятий и ход умозаключений, как их всякий изучает, преподает и применяет, приводят к нелепостям. Где искать надежность и истинность, если даже само математическое мышление дает осечку?».[8] Размышляя над парадоксами теории множеств, Д.Гильберт пришел к заключению, что причины парадоксов следует искать в основаниях математики. Созданная им аксиоматическая теория позволила в дальнейшем Э.Цермело и А.Френкелю ввести Систему Аксиом Цермело-Френкеля, которая запретила рассмотрение парадоксальных множеств.

Однако если Д.Гильберт верил в то, что аксиоматическая теория позволит разрешить гипотезу континуума Г.Кантора в положительном ключе и снимет все сомнения в истинности теории множеств, А.Пуанкаре придерживался на этот счет иного мнения. В трактате «Наука и гипотеза» А.Пуанкаре поставил в противовес Д.Гильберту следующий вопрос: «Являются ли аксиомы, явно формулируемые в руководствах, единственными основаниями геометрии?», – и указал на существование многих скрытых аксиом, содержащихся в доказательствах, которые с формальной точки зрения безупречны.[9]

От математика-интуициониста А.Пуанкаре не могло ускользнуть то обстоятельство, что научные взгляды Р.Дедекинда, Г.Кантора и Д.Гильберта исходили из предположения о внутренней непротиворечивости Евклидовой геометрии. Поскольку теория множеств была непосредственным и вполне логичным ее продолжением, то возникающие в ней парадоксы должны были, по их мнению, тоже иметь полное разрешение. Но А.Пуанкаре, несмотря на то, что Евклидова геометрия мыслилась большинством ученых как наиболее простая, удобная и согласующейся с чувственным опытом, не видел причин, по которым Евклидову геометрию можно было бы называть истинной, то есть, выражаемой одними только инвариантными аксиомами арифметики.

Еще более содержательная критика теории бесконечных множеств прозвучала со стороны другого математика-интуициониста Л.Брауера. В 1911 году он доказал известную в топологии теорему, согласно которой между пространствами с различной размерностью не существует непрерывного перехода (своего рода тезис ex nihilo nihil fit для математики). Раз так, Аксиому Кантора о Стягивающихся Отрезках, предполагавшую существование такого перехода, следовало признать некорректной. Более того, некорректность данной аксиомы означала, что гипотеза континуума Г.Кантора не имела и не могла иметь позитивного разрешения, что позволило Л.Брауеру вынести для всей теории бесконечных множеств весьма неутешительный прогноз: «Учение о трансфинитном есть любопытный патологический казус в истории математики, от которого грядущие поколения придут в ужас».

Предостережения интуиционистов подтвердились в 1931 году, когда К.Гёдель в статье «О формально неразрешимых предложениях Principia Mathematica и родственных систем» опубликовал первую теорему о неполноте, согласно которой любая непротиворечивая теория, включающая арифметику натуральных чисел, не может быть выражена некоторым конечным набором утверждений. Из теоремы о неполноте, в частности, следовало, что для построения непротиворечивой теории бесконечных множеств Системы Аксиом Цермело-Френкеля было недостаточно. Как заметил Д.Хофштадтер: «К.Гёдель показал, что понятие доказуемости уже слабее понятия истинности вне зависимости от того, какую систему мы выбираем (…) ни одна установленная система, какой бы сложной она не была, не может отразить всей сложности целых чисел: 0, 1, 2, 3...».[10]

В 1963 году П.Коэн привел еще одно доказательство, согласно которому ни гипотеза континуума Г.Кантора, ни аксиома выбора Э.Цермело, не зависят от Системы Аксиом Цермело-Френкеля. В соединении с теоремой К.Гёделя это означало, что в рамках данной системы аксиом невозможно ни доказать, ни опровергнуть непрерывность и упорядоченность числовой прямой. Тем не менее, П.Коэн продолжал поддерживать теоретико-множественное направление, которое в середине XX века стало доминирующей математической концепцией, и предложил отказаться от понятия абсолютной истины в математике: «Математика подобна прометееву труду, который полон жизни, силы и привлекательности, но содержит в себе зерно разрушающего сомнения. К счастью, мы редко останавливаемся, чтобы обозреть положение дел и подумать об этих глубочайших вопросах (…) Когда сомнения начинают нас одолевать (что, я надеюсь, происходит нечасто), мы отступаем под безопасные своды теории чисел, откуда, собравшись с духом, снова бросаемся в неверные воды теории множеств. Такова наша судьба – жить, сомневаясь; преследовать цель, в абсолютности которой мы не уверены; короче говоря, понимать, что наша единственная «истинная» наука имеет все ту же смертную, возможно, [всего лишь] опытную природу».[11]

Но далеко не все математики согласились признать понятие истины субъективным суждением. Выдающимся советским математиком и логиком А.А.Марковым была основана школа конструктивизма, в которой получила развитие брауеровская концепция, отрицавшая существование актуальной бесконечности. В своей книге «О философии математики» Г.Вейль выразил различие между теоретико-множественным и конструктивным подходом в следующих словах: «Обладание частями есть основное свойство континуума и брауеровская теория (…) кладет это отношение в качестве базиса для изучения непрерывности. В этом заключается, собственно, основание (…) исходить не из точки, а из интервалов, как из первичных элементов построения».[12] На другое различие, имеющее принципиальное значение для развития науки, обратил внимание математик-фибоначчист А.П.Стахов: в теоретико-множественном подходе при бесконечном измерении «до точки», алгоритм вычисления не влияет на конечный результат. Напротив, в конструктивной математике при измерении «до интервала», между алгоритмами возникает существенная разница в точности измерений.[13] Раз так, сведение всей математики к теории множеств (школа бурбакинистов) будет неизбежно способствовать снижению эффективности алгоритмов вычисления, применяемых на практике.

orthos logos

Основная причина неприятия теории бесконечных множеств со стороны математиков-интуиционистов, а также физика П.Бриджмена и логика Л.Виттгенштейна, была установлена профессором А.А.Зенкиным, которому удалось показать, в чем именно состоит логическая недостаточность доказательства несчетности множества всех действительных чисел. В статье «Ошибка Георга Кантора»,[14] А.А.Зенкин привел доказательство Г.Кантора в соответствие с дедуктивной системой, то есть такой системой, в которой каждое предложение выводится из конечного набора начальных условий доказательства.

(II) Теорема Г.Кантора.

{Тезис A:} Множество действительных чисел Х – несчетно.

Доказательство. Предположим, что множество всех действительных чисел (д.ч.) Х – счетно {Тезис Не-A:}. Тогда существует пересчет всех д.ч. из Х, то есть некоторое взаимно-однозначное соответствие между всеми д.ч. из Х и всеми натуральными числами из N={1,2,3, …}. Пусть существует некоторый искомый произвольный пересчет:

{Тезис B:} x₁, x₂, x₃, … , (1)

Следуя диагональному методу Г.Кантора, пересчет (1) можно поставить во взаимно-однозначное соответствие с диагональным действительным числом, которое образуется последовательностью √2 и отличается по способу построения от всех д.ч. из Х, то есть пусть существует другой пересчет:

{Тезис Не-B:} y₁ =0, y₁₁ y₁₂ y₁₃… (2)

Получаем противоречие, так как оказалось, что счетное множество не содержит всех действительных чисел (отрезок √2 длиннее единичного отрезка), следовательно, множество всех действительных чисел несчетно.

Возражение А.Зенкина состоит в том, что по условию пересчет (1) всех д.ч. из Х потенциально-бесконечен, так как N={1,2,3, …}, и произволен. Поэтому ничто не мешает добавить к исходному бесконечному пересчету (1) пересчет диагонального действительного числа:

y₁ , x₁ , x₂, x₃ , . . . x_n(1.1)

Полученный бесконечный пересчет (1.1) будет содержать все необходимые для утверждения счетности действительные числа {Тезис B:}. Очевидно, к пересчету (1.1) можно снова применить диагональный метод и снова выдвинуть предположение, что в (1.1) не содержится всех д.ч. некоторого другого диагонального числа y₂{Тезис Не-B:}. Но тогда, опираясь на произвольность эталона Х=[0,1] и бесконечность множества Х, не трудно сделать очередной пересчет и показать, что Х может содержать все д.ч. любого диагонального действительного числа, так как любой интервал [0,1] можно построить тем же способом, что диагональное число, как это показано ниже:

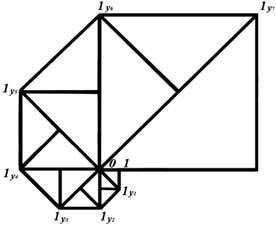график x₁ , x₂, x₃ , . . . x_n;

y₁ , x₁ , x₂, x₃ , . . . x_n;

y₂ , y₁ , x₁ , x₂, x₃ , . . . x_n;

y₃, y₂ , y₁ , x₁ , x₂, x₃ , . . . x_n;

y₄, y₃, y₂ , y₁ , x₁ , x₂, x₃ , . . . x_n и т.д.

Так как в качестве начальных условий Г.Кантор берет, во-первых, произвольность эталона [0,1], во-вторых, потенциальную бесконечность пересчета, то в полном соответствии с дедуктивной системой в доказательстве теоремы (II) мы должны использовать оба начальных условия и не имеем права отбрасывать допущение о счетности {Тезис Не-A:}, пока не будет получено противоречие. Но искомое противоречие не возникает ни на каком шаге доказательства: Не-A®B®Не-B®B®Не-B®B®Не-B® (…), поэтому для утверждения о несчетности множества всех действительных чисел нет никаких оснований.

Г.Кантор размышлял над этой проблемой и считал свое доказательство правильным в силу того, что диагональный метод верно отражает непериодичность десятичной дроби √2. Во всяком случае, он осознавал, что опровержение диагонального метода возможно тогда и только тогда, если окажется, что √2 является соизмеримым отрезком: «Трансфинитные числа стоят или падают вместе с конечными иррациональными числами. По своему внутреннему существу они подобны друг другу, ибо как те, так и другие суть определенно отграниченные образования или модификации (άφωρισμένα) актуально бесконечного».[15] По сути дела, этими словами Г.Кантор констатировал то, что концепция актуальной бесконечности содержится в пифагорейской теории несоизмеримости, с которой был вынужден согласиться Аристотель, не имевший представления о десятичных дробях.

К замечанию Г.Кантора стоит прислушаться, хотя бы потому, что если мы признаем иррациональность √2, то мы вынуждены признать справедливость пифагорейской теоремы о несоизмеримости стороны и диагонали квадрата. Но теорема (I) была справедлива только в Пифагорейской Системе Аксиом, где единица принималась в качестве числа неделимого. Использование десятичных дробей и исключение Аксиомы Неделимости Единицы позволяет обозначить число k в теореме (I) в виде дроби 0,7071…, и тогда n² = 2k² запишется как 1² = 2·(0,7071…)² = 2/2, что является неопровержимым арифметическим и геометрическим фактом.

В самом деле, при непосредственном изучении приближений числа √2, возведенных в квадрат, легко заметить, что в действительности мы сталкиваемся с приближением, имеющим вполне определенную разрядность вида 1, b1 b2 bk 8 а1 а2 а3 аk+1, где bk обозначает количество девяток, аk+1 – количество цифр, среди которых стоят не только девятки:

1,4142² = 1,99996164;

1,41421² = 1,9999899241;

1,414213² = 1,999998409369;

1,4142135² = 1,99999982358225;

1,41421356² = 1,9999999932878736 и т.д.

Получение такой закономерности, связанной с разрядностью, возможно при условии, что десятичная дробь √2 = 1,4142… является периодической десятичной дробью.[16] Так, если разбить некоторый квадрат ABCD на клетки или элементы одинаковой размерности, то сторона квадрата выразится тем же числом элементов, что его диагональ. При этом площадь квадрата ACEF, построенного по основанию квадрата ABCD, будет находиться по формуле: S(АСЕF) = 2S(АВСD) – (2n – 1) или 2n² – (2 n – 1), где n – число элементов стороны квадрата АВСD.

Воспользовавшись этой формулой для нахождения площади квадрата ACEF, построенного по основанию десятичных квадратов: 10², 100², 1000²…, мы получим следующие значения для площадей диагональных десятичных квадратов:

2 · 10² – (2 · 10 – 1) = 181; 2 · 100² – (2 · 100 – 1) = 19801; 2 · 1000² – (2 · 1000 – 1) = 1998001 и т.д.

Извлекая квадратные корни из площадей данных квадратов, мы будем приближаться к десятичному значению числа √2= 1,4142…:

√181 = 13,453624…; √19801 = 140,716026…; √1998001 = 1413,506632… и т.д.

Сравнивая полученные приближения с десятичной дробью √2, можно установить, что на каждом шаге остаток будет приближаться к значению десятичной дроби √2/2 = 0,7071…:

14,142135… – 13,453624… = 0,688511…; 141,421356… – 140,716026… = 0,705330…; 1414,213562… – 1413,506632… = 0,707242… и т.д.

Если соединить найденные значения, переместив запятую целых частей в положение после первой единицы, и сравнить их с дробным значением √2= 1,4142…, можно убедиться, что десятичный остаток второго порядка будет тоже приближаться к значению десятичной дроби √2/2 = 0,7071…:

1,4142135623730950488016887242097… – 1,3453624688511… = 0,0688510… ;

1,4142135623730950488016887242097… – 1,40716026705330… = 0,00705329… ;

1,4142135623730950488016887242097… – 1,413506632707242… = 0,000707240… и т.д.

То есть при получении диагонального квадрата S(ACEF) =199_800_1=1414_²=x², дробь √2= 1,4142… окажется пусть невообразимо большой, но периодической десятичной дробью. Вслед за первым периодом 707_ (где нижнее подчеркивание обозначает недостающие члены последовательности) в дроби 1,414_707_707_(707_) будет следовать второй, за ним третий, четвертый и так до бесконечности, как в любой другой периодической десятичной дроби. Тогда, следуя правилам перевода десятичных дробей в обыкновенные, сторона и диагональ единичного квадрата выразятся отношением двух целых чисел m/n, n≠0:

=1,414_ 707_707_(707_).

Рассмотрим квадраты чисел, образующихся в числителе дроби 1414_707_ −1414_:

147 – 14=133, 133²=17689;

14170 – 141=14029, 14029²=196812841;

1414707 – 1414=1413293, 1413293²=1997397103849;

141427071 – 14142=141412929, 141412929²=19997616488359041;

14142170710 – 141421=14142029289, 14142029289²=199996992410933845521 и т.д.

Разрядность в расположении полученных цифр указывает на приближение к значению 199_700000_1000_, к которому стремится квадрат числителя дроби m/n:

=== 2,00_1.

Получение одного такого дискретного значения 2,00_1, выразимого отношением m/n, находится в полном соответствии с теоремой Л.Брауера, доказавшего, что не существует непрерывного отображения, связывающего два евклидовых пространства Е^a и Е^b при a ≠ b. Если бы отношение m/n для квадратного корня из 2 сводилось к непрерывной десятичной дроби 1,99(9), то для пространств различной размерности существовал бы непрерывный переход, поскольку все несводимые к целым числам корни из числа 2 были бы равны одной и той же десятичной дроби с периодом (9): =1,99(9); =1,99(9)…

Получение, помимо непрерывных десятичных дробей с периодом (9), симметричных им дискретных приближений с избытком (1,9; 1,99; 1,999; 1,9999…∞→2, так же как 2,1; 2,01; 2,001; 2,000…∞1→2), позволяет устанавливать для каждого нецелого корня одно и только одно значение, которое можно записать отношением целых чисел m/n. Так, для это будет точка 2,00_1, для точка 2,000000_1 и так далее. Необходимость и достаточность существования одного дискретного значения 2,00_1 происходит из единственности значения 1,414_, стоящего до начала периода дроби 1,414_707_707_(707_). Только так мы можем задать разрядность, при которой можно найти сколь угодно много десятичных периодов (707_), а именно, ничто не мешает извлекать квадраты из чисел 2,00_00_1; 2,00_00_00_1; 2,00_00_00_00_1, стоящих на числовой прямой ближе к значению 2, и получать более точные приближения к значению бесконечной периодической десятичной дроби 1,414_707_707…; 1,414_707_707_707…; 1,414_707_707_707_707… (то же самое можно сказать о приближениях с недостатком).

Для целостного восприятия приведем геометрическое построение периодической десятичной дроби √2. Во избежание путаницы с Евклидовой геометрией, в которой отрезок √2 считается несоизмеримым, такую геометрию, в которой √2 и другие нецелые корни берутся в качестве периодических значений, назовем геометрией Евдокса или Евдоксовой геометрией. Пусть целое число n элементов одной размерности некоторого квадрата ABCD стремится к бесконечности. Тогда разница его диагонали АС и диагонали x квадрата, равновеликого диагональному квадрату ACEF, выразится пределом:

Такая разница y = √2/2 будет наблюдается при построении квадратов ABCD, состоящих из любого целого числа элементов, так что диагональ заштрихованного элемента (см. ниже) при любом n≠0 будет разделена надвое. Теперь заметим, что существует такое разбиение квадрата ABCD, при котором S(ACEF)=x². Другими словами, повернув элементы диагонального квадрата ACEF=25=x² на 45°, мы обнаружим, что сторона x = АС – y.

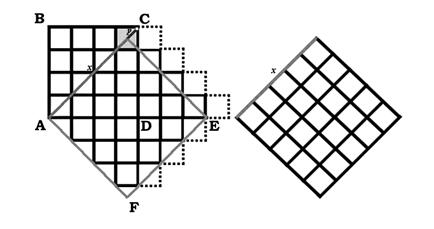
периодичность ЧБ

Построенный по основанию десятичного квадрата S(ABCD) = 1000_² диагональный квадрат S(ACEF) =199_800_1=1414_²=x² можно аналогичным образом развернуть на 45° и обнаружить, что x = АС – y. Тогда для заштрихованного элемента станет возможно дальнейшее разбиение на элементы, кратное числу десятичного квадрата S(ABCD)=1000_²; и для него вновь найдется диагональный квадрат 199_800_1=1414_²=x², а значит, найдется еще более удаленный крайний элемент, диагональ которого будет также разделена надвое. Для наглядности местонахождение этого элемента обозначено белой точкой на диагонали АС. При этом диагональная разница будет определяться тождеством 1414_,707_= АС – y´. Очевидно, что процесс разбиения можно продолжать до бесконечности. Тогда мы перейдем к дискретной решетке, состоящей из бесконечного числа элементов, диагональ которой будет задана как 1414_,707_707_(707_). Переместив запятую в положение после первого знака, мы получим значение 1,414_707_707_(707_), которым соизмеряется сторона и диагональ единичного квадрата.

Все, что было сказано выше об извлечении квадратного корня из 2, можно повторить в Евдоксовой геометрии для любых нецелых корней. Так, для любых нецелых квадратов описанный метод позволяет получить период, равный x/2, для нецелых кубов период, равный x/3, для биквадратов x/4, и т.д., где x – конечная последовательность цифр, стоящая до начала периода соответствующей десятичной дроби.

eо ipso

Любая математическая система, в которой признается справедливость теоремы (I), явно или неявно будет включать Пифагорейскую Систему Аксиом. Поэтому общеупотребительная система Principia Mathematica выглядит в настоящее время следующим образом:

I. Открыто признаваемые Системы Аксиом Арифметики и Геометрии:

1. Евклидова Система Аксиом Геометрии.

2. Не-евклидовы Системы Аксиом Геометрии.

3. Система Аксиом Непрерывности:

a) Аксиома Евдокса-Архимеда;

b) Аксиома Дедекинда;

c) Аксиома Кантора о Стягивающихся Отрезках.

4. Гильбертова Система Аксиом.

5. Система Аксиом Цермело-Френкеля.

6. Система Аксиом Пеано.

И другие публикуемые в математических руководствах аксиоматические системы.

II. Скрытая Система Аксиом:

1. Аристотелева Аксиома Разделения Геометрии и Арифметики.

2. Пифагорейская Система Аксиом:

a) Аксиома Неделимости Единицы;

b) Аксиома Четно-Нечетности Единицы.

На существование фундаментальной Аксиомы Разделения Геометрии и Арифметики неоднократно обращал внимание А.Френкель, который считал, что «преодоление пропасти между областью дискретного и областью непрерывного, или между арифметикой и геометрией, есть одна из главных, – пожалуй, даже самая главная проблема оснований математики».[17] Необходимость в Аксиоме Разделения Геометрии и Арифметики отпадает лишь в том случае, если будет исключена Пифагорейская Система Аксиом, принявшая в основаниях математики скрытый характер. Как уже было отмечено, данная задача находит свое разрешение в рамках Евдоксовой геометрии.

Снятие проблемы скрытых аксиом, появившихся в ходе трансформации Аристотеле-Евклидовой Системы Аксиом, позволяет разрешить комплекс других проблем. В частности, находит свое разрешение Гильбертова проблема непротиворечивости аксиом арифметики: в пифагорейской арифметике единица считалась неделимым числом, в современной арифметике единица бесконечно делима, как и все натуральные числа. Кроме того, в рамках Евдоксовой геометрии подтверждается картезианская гипотеза о «простой природе» несоизмеримых отрезков, а также концепция Л.Брауера, исключающая Аксиому Кантора о Стягивающихся Отрезках и отрицающая идею актуальной бесконечности как внутренне противоречивую.

Онтологический смысл «завершенной бесконечности» наиболее емко был схвачен в философии Николая Кузанского в виде тезиса coincidentia oppositorum (лат. «совпадение противоположностей»). Возникшее в XX веке преобладание в математике, философии и логике идеи актуальной бесконечности приводит, таким образом, к размытию в современной культуре понятий истины и лжи, добра и зла, божественного и демонического, точно так же, как это происходило на закате античной цивилизации. Изучение истории и философии науки имеет поэтому общекультурное значение, которое состоит в восстановлении понятия истинной бесконечности и противопоставлении Хаосу, разрушающему основы человеческой личности, Логоса созидания и творчества.

[1] Лурье С.Я. Архимед. М.-Л., 1945. С.22

[2] Фрагменты ранних греческих философов. Ч.1. М., 1989. С.469

[3] Гайденко П.П. К вопросу о генезисе новоевропейской науки // Философия науки. Вып. 4. М., 1998. С.48

[4] Философы Греции. Основы основ: логика, физика, этика. Харьков, 1999. С.648

[5] Баранов В. Гносеологические основания алгебры Декарта // Sententiae: Наукові праці Спілки дослідників модерної філософії. - VIII-X (1-2/2003, 1/2004). - УНІВЕРСУМ-Вінниця, 2004. С.120-131

[6] Дедекинд Р. Непрерывность и иррациональные числа. Одесса, 1923. С.16

[7] Кантор Г. Труды по теории множеств. М.,1985. С.335-336

[8] Виленкин Н.Я. В поисках бесконечности. М.,1983. С.136

[9] Пуанкаре А. О науке. М., 1983. С.36

[10] Хофштадтер Д.Ф. Гёдель, Эшер, Бах: эта бесконечная гирлянда. Самара, 2001. С.20

[11] Соhen P.J. Comments on the foundations of set theory. Proc. Sym. Pure Math. 13:1 (1971), 9–15

[12] Вейль Г. О философии математики. М.-Л., 1934

[13] Стахов А.П. Введение в алгоритмическую теорию измерения. М., 1977. С.26

[14]Зенкин А.А. Ошибка Георга Кантора // Вопросы философии. 2000, №2, С.165-168

[15]Кантор Г. Труды по теории множеств. М., 1985. С. 284

[16]Клещев Д.С. Возвращение Орфея. Гармония и дисгармония современной математики // Философия и культура. №5, 2009.

[17] Виленкин Н.Я. В поисках бесконечности. М.,1983.С.12