МОДЕЛЬ ВИБРАЦИИ ДВИГАТЕЛЯ С УЧЕТОМ ДИНАМИКИ
Экспериментальная модель вибрации двигателя
Коковин В.Д.,
Калюжный О.Н. (oleg314@mail.ru)
Москва, 2012
В данном материале представлено
описание нового подхода к оценке вибросостояния двигателя. Подход основан на
идентификации моделей вибрации, проводимой в классе дробно-рациональных
функций.
Задача идентификации («подгонки»)
модели, заключающаяся в поиске коэффициентов модели, была выполнена с помощью
программирования методов матричного анализа на языке C++ и протестирована на реальных данных,
полученных при работе двигателей на постоянных режимах. Тестирование показало высокую
устойчивость модели, в том числе – постоянство значений некоторых коэффициентов
на разных двигателях.
Содержание
1. Вибрация двигателей.
2. Аппроксимации Паде.
3. Модель Паде для вибрации двигателя.
4. Расширение модели: анализ остатков.
5. Методы нахождения решений.
6. Результаты.
7. Перспективы.
8. Приложение 1: иллюстрации.
9. Приложение 2: класс MyMatrix.
1. Вибрация двигателей
Основной причиной вибрации двигателей являются колебания роторов, поэтому мощность вибрации двигателя в наибольшей степени зависит от частот вращения РНД и РВД. В нашем исследовании мы не рассматривали механические причины возникновения вибрации, такие, скажем, как прогиб вала под действием центробежной силы, остановившись лишь на эмпирическом подходе к построению модели. Также, в целях упрощения модели, мы на сегодняшний день ограничились изучением лишь одной зависимости – между частотой вращения РВД и виброскоростью. В то же время, существующий у нас сейчас программный продукт способен обрабатывать данные для подгонки более широких моделей, определяющих зависимость от нескольких параметров. То есть, например, моделей зависимости виброскорости от частот вращения роторов, числа M в полете и перегрузок одновременно, а также от производных (любых порядков) от тех или иных параметров.
Исторически сложилось два основных подхода к построению модели вибрации. Это аппроксимация наблюдаемой зависимости рядами Фурье и аппроксимация полиномами (как правило, не более чем второй степени). Мы пошли по третьему пути, обратившись к аппроксимациям Паде.
2.
Аппроксимации Паде
Аппроксимации Паде представляет собой рациональные функции в виде отношения двух полиномов:
![]()
Коэффициенты этих полиномов определяются коэффициентами разложения функции в ряд Тейлора. Этот факт позволяет избежать больших степеней в разложении, что избавляет от появления ошибок, связанных с возведением в большую степень погрешности измерения параметра. В то же время, наличие знаменателя дает нам достаточную кривизну функции, а также позволяет регистрировать особые точки.
Аппроксимации Паде отличаются двумя свойствами, важными для их практического использования:
- высокая точность приближения к аппроксимируемой функции или наблюдаемым данным;
- большая чувствительность к точности вычисления коэффициентов модели, что требует применения эффективных методов линейной алгебры.
В книге известных специалистов в данной области Дж.Бейкера и П.Грейвс-Морриса «Аппроксимации Паде» приводится следующий пример, иллюстрирующий точность приближения на примере функции:
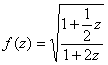
Для этой функции аналитическим образом рассчитаны коэффициенты ряда Тейлора и коэффициенты Паде и построены графики:
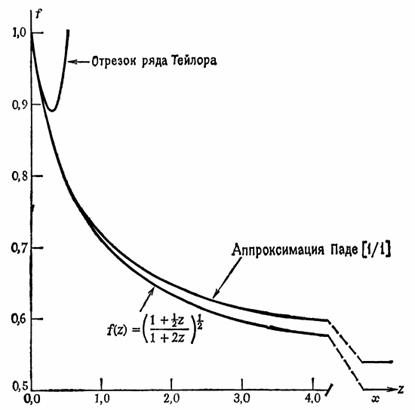
Рис.1
Таким образом, метод Вейерштрасса, основанный на переразложении функций в ряд Тейлора, является скорее общим принципом, чем практическим методом, в то время как метод Паде дает практический результат, если, конечно, удается добиться необходимой точности при подгонке коэффициентов.
Применительно к анализу вибрации двигателя, более «красивой» в сравнении с рядом Тейлора и, главное, более устойчивой получается модель Паде, см. рис.3.
3.
Модель Паде для вибрации двигателя
В качестве анализируемой величины мы выбрали значение виброскорости V, в качестве абсциссы – N2, то есть значение частоты вращения РВД. Простейшая модель имеет вид:
![]() (1)
(1)
Задача построения модели сводится к нахождению коэффициентов Ci , i = 0, … , 4. Мы
ограничились дробью с числителем и знаменателем порядка 2, т.к. недостаток
точности измерения N2 приводит к значительным погрешностям при
арифметических операциях с большими, чем вторая, степенями N2.
Прежде, чем приступить к подгонке модели, необходимо отфильтровать данные вибрации, отбирая только значения на определенных режимах работы двигателя. Реализованный в настоящее время алгоритм фильтрации действует следующим образом:
1. Учитываются только значения V и N2, регистрируемые после прогрева двигателя на частоте вращения РВД = 95% в течение 120 сек.
2. Данные начинают сохраняться на любых частотах вращения > 65% в том случае, если двигатель работал в некотором коридоре частот шириной 2% в течение 17 сек. и прекращают сохраняться после выхода из этого коридора. При стабилизации в другом 2%-ом коридоре частот данные вновь начинают выгружаться.
В результате выгрузки данных мы получаем график следующего вида:
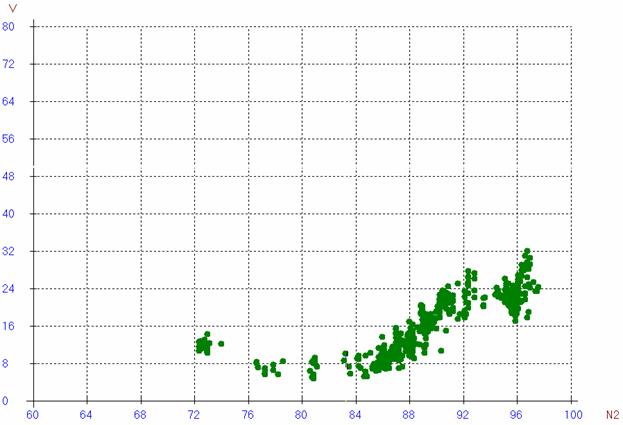
Рис.2
В связи с тем, что на разных участках по N2 получается разная плотность данных, а в местах «скопления» данных мы наблюдаем разброс значений виброскорости, перед началом подгонки модели необходимо специальным образом усреднить значения.
На основе данных, полученных после усреднения, составляются линейные уравнения первой степени, которые решаются с помощью методов линейной алгебры относительно коэффициентов модели.
Для составления линейных уравнений формула (1) преобразуется путем умножения на знаменатель левой и правой части к следующему виду:
V = C0 + C1 *
N2 + C2 * (N2)2 - C3 * N2
* V - C4 * (N2)2 * V (2)
После поступления определенного количества наблюдений (V, N2) мы получаем несовместную систему линейных уравнений, которая преобразуется методом МНК в совместную систему и решается с помощью проекционного алгоритма.
Варьируя некоторые параметры предварительной обработки и решающих алгоритмов, мы получаем некоторое количество приближенных решений, из которых отбираем наилучшее; в качестве критерия качества подгонки используем среднеквадратичное отклонение модельных данных от реальных.
4.
Расширение модели: анализ остатков
Расчет модели вибрации, соответствующей формуле (1), не всегда приводит к удовлетворительному результату. В случае, когда вибрация начинает расти в районе режима Максимал, полученная модельная кривая, как правило, не реагирует на этот рост, так как порядок модели не обеспечивает необходимого количества точек перегиба.
Поэтому в дополнение к описанному алгоритму разработано и запрограммировано следующее расширение модели: к дроби из формулы (1) добавлена аналогичная дробь:
![]() (3)
(3)
В этом случае аналитический переход к линейной форме, аналогичной (2), невозможен. Кроме того, логично предположить, что вклад одной из дробей значительно сильней, чем вклад другой дроби. Поэтому одновременная подгонка коэффициентов обеих дробей, скорее всего, нецелесообразна.
Для этого случая было найдено следующее решение:
1. Выполняется подгонка коэффициентов первой дроби, как в случае формулы (1).
2. Полученные модельные данные вычитаются из реальных, зарегистрированных данных.
3. По полученному остатку выполняется подгонка коэффициентов дроби для формулы:
![]() , (4)
, (4)
где V’ – остаток.
4. Результаты складываются.
Действуя аналогичным образом, можно строить модели, состоящие из произвольного количества дробей.
В случае «простой» модели не удавалось получить удовлетворительный результат для случая, когда вибрация начинала расти в районе режима Максимал. Усложнение модели привело к устранению этого недостатка и к визуальному улучшению результата на других режимах.
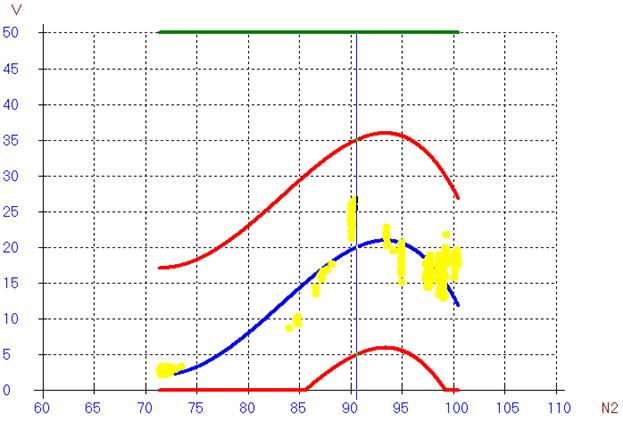
Рис.3а. Аппроксимация рядом Тейлора 4-го
порядка. Здесь и далее синяя линия соответствует модельным данным, красные границы – коридор ±15%.
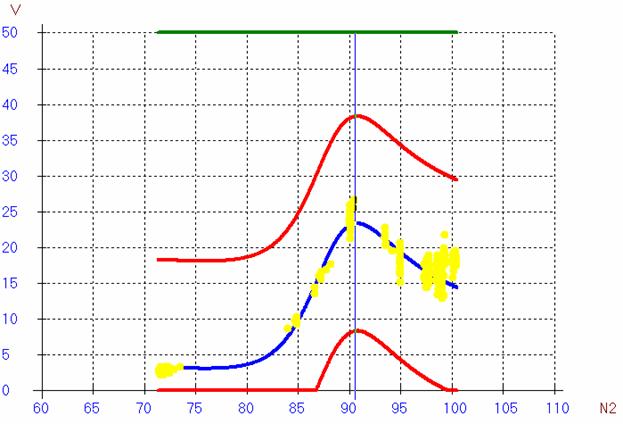
Рис.3б. Простая модель Паде
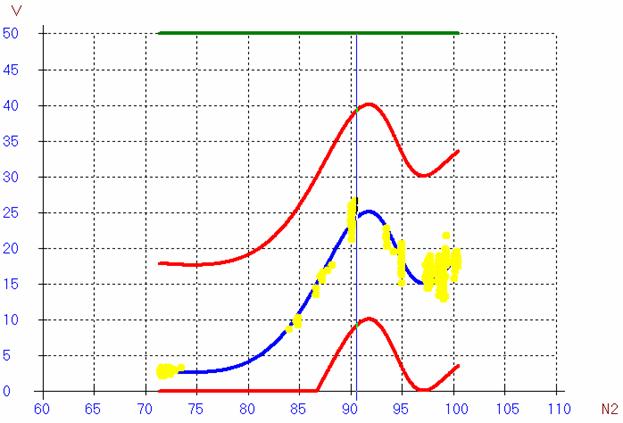
Рис.3в. Расширенная модель Паде (2 дроби)
5.
Методы нахождения решений
На входе решающих алгоритмов мы имеем от нескольких тысяч до нескольких десятков тысяч наблюдений вида (Vi, N2i), где Vi – виброскорость и N2i – частота вращения РВД, i = 1, … , n. На основе этих точек и уравнения (2) можно построить несовместную систему уравнений:
XC = Y , (5)
где:
X = ( 1 , N2
, (N2)2 , N2*V, (N2)2*V )
( N2 – столбец из n наблюдений N2i, (N2)2 – столбец из n квадратов N2i и т.д. );
C – столбец параметров модели;
Y – столбец из n штук Vi.
В получившейся системе количество строк – несколько тысяч или десятков тысяч, количество столбцов равно пяти. Поэтому для ее решения разумно применить метод наименьших квадратов (МНК). После появления на входе первых k наблюдений преобразуем систему (5) к виду:
XkT Xk C =
где XkT – транспонированная матрица наблюдений. Такая система всегда имеет решение.
Затем строки системы (6) по очереди передаются на вход проекционного алгоритма, на выходе которого мы получаем постоянно корректирующееся приближенное решение. После поступления следующих k наблюдений опять используем МНК и снова передаем получившиеся строки в проекционный алгоритм.
Для нахождения приближенного решения мы используем проекционный алгоритм с весовым коэффициентом забывания. Смысл коэффициента забывания W заключается в следующих формулах:
X(k) = W2 *
X(k-1) + X(k) * XT(k) ,
Y(k) = W2 * Y(k-1) + X(k) * y(k) ,
W < 1 .
Коэффициент W обеспечивает "экспоненциальное забывание" прошлых k-1 наблюдений с целью уменьшения их влияния на результаты оценивания параметров модели в момент времени k. Уменьшение коэффициента W обеспечивает большую адаптивность алгоритма оценивания к возможной нестационарности модели объекта, однако при этом снижается точность оценивания параметров за счет уменьшения выборки наблюдений. Адаптивный подход к выбору коэффициента W позволяет получить эффективные оценки параметров нестационарной модели объекта.
Решение системы уравнений (6) относительно C дает оценку вектора параметров C по k наблюдениям вектора входных переменных X(k) и выходной переменной y(k). Для вычисления оценок параметров используются многошаговые проекционные алгоритмы оценивания.
Многошаговые проекционные алгоритмы оценивания позволяют по каждому уравнению вида (6) получать оценки вектора параметров C(k) в соответствии со следующим выражением:
C(k) = C(k-1) + BS * [y(k) – CT(k-1) * X(k)]
, (7)
где:
C(k) - оценка вектора параметров модели размерности L для момента времени k;
BS - вектор коэффициентов коррекции оценок модели размерности L.
Индекс S в выражении (7) означает то количество значений вектора переменных X(k), которое используется для вычисления вектора BS. Величину S принято называть глубиной памяти алгоритма.
Вектор BS вычисляется следующим образом:
BS = Z * (ZT * Z)-1, (8)
Z = A(S-1) * X(k) , (9)
A(S) = A(S-1) – BS * ZT (10)
При S=1:
Z=X(k) и
А(0)=I - единичная квадратная матрица.
Для сокращения количества вычислительных операций в алгоритме следует учитывать диагональную симметричность матрицы А(S) размерности L´L.
Параметр Z2 = ZТ * Z характеризует степень линейной зависимости переменных модели и может быть использован для контроля вырожденности матрицы X(k) в выражении (7).
Блок-схема обобщенного проекционного алгоритма представлена на Рис.4.
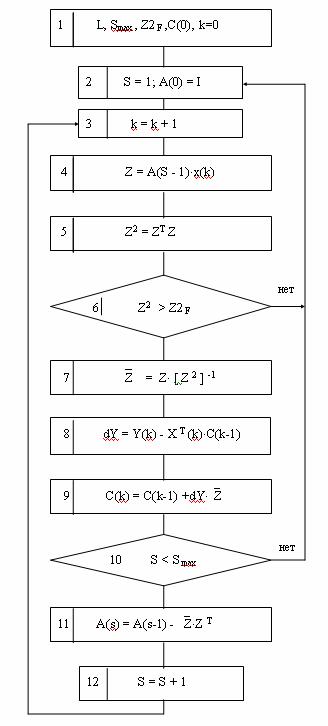
Рис.4. Блок-схема обобщенного проекционного алгоритма
При небольшом количестве зарегистрированных и отфильтрованных данных не всегда получается удовлетворительный результат. Поэтому применяется метод многократной подгонки модели. Заключается он в том, что полученный набор коэффициентов C используется в качестве стартового для повторной подгонки по тем же данным. Эта операция продолжается до тех пор, пока отклонение вновь полученных коэффициентов от предыдущих не перестает превышать некоторую наперед заданную величину.
6. Результаты
Основным положительным результатом проведенных исследований является устойчивость коэффициентов модели, то есть малая изменчивость коэффициентов как при переходе от газовке к газовке, так и при подгонке модели на данных разных двигателей. Наибольшую устойчивость демонстрируют коэффициенты знаменателя: C3 изменяется в интервале [-0.025, -0.019], C4 – в интервале [0.00010, 0.00015]. Пример устойчивости коэффициентов приведен в Таблице 1.
Другим интересным результатом является тот факт, что особые точки модели практически всегда находятся внутри анализируемого интервала и чаще всего – на больших частотах вращения, а именно на тех, где поведение виброскорости является нестабильным. Причем алгоритм находит эти точки независимо от плотности зарегистрированных точек, в том числе и на интервалах, на которых зарегистрированные точки отсутствуют.
Под особыми точками принято понимать значения абсциссы (в нашем случае – N2), при которых знаменатель обращается в нуль. Так как значение дискриминанта знаменателя (d) очень мало, при его расчете образуется значительная погрешность, сильно влияющая на вычисление корней. Поэтому логично ограничиться лишь теми моделями, у которых дискриминант (d) близок к нулю (например, d < 1.0E-6). Тем более, что поиск моделей дает большинство решений именно такого вида. Далее, если дискриминант – положительный, считаем, что он равен нулю и находим единственное решение квадратного уравнения, содержащегося в знаменателе (в нашем случае оно равно –C3 / 2C4). Если дискриминант – отрицательный, но также близок к нулю, поступаем аналогично. Полученное решение считаем особой точкой.
Необходимо пояснить, почему на приведенных здесь графиках не видны разрывы модельной кривой, соответствующие особым точкам. Это связано либо с тем, что дискриминант – отрицательный, хотя и близок к нулю, либо с очень сильной локализацией разрыва (при положительном дискриминанте). Так как программный модуль строит график по дискретной решетке на оси абсцисс с определенным шагом, то, во втором случае, он просто «проскакивает» особую точку.
Исходя из этих результатов, можно наметить два направления использования модели.
1. Визуальный анализ. По характеру полученных модельных кривых и динамике изменения их формы необходимо научиться выявлять те или иные изменения в состоянии двигателя (износ узлов и т.п.).
2. Анализ с помощью коэффициентов модели. Тенденции изменения коэффициентов, вероятно, должны сигнализировать об изменениях в состоянии двигателя и его узлов. Прежде всего, речь должна идти о коэффициентах числителя, т.к. они меняются значительно сильнее, чем коэффициенты знаменателя. Пример тенденции изменения коэффициентов приведен в Таблице 1. Частный случай - анализ с помощью особых точек (–C3 / 2C4). Прослеживается взаимосвязь между особыми точками и частотами вращения, на которых виброскорость нестабильна, то есть значительно меняется как при работе на установившемся режиме, так и при повторном выходе на установившийся режим с такой же частотой вращения. Кроме того, характер распределения особых точек изменяется при износе двигателя.
Так как наблюдаемые данные подвергаются предварительной обработке, и параметры этой обработки варьируются, по данным каждого полета рассчитывается не одна модель, а несколько тысяч удовлетворительных моделей. Поэтому каждый раз мы получаем не просто набор коэффициентов модели C0, … C4, а статистику по этим коэффициентам. При этом на экран выводится одна из моделей – наилучшая в смысле среднеквадратичного отклонения от реальных данных.
Примеры статистик особых точек см. на рис. 6.
Для того, чтобы научиться использовать результаты расчетов, необходимо провести работу по сопоставлению расчетных моделей и тенденций их изменения с известными данными по работе двигателя: износу узлов или изменению условий работы двигателя.
7.
Перспективы
До сих пор мы проводили анализ на данных, полученных на стационарных режимах работы. Таким образом, мы не учитывали свойства объекта, которые способны проявляться лишь в динамике, т.е. на приемистости, при сбросе и т.п. Возможно, параметры модели, построенной на переходных режимах, способны дать нам больше информации о состоянии двигателя.
Следующий подход – модификация модели.
Расширение модели за счет увеличения степени числителя или знаменателя представляется сомнительным, т.к. в этом случае растет ошибка в расчетах. В то же время, можно попытаться пойти по следующему пути: делать предварительную подгонку по модели размерности [2/2], а затем, отталкиваясь от полученных коэффициентов модели, увеличивать размерность, скажем, до [4/4].
Более перспективным видится расширение модели путем добавления в нее таких параметров, как частота вращения РНД, разность между частотами вращения РВД и РНД, перегрузки, число M в полете. Также мы планируем испытать модель, имеющую в качестве аргумента производные от тех или иных параметров.
Вот краткий перечень возможных направлений исследований:
а) Построение моделей на переходных режимах:
- при приемистости
- при сбросе оборотов
- при включении и выключении двигателя
- при включении и выключении форсажа
- при перестройке программ регулирования
б) Расширение модели путем добавления в нее следующих параметров:
- частоты вращения РНД
- разности между частотами вращения РВД и РНД
- перегрузок
- температур
- числа M в полете
- производных от тех или иных параметров
в) Комбинированный анализ вибросостояния двух двигателей в полете.
8.
Приложение 1.
Таблица 1. Пример устойчивости коэффициентов модели (полеты):
|
|
C0 |
C1 |
C2 |
C3 |
C4 |
|
13.03.08 |
13.6 |
-0.326 |
0.00195 |
-0.0234 |
0.000138 |
|
17.03.08 |
14.8 |
-0.362 |
0.00221 |
-0.0239 |
0.000143 |
|
26.03.08 |
11.1 |
-0.263 |
0.00156 |
-0.0233 |
0.000136 |
|
01.04.08 |
12.6 |
-0.293 |
0.00171 |
-0.0225 |
0.000128 |
|
09.04.08 |
15.8 |
-0.386 |
0.00236 |
-0.0238 |
0.000143 |
|
11.04.08 |
16.8 |
-0.410 |
0.00250 |
-0.0239 |
0.000143 |
|
29.04.08 |
15.6 |
-0.381 |
0.00232 |
-0.0238 |
0.000143 |
|
13.05.08 |
16.1 |
-0.381 |
0.00226 |
-0.0229 |
0.000131 |
|
14.05.08 |
13.6 |
-0.323 |
0.00192 |
-0.0230 |
0.000133 |
|
14.05.08 |
14.1 |
-0.335 |
0.00201 |
-0.0225 |
0.000129 |
|
26.05.08 |
15.4 |
-0.372 |
0.00224 |
-0.0230 |
0.000133 |
|
30.05.08 |
12.8 |
-0.321 |
0.00200 |
-0.0247 |
0.000153 |
|
02.06.08 |
14.9 |
-0.354 |
0.00211 |
-0.0229 |
0.000132 |
|
03.06.08 |
11.0 |
-0.267 |
0.00162 |
-0.0229 |
0.000132 |
|
04.06.08 |
12.2 |
-0.284 |
0.00165 |
-0.0227 |
0.000130 |
|
13.06.08 |
11.0 |
-0.244 |
0.00135 |
-0.0212 |
0.000112 |
Примеры модельных графиков:
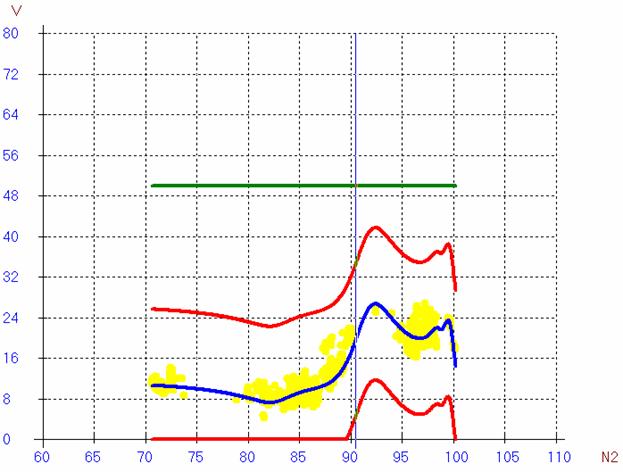
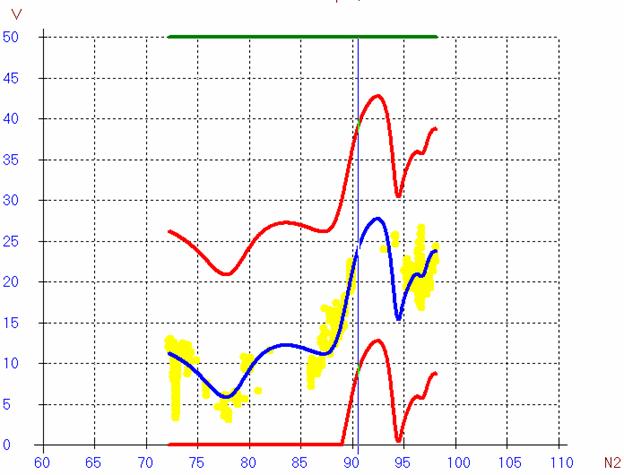
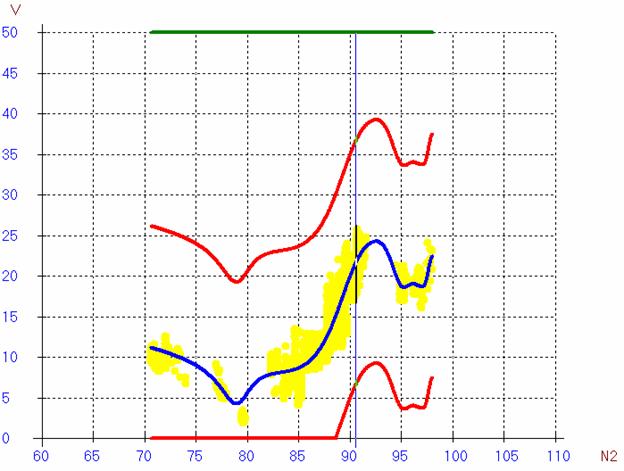
Рис.
5. Модель вибрации, 3 полета.
( две газовки в один день, до регулировки )
( через несколько дней, после регулировки )
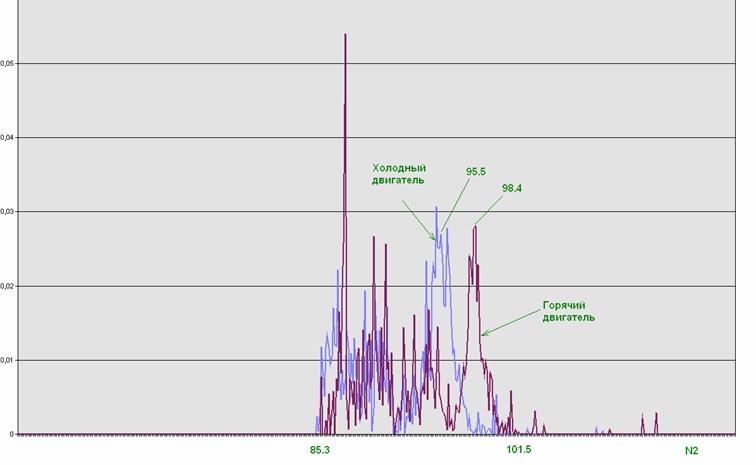
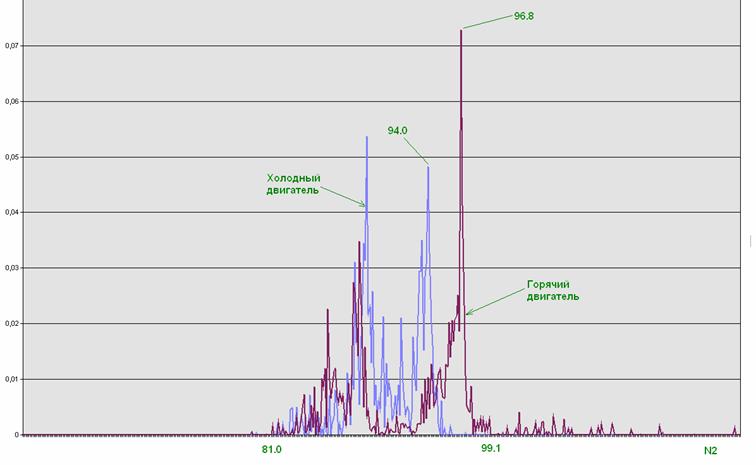
Рис. 6. Статистическое распределение особых точек.
Синий график – холодный двигатель, красный – горячий.
Коллекция графиков распределений на разных двигателях – см. на отдельной странице.
9.
Приложение 2.
Для достижения необходимой
точности расчетов при подгонке модели, реализованных средствами языка
программирования C++, был создан класс, объектами
которого являются матрицы. Класс содержит некоторые функции для работы с
матрицами, а также «перегрузку» операторов сложения, умножения на матрицу,
умножения на число, что позволяет значительно упростить программный код.
Объект «матрица» в нашем классе
имеет не фиксированную, а плавающую размерность. Сделано это для того, чтобы
программа могла оперативно выделять и освобождать память, максимально используя
ресурс компьютера и не допуская, таким образом, переполнения памяти. Такой подход
дал нам возможность для всех переменных – членов любой матрицы определить тип “long double”, то
есть использовать при всех расчетах максимальную точность, что необходимо для
работы с аппроксимациями Паде.
Исходный код класса прилагается:
Файл mymatrix.cpp:
//---------------------------------------------------------------------------
#pragma hdrstop
#include <vcl.h>
#include "mymatrix.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
//---------------------------------------------------------------------------
MyMatrix temp; // Просто глобальная переменная
//---------------------------------------------------------------------------
MyMatrix::MyMatrix()
{
data = NULL;
}
//---------------------------------------------------------------------------
MyMatrix MyMatrix::operator+(MyMatrix
op2)
{
int i, j; // op2 - второй операнд; первый операнд здесь - this,
// n, k, m - члены этого объекта (к которому прибавляем)
if(n!=op2.n || m!=op2.m)
{
Application->MessageBox("Параметры складываемых матриц не совпадают!","",MB_OK);
oblom = true;
return *this; // Возвращаем первый операнд, то есть ничего не делаем
}
temp.data = NULL;
temp.data = new long double*[m];
for (j = 0; j < m; j++)
{
temp.data[j] = new long double[n];
}
temp.n = n; temp.m = m; temp.k = temp.m;
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
{
temp.data[i][j] = data[i+k-m][j] + op2.data[i + op2.k-op2.m][j];
}
return temp;
}
//------------------------------------------------------------------------------
MyMatrix
MyMatrix::operator*(MyMatrix op2)
{
int i, j, s;
long double x;
if(n!=op2.m)
{
Application->MessageBox(" Число столбцов левого множителя\n\n не совпадает\n\n с числом строк
правого множителя!","",MB_OK);
oblom = true;
return *this; // Возвращаем первый операнд, то есть ничего не делаем
}
temp.data = NULL;
temp.data = new long double*[m];
for (j = 0; j < m; j++)
{
temp.data[j] = new long double[op2.n]; // столбцов - столько
же, сколько у второго операнда
}
temp.m = m; // строк - столько же, сколько у первого операнда
temp.n = op2.n; // столбцов - столько же, сколько у второго операнда
temp.k = temp.m;
for (i = 0; i < m; i++) // Идем по строкам первой матрицы
for (j = 0; j < op2.n; j++) // Идем по столбцам второй матрицы
{
x = 0;
for (s = 0; s < n; s++) // Умножаем строку на столбец
{
x = x + (data[i+k-m][s] * op2.data[s+op2.k-op2.m][j]);
}
temp.data[i][j] = x;
}
return temp;
}
//------------------------------------------------------------------------------
MyMatrix MyMatrix::operator*(long
double op2)
{
int i, j;
temp.data = NULL;
temp.data = new long double*[m]; // Выделяем память под temp.data
for (j = 0; j < m; j++)
{
temp.data[j] = new long double[n];
}
temp.n = n; temp.m = m; temp.k = temp.m;
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
{
temp.data[i][j] = data[i+k-m][j] * op2;
}
return temp;
}
//------------------------------------------------------------------------------
MyMatrix MyMatrix::T()
{
int i, j;
temp.data = NULL;
temp.data = new long double*[n];
for (j = 0; j < n; j++)
{
temp.data[j] = new long double[m];
}
temp.m = n; temp.n = m; temp.k = temp.m;
for(i=0; i<temp.m; i++)
for(j=0; j<temp.n; j++)
{
temp.data[i][j] = data[j+k-m][i];
}
return temp;
}
//------------------------------------------------------------------------------
MyMatrix
MyMatrix::operator=(MyMatrix op2)
{
int i, j;
if(oblom || n!=op2.n || m!=op2.m)
{
if(n!=op2.n || m!=op2.m)
Application->MessageBox("Параметры матриц не совпадают (при присвоении)!","",MB_OK);
oblom = true;
if(temp.data) {
temp.de_allocate(); temp.data = NULL; }
return *this; // Возвращаем первый операнд, то есть ничего не делаем
}
for (i = 0; i < m; i++)
for (j = 0; j < n; j++)
{
data[i+k-m][j] = op2.data[i + op2.k-op2.m][j]; // Перегрузка данных всегда происходит из "живого" блока правой матрицы в "живой" блок левой
}
if(temp.data) {
temp.de_allocate(); temp.data = NULL; }
return *this;
}
//------------------------------------------------------------------------------
void __fastcall MyMatrix::de_allocate()
{
for (int i = k-m; i < k && k >= m; i++)
if(data[i]) delete[]
data[i]; // STEP 1: DELETE
THE COLUMNS
delete[] data; // STEP 2:
DELETE THE ROWS
data = NULL;
}
//------------------------------------------------------------------------------
Файл mymatrix.h:
//---------------------------------------------------------------------------
#ifndef mymatrixH
#define mymatrixH
#include <StdCtrls.hpp>
//---------------------------------------------------------------------------
// ЕСЛИ СЧИТАЕМ МАТРИЦУ СТАТИЧЕСКОЙ, ПРИ ЕЕ ОПРЕДЕЛЕНИИ ПИШЕМ: op2.k = op2.m; op2.M = op2.m !!!!!
class MyMatrix
{
public:
int M; // Максимальный номер строки (+ 1)
int k; // Текущий номер последней строки (+ 1)
int m; // THE
NUMBER OF ROWS
int n; // THE
NUMBER OF COLUMNS
long double **data;
bool oblom; // Признак аварийного результата выполнения оператора
TListBox *ListBox11;
void __fastcall
de_allocate(void);
void __fastcall display(void);
MyMatrix T(void);
MyMatrix(); //
Конструктор
MyMatrix operator=(MyMatrix op2);
MyMatrix operator+(MyMatrix op2);
// Сложение матриц
MyMatrix operator*(MyMatrix op2);
// Умножение матриц
MyMatrix operator*(long double op2); // Умножение матрицы на число (справа!)
};
//---------------------------------------------------------------------------
#endif
Литература
1. Коковин В.Д, Семенин В.В., Антонец К.Н. Алгоритмическое обеспечение диагностирования авиационных двигателей с использованием информации БУР на основе методов теории идентификации систем управления. Сборник докладов III научно-практической конференции «Накопители полетных данных». Курск, 2008г.
2.
G.A.Baker,
P.Graves-Morris. Pade
Approximants. Encyclopedia of Mathematics and its Applications, Vol. 13-14, 1981.