Класс DMatrix

Каталог инструментов торгового дома Роберт Кенц

Модель зависимости вибрации двигателя

от скорости вращения вала

Калюжный О.Н.

oleg314@mail.ru

2017

ВВЕДЕНИЕ

Одним из главных показателей «здоровья» двигателя является низкая вибрация на различных режимах работы.

Уровень вибрации имеет общую тенденцию к росту при увеличении частоты вращения. Однако эта зависимость является нелинейной и зависит от скорости изменения оборотов (углового ускорения) и от направления такого изменения (увеличение или сброс оборотов) (см. рис. 1). В случае износа изделия или при врожденных дефектах повышение уровня вибрации происходит неодинаково в разных диапазонах частот вращения.

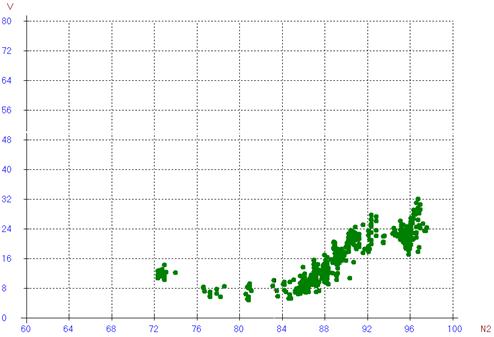
Рис. 1. Фактическая зависимость между оборотами ротора высокого давления ТРД и виброскоростью (виброхарактеристика).

Под уровнем вибрации мы понимаем виброскорость, измеряемую в мм/сек., то есть грубую интегральную характеристику, полученную от датчика виброскорости при низкой частоте регистрации; при такой частоте регистрации спектральный анализ сигнала неэффективен, поэтому мы будем использовать другой подход.

В настоящее время для оценки вибросостояния двигателя принято использовать слишком простые критерии оценки. Как правило, это рост виброскорости от испытания к испытанию, что редко позволяет предугадать отказ работающего двигателя, например, в полете, если имеется в виду двигатель самолета. Поэтому для идентификации «здоровья» двигателя необходимо построить более сложную модель зависимости, которую мы будем искать в виде дифференциального уравнения.

Общий вид дифференциального уравнения обычно получают, отталкиваясь от физической модели, учитывающей механические и (в случае турбореактивного двигателя) термодинамические свойства двигателя. Такой подход реализован в классических трудах по ТРД, например, в книге Ю.А.Кочеткова «Основы автоматики авиационного оборудования». Несмотря на основательность такого подхода, он имеет ряд недостатков, связанных, например, со сложностью современных двигателей. Уравнение, написанное для идеальной модели двигателя, перестает соответствовать реальному процессу при повышении сложности изделия, причем изменяются не только коэффициенты, но и сам вид этого уравнения. В то же время, существование современных персональных компьютеров с большим быстродействием позволяет подбирать вид уравнения в ходе «компьютерного эксперимента».

В данной статье предложен общий вид дифференциального уравнения, полученный в ходе такого эксперимента. Коэффициенты уравнения рассчитываются для каждого отдельного испытания (газовки) двигателя; набор коэффициентов используется для построения мат. модели и вычисления критерия состояния двигателя.

В результате испытаний получен критерий исправности двигателя, основанный на сравнении модельных данных с реальными значениями виброскорости в определенном диапазоне частот вращения вала. Сделан вывод, что в таком диапазоне «невязка» между моделью и реальными данными велика и размер этой невязки тем больше, чем сильнее перекос вала.

ЭКСПЕРИМЕНТ

Рабочим материалом для тестирования модели являлись файлы с записями изменяющихся значений параметров испытаний на вибростенде и наземных испытаний ТРД. Вибростенд состоит из электромотора, вала и поддерживающей опоры (с датчиком частоты вращения), а также датчика виброскорости, закрепленного на станине.

Основными причинами повышения вибрации турбореактивного двигателя является некачественный межроторный подшипник или несоосность различных частей вала. В свою очередь, неисправность подшипника при вращении приводит к биениям вала, то есть непосредственной причиной нештатной вибрации все равно можно с некоторой натяжкой считать перекос вала. Поэтому при испытаниях на вибростенде имитировался перекос, для чего поддерживающая опора была закреплена на шарнире, позволяющем изменять угол наклона опоры по отношению к электромотору.

БАЗОВАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Для обработки результатов испытаний на вибростенде мы использовали дифференциальное уравнение, связывающее виброскорость, частоту вращения вала (угловую скорость) и производную от частоты вращения (угловое ускорение). В случае испытаний турбореактивного двигателя в уравнение были также включены температура воздуха перед воздухозаборником и другие параметры; планируется описать результаты обработки испытаний ТРД в отдельной статье, а здесь будет описан вариант для вибростенда.

Поток данных, поступающий на вход нашего алгоритма, в каждый момент времени представляет собой вектор (V_i, N_i), где V_i – измеренная виброскорость, N_i – измеренная частота вращения ротора. Значения N_i подвергаются предварительной обработке – сглаживанию средним арифметическим с периодом τ. Такое сглаживание применяется с 2-мя целями:

1. Гашение влияния шумов в линии и ошибок округления.

2. Учет инерционности вибрации при росте / падении оборотов. Эта цель является главной, т.к. изменение виброскорости происходит со значительной временной задержкой относительно изменения оборотов.

Обозначим и сформулируем наше базовое уравнение:

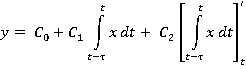
В этом уравнении сглаживание записано в интегральной форме; кроме того, в нем присутствует производная от сглаженного значения. На практике иногда имеет смысл задать разные периоды сглаживания для второго и третьего членов уравнения.

Перепишем третий член в виде:

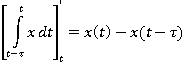
Перейдем от интегральной формы уравнения к виду, более привычному с точки зрения теории автоматики, продифференцировав его левую и правую части:

Применим к уравнению преобразование Лапласа и получим передаточную функцию:

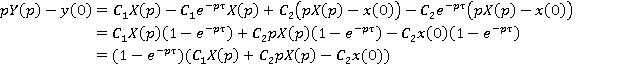
Итого, передаточная функция процесса:

Данную передаточную функцию можно считать соответствующей параллельной системе (раскроем скобки) со звеньями:

– интегрирующее звено;

– интегрирующее звено с дискретным запаздыванием;

–пропорциональное звено;

– звено дискретного запаздывания.

РАСЧЕТ КОЭФФИЦИЕНТОВ МОДЕЛИ

Для расчета коэффициентов уравнения использован специально созданный на языке C++ класс DMatrix. В этом классе реализованы методы решения систем уравнений, позволяющие быстро и с максимальным использованием памяти компьютера обрабатывать поступающий на вход поток значений параметров.

В общем виде, процесс обработки данных выглядит следующим образом.

В компьютер с определенной частотой (с частотой регистрации) поступает набор данных + значение переменной времени. Этот набор может поступать как от датчиков в режиме реального времени, так и из файла. По полученным данным рассчитываются сглаженные значения и производные, входящие в дифференциальное уравнение.

Наша задача – решить уравнение относительно его коэффициентов C_i. После получения n наборов данных мы имеем n линейных уравнений относительно C_i ; этот набор уравнений преобразуется методом МНК к квадратной системе, имеющей единственное решение. Далее полученные уравнения поочередно поступают на вход проекционного решающего алгоритма, задача которого – уточнить решение, полученное на предыдущем шаге. В качестве первого решения берется произвольный набор коэффициентов C_i, на остальных шагах на вход проекционного алгоритма подается предыдущее решение.

Метод решения, реализованный в классе DMatrix, имеет несколько настроек для того, чтобы можно было добиться хорошей скорости подгонки модели. Для этого нужно, с одной стороны, решать на каждом шаге достаточно большую систему уравнений и, с другой стороны, система уравнений не должна быть очень большой, чтобы не отнимать много времени на каждом шаге. Кроме того, скорость решения зависит от способности алгоритма «выскакивать» из локальных потенциальных ям при блуждании решения по фазовому пространству дифференциального уравнения – для решения этой проблемы также предусмотрено 2 настроечных коэффициента. И третий фактор (влияющий на скорость подгонки при расчетах в реальном времени) – это соотношение значимости более свежей информации по отношению к менее свежей. Для этого в нашем проекционном алгоритме существует еще одна настройка – «коэффициент экспоненциального запаздывания».

Познакомиться с примерами использования класса DMatrix и получить исходный текст можно здесь.

Итак, процесс подгонки коэффициентов заключается в последовательном решении N уравнений, составленных по N наборам значений, поступившим на вход от датчиков. Число N есть произведение частоты дискретизации на время эксперимента.

Как правило, для получения качественного результата одного прохода по записи эксперимента недостаточно. Кроме того, мы оказываемся перед выбором: использовать ли все данные, или прореживать их с некоторым шагом. В первом случае полученные коэффициенты скорее отражают физику процесса на конечном временном отрезке испытания и не вполне подходят для начального. Во втором случае мы добровольно теряем полезную информацию (особенно это критично при взятии производных).

Поэтому используется следующий метод. При первом проходе по записи учитываются все точки. При следующем – прореженные с шагом 2. И так далее, до определенного наперед заданного максимального шага – после этого все следующие проходы делаются с этим максимальным шагом.

РАСШИРЕННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Описанная выше базовая модель «работает» на практике, в том смысле, что при подгонке коэффициентов уравнения мы наблюдаем:

- стабильное схождение подгоняемых коэффициентов к некоторому вектору, то есть при достаточно большом количестве шагов на каждом следующем шаге этот вектор почти не изменяется;

- близость значений найденных коэффициентов для разных испытаний одного и того же физического устройства, находящегося в одних и тех же температурных условиях.

Иначе говоря, базовая модель описывает процесс адекватно, хотя и не слишком точно.

Более качественную мат. модель удалось получить путем добавления в нее следующих членов:

1. Полином от сглаженного значения оборотов вращения. То есть вместо

, где ,

запишем

В результате получается:

Идеология этой добавки понятна: зависимость между вибрацией и скоростью вращения при медленном (плавном) изменении оборотов () не является линейной, следовательно, имеет смысл аппроксимировать ее рядом Тейлора.

Надо отметить, что такое усложнение делает наше дифференциальное уравнение нелинейным.

2. Слагаемое . Эта добавка также является нелинейной.

Получается (с учетом полинома) уравнение:

,

где D – константа.

Использование этого уравнения дает наилучший результат.

ПРАКТИЧЕСКИЕ РЕЗУЛЬТАТЫ

Прежде всего, сравним результаты, полученные с использованием базовой мат. модели и с использованием усложненных моделей (на примере одного и того же испытания).

В результате подгонки результатов испытания к базовой модели получаем уравнение:

Как видно на скриншоте, модель (синие точки) отражает линейный тренд, но плохо реагирует на скорость изменения частоты вращения вала (то есть на ).

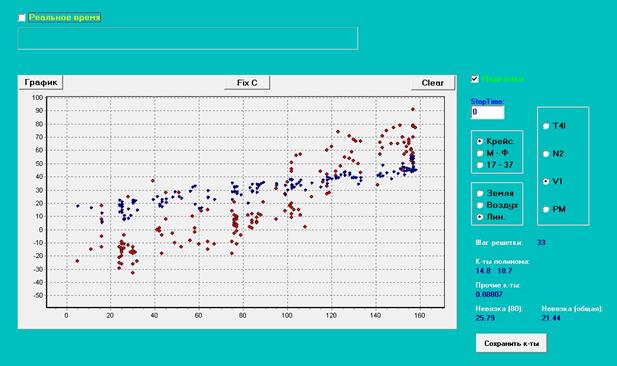
Рис. 2. Результат подгонки к базовой модели.

Ось абсцисс – частота вращения, ось ординат – виброскорость.

Красные точки – реальные наблюдения, синие точки – модельные значения.

Невязка (общая) – среднее отклонение (по модулю) реальных данных от модельных.

Здесь и далее на графиках: на оси ординат отложены значения в мм/сек. за вычетом некоторой константы, на оси ординат – обороты в мин. / 10.

Теперь усложним модель, добавив полином 5-й степени.

Результат:

Точки модели ложатся близко к реальным, модель лучше реагирует на скорость изменения оборотов. Невязка (среднее отклонение по модулю, в правом нижнем углу) – гораздо меньше (8.85 против 21.44 в предыдущем случае).

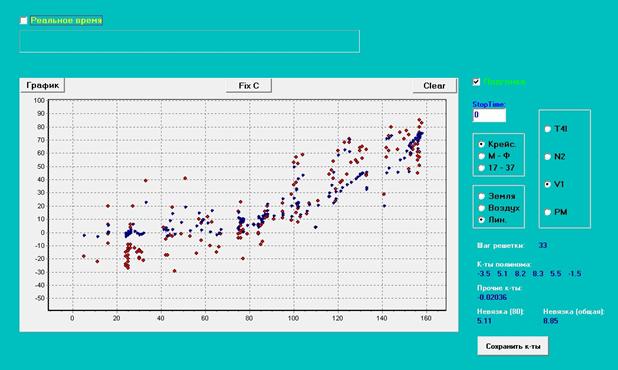
Рис. 3. Результат подгонки к модели с полиномом.

Добавим в уравнение член .

После подгонки получим:

Невязка в этом случае – лучше (6.05), модель еще лучше реагирует на производную:

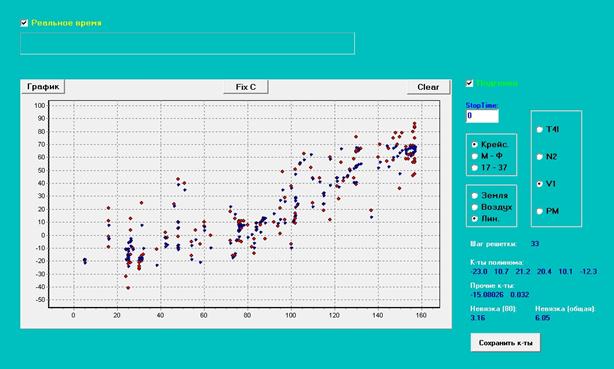
Рис. 4a. Результат подгонки к модели с полиномом и дробной добавкой

(шаг решетки = 33).

При шаге прореживания = 3 (в начале подгонки) видно, что наша модель хорошо реагирует на скорость изменения оборотов, повторяя реальные траектории:

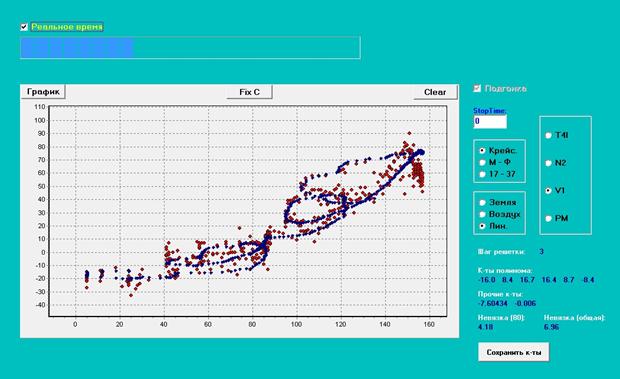
Рис. 4b. Результат подгонки к модели с полиномом и дробной добавкой

(шаг решетки = 3).

Результаты еще двух испытаний на стенде:

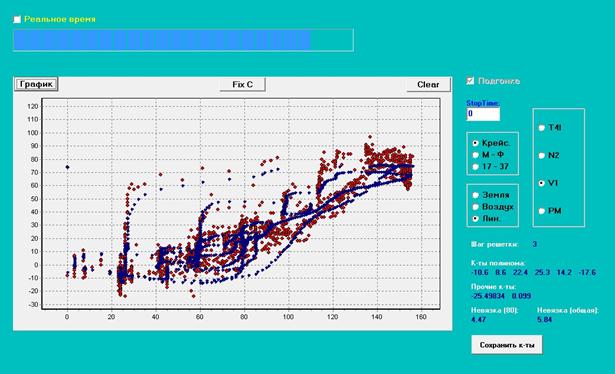
Рис. 5a. Испытание №2, шаг решетки = 3

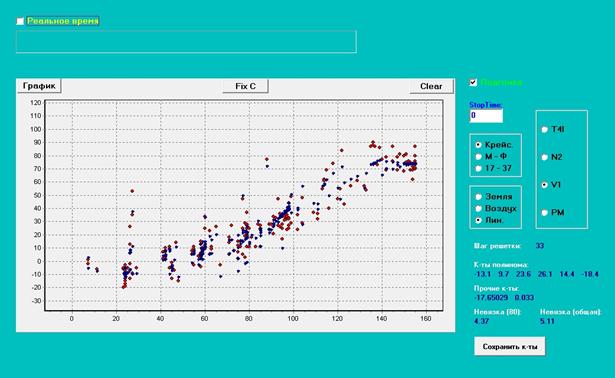
Рис. 5b. Испытание №2, шаг решетки = 33

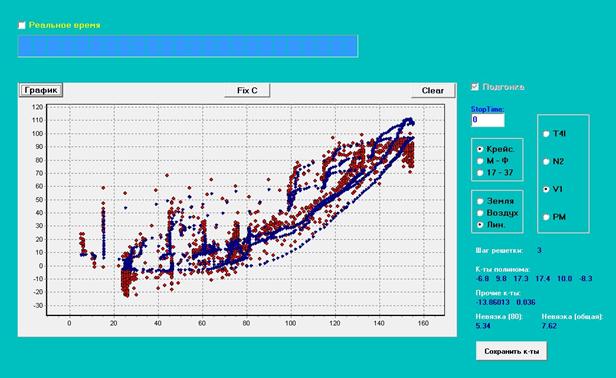
Рис. 6a. Испытание №3, шаг решетки = 3

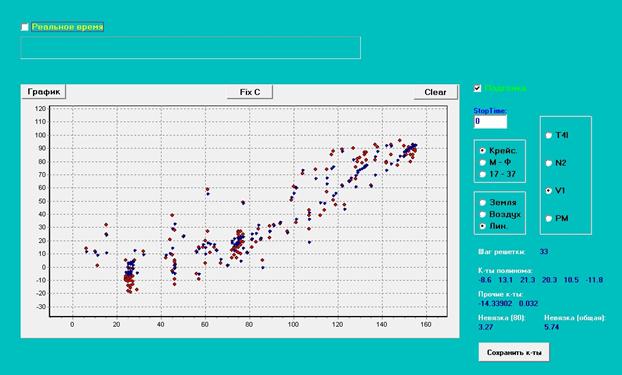
Рис. 6b. Испытание №2, шаг решетки = 33

Обратимся к нашей главной задаче, которая заключается в распознавании двигателей с дефектами, в частности, с перекосом вала. Практика показывает, что при испытаниях такого двигателя зависимость V = V(N) в окрестности некоторых скоростей вращения ведет себя «нестандартно». Поэтому имеет смысл сравнивать невязку, рассчитанную по всем значениям оборотов, с невязкой, рассчитанной в окрестности 750-850 об./мин.

В результате экспериментов выявлена закономерность: если у качественного двигателя общая невязка ≥ локальной невязки, то у двигателя с перекосом наблюдается обратная картина общая невязка < локальной невязки. То есть в окрестности критической точки мотор ведет себя «нестандартно».

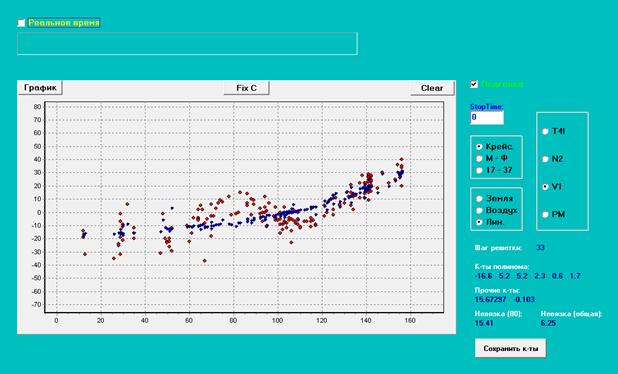
Рис. 7. Испытание мотора с перекосом вала.

Невязка (750-850) = 12.41, невязка общая = 6.25 .

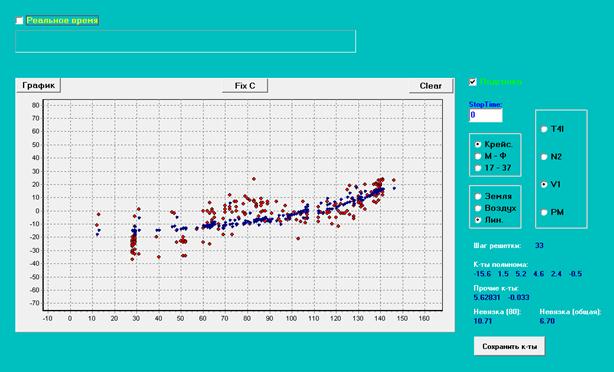
Рис. 8. Испытание мотора с перекосом вала.

Невязка (750-850) = 10.71, невязка общая = 6.70 .

Результаты испытаний с перекосом вала можно интерпретировать еще и по-другому. Как видим на рис. 7,8, рассчитанная мат. модель получилась не очень чувствительной к производной от оборотов. Можно предположить, что сама структура уравнения в случае неисправностей должна быть другой.

Это является еще одним подтверждением правильности выбранного пути исследований. А именно – поиска структуры дифференциального уравнения методом компьютерного эксперимента. Потому что вряд ли возможно, отталкиваясь от положений сопромата и газодинамики, изобретать отдельное уравнение для двигателя с «хорошим» валом и с «плохим» валом, с «правильным» состоянием газовоздушного тракта и с «неправильным» и т.п.

В заключение надо сказать пару слов о двух основных трудностях при использовании вибростенда, мешающих подгонке модели.

1. Резонансы, не связанные с вращением. Такие резонансы возникают на частотах, кратных собственным частотам различных узлов вибростенда. В частности, они могут возникать при неправильном закреплении мотора на станине.

2. Инерция вибрации. Например, слишком большая, но легкая и плохо закрепленная станина продолжает колебаться на «старой» частоте в течение нескольких десятых долей секунды после изменения скорости вращения. В то время как наша модель имеет свою инерцию вибрации, на которую не должна влиять инерция станины.

Исправить эти два недостатка при постановке эксперимента проще всего с помощью придания конструкции необходимой жесткости.

При построении математической модели для турбореактивного двигателя выяснилось, что в этом случае имеет смысл добавить в уравнение члены, содержащие температуру и давление на входе в двигатель, точнее – отношение T1/P1. Но об этом – в другой статье.