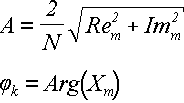Что такое зеркальный эффект.
Предположим, что исходный сигнал состоял из суммы гармоник.
fs(t) = As cos(2πtms / T + φs). Пусть мы этот
сигнал подвергли дискретизации, выполнили над ним прямое и обратное
преобразование Фурье. Представили в виде суммы гармоник Gk(t) = Ak cos(2πtk / T + φk), как
это описано в предыдущей главе. Спрашивается, эти гармоники Gk -
те же самые, что и исходные гармоники fs или нет? Оказывается, нет, не те.
Но кое-какую информацию об исходных гармониках все же можно попытаться восстановить.
Эта задача имеет практический интерес. Пусть нам дан некий сигнал, который физически
получился как сумма гармонических колебаний (или близких к ним). Простейший пример:
кто-то сыграл аккорд, аккорд записан как звуковое колебание в виде mp3 или wav-файла; и надо
восстановить, из каких нот аккорд состоял. Или другой случай. Во время испытаний
самолета возик флаттер (разрушительные нарастающие колебания), самолет разбился, но самописцы
в черном ящике записали изменение перегрузки (суммарное механическое колебание). Надо
посмотреть, из каких гармоник состояло это колебание. Каждой гармонике соответствует
некоторая часть конструкции. В результате можно понять, какие части самолета колебались сильнее
всего и вызвали флаттер.
Вернемся к предыдущей ситуации.
Дана функция f(t) на отрезке [0, T].
Выполнена ее дискретизация, для чего отрезок разбит на
N равных частей в точках tn = Tn/N
и вычислены значения функции в этих точках: {x} : xn = f(tn) = f(Tn/N).
Пусть выполнено прямое дискретное преобразование Фурье (далее - ДПФ) {X} : Xk = NAke jφk, и
функция разложена на сумму из N гармоник:
Gk(t) = Ak cos(2πtk / T + φk)
Теперь предположим, что наша исходная функция сама представляла
собой такую гармонику:
f(t) = A cos(2πtm / T + φ).
Получится ли в результате ее преобразования последовательность {X},
в которой все элементы равны нулю, кроме элемента Xm = NAme jφm,
который дает как раз эту гармонику?
Gm(t) = Am cos(2πtm / T + φm) = f(t), Am = A, φm = φ
Как уже говорилось, нет, нас ждет разочарование. Вместо этой одной гармоники
мы получим две:
Gm(t) = (A/2) cos(2πtm / T + φ) = f(t) / 2 = f'(t)
и
GN-m(t) = (A/2) cos(2πt(N - m) / T - φ) = f''(t)
Как видите у них половинные амплитуды, противоположные фазы, а
частоты зеркально симметрично расположены на отрезке [0, N].
Это - тот самый зеркальный эффект.
Неоднозначность представления суммой гармоник.
Преобразуем сумму этих гармоник по формуле суммы косинусов:
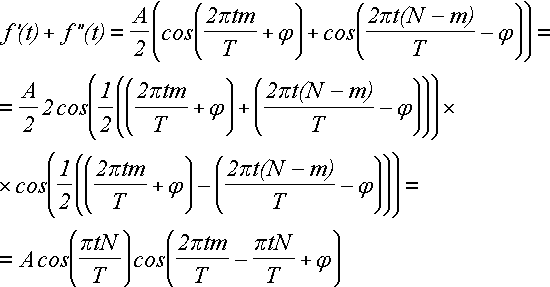
Итого:
f'(t) + f''(t) = A cos(πtN / T) cos(2πtm / T - πtN / T + φ) (30)
А нам требовалось:
f(t) = A cos(2πtm / T + φ) (31)
Однако, формулы (30) и (31) дают один и тот же результат в точках
tn = Tn / N. В самом деле, подставим
Tn / N вместо t сначала в (30):
f'(t) + f''(t) =
= A cos(πTnN / TN)
cos(2πTnm / TN - πTnN / TN + φ) =
= A cos(πn)
cos(2πnm / N - πn + φ) = ...
Второй множитель разложим по формуле косинуса разности, отделив
πn:
... = A cos(πn)
[cos(2πnm / N + φ)
cos(πn) +
+ sin(2πnm / N + φ)
sin(πn)] = ...
Учитывая, что для целого n выполняется sin(πn) = 0
и cos2(πn) = 1, получаем:
... = A cos(πn)
[cos(2πnm / N + φ)
cos(πn)] =
= A cos2(πn)
cos(2πnm / N + φ)
= A cos(2πnm / N + φ)
(32)
Теперь подставим Tn / N вместо t в (31):
f(t) = A cos(2πtm / T + φ)
= A cos(2πTnm / TN + φ) =
= A cos(2πnm / N + φ)
(33)
Формулы (32) и (33) совпадают, что и требовалось доказать.
Из этого примера следует важный вывод. Заданная дискретная
последовательность {x} может быть разложена
в общем случае на разные суммы гармоник
Gk(t). Даже в элементарном случае,
когда исходная функция представляла собой одну гармонику,
в результате можно получить две. То есть, разложение
дискретной последовательности на гармоники неоднозначно.
Этим эффектом мы обязаны именно дискретизации. Дело в том, что
если вместо ДПФ использовать его
непрерывный аналог - разложение в ряд Фурье непрерывной функции
или непрерывное преобразование Фурье
f(t), то мы получим единственую
правильную гармонику Gm(t) = A cos(2πtm / T + φ) = f(t). Если же мы применяем ДПФ,
то получим сумму гармоник, которая только в точках дискретизации
совпадает с исходной функцией:
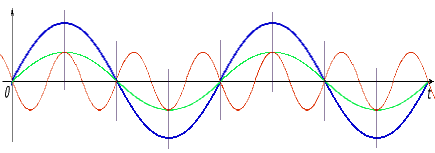
На этом графике для N = 8 и m = 2 синим цветом
показана исходная гармоника f(t) и две гармоники,
которые получаются в результате преобразвания Фурье: f'(t)
зеленым цветом и f''(t)
красным. В точках дискретизации, отмеченных
вертикальными штрихами, сумма гармоник f'(t) и f''(t)
совпадает с гармоникой f(t).
Заметим также, что тот же результат преобразования получился бы, если
бы мы в качестве исходной функции f(t) взяли
2f''(t) или f'(t) + f''(t).
Это следует из того, что в результате
дискретизации была бы получена та же последовательность {x}
и результаты ДПФ, естественно, дали бы то же
самое.
Итак, мы имеем правило:
Разложение на гармоники, когда исходные данные представлены дискретным
набором точек {x} является принципиально неоднозначным.
Функции
f(t) = A cos(2πtm / T + φ),
2f''(t) = A cos(2πt(N-m) / T - φ) и
f'(t) + f''(t) = (A/2) cos(2πtm / T + φ) + (A/2) cos(2πt(N-m) / T - φ)
дают после дискретизации одни и те же исходные данные и те же результаты ДПФ.
Доказательство зеркального эффекта.
В начале главы упоминалось о том, что в результате ДПФ гармонической
функции на практике получаются две гармоники. Однако этот эмпирический
факт не доказывался. Докажем теперь строго, какие гармоники дает
произвольная гармоническая функция
f(t) = A cos(2πtm / T + φ)
при целочисленном
m  [0, N[.
[0, N[.
Напомним формулу прямого ДПФ:
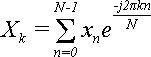
В данном случае
xn =
f(tn) = f(Tn / N) =
A cos(2πTnm / NT + φ) =
A cos(2πnm / N + φ)
Введем обозначения:
wn = 2πn / N
Zk,n = (f(tn) / A) e-j2πkn / N
= cos(wnm + φ) e-jwnk
В результате формула прямого ДПФ упрощается до:
Xk = A Zk,n
Zk,n
Теперь преобразуем Zk,n:
Zk,n = cos(wnm + φ) e-jwnk =
применяем формулу Эйлера:
= cos(wnm + φ) (cos(-wnk) + j sin(-wnk)) =
= cos(wnm + φ) (cos(wnk) - j sin(wnk)) =
раскрываем скобки:
= cos(wnm + φ) cos(wnk) - j cos(wnm + φ) sin(wnk) =
применяем формулы произведения косинусов и синуса на косинус:
= (1/2)[cos((wnm + φ) - wnk) + cos((wnm + φ) + wnk)] -
= - (j/2)[sin(wnk - (wnm + φ)) + sin(wnk + (wnm + φ))] =
перегруппировываем слагаемые:
= (1/2)[cos((wnm + φ) - wnk)
+ cos((wnm + φ) + wnk) -
- j sin(wnk - (wnm + φ))
- j sin(wnk + (wnm + φ))] =
= (1/2)[cos((wnm + φ) - wnk)
+ cos((wnm + φ) + wnk) +
+ j sin((wnm + φ) - wnk)
- j sin((wnm + φ) + wnk)] =
= (1/2)[cos(wnm + φ - wnk)
+ j sin(wnm + φ - wnk) +
+ cos(wnm + φ + wnk)
- j sin(wnm + φ + wnk)] =
применяем формулу Эйлера (только наоборот):
= (1/2)[e j(wnm + φ - wnk)
+ e -j(wnm + φ + wnk)] =
и выносим за скобки все, что можно:
= (1/2)[e jφe jwn(m - k)
+ e -jφe -jwn(m + k)]
Теперь подставляем полученные величины в сумму ДПФ и преобразуем:
Xk = A Zk,n =
Zk,n =
= A (1/2)[e jφe jwn(m - k)
+ e -jφe -jwn(m + k)] =
(1/2)[e jφe jwn(m - k)
+ e -jφe -jwn(m + k)] =
= (A/2)e jφ e jwn(m - k)
+ (A/2)e -jφ
e jwn(m - k)
+ (A/2)e -jφ e -jwn(m + k) =
e -jwn(m + k) =
подставляем wn:
= (A/2)e jφ e j2πn(m - k) / N
+ (A/2)e -jφ
e j2πn(m - k) / N
+ (A/2)e -jφ e -j2πn(m + k) / N =
e -j2πn(m + k) / N =
вводим обозначения для сумм:
= (A/2)e jφS1
+ (A/2)e -jφS2
Легко видеть, что суммы S1 и
S2 являются геометрическими прогрессиями,
а формула суммы геометрической прогрессии нам известна:
SN = a0(qN - 1) / (q - 1), q ≠ 1 (34)
Первый элемент прогрессии в обоих случаях равен a0 = 1.
Знаменатели прогрессий равны
q1 = e j2π(m - k) / N для S1
и
q2 = e -j2π(m + k) / N для S2.
Условие q ≠ 1 вынуждает нас решить уравнения:
e j2π(m - k) / N = 1,
и
e -j2π(m + k) / N = 1,
Учитывая Теорему 0, получим, что условие q ≠ 1
не выполняется при k = m для S1 и
при k = (N - m) для S2.
В случае, когда выполняются оба условия:
k = m и k = (N - m), то есть k = m = N /2 обе суммы нельзя считать по формуле
геометрической прогресии.
В случае k = m для S1 придется
выполнить небольшие дополнительные преобразования:
S1 =  e j2πn(m - m) / N
=
e j2πn(m - m) / N
=  1 = N
1 = N
Аналогично в случае k = N - m для S2:
S2 =  e -j2πn(m + N - m) / N =
e -j2πn(m + N - m) / N =
 e -j2πn =
e -j2πn =
 1 = N
1 = N
В случае k = m = N / 2 имеем:
Xk = (A/2)Ne jφ + (A/2)Ne -jφ =
= (A/2)N(e jφ + e -jφ) =
= (A/2)N(cos φ + j sin φ + cos φ - j sin φ) =
= (A/2)N(2 cos φ) =
= ANcos φ
В случае k = m = 0 имеем:
Xk = (A/2)e jφN + (A/2)e -jφN
= (A/2)N(e jφ + e -jφ) =
= (A/2)N(cos φ + jsin φ + cos φ - jsin φ) = ANcos φ
Наконец, получаем формулу для Xk:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ + (A/2)e -jφ(e -j4πm - 1) / (e -j4πm / N - 1)
Для k = (N - m) ≠ N / 2:
Xk = (A/2)e jφ(e j4πm - 1) / (e j4πm / N - 1) + (A/2)Ne -jφ
Для остальных k:
Xk = (A/2)e jφ(e j2π(m - k) - 1) / (e j2π(m - k) / N - 1) +
+ (A/2)e -jφ(e -j2π(m + k) - 1) / (e -j2π(m + k) / N - 1) (35)
Заметим, что эта формула получена без использования
факта целочисленности m и k.
Теперь учтем целочисленность. Для этого применим Теорему 0 и
заменим в формуле (35) экспоненты на 1 везде, где выполняется это
условие:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ + (A/2)e -jφ(1 - 1) / (e -j4πm / N - 1)
Для k = (N - m) ≠ N / 2:
Xk = (A/2)e jφ(1 - 1) / (e j4πm / N - 1) + (A/2)Ne -jφ
Для остальных k:
Xk = (A/2)e jφ(1 - 1) / (e j2π(m - k) / N - 1) +
+ (A/2)e -jφ(1 - 1) / (e -j2π(m + k) / N - 1)
Сокращаем везде, где получаются нули, и приходим к формулам:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ
Для k = (N - m) ≠ N / 2:
Xk = (A/2)Ne -jφ
Для остальных k:
Xk = 0 (36)
Вывод:
Зеркальный эффект всегда проявляется так, что гармонические
колебания:
f(t) = A cos(2πtm / T + φ),
2f''(t) = A cos(2πt(N-m) / T - φ) и
f'(t) + f''(t) = (A/2) cos(2πtm / T + φ) + (A/2) cos(2πt(N-m) / T - φ)
в процессе дискретного преобразования Фурье представляются
как сумма колебаний
f'(t) + f''(t).
При этом все коэффициенты ДПФ равны нулю за исключением
Xm = (A/2)Ne jφ
и
XN - m = (A/2)Ne -jφ
кроме частных случаев m = N / 2 и m = 0, в которых
единственный ненулевой коэффициент:
Xm = ANcos φ
В этом последнем частном случае зеркальный эффект
выглядит несколько иначе: у исходного гармонического
колебания теряется фаза и искажается амплитуда. Лишь
частота сохраняется прежней.
Исправление зеркального эффекта.
Таким образом зеркальный эффект в подавляющем большинстве случаев
искажает исходную картину, поскольку в действительности очень
редко на вход подается сумма двух гармонических сигналов
f'(t) + f''(t) именно с таким соотношением
частот: m/T и (N - m)/T.
В результате исходный спектр искажается, словно отражаясь в
зеркале:
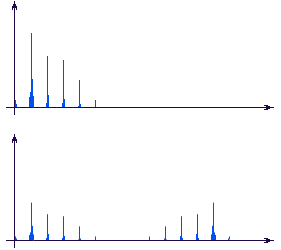
На этом рисунке сверху показан ожидаемый спектр сигнала,
полученный с помощью непрерывного преобразования Фурье, а снизу -
полученный на компьютере с помощью дискретного преобразования Фурье.
Нижний спектр искажен зеркальным эффектом.
Пусть мы обннаружили ненулевой коэффициент Xm.
Выдвинем гипотезу, что этот коэффициент соответствует
исходному гармоническому колебанию. Восстановим его
амплитуду, фазу и частоту.
Xm = (A/2)Ne jφ
f(t) = A cos(2πtm / T + φ).
Частота восстанавливается проще всего: ν = m/T,
где m - индекс найденного ненулевого элемента Xm.
Амплитуда и фаза восстанавливаются по формуле (29):
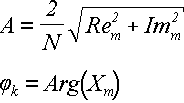
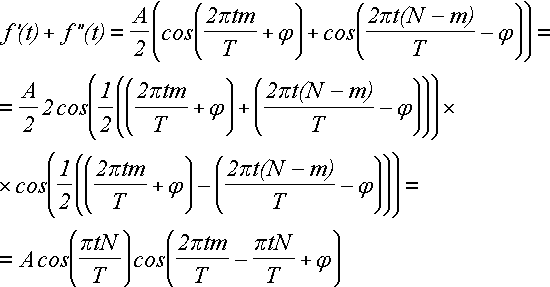

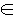 [0, N[
[0, N[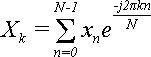
 Zk,n
Zk,n Zk,n =
Zk,n = (1/2)[e jφe jwn(m - k)
+ e -jφe -jwn(m + k)] =
(1/2)[e jφe jwn(m - k)
+ e -jφe -jwn(m + k)] =  e jwn(m - k)
+ (A/2)e -jφ
e jwn(m - k)
+ (A/2)e -jφ e -jwn(m + k) =
e -jwn(m + k) =  e j2πn(m - k) / N
+ (A/2)e -jφ
e j2πn(m - k) / N
+ (A/2)e -jφ e -j2πn(m + k) / N =
e -j2πn(m + k) / N =  e j2πn(m - m) / N
=
e j2πn(m - m) / N
=  1 = N
1 = N e -j2πn(m + N - m) / N =
e -j2πn(m + N - m) / N =
 e -j2πn =
e -j2πn =
 1 = N
1 = N