Для чего нужно быстрое преобразование Фурье или вообще дискретное преобразование Фурье (ДПФ)? Давайте попробуем разобраться.
Пусть у нас есть функция синуса
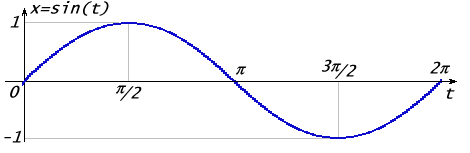
Максимальная амплитуда этого колебания равна
Период колебания равен
Частота колебания обратна периоду:
И, наконец, есть фаза, обозначаемая как φ. Она определяет сдвиг графика колебания влево. В результате сочетания всех этих параметров получается гармоническое колебание или просто гармоника:
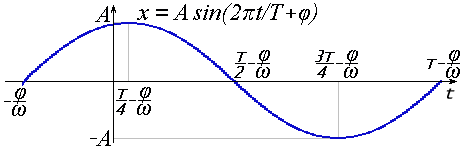
Очень похоже выглядит и выражение гармоники через косинус:
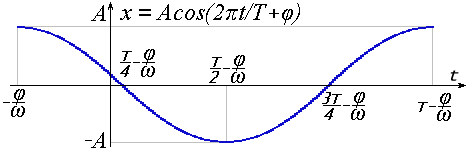
Большой разницы нет. Достаточно изменить фазу на
В природе и технике колебания, описываемые подобной функцией чрезвычайно распространены. Например, маятник, струна, водные и звуковые волны и прочее, и прочее.
Преобразуем (18) по формуле косинуса суммы:
Выделим в (19) элементы, независимые от
По величинам
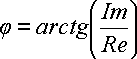 и
и 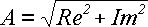 (21)
(21)
Рассмотрим очень распространенную практическую ситуацию.
Пусть у нас есть звуковое или какое-то иное колебание в виде функции
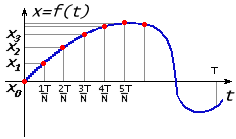
В результате прямого дискретного преобразования Фурье были получены
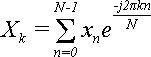 (22)
(22)
Теперь возьмем обратное преобразование Фурье:
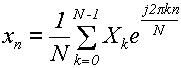 (23)
(23)
Выполним над этой формулой следующие действия: разложим каждое комплексное
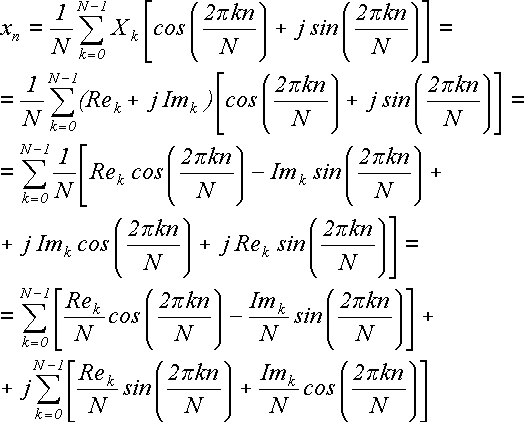 (24)
(24)
Это была цепочка равенств, которая начиналась с действительного числа
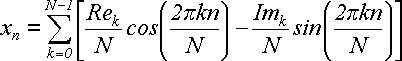 (25)
(25)
Поскольку
при дискретизации мы брали
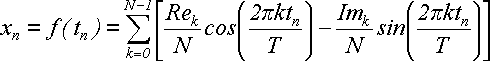 (26)
(26)
Сопоставим эту формулу с формулой (20) для гармоники:
Слагаемые суммы (26) аналогичны формуле (20), а формула (20) описывает
гармоническое колебание. Значит сумма (26) представляет собой сумму из
Выше объяснялось, каким образом формула вида (20) может быть преобразована в формулу вида (18):
Выполним такое же преобразование для слагаемых суммы (26), преобразуем их из вида (20) в вид (18). Получим:
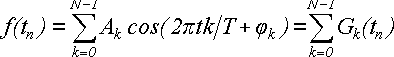 (27)
(27)
Далее будем функцию
называть k-й гармоникой.
Для вычисления
 (29)
(29)
Функция
Итак. Физический смысл дискретного преобразования Фурье состоит в том, чтобы представить некоторый дискретный сигнал в виде суммы гармоник. Параметры каждой гармоники вычисляются прямым преобразованием, а сумма гармоник - обратным.