Что
может быть проще окружности?
Ноябрь 2007
( по
материалам сайта: ustierechi.narod.ru )
Золотая пропорция и число Пи
Число Пи имеет прямое отношение к угловым величинам, и в первую очередь, число Пи – это окружность (360° = 2π).
Окружность в свою очередь, не просто геометрическая фигура, это ещё и круг, траектория, это движение Земли вокруг солнца, это перемещение звезд на небе, это цикличность всех процессов происходящих в мире. Кроме того, окружность в виде сферы – самая распространенная форма во Вселенной. Если бы необходимо было бы выбрать форму, наиболее точно передающую устройство мира, то это была бы окружность.
Если окружность – идеальная геометрическая фигура для описания того, что есть в мире, то Золотая пропорция, это то, что волшебным образом связывает всё то, что есть в мире в единую сущность, и является идеальным описанием гармоничности и целостности Вселенной.
Было бы странно, если бы число Пи и Золотая пропорция, не оказались бы связаны между собой. Забегая вперёд, скажем, что тождественность этих двух величин, является доказанным фактом. Кроме того, известно, что число Пи и Золотая пропорция - иррациональные числа, т.е. числа с бесконечной дробной частью, и тем удивительнее, что их тождественность оказалась абсолютной, т.е. до последнего знака после запятой, даже с учетом тех знаков, которые ещё не вычислены математиками.
Число Пи – угловая величина, а Золотая пропорция – мера деления отрезка (линейная величина), поэтому взаимосвязь этих величин необходимо искать через тригонометрические и обратные им функции (sin, cos, arcsin и т.д).
1) Рассмотрим график какого-либо процесса, в ходе которого взаимосвязано изменяются величины x и y, и графически это - окружность. Точка A – мгновенное значение, на этом графике, может быть задана определенными значениями x и y, а также либо углом α и заданным радиусом окружности, либо углом β и заданным радиусом. Для упрощения задачи, приравняем радиус к единице:
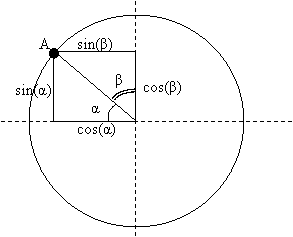
Синус – отношение противолежащего катета к гипотенузе, косинус – отношение прилежащего катета к гипотенузе. Т.к. гипотенуза – это радиус окружности, и он равен единице, то синус, в этом случае, будет равен противолежащему катету, а косинус – прилежащему катету.
Очевидно, что:
|
y = sin(α) = cos(β) |
|
x = cos(α) = sin(β) |
|
α + β = 90° (π/2) |
Некоторым положениям точки A на окружности, будет соответствовать ситуация, когда значения x и y, связаны Золотой пропорцией, т.е.:
|
y / x = 0,61803398875… = φ |
|
x / y = 1,61803398875… = Φ |
y / x = sin(α) / cos(α) = tg(α) = 0,61803398875…= φ
x / y = sin(β) / cos(β) = tg(β) = 1,61803398875…= Φ
Отсюда получим:
α + β = arctg(φ) + arctg(Φ)
α
= 1,01722196790…рад =
58,28…°
β
= 0,55357435890…рад =
31,72…°
|
π/2 = arctan
(Φ) + arctan (φ) |
2) Число Пи и Золотая пропорция взаимосвязаны для углов, кратных 18°:
|
φ / 2 = sin (1π / 10) = sin (9π
/ 10) = cos (4π / 10) = - cos (6π / 10) |
|
Φ / 2 = sin (3π / 10) = sin (7π
/ 10) = cos (2π / 10) = - cos (8π / 10) |
Эти равенства абсолютны, т.е. число Пи и Золотая пропорция в этих равенствах равны без округлений, с точностью до последнего знака после запятой.
Взаимосвязь числа Пи и Золотой пропорции
настолько велика, что не остается сомнений в их тождественности, и можно
говорить о том, что число Пи и Золотая пропорция – это одна и та же
математическая сущность.
3) Решением квадратного уравнения:
|
x2 + x – 1 = 0 |
Будут два корня:
x1 = 0,618033988749895…= φ
x2 = - 1,618033988749895…= - Φ
Это уравнение можно записать, также в виде:
|
x2 + x = 1 |
Нетрудно заметить, что это уравнение – частный случай уравнения окружности, при r = 1, и x = y2:
|
x2
+ y2 = r2 |
x = y2 – это уравнение параболы.

На графике видно, что один из корней ( x2 = - 1,618033988749895… ) не имеет общих точек с графиком окружности.
Другой корень ( x1 = φ = 0,618033988749895…), пересекает график окружности, и в точках пересечения, пересекает также график параболы.
Найдем значения y для точек пересечения:
y1 = 0,786151377757423…
y2 = - 0,786151377757423…
Чем же примечательно это число?
Оказывается y1 = 0,786151377757423… = √φ
Но это еще не всё:
Угол α = arccos (φ) = 51,83…°, и это угол наклона граней пирамид в Гизе. И это также отражает математическую взаимосвязь числа Пи (π) и Золотой пропорции (φ ):
|
π/2 = arcsin (φ) + arccos (φ) = 38,17…° + 51,83…° |
Следует признать, что Золотая пропорция,
есть частный случай уравнения окружности x2 +
y2 = r2.
Иными словами, если есть два параметра,
числа или явления, связанные между собой Золотой пропорцией, то это говорит о
том, что есть и уравнение окружности, связывающее эти параметры.
Теорема Пифагора и Окружность
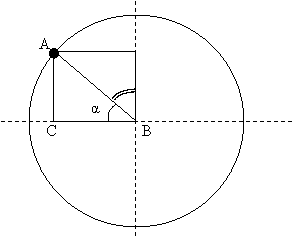
Уравнение окружности задано уравнением:
|
x2
+ y2 = r2 |
Рассмотрим треугольник ABC:
Т.к. величина CB равна значению x для точки A, и величина AC равна значению y для точки A, а радиус окружности равен AB, то уравнение окружности x2 + y2 = r2 можно записать в виде:
|
(CB)2 + (AC)2 = (AB)2 |
А это ничто иное, как уравнение прямоугольного треугольника ABC, с катетами AC, CB, и гипотенузой AB (Теорема Пифагора):
Поэтому, график взаимосвязи x и y, представляет собой, также множество всех точек A прямоугольного треугольника ABC, при изменяемых величинах катетов AC, CB и постоянной величине гипотенузы AB ( r = const ).
Теорема Пифагора и числа Фибоначчи
Числа Фибоначчи —
последовательность целых чисел, заданная с помощью рекуррентного соотношения:
F0
= 0, F1 = 1, F(n+1) = Fn
+ F(n-1)
Последовательность чисел Фибоначчи начинается так:
1,1,2,3,5,8,13,21,34,55,89,144,…
Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен x2 - x - 1 имеет корни φ и -1/ φ., поэтому числа Фибоначчи имеют непосредственное отношение к золотой пропорции φ.
Последние
цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60.
Если от каждого числа брать по две последние цифры, то они образуют
последовательность с периодом, равным 300. Если брать по три последние цифры —
с периодом 1500, и т.д.
Как
известно, «Теорема Пифагора» является едва ли не самой знаменитой теоремой
геометрии, которую помнит каждый человек, который когда-либо учился в средней
школе и, возможно, сумел «начисто забыть» всю математику. Суть этой теоремы
чрезвычайно проста. Теорема утверждает, что в прямоугольном треугольнике катеты
a и b связаны с гипотенузой
с следующим простым соотношением:
a2
+ b2 = c2
Несмотря
на ее предельную простоту, теорема Пифагора, по мнению многих математиков, относится
к разряду наиболее выдающихся математических теорем за всю историю математики.
Особый
интерес всегда вызывали так называемые «пифагоровы треугольники», стороны
которых являются целыми числами. Несомненно, «пифагоровы треугольники» также
относятся к разряду «сокровищ геометрии», а поиски таких треугольников
представляют одну из из
интереснейших страниц в истории математики. Наиболее широко известным из них
является прямоугольный треугольник со сторонами 4, 3 и 5. Он назывался также
«священным» или «египетским», так как он широко использовался в египетской
культуре.
Существует
способ нахождения «пифагоровых треугольников» с использованием чисел Фибоначчи.
Для этого стороны прямоугольного треугольника рассчитываются с использованием 4
любых подряд идущих числа Фибоначчи F(n):
b = F(n)
* F(n+3),
a = F(n+1)
* [ F(n) + F(n+1) + F(n+2) ],
c = F2(n+1) + F2(n+2),
и всегда равна некоторому числу Фибоначчи (5, 13, 34,
89, 610,...).
|
Числа Фибоначи |
Стороны прямоугольного треугольника |
|||||
|
F(n) |
F(n+1) |
F(n+2) |
F(n+3) |
a |
b |
c |
|
1 |
1 |
2 |
3 |
4 |
3 |
5 |
|
1 |
2 |
3 |
5 |
12 |
5 |
13 |
|
2 |
3 |
5 |
8 |
30 |
16 |
34 |
|
3 |
5 |
8 |
13 |
80 |
39 |
89 |
|
8 |
13 |
21 |
34 |
546 |
272 |
610 |
|
13 |
21 |
34 |
55 |
1428 |
715 |
1597 |
|
21 |
34 |
55 |
89 |
3740 |
1869 |
4181 |
|
34 |
55 |
89 |
144 |
9790 |
4869 |
10946 |
Итак, что такое
окружность?
·
Геометрическая
фигура.
·
Траектория
движения, орбита.
·
Цикличность
всех процессов происходящих в мире.
·
Прямая
линия, это крайний случай дуги окружности с бесконечным радиусом. Так как этот случай один из бесконечного числа вариантов, и
окружность с бесконечным радиусов в пределах нашей конечной по размерам
Вселенной существовать не может, то можно утверждать, что в мире нет прямых
линий, также, как и нет прямолинейного движения.
·
Уравнение
окружности можно представить в виде уравнений синуса и косинуса, поэтому все
изменяющиеся синусоидально процессы (а это все электромагнитные излучения,
свет, звук и т.д. т.е. все или почти все процессы во Вселенной), являются
частью процессов, изменяющихся по уравнению окружности.
·
Уравнение,
связывающее катеты и гипотенузу прямоугольного треугольника (Теорема Пифагора),
есть ни что иное, как уравнение окружности.
·
Уравнение
окружности содержит в себе Золотую пропорцию, и это позволяет связать гармонию
и целостность Вселенной, с окружностью.
·
Окружность
в виде сферы – самая распространенная форма во Вселенной.