Другие статьи

К оглавлению

 

 

 

 

Глава 4. ЭНЕРГООПТИМАЛЬНАЯ ГАРМОНИЯ И ОБМЕННЫЙ УЧАСТОК КОРОНАРНОГО РУСЛА

 

 

4.1.Особенности конструкции обменных микрососудов

 

 

Обменный докапиллярный участок составляют несколько последовательных генераций артериол (d»7-100 мкм). Общая поверхность и протяженность сосудов обменного участка в сотни и тысячи раз превосходят таковые на транспортном. Архитектоника микроциркуляторного обменного участка сердца различных видов млекопитающих практически одинакова. На это обстоятельство указывают многие исследователи /Каро и др., 1981/. Установлено поразительное сходство конфигурации и размеров мелких сосудов млекопитающих несмотря на значительное различие по массе тела. К.А.Шошенко /Шошенко и др., 1982/ отмечает аналогию отношений l/d для артерий и вен млекопитающих, рыб и земноводных. Отметим конструктивные отличия микрососудов от других артериальных сосудов. Стенки микрососудов имеют жесткую конструкцию, они практически не растягиваются. Отношение C=l/d для прекапиллярных сосудов значительно превышает величину С для других артериальных сосудов. Отметим еще одно важное отличие. В соответствии с феноменомФареуса-Линдквиста вязкость крови в крупных, средних и мелких артериях транспортного участка постоянна и не зависит от диаметра. Сужению же микрососудов на обменном участке сопутствует значительное снижение вязкости крови (рис. 4.1).


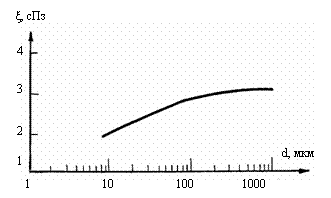
Рис. 4.1. Зависимость вязкости крови от диаметра сосудов /Chien, 1975/. d – диаметр сосуда, ξ – вязкость крови.

 

     Показано /Klitzman, Duling, 1979/, что величина динамического гематокрита, определенная путем центрифугирования порции крови, собранной из микрососудов, практически не отличается от гематокрита крови из транспортных сосудов. Это означает, что соотношение объемов эритроцитов и плазмы, прошедших через микрососуд за единицу времени, не зависит от его калибра.

 

 

 

4.2. Обменные тройники в золотом режиме гипертензии

 

Рассмотрим особенности архитектоники обменных тройников. В обменных сердечных тройниках ветвления терминальных артериол близки к симметричным (H1=H2=0,5, k=1,26) /Голубь, 1978 Шошенко и др., 1982/. Экспериментально и теоретически показано, что в пределах 1>k≤1,26 тройник имеет энергооптимальную структуру /Шошенко и др., 1982/. Ветви обменных тройников приблизительно одинаковы по длине и диаметру. Дополнительной особенностью обменных сосудов по сравнению с транспортными является рост коэффициента их конструкции /Шошенко и др., 1982/; по мере приближения к капиллярам эта величина значительно возрастает (С=3-6). Другим отличием обменных тройников от «эластических» и «мышечных» является то, что вязкость крови в стволе и ветвях неодинакова и зависит от диаметра (рис. 4.1). Вязкость крови от начала и до конца этого участка, наоборот, снижается приблизительно в 2 раза (от 3 до 1,45 сПз).

В микрососудах колебания стенки оказываются сильно «демпфированными», амплитуда пульсовых колебаний по мере снижения калибра коронарных микрососудов быстро угасает /Nellis et al., 1981; Ashikawa et al., 1986/; после 170 мкм отношение систолического даления к диастолическому практически равно 1 /Chillian et al., 1989/. Вследствие указанных особенностей можно считать диаметр и длину сосудов, а также величины вязкости крови x(bЗС), давления ΔP(bЗС) и кровотока q(bЗС), постоянными как в систолу, так и в диастолу, т.е. можно для анализа принять их постоянную величину в течение всего кардиоцикла. Выражения (3.5)-(3.8) для обменных тройников преобразуются следующим образом /Цветков, 2004/,

d1(bЗС) =0,794dС(bЗС),                                      (4.1)

d2(bЗС) =0,794dС(bЗС),                                      (4.2)

l1(bЗС) = 0,794[С1(bЗС)/СС(bЗС)]lС(bЗС),                         (4.3)

l2(bЗС) = 0,794[С2(bЗС)/СС(bЗС)]lС(bЗС).                         (4.4)

где СС(bЗС), С1(bЗС), С2(bЗС) – коэффициенты конструкции ствола и 1 и 2 ветвей в золотом режиме гипертензии. Отметим, что 0,794≈1/, т.е. очевидна связь симметричного варианта ветвления с золотым числом 1,618.

Обменные тройники практически симметричны. В дальнейшем нами будут рассматриваться относительные изменения параметров только для одной из ветвей (j=1, 2). При этом будет подразумеваться, что величины параметров в j-ветви соответствуют их значениям в обеих ветвях.

Покажем, что давление, приложенное к стволу и ветвям обменного тройника, является постоянным и равным давлению на транспортном участке.

Установлена аналогия отношений в одних и тех же органах у животных с очень разными условиями кровотока (например, в скелетных мышцах и сердце у крысы и хариуса) /Шошенко и др., 1982/. При сопоставлении экспериментальных зависимостей ξ=f(d) /Chien, 1975/ и коэффициента конструкции сосуда С=j(d) для сердца /Шошенко и др., 1982/ нами установлено обратно пропорциональное изменение вязкости и длины j-ветви по отношению к стволу (рис. 4.2) /Цветков, 1993, 1994/,

ξj(bЗС)/ξC(bЗС) @ CC(bЗС)/Cj(bЗС),                             (4.5)

l2(bЗС) = 0,794[С2(bЗС)/СС(bЗС)]lС(bЗС).                        (4.6)

где lС(bЗС), lj(bЗС), ξC(bЗС), ξj(bЗС), CC(bЗС), Cj(bЗС) -  соответственно длина, вязкость крови и коэффициент конструкции ствола и j-ветви в золотом режиме гипертензии.

Давление, приложенное к j-ветви,

DPj(bЗС) = qj(bЗС)/Gj(bЗС),

где qj(bЗС), Gj(bЗС) – соответственно кровоток и проводимость j-ветви в золотом режиме гипертензии.

С учетом (4.5) и (4.6) проводимость j-ветви по отношению к стволу,

Gj(bЗС) = 0,5GC(bЗС).


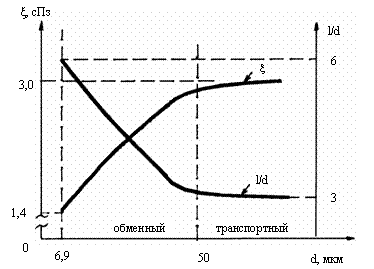
Рис. 4.2. Вязкость крови и отношение  в транспортных и

обменных  сосудах.   ξ – вязкость крови,     d -  диаметр,

l - длина сосуда, l/d - коэффициент конструкции сосуда.

 

Поскольку кровоток и проводимость в ветвях по отношению кстволу изменяются в одинаковой степени, то, очевидно, что в любом тройнике на обменном участке

lj(bЗС) = 0,794[Сj(bЗС)/СС(bЗС)]lС(bЗС).                      (4.7)

Учитывая преемственность обменных тройников по отношению к мышечным,

DPj(bЗС) = 3,5 мм рт. ст.

Как мы могли убедиться выше, эта величина постоянна для всех сосудов сердца как на транспортном, так и обменном участках.

Параметры крови x и b в значительной степени обусловливают потери механической и химической энергии во всяком сосуде с движущейся кровью. Покажем, что в каждой ветви обменного тройника сохраняется линейная зависимость между относительными изменениями x и b.

Для ствола в золотом режиме гипертензии в соответствии с (3.24) для j-ветви

 

ξj(bЗС)/ξC(bЗС) @ CC(bЗС)/Cj(bЗС),                             (4.8)

При переходе от ствола к j-ветви время пребывания эритроцита

ξj(bЗС)/ξC(bЗС) @ CC(bЗС)/Cj(bЗС),                             (4.9)

а величины

lj(bЗС) = 0,794[Сj(bЗС)/СС(bЗС)]lС(bЗС),                       (4.10)

xj(bЗС) = xС(bЗС)/[Сj(bЗС)/СС(bЗС)],                              (4.11)

bj(bЗС) = bС(bЗС)/[Сj(bЗС)/СС(bЗС)].                             (4.12)

Очевидно, что «энергетические» соотношения между стволом и ветвями в обменных тройниках аналогичны таковым в транспортных вследствие обратно пропорциональных изменений величин lj(bЗС) и xj(bЗС). Покажем, что энергетические инварианты обменных тройников и транспортных тройников аналогичны. В соответствии с (4.1), (4.2) и  (4.9) - (4.12) в j-ветви,

γj(bЗС) = WМj(bЗС)/WХj(bЗС) = 0,5,                           (4.13)

в каждом обменном тройнике

 

[W1(bЗС)+ W2(bЗС)]/WС(bЗС ) = 1,                           (4.14)

где WMj(bЗС), WXj(bЗС) – механическая и химическая мощность в j-ветви, WC(bЗС), W1(bЗС), W2(bЗС) - соответственно суммарная мощность в стволе и ветвях в золотом режиме гипертензии.

При сравнении отношений (3.27)-(3.28) для транспортного и (4.13)–(4.14) для обменного тройников очевидна их полная аналогия. Это сходство указывает на то, что на всем протяжении гемоартериального русла «присутствуют» одни и те же универсальные энергетические инварианты. Эти инварианты не зависят от калибра и назначения сосудов. Именно они представляют энергооптимальную гармонию «вхождения» параметров архитектоники и гемодинамики в систему «Обменный участок» в золотом режиме гипертензии.

 

4.3. Обменные тройники в режимах гипертензии

 

Установлено /Козлов, Тупицын, 1982/, что даже при значительной физической нагрузке прекапиллярные сосуды мышц практически не удлиняются и не расширяются. Следовательно, для ствола обменного тройника при гипертензии dС(b)=dС(bЗС), lС(b)=lС(bЗС) и ξС(b)=ξС(bЗС). Другие параметры, определяющие расход механической и химической энергии за единицу времени в стволе, изменяются следующим образом /Цветков, 2004/,

[W1(bЗС)+ W2(bЗС)]/WС(bЗС ) = 1,

[W1(bЗС)+ W2(bЗС)]/WС(bЗС ) = 1,                           (4.15)

tС(b) = tС(bЗС)/b,                                           (4.16)

bС(b) = b2bС(bЗС),                                          (4.17)

где tC(b) – время пребывания эритроцитов, bС(b) – расход химической энергии в единичном объеме крови за единицу времени в стволе в режимах гипертензии. Исходя из (4.15)-(4.17),

WMС(b) = b2WMС(bЗС),                                      (4.18)

[W1(bЗС)+ W2(bЗС)]/WС(bЗС ) = 1,                           (4.19)

[W1(bЗС)+ W2(bЗС)]/WС(bЗС ) = 1,

WС(b) = b2WС(bЗС),                                      (4.20)

где WMС(b), WХС(b), WС(b) – соответственно расход механической, химической и общей мощности в стволе в режиме гипертензии.

Для j-ветви обменного тройника, как и в золотом режиме,

dj(b) = 0,794dС(bЗС),                                      (4.21)

lj(b) = 0,794[Сj(bЗС)/СС(bЗС)]lС(bЗС).                         (4.22)

Отметим, что соотношения (4.21) и (4.22) соответствуют золотому режиму гипертензии. Вязкость крови в обменных сосудах зависит от их диаметра (рис. 4.1), но поскольку диаметр обменных сосудов при гипертензии не меняется, то и вязкость крови в каждом обменном сосуде не зависит от уровня гипертензии. Однако вязкость крови в стволе и ветвях различна ствол, т.к. эти сосуды «вписаны» в наклонный участок кривой x=f(d). В j–ветви по отношению к стволу,

ξj(b) = [СС(bЗС)/Сj(bЗС)]ξС(bЗС).                            (4.23)

С учетом (4.22) и (4.23),

Vj(b) = 0,5[Сj(bЗС)/СС(bЗС)]VC(bЗС),                         (4.24)

Gj(b) = 0,5GC(bЗС),                                       (4.25)

где Vj(b), Vj(b) - соответственно объем и проводимость ствола и j-ветви в режимах гипертензии.

В каждой j-ветви /Цветков, 2004/,

qj(b) = 0,5bqС(bЗС),                                      (4.26)

ΔPj(b) = bΔPС(bЗС),                                      (4.27)

где qj(b), ΔPj(b)– соответственно кровоток и давление, приложенное к j-ветви при гипертензии.

Исходя из (4.24) и (4.26),

tj(b) = [Сj(bЗС)/СС(bЗС)]tС(bЗС)/b,                            (4.28)

где tj(b) - время пребывания эритроцитов в j-сосуде в режимегипертензии.

Перейдем к анализу соотношений затраченной энергии в стволе и ветвях в условиях гипертензии. Параметры крови x и b в значительной степени обусловливают потери механической и химической энергии во всяком сосуде с движущейся кровью. Для j-ветви в режиме гипертензии

bj(b) = 64xj(b)[lj(b)/dj(b)tj(b)]2.

По отношению к стволу с учетом (4.21)-(4.23) и (4.28) в j-ветви

qj(b) = 0,5bqС(bЗС),                                      (4.29)

Следовательно, исходя из (4.24) и (4.29), химическая мощность в j-ветви

WXj(b) = 0,5b2WXС(bЗС).                                   (4.30)

Аналогично, исходя из (4.22), (4.23) и (4.26),

WMj(b) = 0,5b2WMС(bЗС).                                  (4.31)

Как следствие из (4.30) и (4.31),

W1(b) + W2(b) = b2WС(b),                                 (4.32)

где WС(b), W1(b), W2(b)– суммарная мощность ствола, 1 и 2 ветвей в режиме гипертензии. Очевидно, что и в обменных тройниках, так же как и в транспортных, имеет место энергетическое «воспроизводство» ствола ветвями.

Для обменных тройников имеют место те же соотношения гармонии, что и для транспортных,

 [k(b)H1(b)]3/2 + [k(b)H2(b)]3/2 = 1,                           (4.33)

WМ1(b)/WX1(b) = WM2(b)/WX2(b) = WMC(b)/WXC(b) = 0,5,       4.34)

[W1(b) + W2(b)]/WC(b) = 1.                                 (4.35)

Из (4.33)-(4.35) очевидно, что в пределах гипертензии от покоя до максимальной физической нагрузки во всех обменных тройниках инварианты оптимального вхождения одни и те же. Эти отношения аналогичны установленным ранее для транспортных тройников. Полная аналогия указывает на то, что как на обменном участке, так и на транспортном, эти энергооптимальные отношения гармонии одинаковы и неизменны для всех сосудов и тройников независимо от уровня гипертензии. Установленные инварианты универсальны и являются общими для всего докапиллярного участка. Наличие этих отношений обусловливает гармонию оптимального вхождения архитектонических и гемодинамических параметров в систему «Обменный тройник» при любой гипертензии.

Сравнивая выражения (3.37)-(3.39), (3.41)-(3.43) для транспортных тройников и выражения (4.30)-(4.32) для обменных тройников, мы видим, что в первом случае расход энергии при гипертензии возрастает в b3 раз, а во втором – только в b2 раз. Однако это расхождение только кажущееся. При достижении некоторого уровня гипертензии к каждой генерации открытых обменных сосудов параллельно подключаются резервные тройники того же калибра, «окрашенные» в «цвет» уровня гипертензии. Как было показано выше, за счет этого подключения суммарный расход энергии в каждой генерации обменных сосудов возрастает в b3 раз.

В генерациях мышечного типа каждому диапазону гипертензии соответствуют сосуды, «окрашенные» в «свой» цвет с меняющейся интенсивностью «окраски». Это означает, что часть исходно одинаковых сосудов изменяет свои размеры в соответствии с (3.60) и (3.63). Вследствие этого объем и проводимость каждой генерации мышечных сосудов изменяется в одинаковой степени в соответствии с (3.53)-(3.54) и (3.57)-(3.58). В обменных генерациях, так же как и в «мышечных», каждый открытый сосуд окрашен в «свой» цвет, соответствующий определенной гипертензии. Поскольку размеры обменных артериол при гипертензии не меняются, то адекватное изменение объема и проводимости происходит за счет включения дополнительного числа открытых сосудов. К этому следует добавить, что существует физиологический механизм, который позволяет перераспределять функциональную нагрузку /Чернух и др., 1975; Мчедлишвили, 1989/. Действие этого механизма сводится к периодическому «включению» и «выключению» мелких артерий, артериол, капилляров, венул и мелких вен таким образом, что среднее количество функционирующих сосудов сохраняется постоянным, если сохраняется постоянным потребление кислорода и другие факторы, определяющие потребность в кровоснабжении. По-видимому, благодаря этому механизму часть «голодных» клеток, выделяющих аденозин, меняется местами с клетками, не испытывающими до этого кислородного голодания.

В главе 3 (раздел 3.3.2.1) нами было рассмотрено влияние аденозина на мышечные генерации. На уровне терминальных артериол влияние аденозина отсутствует. На этом уровне существуют другие пути регуляции, связанные с величиной клеточного рО2. Оказалось, что периферическое сопротивление изменяется путем закрытия сфинктеров или, наоборот, введением в функциональное состояние части артериол и прекапиллярных сфинктеров, составляющих предпоследнюю генерацию артериол, предшествующую капиллярам при одновременном изменении диаметров резистивных сосудов. Сфинктеры колеблются между открытым и полностью закрытым состояниями. Концентрации Рi и 5`АМФ отражают внутриклеточное состояние восстановления кислорода и поэтому связаны с кислородным обеспечением клеток. При возрастании потребности в кислороде тканевое рО2 падает, что вызывает увеличение концентрации Рi и 5`АМФ с последующим расслаблением мышцы прекапиллярного сфинктера и раскрытием капилляра. По-видимому, каждый резервный капилляр раскрывается в ответ на достижение «своей» величины рО2. Когда сфинктер раскрывается, тканевое рО2 растет и концентрации Рi и 5`АМФ в кардиомиоцитах падают по направлению к новой стабильной величине, адекватной уровню гипертензии. Таким образом, подключение дополнительного числа  артериол и капилляров в условиях гипертензии обусловлено в конечном счете недостаточным кислородным обеспечением сердечных клеток.

Подытоживая проделанный нами анализ архитектоники и гемодинамики докапиллярного артериального русла сердца, можно сказать следующее:

1) несмотря на различную конструкцию эластических, мышечных и обменных тройников основу их организации составляет энергетическая оптимизация;

2) энергетическую оптимизацию всех тройников обусловливают универсальные энергооптимальные отношения, связывающие параметры архитектоники и гемодинамики.

Универсальные энергооптимальные отношения гармонии «присутствуют» во всех режимах гипертензии. Одни и те же универсальные энергетические отношения, независимо от калибра и назначения сосудов, имеют место на протяжении всего гемоартериального русла вплоть до капилляров. Именно эти безразмерные отношения представляют гармонию оптимального «вхождения» параметров архитектоники и гемодинамики в тройники на всем гемоартериальном участке.

 

 

4.4. Обменная поверхность и протяженность артериального русла

 

Газообмен с окружающими тканями - важнейшая функция кровеносного русла. Представляется необходимым рассмотреть основные параметры, связанные с этой функцией, - площадь обменной поверхности, протяженность сосудистой сети и время пребывания эритроцитов в сосудах. Совокупность артериальных сосудов представляет собою своего рода пирамиду, на вершине которой находится первая от аорты коронарная артерия, а в основании - генерация прекапиллярных артериол. Любой тройник имеет отношение к двум соседним генерациям сосудов: к первой генерации относится ствол, ко второй - ветви. Ветви второй генерации, в свою очередь, являются стволами третьей генерации, ветви третьей генерации - стволами четвертой и т.д. В каждой из последующих генераций происходит удвоение количества сосудов. Ближайшие к капиллярам генерации тройников практически симметричны /Голубь, 1978/; именно они составляют более 90% от общей длины и поверхности всего гемоартериального участка. Для упрощения анализа примем все тройники симметричными.

На обменных генерациях имеет место значительное дополнительное увеличение поверхности и протяженности русла за счет «нестандартного» удлинения сосудов (см. (4.3)-(4.4)). Согласно данным /Шошенко и др., 1982; Цветков, 1993, 2004/ в первых двух обменных генерациях, начиная от капилляров, каждый из сосудов по длине эквивалентен двум «стандартным» сосудам (l/d=6). Каждый сосуд из двух последующих генераций эквивалентен по длине 1,67 «стандартным» (l/d=5) и всякий сосуд из трех последующих генераций - 1,33 «стандартным» (l/d=4). При дальнейшем отдалении генераций от капилляров обменные микрососуды становятся «стандартными» (l/d=3). Таким образом, в первых 7 прекапиллярных генерациях универсальное соотношение для «стандартных» сосудов (l/d=3) нарушается. Как мы отмечали раньше, каждому «нестандартному» изменению длины сосуда соответствует обратно пропорциональное изменение вязкости крови том же сосуде. Благодаря этому феномену каждая генерация обменных сосудов потребляет одинаковое количество энергии, поскольку произведение ξl при обратных изменениях ξ и l остается неизменным. Вследствие «нестандартных» изменений длины 7 первых обменных генераций по длине эквивалентны 11,33 «стандартным», что аналогично увеличению «стандартных» генераций на этом участке в 1,62 раза без дополнительных затрат энергии! Нетрудно показать, что и общий объем сосудов и общее время прохождения отдельного эритроцита через 7 «нестандартных» сосудов по сравнению с объемом и временем прохождения через то же количество «стандартных» возрастает также в 1,62 раза. Нельзя не отметить здесь важное обстоятельство - «присутствие» золотого числа 1,62! Отметим важное обстоятельство: эритроциты без дополнительных затрат энергии и дополнительных обменных генераций пребывают в обменных сосудах в 1,62 дольше, чем при том же количестве «стандартных» генераций. Эритроциты в «нестандартных» сосудах «бесплатно» (без дополнительных затрат энергии) отдают значительный объем кислорода! Ниже будет показано (см. раздел 4.5), как за счет «нестандартности» ветвлений достигается наиболее эффективное использование формы кривой дезоксигенации гемоглобина.

Как было показано нами выше, для любой генерации транспортных и обменных сосудов суммарный расход механической и химической энергии одинаков; эта величина равна расходу мощности в стволе первого от аорты тройника. С энергетической точки зрения всю артериальную часть коронарного русла можно было бы заменить одним эквивалентным неразветвленным сосудом. Диаметр этого сосуда был бы равен диаметру ствола первого тройника, а общая длина превосходит длину первого ствола в N раз (N - число генераций сердечных артерий и микрососудов вплоть до капилляра.). Кровоток в «сквозном» сосуде равен кровотоку в первом стволе, а общее давление, приложенное к этому сосуду, равно сумме давлений на всех N генерациях. Какие же преимущества представляет «ветвистая» конструкция («дерево») по сравнению со «сквозной»? Преимущества первой конструкции станут очевидными, как только мы рассмотрим величину обменной поверхности и протяженность сосудов в «сквозной» и разветвленной конструкциях. Например, для собаки весом 20 кг N=29 (эта величина будет использована нами для дальнейших расчетов). Если принять все N генераций стандартными (l/d=3) и симметричными, то по отношению к сквозному варианту суммарная обменная поверхность возрастает приблизительно в 90 раз, а суммарная длина сосудов - в 24.000 раз! Oчевидно несомненное преимущество ветвления перед сквозным вариантом - огромное увеличение обменной поверхности и длины сосудистого русла при том же расходе энергии, крови и сосудистого материала.

В действительности же последние 7 прекапиллярных генераций «нестандартны» (l/d>3). Это означает, что суммарная поверхность и суммарная длина на каждой из этих генераций по отношению к предыдущей возрастают «нестандартно», т.е. более чем в 1,26 и 1,59 раз. Отметим, что для этого участка имеет место реальное симметричное ветвление. С учетом экспериментальных данных /Шошенко и др., 1982/ в 1 и 2 генерациях, начиная от капилляра, обменная поверхность по отношению к «стандартному» варианту дополнительно возрастает в 2 раза, во второй и третьей генерациях - в 1,67 раз и в пятой, шестой и седьмой - в 1,33 раза. За счет этих дополнений суммарная поверхность всего артериального русла возрастает по отношению к «сквозному» варианту в 140 раз, а протяженность артериального русла - в 42.000 раз. Продолжим расчеты для собак с числом генераций N=29. Общая поверхность артериальных сосудов, включая «нестандартные» генерации, равна 3990S1, где S1- площадь поверхности первого от аорты коронарного сосуда. Отметим, что в «стандартных» (транспортных) генерациях вязкость крови постоянна, а отношение l/d=3. При условии, что все генерации были бы «стандартны», суммарная поверхность всего артериального участка составляет 2480S1. За счет «нестандартности» конструкции последних 7 генераций суммарная поверхность артериального участка дополнительно возрастает в 1,6 раза. Очевидно, что бесплатное «золотое» дополнение имеет место и для других млекопитающих, поскольку количество «нестандартных» генераций постоянно независимо от веса животных. Огромное значение имеет величина обменной поверхности. При том же суммарном расходе энергии на перфузию и процессы в крови, что и при «стандартных» генерациях, «нестандартные» генерации позволяют получить значительное дополнительное увеличение обменной поверхности и длины. Дополнительное «бесплатное» увеличение обменной поверхности и длины «отнесено» природой на последние, прекапиллярные, генерации, где газообмен наиболее эффективен. Эти сосуды заполнены наиболее «дешевой» кровью с уменьшающимися величинами ξ и b, что позволяет свести к минимуму расход энергии на перемещение единичного объема крови и поддержание в нем химических процессов. Соответственно «цена» доставки единичного объема потребляемого кислорода в этих сосудах все время снижается, достигая в капиллярах минимальной величины.

Природа стремится увеличить обменную поверхность без дополнительного расхода энергии. Различие между двумя видами тройников (симметричном и асимметричном) при одинаковом расходе мощности, крови и сосудистого материала состоит в том, что суммарная обменная поверхность в симметричном тройнике больше, чем в асимметричном. Причем эта разница тем больше, чем больше асимметрия тройника. В крупных, средних и мелких артериях с выраженной пульсацией сосудов значительны потери энергии, связанные с пульсации стенки. Потери энергии на стенках сосудов пропорциональны боковой поверхности этой части артериального русла и, следовательно, необходима ее минимизация. В этом и заключается преимущество «использования» асимметричного ветвления на транспортном участке. Использование асимметричных тройников в генерациях коронарных артерий выгодно еще и потому, что потребление кислорода в различных участках сердца существенно различается /Weiss et al., 1978/. За счет асимметричности ветвления осуществляется адекватное кровоснабжение различных регионов сердца соответствии с их уровнем потребления кислорода. В микрососудах упругим колебаниям стенки препятствуют вязкие, а не инерционные силы в жидкости. В этих сосудах вязкие силы не дают стенке при движении ее после растяжения проскочить положение равновесия. Поэтому амплитуда пульсационных колебаний в микрососудах быстро угасает. Следовательно, на этом участке практически отсутствуют потери энергии на пульсацию. На обменном участке необходимо иметь другое - максимальную боковую поверхность по отношению к затратам энергии. Это достигается, как мы уже знаем, за счет: 1) симметрии ветвлений и 2) «вписанности» обменного участка в наклонный сегмент кривой x=f(d), что позволяет иметь значительный прирост обменной поверхности без дополнительного расхода энергии, сосудистого материала и крови. За счет последнего феномена возрастает также и отношение поверхности сосуда S к его объемуV (S/V=4/d). Минимально возможному диапазону диаметров обменных сосудов соответствуют максимальные уровни метаболизма в крови. 

Таким образом, энергооптимальная гармония системы «Обменный участок» состоит в обеспечении максимальной обменной поверхности и создания наиболее благоприятных условий для диффузии кислорода.

Очевидно, что распределение асимметричных и симметричных ветвлений на протяжении всего артериального участка имеет оптимальный характер, т.к. оно связано с оптимизацией затрат энергии, крови и сосудистого вещества. Таким образом, достигается энергооптимальная гармония вхождения транспортного и обменного участков в систему «Гемоартериальное дерево сердца».

 

 

4.5. Кислородные параметры в золотом режиме гипертензии

 

Выше нами были рассмотрены параметры архитектоники и гемодинамики, обеспечивающие оптимальный транспорт крови по обменному участку. Необходимо проанализировать «сопряжение» этих параметров с кислородными параметрами на этом участке (разность напряжений и концентраций кислорода на концах сосудов, скорость отдачи кислорода отдельным эритроцитом).

Снова будут рассмотрены терминальные, наиболее близкие к капиллярам генерации артериол. Эти генерации имеют большое значение, т.к. из них в сердечную ткань поступает около 20% от общего количества кислорода, потребляемого миокардом. Кислород начинает поступать в ткани из артериол с диаметром менее 100 мкм /Duling et al., 1979/. Установлено, что в покое перфузируется около 50% всех сердечных артериол диаметромниже 50 мкм /Weiss et al., 1985/. Для анализа нами выбрана цепочка обменных сосудов вплоть до капилляра, двигаясь по которой эритроцит отдает кислород в окружающие ткани (рис. 4.3).

 


 

 

 

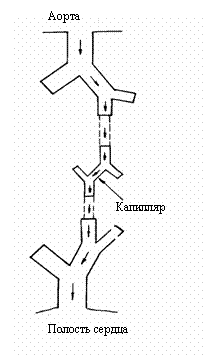
Рис. 4.3. Цепочка сердечных сосудов от аорты до капилляра, по которой движется отдельный эритроцит

 

 

 

Произведем вычисление величин диаметров цепочки сосудов, начиная от капилляра и далее по направлению к аорте (m=1, 2,…7). Диаметры в этом направлении изменяются следующим образом,

dm+1(bЗС) = dm(bЗС)/,                         (4.36)

где dm(bЗС), dm+1(bЗС) - диаметры m- и m+1-сосудов цепочки (начиная от капилляра) в золотом режиме гипертензии. Диаметр сердечного капилляра собак

 

Таблица 1.  Величины гемодинамических и кислородных параметров

в терминальных артериолах

m

dm(bЗС),

мкм

Сm

tm(bЗС),

мсек

Um(bЗС),

%

DHbO2m(bЗС),

%/сек

DpO2m(bЗС),

мм рт. ст.

1

6,9

6

37,0

138,3

5,04

11,0

2

8,7

6

37,0

87,0

3,1

10,5

3

11,0

5

30,9

54,7

1,66

6,9

4

13,9

5

30,9

34,4

1,05

4,9

5

17,5

4

24,6

21,6

0,52

3,6

6

22

4

24,6

13,6

0,30

3,5

7

27,8

4

24,6

8,5

0,14

2,4

8

35,0

3

18,5

5,3

0,08

1,1

9

44,0

3

18,5

-

-

-

10

55,6

3

18,5

-

-

-

 

Примечания: m - номер обменного сосуда цепочки по направлению капилляр – аорта; tm(bЗС) - время пребывания эритроцита в m-сосуде, Um(bЗС) - скорость отдачи кислорода отдельным эритроцитом в поперечном сечении m-сосуда, DHbO2m(bЗС) - количество кислорода, отданного отдельным эритроцитом за время пребывания в m-сосуде, DрО2m(bЗС) – разность напряжений кислорода на концах m-сосуда в золотом режиме гипертензии.

 

dK(bЗС)=5,5 мкм /Bassingthwaighte et al., 1974/. Диаметры сердечных капилляров других млекопитающих  от этой величины отличаются незначительно. Расчетные значения диаметров первых 10 звеньев приведены в табл.1 (столбец 2). Время пребывания эритроцитов в терминальных сосудах можно определить по формуле /Цветков, 1993/

dm+1(bЗС) = dm(bЗС)/,                         (4.37)

Время прохождения эритроцита через артериальный участок сосудистого тракта составляет (15-20)% от общего времени /Ткаченко, 1981/. Впокое общее время пребывания эритроцита в коронарном русле собак при нормальном среднем давлении в аорте составляет 4 с /Bernstein et al., 1962/. Количество артериальных генераций в сердце собак N=27.

Примем время движения эритроцитов по артериальному руслу от аорты до капилляра равным 600 мсек (15% от общего времени). Выражение (4.37) справедливо для любых двух соседних звеньев цепочки, по которой движется отдельный эритроцит. Для сосудов с d>45 мкм коэффициент конструкции Cm(bЗС)=3 (см. табл. 1, столбец 3). Для этих сосудов Сm+1(bЗС)/Сm(bЗС)=1. Для терминальных артериол Сm+1(bЗС)/Сm(bЗС), как нам уже известно, последовательно возрастает в пределах 1,33¸2. В соответствии с представленными величинами время пребывания в каждом «стандартном» сосуде tm(bЗС)=18,5 мcек. Исходя из этой величины, можем рассчитать относительные изменения времени пребывания во всех терминальных сосудах сердца собак (см. табл. 1, столбец 4)

В соответствии с параметрами, известными ранее и вычисленными по (4.36) и (4.37) в первом от капилляра сосуде (m=1) ΔP1(bЗС)=3,5 мм рт. ст., t1(bЗС)=0,037c, ξ1(bЗС)=1,45×10-2 Пз, d1(bЗС)=6,9×10-4см. С учетом этих величин нами получены значения для других параметров: q1(bЗС)=41,9×10-9 см3×с-1, V1(bЗС)=1,53×10-9 см3, G1(bЗС) = 0,91×10-11 г-1×см5×с-1. Используя эти величины и С1(bЗС)=6 в качестве исходных, можно вычислить значения аналогичных параметров для других обменных звеньев цепочки.

Перейдем к непосредственному расчету кислородных параметров. Каждый эритроцит отдает кислород, перемещаясь по цепочке обменных артериол, включая капилляр. Следует учесть, что между капилляром и артериолами много общего. Стенки мельчайших артериол и капилляров имеют весьма сходное строение: эпителий, тончайшая базальная мембрана и сравнительно редкие и очень тонкие пучки гладких мышц. Все эти образования имеют такой же коэффициент диффузии для О2 и СО2, как и окружающие ткани. Эритроциты при перемещении в артериолах с диаметром менее 40 мкм так же, как и в капиллярах, принимают парашютообразную форму /Mochizuki, Kagawa, 1973/. По расчетам Федершпиля и Попеля /Federspiel, Popel, 1986/ эритроциты отдают кислород с одинаковой скоростью независимо от степени их отклонения от продольной оси сосуда. Следовательно, условия для диффузии кислорода аналогичны по всей длине цепочки. Экспериментально установлено /Seiyama et al., 1996/, что количество кислорода, поступающее в ткани через единицу поверхности обменной артериолы за единицу времени, не меняется как при значительном изменении величины кровотока, так и величины гематокрита и степени насыщения эритроцитов кислородом в движущейся крови. Другими словами, за единицу времени сосуд отдает постоянное количество кислорода независимо от представленных изменений в протекающей крови. Скорость отдачи кислорода каждым поперечным сечением сосуда обусловлена только величиной потребления кислорода сердечной тканью, а она по всей длине цепочки одинакова. Следовательно, общее количество кислорода, поступающее за единицу времени из любого поперечного сечения обменных сосудов, всегда одинаково. В крупных микрососудах количество эритроцитов, одновременно находящихся в поперечном сечении, больше, чем в мелких. «Вклад» отдельного эритроцита в общую диффузию из сечения будет тем больше, чем меньше диаметр сосуда. Естественно, что в капилляре отдельный эритроцит отдает кислород с максимальной скоростью. Очевидно, что соотношение скоростей отдачи кислорода отдельным эритроцитом в двух соседних микрососудах обратно пропорционально соотношению их поперечных площадей. Исходя из этих рассуждений, в m-сосуде по отношению к капилляру

dm+1(bЗС) = dm(bЗС)/,                         (4.38)

где Um(bЗС), UK(bЗС), Sm(bЗС), SK(bЗС) - соответственно скорость отдачи кислорода отдельным эритроцитом и площадь поперечногосечения в m-артериоле и капилляре в золотом режиме гипертензии.

 


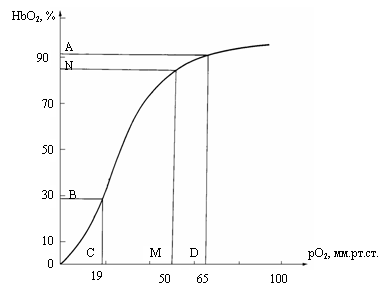
Рис. 4.4. Кривая насыщения гемоглобина человека /Уайт и др., 1981/. По оси абсцисс – рО2 в мм рт. ст.; по оси ординат - HbO2 в %. Точки A, B, C, D – границы логарифмического участка кривой (см. рис. 16). Интервал - CD pO2=19-65 мм рт. ст. интервал AB – HbO2=28,7-91,8%; точкам M и N соответствуют рО2=50 мм рт ст. и HbO2=85% на артериальном конце капилляра в золотом режиме гипертензии.

 

Установлено /Вовенко, Иванов, 1990; Вовенко, Иванов, 1997/, что напряжение кислорода на артериальном концекапилляра в тканях составляет 40-60 мм рт. ст. Примем для дальнейших расчетов в исходном режиме рО2(bЗС)=50 мм рт. ст., а в первой коронарной артерии рО2=95 мм рт. ст. По кривойдиссоциации гемоглобина человека, взятой нами из книги Уайт и др. (1981) (рис. 4.4), этомуинтервалу в эритроците соответствует разность насыщения кислородом ΔHbO2=12%.

Показано /Gayeski et al., 1988/, что в миокарде величины рО2 в крупных, средних и мелких артериях точно следуют изменениям рO2 в аорте. Десатурация начинается в артериолах диаметром 100 мкм и меньше. В микрососудах с диаметром более 50мкм отдача кислорода отдельным эритроцитом очень мала и этой величиной при дальнейших расчетах можно пренебречь. При прохождении m-сосуда разность насыщения кислородом эритроцита кислородом в этом сосуде

ΔHbO2(bЗС) = UK(bЗС)SK(bЗС)tm(bЗС)/Sm(bЗС).

Для расчетов используем первых 10 генераций обменных сосудов (см. Табл. 1, столбец 6); при m>10 расчетные значения Um(bЗС) изменяются всего на сотые доли процента. Общий «разряд» эритроцита на 10 звеньях цепочки

ΔHbO2(bЗС) = UK(bЗС)SK(bЗС)(bЗС)/Sm(bЗС).              (4.39)

Скорость отдачи кислорода эритроцитом в капилляре в золотом режиме можно определить по формуле

UK(bЗС) = [ΔHbO2(bЗС)/SK(bЗС)]/bЗС)/Sm(bЗС).           (4.40)

Приняв ΔHbO2(bЗС)=12%, SK(bЗС)=23,7×10-8 см2 и используя значения dm(bЗС) и tm(bЗС), приведенные в табл. 1, можно вычислить величину UK(bЗС), а также Um(bЗС) и ΔHbO2m(bЗС); последние приведены в табл. 1 (см. столбцы 5 и 6). Расчетное значение UK(bЗС)=215%/с практически равно максимальнойскорости отдачи - 220%. Эта величина была экспериментально установлена и рассчитана для движущихся вплазме эритроцитов с имитацией потребления кислорода /Niesel et al., 1959; Шерман, 1972/. Для дальнейших расчетов будем использовать величину UK(bЗС)=220%/с. В артериолах с диаметром менее 40 мкм скорость отдачи кислорода единичным эритроцитом быстро возрастает. Возрастает и время пребывания эритроцитов в сосуде. Экспериментально установлено /Иванов и др., 1979; Иванов и др., 1982/, что в артериолах мозга и мышц особо резкое падение рО2 происходит в сосудах диаметром 10-15 мкм и ниже. Эта экспериментально установленная тенденция близко совпадает с нашими расчетами (см. Табл. 1, столбец 7). В артериолах с диаметром более 40 мкм отдача кислорода отдельным эритроцитом незначительна. Следует отметить, что время пребывания эритроцита в сердечном капилляре (0,25 с) недостаточно для десатурации гемоглобина от 97% до 30%. Десатурация в этих пределах достигается благодаря тому, что этот процесс начинается в артериолах.

В покое на артериальном конце сердечного капилляра рО2(bЗС)=50 мм рт. ст. /Вовенко, Иванов, 1990; Вовенко, Иванов, 1997/, а на венозном рО2(bЗС)=20 мм рт. ст. /Schuchhardt, 1986/. Большое значение имеет близость прекапиллярных тройников к полной симметрии /Голубь, 1978/. Эритроциты в ветвях терминальных тройников отдают равное количество кислорода и входят в капилляры с приблизительно одинаковыми рО2. В противном случае, т.е. при значительной асимметрии терминальных бифуркаций, степень «разряда»эритроцитов в ветвях была бы различной. Поскольку разряд «докапиллярных» эритроцитов соответствует медленно спадающему участку кривой насыщения гемоглобина (рис. 4.4), то вхождение и выход эритроцитов происходили бы со значительными отклонениями от величин рО2(bЗС)=50 мм рт. ст. и рО2(bЗС)=20 мм рт. ст. Следствием этого были бы неодинаковые условия снабжения кислородом по длине мышечного волокна.

В сущности, как мы уже отмечали, как «поставщики» кислорода обменные артериолы ничем не отличается от капилляров. Добавим к этому, что обменные артериолы, также как и капилляры, параллельны мышечному волокну, которое они обеспечивают кислородом /Hort, 1955/. Как было показано выше, каждое сечение артериол независимо от их диаметра отдает то же количество кислорода, что и сечение капилляра. Представленное сходство ангиотектоники и условий диффузии кислорода в капиллярах и артериолах позволяет сделать вывод, что с «кислородной» точки зрения последние ничем не отличаются от капилляров. Иными словами, количество кислорода, диффундирующегого из микрососуда за единицу времени, определяется его длиной, но не диаметром. Таким образом, «включение» артериол вместо капилляров практически ничего не меняет за исключением одного обстоятельства. Разница заключается в «цене» кислорода. Энергетическая «стоимость» единичного объема кислорода, потребляемого из микрососудов, в артериолах выше, чем в капилляре. Эта «цена» тем больше, чем крупнее микрососуд. В целом можно сказать, что на уровне обменных сосудов существует оптимальная гармония архитектонических, гемодинамических и кислородных параметров. Природа создала высокоэффективное сочетание этих параметров.

Как будет показано в 5 главе (см. рис 5.3), сегмент кривой диссоциации оксигемоглобина, соответствующий рО2=19-65 мм рт. ст., обладает особыми, логарифмическими, свойствами. В связи с этим, как будет показано в дальнейшем, имеет место оптимальное «кислородное» сопряжение докапиллярной и капиллярной частей обменного коронарного русла. Прекапиллярные сосуды являются своего рода переходной конструкцией, где происходит предварительная организация наиболее оптимальных условий для диффузии кислорода в самой эффективной части обменного русла - капиллярах.

Величина U(bЗС)=220%/с в любом поперечном сечении сосудов - кислородный инвариант обменного участка. Этот параметр не зависит ни от диаметрамикрососудов, ни от уровня гипертензии. Последовательность значений Um(bЗС) (см. Табл. 1, столбец 5), включая UK(bЗС), близка к ряду чисел Фибоначчи: 5,3; 8,5; 13,6; 21,6; 34,4; 54,7; 87,0; 138,3; 220 (числа классического» ряда Фибоначчи: 5, 8, 13, 21, 34, 55, 89, 144, 233). Имеет место свое города «восходящий» ряд золотых чисел (см. (2.12))! Представленная последовательность указывает на то, что скорость отдачи кислорода единичным эритроцитом в терминальных артериолах и капилляре изменяется по аналогии с рядом чисел Фибоначчи. Эта аналогия сохраняется при любой гипертензии. Размеры и архитектоника терминальных микрососудов у различных видов млекопитающих практически одинаковы /Каро и др., 1981/. Поэтому можно сказать, что скорость отдачи кислорода отдельным эритроцитом в «одноименных» прекапиллярных сосудах сердца одинакова у всех млекопитающих независимо от их вида и веса. Скорости «разряда» эритроцитов в терминальных артериолах являются инвариантными оптимальными величинами, связанными между собой по аналогии с восходящим рядом золотых чисел.

Суммарная длина генерации артериол тем больше, чем ближе эта генерация к капиллярам. Вспомним, что во всех генерациях общие затраты энергии одинаковы. Следовательно, чем ближе генерация к капиллярам, тем меньше энергетическая «цена» единичного объема отданного кислорода. Происходит резко возрастающее «удешевление» потребляемого кислорода. Естественно, в капиллярах «цена» кислорода минимальна. Поскольку в каждом сосуде отдача кислорода происходит при минимально возможной «цене», то следует говорить об оптимальной «цене» кислородного обеспечения на всем артериолярно-обменном участке. Дополнительно отметим, что чем меньше калибр сосуда, тем больше отношение его поверхности к объему (S/V=4/d). Вследствие этого интенсивность обменных процессов между кровью и тканями по мере продвижения эритроцитов к капиллярам возрастает.

В разделе 3.3.2.1. нами были рассмотрены «мышечные» генерации. На уровне терминальных артериол влияние аденозина на стенки сосудов отсутствует. На этом уровне существуют другие пути регуляции. Оказалось, что наиболее выгодно изменять периферическое сопротивление путем закрытия сфинктеров или, наоборот, введя в функциональное состояние части артериол и прекапиллярных сфинктеров, составляющих предпоследнюю генерацию артериол, предшествующую капиллярам при одновременном изменении диаметров резистивных сосудов. Сфинктеры колеблются между открытым и полностью закрытым состояниями /Honig, Bourdeau-Martini, 1973/. Концентрации Рi и 5`АМФ отражают внутриклеточное восстановление кислорода и поэтому связаны с кислородным обеспечением клеток. При возрастании потребности в кислороде тканевое рО2 падает, что вызывает увеличение концентрации Рi и 5`АМФ с последующим расслаблением мышцы прекапиллярного сфинктера и раскрытием капилляра. По-видимому, в этих условиях каждый резервный капилляр раскрывается в ответ на «свою» величину рО2. Когда сфинктер раскрывается, тканевое рО2 быстро растет и концентрации Рi и 5`АМФ в кардиомиоцитах падают по направлению к стабильной величине, адекватной данному уровню гипертензии.

Таким образом, адекватное подключение дополнительного числа артериол и капилляров вызвано, в конечном счете, недостаточным кислородным обеспечением части сердечных клеток в условиях гипертензии.

 

4.6. Преимущества бифуркационного ветвления и оптимизация

гемоартериального дерева сердца

 

В конце этой главы представляется возможным еще раз показать универсальность энергооптимальной гармонии на пути от «простых» систем к все более и более сложным. 

В наиболее «простой» системе – «m-сосуде с движущейся кровью» - при заданном кровотоке qm(bЗС) величины dm(bЗС), ξm(bЗС) и bm(bЗС) имеют оптимальные значения, при которых суммарный расход механической и химической энергии в единичном объеме сосуда за единицу времени минимален. «Подбор» длины сосуда lm(bЗС) обеспечивает оптимальное время прохождения эритроцитов через артерию tm(bЗС) и оптимальную величину ΔPm(bЗС). Коэффициент оптимальной перфузии одинаков как на транспортном, так и на обменном участках (αm(bЗС)=162 с-1). Таким образом, вхождение каждого из элементов (q(bЗС), ΔP(bЗС), d(bЗС), l(bЗС), t(bЗС), ξ(bЗС), b(bЗС)) в систему «Сосуд, наполненный движущейся кровью» происходит в соответствии с принципом оптимального вхождения.

Тройник конструктивно состоит из ствола и двух ветвей. «Вхождение» в тройник каждого  из трех сосудов имеет оптимальный характер. При заданном кровотоке в стволе и разности давления между концом ствола и концами каждой из ветвей архитектоника сердечного тройника такова, что при этом имеет место минимальный суммарный расход энергии, крови и сосудистого материала. Элементы (сосуды, наполненные движущейся кровью) объединяются в более сложную систему «Тройник» по принципу оптимального вхождения.

Следующим этапом оптимального вхождения является оптимальное ветвление сосудов. Бифуркация является общим типом ветвления сердечных сосудов от крупных артерий до артериол /Zamir, Chee, 1985/. Бифуркация по сравнению с другими возможными вариантами ветвления (3, 4 и более ветвей) имеет значительные преимущества. Рассмотрим в качестве наиболее близкого варианта трифуркацию (ствол и 3 ветви). Предварительно примем, что при бифуркации и трифуркации имеют место одинаковые предварительные условия:

1) равенство кровотока в первой коронарной артерии;

2) одинаковая разность давлений между аортой и артериальным концом капилляров;

3) одинаковая плотность капиллярной сети;

4) равенство диаметра капилляров и диаметра первой коронарной артерии;

5) каждое поперечное сечение капилляров и обменных артериол отдает кислород с максимальной скоростью.

Кроме того, при трифуркации должно существовать такое же оптимальное соотношение между диаметрами сосудов и кровотоками в них, как и при бифуркации. В дальнейшем для простоты расчетов примем все разветвления симметричными, а коэффициент конструкции сосудов постоянным на всем артериальном участке. Исходя из этих предварительных условий,

d1(bЗС)3+ d2(bЗС)3+ d3(bЗС)3= dС(bЗС)3,

l1(bЗС)3+ l2(bЗС)3+ l3(bЗС)3= lС(bЗС)3,

где dС(bЗС), d1(bЗС), d2(bЗС), d3(bЗС), lC(bЗС), l1(bЗС), l2(bЗС), l3(bЗС) - соответственно диаметр и длина ствола и 1, 2 и 3 ветвей в золотом режиме гипертензии. Для симметричного трифуркационного ветвления

d1(bЗС) = d2(bЗС) = d3(bЗС) = 0,694dС(bЗС),                   (4.41)

l1(bЗС) = l2(bЗС) = l3(bЗС) = 0,694lС(bЗС).                     (4.42)

С учетом условия 4) и зависимости (4.41) получается, что для собаки при трифуркации общее число генераций равнялось бы 18 (при бифуркации N=29). Для выполнения условий 1) и 2) необходимо длину всех «трифуркационных» сосудов дополнительно увеличить в 1,6 раза по сравнению с (4.42) (иначе начнется отек тканей). Давление, приложенное к каждому сосуду, при этом также возрастет в 1,6 раза. При таком дополнении общий расход энергии, сосудистого материала и крови для обоих вариантов ветвления будет одинаковым. Однако пришло время вспомнить, что последняя часть генераций приходится на наклонную часть кривой вязкости (рис. 4.1). По мере увеличения числа ветвей (3, 4 и т.д.) количество генераций, «совпадающих» с наклонным сегментом кривой (d<50 мкм), значительно сокращается. На обменный участок в пределах d=5,5¸50 мкм приходится приблизительно 9 бифуркационных разветвлений, тогда как трифуркационных - только шесть. При дальнейшем росте ветвлений количество «совпадений» с наклонным участком будет все меньше и меньше. Если рассматривать обменные генерации, начиная от капилляра (m=1, 2, 3 и т.д.), то преимущества бифуркационного разветвления очевидны. Одноименные генерации при трифуркации имеют больший диаметр, чем бифуркационные. Например, для первой от капилляров генерации при бифуркации d1(bЗС) = 1,26dK(bЗС), при трифуркации d1(bЗС) = 1,44dK(bЗС), при тетрафуркации d1(bЗС) = 1,59dK(bЗС) и т.д. Отметим, что время пребывания эритроцитов в этих сосудах независимо от вида ветвления одинаково. Отдельный эритроцит, проходя через «трифуркационный» сосуд, отдает меньше кислорода, чем в «одноименном» бифуркационном, даже при условии, что время пребывания в них одинаково. В действительности же время пребывания в одноименных генерациях в «бифуркационном» сосуде больше, чем в «трифуркационном». Очевидно, что отдельный эритроцит при прохождении «трифукационной» цепочки не успевает разрядиться до рО2=50 мм рт. ст. Чтобы обеспечить недостающее количество отдаваемого кислорода, необходимо увеличить длину капилляра, что ведет к повышению ΔPK(bЗС). Критическая величина давления на артериальном конце капилляра, выше которой начинается отек тканей, равна 35 мм рт. ст. /БСЭ, т. 13, 1973, с. 1381/. Повышение ΔPK(bЗС) при трифуркации снижает разность между критическим давлением отека тканей и давлением на артериальном конце капилляра. В пределах этой разности снижается верхняя граница допустимого уровня гипертензии (bmax<2, при котором сердечная мышца может адекватно обеспечиваться кислородом без отека тканей. Очевидно, что при дальнейшем росте разветвлений (4, 5 и т.д.) отдельный эритроцит входит в капилляр с все большим рО2. При этом все ниже становится уровень, при котором отсутствует отек сердечной ткани. Очевидно, что при бифуркации уровень максимальный гипертезии имеет наибольшую величину (bmax=2).

Кроме того, с бифуркацией связано еще одно преимущество. При бифуркации всякой генерации обменных сосудов (первой, второй и т.д., начиная от капилляра) по сравнению с «одноименными» генерациями других вариантов ветвлений соответствует наименьшая величина диаметра. Следовательно, величина отношения поверхности к объему сосуда (S/V=4/d) в одноименных генерациях при бифуркации будет наибольшей. Естественно, что в «бифуркационных» сосудах с более высоким отношением S/V уровень метаболизма в крови является максимальным. Отметим, что в интереснейшем математическом исследовании ветвления микрососудов, проведенном В.А.Глотовым /Глотов, 1995/, теоретически доказана невозможность ветвления сосуда более чем на две ветви. «Выбор» бифуркации по сравнению с другими вариантами оптимального ветвления при том же расходе энергии, крови и сосудистого материала обеспечивает максимальную величину «безотечной» гипертензии и условия наиболее интенсивного обмена между кровью и тканями.

Таким образом, «вхождение» сосудов в систему «Тройник» по варианту бифуркации является наиболее эффективным и экономичным. Этот вариант обеспечивает энергооптимальную гармонию между генерациями эластических, мышечных и обменных сосудов.

В заключение рассмотрим «использование» принципа оптимального вхождения в конструкции всей системы «Гемоартериальное коронарное русло».

Всякий тройник своими ветвями дает начало «дочерним» тройникам и т. д. Поскольку сопряжение ствола и ветвей тройников всегда имеет оптимальный характер, то и сопряжение  любых соседних генераций связано с максимальной экономией энергии и вещества.

И, наконец, оптимальное вхождение в систему «Гемоартериальное коронарное русло» – двух основных подсистем: транспортного и обменного участков. Оптимальность их вхождения обеспечивается:

1) асимметрией эластических и мышечных тройников;

2) симметрией обменных тройников;

3) оптимальной «вписанностью» этих участков в определенные сегменты кривой вязкости крови.

Благодаря оптимальной гармонии сопряжения «противоположностей» - транспортного и обменного участков - в системе «Гемоартериальное русло» перемещение единичного объема потребляемого кислорода по артериальному руслу в целом обеспечивается при минимуме затрат энергии, крови и сосудистого вещества. Мы могли убедиться в «присутствии» принципа оптимального вхождения на всей цепочке гемоартериальных систем возрастающей сложности. Этот феномен еще раз указывает на универсальность «использования» Природой принципа оптимального вхождения в сердечных системах различной сложности.

Необходимо указать на разнообразие конструкции генераций, исполненных Природой в соответствии с законами (3.56)-(3.58). Во всех генерациях эластического типа соответствие этим законам происходит за счет одинакового относительного изменения диаметров и длин во всех сосудах. На мышечной части транспортного участка соответствие законам (3.56)-(3.58) обеспечивается аналогичным изменением размеров одинаково «окрашенных» сосудов в каждой генерации. На обменном участке соответствие обеспечивается аналогичным подключением дополнительного числа обменных сосудов постоянного размера. Во всех трех вариантах ветвления найден наиболее эффективный способ включения той или иной генерации в условиях гипертензии. Бифуркационное «дерево» сердца имеет энергооптимальную фрактальную конструкцию /Цветков, 2003/.

 

4.7. Фракталы и артериальное «дерево»

 

Одним из методологических инструментов, позволяющих вскрыть основу организации живых систем – законы их композиции - является учение о фракталах. Основоположник фрактальной геометрии Б. Мандельброт поясняет понятие фрактала как некоего образования, самоподобного в том или ином смысле /Пайтген., Рихтер П., 1993/. Фрактальным множествам присуща масштабная инвариантность (самоподобие) их внутренней структуры: любая малая часть фрактала воспроизводит всю его структуру. Важным показателем фрактальных зависимостей является фрактальная размерность, которая, как правило, бывает дробной и не совпадает с топологической размерностью. Последняя, как известно, для линии равна 1, для поверхности – 2, для объема – 3. Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии. Многие объекты живой природы имеют ярко выраженную фрактальную структуру (деревья, кровеносные сосуды, легкие и др.). Создана своеобразная фрактальная геометрия. Системы фрактальных зависимостей образуют целый мир объектов (структур) и явлений (процессов), отличающихся от непрерывных систем своеобразной «рваной структурой». Важным свойством фракталов является самоподобие. Проявление общей биоэнергетической направленности структур и функций живых систем обнаружено на всех уровнях организации живой природы: от макромолекулярного до биосферного, что сродни проявлению свойства самоподобия объектов, отображаемых фрактальными зависимостями. Как видим, важные свойства фракталов близки важным общим свойствам главных энергетических законов природы. Это дает основание предполагать, что наиболее общим свойством природных объектов, отображаемых фрактальными зависимостями, является их энергоемкость. Последовательность чисел Фибоначчи, которые отражают аналитическое выражение золотого сечения, в своей основе родственна фракталам.

Артериальное «дерево» сердца, как будет показано ниже, имеет энергооптимальную фрактальную конструкцию. Основополагающей структурной единицей «дерева» является сосудистый тройник. Выше нами было показано, что бифуркация является оптимальным вариантом ветвления сосуда (по сравнению, например, с трифуркацией и т.д.). Каждый тройник состоит из ствола и двух ветвей. Каждая ветвь, в свою очередь, является стволом и разделяется на две ветви и т.д. Таким образом, первый тройник по форме последовательно воспроизводится в нисходящем масштабе (см. рис. 3.6).

По мере продвижения крови каждая бифуркация конструктивно повторяет предыдущую в уменьшенном масштабе. Выше нами было показано, что последовательное сопряжение тройников сердца связано с оптимальными соотношениями параметров ствола и ветвей. Элементарной единицей тройника является сосуд с движущейся кровью. В каждом сосуде имеет место двоякий расход энергии: 1) механической - на перемещение крови и 2) «химической» - на обеспечение процессов метаболизма в крови и воспроизводства эритроцитов. На основе анализа экспериментальных данных нами установлено, что во всех сердечных артериальных и капиллярных сосудах суммарный расход энергии по отношению к единичному объему транспортируемой крови минимален (режим «минимальной работы»). Режим «минимальной работы» обеспечивается «подбором» оптимального диаметра сосуда для заданной величины кровотока, симметрией движения эритроцитов относительно продольной оси сосуда, ламинарно-вращательной формой движения и оптимальной температурой крови. Кроме того, в каждом сосуде поддерживается оптимальная величина гематокрита и оптимальное соотношение скоростей составляющих крови: плазмы и эритроцитов. В любом сосуде имеют место оптимальные соотношения между затратами механической и химической энергии.

Мощности для отдельного сердечного -сосуда

γ(β) = WM(β)/WX(β) = WM(bЗС)/WX(bЗС) = 0,5,

где WM(bЗС), WX(bЗС), WM(β), WX(β)– соответственно расход механической и химической энергии за единицу времени в сосуде в золотом и других режимах гипертензии. Величина γ(β) является постоянной энергооптимальной оптимальной величиной (инвариантом) для всех артериальных сосудов сердца млекопитающих, включая и капилляры.

Артериальное русло состоит из асимметричных и симметричных тройников. Первые относятся к генерациям крупных, средних и мелких сердечных артерий, вторые – к генерациям микрососудов. Конструктивные особенности всякого тройника в режимах гипертензии можно представить тремя коэффициентами: коэффициентом ветвления k(β)=k(bЗС) и коэффициентами относительного сечения ветвей H1(β)=H1(bЗС). Параметры H1(β) и H2(β) позволяют оценить степень асимметрии ветвления, а коэффициент k(β) показывает превышение суммарной площади поперечного сечения ветвей по отношению к площади ствола. Во всех сердечных тройниках 1< k(β)≥1,26, что соответствует режиму «минимальной работы» в стволе и ветвях. Для асимметричных тройников 1<k(β)<1,26, H1(β)≠H2(β), для симметричных k(β)=1,26, H1(β)=H2(β)=0,5. Оптимальная архитектоника сердечных тройников, и асимметричных и симметричных, во всех режимах гипертензии соответствует выражению

[k(β)H1(β)]3/2 + [k(β)H2(β)]3/2 = [k(βЗС)H1(bЗС)]3/2+ [k(bЗС)H2(bЗС)]3/2 = 1.

Рассмотрим отдельно асимметричные и симметричные тройники. Характерной особенностью сосудов асимметричных тройников сердца во всех режимах гипертензии является постоянство отношения диаметра к длине: lC(β)/dC(β)=l1(β)/d1(β)=l2(β)/d2(β)=const. Вязкость крови в асимметричных тройниках практически также постоянна (не зависит от диаметра). Вследствие этих особенностей в этих тройниках имеет место феномен самоподобия - неизменное суммарное «воспроизводство» ствола ветвями по объему крови и сосудистого материала. Это означает, что суммарный объем крови, заключенный в сосудах ветвей и суммарная масса стенок ветвей равны величине этих параметров в стволе. Аналогично, во всех режимах гипертензии суммарный расход энергии за единицу времени в ветвях асимметричного тройника равен ее расходу в стволе,

λ(β) = [(W1(β) + W2(β)]/WС(β) = [(W1(bЗС) + W2bЗС)]/WС(bЗС) = 1,

где WС(β), W1(β), W2(β) – соответственно общие затраты механической и химической энергии за единицу времени в стволе и ветвях. Каждая из ветвей исходного тройника является стволом для последующих тройников и т.д. При последующем снижении калибра тройников в каждой новой генерации имеет место очередное суммарное «воспроизводство» самого первого, исходного, ствола по энергии, крови и сосудистому веществу. Фрактальное подобие последовательности тройников представлено отношениями γ(β) и λ(β). Оптимальность этого подобия последовательности тройников заключается в том, что все асимметричные тройники имеют структуру, позволяющую пропускать «свой» кровоток с минимальными затратами энергии, крови и сосудистого материала.

Симметричные тройники составляют обменный микроциркуляторный участок артериального русла сердца. На обменном участке l1(β)/d1(β)=l2(β)/d2(β), но эта величина в отличие от транспортного участка всегда больше, чем lC(β)/dC(β). Для каждой последующей генерации тройников неравенство сохраняется (при этом отношения lC(β)/dC(β), l1(β)/d1(β) и l2(β)/d2(β) по мере продвижения к капиллярам возрастают). Особенность этих тройников состоит в том, что в них величина коэффициента k(β), отношения dС(β)/d1(β) и dС(β)/d2(β) приблизительно равны числу 1,26. Отметим связь этого числа с золотым числом 1,618 (1,26≈√1,618=1,27). Таким образом, оптимальная архитектоника симметричных тройников связана с золотыми числами. В асимметричных тройниках «золотые» соотношения отсутствуют. Дополнительное, «нестандартное», удлинение ветвей должно было бы привести к дополнительным затратам энергии. Однако на обменном участке в соответствии с эффектом Фареуса-Линдквиста уменьшение вязкости крови по мере уменьшения диаметра обратно пропорционально «дополнительному» удлинению сердечных микрососудов, что позволяет скомпенсировать дополнительные потери энергии. Как следствие этого, в симметричных тройниках, так же как и в асимметричных, ветви суммарно «воспроизводят» ствол по затратам энергии (λ(β)=1).

В итоге можно сказать, что основу «энергетического» фрактального подобия всех тройников независимо от калибра сосудов и их назначения составляет отношение λ(β)=1. На обменном участке фрактальное сопряжение тройников связано с золотыми числами.

 

4.8. «Цена» транспорта кислорода на артериальном участке

 

Перейдем к анализу оценки затрат энергии на транспорт единичного объема кислорода в режимах гипертензии. Было показано /Цветков, 2004/, что в условиях гипертензии в любой  i-генерации сердечных артерий,

WМi(b) = b3WМi(bЗС),

WХi(b) = b3WХi(bЗС).

где WМi(bЗС), WМi(b), WХi(bЗС), WХi(b) - средняя за сердечный цикл механическая и химическая мощность, расходуемая в i-сосуде в золотом и других режимах гипертензии. Очевидно, что суммарный расход механической и химической энергии за единицу времени возрастает в b3 раз как на i-генерации, так и на всей совокупности «стандартных» генераций,

W(b) = b3W(bЗС),                                        (4.43)

где W(bЗС), W(b) - расход механической и химической энергии за единицу времени на «стандартном» участке в золотом и заданном режимах гипертензии.

Увеличение затрат энергии в b3 раз при гипертензии имеет место также и на «нестандартном», обменном участке. На этом участке при гипертензии средние значения давления, отнесенные к длительности кардиоцикла, во всех сосудах увеличиваются в b раз. «Подключение» резервного сосуда при гипертензии имеет следствием то, что кровоток увеличивается в b раз в основном сосуде и в b(b-1) раз в резервном, суммарный же кровоток возрастает в b3 раз. При этом давление, приложенное к каждому сосуду, возрастает в b раз. Следовательно, расход механической мощности на генерации «нестандартных» сосудов, а также и на всем «нестандартном» участке возрастает в b3 раз. Аналогично, расход химической энергии за единицу времени в основном сосуде возрастает в b3 раз, а в резервном в b2(b-1) раз. Суммарный расход химической мощности в обеих ветвях увеличивается в b3 раз. Очевидно, что и на «нестандартном», микрососудистом участке имеет место возрастание общего расхода механической и химической мощности в b3 раз по аналогии с (4.43).

Таким образом, общий расход мощности на всем артериальном участке в режимах гипертензии,

SW(b) = b3SW(bЗС).                                      (4.44)

Из вышеизложенного очевидно, что вся система докапиллярного транспорта кислорода при гипертензии расходует энергию на перфузию и процессы в крови в b3 раз больше, чем в покое. Средняя за кардиоцикл скорость потребления кислорода миокардом в том же режиме гипертензии увеличивается в b3 раз /Цветков, 1997/,

 

SB(b) = b2SB(bЗС),                                       (4.45)

где SB(bЗС), SB(b) – суммарное потребление кислорода сердечной мышцей в золотом и других режимах гипертензии. Исходя из (4.44) и (4.5) очевидно, что в условиях гипертензии «цена» доставки единичного объема потребляемого кислорода по артериальному участку коронарного русла линейно пропорциональна росту гипертензии,

V(b) = SW(b)/SB(b) = bV(bЗС).

Каким образом меняется «цена» транспорта единичного объема потребленного кислорода в отдельных генерациях артериальных сосудов? Поскольку скорость диффузии кислорода из любого сечения каждой артериолы одинакова, то объем кислорода, отдаваемого сосудом за единицу времени, линейно зависит от длины сосуда. Во всех терминальных тройниках

D1(bЗС) + D2(bЗС) = 1,588[С1(bЗС)/СС(bЗС)]DС(bЗС),

W1(bЗС) + W2(bЗС) = WС(bЗС),

где DС(bЗС), D1(bЗС), D2(bЗС) - соответственно средний за кардиоцикл объем кислорода, отдаваемый за единицу времени стволом, 1 и 2 ветвями тройника, WC(bЗС), W1(bЗС), W2(bЗС) - средняя за кардиоцикл энергия, расходуемая за единицу времени в стволе, 1 и 2 ветвях в золотом режиме гипертензии. Если бы в обменных тройниках отношение С1(bЗС)/СС(bЗС)= С2(bЗС)/СС(bЗС)=3, то суммарная величина потребляемого кислорода в ветвях по отношению к стволу увеличивалась бы в 1,588 раз (отметим близость этого числа к золотому числу 1,618!). Фактически же отношение длины к диаметру в обменных сосудах больше 3. Если рассматривать генерации микрососудов по мере убывания их диаметра, то очевидна следующая тенденция: в очередной генерации (n=2, 3,...,7) отдаваемый объем кислорода возрастает более, чем в 1,588n раз, а расходуемая мощность остается прежней. Таким образом, по мере приближения к капиллярам энергетическая «цена» объема отдаваемого кислорода стремительно падает, достигая минимального значения в капилляре. В режимах гипертензии тенденция падения сохраняется; при этом «цены», полученные для каждого сосуда в золотом режиме, следует умножить на величину b.

Из вышеизложенного можно сделать следующие выводы:

1) в любом режиме гипертензии общий расход энергии на транспорт потребленного кислорода по артериальному руслу, включая транспортный и обменный участки, имеет оптимальную, т.е. минимально возможную для каждого режима, величину;

2) самый «дешевый» кислород поставляется в сердечную мышцу в золотом режиме, а самый «дорогой» - в режиме максимальной гипертензии;

3) в каждом режиме наиболее «дешевый» кислород поступает из микрососудов наименьшего диаметра, а самый «дорогой» - из наиболее крупных сосудов.

Увеличение «стоимости» транспорта при росте гипертензии вызвано необходимостью создать в сердечных клетках концентрацию кислорода выше летальной для данного уровня гипертензии. Чем больше гипертензия, тем выше значение рО2, ниже которого начинается гибель клеток. Природа «пошла» на дополнительный расход энергии, достаточный для устранения летальной ситуации в клетках. Естественно, что чем значительнее уровень гипертензии, тем больше дополнительный расход энергии, а следовательно, и «цена» транспорта кислорода. За счет дополнительного расхода энергии обеспечивается прирост рО2 в сердечной ткани на величину /Цветков, 1997/

δpO2(b) = 42lgb.                                                     (4.45а)

С величиной δpO2(b) связан рост «цены» доставки единичного объема кислорода. Дополнительные затраты энергии обеспечивают «качество» потребляемого кислорода адекватно уровню активности сердечной мышцы. Таким образом, оптимальная организация системы докапиллярного транспорта кислорода обеспечивает в каждом режиме гипертензии:

1) минимум транспортных расходов на доставку единичного потребленного объема кислорода;

2) защиту сердечных клеток от гибели.

Очевидно, что при любом уровне гипертензии обеспечивается оптимальное кислородное обеспечение сердца по «количеству» (4.45) и «качеству» (4.45а).

Отметим при этом, что благодаря оптимальной организации мышечной массы (см. раздел 2.4) объем потребляемого сердцем кислорода «сведен» к минимальной величине. Таким образом, в сердце имеет место двойная экономия по отношению к кислороду: 1) минимизация потребности в кислороде вследствие минимизации мышечной массы миокарда и 2) минимизация «цены» доставки необходимого объема кислорода к месту диффузии. Таким образом, имеет место энергооптимальная гармония между минимизацией объема кислорода, используемого в миокарде в энергетических процессах, и минимизацией затрат энергии на доставку кислорода к месту потребления.

 

 

К оглавлению