Другие статьи

К оглавлению

---

Глава 3. ЭНЕРГООПТИМАЛЬНАЯ ГАРМОНИЯ И ТРАНСПОРТНЫЙ УЧАСТОК КОРОНАРНОГО РУСЛА

3.1. Интегратизм и «сборка» сложных систем

Науке известны законы, отражающие стабильность мирового порядка, - законы сохранения. Однако науке недостает законов возникновения «сложного из простого». Причина такой парадоксальной ситуации в том, что до последнего времени наука развивалась главным образом редукционистским путем, что подразумевает расчленение сложного целого на простые части, синтезом же как таковым пренебрегали. Редукционизм обозначает принцип, основанный на убеждении, что путь к познанию сложного лежит через расчленение этого сложного на все более и более простые составляющие и изучение их природы и свойств. Редукционизм предполагает необходимость разложения явления на составляющие его детали и механизмы. Считается, что, зная механизмы данного явления, мы можем судить о явлении в целом. Успех редукционизма породил в науке так называемый механистический подход к пониманию явлений природы. Благодаря своим успехам в исследовании вещественно-энергетических свойств природы, механистический подход прочно утвердился в психологии не только ученых, но и людей, далеких от науки. Сложившиеся стереотипы мышления до сих пор не позволяют существенно сдвинуться в понимании так называемых «сложных систем», к числу которых, в частности, относятся все биосистемы. «Жизнь не является простой суммой своих составных частей…Чем дальше вы расчленяете живые комплексы, тем дальше вы уходите от биологии и в конце концов вам остаются только …законы неживой природы» /Казначеев и др., 1997, с. 111/. Деятельность живых систем не удается объяснить в рамках механистического подхода. При механистическом подходе предполагается, что, сводя сложное к совокупности его частей, можно, изучив последние, получить сведения о свойствах исходного целого. В результате редукционистского подхода объект исчезает как целое, как система со всеми присущими ей признаками. Как иронически отметил Бернард Шоу, ситуация в научном мире идет к тому, что исследователь будет знать «все ни о чем и ничего обо всем». И, тем не менее, надежды ученых всего мира понять феномен жизни, исходя из принципов редукционизма, живы и по сей день. От понимания многих исследователей ускользает «природа целесообразности», в соответствии с которой происходит организация взаимодействия всех подсистем организма, и не только организма, но и всей живой природы в целом.

Как противовес редукционисткому методу в современной науке возникает обратное, интегративистское течение, т.е. системный подход к объекту, подразумевающий «сборку» объекта из ранее изученных частей. Это направление получило наименование «интегратизм». Метод интегратизма в современной науке приобретает все большее значение. Как писал академик В.А.Энгельгардт, основная сущность этого направления состоит «в познании того, каким образом происходит включение, интеграция элементов более примитивных в новые целостности, стоящие на более высокой ступени организационной иерархии, с иными степенями упорядоченности» /Энгельгардт, 1984, с. 207/. В соответствии с принципом интеграции исследователь идет в обратном редукционизму направлении – «от простого к сложному».

Интегратизм предполагает «сборку» сложной живой системы из ранее изученных частей («простых» систем). Однако на пути к этой цели существуют значительные трудности. Редукционизм предполагает дробление изучаемых биообъектов на все более мелкие элементы. Естественно, что при движении в таком направлении теряется значительная часть информации о связях внутри объекта. (Например, если некую систему представить как А+В, где «+» - связь, объединяющая А и В в единое функциональное целое, то при дроблении системы «+» исчезает.) В этом плане большой теоретический интерес для биологов представляет системный подход к изучаемому объекту /Урманцев, 1974, 1978/. В разработанном Ю.А.Урманцевым варианте общей теории систем (ОТС) впервые, помимо универсальных понятий «объект» и «объект-система», введено понятие «закон композиции (организации)» объекта. «Объектом» по Урманцеву признается любой предмет мысли, т.е. предметы объективной и субъективной реальности, и не только вещи, но также качества, свойства, отношения, процессы и т.д. «Объект-система»– это единство, созданное определенного сорта «первичными» элементами + связывающими их в целое отношениями + ограничивающими эти отношения условиями (законом композиции). Исходя из этого определения системы, в качестве первичных «элементов» в рассматриваемых нами кардиосистемах можно представить те или иные параметры деятельности сердца (давление, кровоток, время изгнания крови, длина и диаметр сосудов и т.д.). Аспект «закон композиции», выдвинутый Ю.А.Урманцевым, значительно расширяет возможности исследователя. Следует сказать, что законам организации в биологических науках не уделяется должного внимания. До сих пор организация живого объекта многими биологами чаще всего воспринимается как некая второстепенная данность Природы, которая не подлежит изучению. Однако невозможно говорить о гармонии живого объекта, не изучив предварительно его организацию.

Отметим, что одной из проблем, исходящих из интегрального подхода, является выявление законов и критериев гармонии стабильных, самоорганизующихся систем. По общепринятому определению «гармония – это соразмерность частей и целого, слияние различных комплексов объекта в единое органическое целое» /Лосев, 1971, с. 128/. Как уже было показано в 2 главе этой книги, мерой гармонии, «соразмерности частей и целого», является золотое сечение, объединяющее «противоположности» объекта (ССЦ) в единое целое. Большим вкладом в решение проблемы меры «противоположностей» являются исследования белорусского философа Э.М.Сороко /Сороко, 1984/. В настоящее время остается открытым вопрос: «По какому критерию происходит «слияние различных частей объекта в единое целое»? Ответ на этот вопрос, по нашему представлению, следует искать на пути интегратизма и системного подхода. Интегратизм неразрывно связан с системным подходом, который приобретает в настоящее время огромное значение (особенно в биологии). Однако на этом пути предстоит преодолеть большие трудности. Для «сборки» живой системы необходимо иметь большой объем экспериментальных данных. Большинство биологических объектов по причине их исключительной сложности чаще всего изучены очень «мозаично». Вследствие этого невозможно произвести достаточно полный и глубокий системный анализ большинства живых систем. Сердце человека и млекопитающих по причине значительной «вертикальной» (иерархия систем) и «горизонтальной» (множество параметров деятельности) изученности представляется не только наиболее подходящим объектом для «сборки», но также и «полем поиска» законов и критериев гармоничного вхождения «простых» систем в более сложные.

На основе проведенного нами системного анализа огромного объема экспериментальных данных впервые была установлена энергооптимальная гармония сердечных систем независимо от уровня их сложности /Цветков, 1993, 1997, 2004/. Эта универсальная особенность организации систем сердца получила обозначение – «принцип оптимального вхождения». Сущность этого принципа состоит в том, что «Всякая из сердечных систем, совместно образующих сложную кардиосистему, включается в последнюю оптимальным образом, вследствие чего сложная система исполняет свою функцию с минимальным расходом энергии и строительного материала». Поскольку сердечные системы представляют собой стабильные самоорганизующиеся системы, то принцип оптимального вхождения является условием образования стабильных сердечных систем. Гармония оптимального «вхождения» кардиосистем имеет место как в условиях покоя, так и физической нагрузки.

Рассмотрим одну из «сложных» сердечных систем. Сердце для исполнения своей функции нуждается в адекватном количестве кислорода. Ниже нами будет представлен процесс «сборки» функционально связанных сердечных систем возрастающей сложности по направлению от самой «простой» системы - эритроцита - до системы кислородного обеспечения сердца в целом.

Существующие к настоящему времени модели кислородного обеспечения сердца страдают существенными недостатками. Так в монографии Е. Вейбеля /Weibel, 1984/, написанной как учебное пособие для студентов Гарвардского университета в США, использованы устаревшие концепции А. Крога транспорта кислорода в тканях. В современном учебнике по физиологии, изданном в Штуттгарте в 1999 г. под редакцией известного специалиста по транспорту кислорода Г. Тевса /Thews et al., 1999/, анализ транспорта кислорода также производится по модели Крога. В этих книгах не представлены новейшие открытия в области кислородного снабжения органов, в частности, то, что кислород поступает в ткани не только из капилляров, но также из артериол и венул /Duling et al., 1979; Иванов и др., 1979/. В более продвинутых моделях /Grunewald, Sowa, 1978/ не представлено сопряжение кислородных параметров в ткани с параметрами архитектоники и гемодинамики снабжающих микрососудов, что не позволяет выявить конечную «цель» Природы: «Почему эта система организована таким, а не иным образом?». Для решения этой задачи произведем «сборку» системы обеспечения кислородом сердца по направлению «от простого к сложному».

3.2. Кислороднесущие системы возрастающей сложности

Гемоартериальное русло сердца по отношению к транспорту и потреблению кислорода можно разделить на два участка. На первом участке (крупные, средние и мелкие артерии) кислород в окружающие ткани не поступает. Газообмен осуществляется на другом участке, включающем генерации прекапиллярных микрососудов. Первый участок русла можно назвать транспортным, а второй – обменным. Кроме этих участков существует капиллярный участок, на котором осуществляется основной обмен между кровью и сердечной тканью. В этой главе нами будут рассмотрены особенности архитектоники и гемодинамики транспортного участка, а также произведена их «сборка» по направлению от «простого к сложному». «Сборка» производится по цепочке функционально связанных систем возрастающей сложности: эритроцит → кровь → сосуд с движущейся кровью → гемососудистый тройник → генерации тройников

3.2.1. Эритроцит

Для всех позвоночных универсальным признаком является заключение гемоглобина в специальные клетки – эритроциты. Основная масса эритроцита состоит главным образом из воды (65%) и молекул гемоглобина (34%). Концентрация гемоглобина одинакова у разных видов млекопитающих; причем эта концентрация не зависит от диаметра и объема эритроцитов и их возраста /Тринчер, 1965/. Эритроцит обладает целым рядом свойств, аналогичных для различных видов млекопитающих:

1) отделяет дыхательный пигмент от плазмы и создает наиболее благоприятную ионную среду для выполнения им специфических кислороднесущих функций;

2) содержит химические регуляторы функции дыхательного пигмента;

3) внутри эритроцита концентрация гемоглобина может достигнуть достаточно высокой степени, что необходимо для сохранения пигментом сложного строения, обеспечить ему кооперативный эффект и своеобразную форму кривой диссоциации оксигенированной его формы;

4) высокая концентрация гемоглобина внутри эритроцита и изоляция пигмента от плазмы позволяет резко повысить кислородную емкость крови без увеличения онкотического давления в плазме, что имеет огромное значение для обмена воды и электролитов между тканями и кровью в тканевых капиллярах;

5) эритроциты обладают способностью уменьшать вязкость крови в самом ответственном для обмена веществ звене кровеносного русла – в артериолах и капиллярах;

6) эритроциты млекопитающих – безъядерные образования с чрезвычайно низким собственным дыханием, что увеличивает продолжительность их жизни;

Молекулы гемоглобина обладают важными оптимизирующими свойствами:

1) кооперативное связывание кислорода повышает эффективность гемоглобина как переносчика кислорода /Стайер, 1984/

2) молекулы гемоглобина в эритроците имеют паракристаллическую упаковку; их концентрация в клетке близка к предельной /Щерба, 1968/;

3) концентрация гемоглобина в эритроците у различных видов млекопитающих одинакова, несмотря на различные размеры клеток /Коржуев, 1964/.

Отметим конструктивные особенности эритроцита. Равномерное распределение молекул гемоглобина в эритроците обусловливает равномерное распределение внутриклеточной воды. Молекулы гемоглобина располагаются на внутренней стороне мембраны эритроцита. Между двумя молекулами гемоглобина находятся две молекулы воды. Вода в этой конструкции выполняет две взаимно противоположные функции. С одной стороны, поддерживает жесткую структуру, что позволяет сохранять автономность каждой молекулы гемоглобина. С другой – обеспечивает изменчивость формы при прохождении через капилляры. Физическая особенность внутриклеточной воды заключается в ее квазикристаллической структуре при сохранении низкой вязкости жидкости. Внутриклеточная вода одновременно находится в двух качественно различных состояниях - кристалла и жидкости, она сопряжена с непрерывными метаболическими функциями живой клетки /Тринчер, 1965/. Очевидно, что особое состояние воды и пространственное расположение молекул воды и гемоглобина обеспечивает гармонию «противоположностей»: 1) жесткость и изменчивость оболочки эритроцита и 2) свойства жидкой и кристаллической структур воды. Высокая концентрация гемоглобина в эритроците и практически полное отсутствие его в плазме уменьшает онкотическое давление плазмы; при этом предотвращается обезвоживание тканей и исключается потеря гемоглобина вследствие его фильтрации в клубочках почек /Иванов, 1993, т. 2, с. 164/. Нахождение молекул гемоглобина внутри эритроцита обеспечивает по сравнению с растворением такого же количества гемоглобина в плазме уменьшение вязкости крови в несколько раз /Физиология человека, 1985/. Можно сказать, что конструктивное сопряжение гемоглобина и воды обеспечивает оптимальную гармонию «противоположностей» в структуре эритроцита. Отметим, что время перехода от Hb к HbO₂ в легких при естественной величине рН 7,26 равно минимальной величине /Mochizuki, 1966/.

У всех млекопитающих от крошечной землеройки до кита эритроциты имеют вид двояковогнутых дисков: диаметр эритроцитов приблизительно одинаков и составляет 7-10 мкм. Концентрация гемоглобина составляет 15 г на 100 мл крови; даже небольшое увеличение его содержания резко увеличивает вязкость крови /Шмидт-Нильсен, 1987/. Эритроциты придают крови свойства неньютоновской жидкости, которая последовательно уменьшает свою вязкость, проходя через микрососуды и капилляры.

Главная функция эритроцитов заключается в транспорте кислорода к месту его потребления с последующим газообменом между кровью и окружающими тканями. Оптимальность организации эритроцита определяется прежде всего его геометрией и внутренней структурой. Оптимальная форма должна: 1) обеспечить при данном объеме клетки «складирование» максимального количества молекул гемоглобина; 2) обеспечить минимум потерь энергии при движении в плазме крови. Этими двумя предварительными условиями обусловливается минимальная энергетическая «цена» транспорта молекулы гемоглобина.

Рис 3.1. Дискообразная форма эритроцита.

dкл - диаметр клетки,

dвып - диаметр наиболее выпуклой части клетки,

dвг - диаметр вогнутой части клетки,

Н – толщина выпуклой части клетки,

h - толщина вогнутой части клетки

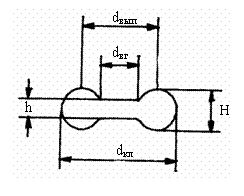
Эритроцит человека и млекопитающих имеет форму двояковогнутого диска (рис. 3.1). При анализе возможных дискообразных форм эритроцита постоянного объема было показано /Lenard, 1974/, что форма эритроцита человека, соответствующая естественной, обеспечивает максимальное отношение его поверхности S к объему V, равное 1,638 (для сравнения для шара S/V=0,55). Молекулы гемоглобина располагаются непосредственно под мембраной эритроцита; их взаимное расположение соответствует предельно плотной, паракристалической упаковке /Щерба, 1968/. Очевидно, что доставка необходимого количества кислорода к месту потребления достигается при минимальном количестве «суденышек» – эритроцитов! Отметим, что величина S/V должна удовлетворять двум противоречивым условиям. С одной стороны, чтобы разместить большее количество молекул гемоглобина под поверхностью клетки это отношение должно быть минимальным (размер эритроцита должен возрастать), а с другой стороны, при росте размера эритроцита снижается уровень метаболизма клетки. Природа нашла оптимальное соотношение этих «противоположностей» при величине S/V=1,638. Эритроцит – безъядерная клетка, поэтому для обеспечения ее жизнедеятельности требуется незначительные затраты энергии. Таким образом, эритроцит транспортирует максимальное количество молекул гемоглобина при минимальном расходе энергии как внутри клетки, так и вне ее (гидродинамика). Следует отметить «роль» чисел Фибоначчи в формообразовании эритроцита (рис. 1) /Суббота, 1994/. Оптимальная конструкция эритроцитов связана именно с этими числами!

Хаотическое расположение эритроцитов в крови исключается /Чижевский, 1959; Куприянов, Ананин, 1988/. Эритроцит движется вдоль сосуда своей узкой стороной. При таком расположении, находясь в слоях плазмы разных скоростей, эритроцит получает вращение вокруг своего центра симметрии по оси, перпендикулярной к его вогнутым сторонам. Система морфологических и корпускулярных элементов крови окутана силовыми линиями электрического поля. Между отдельными элементами действуют силы электростатического распора, препятствующие полному сближению и соприкосновению элементов. Дискоидная форма эритроцитов обеспечивает симметричность их движения по отношению к продольной оси сосуда; благодаря этому обстоятельству обеспечивается минимальная вязкость крови /Sugihara-Seki, Skalak, 1988/. Показано /Каро и др., 1981/, что при этом: 1) исключается тенденция частиц к оседанию и 2) минимизируется энергия, рассеиваемая потоком, т.е. минимизируется расход механической энергии на транспорт молекулы гемоглобина. Дискоидная форма эритроцита и его размер являются оптимальным решением «противоположных» требований к этому элементу крови.

Рис. 3.2. Зависимость эластичности мембраны эритроцита от его формы /Глазер, 1978/

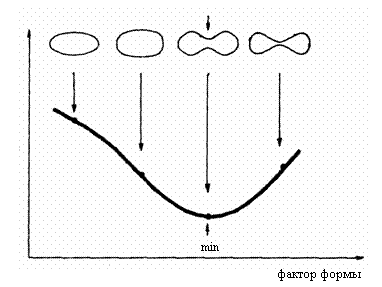
Показано /Глазер, 1978/, что при естественном отношении S/V=1,638 энергия деформации мембраны имеет минимальную величину (рис. 3.2). Вследствие этого свойства преобразование формы эритроцитов в микрососудах происходит с минимом потерь энергии. Вода составляет 65-70% от объема эритроцита /Розен, 1969/. Вода – единственная жидкость на Земле (кроме ртути), для которой зависимость удельной теплоемкости от температуры имеет минимум. Эта жидкость играет главную роль в процессах регулирования теплообмена человека и других млекопитающих, позволяет им поддерживать комфортное состояние при минимуме энергетических затрат. Вода внутри клетки находится в состоянии максимальной упорядоченности – в состоянии, достигаемом в неживых системах только при абсолютном нуле температуры. Это состояние характеризуется отрицательным значением энтропии: квазикристаллическая структура внутриклеточной воды непрерывно разрушается при температуре жизни клетки (36,8^оС) и непрерывно возникает заново в процессе расходования энергии метаболизма. Были установлены два фундаментальных, отличительных свойства живой клетки /Тринчер, 1965/. Во-первых, при температуре жизнедеятельности структура клетки является термолабильной в связи с квазикристаллической термолабильной (негэнтропийной) структурой внутриклеточной воды, подвергающейся непрерывным фазовым переходам (кристалл – жидкость). Во-вторых, все неводные компоненты живой клетки (белки, нуклеиновые кислоты и т.д.) при обеспечении температуры воды обладают термостабильностью при температуре обмена веществ. Молекула жидкой воды имеет V-образную форму, где расстояния между атомами О и Н соотносятся между собою по золотой пропорции /Цветков, 1997; Белянин, Романова, 2003/. Это сильно отличает молекулу Н₂О от линейных молекул, в которой все атомы расположены цепочкой. Именно такое особое расположение атомов в молекуле воды и позволяет ей иметь множество необычных свойств.

На внутренней поверхности эритроцита молекула гемоглобина располагается между двумя молекулами воды, что позволяет сохранять автономность каждой молекулы гемоглобина и обеспечивает эластичность формы клетки. Высокая деформируемость мембраны обеспечивает текучесть содержимого эритроцитов (концентрированного раствора гемоглобина и энзимов при отсутствии эластических структур внутри). При движении клетки происходит вращательно-поступательное движение мембраны вокруг содержимого эритроцита (оболочка эритроцита движется подобно гусенице танка) /Schmidt-Schonbein et al., 1980/. Вследствие этого эритроциты ведут себя в сосудах подобно капелькам жидкости /Fung, 1984/. Вязкость крови в сосудах значительно ниже, чем вязкость других суспензий и эмульсий с сопоставимым соотношением между величиной частиц и диаметром сосудов /Мчедлишвили, 1989/.

Вода участвует в большинстве биохимических реакций в организме. Ткани человека и млекопитающих содержат 70% Н₂О, кровь – 79%, а лимфа – 96%. Температура 36,8^оС в клетке является точкой оптимального соотношения долей двух «противоположных» состояний воды: жидкого и «льда». Вода при температуре 36,8^оС обладает уникальными свойствами. При этой температуре структура воды в клетках обладает особой, квазикристаллической упорядоченностью, при которой количество разорванных и сохранившихся тетрамерных связей примерно одинаково /Колясников, 1995/. Такое соотношение обеспечивает равновероятное протекание биопроцессов в обоих направлениях.

При температуре жизнедеятельности структура клетки является термолабильной в связи с квазикристаллической структурой внутриклеточной воды, подвергающейся непрерывным фазовым переходам (кристалл – жидкость) /Тринчер, 1965/. Кроме того, температура 36,8^оС позволяет создать в эритроците условия теплового комфорта, при котором расходуется минимальная энергия на поддержание оптимальной температуры в клетке (рис. 3.3). Эта температура разделяет жидкую фазу воды приблизительно в соотношении золотой пропорции. Отметим, что t=36,8^oC обеспечивает энергооптимальную гармонию структурных «противоположностей» воды в эритроците.

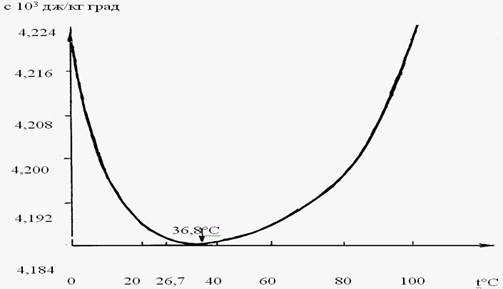
Рис. 3.3. Зависимость теплоемкости воды от температуры /Бочков, 1974/.

Оптимальное «вхождение» каждого из гемодинамических и структурных параметров в систему «Эритроцит» обеспечивает свой «вклад» в общую экономию энергии и вещества при транспорте кислорода. В эритроците имеет место гармония энергооптимального «вхождения».

3.2.2. Кровь

Функция крови - транспортировка и распределение по организму газов, питательных веществ и клеточных элементов. Газообмен является одной из главнейших функций крови. Эта функция осуществляется при движении крови по артериальным микрососудам и капиллярам. Основными элементами крови являются плазма, эритроциты, лейкоциты и тромбоциты. Два последних элемента занимают незначительную часть объема крови и не являются поставщиками кислорода, поэтому мы не будем их рассматривать. Представляет интерес «вхождение» в кровь первых двух элементов – эритроцитов и плазмы.

Оптимальная величина концентрации эритроцитов в крови обусловлена двумя противоречивыми условиями. С одной стороны, желательно иметь большую концентрацию эритроцитов, поскольку при этом возрастает концентрация кислорода в единичном объеме крови. С другой стороны, неограниченный рост гематокрита связан с повышением вязкости крови, а, следовательно, и с возрастанием расхода механической энергии на транспорт кислорода. Это противоречие устраняется, если отношение ξ/Ht=min, где ξ - вязкость крови, Ht – гематокрит /Moll, Bartels, 1968; Chien, 1975/. Такое оптимальное отношение соответствует естественной величине Ht=42% при нормальном артериальном давлении и напряжении сдвига τ=10³ дн/см² (рис. 3.4).

По расчетам И.Ф. Образцова и М.А.Ханина /Образцов, Ханин, 1989/ величине Ht=42% соответствует оптимальная концентрация эритроцитов С=5,2·10⁹ 1/мл крови. Величина гематокрита и вязкости крови в крупных, средних и мелких артериях (примерно до 100 мкм) постоянна /Chien, 1975/. Величина вязкости не меняется также при линейной скорости эритроцитов свыше 500 мкм/с /Lipowski et al., 1980/. Даже в капиллярах скорость эритроцитов значительно превышает эту величину. Необходимо сделать некоторые пояснения к определению гематокрита в микрососудах. Величина гематокрита соответствует отношению массы эритроцитов к массе плазмы после центрифугирования в пробирке. При наблюдениях за микрососудами и, особенно, за капиллярами всегда можно заметить движущиеся эритроциты, разделенные промежутками плазмы. При фотографировании этой картины возникает стремление определить объемное отношение эритроциты - плазма. При расчетах оказывается, что в капилляре отношение массы эритроцитов к плазме намного меньше, чем в порции крови, выпущенной из сосуда. Отсюда возникла проблема так называемого динамического гематокрита в микрососудах /Иванов, 1993, т. 2, с. 137/.

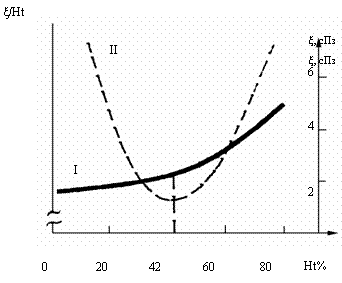
Рис. 3.4. Соотношение между концентрацией эритроцитов и вязкостью крови. ξ– вязкость крови, Ht – гематокрит, I - кривая вязкости крови, II - отношение вязкости к гематокриту. При гематокрите 42% отношение ξ/Ht=min

Гематокрит, определенный путем центрифугирования порции крови из артериол и венул диаметром 100-200 мкм, дал величину, которая почти не отличается от гематокрита крови из магистральных сосудов /Barnard et al., 1968; Klitzman, Duling, 1979/. Каким образом, гематокрит в капилляре и артериоле может быть меньше, чем в магистральных сосудах? Между эритроцитами и стенкой капилляра имеется слой плазмы, который благодаря трению о стенку сосуда движется со скоростью меньшей, чем у эритроцитов. При отношении скорости эритроцитов к скорости пристеночного слоя плазмы, равном приблизительно 1,6, соотношение объемов эритроцитов и плазмы, проходящих через микрососуды в единицу времени, практически не будет отличаться от гематокрита в транспортных сосудах, полученного путем центрифугирования крови /Klitzman, Duling, 1979/. Это означает, что гематокрит крови, движущейся через крупные, средние и мелкие артерии и микрососуды, постоянен и не зависит от их диаметра. (Отметим кстати, что отношение 1,6 практически соответствует золотому числу 1,618!) Таким образом, гармония «противоположных» компонентов крови - объектов с замкнутой поверхностью (эритроциты) и несущей их жидкости (плазма) - имеет энергооптимальную основу. Энергооптимальное соотношение концентраций эритроцитов и плазмы имеет место на всем артериальном участке, включая и капилляры, тем самым минимизируется «цена» транспорта единичного объема кислорода. В микрососудах эта «цена» дополнительно снижается за счет снижения величины вязкости крови.

Температура 36,8^оС имеет важнейшее значение оптимального функционирования плазмы. Вблизи этой температуры кровь с гематокритом Ht=42% имеет минимальную вязкость /Суббота, 1994/. Плазма крови млекопитающих на 90% состоит из воды. Расход энергии на нагрев воды при 36,8°С на 1°С минимален /Бочков, 1974/. Согласно модели, представленной Ю.А. Колясниковым /Колясников, 1995/, при 36,8°С выравниваются массы квазикристаллической воды (жидкий лед) и обычной воды, что обеспечивает равновероятность течения обратимых биохимических реакций в обе стороны. При этом способность перехода воды из одного состояния в другое максимальна. Очевидно, что при температуре 36,8^оС в плазме создаются наиболее благоприятные условия для протекания биологических процессов с минимальными затратами энергии на их поддержание.

Подытожим. Минимизация затрат механической энергии на перемещение крови происходит благодаря созданию минимально возможной вязкости (форма эритроцитов, продольная симметрия кровотока, оптимальная концентрация эритроцитов и оптимальная температура). С другой стороны, обеспечивается максимальная концентрация молекул гемоглобина в эритроците и наиболее благоприятные условия для протекания биопроцессов в крови. Все параметры крови (гематокрит, вязкость и температура) «подобраны» оптимальным образом. Оптимальное «вхождение» этих параметров в систему «Кровь» обеспечивает минимум потерь механической и тепловой энергии по отношению к перемещению единичного объема кислорода к месту его потребления. Таким образом, в системе «Кровь» имеет место энергооптимальная гармония «вхождения» отдельных систем в соответствии с принципом оптимального вхождения.

Интересна связь элементов крови с золотой пропорцией и числами Фибоначчи /Симонян, 1971/. Основные элементы (эритроциты, лейкоциты и тромбоциты) в глобулярном объеме крови сбалансированы как соотношение чисел 62:32:6; нетрудно увидеть, что отношение первого члена к сумме двух других равно золотому числу 1,618. Было установлено, что отношение объема циркулирующей крови к плазматическому объему в организме равно 5:3, а отношение плазматического объема к глобулярному – 3:2 (числа Фибоначчи). Распределение людей по 3 группам крови отвечает отношению чисел Фибоначчи – 8:21:34. С большой степенью вероятности можно предположить, что за этими соотношениями скрываются дополнительные аспекты экономии энергии и вещества.

3.2.3. Сосуд с движущейся кровью

В любом сосуде расход энергии, связанный с движущейся кровью, разделяется на «механическую» и «химическую» составляющие. Механическая энергия расходуется на перемещение крови в сосуде, а химическая энергия связана с химическими аспектами «стоимости» крови.

Рассмотрим механическую составляющую затрат энергии. Выше нами были рассмотрены пути оптимизации вязкости крови («подбор» гематокрита и температуры крови). В сосуде возникают дополнительные факторы минимизации вязкости, связанные с конфигурацией движущейся крови. Вследствие дискообразной формы эритроцитов происходит их симметриализация относительно продольной оси сосуда, что обусловливает дополнительное снижение вязкости крови /Sugihara-Seki, Skalak, 1988/. Дискообразная форма эритроцитов исключает также тенденцию к их оседанию на стенки сосуда /Каро др., 1981/. Таким образом, минимальная величина вязкости крови в сосуде обусловлена оптимальным «подбором» гематокрита, температуры, формы эритроцитов, а также симметрийным способом движения последних. Снижение вязкости крови является одним из важнейших факторов, позволяющих минимизировать потери механической энергии, связанной с вязкой диссипацией. Существуют и другие аспекты экономии механической энергии в сосуде. Установлено /Куприянов, 1983; Куприянов, Ананин, 1988/, что движение крови в артериальных сосудах имеет ламинарно-спиральный характер. Спиралевидная ориентация мышечных волокон в стенках артерий представляет собой своего рода универсальную закономерность /Куприянов, 1983/. Осуществление спиральных конструкций и процессов способствует экономии энергии и материала, обеспечивает повышенную прочность системы и надежность ее деятельности. По мнению академика В.В.Куприянова, пропульсация по спирали обеспечивает значительную экономию энергии на перемещение крови в сосуде. Установлено также тесное соответствие ориентации эндотелиальных клеток протекающему кровотоку /Lowell, Adamson, 1980/. Наблюдения показали высокоупорядоченное распределение клеточных и плазменных компонентов в крови (можно провести некоторую аналогию с движением пули в стволе с винтовой нарезкой). Такой тип движения универсален и происходит c минимальной потерей энергии /Marinelli et al., 1995; Гареев и др., 2000/. Естественно, что при таком способе движения перемещение единичного объема крови в сосуде сопряжено с минимумом затрат механической энергии. Таким образом, налицо различные аспекты минимизации «механической» части общей энергии, расходуемой в сосуде (гематокрит, температура, вязкость, симметриализация кровотока и спирально-ламинарный характер движения).

Механическая мощность, расходуемая в сосуде с движущейся кровью (рис. 3.5),

W_M = 128q²ξl/πd⁴,

где q – кровоток, ξ – вязкость крови, l, d – длина и диаметр сосуда.

Химическая мощность, потребляемая в сосуде,

W_X = (π/4)bd²l,

где b – расход химической энергии в единичном объеме крови за единицу времени.

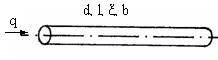
Рис. 3.5. Сосуд с движущейся кровью. q - объемный кровоток,
за единицу времени. d, l- диаметр и длина сосуда, ξ - вязкость крови, b - удельный расход химической энергии

При первом же взгляде на эти зависимости очевидно, что механическая и химическая составляющие суммарной мощности зависят от диаметра сосуда в различной степени. Более того, при изменении величины диаметра они изменяются в противоположных направлениях. Следовательно, при заданной величине кровотока Q минимальный суммарный расход механической и химической мощности соответствует некоторому оптимальному диаметру d. Режим движения крови в сосуде при минимальном суммарном расходе энергии получил обозначение - режима «минимальной работы» /Murray, 1926b/. В соответствии с расчетами Мюррея в этом режиме кровоток в сосуде связан с его оптимальным диаметром и параметрами крови, следующим отношением

q/d³ = (π/32),

где d, l –диаметр и длина сосуда, b – расход химической энергии в единичном объеме крови за единицу времени, x - вязкость крови

Из условий гемодинамики можно показать, что

Q/d³ = (π/4)l/dt.

Во всех сердечных сосудах энергооптимальный режим имеет место /Цветков, 2004/, при этом

/8 = l/dt. (3.1)

Оптимальное соотношение гемодинамических параметров в сосуде

a =l/dt = 162 с^-1. (3.2)

Эта величина обозначена нами как коэффициент оптимальной перфузии. Величина a = 162 с^-1 является условием минимальности потерь энергии при перфузии любого сердечного сосуда. В условиях гипертезии величина коэффициента оптимальной перфузии будет возрастать, но в одинаковой степени для всех сосудов /Цветков, 1997, 2004/.

Другим показателем энергетических затрат в сосуде с движущейся кровью является оптимальное отношение механической и «химической» мощностей. Соотношение механической и химической мощностей равно постоянной, оптимальной, величине для всех сердечных артерий, артериол и капилляров не только в покое, но и при различных уровнях физической нагрузки /Цветков, 2004/,

g = W_M/W_X = 0,5. (3.3)

Исходя из (3.1)-(3.3), в каждом сердечном сосуде имеет место энергооптимальная гармония «противоположных» мощностей W_M и W_X. Кроме того, в системе – «Сердечный сосуд с движущейся кровью» – имеет место гармония энергоооптимального «вхождения» конструктивных, гемодинамических, химических и температурных параметров крови. Единичный объем крови проходит через сердечный сосуд с минимальными затратами энергии. Тем самым обеспечивается минимальность затрат энергии на транспорт единичного объема кислорода в каждом сосуде.

3.3. Транспортный участок

Артерии представляют собой цилиндрические трубки с весьма сложным строением стенки. В стенке артерии имеются 3 оболочки: внутренняя, средняя и наружная. В составе стенок крупных сосудов преобладает межклеточное вещество в виде эластических волокон и мембран. Подобные артерии являются сосудами эластического типа строения. В стенках сосудов мелкого и отчасти среднего калибра преобладает гладкая мышечная ткань с небольшим количеством межклеточного вещества. Такие артерии относят к мышечному типу строения. Наиболее высокого развития строма достигает в стенке аорты и отходящих от нее артерий, имеющих эластический тип строения. В артериях среднего и мелкого калибра в эластической строме остаются лишь внешние и внутренние мембраны, при этом между слоями мышечных клеток находятся лишь тонкие сети эластических волокон. В стенках самых мелких артерий и прекапиллярных артериол эластическая строма совершенно теряется. Изменения размеров артерий эластического типа происходят за счет механического растяжения приложенным давлением. Сосуды мышечного типа изменяют свои размеры за счет механических и биохимических факторов. Обменные микрососуды (артериолы и капилляры) своих размеров практически не меняют ни при механическом, ни при биохимическом воздействии на их стенки.

Гемоартериальный участок коронарного русла следует разделить на последовательные генерации в зависимости от особенностей устройства стенок артерий. В первые генерации входят артерии эластического типа с диаметром более 500 мкм (ниже начинается реагирование стенки на аденозин /Harter et al., 1982/). В следующие генерации включаются артерии мышечного типа с диаметром приблизительно от 500 до 100 мкм /Чернух и др., 1975; Мчедлишвили, 1989/. В завершающие генерации входят артериолы с диаметром менее 100 мкм и капилляры. Первые две градации представляет транспортный участок, по которому кровь перемещается без газообмена с окружающими тканями. Обменные генерации представляют собою участок гемоартериального русла, на котором кислород через стенки сосудов поступает в окружающие ткани. Транспортный участок включает в себя генерации сосудов эластического и мышечного типа. Ниже представлен математический анализ с целью выявления гармонии в этих генерациях.

3.3.1. Генерации сосудов эластического типа

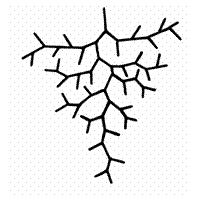
Транспортный участок в целом можно представить как совокупность последовательных генераций тройников – артериальное «дерево» (рис. 3.6). Бифуркация является общим типом разветвления коронарных артерий независимо от их диаметра, включая и артериолы /Zamir, Chee, 1985/.

Отдельный тройник состоит из трех сопряженных сосудов с движущейся кровью (ствол и две ветви). Тройник является системой, в которую каждый из сосудов включен в качестве более «простой» системы. Длина элемента тройника равна расстоянию по стволу от вершины угла предыдущего разветвления, при котором образовался этот ствол, до вершины угла, при котором он распался на ветви (рис.3.7). Поскольку все сосуды в тройнике принадлежат к эластическому типу, то такие тройники будем называть «эластическими».

Установлено /Ross, 1967/, что во всех коронарных артериях эластического типа протекает пульсирующий кровоток. Анализ кривых кровотока показал /Цветков, 1993/, что в каждом пульсирующем сосуде (крупные, средние и мелкие артерии) средние за систолу (напряжение) и диастолу (расслабление) значения коронарного кровотока приблизительно равны друг другу. На пути перемещения крови к сердечнымсосудам меньшего диаметра пульсации давления (а следовательно, и кровотока) все более сглаживаются, в микрососудах с диаметром менее 100 мкм они незначительны /Duling, Klitzman, 1980; Toyotaka et al., 1994/. С учетом равенства средних значений давления и кровотока за систолу и диастолу, а также за кардиоцикл в целом, отпадает необходимость раздельного анализа систолических и диастолических значений сердечных параметров (давление, кровоток, проводимость, объем и т.д.). Вследствие этого, в эластических тройниках мы не будем рассматривать отдельно средние систолические и средние диастолические величины параметров, а только их значения, усредненные за сердечный цикл.

Нашей задачей является показать особенности архитектоники и гемодинамики эластических тройников сердца в условиях физиологического покоя и физической

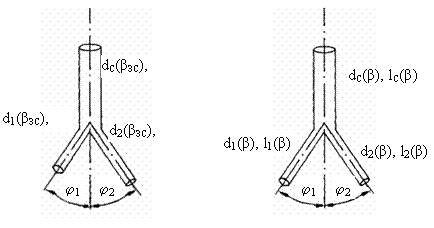
Рис. 3.7. Сосудистые тройники. А – асимметричный тройник, Б – симметричный тройник. d_С(β_ЗС), d₁(β_ЗС), d₂(β_ЗС), l_С(β_ЗС), l₁(β_ЗС), l₂(β_ЗС) – соответственно диаметр и длина ствола и 1 и 2 ветвей, φ₁(β_ЗС), φ₂(β_ЗС) - углы отклонения 1 и 2 ветвей в золотом режиме гипертензии.

нагрузки. Рост физической нагрузки вызывает гипертезию, повышение среднего давления в аорте. Режим кровоснабжения здорового сердца млекопитающих в покое связан с пропорцией золотого сечения и числами Фибоначчи и обозначен нами как золотой режим гипертензии /Цветков, 1993/. Этот режим приблизительно соответствует физиологическому покою организма. Ранее нами было показано /Цветков, 1993, 1997/, что при физической нагрузке относительные изменения многих сердечных параметров в той или иной степени связаны с показателем уровня гипертензии

β = P(ν)/P(ν_ЗС),

где ν_ЗС, ν - частота сердцебиений в золотом и заданном режиме гипертензии, P(ν_ЗС), P(ν) – среднее давление в аорте в золотом и некотором режиме гипертензии. Естественно, что в золотом режиме показатель роста гипертензии β_ЗС=β=1. Максимальной гипертензии соответствует β=2 /Цветков, 1993/. В дальнейшем при расчетах изменений сердечных параметров будем считать золотой режим гипертензии исходным.

3.3.1.1. Эластические тройники в золотом режиме гипертензии

Конструкционные особенности тройников в золотом режиме гипертензии представлены тремя коэффициентами: 1) коэффициент ветвления k(β_ЗС), 2) коэффициенты относительного сечения ветвей Н₁(β_ЗС) и H₂(β_ЗС) (см. раздел 2.6.2).Теоретически доказано /Шошенко и др., 1982/, что величинам 1<k£1,26 в тройниках соответствует оптимальный режим «минимальной работы». В этой же работе авторами представлена экспериментальная зависимость k=f(H) для сердечных сосудов, где k=1,10-1,20. При этих значениях движение крови в тройниках сердца в покое имеет энергооптимальную основу. Подобное распределение кровотоков соответствует оптимальному соотношению диаметров в тройнике /Розен, 1969/,

d₁(b_ЗС)³ + d₂(b_ЗС)³ = d_С(b_ЗС)³. (3.4)

Для оценки взаимосвязи между длиной и диаметром сердечных сосудов введем дополнительный параметр конструкции сосуда,

C(b_ЗС)=l(b_ЗС)/d(b_ЗС),

где l(b_ЗС) – длина сосуда в золотом режиме гипертензии. Для сердечных артериальных сосудов с диаметрами более 40 мкм С(b_ЗС)=3 /Шошенко и др., 1982; Цветков, 1993/. Эластические сосуды значительно превышают по диаметру 50 мкм. Следовательно, на этом участке отношения С₁(b_ЗС)/С_С(b_ЗС)=С₂(b_ЗС)/С_С(b_ЗС)=1. Рассмотрим соотношения между диаметрами и длинами ствола и ветвей в некотором тройнике с привлечением коэффициентов k(b_ЗС), H(b_ЗС) и C(b_ЗС). Связь между ветвями и стволом может быть представлена следующими выражениями /Цветков, 1993/:

d₁(b_ЗС) = d_С(b_ЗС), (3.5)

d₂(b_ЗС) = d_С(b_ЗС), (3.6)

l₁(b_ЗС) = l_C(b_ЗС), (3.7)

l₂(b_ЗС) = l_C(b_ЗС). (3.8)

В соответствии с (3.5) и (3.6) выражение (3.4) можно преобразовать,

[k(β_ЗС)H₁(β_ЗС)]^3/2+ [(k(β_ЗС)H₂(β_ЗС)]^3/2= 1. (3.9)

С учетом этого обстоятельства покажем, что в покое для всех сосудов на «эластическом» участке коэффициент оптимальной перфузии одинаков (α(b_ЗС)=162 с^-1). Для этого необходимо рассмотреть изменения ветвей по отношению к стволу для параметров d(b_ЗС), l(b_ЗС) и t(b_ЗС), входящих в α(b_ЗС). Преобразования d(b_ЗС) и l(b_ЗС) для ветвей представлены в (3.5)-(3.8). Время пребывания эритроцитов в сосуде

t(b_ЗС) = V(b_ЗС)/q(b_ЗС).

В соответствии с (3.5)-(3.8) объемы крови V в ветвях и стволе соотносятся следующим образом,

V₁(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2V_С(b_ЗС), (3.10)

V₂(b_ЗС) = [(k(b_ЗС)H₂(b_ЗС)]^3/2V_С(b_ЗС), (3.11)

где V_С(b_ЗС), V₁(b_ЗС), V₂(b_ЗС) - объемы ствола и ветвей в золотом режиме. Очевидно, что суммарный объем ветвей равен объему ствола,

V₁(b_ЗС) + V₂(b_ЗС) = V_С(b_ЗС).

Кровотоки в стволе иветвях в режиме «минимальной работы» связаны выражениями /Шошенко и др., 1982/

d₁(b_ЗС) = d_С(b_ЗС), (3.12)

q₂(b_ЗС) = [k(b_ЗС)H₂(b_ЗС)]^3/2 q_С(b_ЗС), (3.13)

где q_С(b_ЗС), q₁(b_ЗС), q₂(b_ЗС) - кровотоки в стволе и ветвях в золотом режиме.

Исходя из (3.10) - (3.13),

t₁(β_ЗС) = V₁(β_ЗС)/q₁(β_ЗС) = t_С(β_ЗС), (3.14)

t₂(β_ЗС) = V₂(β_ЗС)/q₂(β_ЗС) = t_C(β_ЗС), (3.15)

где t_С(b_ЗС), t₁(b_ЗС), t₂(b_ЗС) - время пребывания эритроцитов в стволе и ветвях в золотом режиме гипертензии. Очевидно, что время пребывания эритроцитов в сосудах любого эластического тройника независимо от их калибра одинаково: t₁(b_ЗС)=t₂(b_ЗС)=t_С(b_ЗС). Показано /Цветков, 2004/, в сосудах в любой j-генерации, где С=l/d=3, величина t_j = 18,5 мсек (см. Табл. 1). C учетом этих данных коэффициент перфузии для любого сосуда равен оптимальной величине

α(b_ЗС) = l(b_ЗС)/d(b_ЗС)t(b_ЗС) = 162 c^-1. (3.16)

Для артерий в тройнике отношение h/d =const /Cohn, 1954, 1955; Kamiya, Togawa, 1972/, где d – диаметр, h – толщина стенки сосуда. Исходя из этого,

V_СТ1(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2V_СТС(b_ЗС), (3.17)

V_СТ2(b_ЗС) = [k(b_ЗС)H₂(b_ЗС)]^3/2V_СТC(b_ЗС), (3.18)

где V_СТС(b_ЗС), V_СТ1(b_ЗС), V_СТ2(b_ЗС) - объемы стенок ствола и ветвей. Суммарный объем стенок ветвей равен объему стенки ствола,

V_СТ1(b_ЗС) + V_СТ2(b_ЗС) = V_СТC(b_ЗС).

Очевидна интересная особенность архитектоники эластических тройников – суммарный объем сосудистой массы и суммарный объем крови в ветвях соответственно равны объему сосудистого материала и объему крови в стволе. Ветви по этим параметрам «воспроизводят» ствол! Отметим, что воспроизводство объемов крови и сосудистого материала имеет место не только при симметрии, но и при асимметрии (1<k(b_ЗС)<1,26, H₁(b_ЗС)≠H₂(b_ЗС)). Показано /Kamiya, Togawa, 1972; Kamiya et al., 1974/, что при заданном кровотоке через тройник и заданном давлении между началом ствола и концами ветвей именно в режиме «минимальной работы» общий объем крови в сосудах тройника имеет минимальную величину. Установлено /Cohn, 1954, 1955/, что минимальный суммарный расход сосудистого материала в тройнике имеет место при архитектонике тройника, соответствующей режиму «минимальной работы» (1<k(b_ЗС)£1,26). Таким образом, эластические тройники сердца пропускают через себя кровоток с минимальными затратами крови и сосудистого материала.

Покажем, что давление, приложенное к отдельному сосуду, постоянно для всех эластических генераций.

Давление, приложенное к стволу тройника,

DP_C(b_ЗС) = Q(b_ЗС)/G_C(b_ЗС),

где DP_C(b_ЗС), G_C(b_ЗС) - соответственно давление, приложенное к стволу, и проводимость ствола в золотом режиме гипертензии.

Проводимость ветвей тройника сосуда на «эластическом» участке, где коэффициент конструкции сосуда С(b_ЗС) и вязкость крови x(b_ЗС) постоянны, в соответствии с (3.6)-(3.8)

G₁(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2G_Cb_ЗС), (3.19)

G₂b_ЗС) = [k(b_ЗС)H₂(b_ЗС)]^3/2G_C(b_ЗС), (3.20)

где G_Сb_ЗС), G₁(b_ЗС), G₂(b_ЗС) – соответственно проводимость ствола, 1 и 2 ветвей в золотом режиме гипертензии. Очевидно, что и по проводимости также имеет место «воспроизводство» ствола ветвями,

G₁(b_ЗС)G₂(b_ЗС)= G_С(b_ЗС).

Поскольку кровоток и проводимость в каждой ветви по отношению к стволу изменяются в одинаковой степени, то 

DP₁(b_ЗС)=DP₂(b_ЗС) =DP_С(b_ЗС).

В любом «эластичном» j-сосуде /Цветков, 2004/

DP_j(b_ЗС) = 3,5 мм рт. ст.

Отметим, что величина DP_j(b_ЗС)=3,5 мм рт. ст. имеет место также и в «мышечных», и в обменных сосудах. Нами было показано /Цветков, 2004/, что независимо от веса млекопитающих в пределах 0,1-100.000 кг значение DP_j(b_ЗС)»3,5 мм рт. ст. (см. раздел 4.8, Табл. 2). Величина DP(b_ЗС)=3,5 мм рт. ст. является своего рода инвариантом для различных видов млекопитающих.

В общем виде закон структурно-динамической композиции любого j-сосуда тройника можно представить выражением

DP_j(b_ЗС)t_j(b_ЗС) = 32ξ_j(b_ЗС)[l_j(b_ЗС)/d_j(b_ЗС)]². (3.21)

В золотом режиме гипертензии для эластических сердечных сосудов (d>100 мкм) имеем l_j(b_ЗС))/d_j(b_ЗС)=3 /Шошенко и др., 1982/, ξ_j(b_ЗС)=3×10^{-2 ×}г ×см^-1 с^-1 /Haynes, 1960/ и расчетные величины ΔP_j(b_ЗС)=3,5 мм рт. ст.=465,5 г××см^-2×с^-2 и t_j(b_ЗС)=18,5×10^-3 сек. Подставив эти данные, полученные экспериментальным путем и в результате расчетов, в (3.21), убедимся, что расхождение между левой и правой частями этого равенства незначительно, что указывает на достаточно точное определение расчетных величин ΔP_j(b_ЗС) и t_j(b_ЗС). В этом выражении левая часть отображает динамические параметры, т.е. давление, приложенное к j-сосуду, и время пребывания эритроцитов в j-сосуде. В правой части представлены структурные параметры - кажущаяся вязкость крови, длина и диаметр сосуда. Очевидна гибкость оптимального «подбора» размеров сосудов. Если «подбором» диаметров обусловливается энергооптимальный характер движения кровотока в сосудах и количество ветвлений до капилляров, то «подбор» длины обеспечивает оптимальную величину давления на каждом сосуде. Учитывая полную аналогию архитектоники артериального участка сердца различных видов млекопитающих /Каро и др., 1981/, можно сказать, что оптимальный «подбор» конструктивных величин d, l, ξ и динамических - DP и t для каждого сосуда составляет основу энергетической оптимизации кровоснабжения сердца млекопитающих. Как отмечал А.Л.Чижевский, «кровяное русло должно быть в высокой степени упорядочено геометрически, физически и химически» /Чижевский, 1959, с. 13/.

Рассмотрим соотношение затрат механической и химической энергий в ветвях и стволе - энергетическую основу транспорта крови по цепочке артериальных сосудов. Во всяком сосуде общийрасход энергии за единицу времени (мощности) складывается из потерь на перфузию и биопроцессы в крови.

Механическая, мощность в стволе в золотом режиме гипертензии,

W_МС(b_ЗС) = 128q_С(b_ЗС)²[ξ_C(b_ЗС)l_C(b_ЗС)]/πd_C(b_ЗС)⁴,

«химическая» мощность в стволе

W_ХС(b_ЗС) = (π/4)b_С(b_ЗС)[d_С(b_ЗС)]²l_С(b_ЗС),

где b_С(b_ЗС)- потребление химической энергии в единичном объеме крови за единицу времени.

С учетом (3.5)-(3.8), (3.12)-(3.13) в 1 и 2 ветвях,

W_М1(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2W_МС(b_ЗС), (3.22)

W_М2(b_ЗС) = [k(b_ЗС)H₂(b_ЗС)]^3/2W_МС(b_ЗС), (3.23)

где W_М1(b_ЗС), W_М2(b_ЗС) - механическая мощность в 1 и 2 ветвях в золотом режиме.

Исходя из (3.1),в j-сосуде

b_j(b_ЗС) = 64ξ_j(b_ЗС)[l_j(b_ЗС)/d_j(b_ЗС)t_j(b_ЗС)]². (3.24)

Поскольку во всех эластических генерациях ξ(b_ЗС) = 3 10^-2 Пз и l(b_ЗС)/d(b_ЗС)t(b_ЗС) = 162 с^-1, очевидно, что в каждом j-сосуде

b_j(b_ЗС) = 50.390 эрг см³ с^-1.

С учетом этой величины и исходя из (2.5)-(2.8),

W_Х1(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2W_XС(b_ЗС), (3.25)

W_Х2(b_ЗС) = [k(b_ЗС)H₂(b_ЗС)]^3/2W_XС(b_ЗС), (3.26)

Из выражений (3.22)-(3.23) и (3.25)-(3.26) очевидно, что

W_М1(b_ЗС)/W_Х1(b_ЗС) = W_М2(b_ЗС)/W_Х2(b_ЗС) = W_МС(b_ЗС)/W_XС(b_ЗС).

Исходя из выражений, соответствующих W_М(b_ЗС) и b(b_ЗС), легко показать, что на эластическом участке для всякого сосуда соотношение механической и химической энергии одинаково /Цветков, 2004/,

W_Х1(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2W_XС(b_ЗС), (3.27)

Исходя из (3.22) –(3.26) и (3.27), отношение общих затрат мощности в стволе и ветвях эластического тройника

W_Х1(b_ЗС) = [k(b_ЗС)H₁(b_ЗС)]^3/2W_XС(b_ЗС), (3.28)

В (3.27) отображена энергооптимальная гармония «противоположностей» в каждом из сосудов тройника. В (3.28) представлена гармония энергооптимального «вхождения» ствола ветвей в систему «Эластический тройник». В этих тройниках ветви «воспроизводят» ствол по затратам энергии, крови и сосудистого материала. Каждая генерация сосудов «повторяет» предыдущую по затратам энергии и живого вещества. В сущности, каждая генерация сосудов суммарно равна по этим параметрам стволу первого эластического тройника. Однако при тех же затратах энергии, крови и сосудистого материала каждая генерация имеет большую суммарную поверхность и протяженность сосудов, чем предыдущая. Этот феномен имеет огромное значение для обменной части коронарного русла. В конечном же счете, эластический отдел транспортного участка «пропускает» через себя единичный объем кислорода с минимальными затратами энергии, крови и сосудистого вещества.

3.3.1.2. Эластические тройники в режимах гипертензии

При переходе от покоя к физической нагрузке среднее давление в аорте и средний коронарный кровоток возрастают. При фиксированной величине физической нагрузки через 3-5 минут устанавливаются стабильные значения давления, кровотока и других архитектонических и гемодинамических параметров. При нагрузке во всех коронарных артериях наблюдаются аналогичные изменения. При нагрузке имеет место аналогия отношений средних кровотоков по отношению к их величинам в покое в каждой из ветвей левой коронарной артерии /Khouri et al. 1965, Vatner et al., 1972/. Соотношение средних кровотоков в эндо- и эпикардиальных слоях постоянно в покое и при любой мышечной нагрузке /Ball, Bache, 1976/. Не меняется отношение среднего кровотокав коронарном синусе к общему среднему коронарному кровотоку /Lafontant et al., 1962/ и среднему кровотоку в левой коронарной артерии /Rayford et al., 1959/ при изменении давления в аорте и сжатии легочной артерии. Установленные явления возможны лишь в том случае, если при гипертензии в каждом сосуде средняя за систолу, средняя за диастолу и средняя за кардиоцикл величины кровотока равны друг другу и при гипертензии изменяются в одинаковой степени. Феномен равенства среднесистолического, среднедиастолического и среднего значений относится и к другим гемодинамическим параметрам отдельного сосуда (давление, проводимость, объем и т.д.) /Цветков, 1993, 1997/. Вследствие этого можно говорить об аналогичности относительных изменений среднесистолического, среднедиастолического и среднего значений того или иного параметра при переходе на новый уровень гипертензии. Этот феномен позволяет нам не производить анализ рассматриваемых параметров раздельно для систолы, диастолы и сердечного цикла. В дальнейшем при рассмотрении изменений какого-либо параметра в условиях гипертензии мы будем использовать его среднее значение за сердечный цикл.

Кровоснабжение сердца обусловлено величиной среднегодавления в аорте. По этой причине в дальнейшем для анализа параметровархитектоники и гемодинамики при гипертензии будем использовать коэффициент роста гипертензии b. Этот коэффициент связан сизменением среднего давления в аорте по отношению к золотому режиму,

b = P(b)/P(b_ЗС),

где P(b_ЗС), P(b) – среднее давление в аорте в золотом и некотором режимах гипертензии. Для человека и млекопитающих в естественных пределах вариации физической нагрузки от покоя до максимальной нагрузки β=1-2. В качестве исходного режима примем золотой режим гипертензии (b=b_ЗС=1).

В эластических тройниках размеры сосудов (длина и диаметр) изменяются за счет изменения приложенного давления. Ниже нами будут рассмотрены изменения параметров архитектоники и гемодинамики этих тройников в условиях гипертензии. В режимах гипертензии среднее давление в аорте P(b), общий коронарный кровоток q(b) и время прохождения эритроцитами кровеносного русла сердца t(b) изменяются следующим образом /Цветков, 1993, 1997/,

P(b) = bP(b_ЗС),

q(b) = b²q(b_ЗС),

t(b) = t(b_ЗС)/b.

В режимах гипертензии для любого сосуда j-генерации

ΔP_j(b) = bΔP_j(b_ЗС), (3.29)

q_j(b) = b²q_j(b_ЗС), (3.30)

t_j(b) = t_j(b_ЗС)/b. (3.31)

Исходя из выражений (3.29)-(3.31),

V_j(b) = bV_j(b_ЗС),

G_j(b) = bG_j(b_ЗС),

где V_j(b_ЗС), V_j(b), G_j(b_ЗС), G_j(b) - соответственно объем и проводимость j-сосуда в золотом и других режимах гипертензии.

Эластические артерии при гипертензии расширяются и удлиняются. Морфологически феномен одновременного расширения и удлинения сосудов объясняется спиральным расположением мышечных клеток в стенках сосудов /Куприянов, 1983/. Из анализа экспериментальных данных /Valenta et al., 1994, c. 172/ следует, что при увеличении давления в артериальном сосуде его диаметр и длина изменяются в одинаковой степени,

d/d₀ = l/l₀ = (P/P₀)^1/3,

где P₀, d₀, l₀, P, d, l – соответственно исходные величины давления, приложенного к сосуду, диаметра и длины сосуда и их значения, соответствующие возросшему артериальному давлению.

Очевидно, что при гипертензии

ΔP_j(b) = bΔP_j(b_ЗС), (3.32)

l_j(b) = b^1/3l_j(b_ЗС), (3.33)

где d_j(b), l_j(b) - соответственно диаметр и длина j-сосуда в режиме гипертензии.

Оптимальную структурно-динамическую композицию любогоj-сосуда в некотором режиме гипертензии можно представитьвыражением

ΔP_j(b) = bΔP_j(b_ЗС), (3.34)

В данном выражении ξ_j(b)=ξ_j(b_ЗС), поскольку при гипертензии в пределах изменения калибра сосудов вязкость крови на всем транспортном участке не меняется. В (3.34) отображены относительные изменения структурно-динамических параметров, представляющих расход механической энергии в сосудах транспортного участка.

Исходя из (3.32), можно показать, что k(b) = k(b_ЗС), H₁(b) = H₁(b_ЗС), H₂(b) = H₂(b_ЗС). Таким образом, во всех режимах гипертензии условия энергетической оптимальности эластических тройников сохраняются (см. (3.4) и (3.9)),

ΔP_j(b) = bΔP_j(b_ЗС), (3.35)

[k(b)H₁(b)]^3/2 + [k(b)H₂(b)]^3/2 = 1. (3.36)

Таким образом, условие энергооптимального вхождения конструкционных и гемодинамических параметров в систему «Эластический тройник» сохраняется и для нагрузки.

Рассмотрим раздельно изменения механической и химической мощностей в условиях гипертензии. Механическая мощность в стволе и ветвях с учетом (3.30), (2.32) и (2.33)

W_МС(b) = b³W_МС(b_ЗС), (3.37)

W_М1(b) = b³[k(b_ЗС)H₁(b_ЗС)]^3/2W_МС(b_ЗС), (3.38)

W_М2(b) = b³[k(b_ЗС)H₂(b_ЗС)]^3/2W_МС(b_ЗС), (3.39)

В соответствии с (3.24) и (3.31)-(3.33)

b_j(b) = b²b_j(b_ЗС). (3.40)

Соответственно, химическая мощность в стволе и ветвях с учетом (3.32), (3.33) и (340),

W_ХС(b) = b³W_ХС(b_ЗС), (3.41)

W_Х1(b) = b³[k(b_ЗС)H₁(b_ЗС)]^3/2W_ХС(b_ЗС), (3.42)

W_Х2(b) = b³[k(b_ЗС)H₂(b_ЗС)]^3/2W_ХС(b_ЗС). (3.43)

При анализе (3.36)-(3.39) и (3.41)-(3.43) для тройника очевидна полная аналогия относительных изменений «механических» и «химических» мощностей при переходе от золотого режима к гипертензии. Как следствие этого, в каждом j-сосуде, как и в золотом режиме, сохраняется отношение

W_Мj(b)/W_Хj(b) = W_Мj(b_ЗС)/W_Хj(b_ЗС) = 0.5. (3.44)

Очевидно, что и отношение общих затрат мощности в стволе и ветвях при гипертензии то же, что и в золотом режиме,

W_С(b)/[W₁(b) + W₂(b)] = 1. (3.45)

В заключение можно сказать, что имеет место полная аналогия отношений (3.9), (3.27) и (3.28) в покое и (3.36) (3.44) и (3.45) при гипертензии. Эти инварианты составляют основу энергооптимальной гармонии «противоположностей» в системе «Эластический тройник» как в покое, так и при физической нагрузке.

3.3.2. Генерации сосудов мышечного типа

3.3.2.1. Особенности регуляции размеров мышечных сосудов

Качественная сторона изменений архитектоники тех или иных параметров коронарного русла в условиях гипертензии в настоящее время достаточно хорошо изучена. Однако структура изменений размеров сосудов в мышечных генерациях до сих пор математически не обоснована. Ниже нами выдвигается гипотеза регуляции размеров сосудов в каждой генерации и предлагаются математические структуры таких изменений.

Около 70% сопротивления коронарного русла контролируется мышечными микрососудами с диаметром менее 200 мкм /Chillian et al., 1990/. Существуют три механизма регуляции диаметра коронарных мышечных сосудов: 1) метаболический, 2) миогенный и 3) эндогенный /Liao, Kuo, 1997/. Первый механизм увеличения диаметра связан с выделением аденозина из кардиомиоцитов в ответ на возросшее потребление кислорода /Feifl, 1983/. Второй механизм обеспечивает расширение сосуда в ответ на понижение давления в его просвете или, наоборот, его сужение при повышенном давлении /McHale et al., 1987; Kuo et al., 1992/. Tретий механизм связан с изменением напряжения сдвига в стенке сосуда; при этом происходит выделение вазодилятаторов из эндотелия /Holtz et al., 1984; Kuo et al., 1991/. Расширение кровеносных сосудов в ответ на увеличения напряжения сдвига (или увеличения коронарного кровотока) называют кровотоковой дилятацией.

Рассмотрим первый тип регуляции. Роль аденозина в регуляции коронарного кровотока установлена еще в 60-70-х годах прошлого столетия. Было показано, что содержание аденозина в межклеточной жидкости является необходимым условием адекватного кровоснабжения здорового сердца /Rubio, Berne, 1969; Freud, Laarse, 1977; Berne, 1980/. Аденозин легко проходит через мембрану кардиомиоцита в межклеточное пространство и вызывает расслабление мышечных клеток в стенках коронарных артерий /Rubio, Berne, 1969; Olsson, 1970; Olsson et al., 1976/. Образование аденозина и его выход в межклеточное пространство происходит в ответ на кислородное голодание клеток. При окклюзии коронарной артерии уже через 5 сек уровень аденозина в миокарде возрастает почти в 3 раза /Olsson, 1970/. Концентрация аденозина и его производных в течение систолы значительно выше, чем в диастоле /Thompson et al., 1980/. Отмечено воздействие аденозина на стенки коронарных артерий вплоть до d=500 мкм /Harder et al., 1979/. Установлено /Kuo et al., 1992/, что изолированные коронарные артерии (d=30-200 мкм) расширяются в ответ на воздействие аденозина в различной степени; воздействие аденозина постепенно снижается с увеличением размеров сосудов /Gellai et al., 1973/. На интактном сердце было показано, что аденозин воздействует в наиболее значительной степени на микрососуды с диаметром менее 150 мкм /Kanatsuka et al., 1989; Jones et al., 1995/.

Установлено /Watkinson et al., 1979; McKenzie et al., 1980; Ely et al., 1983; Matsunaga et al., 1996/, что в условиях гипертензии, вызванной физической нагрузкой, существует прямая зависимость между ростом потребления кислорода миокардом и последующим увеличением концентрации аденозина и проводимости коронарного русла. Механизм адекватного соответствия работает в следующей последовательности. Физическая нагрузка вызывает рост среднего давления в аорте (гипертензию), возрастание силы сокращений миокарда и потребления кислорода. Происходит перестройка коронарного кровообращения адекватно возросшему уровню потребления кислорода. Вследствие временного дефицита кислорода в межклеточное пространство из кардиомиоцитов выделяется дополнительный объем аденозина. Возросшая концентрация аденозина и его производных обеспечивает расслабление мышечных клеток в стенках сосудов в «нижних» генерациях мышечных сосудов (d<150 мкм). (Отметим кстати, что кротоковая дилятация наиболее выражена в микрососудах с диаметром более 150 мкм /Liao, Kuo, 1997/.) После этого в верхних генерациях (d>150 мкм) снижается давление, возрастает кровоток, за счет чего увеличивается напряжение сдвига в этих сосудах /Liao, Kuo, 1997/; при этом происходит выделение вазодилятаторов из эндотелия, вызывающих расслабление мышечной стенки этих сосудов /Kuo et al., 1991/. Такая последовательность вызывает дополнительный рост кровотока в верхних и нижних генерациях, что увеличивает транспорт кислорода и снижает его дефицит в клетках. Как следствие, снижается концентрация аденозина в межклеточной жидкости и на стенках сосудов. Действие механизма сопряжения нижних и верхних генераций продолжается до тех пор, пока дефицит кислорода не будет полностью устранен; при этом размеры сосудов и кровотоки в сосудах устанавливаются на уровне, адекватном уровню гипертензии.

По-видимому, одним из факторов, ограничивающим увеличение просвета «верхних» сосудов, является напряжение сдвига на их стенке. Показано /Zamir, 1977/, что в оптимальном режиме «минимальной работы» напряжение сдвига имеет постоянное значение независимо от калибра сосуда,

τ=8ξс/d = 8ξl/dt,

где τ – напряжение сдвига на стенке, ξ – вязкость крови, с – линейная скорость эритроцитов в сосуде, d, l – диаметр и длина сосуда. Несложно показать в соответствии с (3.16), что для любого j–сосуда в золотом режиме гипертензии

τ_j(b_ЗС) = 8ξ_j(b_ЗС)l_j(b_ЗС)/d_j(b_ЗС)t_j(b_ЗС)=const.

Соответственно, в режимах гипертензии

τ_j(b) = bτ_j(b_ЗС).

Высказано предположение /Шошенко и др., 1982/, что рост просвета сосуда прекращается, когда достигается необходимое, по-видимому, оптимальное, соотношение между диаметром d и скоростью движения эритроцитов в сосуде. В частности, установлено /Nakache, Peronneau, 1979/, что каталитическая активность фермента b-галактозидазы на внутренней стенке меняется с изменением скорости протекания жидкости. В каждом режиме гипертензии устанавливается новое, оптимальное, соотношение между скоростью и диаметром j-сосуда; это соотношение одинаково для всех сосудов. При переходе к большей или меньшей гипертензии концентрация аденозина и других вазодиляторных агентов, а также кровоток в «нижних», и «верхних» микрососудах, соответственно возрастают или уменьшаются вплоть до полного соответствия между количеством доставляемого и потребляемого кислорода.

Миогенная регуляция проявляется, по-видимому, в тех случаях, когда напряжение в аорте выше или ниже нормальной величины. В первом случае за счет этого вида регуляции падение давления на резистивных генерациях возрастает, а во втором, наоборот, падает. В итоге на генерациях обменных микрососудов устанавливается величина давления, оптимальная для нормального, адекватного обеспечения кислородом сердечной мышцы. Этот механизм имеет огромное значение для компенсации отклонений давления в аорте от нормы. С другой стороны, показано /Liao, Kuo, 1997/, что в норме реакция миогенного механизма регуляции в ответ на возрастание концентрации аденозина незначительна.

Необходимо отметить еще одно важное обстоятельство: толщина мышечной массы в стенках генерации артериальных микрососудов одинакового калибра различна /Аветисян, 1982/. Напряжение в мышечном слое определяется действием механизмов нейро-гуморальной регуляции. Очевидно, что реакция сосудов одинакового диаметра, но с разной толщиной мышечного слоя, будет различной при одной и той же концентрации аденозина и эндотелиальных вазодилятаторов. Таким образом, для каждой генерации мышечных сосудов существуют два основных фактора регуляции:

1) различная реакция сосудов на концентрацию аденозина и эндотелиальных вазодилятаторов и

2) различие в толщине мышечного слоя стенках сосудов одной и той же генерации, что позволяет избирательно изменять размеры в пределах изменения «своего» давления и «своей» концентрации вазодилятаторов.

В этих условиях распределение сосудов по толщине их стенки должно приводить к определенному распределению по критической концентрации аденозина на стенке и приложенному давлению. Следствием этих механизмов является то, что каждый сосуд изменяет свои размеры в пределах «своего» давления и «своих» концентраций аденозина и эндотелиальных вазодилятаторов. После превышения этих пределов сосуд перестает удлиняться и расширяться. Чем меньше калибр микрососуда, тем ниже предельное давление и концентрация вазодилятаторов, при которых сосуд перестает увеличивать свои размеры.

Таким образом, налицо гармония метаболического, миогенного и эндогенного механизмов регуляции диаметра и длины мышечных сосудов, обеспечивающих, в конечном счете, энергооптимальное обеспечение сердца кровью и кислородом при любом уровне гипертензии.

3.3.2.2. Гемодинамические параметры генераций мышечных

сосудов в режимах гипертензии

При гипертензии в генерациях эластического типа размеры сосудов изменяются за счет механического растяжения давлением (см. (2.32) и (2.33)). На эластическом участке увеличение общей проводимости и объема каждой генерации происходит за счет аналогичного увеличения размеров всех сосудов во всех генерациях. В генерациях мышечного типа, приблизительно соответствующих коронарным артериолам с диаметром от 500 до 100 мкм, изменение размеров не одинаково и в разной степени связано с величиной приложенного давления и с концентрацией вазодиляторного агента аденозина на мышечной стенке этих сосудов.

Архитектоника «мышечных» тройников в золотом режиме гипертензии в своей основе аналогична архитектонике «эластических» тройников. Аналогия заключается в том, что эти тройники, как и в эластических генерациях, симметричны, а коэффициенты конструкции в тройниках одинаковы: С(b_ЗС)=l₁(b_ЗС)/d₁(b_ЗС)=l₂(b_ЗС)/d₂(b_ЗС)= l_С(b_ЗС)/d_С(b_ЗС)=3. Можно произвести анализ параметров архитектоники и гемодинамики мышечных тройников в золотом режиме гипертензии и в итоге получить те же соотношения, что и для эластических генераций. Однако в режимах гипертензии эти соотношения у мышечных и эластических тройников будут разными. Рассмотрим архитектонику и гемодинамику мышечных генераций и связь между ними в условиях гипертензии.

Если при гипертензии давление в аорте увеличивается в b раз,

P(b) = bP(b_ЗС), (3.46)

то общий коронарный кровоток по отношению к покою возрастает в b² раз /Цветков, 1993/,

q(b) = b²q(b_ЗС). (3.47).

Исходя из этих изменений, общая проводимость коронарного русла при гипертензии возрастает в b раз,

G(b) = b²q(b_ЗС)/P(b_ЗС)= bG(b_ЗС). (3.48)

Время прохождения эритроцитов по сердечному сосудистому руслу в условиях гипертензии уменьшается в b раз /Bernstein et al., 1962, Цветков, 1993/,

t(b) = t(b_ЗС)/b. (3.49)

Следовательно, общий объем коронарного русла увеличивается в b раз,

V(b) = b²q(b_ЗС)t(b_ЗС)/b = bV(b_ЗС). (3.50)

Естественно предположить, что одинаковые изменения суммарной проводимости и суммарного объема всего коронарного русла возможны только при аналогичных относительных изменениях этих параметров во всех генерациях эластических, мышечных и обменных сосудов. Такое предположение подтверждается большим количеством экспериментальных данных. Как уже отмечалось выше, соотношения кровотоков в ветвях левой коронарной артерии остаются неизменными в покое и приразличных уровнях физической нагрузки /Khouri et al., 1965, Vatner et al., 1972/. Соотношение кровотоков в покое и прилюбой мышечной нагрузке постоянно также и в эндо- и эпикардиальных слоях миокарда /Ball, Bache, 1976/. Не меняется отношение кровотокав коронарном синусе к общему коронарному кровотоку /Lafontant et al., 1962/ и кровотоку в левой коронарной артерии при изменении давленияв аорте и сжатии легочной артерии /Rayford et al., 1959/. Представленные выше феномены возможны лишь в том случае, когда суммарный кровоток во всех генерациях артерий, артериол, капилляров, венул и вен коронарного русла изменяются в одной и той же степени - в b² раз.

Очевидно, что для всякой j-генерации коронарных сосудов любого типа

q_j(b) = b²q_j(b_ЗС). (3.51)

где q_j(b_ЗС), q_j(b) – соответственно общий кровоток в j-генерации в золотом и различных режимах гипертензии.

Экспериментально установлена линейная зависимость между изменениями давления в аорте и сосудах различных органов млекопитающих /Duling, Klitzman, 1980/. Следовательно, при возрастании давления в аорте в b раз на j-генерации

∆P_j(b) = b∆P_j(b_ЗС). (3.52)

В условиях гипертензии для мышечных j-сосудов, как и для эластических, С(b_ЗС)= b^1/3l_j(b_ЗС)/b^1/3d_j(b_ЗС) = 3 и ξ_j(b)=ξ_j(b_ЗС). Исходя из (3.34), (3.51) и (3.52),

G_j(b) = bG_j(b_ЗС), (3.53)

V_j(b) = bV_j(b_ЗС), (3.54)

t_j(b) = t_j(b_ЗС)/b, 

где ∆P_j(b_ЗС), ∆P_j(b), V_j(b_ЗС), V_j(b), G_j(b_ЗС) G_j(b), t_j(b_ЗС), t_j(b) – соответственно давление, приложенное к j-генерации мышечных сосудов, проводимость, объем и время пребывания эритроцитов в золотом и других режимах гипертензии.

Таким образом, относительные изменения общего кровотока, общей проводимости, общего объема и времени пребывания в каждой генерации эластических и мышечных сосудов аналогичны.

Для каждой генерации мышечных сосудов, как было представлено выше, существуют два основных фактора регуляции: различие в толщине мышечного слоя стенках сосудов одной и той же генерации и различная реакция сосудов на концентрацию аденозина и эндотелиальных вазодилятаторов. Эти особенности позволяют сосудам одинакового калибра, но с разной толщиной стенки, избирательно изменять размеры в пределах изменения «своего» давления и «своей» концентрации вазодилятаторов. После превышения «своего» давления и «своей» концентрации размеры сосуда больше не изменяются. Таким образом, всякую мышечную генерацию составляет совокупность сосудов с различной «чувствительностью» к давлению и концентрации сосудорасширяющих веществ. По-видимому, часть сосудов во всех генерациях при превышении золотой гипертензии своих размеров не меняет. Длина и диаметр этих сосудов остаются постоянными в золотом и других режимах гипертензии. Исходя из этого весьма вероятного предположения, общий коронарный кровоток (см. (3.47)) можно представить как сумму двух составляющих,

b²q(b_ЗС) = bq(b_ЗС) + r(b)q(b_ЗС),

где bq(b_ЗС) – часть общего кровотока при гипертензии, которая протекала бы через коронарное русло при сохранении исходных, «золотых» размеров сосудов. Приращение кровотока r(b)q(b_ЗС) =b(b-1)q(b_ЗС) обеспечивается за счет изменения размеров сосудов в условиях гипертензии.

Структура общего кровотока для j–генерации может быть представлена следующим образом,

b²q_j(b_ЗС) = bq_j(b_ЗС) + b(b-1)q_j(b_ЗС). (3.56)

Как и для кровотока, в соответствии с (3.48) и (3.49), при гипертензии величины объема V_j(b) и проводимости G_j(b) можно представить в качестве суммы двух составляющих,

bG_j(b_ЗС) = G_j(b_ЗС) + x(b)G_j(b_ЗС),

bV_j(b_ЗС) = V_j(b_ЗС) + x(b)V_j(b_ЗС),

где G_j(b_ЗС), V_j(b_ЗС), - общая проводимость и общий объем j-генерации в золотом режиме гипертензии. Приращения к основной части проводимости и объема за счет увеличения размеров сосудов в условиях гипертензии

х(b)G_j(b_ЗС) = (b-1)G_j(b_ЗС),

х(b)V_j(b_ЗС) = (b-1)V_j(b_ЗС),

Следовательно, структуру этих параметров для j-генерации можно представить выражениями,

bV_j(b_ЗС) = V_j(b_ЗС) + (b-1)V_j(b_ЗС), (3.57)

bG_j(b_ЗС) = G_j(b_ЗС) + (b-1)G_j(b_ЗС). (3.58)

В выражениях (3.56)-(3.58) представлены структуры общего коронарного кровотока, общего объема и общей проводимости для любой j-генерации мышечных сосудов. В условиях гипертензии каждый из этих параметров как бы разделен на две части: «золотую» и «приращение». «Золотая» часть соответствует той части генерации, в которой размеры сосудов равны «золотым»; эти размеры остаются постоянными при всех уровнях гипертензии. «Приращение» происходит за счет избирательного увеличения размеров остальных сосудов. Исходя из такого разделения, мы можем перейти к анализу сопряжения мышечных генераций.

3.3.3. Генерации мышечных сосудов в режимах гипертензии

Транспортный участок сердца условно можно разделить на генерации двух типов. В генерациях первого, эластического типа размеры сосудов при гипертензии изменяются за счет их «механического» растяжения давлением (см. (3.32) и (3.33)). В генерациях второго, мышечного» типа изменения размеров обусловлены и давлением, и воздействием вазодилятаторов.

Генерации, соответствующие эластическому типу, рассмотрены нами выше. В этих генерациях все сосуды изменяют свои размеры аналогично по законам (3.32)-(3.33). Эластические тройники можно считать «подобными», поскольку у них при гипертензии каждый из параметров ствола и ветвей изменяются в равной степени («подобно»). Аденозин не оказывает воздействия на стенки этих сосудов. В генерациях мышечного типа стенки сердечных сосудов реагируют расслаблением на увеличение концентрации аденозина в межклеточной жидкости и эндотелиальных вазодилятаторов. В соседних генерациях мышечного типа сосуды имеют разную чувствительность не только к изменению давления, но и к концентрации вазодиляторных агентов.

Нам представляется наиболее вероятным следующий механизм регуляции размеров сосудов в мышечных генерациях. Для удобства анализа сопряжения мышечных генераций введем систему – «сквозная цепочка сосудов». В нашем случае это цепочка последовательно соединенных мышечных сосудов приблизительно от 500 до 100 мкм (вплоть до микрососудов). В конце каждого звена сквозной цепочки отходят две боковых цепочки (бифуркационное ветвление). Рассмотрим изменения размеров артерий в сквозной и боковых цепочках в ответ на изменение давления и концентрации вазодилятаторов.

Начнем мысленно перемещаться по сквозной цепочке в направлении от мелких звеньев к более крупным. В исходном, золотом режиме гипертензии условно «окрасим» всю сквозную цепочку красным цветом. Естественно этим же цветом будут окрашены и все боковые цепочки сосудов исходного, «золотого», размера. Это означает, что все сосуды генераций окрашены в красный цвет, соответствующий золотому режиму гипертензии. В дальнейшем по мере возрастания гипертензии для окраски будем последовательно пользоваться другими цветами (оранжевым, желтым, зеленым, голубым и т.д.). При превышении золотого режима в некотором диапазоне β_ЗС<β≤β₁ все сосуды сквозной цепочки «выше» определенного количества начальных звеньев начинают «оранжеветь» (за исключением первых звеньев). Первые звенья и отходящие на этом участке боковые цепочки сохраняют «красный» цвет, соответствующий золотому режиму. Каждая генерация теперь окрашена в два цвета (в каждой генерации одинаковых сосудов происходит перекрашивание части «красных» сосудов в «оранжевый» цвет). «Оранжевые» сосуды увеличивают свои размеры в соответствии со своим «оранжевым» давлением (см. (3.32) и (3.33)). В следующем диапазоне гипертензии β₁<β≤β₂ при превышении уровня β₁ звенья сквозной цепочки будут «желтеть» (за исключением расположенных ниже «красных» и «оранжевых» звеньев и их боковых цепочек). Всякая j-генерация сосудов исходно одинакового калибра теперь будет «окрашена» в «красный», «оранжевый» и «желтый» цвета (произошло «перекрашивание» части «оранжевых» сосудов в «желтый» цвет). «Желтые» сосуды увеличиваются в размерах соответственно «своей» величине гипертензии (см. (3.32) - (3.33)). В диапазоне β₂<β≤β₃ звенья сквозной и боковые цепочки «зеленеют» за исключением расположенных ниже «красных», «оранжевых» и «желтых» звеньев и их боковых цепочек. При достижении гипертезии β₃ каждая j-генерация исходно одинаковых сосудов будет окрашена в четыре «цвета»: красный, оранжевый, желтый и зеленый (при этом происходит «перекрашивание» части «желтых» сосудов в «зеленый» цвет). Подобное «перекрашивание» можно продолжать вплоть до максимальной гипертензии (β=2). В итоге j-генерация сосудов исходно одинакового калибра будет окрашена «во все цвета радуги». Размеры одинаково окрашенных сосудов «законсервированы» на уровне соответствующего им диапазона гипертензии. Исходя из (3.32) и (3.33), очевидно, что в каждой генерации «зеленые» сосуды превосходят по размерам «желтые», а «желтые», в свою очередь, больше «оранжевых» и т.д. Естественно, что размеры сосудов последней «расцветки» будут наибольшими, т.к. они соответствуют максимальной гипертензии. Можно сказать, что в каждой j-генерации могут быть представлены сосуды всех размеров, соответствующих режимам гипертензии от золотого до максимального (β=2).

Каждому поддиапазону гипертензии (β_n<β≤β_n+1) соответствует «свое» звено сквозной цепочки. При возрастании величины β в пределах этого поддиапазона интенсивность окраски «своего» и выше расположенных звеньев возрастает. При достижении величины β_n+1 эта часть сквозной цепочки имеет наиболее интенсивную окраску. При переходе границы β_n+1 все выше расположенные звенья приобретают «окраску» следующего поддиапазона β_n+1<β≤β_n+2. «Свое» звено сохраняет «свою» наиболее интенсивную окраску, которая сохраняется при дальнейшем росте гипертензии. Сохраняется также наиболее насыщенная, для каждого «своя», окраска и для ниже расположенных звеньев сквозной цепочки.

Каким же образом реализуется плавное изменение интенсивности «окраски» сосудов в каждой генерации в пределах всякого поддиапазона гипертензии? Ответ очевиден: за счет изменений «внутри» боковых цепочек, отходящих от «своих» звеньев сквозной цепочки. Каждая боковая цепочка имеет «свой» поддиапазон гипертензии (соответственно или β_ЗС>β≤β₁, или β₁>β≤β₂, или β₂>β≤β₃ и т.д.). Для этого поддиапазона она является, в свою очередь, «сквозной», и у нее есть свои «боковые» цепочки. Для каждой из этих цепочек имеется «свой» поддиапазон поддиапазона. Естественно, что это дробление можно продолжить. При росте гипертезии в пределах поддиапазонов происходит полная аналогия процедуры интенсивности «окрашивания» последовательности звеньев боковой цепочки, как это имеет место на сквозной цепочке. Различие только в том, что эта процедура относится только к «своему» цвету. По мере возрастания гипертензии в генерации происходит изменение размеров сосудов возрастающей интенсивности «расцветки». Например, «оранжевая» фракция сосудов в генерациях расслаивается на «оттенки» от минимальной до максимальной насыщенности. Естественно, аналогичным же образом происходит «окраска» сосудов в другие «цвета». Всякая генерация сосудов исходно одинакового калибра при максимальной гипертензии оказывается плавно окрашенной «во все цвета радуги». Размеры каждого из «окрашенных» сосудов соответствуют «своей» величине гипертензии. Соотношение между «окрашенными» сосудами аналогично для всех генераций. Поэтому при любом уровне гипертензии обеспечивается равенство всех мышечных генераций по давлению, кровотоку, объему и проводимости независимо от их калибра. Оптимальное распределение сосудов по размерам обусловливает оптимальное сопряжение мышечных генераций при любом уровне гипертензии. Это правило в соответствии с принципом оптимального вхождения лежит, по нашему представлению, в основе энергооптимальной гармонии мышечного участка коронарного русла.

Очевидно, что изменения суммарных величин кровотока, проводимости и объема в мышечных генерациях аналогичны изменениям этих параметров в эластических генерациях. В последующих за мышечными обменных генерациях размеры сосудов остаются постоянными при любой гипертензии. Поэтому изменения кровотока, объема и проводимости в этих генерациях происходят только за счет вновь открытых артериол и капилляров. Вновь открытые микрососуды также «окрашиваются» в разные «цвета», каждый из них принадлежит к «своей» величине гипертензии. В режимах гипертензии в обменных генерациях соотношения параметров гемодинамики между «окрашенными» сосудами различного «цвета» те же самые, что и для мышечных. Поэтому изменения кровотока, объема и проводимости в этих генерациях происходят только за счет вновь открытых микрососудов и капилляров. В режимах гипертензии в обменных генерациях соотношения параметров гемодинамики между «окрашенными» сосудами те же самые, что и для мышечных генераций.

3.3.4. Мышечные тройники в режимах гипертензии

Транспортные эластические тройники в условиях гипертензии рассмотрены нами выше. В этом варианте все элементы тройника (ствол и обе ветви) изменяют свои размеры аналогично по законам (3.32)-(3.33). Поэтому эластические тройники можно обозначить как «подобные» Перейдем к непосредственному анализу переходных тройников, Рассмотрим тройники, у которых при гипертензии размеры ствола и каждой из ветвей изменяются по различным законам (рис. 3.8). Такие тройники мы обозначили «переходными». Ствол и одна из ветвей переходного тройника являются звеньями сквозной цепочки; другая ветвь является первым звеном боковой цепочки.

Три составляющих каждого параметра в структурах (3.56)-(3.58) можно «перенести» на переходной тройник. Левая часть этих равенств соответствует стволу, первый элемент правой части («сквозной») - 1 ветви и второй элемент («боковой») – 2 ветви. Первую ветвь можно было бы обозначить «сквозной», а вторую – «боковой». Однако для удобства в дальнейшем будем обозначать «сквозную» и «боковую» соответственно как 1 и 2 ветви.

Рассмотрим в качестве примера законы изменения архитектоники и гемодинамики переходного тройника в некотором диапазоне гипертензии b_n-1<b£b_n. В пределах этого диапазона диаметр и длина ствола изменяются подобно эластическому сосуду, т.е. в соответствии с (3.32) и (3.33). Размеры 1 ветви «законсервированы» на уровне, достигнутом на верхней границе предыдущего диапазона b_n-1. Размеры 2 ветви изменяются по «своим» законам, отличным от (3.32) и (3.32). На всем «мышечном» участке для упрощения вычислений все ветвления в исходном, золотом режиме гипертензии примем симметричными, т.е. d₁(b_ЗС)=d₂(b_ЗС)=0,794d_С(b_ЗС), l₁(b_ЗС)=l₂(b_ЗС)=0,794l_С(b_ЗС). Коэффициент конструкции для всех мышечных сосудов в покое и при гипертензии С_С(b)=С₁(b)=С₂(b)=3.

Величина давления, приложенного к стволу и ветвям, одинакова: ΔP₁(b_ЗС) =ΔP₂(b_ЗС) =ΔP_С(b_ЗС) =3,5 мм рт. ст. /Цветков, 2004/. В соответствии с этими условиями и выражением (3.56) кровотоки в стволе, 1 и 2 ветвях при b_ЗС<b£b₁ в каждом переходном тройнике изменяются следующим образом,

q_С(b) = b²q_С(b_ЗС),

q₁(b) = 0,5bq_С(b_ЗС),

q₂(b) = b(b-0,5)q_С(b_ЗС).

Для любого диапазона гипертензии b_n-1<b£b_n

q_С(b) = b²q_С(b_ЗС), (3.59)

q₁(b) = 0,5bb_n-1q_С(b_ЗС), (3.60)

q₂(b) = b(b-0,5b_n-1)q_С(b_ЗС), (3.61)

где q_C(b), q₁(b), q₂(b) – соответственно кровотоки в стволе, 1 и 2 ветвях в диапазоне гипертензии b_n-1<b£b_n.

Исходя из (3.59)-(3.61), структуру кровотока в стволе и ветвях переходного тройника можно представить следующим выражением,

b²q_С(b) = 0,5bb _n-1q_С(b_ЗС) + b(b-0,5b_n-1)q_С(b_ЗС).

В соответствии с (3.57) распределение объема в переходном тройнике для b_n-1<b£b_n происходит следующим образом:

V_С(b) = bV_С(b_ЗС), (3.62)

V₁(b) = 0,5b_n-1V_С(b_ЗС ), (3.63)

V₂(b) = (b-0,5b_n-1)V_С(b_ЗС), (3.64)

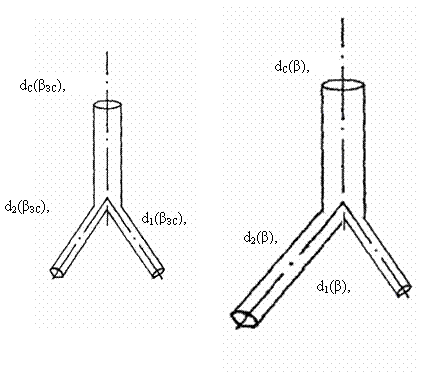
Рис. 3.8. Переходные тройники в диапазоне гипертензии β_ЗС<β≤β₁.

А – тройник в золотом режиме, Б – тройник в режиме гипертензии: d₁(β)=0,794d_С(β_ЗС), d₂(β)=[β-0,5]^1/3d_С(β_ЗС), d_С(β)=β^1/3d_С(β_ЗС), l₁(β)=0,794l_С(β_ЗС), l₂(β)=[β-0,5]^1/3l_С(β_ЗС), l_С(β)=β^1/3l_С(β_ЗС).

где V(b_ЗС)-объем ствола, соответствующий золотому режиму гипертензии; V_С(b), V₁(b), V₂(b) – соответственно объем ствола, 1 и 2 ветвей в диапазоне b_n-1<b£b_n.

Аналогично, в соответствии с (3.58) распределение проводимостей в тройнике

G_С(b) = bG_С(β_ЗС), (3.65)

V₁(b) = 0,5b_n-1V_С(b_ЗС),

V₁(b) = 0,5b_n-1V_С(b_ЗС), (3.66)

G₂(b) = (b-0,5b_n-1)G_С(β_ЗС), (3.67)

где G_С(β_ЗС) - проводимость ствола, соответствующая золотому режиму гипертензии; G_С(b), G₁(b), G₂(b) –проводимость ствола, 1 и 2 ветвей в диапазоне гипертензии b_n-1<b£b_n.

В режиме «минимальной» работы диаметры ствола и ветвей в тройнике связаны выражением /Розен, 1969/

d₁(b)³ + d₂(b)³=d_С(b)³.

В соответствии с (3.32)-(3.33) и (3.62)-(3.64) в пределах b_n-1£b£b_n диаметры ствола и ветвей,

d_С(b) = b^/3d_С(b_ЗС), (3.68)

d₁(b) = 0,794b_n-1^/3d_С(b_ЗС), (3.69)

d₂(b) = [b-0,5b_n-1]^1/3d_С(b_ЗС), (3.70)

где d_С(b_ЗС) – диаметр ствола в золотом режиме гипертензии; d_С(b), d₁(b), d₂(b) – диаметр ствола, 1 и 2 ветвей в режиме гипертензии.

Соответственно, поскольку для всех мышечных сосудов l/d=const,

l_С(b) = b^/3l_С(b_ЗС), (3.71)

l₁(b) = 0,794b_n-1^/3l_С(b_ЗС), (3.72)

l₂(b) = [b-0,5b_n-1]^1/3l_С(b_ЗС), (3.73)

где l_С(b_ЗС) –длина ствола в золотом режиме гипертензии; l_С(b), l₁(b), l₂(b) – длина ствола, 1 и 2 ветвей в диапазоне b_n-1<b£b_n.

Мышечные тройники отличаются от эластических тем, что все их элементы (ствол и ветви) при одном и том же уровне гипертензии изменяются в различной степени. Покажем, что оптимальные отношения мощностей (3.44) и (3.45), соответствующие подобным тройникам, справедливы и для переходных тройников.

В стволе переходного тройника механическая, химическая и суммарная мощности в режимах гипертензии b_n-1<b£b_n изменяются в соответствии с (3.37) и (3.41),

W_МС(b) = 0,5b³W_МС(b_ЗС), (3.74)

W_ХС(b) = 0,5b³W_ХС(b_ЗС). (3.75)

Естественно, что суммарная мощность в стволе

W_С(b) = b³W_С(b_ЗС). (3.76)

В первой ветви при гипертензии, соответствующей b_n-1, механическая мощность увеличивается в b_n-1³ раз. При дальнейшем росте гипертензии за счет увеличения ∆P₁(b_n-1) и q₁(b_n-1) в b/b_n-1 раз

W_М1(b) =0,5b²b_n-W_МС(b_ЗС). (3.77)

Определим химическую мощность в 1 ветви. В соответствии с (3.51) и (3.54), время пребывания эритроцитов в 1 ветви в диапазоне b_n-1<b£b_n

t₁(b) = t_С(b_ЗС)/b. (3.78)

Несложно показать, что и

t₂(b) = t_С(b_ЗС)/b,

t_С(b) = t_С(b_ЗС)/b.

Очевидна «временная» аналогия в стволе и ветвях, принадлежащих к различным генерациям мышечных сосудов. Исходя из (3.24) и (3.78), потребляемая в этом сосуде удельная химическая энергия за единицу времени,

b₁(b) = b²b_С(b_ЗС). (3.79)

В соответствии с (3.53) и (3.79) химическая мощность в 1 ветви

W_Х1(b_n-1) = 0,5b²b_n-W_ХС(b_ЗС). (3.80)

Общая мощность в 1 ветви переходного тройника

W₁(b) = b²b_n-W_С(b_ЗС). (3.81)

В 2 ветви переходного тройника

DP₂(b) = bDPс(b_ЗС),

q₂(b) = 0,5b(b-b_n-1)q_C(b_ЗС).

Исходя из этого, механическая мощность в 2 ветви

W_М2(b) = 0,5b²(b-0,5b_n-1)W_МС(b_ЗС). (3.82)

В этой же ветви,

b₂(b)=b²b_С(b_ЗС),

V₂(b) = (b-0,5)V_С(b_ЗС).

Следовательно,

W_Х2(b) = b²(b-0,5b_n-1)W_ХС(b_ЗС). (3.83)

Соответственно, общая мощность, потребляемая во 2 ветви

W₂(b) = b²(b-0,5b_n-1)W_С(b_ЗС). (3.84)

Суммарная мощность в 1 и 2 ветвях переходного тройника

W(b) = W₁(b) + W₂(b) = b³W_С(b_ЗС). (3.85)

Из анализа выражений (3.77) и (3.80), (3.82) и (3.83) очевидно, что отношение механической и химической мощностей в стволе и ветвях любого переходного тройника одинаково и не зависит от уровня гипертензии

W(b) = W₁(b) + W₂(b) = b³W_С(b_ЗС). (3.86)

Из анализа выражений (3.76) и (3.85) следует, что

W(b) = W₁(b) + W₂(b) = b³W_С(b_ЗС). (3.87)

Очевидно, что отношение (3.86) полностью аналогично отношению (3.44). Эта аналогия указывает на то, что на всем транспортном участке этот инвариант одинаков для всех сосудов при всех уровнях гипертензии. Отношения (3.87) и (3.45) аналогичны для всех «подобных» и «переходных» тройников независимо от уровня гипертензии. Наличие этих отношений обусловливает энергооптимальную гармонию вхождения элементов тройников в системы «Подобный тройник» и «Переходной тройник» при любой гипертензии. Оптимальная природа эластических и мышечных тройников обеспечивает, в конечном счете, минимальные затраты энергии, крови и сосудистого материала для перемещения кислорода на транспортном участке.

---

К оглавлению