Глава
2. «ЗОЛОТАЯ» ГАРМОНИЯ СТРУКТУР СЕРДЕЧНЫХ ЦИКЛОВ И ПРОЦЕССОВ
Гармония - начало, объединяющее «противоположности» в
системе. Традиция подхода к объекту как совокупности противоположностей берет
начало в Древней Греции. «Бог, - учили пифагорейцы, - положил числа в основу
мирового порядка. Бог – это единство, а мир – множество и состоит из
противоположностей. То, что приводит противоположности к единству и создает
все в космосе, есть гармония. Гармония является божественной и заключается в числовых отношениях…Блаженство есть знание
совершенства чисел души» / по Варден, 1959, с. 129/. Пифагор первым поверил в
рациональное устройство мироздания и возможность описания этого устройства с
помощью чисел и их отношений. В наши дни идея гармонии «противоположностей»
приобретает все большее признание. «Гармония, - указывает
белорусский философ Э.М.Сороко, - не обладает каким-либо смыслом вне
противоречивости» /Сороко, 1984, c. 80/.
«Великая карта оптимальных состояний природы, - пишет Сороко, - согласно
которой та создает свои порядки, написана языком противоположностей, контрарностей, противодействий» /Сороко,
1984, с. 101/. Гармония систем при рассмотрении ее с исходных позиций
предполагает отправной точкой брать единство противоположностей. Можно
ли вообще измерить гармонию «противоположностей»? В чем заключается
первоисточник гармонии, и какова специфика ее объективных законов? Это всего
лишь отдельные стороны проблемы сущности гармонии. Эти вопросы, как будет нами
показано ниже, имеют непосредственное отношение к структуре сердечных циклов
человека и млекопитающих (ССЦ) и других биопроцессов.
2.1. Структуры
сердечного цикла в условиях покоя и физической нагрузки
2.1.1 Система «Структура
сердечного цикла (ССЦ)»
Фазовая структура каждого
сердечного параметра отображает его качественные изменения в течение
кардиоцикла в соответствии с некоторыми функциональными состояниями. Необходимо
решить, каким образом произвести раздел «противоположных» состояний в пределах
сердечного цикла, чтобы получить информацию о наиболее глубоких законах
организации и гармонии сердца. Основой деятельности сердца является
периодическая смена двух противоположных, взаимно дополняющих друг друга
состояний сердечной мышцы - систолы (напряжения) и диастолы (расслабления). Благодаря смене этих
«противоположностей» сердце исполняет свою функцию мышечного насоса, перекачивающего
кровь из артерий в вены. Исходя из этого, нами выбраны для гармонического
анализа структуры сердечного цикла (ССЦ), объединяющие систолическую и
диастолическую «противоположности» важнейших сердечных параметров. По
разделению «противоположностей» всякая ССЦ включает в себя в качестве составляющих
систолическое и диастолическое значения рассматриваемого параметра и их
сумму.
Согласно общей теории систем
(ОТС) Ю.А.Урманцева /Урманцев, 1974, 1978/ любую ССЦ можно представить как
объект-систему. В каждой объект-системе необходимо выделить следующие аспекты:
1) первичные элементы, рассматриваемые на данном уровне исследования как неделимые; 2) отношения
единства между этими элементами и 3) законы композиции (организации),
определяющие границы этих
отношений. Первичными элементами
структур сердечного цикла (ССЦ) по основанию «противоположность» является
систолическое, диастолическое и суммарное значения рассматриваемого параметра.
Отношением единства между этими элементами является их функциональная связь, а
законом композиции - математическое выражение определенного вида, связывающее
эти элементы в единое целое. На основе 1) - 3) нами были
построены ССЦ, представляющие наиболее важные параметры деятельности сердца, -
временная, объемная, механическая и кровотоковая ССЦ /Цветков, 1993, 1997/.
Временная ССЦ состоит из длительностей систолы, диастолы и кардиоцикла. Объемная ССЦ включает в себя объем изгнанной крови, объем
оставшейся крови и конечнодиастолический объем левого желудочка. Механическая ССЦ представляет собой отнесенные к длительности
сердечного цикла среднее систолическое и среднее диастолическое давления в
аорте и среднее за сердечный цикл давление в аорте. Кровотоковая
ССЦ включает в себя отнесенные к длительности сердечного цикла средний
систолический и средний диастолический коронарные кровотоки и средний за
кардиоцикл коронарный кровоток. Пределы предпринятого исследования
ограничены. Нами будут рассмотрены структуры сердечного цикла здоровых взрослых
людей и животных, находящихся в покое и в пределах допустимой физической нагрузки.
Особи репродуктивного возраста в течение экспериментов находились в нормальных
условиях (нормальные состав, влажность и атмосферное давление вдыхаемого
воздуха, естественная температура окружающей среды, нормальное питание,
отсутствие стрессовых ситуаций и т.д.). В качестве «возмущающего» фактора,
влияющего на величину параметров сердца, избрана градуированная физическая
нагрузка. Естественно, что для каждого вида млекопитающих величины сердечных
параметров связаны с весом животных. Совокупность всех реально существующих
временных, механических, объемных и кровотоковых ССЦ животных различной массы
(веса) в условиях вариации физической нагрузки от покоя до максимума составляет
некоторое «пространство» ССЦ. Нашей конечной задачей является представление законов
композиции этого «пространства» и анализ его особенностей (гармонии).
2.1.2. Обобщенное
представление ССЦ
В общем виде любую структуру сердечного
цикла (ССЦ), по отношению к весу животного и физической нагрузке можно
представить выражением
CSj(d,W) + Cdj(d,W) = Cj(d,W),
где W - вес животного; d - относительное изменение минутного выброса сердца
при заданной физической нагрузке по отношению к минутному выбросу в покое, δ - опосредованный показатель изменения
кровоснабжения организма при вариации нагрузки; Csj(δ,W), Cdj(δ,W),
Cj(δ,W) - систолическое,
диастолическое и суммарное значения некоторого j-параметра, соответствующие
величинам W и δ. Значения Csj(δ,W), Cdj(δ,W)
и Cj(δ,W) соответствуют
установившимся режимам кровоснабжения организма в покое или после
кратковременной градуированной нагрузки (5-10 мин). Показатель d = n/nпок, где nпок, n - соответственно частота сердцебиений за минуту в покое и при
нагрузке.
В выражении (2.1)
систолическим и диастолическим элементам механической и кровотоковой ССЦ соответствуют средние за
систолу и диастолу величины рассматриваемого параметра, отнесенные к
длительности сердечного цикла. При
весе животного W и частоте сердцебиений n, соответствующей некоторой величине d,
![]() = (1/T(n,W))
= (1/T(n,W)) ![]() ,
,
![]() = (1/T(n,W))
= (1/T(n,W)) ![]() ,
,
где tS(n,W), td(n,W), T(n,W) - соответственно длительность
систолы, диастолы и кардиоцикла, cj(n,W,t) - мгновенное значение j-параметра, ![]() ,
, ![]() - соответственно среднее за
сердечный цикл систолическое и среднее за сердечный цикл диастолическое
значения j-параметра некоторого животного при сердечном ритме n. Естественно, что при одной и той же величине d частота сердцебиений n для различных видов животных будет зависеть от их
веса.
- соответственно среднее за
сердечный цикл систолическое и среднее за сердечный цикл диастолическое
значения j-параметра некоторого животного при сердечном ритме n. Естественно, что при одной и той же величине d частота сердцебиений n для различных видов животных будет зависеть от их
веса.
Среднее за кардиоцикл значение параметра
для механической и
кровотоковой ССЦ
![]() = (1/T(n,W))
= (1/T(n,W))![]() ,
,
где ![]() - среднее за сердечный цикл значение
j-параметра, соответствующее частоте n. В дальнейшем для механической и кровотоковой ССЦ
среднее за кардиоцикл значение параметра будем для краткости обозначать
«средним значением», а длительность сердечного цикла и конечнодиастолический
объем – «суммарным».
- среднее за сердечный цикл значение
j-параметра, соответствующее частоте n. В дальнейшем для механической и кровотоковой ССЦ
среднее за кардиоцикл значение параметра будем для краткости обозначать
«средним значением», а длительность сердечного цикла и конечнодиастолический
объем – «суммарным».
Нами было установлено
/Цветков, 1993, 1997/, что в определенном режиме кровоснабжения организма
систолическое, диастолическое и суммарное (или среднее) значения параметра для
временной, механической, объемной и кровотоковой ССЦ
соотносятся по золотому сечению. Этот режим приблизительно
соответствует покою организма для различных видов млекопитающих независимо от
их веса. Режим кровоснабжения организма, связанный с золотой пропорцией,
был обозначен нами «золотым». Этот режим для всякого вида животных
соответствует своей «золотой» частоте сердцебиений nЗС, при которой длительности систолы, диастолы и кардиоцикла
соотносятся между собою по золотому сечению. Частота nЗС различна для различных видов млекопитающих (для человека nЗС»nпок=63 уд/мин, для собаки nЗС»nпок=94 уд/мин и т.д.). В дальнейшем избираем золотой режим
кровоснабжения в качестве исходного при анализе изменений, соответствующих
вариации физической нагрузки от покоя до максимума (для различных животных этот
предел соответствует δ»1-4). В золотом режиме кровоснабжения
δ = δЗС=1. С учетом этого, для механической
и кровотоковой ССЦ в золотом режиме
![]() , = 0,382
, = 0,382![]() , (2.2)
, (2.2)
![]() =
0,618
=
0,618![]() ,
(2.3)
,
(2.3)
где![]() ,
, ![]() - соответственно среднее за кардиоцикл
систолическое, среднее за кардиоцикл диастолическое
и суммарное значения рассматриваемого
j-параметра при dЗС. При физической нагрузке между изменениями минутного
выброса сердца и частоты сердцебиений
существует прямая линейная зависимость /Цветков, 1993/; следовательно, для
каждого животного d=n/nЗС. В золотом режиме кровоснабжения закон композиции для ССЦ
рассматриваемых параметров можно представить следующим выражением
- соответственно среднее за кардиоцикл
систолическое, среднее за кардиоцикл диастолическое
и суммарное значения рассматриваемого
j-параметра при dЗС. При физической нагрузке между изменениями минутного
выброса сердца и частоты сердцебиений
существует прямая линейная зависимость /Цветков, 1993/; следовательно, для
каждого животного d=n/nЗС. В золотом режиме кровоснабжения закон композиции для ССЦ
рассматриваемых параметров можно представить следующим выражением
0,382![]() + 0,618
+ 0,618![]() =
= ![]() , (2.4)
, (2.4)
Известно /Цветков, 1993/,
что в покое зависимость рассматриваемых средних и суммарных ![]() значений сердечных
параметров от веса i-животного
можно представить аллометрическими выражениями
значений сердечных
параметров от веса i-животного
можно представить аллометрическими выражениями
![]() = ajWibj (2.5)
= ajWibj (2.5)
где Wi - вес i-животного; aj , bj
- величины, соответствующие j-параметру
деятельности сердца (эти величины имеют постоянные значения независимо от веса
животных). С учетом (2.3) – (2.5),
0,382ajWibj + 0,618ajWibj = ajWibj. (2.6)
Влияние физической нагрузки на величину
элементов рассматриваемых ССЦ можно представить в
обобщенной форме /Цветков, 1993, 1997/
0,382![]() ajWibj +0,618
ajWibj +0,618![]() ajWibj @
ajWibj @![]() ajWibj, (2.7)
ajWibj, (2.7)
где kj - величина, соответствующая j-параметру; эта величина
не зависит от уровня физической нагрузки и веса животных.
Итак, в (2.7) представлен обобщенный
закон композиции «пространства»
временных, механических, объемных и кровотоковых структур сердечного цикла.
«Пространство» (2.7) образуют 3 «переменных»: j-параметр (коэффициенты aj , bj , kj), вес i-животного
(величина Wi), нагрузка (величина
δ). В этом выражении представлена универсальная роль золотого сечения, а
также отображено влияние веса животных и мышечной нагрузки на величину
рассматриваемых параметров. Закон (2.7) отображает совокупность важнейших
параметров, связывающих сердце с кровоснабжением организма. В результате
проведенного анализа работ /Stahl, 1962, 1965, 1967; Noordegraaf, Li, 1979; Li, 1983; Цветков, 1993, 1997/ установлены следующие значения kj , aj
и bj :
для временной ССЦ - kj =-2, aj=0,249, bj
=0,250, [Сj]=cек; для
объемной ССЦ - kj =-1, aj =1,76, bj =1,02,
[Сj]=мл; для механической ССЦ
- kj =1, aj=1,47×105 , bj =0,033, [Сj]=дн/см2 и для кровотоковой ССЦ - kj =2, aj =7,48,
bj =0,81, [Сj]=мл/мин. Во всех расчетах [Wi] принимается в кг.
2.1.3. Гармония «пространства» ССЦ и «особые» числа
Обобщенный закон (2.7) можно представить
в следующем виде,
[0,382![]() +
0,618
+
0,618![]() )]
)]![]() ajWi
ajWi![]() @
@ ![]() ajWi
ajWi![]() .
.
Очевидно, что основу (2.7) составляет
приблизительное тождеств
0,382![]() + 0,618
+ 0,618![]() @ 1. (2.8)
@ 1. (2.8)
Первый член (2.8) представляет долю систолической
«противоположности» параметров в условиях покоя и нагрузки,
nS(δ) = 0,382![]() , (2.9)
, (2.9)
а второй – долю «диастолической»
противоположности (рис. 2.1)
nd(δ) = 0,618![]() . (2.10)
. (2.10)
|
|
В (2.8) представлена основа гармонии
«противоположностей» сердечных параметров в покое и при любом уровне нагрузки.
Как будет представлено ниже, величины nS(δ) и nd(δ) являются своего рода мерой
энергооптимальной гармонии противоположностей ССЦ при заданном
относительном уровне нагрузки для всех животных.
Относительное расхождение между левой и
правой частями приблизительного тождества (2.8) в заданных пределах (![]() =1-2) составляет не более (-3-+7)%. Отметим, что это расхождение
находится в пределах ±(5-6)%-отклонения параметра от его
оптимального значения, при котором оптимальность системы еще сохраняется
/Бочков, 1974/. При замене
=1-2) составляет не более (-3-+7)%. Отметим, что это расхождение
находится в пределах ±(5-6)%-отклонения параметра от его
оптимального значения, при котором оптимальность системы еще сохраняется
/Бочков, 1974/. При замене ![]() =х и умножении правой части
на х0 =1, выражение (2.8) предстает
в следующей форме
=х и умножении правой части
на х0 =1, выражение (2.8) предстает
в следующей форме
0,382х + 0,618х-1 @ 1х0. (2.11)
В (2.11), а,
следовательно, и в (2.8) можно отметить интересные особенности. В их
структуре имеет место «пересечение» двух
геометрических прогрессий: 1) «золотой»: j-2 =
0,382, j-1 =
0,618, j0 = 1 и 2)
х-1 , х0 , х; первая из них
обладает, как известно, также свойствами аддитивного ряда. Отметим, что
разность показателей крайних членов обеих прогрессий равна 2. Отношение хmax/хmin
=2 имеет характерную особенность: оно соответствует отношению верхнего и
нижнего значений двух соседних октав (![]() ). Это соотношение соответствует 2 интервалам качественной
симметрии /Марутаев, 1990/. Таким образом,
особенности композиции (2.8) связаны с золотым числом j и числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/.
). Это соотношение соответствует 2 интервалам качественной
симметрии /Марутаев, 1990/. Таким образом,
особенности композиции (2.8) связаны с золотым числом j и числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/.
В каждом члене (2.7) имеет
место перемножение двух выражений: ![]() ajWi
ajWi![]() ,
, ![]() ajWi
ajWi![]() ,
, ![]() ajWi
ajWi![]() ; первый из этих сомножителей безразмерен, а другой имеет размерность
параметра. Как нам представляется, здесь
имеет место важный феномен. И размерный и
безразмерный сомножители имеют аллометрическую форму, что указывает на универсальность этой формы для
представления изменений параметра как по отношению к нагрузке, так и весу
животных. Следует вспомнить при этом,
что аллометрическая форма относительного изменения имеет место и при росте
растений /Huxley,
1932; Боднар, 1992, 1994/, что указывает на особое «благоволение» живой природы
к подобной форме преобразований.
; первый из этих сомножителей безразмерен, а другой имеет размерность
параметра. Как нам представляется, здесь
имеет место важный феномен. И размерный и
безразмерный сомножители имеют аллометрическую форму, что указывает на универсальность этой формы для
представления изменений параметра как по отношению к нагрузке, так и весу
животных. Следует вспомнить при этом,
что аллометрическая форма относительного изменения имеет место и при росте
растений /Huxley,
1932; Боднар, 1992, 1994/, что указывает на особое «благоволение» живой природы
к подобной форме преобразований.
В законе (2.7) присутствует также своего
рода «иерархия» постоянных безразмерных величин. Прежде всего, это золотые
числа, обусловливающие универсальность
всего «пространства» ССЦ. Числа 0,382 и 0,618 характеризуют гармонию
противоположных «состояний» сердечной
мышцы в золотом режиме кровоснабжения; эти числа являются общими для всех животных и всех рассматриваемых параметров.
Диапазон изменения нагрузки δ=1-4 приблизительно сохраняется независимо от
веса для всех животных /Цветков, 1993, 1997/.
Величины kj , aj и bj по отношению к некоторому j-параметру аналогичны для всех животных и не
зависят от уровня нагрузки. В конечном счете, только величина Wi
«индивидуализирована», т.е. имеет
размерность и относится к отдельному i-животному.
Таким образом, в законе (2.7) имеем
следующий ряд универсальных величин: 1)
числа 0,382 и 0,618; 2) диапазон чисел d =1-4 и 3)
значения kj, aj и
bj . Эти величины представляют числовой «каркас» - основу гармонии
«пространства» ССЦ. В соответствии с принципом оптимального вхождения
«вхождение» представленных чисел («простых» систем) в сложную систему
(«пространство» ССЦ) должно иметь оптимальную основу. Ниже будет представлено
энергооптимальное содержание этого «каркаса».
Прежде всего, следует
отметить оптимальность веса (массы) тела
млекопитающих. И.Ф.Образцов и М.А.Ханин /Образцов, Ханин, 1989/
показали, что наблюдаемые в природе веса
тел млекопитающих весьма близки к
оптимальным величинам, допустимым с точки зрения энергетики. Зависимость средних и суммарных значений параметров от веса животных
представлена выражением (2.5). Покажем, что в
покое средние и суммарные значения
рассматриваемых параметров (среднее артериальное давление, средний коронарный
кровоток, длительность кардиоцикла и конечнодиастолический объем левого желудочка) энергооптимальны по
отношению к весу млекопитающих.
Оптимальная масса сердца определяется
влиянием двух «противоположных» энергофакторов: 1) артериальное давление и 2)
воспроизводство эритроцитов /Образцов, Ханин, 1989/.
При увеличении артериального давления уменьшается объем циркулирующей крови и, следовательно, энергетические
затраты, связанные с эритропоэзом. С
другой стороны, при этом возрастает механическая работа сердца и увеличивается масса сердца.
Природа нашла оптимальное соотношение между затратами мощности на
воспроизводство эритроцитов и мощности,
потребляемой сердцем, при котором их сумма равна минимальной величине. Вес сердца в этом
случае оптимален, т.е. имеет минимально
возможную величину. Соотношение энергетических «противоположностей» двух систем, составляющих единое целое представляет собой гармонию
оптимальных затрат энергии. Очевидно, что веса сердца и организма соотносятся
между собою оптимальным образом; это
отношение является инвариантным для различных
видов животных и составляет приблизительно 0,06 /Stahl, 1965; Prothero, 1979/.
Установлено /Ханин и др.,
1978; Образцов и Ханин, 1989/, что в покое среднее артериальное давление и
минутный выброс сердца оптимальны по отношению к массе (весу) организма
животных. Эти параметры оптимальны с точки зрения минимальности энергозатрат на
кровоснабжение организма. Было показано /Цветков, 1986, 1993/, что в покое
среднее давление в аорте и средний коронарный кровоток имеют оптимальные
значения, которые позволяют с минимальным расходом энергии обеспечить снабжение
сердечной мышцы кровью и кислородом. Средний коронарный кровоток и минутный
выброс имеют в покое энергооптимальные значения и связаны между собою
одинаковым для млекопитающих отношением 0,04-0,05 /Фолков, Нил, 1976; Sasaki, Wagner, 1971/. Очевидно, что и
коронарный кровоток оптимален по отношению к весу животных. В
покое естественный объем изгнанной крови за одно сокращение (ударный объем) по
отношению к естественному конечнодиастолическому (полному) объему левого
желудочка составляет энергооптимальную долю /Suga, 1979/. Поскольку минутный сердечный выброс и ударный объем
оптимальны по отношению к весу, то, очевидно, что оптимальна по отношению к
весу и частота сердцебиений, а, следовательно, и длительность сердечного цикла.
Таким образом, средние и суммарные
значения представленных видов ССЦ в золотом режиме энергооптимальны по отношению
к весу отдельных животных. Поскольку и вес и средние
и суммарные значения параметров оптимальны, то, очевидно, что «подбор» чисел aj
и bj обусловливает
оптимальное соотношение между весом организма и величиной того или иного
сердечного параметра в золотом режиме кровоснабжения организма.
В «незолотых», режимах
кровоснабжения организма все представленные j–параметры также имеют энергооптимальную
«основу». Показано, что при нормальных условиях сердце млекопитающих в покое /Burkhoff, Sagawa, 1986; Myhre et al., 1988/ и при любой физической нагрузке /Hayashida et al., 1992/ исполняет свою функцию с минимально возможными
затратами энергии. Показано /Цветков, 1993/, что расход механической энергии на
изгнание единичного объема крови из желудочков оптимален при любом уровне
нагрузки. За физиологическими пределами
работа сердца или невозможна или ее эффективность значительно снижается,
что приводит к нарушениям адекватного кровоснабжения организма. Очевидно, что
лишь в диапазоне d=1-4 обеспечивается оптимальная
деятельность сердца. Следует отметить, что чем больше d, тем менее экономна работа сердца
/Цветков, 1993, 1997/. Тем не менее, каждому значению d соответствует «свой» оптимальный режим
работы сердца. Диапазон d=1-4
предстает как интервал величины d, в котором
сохраняется энергооптимальное соотношение между «возможностями»
сердечно-сосудистой системы организма и допустимыми пределами физической
нагрузки.
В покое
«противоположности» в рассматриваемых ССЦ
разделяются в соотношении 0,382:0,618. Золотое сечение представляет наиболее
энергоэкономное с точки зрения энергетики сопряжение «противоположностей» в
сердечном цикле. В золотом режиме сердце функционирует с наибольшей
эффективностью /Цветков, 1993, 1997/.
Таким образом, мы могли
убедиться, что все «голые» числа в законе (2.7) имеют оптимальное
«обоснование», что указывает на их особую роль в организации
оптимальной, наиболее эффективной, деятельности сердца млекопитающих.
«Вхождение» этих чисел в «пространство» ССЦ обеспечивает энергооптимальную гармонию
деятельности сердца в золотом режиме кровоснабжения организма. Следует в связи
с этим указать на весьма важные, по нашему мнению, теоретические соображения о «качестве» особых
чисел, их роли в организации окружающего
нас мира, представленные в работах Г.Б.Аракеляна (1981) и М.А.Марутаева (1990).
2.1.4.
Энергооптимальность «противоположностей» ССЦ в условиях нагрузки
Отметим, что оптимальной композицией ССЦ при
физической нагрузке является такая композиция, при которой исполнение функции
сердца сопряжено с минимально возможным для заданного уровня нагрузки расходом
механической энергии. Эффективность работы сердца определяется как отношение
производимой механической работы к объему потребляемого кислорода. При любом
режиме гипертензии, связанном с физической нагрузкой, средние и суммарные
значения ССЦ энергооптимальны. Показано /Цветков,
1986, 1993, 1994/, что во всех режимах гипертензии имеют место оптимальные
значения среднего аортального давления и среднего кровотока. Потребление
энергии сердцем всегда минимально в том случае, если конечнодиастолический и
ударный объем объемы левого желудочка равны их естественным величинам для
данного режима сокращений. Поскольку при нагрузке и минутный выброс /Образцов,
Ханин, 1989/ и ударный объем /Muhre et al., 1988/ энергооптимальны, то естественно, что для любого
уровня нагрузки оптимальна и длительность сердечного цикла.
Рассмотрим оптимальность «вхождения» фазовых
составляющих в структуры сердечных циклов. Предварительно отметим, что между
утилизацией кислорода, синтезом молекул АТФ и потреблением энергии в сердечных
клетках в естественных условиях существует линейная зависимость
/Ленинджер, 1974; Coulson, 1979/. Установленно /Bache et al., 1970; Buckberg et al., 1975/, что при искусственной электрической стимуляции
механическая работа сердца остается неизменной и равной естественной величине
до стимуляции. В то же время потребление кислорода при возрастании
стимулированного сердечного ритма возрастает (минимальное значение при
естественной частоте сердцебиений) /Laurent et al., 1956; Vinten-Johansen et al.,
1980/. При электрической стимуляции долевой временной состав сердечных циклов
соответствует их естественному составу при той же частоте /Бабский,
Ульянинский, 1961/. Следовательно, естественный долевой состав
«противоположностей» (длительностей систолы и диастолы) обусловливает
минимальный расход химической энергии АТФ по отношению к неизменной
механической работе сердца (постоянное давление и сердечный выброс за минуту).
Этот феномен отражает энергооптимальность фазового состава временных
ССЦ при естественном изменении
сердечного ритма при нагрузке.
Сохраняя естественными
уровень кровоснабжения организма и частоту сердцебиений, давление в аорте можно менять за счет вариации
периферического давления (эффект Анрепа). При этом
установлено /Sarnoff et al.,
1958/, что минимальное потребление кислорода сердечной мышцей имеет место при
естественном периферическом сопротивлении, т.е. при естественном среднем
давлении и его долевом составе. Следовательно, в условиях нагрузки минимальный
расход химической энергии АТФ имеет место при естественной для этого уровня нагрузки композиции
механической ССЦ.
Сравним изменения работы сердца по
изгнанию крови и работы на перфузию сердечной мышцы за минуту при росте частоты
электрической стимуляции. Первая работа остается неизменной, в то время как
вторая возрастает за счет увеличения среднего коронарного кровотока /Laurent et al., 1956; Vinten-Johansen, 1980; Новикова. 1980/. Очевидно, что
минимальная работа по перфузии коронарных сосудов имеет место тогда, когда
электроритм совпадает с естественным ритмом. Следовательно, минимальные затраты
энергии на перфузию для всякого уровня физической нагрузки соответствует
естественной, оптимальной композиции кровотоковой ССЦ.
Как уже было отмечено
выше, одна и та же работа по изгнанию постоянного объема крови из левого
желудочка при постоянном сердечном ритме и среднем давлении в аорте
сопровождается минимальным потреблением «сердечного» кислорода в том случае,
когда соотношение между изгнанной и оставшейся кровью в желудочке равно
естественному /Suga,
1979/. Следовательно, при всякой нагрузке минимальные затраты химической
энергии АТФ на изгнание единичного объема крови из желудочков имеют место при естественной
композиции объемной ССЦ.
Таким образом, минимальные затраты «сердечной»
химической энергии на обеспечение адекватного кровоснабжение организма
млекопитающих имеют место в том случае, когда композиции временной,
механической, объемной и кровотоковой ССЦ соответствуют их естественным
аналогам. Коэффициент полезного действия (КПД) сердца равен отношению ударной
механической работы к количеству химической энергии, выделенной в сердечных
клетках при утилизации кислорода за одно сокращение. Теоретически
и экспериментально показано, что при нормальных физиологических условиях КПД
сердца максимален и составляет 18-20% /Burkhoff, Sagawa, 1986/. Можно сказать, что всякая «естественная»
ССЦ «пространства» (2.7) оптимальна дважды: 1) за счет оптимальности величин ее
элементов по отношению к весу животного и 2) за счет оптимального соотношения
между ее элементами в покое и при физической нагрузке. За счет этих
факторов обеспечивается наиболее эффективная работа сердца млекопитающих.
Подытожим. Нами было проанализирована
гармония «противоположностей» в структурах сердечного цикла. Оптимизация ССЦ
как бы происходит в два этапа. Первый этап – подбор энергооптимальных средних и
суммарных значений параметров по отношению к весу животного, второй этап –
энергооптимальное разделение «противоположностей» внутри ССЦ. Очевидно, что
гармония противоположностей в каждой отдельной ССЦ «подобрана» Природой таким
образом, что именно при таком «раскладе» (и никаком другом!) обеспечивается
минимальность затрат «сердечной» энергии. Оптимальное сопряжение «противоположностей»
в покое и при нагрузке обусловлено золотым сечением, его замечательными
свойствами. Количественную меру гармонии ССЦ составляют величины nS(δ) и nd(δ).
Согласно определения системы по Ю.А. Урманцеву /Урманцев, 1974/,
первичными элементами «пространства» ССЦ являются отдельные ССЦ, отношением
единства между ними – функционирование сердца, законом композиции – выражение (2.7). «Вхождение» всякой ССЦ совместно с другими
при одном и том же уровне нагрузки отдельного животного в совокупность ССЦ этой
особи обеспечивает минимальность затрат энергии на исполнение функции сердца.
Минимальность затрат энергии с ростом нагрузки возрастает. Нами в работах
/Цветков, 1993, 1997, 2004/ был выдвинут критерий организации
кардиосистем различной сложности – принцип оптимального вхождения. Суть этого
принципа заключается в следующем: Всякая сердечная система
совместно с другими включается в более сложную кардиосистему оптимальным
образом, вследствие чего последняя исполняет свою функцию с минимальными
затратами энергии и строительного материала. Согласно современному представлению, «гармония – соразмерность частей и
целого, слияние различных комплексов объекта в единое органическое целое»
/Лосев, 1971, т. 6, с. 128/. Очевидна некоторая аналогия между определением
понятия гармония и принципа оптимального вхождения, т.к. «слияние различных
комплексов объекта в единое органическое целое» подразумевает их вхождение в
систему. Из проведенного выше анализа «пространства» ССЦ следует: принцип
оптимального вхождения является критерием гармонии всех ССЦ, составляющих эту
систему. Неизменная экономия энергии, сопутствующая «вхождению» каждой ССЦ
в «пространство» (2.7) является условием энергооптимальной гармонии этого
«пространства».
2.2.
Золотое сечение и «эстафета противоположностей» в сердечных процессах
Как правило, «золотая» точка раздела отдельного
сердечного цикла является границей перехода системы в качественно новое
состояние. В кардиоцикле главенствующей «противоположностью», несомненно,
является систола. За систолу сердце потребляет 91% кислорода от общего
количества за сердечный цикл, а за диастолу - только 9% /Monroе, 1964/.
Очевидно также, что объем сердечной мышцы в основном определяется ее работой во
время систолы. Систолическая часть временной ССЦ является «системой», состоящей
из своих временных «элементов». Такими элементами для систолической части
являются длительности напряжения мышечных волокон в течение отдельных фаз
систолы (рис. 2.2). Напряжению мышечных
волокон миокарда в течение систолы
соответствуют следующие активностные состояния: 1) интервал асинхронного напряжения (0-1); 2) интервал
синхронного напряжения (1-2); 3) интервал сокращения (2-3). С активностной
точки зрения первые два интервала соответствуют фазе напряжения при
постоянной длине волокон, а третий -
фазе напряжения при укорочении волокон. С
функциональной точки зрения первые два интервала приходятся на фазу
подготовки к изгнанию крови из желудочков, а третий временной интервал
соответствует фазе изгнания. Для человека интервал асинхронного напряжения, интервал синхронного напряжения,
фаза напряжения при неизменной длине мышечных волокон, интервал сокращения 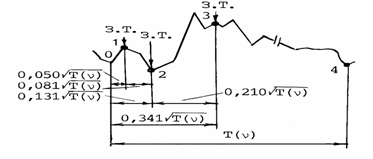
Рис. 2.2. Динамокардиограмма
человека./Цветков, 1984/. υ - частота сердцебиений; T(υ) – длительность сердечного цикла
при частоте υ Активностные состояния сердечной мышцы: 0-1
– интервал асинхронного напряжения; 1-2 – интервал синхронного напряжения; 0-2
– фаза напряжения при постоянной длине мышечных волокон; 2-3 – интервал
мышечного сокращения; 0-3 – длительность систолы; 0-4 – длительность
кардиоцикла. З.Т. – золотые точки интервалов 0-2 (т. 1), 0-3 (т. 2), 0-4 (т. 3
делит сердечный цикл по золотому сечению только при υ= υЗС).
и
длительность систолы соответственно равны /Бабский, 1957; Бабский,
Карпман, 1963; Цветков, 1984а/: 0,050![]() , 0,081
, 0,081![]() , 0,131
, 0,131![]() , 0,210
, 0,210![]() , 0,340
, 0,340![]() , где υ - частота сердцебиений; T(υ)
- длительность сердечного цикла, соответствующая частоте υ . Очевидна аналогия представленного ряда длительностей
числам классического ряда Фибоначчи - 5, 8, 13, 21, 34.
, где υ - частота сердцебиений; T(υ)
- длительность сердечного цикла, соответствующая частоте υ . Очевидна аналогия представленного ряда длительностей
числам классического ряда Фибоначчи - 5, 8, 13, 21, 34.
Предварительно рассмотрим ряды (последовательности)
золотых чисел. Золотое сечение для единичного отрезка можно представить в виде
пропорции
0,382:0,618=0,618:1 =0,61803…
Долевой состав единичного отрезка при таком делении
0,382+0,618=1.
В
соответствии с этими соотношениями единичный отрезок в свою очередь является
меньшей частью для следующего «золотого деления»: 1:1,618=1,618:2,618=0,618.
Такую последовательность можно продолжать до бесконечности, в результате чего
имеем ряд «золотых» чисел: …0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854;
11,090... Он одновременно представляет собой геометрическую прогрессию, в
которой всякое число ряда больше предыдущего в 1,618 раз, и аддитивный
рекуррентный ряд чисел, в котором каждое
число равно сумме двух предыдущих. Очевидно, что свойства геометрической
прогрессии и рекуррентности сохраняются для всякого другого ряда:
0,382A,
0,618A, А, 1,618А, 2,618А, 4,236А, 6,854А, 11,090А,… (12)
где А может иметь любую
величину и размерность (см, см3, сек, г, кал и т.д.). Двигаясь слева направо, получаем последовательность (2.12), которая
обозначается как восходящий ряд золотых чисел. Очевидно, что, расположив
ряд (2.12) в обратной последовательности, можно получить нисходящий ряд
золотых чисел
11,090А, 6,854А, 4,236А,
2,618А, 1,618А, А, 0,618A, 0,382A, … (2.13)
Покажем, последовательное
деление систолы точками фазовых переходов аналогично ряду (2.12). Фазу
напряжения при постоянной длине сердечных волокон составляют длительности
«противоположных» интервалов асинхронного
и синхронного напряжения,
0,050![]() + 0,081
+ 0,081![]() = 0,131
= 0,131![]() .
(2.14)
.
(2.14)
Аналогично всю систолу в целом можно
подразделить на два противоположных состояния: напряжение при постоянной длине
волокон и напряжение при укорочении
волокон. Длительность систолы состоит из временных интервалов
напряжения мышечных волокон при
постоянной длине и укорочения. Закон композиции временных «противоположностей»
всей систолы,
0,050![]() + 0,081
+ 0,081![]() = 0,131
= 0,131![]() .
(2.15)
.
(2.15)
Из выражений (2.14) и (2.15) очевидно, что
в каждой из представленных временных систем смена «противоположных» состояний мышцы
происходит в точке, которая делит
длительность интервала по пропорции золотого сечения. В
(2.14) и (2.15) представлена эстафета «временных» золотых сечений по всей
систоле в соответствии с восходящим
рядом (2.12): 0,050![]() , 0,081
, 0,081![]() , 0,131
, 0,131![]() , 0,340
, 0,340![]() . В этом ряду представлена эстафета золотых сечений
систолы. Для систолы «золотые» соотношения между противоположными состояниями не зависят от длительности сердечного
цикла и сохраняются при любой частоте сердцебиений. «Золотое» временное
разделение основных «противоположностей» сердечного цикла - систолы и диастолы
– имеет место только при золотом сердечном ритме (ν=νЗС).
Отметим, что в золотом режиме изгнание единичного объема крови происходит при
минимальном расходе энергии /Цветков, 1997/, т.е. имеет место энергооптимальная
гармония «противоположностей». По аналогии с основным делением
«противоположностей» с большой степенью вероятности можно предположить, что в
основе золотых «противоположностей» систолы также лежит энергооптимальная
гармония. Сердечная мышца в течение систолы работает с минимальным
потреблением энергии.
. В этом ряду представлена эстафета золотых сечений
систолы. Для систолы «золотые» соотношения между противоположными состояниями не зависят от длительности сердечного
цикла и сохраняются при любой частоте сердцебиений. «Золотое» временное
разделение основных «противоположностей» сердечного цикла - систолы и диастолы
– имеет место только при золотом сердечном ритме (ν=νЗС).
Отметим, что в золотом режиме изгнание единичного объема крови происходит при
минимальном расходе энергии /Цветков, 1997/, т.е. имеет место энергооптимальная
гармония «противоположностей». По аналогии с основным делением
«противоположностей» с большой степенью вероятности можно предположить, что в
основе золотых «противоположностей» систолы также лежит энергооптимальная
гармония. Сердечная мышца в течение систолы работает с минимальным
потреблением энергии.
Рассмотрим «эстафету» золотых сечений в
точках «качественного» перехода при наполнении и опорожнении предсердий и
желудочков. Показано /Toma et al., 1987/, что за
интервал раннего наполнения в левое
предсердие человека поступает 37%, а в фазу позднего наполнения - 63% от общего
количества крови, поступившей в предсердие за интервал закрытого митрального клапана; это
соотношение практически соответствует
золотому сечению. Границей раздела «противоположных» состояний (раннего и
позднего наполнения) служит момент, в который прекращается падение и начинается
рост давления в левом предсердии. Следует отметить, что максимальный и минимальный объем обоих
предсердий и их разность в течение сердечного цикла также приблизительно
составляют золотую пропорцию /Tsarikis et al., 1977/. Через
открытый митральный клапан в течение
времени, когда предсердие представляет
собою трубку, открытую с двух сторон, в левый желудочек поступает 58% крови от общего количества, а остальные
42% - в течение систолы предсердия /Grant et al., 1964/. Соответственно, фазу изгнания крови из
желудочков можно разделить на два
противоположных периода - возрастающего и
редуцированного изгнания. Период возрастающего изгнания для левого желудочка начинается в момент подъема
давления в аорте и заканчивается в
момент, приблизительно соответствующий
максимальному давлению в желудочке; конец замедленного изгнания соответствует началу резкого подъема давления
в аорте. Установлено /Vrettos, Gross,
1994/, что естественной форме кривой изгнания для желудочков соответствует
минимальная мощность выброса единичного объема крови. Показано /Цветков, 1993/, что объемы крови,
изгнанные за период возрастающего и
период редуцированного изгнания, соотносятся между собою по пропорции золотого
сечения. Следует напомнить, что в покое отношение объема изгнанной крови, объема
оставшейся крови и конечнодиастолического объема желудочков приблизительно соответствует золотой пропорции /Holt et al., 1962; Holt et al., 1968/. Итак, в покое
«объемная» картина наполнения и опорожнения предсердий и желудочков,
представленная по принципу «противоположностей» в этих процессах, неизменно связана с пропорцией
золотого сечения. Установленные
соотношения позволяют представить процесс
наполнения и опорожнения предсердий и
желудков как гармонию «золотых» противоположностей
Установлено /Vrettos, Gross, 1994/,
что естественной форме кривой изгнания для желудочков соответствует минимальная мощность выброса
единичного объема крови. В течение систолы желудочки находятся в двух
противоположных состояниях: замкнутом
(подготовка к изгнанию) и открытом (изгнание
крови). В момент размыкания полулунного клапана в
аорте давление в левом желудочке
составляет 62% от максимального /Цветков, 1993/
(рис. 2.3). Следовательно, соотношение
между минимальным и максимальным
давлениями в аорте соответствует золотому сечению; это соотношение сохраняется
при любом уровне физической нагрузки.
Поскольку величины среднего давления в аорте, как было показано выше, равны
энергооптимальным значениям во всех режимах кровоснабжения, то и гармония
максимального, минимального и пульсового давлений в аорте имеет оптимальную основу.
|
|
Рис. 2.3. Кривая
давления в аорте. υ
- частота сердцебиений; p(υ,t)
- мгновенное значение давления, P(υ) -
максимальное давление в течение фазы
изотонического напряжения, P*(υ)max
- максимальное давление в левом
желудочке в течение фазы изометрического
напряжения, DP(υ) - пульсовое
давление при частоте сердцебиений
Итак, рассмотренные временные, объемные
и механические цепочки «противоположностей» неизменно связаны с пропорцией
золотого сечения. Форма их временного и пространственного «пересечения»,
естественно, не случайна и имеет энергооптимальную основу.
2.3. Золотые «противоположности» в процессах
аккумуляции и
рассеяния
энергии
Рассмотрим каскад
последовательных «золотых» преобразований световой энергии в растительных и
животных клетках. Процесс расхода энергии, поступающей в растительные и
животные клетки, происходит в двух качественно различных формах: 1) аккумуляция
в энергосвязывающих химических образованиях и 2) тепловое рассеяние. Необходимо
отметить, что непосредственное измерение аккумулируемой и тепловой энергии в
интактных клетках до сих пор
представляет большие трудности. По этой причине нами проанализированы процессы
аккумуляции и рассеяния для реакций, протекающих в стандартных условиях (рН
7,0, температура 37оС, избыток Mg2+,
Баланс энергии в растительной клетке. Расход энергии световых квантов в
растительных клетках происходит в 2-х качественно «противоположных» формах: 1)
рассеяние в виде тепла и 2) консервация в химических образованиях - углеводах.
Для синтеза одной молекулы гексозы из 6 молекул СО2
необходимо 48 световых квантов. 48 квантов соответствуют 1920 ккал, т.к.
возбужденный хлорофилл при длине волны 700 нм испускает световые кванты с
энергией примерно 40 ккал. Стандартная свободная энергия для синтеза молекулы
гексозы из СО2 и воды равна DGo/=686
ккал/моль, следовательно, энергия, рассеиваемая при этом в виде тепла,
составляет 1234 ккал/моль. Соответственно, доли световой
энергии, расходуемой в клетке на синтез гексозы и тепло, составляют 686/1920= 0,36 и 1234/1920=0,64; эти
величины весьма близки к «золотым» величинам - 0,38 и 0,62 (отклонение составляет ~5% и соответствуют
экспериментальным данным ./Asawa,
1994, р. 553/.
Гидролиз молекулы глюкозы. В животных клетках энергия, выделяемая при гликолизе
глюкозы, частично рассеивается в виде тепла, остальная сохраняется в химически
связанной форме в молекулах АТФ. Уравнение полного окисления глюкозы до СО2 и воды в процессе гликолиза и через цикл трикарбоновых
кислот можно представить в следующем виде
Глюкоза+6О2+36Фн+36АДФ![]() 6СО2+36АТФ+42Н2О
6СО2+36АТФ+42Н2О
Экзергонический компонент
Глюкоза+6О2 ![]() 6СО2+6Н2О DGo/=-686
ккал/моль
6СО2+6Н2О DGo/=-686
ккал/моль
Эндергонический компонент
36Фн+36АДФ ![]() 36АТФ+36Н2О DGo/=+263
ккал/моль
36АТФ+36Н2О DGo/=+263
ккал/моль
Таким образом, энергия, выделившаяся при гидролизе
молекулы глюкозы, распределяется в следующем соотношении «противоположностей»:
аккумуляция в АТФ - 263/686=0,383 и рассеяние в виде тепла 423/686=0,617, что соответствует пропорции золотого сечения.
Стандартная
свободная энергия гидролиза АТФ. Стандартная свободная энергия гидролиза АТФ DGo/АТФ составляет
DGo/АТФ=-7,3 ккал/моль.
Для гидролиза концевой фосфатной группы аденозиндифосфата (АДФ) при рН
7,0 значение стандартной свободной энергии
АДФ+Н2О ![]() АМФ+Фн
АМФ+Фн
DGo/=-7,3 ккал/моль.
Отщепление последней фосфатной группы от
аденозинфосфата (АМФ) характеризуется величиной стандартной DGo/
АМФ+Н2О ![]() Аденозин+Фн
Аденозин+Фн
DGo/=-3,4 ккал/моль
Таким образом, при гидролизе АТФ до аденозина
суммарное выделение свободной энергии составляет
DGo/=
-7,3+(-7,3)+ (-3,4)=-7,3+(-10,7)=-18 ккал/моль.
Энергетический «заряд» Е системы АТФ – АДФ – АМФ, характеризующий долю
энергии, используемой на исполнение химических процессов в клетке, можно
определить из отношения
Е = ([АДФ] + 2[АТФ])/2([АМФ] + [АДФ] + [АТФ])
где [АМФ], [АДФ], [АТФ] – соответственно концентрации
молекул АМФ, АДФ и АТФ в клетке. Величина Е = 0,611, что практически совпадает с золотым
числом 0,618.
Таким образом, на всем пути
преобразования световой энергии имеет место золотая гармония энергетических
«противоположностей». Преобразование
световой энергии на пути от растительной клетки до молекул аденозинтрифосфата
(АТФ) происходит в соответствии с нисходящим рядом золотых чисел (2.13): 1234, 686, 263, 162,5, 100,5. Можно сказать, что во всей рассмотренной
последовательности биохимических процессов энергия расходуется в одном и
том же, «золотом», отношении. Аккумуляция энергии в химических образованиях или макроэргических связях АТФ неизменно
составляет приблизительно 38%; остальные 62% рассеиваются в виде тепла
или составляют базовый запас энергии. Имеет место своего рода «золотой каскад»
дробления световой энергии на всем пути преобразований, начиная от молекулы
гексозы в растительных и кончая гидролизом молекул АТФ. Аккумулируемая часть
энергии представляет собой свободную энергию, используемую для протекания
биохимических процессов в клетках; эта часть является наиболее важной,
доминирующей частью общей энергии. Рассеиваемая, тепловая, часть энергии, также
имеет важное значение. Эта часть расходуемой энергии
обеспечивает создание в клетках температурных условий (36,6оС),
наиболее благоприятных для протекания биологических процессов /Тринчер, 1965;
Колясников, 1995/. Протекание биологических процессов при температуре 36,6оС
происходит с
минимальным потреблением энергии. Таким
образом, и в этом случае можно считать, в основе преобразования световой
энергии лежит золотая энергооптимальная гармония.
В заключение необходимо отметить, что
«золотое» разделение на доминирующую и вспомогательную «противоположности»
присуще многим сложным процессам. В частности, нами установлено золотое
соотношение противоположностей в циклах сердечных параметров, соответствующих
покою организма млекопитающих /Цветков, 1993, 1997/. В каждом из этих циклов
доминирующей, систолической, «противоположности» (напряжение миокарда)
соответствует 38% от общей величины параметра, а 62% - диастолической
(расслабление миокарда), имеющей вспомогательное значение. Вследствие такого
«расклада» сердце исполняет свою функцию с минимальными затратами энергии и
строительного материала. Таким образом, можно сделать вывод о том, что
«тяготение» 38%-части энергии к доминирующей противоположности, а 62% к
вспомогательной, отнюдь не является случайностью, а напротив, может быть
представлена как закономерность. Это
своего рода золотая гармония противоположных состояний энергии на каждом
этапе ее преобразования. По-видимому, этот феномен обусловливает наиболее
энергетически оптимальный вариант распределения
расхода энергии в живых клетках.
2.4. Биофизические основы энергооптимальной
деятельности сердца
Мышечная масса сердца имеет оптимальную
конструкцию. Мускулатура левого желудочка состоит из трех слоев - двух
косых (наружный и внутренний) и один
циркуляторный (поперечный). Угол
начального наклона «косых» волокон на поверхности эндокарда составляет 52,4о /Sallin, 1969/; этот угол незначительно отличается от «золотого» угла 51,9о. Свойства прямоугольного
треугольника с углом 51,9о при основании
использовались еще в Древнем Египте при
строительстве пирамиды Хеопса /Васютинский, 1990/. Этот треугольник
обладает замечательным свойством - его
стороны соотносятся между собою по геометрической прогрессии - 1,6180,
![]() , 1,618 (или 1, 1,272, 1,618). «Косое» направление силы в
мышечных слоях задает струе крови вращательно-поступательное движение от
верхушки желудочка по направлению к полулунному клапану, что значительно
сокращает время изгнания единичного объема крови. Саллин (1969), принимая форму
левого желудочка близкой к эллипсоиду
вращения, показал с учетом угла 52,4°, что ударный выброс крови при этих условиях составляет 36% от
конечнодиастолического объема. Величина
36% весьма близка к «золотой» - 38%, которая, как мы показали выше, соответствует оптимальной величине ударного
объема в покое. При угле 52,4° распределение «косой» силы F по взаимно
перпендикулярным осям желудочка происходит в «золотом» отношении: FГ @(1/1,272)F, FВ @(1/1,618)F, где Fг, Fв
- проекции силы F на горизонтальную и вертикальную оси желудочка. При естественной конфигурации
сердца и при естественной нагрузке выброс ударного объема крови происходит при
минимальном потреблении кислорода /Suga, 1979/. Следовательно, 52,4° является оптимальным углом, при котором выброс адекватного количества крови происходит с минимальными
затратами энергии. Таким образом, и на этом уровне очевидна роль золотых чисел
в организации энергооптимальной деятельности сердца.
, 1,618 (или 1, 1,272, 1,618). «Косое» направление силы в
мышечных слоях задает струе крови вращательно-поступательное движение от
верхушки желудочка по направлению к полулунному клапану, что значительно
сокращает время изгнания единичного объема крови. Саллин (1969), принимая форму
левого желудочка близкой к эллипсоиду
вращения, показал с учетом угла 52,4°, что ударный выброс крови при этих условиях составляет 36% от
конечнодиастолического объема. Величина
36% весьма близка к «золотой» - 38%, которая, как мы показали выше, соответствует оптимальной величине ударного
объема в покое. При угле 52,4° распределение «косой» силы F по взаимно
перпендикулярным осям желудочка происходит в «золотом» отношении: FГ @(1/1,272)F, FВ @(1/1,618)F, где Fг, Fв
- проекции силы F на горизонтальную и вертикальную оси желудочка. При естественной конфигурации
сердца и при естественной нагрузке выброс ударного объема крови происходит при
минимальном потреблении кислорода /Suga, 1979/. Следовательно, 52,4° является оптимальным углом, при котором выброс адекватного количества крови происходит с минимальными
затратами энергии. Таким образом, и на этом уровне очевидна роль золотых чисел
в организации энергооптимальной деятельности сердца.
Майром с соавт. /Myhre et al., 1988/ было установлено, что в
нормальных, естественных условиях правый и левый желудочки работают в
оптимальном режиме, т.е. при максимальном выделении мощности на нагрузке -
артериальной системе. В этом
случае имеет место энергооптимальная гармония между
«противоположностями»: производством механической энергии и
ее потреблением на нагрузке. Основу экономии энергии составляют
следующие факторы. Показано /Kenner, 1986/,
что максимальная энергия выделяется на
нагрузке в том случае, когда внутреннее сопротивление насоса (сердца) и сопротивление нагрузки
(артериальная система) равны; это соотношение реализовано в кардиоваскулярной
системе. Максимальному
выделению мощности на нагрузке способствует то обстоятельство, что коэффициенты растяжимости стенок левого
желудочка и аорты одинаковы /Little,
Cheng, 1991, Suginawa et al.,
1985/. Аорта геометрически подобна каналам, в которых движение жидкости
происходит с минимальными потерями
энергии /Роева, 1980/. Внутренняя поверхность левого желудочка (сосочковые мышцы и трабекулярный
аппарат) образуют спиральную структуру /Углов и др., 1984/, которая закручивает
струю крови, придавая ей вращательно-поступательное движение. За счет
этого обстоятельства сокращается время изгнания единичного объема крови без
дополнительных затрат мышечной ткани. Таким образом, оптимальное сопряжение сердца с нагрузкой за
счет перечисленных факторов позволяет сэкономить дополнительное количество
потребляемой энергии и мышечного
материала.
Сердце включает в себя кроме мышечных
волокон элементы, непосредственно не производящие механической работы (сосуды
с кровью, проводящая и нервная системы и
т.д.). Отмечено практически линейное
отношение между весом сердца млекопитающих и количеством мышечных волокон /Prothero, 1979/; следовательно, у всех животных можно считать постоянным соотношение весов мышечных
и «вспомогательных» тканей сердца независимо от веса организма. Объем мышечной
ткани по отношению к общему объему сердечных тканей составляет 37% (личное сообщение акад. РАМН В.А.Ткачука). В этом
случае снова имеет место сопряжение «противоположностей» по золотому сечению.
По-видимому, это отношение также имеет
оптимальную природу и его следует считать инвариантной величиной для всех
млекопитающих.
Интересно отметить также следующее обстоятельство. Установлено /Кирьянов, 1990/,
что веса стенки левого желудочка и межжелудочковой перегородки, а также
межжелудочковой перегородки и стенки правого желудочка, млекопитающих соотносятся
между собою как числа Фибоначчи (3:2).
Вес межжелудочковой перегородки является среднегеометрической величиной между
весами левого и правого желудочков. Можно утверждать с большой степенью
вероятности, что и для «верхней» части сердца (предсердий) следует ожидать аналогичного, «золотого», соотношения между
весами стенок левого и правого предсердий и их перегородки. По-видимому,
соотношения по числам Фибоначчи между стенками желудочков и межжелудочковой
перегородкой, а также для их предсердечных аналогов, обеспечивают оптимальное сопряжение
между работой левого и правого желудочков, а также левого и правого предсердий,
а в целом оптимальное сопряжение работы левого и правого сердец. В
фибоначчиевых соотношениях представлено энергооптимальное сопряжение
всех камер сердца млекопитающих. В целом такое сопряжение является еще одним
аспектом экономии энергии и мышечного вещества. Оно является еще одним
энергооптимальным инвариантом сердца млекопитающих.
Итак, налицо цепочка золотых
оптимальностей на мышечных слоях, сердечной мышце, камерах сердца, системе
«желудочек-нагрузка». Эта цепочка является своего рода иллюстрацией к представленному нами принципу
оптимального вхождения. Принцип оптимального вхождения является критерием
энергооптимальной гармонии. Мы могли убедиться, что природа экономит на всех
уровнях «мышечных» систем независимо от их сложности. Нельзя не вспомнить при этом, что еще Аристотель говорил, что
природа не делает при помощи большего, если это же можно сделать при помощи
меньшего! В этой связи необходимо еще
раз указать на важнейшую роль в этом феномене золотого сечения и чисел
Фибоначчи.
2.5. «Цена» изгнания единичного объема крови
Покажем, что золотой режим
кровоснабжения организма является для
сердца самым экономичным по отношению к затратам механической мощности на изгнание единичного объема крови.
Исполняемая сердцем механическая работа приходится на фазу изгнания крови из
желудочков. Механическая (ударная)
мощность A(νЗС), производимая в течение фазы изгнания, вычисляется в золотом режиме по следующей
формуле
A(νЗС ) = (1/t*S(υЗС))![]() q*(υЗС,t)q*(υЗС,t)dt, (2.16)
q*(υЗС,t)q*(υЗС,t)dt, (2.16)
где t*S(υЗС)
- длительность фазы изгнания, q*(υЗС,t), q*(υЗС,t) - мгновенные
значения объемной скорости изгнания крови из желудочка и давления в левом желудочке во время фазы
изгнания при частоте υЗС.
Для левого желудочка в некотором режиме
кровоснабжения (при физической нагрузке)
по отношению к золотому режиму /Цветков, 1993/
t*S(υ) = t*S(υЗС)/![]() . (2.17)
. (2.17)
В аналогичных характерных
точках кардиоциклов, соответствующих
частотам nЗС и n /Цветков, 1993/:
p*(υ,t) = ![]() p*(υЗС,t),
(2.18)
p*(υЗС,t),
(2.18)
q*(υ,t)= ![]() q*(υЗС,t).
(2.19)
q*(υЗС,t).
(2.19)
Исходя из предварительных условий
(2.17)-(2.19),
A(υ) = ![]() A(υЗС), (2.20)
A(υЗС), (2.20)
где A(υ) -
ударная работа сердца в заданном режиме кровоснабжения при частоте сердцебиений υ.
Величина объема крови, выброшенного
желудочком за одно сокращение при
частотах υ и υЗС,
V(υ) = ![]() q*(υЗС,t)dt, (2.21)
q*(υЗС,t)dt, (2.21)
V(υ) = ![]() q*(υЗС,t)dt = z(υЗС), (2.22)
q*(υЗС,t)dt = z(υЗС), (2.22)
где V(υЗС), V(υ) -
соответственно ударный объем крови в золотом и
заданном режимах кровоснабжения организма; из
(2.22) очевидно их равенство.
Эффективность работы сердца по отношению к его функции определяется количеством механической
энергии, затраченной на изгнание
единичного объема крови. Исходя из (2.20) и (2.22), имеем отношение, характеризующее «цену» изгнания
крови в том или ином режиме,
h(υ) = С(υ)/С(υЗС) = ![]() h(υЗС), (2.23)
h(υЗС), (2.23)
где h(υЗС), h(υ)
- соответственно «цена» изгнания единичного объема крови в золотом и заданном режимах кровоснабжения.
Поскольку δ=υ/υЗС, то (2.23) можно представить в
следующем виде,
h(δ) = ![]() h(δЗС) (2.24)
h(δЗС) (2.24)
В работах /Gregg, Fisher, 1963; Suga, 1979/
экспериментально показано, что работа сердца
энергооптимальна как в покое, так и при всяком уровне физической нагрузки. Однако, как очевидно из (2.24), «цена» оптимальности различна: в
золотом режиме (δ= δЗС=1) «цена» изгнания единичного объема крови минимальна, а при наибольшей
нагрузке (δ=4) максимальна. Энергооптимальная гармония
«противоположностей» в ССЦ в соответствии со свойствами золотого сечения
обеспечивает «экономное» изгнание крови во всех режимах кровоснабжения
организма. Наиболее экономный, золотой, режим соответствует
физиологическому покою организма. Это состояние (сон, отдых, незначительные
физические нагрузки) является преобладающим в течение жизни даже для животных,
ведущих активный образ жизни. Сердце в течение всей жизни животного в
основном работает в наиболее экономичном золотом режиме.
2.6. Гармония
«противоположностей» ССЦ
гемоартериальной системы
сердца
Обеспечение сердца кровью и кислородом
представляет замкнутый на себя цикл: 1) сокращение сердца обеспечивает
поступление крови и кислорода в сердечную мышцу и 2) утилизация кислорода в
кардиомиоцитах обеспечивает очередное сокращение сердца. Основу деятельности
системы крово-кислородного обеспечения сердца составляет взаимодействие трех
«партнеров»: 1) переносчика кислорода - крови; 2) транспортного тракта
- сосудистого русла и 3) движущего фактора - давления в аорте. С
первыми двумя «партнерами» связаны структурные аспекты системы, с третьим
-динамические.
С кровью переносятся все необходимые для
жизни клеток вещества (глюкоза, аминокислоты, жирные кислоты, соли, вода и
т.д.).Однако количество крови, протекающее через миокард, обусловлено прежде всего его потребностью в кислороде.
Транспорт кислорода - одна из важнейших функций движущейся крови. Среднее
давление в аорте рефлекторно задает уровень кровотока в коронарных сосудах, а также
уровень потребления кислорода сердечными клетками. В нашу задачу входит
рассмотреть основы гармонической взаимосвязи давления, архитектоники
коронарного русла, движущейся по нему крови и кислородного потребления в
условиях покоя и физической нагрузки в соответствии с принципом оптимального
вхождения.
Повышение артериального давления как
следствие физической нагрузки, а также других «возмущающих» факторов, принято
называть гипертензией. Связь между гипертензией и кровоснабжением организма
млекопитающих в условиях физической нагрузки можно представить отношением /Цветков, 1993/,
![]() /
/![]() =
= ![]() =
= ![]() , (2.25)
, (2.25)
где nЗС, n - соответственно частоты сердцебиений в золотом режиме кровоснабжения
организма и при некотором уровне физической
нагрузки; Q(nЗС), Q(n), ![]() ,-
,-![]() минутный выброс
сердца и среднее давление в аорте в золотом режиме кровоснабжения и при
нагрузке, δ – уровень относительного кровоснабжения организма.
Кровоснабжение сердца обусловлено величиной среднего давления в аорте. В
дальнейшем для анализа будем использовать отношение, связанное с изменением
давления /Цветков, 1993/,
минутный выброс
сердца и среднее давление в аорте в золотом режиме кровоснабжения и при
нагрузке, δ – уровень относительного кровоснабжения организма.
Кровоснабжение сердца обусловлено величиной среднего давления в аорте. В
дальнейшем для анализа будем использовать отношение, связанное с изменением
давления /Цветков, 1993/,
β =![]() =
=![]() /
/![]() (2.26)
(2.26)
Значение β представляет уровень относительной
гипертензии; для млекопитающих в естественных пределах вариации физической
нагрузки β=1-2. В качестве исходного режима гипертензии примем «золотой»
режим гипертензии, соответствующий золотому режиму кровоснабжения всего
организма (β =βЗС
=1).
Нашей задачей является установление
критерия гармонии между систолической и диастолической «противоположностями»
ССЦ параметров, составляющих основу деятельности гемососудистой системы сердца.
2.6.1. Особенности организации гемоартериальной
системы сердца
Установлено /Ross, 1967/, что форма кривых кровотока в
крупных коронарных артериях совершенно аналогична. Это
означает, что средние за сердечный цикл кровотоки в каждой из этих артерий находятся
в одном и том же отношении к их максимальным и минимальным значениям /Цветков,
1993/. Анализ показал, что в пульсирующих сосудах (крупные и средние артерии)
средние за электромеханическую систолу и диастолу значения кровотока и средний
за кардиоцикл кровоток приблизительно одинаковы. По мере перемещения
крови к сердечным cосудам меньшего диаметра пульсации
давления (а, следовательно, и кровотока) в этих сосудах все более сглаживаются;
в микрососудах (d<100 мкм) они практически затухают /Duling, Klitzman, 1980; Toyotaka et al., 1994/. Эти экспериментальные данные
позволяют судить о том, что на уровне микрососудов пульсации размеров,
кровотоков и давлений или незначительны или совсем отсутствуют. Следовательно,
и в микрососудах средние значения параметров за систолу, диастолу и сердечный
цикл также равны одной и той же величине. Следует отметить еще одно
обстоятельство – аналогию относительных изменений кровотоков во всех коронарных
артериях независимо от их калибра. Отмечена неизменность соотношений кровотоков
между ветвями левой коронарной артерии в покое и при различных уровнях
физической нагрузки /Khouri et al., 1965; Vatner et al., 1972/. Так же постоянно в покое и при
любой мышечной нагрузке соотношение кровотоков в эндо- и эпикардиальных слоях /Ball, Bache, 1976/. Не меняется отношение
кровотока в коронарном синусе к общему коронарному кровотоку /Gregg, Shiple, 1947/ и кровотоку в
левой коронарной артерии /Rayford et al.,
1959/ при изменении давления в аорте и сжатии легочной артерии.
Представленные явления возможны только в том случае, если средние за систолу, диастолу и кардиоцикл значения кровотока в
отдельном сосуде при нагрузке изменяются в одинаковой степени. Очевидно, что
феномен равенства среднесистолического, среднедиастолического и среднего
значений относится и к другим гемодинамическим параметрам отдельного сосуда
(давление, проводимость, объем, время пребывания эритроцита и т.д.).
Это обстоятельство упрощает задачу, т.е. можно не производить анализ параметра
отдельно для систолы, диастолы и сердечного цикла. В дальнейшем при
рассмотрении изменений какого-либо параметра в условиях гипертензии мы будем
использовать его среднее за сердечный цикл значение; для краткости будем
обозначать эту величину «средним значением» параметра.
2.6.2. «Стандартные» и «нестандартные» тройники
Артериальное русло сердца условно можно
разделить на «стандартный» и «нестандартный» участки. Все коронарное русло
состоит из тройников. На «стандартном» участке каждый ствол тройника
разветвляется на две несимметричных ветви; этому участку соответствуют сосуды
диаметром d>100мкм. На «нестандартном» участке (5,5<d<100 мкм) всякий сосуд делится на две приблизительно
симметричных ветви. «Стандартный» участок исполняет в основном транспортную
функцию, обмен между кровью и сердечными клетками происходит на «нестандартном»
участке и капиллярах. По аналогии будем обозначать тройники на этих участках
«стандартными» и «нестандартными».
Для нас особый интерес представляют
микрососудистые тройники, поскольку в микрососудах происходит газообмен между
кровью и тканями. Отдельный эритроцит отдает кислород, двигаясь по цепочке
микрососудов сосудов, включая капилляр. Каждые два соседних звена этой цепочки
представляют соответственно ствол и одну из ветвей «нестандартного» тройника.
Особенности архитектоники тройника в золотом режиме гипертензии можно
представить тремя коэффициентами /Шошенко и др., 1982/:
1) коэффициент ветвления
k(βЗС) = [d1(βЗС)2 + d2(βЗС)2]/dС(βЗС)2,
(2.27)
k(βЗС) = [d1(βЗС)2 + d2(βЗС)2]/dС(βЗС)2,
2) коэффициенты относительного сечения ветвей,
H1(βЗС)
= d1(βЗС)2/[d1(βЗС)2 + d2(βЗС)2],
2.28)
H2(βЗС)
= d2(βЗС)2/[d1(βЗС)2 + d2(βЗС)2],
(2.29)
где dС(βЗС),
d1(βЗС), d2(βЗС)
– диаметры ствола, 1 и 2 ветвей в золотом режиме гипертензии. В выражениях (2.27) - (2.29) представлены средние за сердечный цикл
(средние) значения диаметров микрососудов в золотом режиме
гипертензии. Для симметричных «нестандартных»
тройников /Цветков, 1993, 1997/ k=1,26, Н1=Н2=0,5.
Диаметр микрососудов (d£100 мкм) практически не изменяется как в
течение кардиоцикла, так и при гипертензии /Цветков, 1997, 2004/.
Следовательно, для каждого микрососудистого
тройника k(b)=k(βЗС)=1,26, Н1(b)=Н1(βЗС)=0,5
и Н2(b)=Н2(βЗС)=0,5
во всех режимах гипертензии.
2.6.3. Условия оптимального движения крови в отдельном
сердечном сосуде
В любом сосуде расход энергии, связанный
с движущейся кровью, разделяется на следующие составляющие /Образцов, Ханин, 1989/:1) расход энергии, теряемой в результате
вязкой диссипации; 2) расход энергии, потребляемой в связи с генерацией
клеточных элементов крови взамен погибающих;3) расход энергии,
затрачиваемой особью на передвижение в связи с необходимостью «переносить»
кровь; 4) расход энергии на метаболизм клеточных элементов крови. Затраты
энергии, представленные в 2)-4), составляют «стоимость» крови. С.Мюррей
/Murray, 1926 б/
отмечает, что четвертый фактор «стоимости» существенно меньше второго и
третьего. В дальнейшем будем обозначать энергию, расходуемую на перфузию
сосуда, «механической», а энергию, связанную со «стоимостью» крови, -
«химической».
При заданном кровотоке в
сосуде с увеличением диаметра последнего расход «механической» энергии падает,
а «химической», наоборот, возрастает. Очевидно, что для некоторого диаметра
суммарный расход энергии в сосуде будет минимальным. В соответствии с принципом
«минимальности работы», выдвинутым Мюрреем /Murray, 1926b/, заданный объемный кровоток в сердечном сосуде q связан с его диаметром d и
параметрами крови оптимальным соотношением
q/d3= (π/32)![]() ,
,
где x - вязкость
крови, b - расход химической энергии в единичном объеме крови за единицу
времени.
В соответствии с принципом
оптимального вхождения гармония энергетических «противоположностей» в коронарном
сосуде имеет место /Цветков, 2004/, если
α = l/dt = ![]() /8 = 162 с-1,
(2.30)
/8 = 162 с-1,
(2.30)
где d, l, t - соответственно диаметр и длина сосуда,
время пребывания эритроцитов в сосуде, α – коэффициент оптимальной перфузии.
В левой части
(2.30) представлены конструкционные и динамические параметры сосуда, в
правой – параметры крови. Элементом, функционально объединяющим обе части
равенства, является диаметр сосуда, поскольку параметры крови ξ и b
зависят от величины d /Цветков, 1986, 1993/.
Показателем минимальных затрат энергии в сосуде с движущейся кровью является
отношение механической и химической мощностей /Цветков, 2004/,
g(β) = WM(β)/WX(β) = 0,5, (2.31)
где WM(β), WX(β) – соответственно механическая и
химическая энергия, расходуемая в сосуде за единицу времени в некотором режиме
гипертензии. Величина g(β)=0,5 является постоянной в покое и
во всех режимах гипертензии /Цветков, 2004/. Значение g(β)=0,5 обусловливает энергооптимальную гармонию затрат
механической и химической энергии в каждом сердечном сосуде во всех режимах
гипертензии.
2.7. Гармония
«противоположностей» ССЦ на «нестандартном» участке артериального русла
2.7.1. Гемодинамические параметры «нестандартных»
тройников в режимах гипертензии
Установлено /Голубь, 1978/,
что микрососудистые тройники приблизительно симметричны, т.е. d1(βЗС)=d2(βЗС), l1(βЗС)=l2(βЗС) (рис.
2.4).
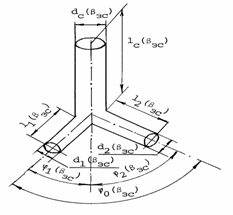
Рис. 2.4. Схема
сосудистого тройника. dC(βЗС),d1(βЗС), d2(βЗС), lС(βЗС), l1(βЗС), l2(βЗС)
- соответственно диаметр и длина ствола и 1 и 2 ветвей, j1(βЗС), j2(βЗС) - углы отклонения 1 и 2 ветвей,
j0(βЗС) - угол разветвления в золотом
режиме гипертензии.
Исходя из (2.27)-(2.29),
с некоторой погрешностью для всех «нестандартных» тройников примем k(βЗС)=1,26 и H1(βЗС)=H2(βЗС)=0,5. Рассмотрим соотношения
диаметров и длин ствола и одной из ветвей тройника (последовательных звеньев
цепочки) с привлечением коэффициентов k(βЗС)
и H(βЗС). Очевидно, что
полученные величины параметров для первой из ветвей будут те же, что и во
второй. Для оценки взаимосвязи между длиной и диаметром сосуда введем параметр
конструкции С(βЗС)=l(βЗС)/d(βЗС).
К.А.Шошенко и др. (1982) отмечает, что распределение
этого параметра по цепочке коронарных сосудов аналогично и для млекопитающих, и
для рыб, и для земноводных. Установлены особенности распределения
величины параметра конструкции при движении по цепочке по направлению к
капилляру. Так для участка цепочки, где d(βЗС)>50 мкм, С(βЗС)=3, а для участка, где d(βЗС)<50
мкм, величина С меняется от 4 до 6 (С(βЗС)=4-6). По мере
сужения сосудов величина С возрастает. Размеры
микрососудов при гипертензии практически не меняются. Естественно, что во всех
режимах гипертензии для этих сосудов параметр C1(β)=C1(βЗС),
C2(β)=C2(βЗС), CС(β)=CС(βЗС).
Представленная в книге К.А. Шошенко и др. /Шошенко и др., 1982/
экспериментальная зависимость k=f(H) позволила установить, что для
артериального участка коронарного русла k=1,10-1,20. В этой же работе авторами
теоретически доказано, что величинам 1<k£1,26в
тройниках соответствует оптимальный режим «минимальной работы», установленный
Мюрреем /Murray,
1926a, 1926b/. Очевидно, что движение крови по
артериальному коронарному руслу имеет энергооптимальную основу.
Особенность «нестандартного»
участка (d£100мкм) сердца составляют противоположно
направленные изменения вязкости крови x и параметра конструкции С при
переходе от ствола к ветвям /Цветков, 1986, 1993/,
x1(βЗС)/xС(βЗС) @ СС(βЗС)/С1(βЗС),
x2(βЗС )/xС(βЗС) @ СС(βЗС)/С2(βЗС).
Диаметр и длина сосуда при гипертензии не меняется. На
участке кривой x=f(d), соответствующем d<100 мкм, x1(b)= x1(βЗС),
x2(β)=x2(βЗС)
и xС(b)=xС(βЗС).
Соответственно, для «нестандартных», симметричных тройников имеем обратные
изменения x, l и t /Цветков, 1993/,
x1(βЗС) = x2(βЗС) = [С1(βЗС)/СС(βЗС)]xС(βЗС),
l1(βЗС) = l2(βЗС) = 0,794[СC(βЗС)/С1(βЗС)]lС(βЗС),
t1(βЗС) = t2(βЗС) = 0,794[СC(βЗС)/С1(βЗС)]tС(βЗС).
Для любого сосуда
«нестандартного» участка коэффициент оптимальной перфузии тройника одинаков
/Цветков, 2004/
αА(βЗС) = 162 с-1.
(2.31а)
В условиях гипертензии, вызванной
физической нагрузкой, происходит перестройка всего коронарного русла в целом и
его артериального участка в частности. Для анализа этих изменений разделим
артериальное русло, как и прежде, на «стандартные» (l/d=3) и «нестандартные»
(l/d>3) генерации. При анализе соотношений рассматриваемых параметров на
«нестандартном» участке будем рассматривать их значения, усредненные за
сердечный цикл. В «нестандартном» симметричном тройнике при гипертензии
(k(β)=1,26 и H1(β)=H2(β)=0,5)
гемодинамические параметры изменяются следующим образом /Цветков, 1993, 1997/,
d1(β) = d2(β)
= 0,794dC(βЗС),
(2.32)
l1(β) = l2(β)
= 0,794[C1(βЗС)/CC(βЗС)]lC(βЗС), (2.33)
ξ1(β) = ξ2(β)
= [CC(βЗС)/C1(βЗС)]ξC(βЗС), (2.34)
t1(β) = t2(β)
= [C1(βЗС)/CC(βЗС)]tC(βЗС)/β, (2.35)
q1(β) = q2(β)
= 0,5βqC(βЗС), (2.36)
ΔP1(β) = ΔP2(β) =
ΔPC(βЗС), (2.37)
b1(β) = b2(β)
= bc(β) = β2bc(βЗС), (2.38)
где ΔP1(β), ΔP2(β),
q1(β), q2(β), t1(β), t2(β),
b1(β), b2(β) -
соответственно приложенное давление, кровоток, время пребывания
эритроцита, удельное потребление химической мощности в 1 и 2 ветвях тройника в
режиме гипертензии. В условиях гипертензии коэффициент оптимальной перфузии
αА(β) = βαА(βЗС).
(2.38а)
2.7.2. Оптимизация энергетических параметров в режимах
гипертензии
В условиях гипертензии, вызванной
физической нагрузкой, происходит перестройка всего коронарного русла в целом.
Артериальное русло условно можно разделить на «стандартные» (l/d=3) и
«нестандартные» (l/d>3) генерации. Нас более всего интересует «нестандартный»
участок, т.к. на этом участке происходят обменные процессы между кровью и
сердечными клетками.
Исходя из (2.32)
– (2.38), затраты мощности в стволе на перфузию и поддержание биопроцессов
в крови в «нестандартном» тройнике /Цветков, 1993,
1997/
WМС(β)
= β2WМС(βЗС), (2.39)
WХС(β)
= β2WХС(βЗС), (2.40)
где WМС(βЗС),
WХС(βЗС), WМС(β), WХС(β)
– соответственно суммарные затраты энергии за единицу времени на перфузию и на
процессы в крови в стволе в золотом и других режимах гипертензии.
Соответственно,
WМ1(β)
= WМ2(β) = 0,5β2WМС(βЗС), (2.41)
WХ1(β) = WХ2(β) = 0,5β2WХС(βЗС), (2.42)
где WМ1(β),
WМ2(β), WХ1(β), WХ2(β)
- суммарные затраты мощности на перфузию и процессы в крови в 1 и 2 ветвях
тройника в режиме гипертензии. Очевидно, что и в покое и при гипертензии ветви
«нестандартных» тройников по затратам энергии суммарно «воспроизводят» затраты
ствола. При этом каждая составляющая энергетических затрат в ветвях и стволе
возрастает в β2 раз по
отношению золотому режиму. Как следствие этого,
g(β) = WМ1(β)/WХ1(β)
= WМ2(β)/WХ2(β) = WМС(β)/WХС(β)
= 0,5. (2.43)
По аналогии с симметричным вариантом
ветвления «нестандартных» тройников можно показать, что и при асимметричном
варианте для «стандартных» тройников механическая и химическая мощности в
стволе, 1 и 2 ветвях возрастают в одинаковой степени – в β2 раз
/Цветков, 1997/. Следовательно, для любой генерации «стандартных» и
«нестандартных» тройников
l(β) = [W1(β) + W2(β)]/WС(β) = 1,
(2.44)
это отношение является безразмерным
энергооптимальным критерием гармонии сопряжения сердечных тройников. Другим
безрамерным энергооптимальным показателем гармонии всех тройников является
выражение /Шошенко и др., 1982/
[k(β)H1(β)]3/2+ [k(β)H2(β)]3/2 = 1. (2.45)
Это выражение характеризует энергооптимальную
архитектонику тройников.
Таким образом, во всех
«стандартных» и «нестандартных» тройниках артериального русла имеют место одни
и те же условия: 1) оптимальное отношение g(β)=0,5 остается
неизменным для любого сосуда при любом уровне гипертезии; 2) оптимальная
величина l(β)=1 и [k(β)H1(β)]3/2+[k(β)H2(β)]3/2
=1 неизменны для всех тройников при всяком уровне гипертензии. Если g(β)=0,5 отражает
гармонию «противоположных» энергий (механической и химической) в каждом
артериальном сердечном сосуде, то l(β)=1 и [k(β)H1(β)]3/2+
[k(β)H2(β)]3/2 = 1 представляет гармонию
энергооптимального вхождения ствола и ветвей в единое целое – тройник. Эти
величины являются энергооптимальными критериями гармонии всех артериальных
тройников при любом уровне нагрузки. Организация «сердечного» дерева как
совокупности оптимальных тройников позволила в итоге получить максимально
экономную систему транспорта крови и кислорода.
2.8. Микроциркуляторное «пространство» ССЦ и его
особенности
Рассмотрим прекапиллярные генерации
микрососудов. Установлено, что кислород начинает поступать в ткани из этих
сосудов /Иванов и др., 1979, Duling
et al.,
1979/. Архитектоника микроциркуляторного участка
различных видов млекопитающих аналогична. На это обстоятельство указывают
многие исследователи. Каро /Каро и др., 1981/ обращает
внимание на поразительное сходство размеров мелких сосудов млекопитающих несмотря
на значительное различие по массе тела. К.А.Шошенко /Шошенко и др.,
1982/ отмечает аналогию отношений l/d для коронарных артерий различных
видов млекопитающих. Ветвления терминальных обменных артериол
близки к симметричным (H1=0,5, H2=0,5, k=1,26) /Голубь,
1978/. Отметим еще одну важную особенность - размеры терминальных сердечных
артериол практически постоянны в течение сердечного цикла /Toyotaka et al., 1994/. Можно считать, что в любом m-сосуде
рассматриваемой нами микроциркуляторной части цепочки начиная от
капилляра, величины ΔPm(βЗС), dm(βЗС), lm(βЗС) и ξm(βЗС) постоянны в течение всего
кардиоцикла. Естественно, что не меняются во время сердечного цикла и
производные от вычислений с использованием этих величин - qm(βЗС), tm(βЗС), Vm(βЗС) и Gm(βЗС). Величина скорости отдачи
кислорода отдельным эритроцитом Um(βЗС)
и разности концентраций кислорода в крови m-сосуда также постоянны в течение
сердечного цикла /Цветков, 1993, 1997/.
Газообмен между кровью и тканями на микроучастке происходит на 7 прекапиллярных
генерациях /Цветков, 1993, 1997/, т.е. m=1, 2, …7.
Представленные выше параметры обозначим
общим символом Аm(βЗС),
Аms(βЗС)= Аmd(βЗС)
= ![]() ,
,
где Аms(βЗС), Аmd(βЗС), ![]() -
соответственно средние значения параметров за систолу, диастолу и сердечный
цикл в золотом режиме гипертензии.
-
соответственно средние значения параметров за систолу, диастолу и сердечный
цикл в золотом режиме гипертензии.
Необходимо установить «вклад»
систолической и диастолической составляющих в среднее за кардиоцикл значение
параметра ![]() .Средние за сердечный цикл систолические и
диастолические значения параметров в обобщенной форме,
.Средние за сердечный цикл систолические и
диастолические значения параметров в обобщенной форме,
![]() = Аms(βЗС)ts(βЗС)/T(βЗС),
= Аms(βЗС)ts(βЗС)/T(βЗС),
![]() = Аmd(βЗС)td(βЗС)/T(βЗС),
= Аmd(βЗС)td(βЗС)/T(βЗС),
где ![]() ,
, ![]() - средние за
кардиоцикл систолические идиастолические величины параметров в m-сосуде, T(βЗС),
ts(βЗС), td(βЗС) - длительность систолы,
диастолы и сердечного цикла в золотом режиме гипертензии. В обобщенном
виде для золотого режима структура сердечного цикла (ССЦ) для всякого
микроциркуляторного j-параметра,
- средние за
кардиоцикл систолические идиастолические величины параметров в m-сосуде, T(βЗС),
ts(βЗС), td(βЗС) - длительность систолы,
диастолы и сердечного цикла в золотом режиме гипертензии. В обобщенном
виде для золотого режима структура сердечного цикла (ССЦ) для всякого
микроциркуляторного j-параметра,
0,382![]() + 0,618
+ 0,618![]() =
= ![]() . (2.46)
. (2.46)
С учетом (2.8) и (2.46) при
гипертензии закон композиции ССЦ для рассматриваемых гемодинамических и
кислородных параметров на терминальном участке цепочки можно представить
обобщенным выражением /Цветков, 1997/,
0,382 βЗС![]()
![]() + 0,618 βЗС
+ 0,618 βЗС![]()
![]() = βЗС
= βЗС![]()
![]() , (2.47)
, (2.47)
где m-номер сосуда, kj -
показатель степени, соответствующий j-параметру; эта величина постоянна и не
зависит от номера сосуда.
В законе (2.47) представлено
«пространство» ССЦ рассматриваемых выше параметров. Очевидна аналогия закона
(2.47) с обобщенным законом (2.7). Вследствие полного сходства
микроциркуляторного участка всех млекопитающих очевидна независимость
параметров этого участка от веса животных. Величина
j-параметра обусловлена только порядковым номером сосуда m и величиной
β. Для конкретизации закона (2.47) рассмотрим изменение параметров ![]() по цепочке как результат
преобразования
по цепочке как результат
преобразования ![]() , т.е. при «движении» параметра от первого звена к
последующим по направлению к аорте. Это преобразование можно представить
следующим образом,
, т.е. при «движении» параметра от первого звена к
последующим по направлению к аорте. Это преобразование можно представить
следующим образом,
![]() =
= ![]()
![]()
![]() ,
(2.48)
,
(2.48)
где С1(βзс), Сm(β) - соответственно
коэффициенты конструкции первого и m-сосуда в золотом режиме гипертензии; aj
и bj -постоянные коэффициенты, соответствующие j-параметру.
При гипертензии диаметр и длина микрососудов не меняются, очевидно, что Сm(β)/С1(β) = Сm(βЗС)/С1(βЗС), km(β)Hm(β)
= km(βЗС)Hm(βЗС) =0,63 при любом уровне
гипертензии. При любой степени гипертензии
![]() =
=![]() =0,794.
=0,794.
Исходя из выражений (2.47) и (2.48), можно представить обобщенный закон композиции
микроциркуляторного «пространства» ССЦ в следующем виде /Цветков, 1993/,
0,382 βЗС![]() [(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1)
[(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1)![]()
![]() +
+
0,382 βЗС![]() [(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1)
[(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1)![]()
![]() +
+
+0,618 βЗС![]() [(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1)
[(Cm(βЗС)/С1(βЗС)]aj 0,794bj(m-1) ![]() @
@
@ βЗС![]() ((Cm(βЗС)/С1(βЗС))aj 0,794bj(m-1)
((Cm(βЗС)/С1(βЗС))aj 0,794bj(m-1) ![]() . (2.49)
. (2.49)
Нами были установлены следующие
значения величин в (2.49) /Цветков, 1997/. Величины kj, aj
и bj для сердечных параметров: давление- kj =0, aj
=0, bj =0, кровоток - kj =1, aj =0, bj
=-3, объем сосуда -kj =0, aj =1, bj
=-3, проводимость сосуда - kj =0, aj=0, bj=-3,
время пребывания эритроцита - kj =-1, aj =1, bj
=0, скорость отдачи кислорода
отдельным эритроцитом - kj =0, aj =0, bj =2,
разность концентраций кислорода - kj =-1, aj =1,
bj =2. Для m=1-2 величина Cm(βЗС)=6, для m=3-4 - Cm(βЗС)=5,
для m=4-7 - Cm(βЗС)=4,
для m<7 - Cm(βЗС)=3.
Представим конкретные
значения параметров ![]() . Величины
. Величины ![]() для некоторых
параметров представлены в разделе 4.5 (см. табл. 1). Величины, приведенные в
таблице 1, одинаковы и для систолы, и для диастолы. Естественно, что средние за сердечный цикл значения этих параметров имеют те же
значения. Вычислены значения следующих параметров
/Цветков, 2004/: давление
для некоторых
параметров представлены в разделе 4.5 (см. табл. 1). Величины, приведенные в
таблице 1, одинаковы и для систолы, и для диастолы. Естественно, что средние за сердечный цикл значения этих параметров имеют те же
значения. Вычислены значения следующих параметров
/Цветков, 2004/: давление ![]() =3,5 мм рт. ст., скорость отдачи кислорода отдельным
эритроцитом
=3,5 мм рт. ст., скорость отдачи кислорода отдельным
эритроцитом ![]() =127,6%/с, разность концентраций кислорода в крови
сосуда
=127,6%/с, разность концентраций кислорода в крови
сосуда ![]() =5,49% и время пребывания
=5,49% и время пребывания ![]() =0,037с. По известным значениям ΔP1(βЗС),
t1(βЗС), ξ1(βЗС)=1,45×10-2 Пз, d1(βЗС)=6,9×10-4см, и С1(βЗС)=6,одинаковым
за систолу и диастолу, нами получены значения
=0,037с. По известным значениям ΔP1(βЗС),
t1(βЗС), ξ1(βЗС)=1,45×10-2 Пз, d1(βЗС)=6,9×10-4см, и С1(βЗС)=6,одинаковым
за систолу и диастолу, нами получены значения ![]() для других
параметров первого звена цепочки:
для других
параметров первого звена цепочки: ![]() =41,9×10-9см3с-1,
=41,9×10-9см3с-1,
![]() =1,53×10-9см3,
=1,53×10-9см3, ![]() =9,1×10-11г-1см5с-1.
Используя эти величины и С1(βЗС)=6
в качестве исходных, можно вычислить средние значения параметров для других
звеньев цепочки.
=9,1×10-11г-1см5с-1.
Используя эти величины и С1(βЗС)=6
в качестве исходных, можно вычислить средние значения параметров для других
звеньев цепочки.
В законе (2.49), как и в
законе (2.7) можно отметить интересные особенности. В его структуре имеет место
«пересечение» двух геометрических прогрессий: 1) «золотой»: j-2 = 0,382, j-1 = 0,618, j0 = 1 и 2) х-1 , х0
, х; первая из них обладает также свойствами аддитивного ряда. Разность показателей крайних членов
обеих прогрессий равна 2. Отношение хmax /хmin =2 имеет характерную
особенность: оно соответствует отношению верхнего и нижнего значений двух соседних октав (![]() ) /Марутаев, 1990/. Таким образом, особенности композиции (2.49) связаны с
числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/. Золотое число j также
является «особым» числом.
) /Марутаев, 1990/. Таким образом, особенности композиции (2.49) связаны с
числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/. Золотое число j также
является «особым» числом.
В (2.49) отображена уникальная роль
золотого сечения в организации «противоположностей» этого «пространства», а
также представлено влияние на ССЦ уровня гипертензии
и порядкового номера звена цепочки. Числовой каркас (2.49) имеет иерархию,
сходную с «пространством» (2.7). Золотые числа 0,382 и 0,618 характеризуют
гармонию «противоположностей»; они «присутствуют» в ССЦ всех рассматриваемых
параметров в каждом из звеньев цепочки в золотом режиме гипертензии. Диапазон
гипертензии b=1-2 постоянен для любого параметра и
номера сосуда. Каждому j-параметру соответствуют свои величины kj, aj и bj. Особенностью этого «пространства»
является полная независимость величины параметров от веса животных.
В каждом члене тождества
(2.49) имеет место перемножение выражений: [(Сm(β)/С1(βЗС)]aj и 0,794bj(m-1), каждый из которых характеризует оптимальность «вхождения»
рассматриваемых параметров в «пространство» (2.49). Величины βkj+1, βkj-1 и βkj представляют гармонию оптимальных
«противоположностей» при различных уровнях гипертензии. Аналогия «пространств»
(2.7) и (2.49) заключается в том, что в основе того и другого лежит
энергооптимальное тождество (2.8). Основу микроциркуляторного «пространства»,
как и «пространства» (2.7), составляют отношения гармонии «противоположностей»,
nS(β) = 0,382β, (2.50)
nd(β) = 0,618/β, (2.51)
где nS(β), nd(β)
- соответственно отношение среднесистолической и среднедиастолической величин j-параметра, отнесенных к сердечному циклу, к среднему
за сердечный цикл значению этого параметра при различных уровнях
гипертензии.
В каждом микрососуде величины nS(b) и nd(b) являются мерой энергооптимальной гармонии
«противоположностей» при вариации уровня гипертензии. Исходя из проведенного выше анализа системы -
микроциркуляторное «пространство» ССЦ, -
очевидно, что принцип оптимального вхождения является общим критерием
гармонии «противоположностей» для совокупности всех ССЦ, составляющих эту
систему. «Архитектоническая», «гемодинамическая» и «кислородная» организация
терминального участка артериального русла сердца для различных видов
млекопитающих одинакова. По этой причине микроциркуляторные «пространства» ССЦ
для животных различного веса аналогичны, практически можно говорить об их
полном тождестве. Мы можем констатировать, что в организации
микроциркуляторного «пространства» ССЦ (2.49) участвуют те же критерии (2.50) и
(2.51), что и в организации «пространства» (2.7) всего
сердца.
2.9. «Цена» транспорта единичного объема потребляемого
кислорода
Перейдем к оценке затрат энергии на
транспорт единичного объема потребляемого кислорода по артериальному руслу. В
каждой «стандартной» i-генерации в
условиях гипертензии /Цветков, 1993/
WMi(β) = β3WMi(βЗС), (2.52)
WXi(β) = β3WXi(βЗС), (2.53)
где Wмi(βЗС), Wмi(β), Wхi(βЗС),
Wхi(β) - средняя за сердечный
цикл механическая и химическая мощность, расходуемая в i-сосуде в золотом и
заданном режимах гипертензии. Суммарный расход механической и химической
энергии за единицу времени возрастает в β3
раз как на i-генерации, так и на всей совокупности «стандартных» генераций
сосудов,
SWст(β) = β3SWст(βЗС), (2.54)
где SWст(βЗС),
SWст(β) - суммарный
расход механической и химической энергии за единицу времени на «стандартном»
участке в золотом и заданном режимах гипертензии.
Увеличение затрат энергии в β3 раз в условиях гипертензии имеет
место также и на «нестандартных» генерациях /Цветков,
1997, 2004/. На этом участке при гипертензии средние значения давления,
отнесенные к длительности кардиоцикла, во всех сосудах увеличиваются в β раз. При гипертензии «подключение» резервных
сосудов имеет следствием то, что кровоток увеличивается в β раз в основных сосудах и в β(β-1)
раз в резервных, суммарный же кровоток возрастает в β3
раз. Таким образом, расход механической и химической энергии за единицу времени
на всем «нестандартном» участке по аналогии с (2.54)
возрастает в β3 раз. Таким образом, средний за кардиоцикл расход мощности на
всем артериальном участке при гипертензии,
SW(β) = β3SW(βЗС). (2.55)
Из вышеизложенного очевидно,
что вся система докапиллярного транспорта кислорода при гипертензии расходует
мощность на перфузию и процессы в крови в β3 раз больше, чем в
покое. Средняя за кардиоцикл скорость потребления кислорода миокардом в том же
режиме гипертензии увеличивается только в β2 раз /Цветков,
1993/,
SB(β) = β2SB(βЗС), (2.56)
где SB(βЗС),
SB(β) - средняя за сердечный цикл
скорость потребления кислорода сердечной мышцей в золотом и заданном режимах
гипертензии. Исходя из (2.55) и (2.56) очевидно,
что в условиях гипертензии «цена» доставки единичного объема потребляемого
кислорода по артериальному участку возрастает в β
раз, т.е. прямо пропорционально росту гипертензии,
V(b) = SW(β)/SB(β) = bV(βЗС). (2.57)
Таким образом, можно
заключить, что энергооптимальная гармония «противоположностей» в структурах
микроциркуляторного «пространства» ССЦ обеспечивает минимальную «цену»
доставляемого кислорода.
Самая низкая «цена» транспорта единичного объема кислорода соответствует
золотому режиму гипертензии (физиологический покой организма).
2.10. Капиллярное
«пространство» ССЦ
Особенности организации капиллярного
русла, т.е. плотность расположения капилляров, строение капиллярной стенки, а
также рисунок капиллярной сети, во многом обусловлены
особенностями тканей органа /Джавахишвили, Комахидзе, 1987; Куприянов и др.,
1975; Чернух и др., 1975/. Несомненно, что для организации капиллярной сети определяющими
является и гемодинамика и газообмен. С этой точки зрения, каждый сердечный
капилляр одновременно является звеном двух цепочек сосудов – «гемодинамической»
и «диффузионной». Первая представляет последовательность артериальных сосудов,
по которой отдельный эритроцит доставляет кислород к капилляру. Вторую цепочку
составляет ряд последовательно соединенных между собою капилляров, параллельных
мышечному волокну. Таким образом, необходимо рассмотреть две системы: 1)
гемокапиллярного обеспечения и 2) капиллярно-кислородного обеспечения. В каждую
из этих систем капилляр входит в качестве отдельного элемента. Анализ первой
системы позволяет установить особенности «гемодинамического» сопряжения тройника:
терминальной артериолы (ствола) и капилляров (ветвей). Выявление количественных
взаимосвязей во второй системе открывает возможность показать особенности
«диффузионного» сопряжения цепочек сердечных капилляров и мышечных волокон. В
нашу задачу входит показать оптимальное «сцепление» архитектонических,
гемодинамических и кислородных параметров в этих системах.
Вхождение ССЦ этих
параметров капиллярное «пространство» будет представлено в законе (2.75).
2.10.1. Особенности конструкции гемокапиллярной сети
Плотность васкуляризации отдельных
регионах сердца (основание и верхушка, эндокард и эпикард, предсердия и
желудочки и т.д.) имеет существенные различия. Тем не менее, организации
капиллярного русла присущи характерные признаки, общие для всего объема
сердечной мышцы.
1. В сердечной мышце капилляры вытянуты
по ходу мышечных волокон и приблизительно параллельны
друг другу /Toborg,
1972/.
2. Размеры капилляров
одинаковы по всему объему сердца /Tomanec et al., 1986/.
3. Независимо от степени
механического сжатия диаметр, длина, площадь и конфигурация внутренней
поверхности капилляров остаются неизменными /Мчедлишвили, 1958, Tilton et al., 1979/.
4. В случае возрастания
активности сердца количество перфузируемых капилляров увеличивается /Barnard et al., 1977/.
5. Движение крови в
капиллярах имеет ламинарный характер /Регирер, 1971/.
Гемодинамические
«капиллярные» параметры связаны определенными соотношениями с изменениями
среднего аортального давления. На входе артериальной системы всегда имеет место
значительная пульсация давления. На уровне микрососудов пульсация
незначительна, а в капиллярах практически отсутствует /Каро и др., 1981/.
Эффективное гашение пульсовой волны до капилляра обеспечивается в значительной
степени за счет извитого пути артериол /Гавриш, 1984/. Максимальное сглаживание
пульсовых колебаний обеспечивает постоянство капиллярных параметров в течение
всего кардиоцикла. Как следствие этих особенностей средние значения капиллярных
параметров за систолу, диастолу и за сердечный цикл одинаковы. В дальнейшем
будем рассматривать только средние значения параметров за кардиоцикл.
2.10.2. Законы изменения капиллярных параметров в
режимах гипертензии
При гипертензии размеры капилляров и
вязкость крови в капиллярах не меняются,
dK(β) = dK(βЗС), (2.58)
lK(β) = lK(βЗС), (2.59)
ξK(β) = ξK(βЗС), (2.60)
где dK(βЗС), dK(β), lK(βЗС),
lK(β), ξK(βЗС),
ξK(β)
- соответственно диаметр, длина и вязкость крови в капилляре в золотом и
заданном режимах гипертензии. Исходя из (2.58)-(2.60),
dK(β) = dK(βЗС), (2.61)
GK(β) = GK(βЗС), (2.62)
где VK(βЗС), VK(β), GK(βЗС),
GK(β) -
соответственно объем и проводимость капилляра в золотом и заданном режимах
гипертензии.
Гемодинамические параметры в условиях
гипертензии /Цветков, 1993, 1997/,
ΔPK(β) = βΔPK(βЗС), (2.63)
dK(β) = dK(βЗС), (2.64)
tK(β) = tK(βЗС)/β, (2.65)
где ΔPK(βЗС),
ΔPK(β),
qK(βЗС),
qK(β) -
соответственно давление, приложенное к капилляру, и кровоток в нем, tK(βЗС),
tK(β) - время
пребывания эритроцитов в капилляре в золотом и других режимах гипертензии.
В общем виде связь
между параметрами (2.58)-(2.65) в золотом и других режимах гипертензии может
быть представлена выражениями
ΔPK(βЗС)tK(βЗС) = 32ξK(βЗС)(lK(βЗС)/dK(βЗС))2, (2.66)
βΔPK(βЗС)tK(βЗС)/β = 32ξK(βЗС)(lK(βЗС)/dK(βЗС))2. (2.67)
В левой части законов композиции системы
(2.66) и (2.67) представлены гемодинамические,
а в правой - конструктивные параметры капилляра и крови. Коэффициент
оптимальной перфузии для сердечных капилляров в золотом и других режимах
гипертензии /Цветков, 2004/
αK(βЗС)
= lK(βЗС)/dK(βЗС)tK(βЗС)
= 160 с-1, (2.68)
αK(β) = lK(βЗС)/dK(βЗС)tK(βЗС)/β
= 160β с-1.
(2.68а)
Очевидно, что βK(βЗС)=aА(βЗС), а βK(β)=aА(β). Это означает, что перфузия артериального и капиллярного участков имеет
энергооптимальную основу.
2.10.3. Терминальные тройники
Большой интерес представляет «стык»
между артериальными и капиллярными сосудами. Рассмотрим тройник, где стволом
является терминальная артериола, а ветвями - капилляры. Капиллярное ветвление
практически симметрично. В соответствии с критерием «минимальной работы» - dK(βЗС)=0,794dC(βЗС);
это соотношение аналогично полученному ранее для
микрососудистого участка. Однако на этом сходство кончается, поскольку длина
ветви (капилляра) не уменьшается по сравнению со стволом, а наоборот,
значительно возрастает; причем это возрастание не компенсируется полностью, как
это происходит на терминальном участке, «обратным» изменением вязкости крови.
Естественно возникает вопрос: воспроизводят ли энергетически капиллярные
«ветви» артериолярный «ствол» в золотом и других режимах гипертензии?
Мощность, расходуемая на перфузию и
кровь капилляра /Цветков, 1997/,
WМK(βЗС)
= 0,63mKcKWМС(βЗС),
WХK(βЗС)
= 0,63m KcKWХС(βЗС),
где WМС(βЗС),
WМK(βЗС),
WХС(βЗС), WХK(βЗС)
- соответственно механическая и химическая мощность, расходуемая в стволе и
капилляре за единицу времени, mKlK(βЗС)/lC(βЗС)>1, cKξK(βЗС)/ξC(βЗС)<1,
- коэффициенты перехода от ствола к капилляру по длине и вязкости крови. При известных значениях /Цветков, 2004/
ξC(βЗС)=1,4×10-2
Пз, ξKβЗС)=1,15×10-2
Пз, lCβЗС)=3,2 мкм и lK(βзс) =220 мкм, mK=4,6 и cK=0,82. Исходя
из этих величин,
WМK(βЗС)
= 2,6WМС(βЗС),
WХK(βЗС)
= 2,6WХС(βЗС).
Соответственно, в условиях гипертензии,
WМK(β) = 2,6b2WМС(βЗС), (2.69)
WХК(β)
= 2,6b2WХС(βЗС), (2.70)
где WМK(β), WХК(β) – средние за сердечный цикл величины
механической и химической мощности в режиме гипертензии. Сопряжение ствола
(терминальная артериола) тройника с ветвями (капиллярами) осуществляется через
оптимальную величину kH=0,63. Эта величина обусловливает энергооптимальное
сопряжение гемодинамических параметров артериолы и капилляра. Можно считать,
что ствол и ветви «входят» в тройник в соответствии с принципом оптимального
вхождения. Тем самым обеспечивается энергооптимальная гармония всех
артериолярно-капиллярных тройников.
Исходя из (2.43), (2.69) и (2.70), отношения механической и химической
мощностей в стволе (артериоле) и ветвях (капилляры) аналогичны,
αK(βЗС)
= lK(βЗС)/dK(βЗС)tK(βЗС)
= 160 с-1, (2.71)
Инвариант
g(b)=0,5 представляет оптимальное соотношение затрат
«противоположных» энергий во всех режимах гипертензии. Это соотношение является
условием энергооптимальной гармонии для всего обменного
артериально-капиллярного участка коронарного русла во всех режимах гипертензии.
2.10.4. Капиллярное
«пространство» ССЦ и особенности его организации
Размеры капилляра, вязкость крови и
давление остаются постоянными в течение всего сердечного цикла. Следовательно,
средние значения всех гемодинамических параметров капилляра за систолу и
диастолу равны друг другу: ΔPS(βЗС)=ΔPd(βЗС), qS(βЗС)=qd(βЗС), tS(βЗС)=td(βЗС), VS(βЗС)=Vd(βЗС) и GS(βЗС)=Gd(βЗС). Показано /Цветков, 1997, 2004/, что скорость отдачи кислорода
в капилляре, разность концентраций и напряжений кислорода в крови на концах
капилляра также неизменны в течение кардиоцикла, т.е. US(βЗС)=Ud(βЗС), ΔHbO2S(βЗС)=ΔHbO2d(βЗС) и ΔpO2S(βЗС)=ΔpO2d(βЗС). Индексы s и d указывают на
систолическую и диастолическую части капиллярного параметра; под систолическими
и диастолическими значениями параметров подразумеваются их средние значения за
систолу и диастолу.
В обобщенном виде средние за сердечный
цикл систолическое и диастолическое значения
некоторого j-параметра в режиме гипертензии,
![]() = Asj(β)tS(β)/T(β),
= Asj(β)tS(β)/T(β),
![]() = Adj(β)td(β)/T(β),
= Adj(β)td(β)/T(β),
где ASj(β), Adj(β), ![]() ,
, ![]() - соответственно средние за систолу и диастолу, средние за сердечный цикл систолическое и диастолическое
значения j-параметра, tS(β), td(β),
T(β) - длительность систолы, диастолы и
кардиоцикла в режиме гипертензии.
- соответственно средние за систолу и диастолу, средние за сердечный цикл систолическое и диастолическое
значения j-параметра, tS(β), td(β),
T(β) - длительность систолы, диастолы и
кардиоцикла в режиме гипертензии.
Поскольку в золотом режиме гипертензии
длительности систолы, диастолы и кардиоцикла связаны между собою пропорцией
золотого сечения, а значения параметров постоянны в течение всего сердечного
цикла, то законы их композиции можно представить в обобщенной форме,
![]() = 0,382
= 0,382![]() ,
,
![]() = 0,618
= 0,618![]() ,
,
0,382![]() + 0,618
+ 0,618![]() =
=![]() ,
(2.74)
,
(2.74)
где ![]() - величина j-параметра в золотом режиме гипертензии.
Поскольку все величины капиллярных параметров одинаковы в течение сердечного
цикла, то очевидно, величина gK(b) = 0,5 имеет место как в
систолу, так и в диастолу.
- величина j-параметра в золотом режиме гипертензии.
Поскольку все величины капиллярных параметров одинаковы в течение сердечного
цикла, то очевидно, величина gK(b) = 0,5 имеет место как в
систолу, так и в диастолу.
Преобразования ССЦ всех капиллярных
параметров в условиях гипертензии можно представить следующим обобщенным
выражением /Цветков, 1997/
0,382b![]()
![]() + 0,618b
+ 0,618b![]()
![]() @ b
@ b![]()
![]() , (2.75)
, (2.75)
где kj-
показатель, соответствующий j-параметру. Закон (2.75) представляет собой
капиллярное «пространство» ССЦ.
В (2.75) гемодинамические и
кислородные параметры капилляра при гипертензии имеют следующие значения: для
давления и кровотока - kj=1, для объема, проводимости, скорости отдачи кислорода и разности напряжения
кислорода - kj=0 и для разности концентраций кислорода в крови и
времени пребывания - kj=-1. Величины других капиллярных параметров:
qK(βЗС)=20,9×10-9см3с-1, dK(βЗС)=5,5
мкм, ξK(βЗС)=1,15×10-2 Пз, tK(βЗС)=0,25
с и lK(βЗС)=220
мкм. Средние за сердечный цикл величины ![]() имеют значения:
имеют значения: ![]() =15,5 мм рт. ст.,
=15,5 мм рт. ст., ![]() =4,8×10-9см3,
=4,8×10-9см3,![]() =0,95×10-11г-1см5с-1.
Соответственно, величины
=0,95×10-11г-1см5с-1.
Соответственно, величины ![]() = 215%/c,
= 215%/c, ![]()
![]() = 55% и
= 55% и ![]() =
=
В «пространстве» (2.75)
можно отметить совпадение особенностей его структуры с «пространством» (2.7). В
структуре (2.7) имеет место «пересечение» двух геометрических прогрессий: 1)
«золотой»: j-2 = 0,382, j-1=0,618, j0 =1 и 2) х-1 , х0 ,
х; первая из них обладает также свойствами аддитивного ряда. Разность показателей крайних членов
обеих прогрессий равна 2. Отношение хmax /хmin =2 имеет характерную
особенность: оно соответствует отношению верхнего и нижнего значений двух соседних октав (![]() ) /Марутаев, 1990/. Таким образом, особенности композиции (2.75) связаны с
числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/. Золотое
число j также является «особым» числом. Таким
образом, структура (2.75) «сконструирована» с использованием особых чисел.
) /Марутаев, 1990/. Таким образом, особенности композиции (2.75) связаны с
числом 2, которое наряду с числами p, e и i имеет широкое «представление» в
законах физики /Аракелян, 1981/. Золотое
число j также является «особым» числом. Таким
образом, структура (2.75) «сконструирована» с использованием особых чисел.
В законе (2.7) отображена
уникальная роль золотого сечения в организации «противоположностей» этого
«пространства», а также представлено влияние на ССЦ уровня гипертензии.
Числовой каркас (2.75) имеет иерархию, сходную с «пространством» (2.7). Золотые
числа 0,382 и 0,618 характеризуют гармонию «противоположностей»; они
«присутствуют» в ССЦ всех рассматриваемых параметров в золотом режиме
гипертензии. Диапазон гипертензии b=1-2
постоянен для всех животных и капилляров. Особенностью «пространства» (2.75)
является полная независимость его параметров от «номера» капилляра и веса
животных. Величины βkj+1, βkj-1 и βkj представляют оптимальное соотношение
«противоположностей» при различных уровнях гипертензии. При сравнении
«пространств» ССЦ (2.7), (2.49) и (2.75) следует отметить важную особенность
- их «вырождение». В
первом «пространстве» величина j-параметр
зависит от веса животных, во втором – только от «номера» сосуда, в третьем же –
исчезает зависимость даже от «номера» капилляра. Во всех «пространствах»
сохраняется зависимость j-параметра от внешнего фактора – физической нагрузки. Аналогия
«пространств» (2.7), (2.49)и (2.75) заключается в том, что в условиях
гипертензии их энергооптимальная гармония обусловлена отношениями
nS(β) = 0,382β, (2.76)
nd(β) = 0,618/β, (2.77)
где nS(β), nd(β)
- соответственно отношение среднесистолической и среднедиастолической величин
параметра, отнесенных к сердечному циклу, к среднему за сердечный цикл значению
параметра при различных уровнях гипертензии.
Величины nS(b) и nd(b) являются мерой энергооптимальной гармонии
«противоположностей» в капиллярных ССЦ любого животного во всех режимах
гипертензии. Тем самым обеспечивается
энергооптимальная гармония всего артериолярно-капиллярного комплекса.
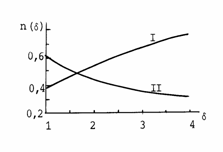 Рис. 2.1.
Инварианты ССЦ в условиях относительного кровоснабжения организма. Кривые
Рис. 2.1.
Инварианты ССЦ в условиях относительного кровоснабжения организма. Кривые