2.5. Золотое сечение, числа Фибоначчи и  биофизические основы оптимальной деятельности сердца 

 

 

Выше нами на основе экспериментальных данных было показано,  что "пространство" (2.7) организовано в соответствии с принципами  максимальной экономии энергии, оптимального преобразования и  оптимального вхождения. Принцип оптимального вхождения, как нам  представляется, является основным из этих принципов. Покажем на  примере сердечных систем различной сложности неизменность  оптимального включения "простых" систем в более сложные. 

Начнем с анализа "вхождения" субклеточных структур (элементов)  в систему (кардиомиоцит). Длина растянутого саркомера, которой  соответствует максимальная механическая работа при сокращении,  составляет 2,20 мкм; отметим, что в покое длина сердечного  саркомера в конце диастолы у млекопитающих равна той же величине  [263, 265]. Следовательно, нормальное сокращение кардиомиоцитов  связано с участием наиболее "сильных" саркомеров, имеющих  оптимальную длину. Очевидно, что вследствие этого для производства  необходимой механической работы кардиомиоцит обходится минимальным  количеством саркомеров. Известно также [262], что наиболее  "сильные" саркомеры на единицу производимой работы потребляют  минимальное количество кислорода. Таким образом, механическая  деятельность мышечной клетки осуществляется оптимальным образом как  по отношению к расходу "движущего" материала, так и к затратам  энергии АТФ. Известно, что вода в диапазоне температур 36-42°C  обладает особыми свойствами, благоприятными для протекания в ней  биологических процессов [71]. При температуре около 37^оС  в воде разорвана ровно половина межтетрамерных Н-связей, что обеспечивает равновероятность течения в обе стороны обратимых биохимических реакций в клетках. При 36,8°C, соответствующей температуре в  клетке, теплоемкость воды минимальна [22]. Следовательно, для  поддержания в клетке температуры, равной 36,8°C, можно обойтись  минимальным количеством энергии. Установлено [183], что  максимальная скорость утилизации кислорода в митохондриях сердечных  клеток млекопитающих происходит при рН 7,4 во внеклеточной  жидкости. Отметим, что pH 7,4 во внеклеточной жидкости  соответствует норме для кардиомиоцитов [292]. Вследствие  представленных выше феноменов ясно, что клетка для обеспечения  своей жизнедеятельности может обойтись минимальным количеством  митохондрий. Показано также [113], что при увеличении нагрузки в  несколько раз содержание молекул АТФ и КФ в сердечной клетке  практически не меняется; относительное постоянство содержания  макроэргических фосфатов достигается путем ускорения оборота этих  соединений. Таким образом, "сильные" саркомеры, максимальная  скорость дыхания митохондрий, минимальная теплоемкость "клеточной"  воды обеспечивают в кардиомиоците максимально возможную экономию  энергии и "строительного" материала. Мы могли убедиться в  оптимальности вхождения элементов (субклеточных структур) в  сердечную систему - кардиомиоцит. 

Покажем роль золотого сечения и чисел Фибоначчи в  оптимизации деятельности кардиомиоцита и более сложных сердечных  систем.

Очевидно, что функционирование кардиомиоцита невозможно без  внутриклеточной воды. Особые свойства воды имеют огромное значение  для оптимального протекания биологических процессов в любой клетке.  По этой причине следует познакомиться с особенностями структуры  воды. 

Молекула воды построена из атомов, которые сильнее различаются  по элетроотрицательности по сравнению с атомами других гомологов  (H₂S, H₂Se, H₂Te,... ); из этого следует, что связь в молекуле Н₂О  наиболее прочная. Молекула Н₂О обладает максимальной энергией связи  и наибольшим потенциалом ионизации среди указанных молекул. Она  имеет наибольший по величине дипольный момент и наибольший угол  молекулы (НОН). В строении молекул Н₂О симметрия выражается в  тетраэдрическом характере водородных связей [9]. Молекула воды  имеет структуру равнобедренного треугольника. Атом кислорода  занимает вершину треугольника, а оба атома водорода расположены в  его основании; величина угла при вершине равна 104,6 [58].  Молекула воды имеет зеркальную симметрию относительно оси,  проходящей через атом кислорода. Легко показать, что отношение  расстояний от атома водорода до другого атома водорода и до атома  кислорода приблизительно соответствует золотому сечению. Благодаря  этому обстоятельству вода имеет целый ряд аномальных свойств  (высокая диэлектрическая постоянная, необычайно высокая  растворимость и т.д.). Как показано в недавних исследованиях [59],  вода состоит из квантов (57 молекул, сцепленных в подобие  тетраэдра). Тетраэдр состоит из 4 додекаэдров (правильных  12-гранников). 16 квантов образуют структурный элемент, состоящий  из 912 молекул воды. Вода на 80% состоит из таких элементов, 15% -  кванты-тетраэдры и 3% - классические молекулы Н₂О. Хаотически  двигаются не отдельные молекулы Н₂О, а структурные элементы.  Отметим, что структура воды связана с платоновыми телами (тетраэдр,  додекаэдр), форма которых связана с золотой пропорцией. Ядро  кислорода также имеет форму платонова тела (тетраэдра) [121]. 

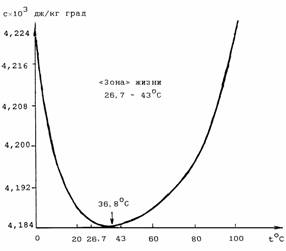
В интервале 30-45°C массы квазикристаллической и жидкой воды  приблизительно равны друг другу. В этом температурном диапазоне  наблюдается максимальная сжимаемость и минимальная теплоемкость  воды, что предопределяет ее особую роль в биологических процессах.  "Зона жизни", в которой сохраняются условия для протекания в воде  биологических процессов, простирается в пределах 26,7°C-43°C [22]  (рис. 2.6). Интересно, что температура 36,8°С делит этот интервал  приблизительно по золотой пропорции - 16,3:10,1 = 10,1:6,2.  Температура 36,8°С разделяет интервал жидкой фазы воды (0-100°C) в  отношении, также весьма близком к золотому. Отметим кстати, что  интервал плотностей всех существующих жидкостей разделяется водой в  "золотом" отношении [73]. Таким образом, особые свойства воды во  многом определяются "золотыми" соотношениями. Связь структуры  важнейшего фактора жизни - воды - с золотым сечением несомненна.  Эта связь проявляется, как мы могли убедиться, на уровне структуры  отдельной молекулы и структуры воды в жидком состоянии. 

 

 

 

 

Рис. 2.6. Удельная теплоемкость воды [22].

 

 

 

 

 

 

 

 

 

 

 

 

Источником энергии в клетках являются молекулы  аденозинтри-фосфата (АТФ). Установлено [258], что в изотоническом  режиме деятель-ности сердца (в этом режиме мы-шечные волокна  сокращаются) энергия АТФ, расходуемая на сократительную  деятельность кардиомио-цитов, делится в следующем отношении: 61,8%  расходуется непосред-ственно на механическую работу и 38,2%  рассеивается в виде тепла. Однако мышечные волокна в течение части  систолы не меняют своей длины (изометрический режим напряжения). В  изометрическом режиме энергия АТФ распределяется следующим образом:  95% энергии рассеивается в виде тепла и только 5% расходуется на  механическую работу. С учетом этого обстоятельства в целом за  систолу непосредственно на механическую работу используется около  40% энергии АТФ и остальные 60% расходуется на производство тепла;  такое соотношение приблизительно соответствует золотой пропорции.  Таким образом, распределение энергии АТФ как в фазу изгнания, так и  за всю систолу в целом происходит по золотой пропорции. 

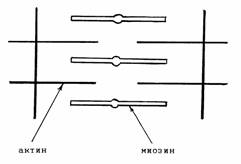
Важное значение золотое сечение и числа Фибоначчи имеют и для  организации "движущих" структур кардиомиоцита (рис. 2.7). Длины  актиновых и миозиновых нитей, составляющих "силовую единицу" (саркомер), соответственно равны 1,0 и 1,5 мкм [43]; эти числа  соотносятся между собою как числа Фибоначчи - 2:3. Оптимальная  длина саркомера в конце диастолы составляет 2,20 мкм, укорачиваясь  к концу сокращения до 1,73 мкм [264]. Относительное укорочение  саркомера за время сокращения равно 2,20/1,73 =1,272 =Ö1,618;  следовательно, и здесь имеет место золотое число. Следует отметить,  что и для спирали ДНК отношение диаметра d=33,8А  к шагу h=21,1А   весьма близко к золотому числу 1,618 (d/h=1,602) [34]. 

 

 

Рис. 2.7. Конструкция саркомера.

 

 

 

 

 

 

 

 

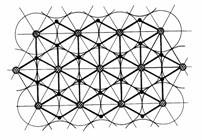
Каждая актиновая нить в поперечном сечении клетки  взаимодействует с 3 соседними миозиновыми ("вершинами"  равностороннего треугольника), а всякая миозиновая нить - с 6  актиновыми, расположенными по "вершинам" правильного шестиугольника  (рис. 2.8).

 

 

Рис. 2.8. Взаимное расположение актиновых и миозиновых нитей.

 · - актиновые нити ,    

      -  миозиновые нити.

 

Размещение пар мостиков по длине миозиновой нити  осуществляется по винтовой линии с интервалом 120° . В  этой конструкции имеет место симметрия винтового движения,  включающая в себя поворотную симметрию и симметрию скольжения.  Такого рода симметрию можно представить инвариантом - дробью m/l,  где m - количество полных винтовых линий, в конце которого два  мостика по вертикальной линии расположены друг над другом, а l -  число мостиков на общей длине этих линий. Винтовая линия,  соединяющая точки крепления двух мостиков, расположенных на одной  линии друг над другом, делится промежуточными мостиками на три  равные части [83]. Для винтовой линии, разделенной мостиками на 3  равные части, двойное отношение W=4a² /3a² =1,33, где а - расстояние  между двумя соседними мостиками; очевидно, что величина 1,33  практически совпадает со значением золотого вурфа W=1,309. 

Большой интерес представляет минимизация объема кардиомиоцита,  поскольку пространство внутри мышечной клетки должно использоваться  с максимальной эффективностью. С этой целью рассмотрим минимизацию  объема некоторых структур кардиомиоцита. Так расположение линейных  полимеров ДНК по двойной спирали позволяет осуществить их наиболее  плотную упаковку и свести к минимуму объем ядра клетки. Можно также  показать, что плотность "упаковки" актиномиозинового комплекса  максимальна. В плоскости, перпендикулярной направлению саркомеров,  сечения миозиновых нитей располагаются по вершинам равносторонних  треугольников, а актиновых - в их центре (рис.2.8) [219]. Такой способ  упаковки соответствует наиболее плотному взаимному расположению  множества взаимодействующих элементов двух видов на заданной  площади [127]. Расположение актиновой нити в центре равностороннего  "миозинового" треугольника позволяет получить наименьшую сумму длин  3 мостиков, чем при любом смещении от центра. Отметим при этом, что  расстояния в треугольнике от любой миозиновой нити до актиновой и  соседней миозиновой соотносятся между собою как числа Фибоначчи - 2  и 3. Центральное положение нити позволяет получить значительную  экономию "мостикового" материала. Максимальная плотность упаковки позволяет  значительно улучшить условия взаимодействия актиновых и миозиновых  нитей и свести к минимуму объем, занимаемый в клетке "силовыми"  структурами. 

Эффективно "используют" пространство кардиомиоцита и  энергопроизводящие структуры кардиомиоцита. В сердечной клетке  млекопитающих митохондрии располагаются между миофибриллами, под  сарколеммой и у полюсов ядер [43]. Такое расположение позволяет  свести к минимуму пространство, разделяющее энергопроизводящие и  -потребляющие структуры. Снаружи каждая митохондрия покрыта  3-слойной ограничивающей мембраной. Лежащая под ней трехслойная же  мембрана образует многочисленные складки и впячивания - кристы,  направленные в глубь митохондрий. С внутренними мембранами связаны  ферменты, катализирующие процессы переноса электронов и синтеза  АТФ. Складчатая поверхность по отношению к гладкой имеет то  преимущество, что при том же занимаемом объеме позволяет разместить  под мембраной значительно большее количество функциональных частиц.  Таким образом, "складчатость" структуры митохондрий также позволяет  значительно уменьшить размеры клетки. 

Очевидно, что максимально плотная упаковка ядра, миофибрилл,  митохондрий и, по-видимому, других структур в итоге позволила  свести объем мышечной клетки к минимуму. Минимизация объема связана  в основном с уменьшением диаметра клетки, что дает большой выигрыш  в повышении уровня метаболизма кардиомиоцита. Суть этого явления  заключается в следующем. Объем V и площадь обменной боковой  поверхности S кардимиоцита, поскольку он имеет цилиндрическую  форму, связаны с его длиной и диаметром. Для цилиндра S/V=4/d (d -  диаметр). Очевидно, что увеличение S/V может происходить лишь за  счет "сжатия" кардиомиоцита по диаметру; в то же время длина клетки  может быть любой, поскольку она не влияет на величину S/V. По этой  причине природа "выбрала" энергетически оптимальную длину  саркомера, равную 2,20 мкм при растяжении и 1,73 мкм при  сокращении. Максимальное отношение S/V обеспечивает прежде всего  значительную экономию "мембранного" материала. С другой стороны, в  этом случае единичному объему клетки соответствует максимальная  площадь обменной поверхности. Благодаря этому в единичном объеме  клетки протекают метаболические процессы максимальной интенсивности  по сравнению с теми, которые соответствовали бы менее плотной  упаковке. 

Нам представляется также важным отметить, что в сердечной  клетке отношение объемов энергопроизводящих элементов (митохондрий)  и энергопотребляющих соответственно составляет 0,34:0,66 [246]; это  соотношение соответствует отношению чисел Фибоначчи - 1:2.  Несомненно, что минимизация суммарных объемов энергопроизводящих и  -потребляющих элементов по числам Фибоначчи связана в конечном  счете с оптимизацией деятельности клетки в целом. Можно сказать,  что кардиомиоцит по отношению к исполняемой функции  "сконструирован" природой оптимальным образом как по отношению к  энергии, им потребляемой, так и к строительному материалу,  необходимому для его структур. Более того, он в высшей степени  упорядочен и пространственно, что позволяет иметь наиболее высокий  уровень метаболизма в расчете на единичный объем клетки.  Конструкция кардиомиоцита, как мы могли убедиться, обусловлена  принципом максимальной экономии энергии. Экономия живого вещества  не отменяет сути этого принципа, поскольку для воспроизводства и  питания дополнительного объема субклеточных структур потребовались  бы дополнительные затраты энергии. Следовательно, экономия вещества  в конечном счете означает экономию энергии. 

Интересно в связи с вышеизложенным обратить внимание на  параметры сферической клетки, связанные с ее ростом и делением.  Покажем "участие" в этих процессах золотых чисел. При росте объем и  площадь поверхности клеток возрастают в разной степени. Если  считать клетку сферой, то ее объем до деления надвое возрастает пропорционально  (aR₀)³ , а поверхность - (aR₀)² , где R₀ - радиус клетки сразу после  деления, а a=R/R₀ - коэффициент увеличения радиуса R₀ при росте. При  росте клетки увеличение живой протоплазменной массы происходит в  3-й степени, а поверхности клеточной мембраны , через которую  осуществляется обмен веществ, только во 2-й степени. Естественно,  что наступает момент, когда радиус клетки достигает критической  величины (R=a_крR₀), выше которой адекватное обеспечение  увеличивающейся протоплазмы через поверхность уже невозможно. На  это обстоятельство обращал внимание известный физиолог  И.А.Аршавский [5]. По-видимому, двойное увеличение объема  (R=1,26R₀) является пороговой величиной отношения S/V. При этом  поверхность клетки S возрастает в 1,59, а отношение V/S в 1,26 раз;  отметим, что числа 1,59 и 1.26 практически совпадают с золотыми  числами 1,618 и 1,272 =Ö1,618. Таким образом, критический предел  роста и деления клетки обусловлен золотыми числами. Естественно,  что отношения R /R₀ =1,26, S /S₀ =1,59 и V /V₀ =2 являются  инвариантами роста всех делящихся клеток. Таким образом, как мы  могли убедиться, золотое сечение и числа Фибоначчи имеют решающее  значение в экономичной, оптимальной организации деятельности не  только кардиомиоцитов, но и делящихся клеток. 

Исходя из предыдущих "экономий" следует ожидать, что и  мышечная масса сердца в целом должна иметь оптимальную конструкцию.  Мускулатура левого желудочка состоит из трех слоев - двух косых  (наружный и внутренний) и один циркуляторный (поперечный). Угол  начального наклона "косых" волокон на поверхности эндокарда  составляет 52,4^о [253]; этот угол незначительно отличается от  "золотого" угла 51,9^о . Свойства прямоугольного треугольника с углом  51,9^о при основании использовались еще в Древнем Египте при  строительстве пирамиды Хеопса [27]. Этот треугольник обладает  замечательным свойством - его стороны соотносятся между собою по  геометрической прогрессии - 1,618⁰: Ö1,618: 1,618 (или  1:1,272:1,618). "Косое" направление силы в мышечных слоях задает  струе крови вращательно -поступательное движение от верхушки  желудочка по направлению к полулунному клапану, что значительно  сокращает время изгнания единичного объема крови. Саллин [253]  показал с учетом угла 52,4° и принимая форму левого желудочка  близкой к эллипсоиду вращения, что ударный выброс крови при этих  условиях составляет 36% от конечнодиастолического объема. Величина  36% весьма близка к "золотой" - 38%, которая, как мы показали выше,  соответствует оптимальной величине ударного объема в покое.  "Золотой" угол 52,4° обеспечивает распределение "косой" силы F по  осям желудочка в золотом отношении: F_Г @(1/1,272)F, F_В @(1/1,618)F,  где F_г, F_в - проекции силы F на горизонтальную и вертикальную оси  желудочка. При естественной конфигурации сердца и при естественной  нагрузке выброс ударного объема крови происходит при минимальном  потреблении кислорода [269]. Следовательно, с углом 52,4° связан  "подбор" оптимального угла, при котором выброс адекватного  количества крови происходит с минимальными затратами энергии. Таким  образом, и на этом уровне очевидна роль золотых чисел и золотого  сечения в организации оптимальной деятельности сердца. 

Показано [223], что максимальная энергия выделяется на  нагрузке в том случае, когда внутреннее сопротивление насоса  (сердца) и сопротивление нагрузки (артериальная система) равны; это  соотношение реализовано в кардиоваскулярной системе. Майром с  соавт.[241] было установлено, что в нормальных условиях правый и  левый желудочки работают в оптимальном режиме, т.е. при  максимальном выделении мощности на нагрузке - артериальной системе.  Искусственно изменялось сопротивление выбросу крови, при этом  максимум мощности выделялся на нагрузке, соответствующей  естественному, нормальному объему изгнанной крови. Максимальному  выделению мощности на нагрузке способствует то обстоятельство, что  коэффициенты растяжимости стенок левого желудочка и аорты одинаковы  [232, 271]. Необходимо при этом отметить, что аорта геометрически  подобна каналам, в которых движение жидкости происходит с  минимальными потерями энергии [10]. Внутренняя поверхность левого  желудочка (сосочковые мышцы и трабекулярный аппарат) образуют  спиральную структуру [130], которая закручивает струю крови, т.е.  придает ей вращательно-поступательное движение. За счет этого  обстоятельства сокращается время изгнания единичного объема крови  без дополнительных затрат мышечной ткани. Таким образом,  оптимальное сопряжение сердца с нагрузкой позволяет сэкономить  дополнительное количество потребляемой энергии и мышечного  материала. 

Сердце включает в себя кроме мышечных волокон элементы,  непосредственно не производящие механической работы (сосуды с  кровью, проводящая и нервная системы и т.д.). Отмечено практически  линейное отношение между весом сердца млекопитающих и количеством  мышечных волокон [247]; следовательно, у всех животных можно  считать постоянным соотношение весов мышечных и "вспомогательных"  тканей сердца независимо от веса организма. По-видимому, это  отношение также имеет оптимальную природу и его следует считать  инвариантной величиной. Интересно отметить также следующее  обстоятельство. Установлено [68], что веса стенки левого желудочка  и межжелудочковой перегородки, а также межжелудочковой перегородки  и стенки правого желудочка млекопитающих соотносятся между собою  как числа Фибоначчи - 3:2. Можно утверждать с большой степенью  вероятности, что и для "верхней" части сердца следует ожидать  аналогичного, "золотого", соотношения между весами стенок левого и  правого предсердий и их перегородки. Вес межжелудочковой  перегородки является среднегеометрической величиной между весами  левого и правого желудочков. Это соотношение является еще одним  конструкционным инвариантом сердца млекопитающих. 

Итак, налицо цепочка "золотых" оптимальностей на  кардиомиоците, мышечном волокне, мышечных слоях, сердечной мышце и  и системе "желудочек-нагрузка". Эта цепочка является своего рода  иллюстрацией к представленному нами принципу оптимального  вхождения. Мы могли убедиться, что природа экономит на всех уровнях  "мышечных" систем независимо от их сложности. Нельзя не вспомнить  при этом, что еще Аристотель говорил, что природа не делает при  помощи большего, если это же можно сделать при помощи меньшего! В  этой связи необходимо еще раз указать на важнейшую роль золотого  сечения и чисел Фибоначчи в этом феномене.