Другие статьи

---

Фотонная теория элементарных частиц

Сухих Иван Николаевич

г. Щёкино, Тульская обл.

Получить исходную версию статьи в формате *.doc

АННОТАЦИЯ

В статье описываются два вида движений (прямолинейное и круговое) двух видов фотонов (положительных и отрицательных). С данной точки зрения объяснены строение элементарных частиц и квантов излучения и разнообразные физические эффекты.

In the article two kinds movements (straight and circle) of two kinds photons (positive and negative) are described. From this point of view structure of elementary particles and of quants of radiation and various physical effects are explained.

1. ФОТОНЫ.

1.1. ОБЩИЕ ПОЛОЖЕНИЯ.

Существует два вида фотонов: положительные («+» - фотоны) и отрицательные (« - » - фотоны).

Частицы с положительным электрическим зарядом испускают «+» - фотоны, частицы с отрицательным электрическим зарядом испускают « - » - фотоны. Фотоны, испущенные зарядом данного знака («+» или «-» ), поглощаются зарядом того же знака, (частица получает однонаправленный импульс) и вызывают выбивание фотона (индуцированное излучение) у заряда противоположного знака (частица получает противоположно направленный импульс). Фотоны могут двигаться только двумя способами:

1. прямолинейно;

2. по круговой орбите вокруг общего «центра масс» (орбита является окружностью, но плоскость орбиты постоянно меняется, поэтому за относительно длительный промежуток времени движение фотонов происходит как бы по сфере). При этом скорость фотонов постоянна и равна скорости света с (относительно «центра масс» данной круговой системы при движении второго типа или при их испускании из данной круговой системы и дальнейшем прямолинейном движении — при условии, что данная круговая система обладает свойствами инерциальной системы отсчета). При прямолинейном движении фотоны обладают свойствами квантов энергии, а при движении в круговой системе совокупность фотонов обладает свойствами элементарных частиц (рнс.1).

а) кванты б) элементарная частица

Рис. 1.

1.2. ВИДЫ КВАНТОВ.

Прямолинейное движение фотонов описывается уравнением:

Еф∙ 2 tф =	h	(1),
	2

где Е_ф - энергия одного фотона, t_ф - характерное фотонное время, в течение которого происходит один акт излучения (или поглощения) фотонов данной элементарной частицей, т.е. излучается (или поглощается) группа фотонов в виде одной порции, h - постоянная Планка. Один квант состоит из одного или нескольких фотонов одного знака. За 1 сек. вдоль одной прямой через одну ее точку пролетело бы 2υ фотонов (υ - частота кванта, почему 2υ - см. ниже), за время 2t_ф реально пролетит 2t_ф ∙ 2υ фотонов, которые имеют энергию:

Е_ф ∙2t_ф ∙2υ = (h/2)∙2υ = hυ. Таким образом, hυ - это энергия кванта – группа фотонов, которые испускаются (или поглощаются) за один акт излучения (или поглощения). Если квант состоит из одного фотона, будем называть его виртуальным (его частота 2υ₀ = const), если квант состоит из нескольких фотонов одного знака, будем называть его реальным (его частота 2υ > 2υ₀ может быть разной). Если частота кванта 2υ > 2υ₀, то будем его называть радиоквантом. Виртуальные кванты испускаются постоянно с частотами 2υ₀ всеми невозбужденными элементарными частицами, участвующими в электрическом взаимодействии. Реальные кванты испускаются только возбужденными элементарными частицами при переходе на более низкий энергетический уровень. Радиоквант представляет собой совокупность летящих вдоль одной прямой фотонов, каждый из которых является виртуальным квантом, испущенным вдоль данной прямой заряженной частицей при её (частицы) колебаниях. Частота радиокванта равна частоте колебания частицы, радиокванты формируют радиоволны, инфракрасное, оптическое и ультрафиолетовое излучения.

1.3. КОЛЕБАНИЯ ЭЛЕКТРОНА В ПРОВОДНИКЕ.

Рассмотрим движение (колебательный дрейф) электрона в проводнике при электрических колебаниях. Электрон через промежутки времени

2t_ф (t_ф излучения + t_ф поглощения) испускает в разные стороны фотоны (виртуальные кванты). Будем рассматривать лишь те фотоны, которые электрон испускает относительно себя в направлении х, перпендикулярном направлению колебаний у (длине проводника) (рис. 2).

у E

2 ● 1 ● 1

•

1 • 3 ● ●

• 2 4 t

4 ●

3

х

а) колебательный дрейф б) колебание электрической напряженности

электрона в проводнике в электромагнитной волне

Рис. 2.

При установившихся колебаниях моментом 1 изберем момент времени, когда электрон находится в точке «равновесия», где он находился до начала колебаний. В момент 1 скорость электрона равна V_max (по модулю) и однонаправлена у. Фотон, испущенный в момент 1, имеет импульс р_ф, который относительно данного проводника можно разложить на p_x и р_у, где (по модулю) р_ф= m_ф c (m_ф — масса фотона, с — скорость света), р_у = m_ф ∙ V_max , р²_ф= р²_х + р²_у (рис.3).

р_ф

p_y

p_x

момент времени 1

Рис. 3.

В момент времени 2 электрон находится в «крайней» точке колебаний и его скорость равна нулю. Фотон, испущенный в момент 2, имеет импульс

р_ф =р_х= m_фс (здесь р_у = 0).

В момент времени 3 электрон опять находится в точке «равновесия», но его скорость V_max направлена противоположно его скорости в момент 1. Соответственно, импульс фотона, испущенного в момент 3, относительно проводника будет р²_ф = р²_х+р²_у, где р_у = - m_ф V_max , р_ф= m_фс (рис.4).

p_x

р_ф р_у

момент времени 3

Рис. 4.

В момент времени 4 электрон находится в противоположной «крайней» точке колебаний, его скорость равна нулю. Фотон, испущенный в момент 4, имеет импульс р_ф = р_х= m_фс ( р_у = 0) - такой же, как в момент 2. Итак, компонент импульса фотонов р_х квазипостоянен постоянен во времени и приблизительно равен р_х ≈ m_фс = р_ф (так как V_max << с) - он вызывает стойкое смещение свободных электронов в параллельном проводнике - приемнике 2 в сторону его поверхности, противоположной проводнику - излучателю 1, перпендикулярно длине проводников 1 и 2. Компонент импульса фотонов р_у меняется во времени по закону косинуса (соответственно изменению скорости колебательного дрейфа электронов в проводнике 1, так как р_у = m_фV, где V –скорость дрейфа электронов) и достигает максимума (по модулю) р_уmax в моменты 1 и 3, т.е. р_у = р_уmaxcos ωt, где ω – угловая частота электрических колебаний, t- время. Именно компонент импульса фотонов (виртуальных квантов) p_y, испущенных колеблющимися электронами проводника 1, вызывает колебания электрической напряженности Е в электромагнитной волне в той же фазе Е = Е_max cos ωt и колебания электронов в параллельном проводнике 2 с той же частотой, что и в проводнике 1. Если проводник 2 перпендикулярен проводнику 1, то колебания электронов в нем будут происходить в направлении длины проводника 1 (т.е. толщины проводника 2) на участке длины проводника 2 равной толщине (диаметру) проводника 1: в случае, если проводники 1 и 2 являются отрезками проволоки, то этот участок представляет собой практически точку (прямая проекция проводника 1 на проводнике 2) (рис.5) на проводнике 2, т.е. практически

Рис. 5.

колебания в проводнике 2 происходить не будут – вот почему электромагнитная волна является поперечной. От данного электрона проводника 1, который в моменты времени 1 и 3 находится в точке А, фотоны будут лететь к проводнику 2: в момент 1 – по направлению АС₁, в момент 3 – по направлению АС₃ (точки С₁ и С₃ лежат на проводнике 2) (рис. 6). Момент времени 1 бывает один раз в период колебаний (с частотой υ), так же как и момент времени 3. Поэтому фотоны по лучу АС₁ (или АС₃ ) будут лететь с частотой υ, и расстояние между ними будет λ =с/ υ

В

С₁

А Рис. 6.

С₃

1 2

Но данный электрон в точке А бывает дважды за период колебаний через промежутки времени равные полупериоду колебаний (в моменты времени 1 и3). Поэтому из точки А (произвольно взятой на проводнике 1) данный электрон будет испускать фотоны с частотой 2υ. В точку С₁ на проводнике 2 фотоны от проводника 1 прилетают не только из точки А, но и из точки В (луч ВС₁ параллелен лучу АС₃ – фотоны, летящие по этим лучам, испускаются в момент времени 3). Поэтому в точку С₁ (а также в любую другую точку проводника 2) фотоны от проводника 1 прилетают с частотой 2υ. Следовательно, при рассмотрении электромагнитной волны для полёта фотонов надо пользоваться величинами υ и λ (λ - расстояние между фотонами в радиоквантах), а для испускания и поглощения фотонов (радиоквантов) надо пользоваться величинами 2υ и λ/2. При рассмотрении виртуальных и реальных квантов (так как они не связаны с колебаниями заряженной частицы) надо всегда (для полёта испускания и поглощения фотонов) пользоваться величинами 2υ и λ/2 (λ/2 – расстояние между фотонами в виртуальных и реальных квантах).

1.4. СТРОЕНИЕ КВАНТОВ.

Заряженная частица, имеющая элементарный заряд е, (и некоторые незаряженные частицы) за промежуток времени t_ф излучает один фотон (виртуальный квант) в одном направлении (по одному лучу), число таких лучей d, т.е. данная элементарная частица за один t_ф излучает d виртуальных квантов. В следующий промежуток времени t_ф данная частица поглощает d виртуальных квантов (один виртуальный квант из одного луча). Направления лучей испускания распределены равномерно в пространстве (более точно – см. ниже), направления лучей поглощения распределены неравномерно – их больше со стороны более сильного электрического поля. Промежутки времени t_ф (излучения) и

t_ф (поглощения) у данной элементарной частицы попеременно следуют друг за другом. t_ф = cоnst – для всех элементарных частиц. В одном атоме t_ф (излучения) электронов соответствуют t_ф (поглощения) протонов и наоборот, t_ф (поглощения) электронов соответствует t_ф (излучения) протонов. Следовательно, t_ф (излучения) у всех протонов (как потом и у всех электронов) одного атома возникает одновременно. Поэтому в одном атоме не происходит электрического отталкивания протонов друг от друга и электронов друг от друга, так как за

время t_ф фотон пролетает расстояние ℓ₀ = с∙t_ф , которое (как увидим ниже) много больше размеров атомов. ℓ₀ – расстояние, на котором вдоль прямой располагаются фотоны в реальном кванте (различной частоты) (рис. 7). Так как виртуальные кванты (фотоны) испускаются (по одному лучу) через промежутки времени 2t_ф, то λ₀/2 = 2ℓ₀ - длина волны виртуального кванта. Радиокванты (у которых λ/2 > λ₀/2) могут иметь только кратные длины волн:

λ	=	nλ0	, 2υ =	2υ0	, где n ≥ 2 – целое число (2)
2		2		N

Реальные кванты (у которых λ/2 < λ₀/2) могут иметь только дольные длины волн:

λ	=	1	*	Λ0	=	ℓ0	, 2 υ = 2n·2 υ0 , (3)
2		n		4		n

где n ≥ 1 – целое число, (n + 1) – число фотонов в реальном кванте

● ● ● ● ● ● ● ● ● ● ● ● реальные кванты

● ● ● виртуальные кванты

● ● радиокванты

ℓ₀

λ₀/2 Рис. 7.

1.5. ВЗАИМОДЕЙСТВИЕ ЗАРЯДОВ.

Рассмотрим взаимодействие неподвижных заряда q₁ (заряд 1, создающий рассматриваемое электрическое поле) и заряда q₂ (заряд 2, на который рассматриваемое электрическое поле действует с силой F_э). Выберем такую инерциальную систему отсчёта, в которой заряд 1 покоится, направим ось x от заряда 1 к заряду 2, для определённости предположим, что эти заряды положительные, расстояние между зарядами равно R. Взаимодействие осуществляется путём обмена фотонами (в данном случае заряд 2 поглощает фотоны поля и приобретает сонаправленный с фотонами поля импульс, если бы заряды были разноимёнными, то фотоны поля выбивали бы фотоны противоположного знака из заряда 2, в результате чего заряд 2 приобретал бы импульс отдачи, противоположно направленный с импульсом фотонов поля). Сила – это изменение импульса за 1 сек.: F_э = ∆р /∆t . Поэтому сила Fэ равна суммарному импульсу фотонов, испущенных зарядом 1 и поглощённых зарядом 2 за 1 сек. (испускание фотонов происходит равномерно по всем направлениям и поэтому не меняет импульс заряда 1):

Fэ =	q1 q2	=	q1 q2	где S – площадь сферы радиусом R –заряд 1 находится
	4πε0R^2		ε0S	в центре сферы, заряд 2 – на её поверхности. Если

скорость заряда 1 постоянна, то скорость фотонов поля относительно него по всем направлениям равна скорости света с. Сила F_э прямо пропорциональна напряжённости поля Е = q₁ / ε₀S. За 1 сек заряженная элементарная частица (её заряд равен е) испускает по всем направлениям

Nе = 2 υ0 d =	d	фотонов. (4)
	2tф

Заряд 1 Кл за 1 сек испускает

N0 =	Nе	фотонов. (5)
	е

Заряд q испускает за 1 сек

Nu = Nо q =	q Nе	(6)
	Е

фотонов по всем направлениям. Тогда за 1 сек. 1 кв. метра сферический поверхности, на которой находится заряд 2, достигнет n = N_u /S фотонов

(n- поверхностная концентрация фотонов).

n =	N0 q1	=	q1 Nе	=	q1 d	(7),
	S		S е		S∙2tф е

что создает напряжённость Е поля

Е =	Nu	= a n (8),
	N0 ε0S

где а = 1/ N₀ ε₀ = const, – константа (по смыслу – это напряжённость электрического поля, созданного в ситуации, когда 1 кв. метра сферической поверхности достигает 1 фотон за 1 сек.). (Единицы: N_u –c^-1, N₀ –c ^-1 Кл ^-1,

n–c ^-1 м^-2 , а –В·с·м). Отсюда:

F_э = q₂ а n (9)

С другой стороны

F_э = N_n m_ф с (10),

где N_n – число поглощённых зарядом 2 фотонов (из испущенных зарядом 1) за 1 сек, m_ф с - импульс 1 фотона. N_n пропорционально q₂ :

N_n = b q₂ n (11),

где b – константа (число фотонов, поглощённых зарядом 2 (1 Кл) за 1 сек при

n = 1 c ^–1 м ^–2 , единицы b -м² Кл ^–1 ). Из определения ясно, что 0 < b < 1, т.е.

b – это доля числа фотонов, поглощённых зарядом 2 (1Кл) за 1 сек, к числу фотонов, достигших 1 кв. метра сферической поверхности, на которой находится заряд 2, за 1 сек. Отсюда:

F_э = b q₂ n m_ф c = q₂ аn и b m_ф c = a (12).

Тогда m_ф = а / b c = const – масса фотона является постоянной величиной. Из третьего закона Ньютона следует, что число фотонов, испущенных зарядом 1 и поглощённых зарядом 2 за 1 сек, равно числу фотонов, испущенных зарядом 2 и поглощённых зарядом 1 за 1 сек. Тот же вывод получается при рассмотрении движения тела 1 по орбите вокруг тела 2: Е_р = FR, где F – сила взаимодействия тел 1 и 2, R – расстояние между ними, Е_р - потенциальная энергия взаимодействия тел 1 и 2, Е_к = mV ²/ 2, где Е_к - кинетическая энергия тела 1, m- масса тела 1, V –скорость тела 1, а так как F = mV ²/R, то Е_к = FR /2 = Е_p / 2, т.е. кинетическая энергия тела 1 равна ½ части потенциальной энергии взаимодействия тел 1 и 2 (природа взаимодействия – электрическое или гравитационное – значения не имеет). Итак, в результате электрического (или гравитационного – см. ниже) взаимодействия (обмена виртуальными квантами) изменяется скорость тела и его кинетическая энергия, но общая энергия и масса тела не меняются. При изменении скорости тела меняется векторная сумма (равнодействующая) импульсов частиц, составляющих тело, но скалярная сумма модулей импульсов этих частиц не меняется и равна m c (m –масса тела, с – скорость света). При переходе из одной в другую инерциальную систему отсчёта меняются скорость и кинетическая энергия тела, а общая энергия и масса тела не меняются. Изменение общей энергии и массы тела происходит только в результате излучения или поглощения реальных квантов.

1.6. МАГНИТНАЯ ЭЛЕКТРИЧЕСКАЯ СИЛА.

Рассмотрим случай, когда к неподвижному заряду 1 приближается с постоянной скоростью V заряд 2 по прямой а, проходящей через центр заряда 1 (рис.8).

с t₁

V t₂ с t₂

(2) 2 (2) 1

V t₂ с t₁ a

1

с t₂

Рис. 8.

Сила взаимодействия зарядов F ~ n, поверхностная концентрация фотонов n ~ 1/ R², где R - расстояние между зарядами, тогда F ~ 1/ R². Обозначим: F_э – сила взаимодействия, если бы заряд 2 был неподвижен, F_v – сила взаимодействия, когда заряд 2 приближается со скоростью V к заряду 1, R₁ – расстояние между зарядами, на котором рассматривается их взаимодействие, R₂ – расстояние между зарядами в тот момент времени, когда заряда 2 достигает фотон, испущенный зарядом 1 в момент времени, когда расстояние между зарядами было R₁ . Тогда

F_э ~ 1/ R₁² , F_v ~ 1/ R₂² Так как R₁ = ct₁, R₂ = ct₂ (с - скорость света, t₁ – время пролёта фотоном расстояния R₁ , t₂- время пролёта фотоном расстояния R₂), то F_э ~ 1/ t₁² , F_v ~ 1/ t₂² . Тогда

Fv =	t1^2	∙ Fэ (13)
	t2^2

Из с t₁ = с t₂+ V t₂ (рис. 8) следует

F_v = 1 +

V

2

F_э (14)

c

Если заряд 2 удаляется от заряда 1 с постоянной скоростью V по прямой а, то из с t₁ = с t₂ – V t₂ (рис.8) следует

Fv = 1 -	V	2 Fэ (15)
	c

Если заряд 2 приближается к заряду 1 по прямой а′, не проходящей через центр заряда 1, и его скорость по прямой а′, равна V, то скорость приближения заряда 2 к заряду 1 равна V cos£, где £- угол между прямой a′ и прямой, соединяющей центры зарядов (рис.9)

V t₂ (2) 2 £ V t₂

2 £ 180° -£ (2) а′

сt₂

сt₁ сt₁ сt₂

£

1 а

Рис. 9.

Тогда (14) записывается в виде :

F_v = 1 +

V cos£

2

F_э (16)

c

При удалении заряда 2 от заряда 1 по прямой а′ с той же скоростью (15) записывается в виде:

F_v = 1 -

V cos£

2

F_э (17)

с

Можно записать (16) в виде F_v = F_э + F_м, где

F_м = 1 +

V cos£

2

- 1 F_э =

2 V cos£

+

V ²cos²£

F_э (18)

с

c

c²

интерпретируется как появление магнитной силы. Аналогично, (17) можно записать в виде: F_v = F_э - F_м, где

F_м = 1 - 1 -

V cos£

2

F_э =

2 V cos£

-

V ²cos²£

F_э (19)

с

c

c²

также является магнитной силой.

При сближении зарядов направления F_э и F_м совпадают, при отдалении зарядов F_э и F_м противоположно направлены. Но в (16) и в (17) мы пренебрегли изменением угла £ за промежуток времени t₂. Это допустимо при V<<с, но в общем случае необходимо пользоваться геометрическими соотношениями (рис. 9). Тогда вместо V cos£ при приближении заряда 2 надо брать (сt₁ - сt₂ ) / t₂ = =с(t₁ / t₂ – 1), а при удалении (сt₂ - сt₁)/ t₂ = с(1 - t₁ / t₂). Подставляя эти значения в (16) и в (17) соответственно, получаем в обоих случаях (13). Зная R₁ = ct₁, V, угол £, пользуясь теоремой косинусов, составляем уравнение: при сближении зарядов

(сt₁)² + (V t₁)² – 2Vсt₁ t₂ cos£ – (сt₂)² = 0, при отдалении зарядов (вместо угла £ берём угол (180 –£)) (сt₁)² + (V t₂)² + 2Vсt₁ t₂ cos£ – (сt₂)² = 0. Решаем уравнение относительно t₂, найденное значение подставляем в (13). В любом случае справедливы формулы (14) и (15), если рассматривать V как скорость приближения заряда 2 к заряду 1, или, соответственно, как скорость удаления заряда 2 от заряда 1 (в данный момент времени).

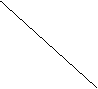
Опустим из центра заряда 1 на прямую а′, по которой с постоянной скоростью V движется заряд 2, перпендикуляр, который пересечёт прямую а′ в точке О (рис.10).

А V t₂ O V t₂́ В

2 а΄

сt₁ сt₂ сt₁́ сt₂ ́́

Рис. 10.

1 а

Рассмотрим действие заряда 1 на заряд 2 в момент прохождения зарядом 2 точки О. Пусть заряд 2 приближается к заряду 1. В тот момент времени, когда заряд 2 находился в точке А, заряд 1 испустил фотон, который достигнет заряда 2 через промежуток времени t₂, когда заряд 2 будет находиться в точке О. Тогда на заряд 2, находившийся в точке А, со стороны заряда 1 действовала сила

F_v = (t₁² / t₂² )F_э . Из соотношения (сt₁)² = (V t₂)² + (сt₂)² (рис. 10) находим:

F_v = 1 +

V ²

F_э = F_э + F_м, где

c²

Fм =	V ^2	Fэ (20).
	с^2

Пусть в тот момент времени, когда заряд 2 находится в точке О, заряд 1 испустил фотон, который достигнет заряда 2 через промежуток времени t_́2́, когда заряд 2 будет находиться в точке В (рис. 10). Тогда на заряд 2, находящийся в точке О, со стороны заряда 1 действует сила F′_v = (t′₁ / t′₂)² ∙F′_э . Из соотношения (сt′₂)² = (сt′₁)² + (V t′₂)² находим:

F′_v = 1 -

V ²

F′_э = F′_э - F′_м, где

c²

F′м =	V ^2	F′э (21).
	с^2

1.7. ВЗАИМОДЕЙСТВИЕ ТОКОВ.

Пусть а и а′ – два тонких длинных параллельных проводника (рис. 10), по которым с постоянной скоростью V движутся свободные заряды (так как проводники одинаковые, то равенство | V | означает, равенство силы тока I). В проводнике каждому свободному движущемуся отрицательному элементарному заряду (электрону) соответствует неподвижный положительный элементарный заряд (протон). Неподвижные протоны и движущиеся с постоянной скоростью V электроны являются инерциальными системами отсчёта, поэтому в качестве заряда 1 проводника а (рис. 10) можно рассматривать любой из них, который взаимодействует с противоположно находящимся в точке О подвижным зарядом 2 (находившимся в момент испускания фотона зарядом 1 в точке А) и неподвижным зарядом, лежащим в точке А. Тогда сила взаимодействия заряда 1 с подвижным относительно него зарядом 2 будет F_v = (1 + V ² / c²)F_э, где F_э – сила взаимодействия с неподвижным зарядом 2. Пусть расстояние между проводниками а и а΄ 1м и по ним текут токи силой 1А. Рассмотрим взаимодействие отрезка в 1м проводника а c ближайшим к нему отрезком в 1 м проводника а΄. Пусть токи противоположно направлены ( ). Тогда электроны проводника а΄ движутся относительно электронов проводника а со скоростью 2V, относительно протонов проводника а со скоростью V, протоны проводников относительно друг друга неподвижны. Сила отталкивания

1+

(2V)²

F_э + F_э = 2 +

4V ²

F_{э ,} сила притяжения

с²

с²

1+

V ²

F_э + 1 +

V ²

F_э = 2 +

2V ²

F_{э .} Результирующая сила

с²

с²

с²

имеет вид отталкивания между проводниками, её модуль:

2V ^2	Fэ (22)
с^2

Пусть токи одинаково направлены ( ). Тогда электроны проводников относительно друг друга неподвижны, а относительно протонов двигаются со скоростью V, протоны относительно друг друга неподвижны. Сила притяжения

1+

V ²

F_э + 1 +

V ²

F_э = 2 +

2V ²

F_{э .} Сила отталкивания

с²

с²

с²

F_э + F_э = 2F_э . Результирующая сила имеет вид притяжения между проводниками, её модуль: (2V ² / с² ) F_э (совпадает с (22)). Вычислим F_э . При токе силой 1А за 1 сек через поперечное сечение проводника проходит заряд

1 Кл, что соответствует сумме свободных зарядов в V метрах проводника. Тогда в 1 м проводника сумма свободных зарядов равна 1/ V Кл. Итак,

F_э = k(q₁q₂ /R²) = k / V ² Н, где q₁ = q₂ = 1/ V, R = 1, k = 1/ 4πε₀ = 8,987·10⁹. Тогда сила взаимодействия между отрезками проводников а и а΄ в 1м будет

(2V² / с² ) F_э = 2k/ с² = 2·8,987·10⁹ / 8,987·10¹⁶ = 2·10 ^–7 Н. Именно данное значение магнитной силы между проводниками входит в определёние силы тока в 1А.

1.8. ЭЛЕКТРОМАГНИТНАЯ САМОИНДУКЦИЯ.

Рассмотрим случай, когда приближающийся заряд 2 изменил свою скорость V относительно заряда 1 (в проводнике а) (рис. 8). Если V увеличилось, то магнитная сила F_м тоже увеличится, если V уменьшилась, то F_м тоже уменьшится. В проводниках внешнее электрическое поле вызывает движение (дрейф) свободных зарядов “первого слоя”. Расстояние между свободными зарядами “первого и второго слоёв” уменьшается, отталкивание между ними усиливается, из-за этого свободные заряды второго слоя начинают дрейф в том же направлении. Так происходит слой за слоем (расстояние между слоями равно дебаевскому радиусу). В результате возникает движение всех свободных зарядов проводника. Вследствие отталкивания между свободными зарядами соседних слоёв будет происходить не только увеличение скорости зарядов следующего слоя, но и уменьшение скорости зарядов данного слоя. Поэтому при увеличении напряжённости внешнего поля отталкивание между слоями усиливается – заряды данного слоя увеличивают свою скорость дрейфа постепенно, при уменьшении напряжённости внешнего поля отталкивание между слоями ослабляется – заряды данного слоя уменьшают свою скорость дрейфа постепенно. В классической физике это явление интерпретируется как электромагнитная самоиндукция, подчиняющаяся правилу Ленца.

1.9. ЭФФЕКТ ДОПЛЕРА.

При электрическом взаимодействии элементарный заряд за время t_ф поглощения может провзаимодействовать не более чем с одним фотоном, прилетающим из данного направления (по данному лучу). Магнитные явления зависят от скорости зарядов друг относительно друга потому, что за время пролёта фотонов меняется расстояние между зарядами и, следовательно, поверхностная концентрация фотонов на этих расстояниях, от которой зависит сила взаимодействия между зарядами. Действие излучений (радиоквантов) также зависит от скорости источника относительно приёмника (эффект Доплера), но здесь дело в другом.

Пусть источник приближается к приёмнику со скоростью V, тогда скорость фотонов (радиоквантов) относительно приёмника будет с + V = λυ, где с = λ υ₀ – скорость фотонов (света) при неподвижном источнике, υ₀ – частота излучения при неподвижном источнике (частота излучения относительно источника), υ –частота излучения относительно приёмника при движущемся источнике, λ - длина «волны» (зависит только от υ₀ и не зависит от скорости источника относительно приёмника). Поэтому

υ =	с + V	=	с + V	υ0 (23)
	Λ		с

Пусть источник удаляется от приёмника со скоростью V. Тогда скорость фотонов относительно приёмника будет с – V = λυ. Поэтому

υ =	с – V	=	с – V	υ0 (24)
	Λ		с

Итак, эффект Доплера в отношении излучений доказывает, что скорость фотонов относительно приёмника зависит от скорости источника относительно приёмника.

1.10. СТРУКТУРНЫЕ ЧАСТИЦЫ ТЕЛА.

Полная энергия тела E_t = E_р + E_к, где E_к – кинетическая энергия тела как целого, E_р – некинетическая (потенциальная) энергия тела как целого (сумма кинетических энергий разнонаправленного движения частиц, составляющих тело). Пусть в системе отсчёта 1 тело имеет скорость V, тогда E_к1 = m V ² / 2 (m- масса тела), E_р1 = E_р (1 - (V ² / с²)) (E_р – некинетическая энергия тела в системе отсчёта, в которой оно покоится и E_к = 0. Это следует из (21) и E_р =FR). Пусть в системе отсчёта 2 тело имеет скорость V + ∆V, тогда E_к2 = (m(V + ∆V)²) / 2,

E_р2 = E_р 1-

(V + ∆V)²

Полная энергия тела во всех системах отсчёта

с²

одинаковая E_к = E_к1 + E_р1 = E_к1 + E_{р1 ,} Тогда

m V ²

+ E_р 1 -

V ²

=

m(V + ∆V)²

+ E_р 1-

(V + ∆V)²

2

с²

2

с²

Проведя преобразования, получаем E_р = m с² /2, тогда

Et = Eк1 + Eр1 =	m с^2	(25)
	2

Значит, все элементарные структурные частицы, составляющие тело, движутся со скоростью «света» с ( в системе отсчёта, в которой тело покоится). Естественно сделать вывод, что такой элементарной структурной единицей является фотон, энергия которого

Eф =

mф с^2

/2 = const (26)

При движении второго рода (см. выше) фотоны формируют «элементарные» частицы, которые формируют атомы, которые формируют тело. Отсюда также следует, что не существует частиц в данном теле, которые движутся быстрее фотонов в данной системе отсчёта. Значит, фотоны между собой гравитационно взаимодействовать не могут. Нет необходимости вводить особые частицы (гравитоны) для переноса гравитационного взаимодействия. Гравитационное взаимодействие осуществляется также путём обмена фотонами (см. ниже).

Заметим ещё, что два взаимодействующих тела (электрически или гравитационно) не могут двигаться со скоростью большей с друг относительно друга (при отдалении – фотоны от одного тела не достигнут другого, тела, если его скорость равна с, при сближении – фотоны, испущенные телом 1, не смогут передать дополнительный импульс телу 2, если импульс тела 2 относительно тела 1 уже достиг значения mс ). Однако два не взаимодействующих тела могут двигаться друг относительно друга (вследствие относительности движения) со скоростью большей с (тахионы – по отношению друг к другу).

1.11. ГРАВИТАЦИОННОЕ ВЗАИМОДЕЙСТВИЕ.

Рассмотрим гравитационное взаимодействие двух протонов. Протон имеет электрическую и гравитационную части (см. ниже). В стабильном состоянии из электрической части за время t_ф по каждому из d направлений вылетает один “+” - фотон (виртуальный квант), 2t_ф - время между двумя вылетами в одном направлении; это определяет участие протона в электрическом взаимодействии. Независимо от этого из гравитационной части за время t_g (гравитационное время) в одном направлении также вылетает по одному фотону: по d/2 направлениям «+» – фотоны и по d/2 направлениям «-» -фотоны. 2t_g – время между двумя вылетами в одном направлении. Каждый из этих фотонов выбивает фотон противоположного знака у другого протона, что вызывает его притяжение к данному протону – гравитационное взаимодействие. Вакантное место быстро заполняется фотоном того же (что и выбитый) знака, чьё направление импульса совпадает с направлением движения данного вакантного места в данный момент (в окружающем пространстве имеется множество фотонов обоих знаков). 2 протона на расстоянии R друг от друга электрически взаимодействуют с силой

F_э = ke²/R² = (2,306∙10 ^–28 / R² ) Н, гравитационно взаимодействуют с силой

F_g = Gm_р / R² = (1,860∙10 ^–64 / R² ) Н (m_р – масса протона).

Значит сила электрического взаимодействия протонов больше силы гравитационного взаимодействия в

Fэ	=1,24∙10^36 раз (27),
Fg

т.е. из одного протона за одно и то же время в одном и том же направлении вылетает в 1,24∙10³⁶ раз меньше число фотонов для гравитационного взаимодействия, чем число фотонов для электрического взаимодействия. Тогда

2t_g = 1,24∙10³⁶ · 2 t_ф (28).

Так как протон состоит (см. ниже) из n_р фотонов (всего – обоих знаков), то за время

tv = 2 tg	nр	(29)
	d

в результате гравитационного взаимодействия произойдёт полное замещение фотонов в данном протоне, что можно интерпретировать как время жизни протона.

Забегая вперёд, относительно гравитационного взаимодействия других частиц заметим следующее. Нейтрон имеет гравитационную часть и две электрических части, протоны и нейтроны в ядре за короткое время (по сравнению с t_g) превращаются друг в друга, поэтому сильное взаимодействие на гравитационное взаимодействие не влияет. Электрон не имеет гравитационной части. Другие частицы нестабильны (их время жизни намного меньше t_g ). Поэтому, кроме нуклонов, другие частицы в гравитационном взаимодействии не участвуют.

1.12. МАГНИТНАЯ ГРАВИТАЦИОННАЯ СИЛА.

Гравитационная сила F_g имеет ту же природу, что и электрическая сила F_э – обмен фотонами, но меньшей интенсивности. Следовательно, существует и гравитационная магнитная сила F_gм, зависящая от скорости одного тела относительно другого тела, которая вычисляется по тем же формулам, что и электрическая магнитная сила F_м ((13) – (21)):

Fgv =

t1 t2

^2· Fg = Fg ± Fgм (30),

где F_g = G m₁ m₂ / R² (закон всемирного тяготения), «+» берётся при сближении тел, «-» - при удалении.

В частности, при движении тела 1 по орбите вокруг тела 2 имеем :

Fgv = 1 -	V^2	Fg = Fg – Fgм (31)
	c^2

(где F_gм = (V² / с² ) F_g , V - скорость тела 1 по орбите), так как движущееся по орбите тело 1 за время пролёта фотона от тела 2 к телу 1 переходит из точки О в точку В (рис. 10 и рис.11). V t₂

1

сt₁ сt₂

2 Рис. 11.

Для примера, рассмотрим движение Меркурия по орбите вокруг Солнца. Cреднее расстояние от Солнца R = 0,387 а.е. = 5,78952·10¹⁰ м. Период обращения Т = 88 сут. = 7,6032·10⁶ сек. Скорость движения по орбите V = 2πR/ Т = =4,78438·10⁴ м/с. Откуда F_gм / F_g = V² / с² = 2,54693·10^–8 Период обращения

в 88 сут. означает, что сила F_g за 88 сут. вызывает движение в 360° , тогда за

100 лет =36525сут. cила F_g вызовет движение в 360·36525/88 =149420,45° Так как сила F_gм меньше по интенсивности в F_gм / F_g раз, то она вызовет за 100 лет движение ( отклонение в движении ) во столько же раз меньшее :

2,54693·10^–8 · 149420,45 = 0,0038056° = 13,7″. Именно отклонение в движении Меркурия в 13,7″ за 100 лет невозможно объяснить с помощью только законов Ньютона.

1.13. ИНТЕРФЕРЕНЦИЯ СВЕТА.

Все тела обмениваются виртуальными квантами (из-за наличия в электроне, протоне и нейтроне электрических частей – см. ниже). Если за время

t_ф поглощения к данному, например, электрону прилетят по одному «-»-фотону по каждому из d направлений, то все они поглотятся как виртуальные кванты. Если за t_ф поглощения, кроме этих фотонов, по одному (или нескольким) направлению прилетят ещё один (или несколько) «-»-фотонов, то два (или более) фотонов из этого (или этих) направления поглотятся как реальный квант (или кванты), что ведёт к возбуждению электрона и последующим эффектам (увеличению внутренней энергии тела, химическим реакциям, рентгеновскому излучению и т.д.). Электрон способен «нормально» поглотить только те прилетающие из разных направлений за t_ф поглощения «-»-фотоны, которые прилетают к данному электрону через промежуток времени равный или больший t_е от момента прилёта поглощённого предыдущего «-»-фотона (t_е – время обращения фотонов в электроне – см. ниже) – при интерференции это даёт минимум. Если промежуток времени от момента прилёта предыдущего поглощённого “- ”- фотона до момента прилёта данного “-” фотона меньше t_е, то данный фотон не может нормально поглотиться данным электроном и “отражается”, т.е. излучается в следующий же t_ф испускания – при интерференции это даёт максимум. При наличии в окружающем тело пространстве излучения (например, оптического) существует вероятность (прямо пропорциональная интенсивности излучения вследствие его некоггерентности в обычных условиях), что кванты излучения прилетят к электронам поверхностных слоёв тела вместе с виртуальными квантами от другого тела и поглотятся в виде реальных квантов или отразятся.

Рассмотрим интерференцию коггерентного света при полёте фотонов от двух щелей (А и В) к произвольно выбранной на экране точке С (рис. 12).

|АС-ВС| = ∆L - разница длины пути полёта фотонов. Расстояние между соседними фотонами в луче равно длине волны λ. Если

∆L = n λ (32)

(n – натуральное число), то фотоны, летящие по лучам АС и ВС, попадают в точку С одновременно (с частотой υ ) – они не могут «нормально» поглотиться и отражаются (испускаются в следующий же t_ф испускания) с той же частотой υ – возникает максимум. Если

∆L = (2n + 1)	λ	(33)
	2

то фотоны из лучей АС и ВС попадают в точку С попеременно (с частотой 2υ ) – поверхностный электрон в точке С за t_ф поглощения «нормально» поглощает фотоны излучения в виде виртуальных квантов – возникает минимум.

В

С

А

Рис. 12.

Рассмотрим пролёт через две щели параллельного потока элементарных частиц, например электронов, и картину, возникающую при этом на экране (рис.13). Расстояние между электронами в одном луче равно λ_бе/2 - длина волны де Бройля для электрона (см. ниже).

В

С

А

Рис. 13.

Если

∆L = n	λб	(34)
	2

то электроны от щелей А и В в данную точку C экрана прилетают одновременно, если

∆L =	2n + 1	·	λбе	(35),
	2		2

то электроны прилетают попеременно. Так как взаимодействие между прилетающими электронами и электронами поверхностных слоёв экрана происходит путём обмена фотонами, то возникающая на экране картина соответствует интерференции лучей фотонов с длиной волны λ_б/2. При открытой только одной щели возникает картина (рис. 14), так как в пространстве всегда есть свободные молекулы, атомы и элементарные частицы, на которых происходит рассеяние параллельного потока электронов – на больший угол отклоняется меньшее число электронов – с удалением от прямой проекции щели уменьшается засветка экрана.

Рис. 14.

1.14. ДВИЖЕНИЕ ЭЛЕКТРОНА В АТОМЕ.

В атоме водорода движение электрона описывается уравнениями:

mV^2	=	ke^2	(закон Кулона) (36),
r		r^2

m V r = n ħ (37),

Т =	2π r	(38),
	V

где m – масса электрона, V – скорость его движения по орбите, r- радиус атомной орбиты электрона, е – элементарный заряд, k = 1/ 4πε₀ – коэффициент из закона Кулона, Т – период обращения электрона по орбите, ħ = h/ 2π – постоянная Планка, n- натуральное число – номер атомной орбиты. Из (36) –(38) находим:

rn =	ħ^2n^2	= r1n^2(39),
	e^2 km

Vn =	k e^2	=	V1	(40),
	ħ n		n

Tn =	2π ħ^3 n^3	= T1 n^3 (41),
	E^4 k^2m

где r_1н = 5,29·10 ^–11 м (42),

V_1н = 2,187·10 ⁶ м/c (43),

T_1н = 1,5198·10 ^–16 c (44) -

характеристики первой орбиты в атоме водорода, r_n, V_n, T_n, - те же характеристики для n-ной орбиты. Это следует из теории Бора, экспериментально подтверждённой для атома водорода. Для атомов с зарядом ядра Z>1 надо вместо е² брать (Z-σ) е², вместо е⁴ надо брать (Z-σ)² е⁴, где σ – константа экранирования из закона Мозли. Для первой орбиты для всех элементов σ = 0, для второй орбиты для элементов

2-7 периодов σ = 1, для третьей орбиты для элементов 3-7 периодов σ = 7,5, для четвёртой орбиты для элементов Z = 19 и Z = 20 (4-го периода) σ = 15,75, для последующих элементов (Z ≥ 21) для четвёртой, пятой, шестой и седьмой орбит σ имеет индивидуальное значение для каждого элемента, так как идёт заполнение внутренних орбит атомов – усовершенствованная теория Бора.

Но движение электрона по первой орбите описывается (подобно испусканию фотонов – уравнение (1)) также уравнением:

Еk1 · 2tа =	h	(45),
	2

где Е_k = mV²/2 – кинетическая энергия электрона на первой орбите, t_а – характерное время электрона в атоме. Из (37) и (45) следует, что

ta =	π r1	=	T1	(46) -
	V1		2

полупериод обращения электрона по первой орбите. За это время электрон пролетает расстояние

ℓ_а = π r₁ (47)-

характерное расстояние электрона в атоме – половина длины первой орбиты – минимальное расстояние по орбите (дуга орбиты), на котором могут находиться друг от друга электроны ( t_а и ℓ_а – индивидуальны для каждого химического элемента, так как они зависят от Z). Длина n-ной орбиты

ℓ_n = 2π r_n = 2π r₁ n² = 2 n² ℓ_а (48),

поэтому на n-ной орбите могут разместиться максимум 2n² электронов. Можно сказать, что n-ная орбита имеет 2n² узловых точек. Электроны в соседних узловых точках орбиты имеют противоположно направленный спин и движутся по орбите навстречу друг другу (электроны проходят друг сквозь друга – см. ниже строение электрона) электроны в узловых точках «через одну» имеют одинаково направленный спин и движутся по орбите в одну сторону (рис. 15). Поэтому суммарные M_S (спинновой момент импульса) и M_L (орбитальный момент импульса) заполненной орбиты равны нулю. При застраивании электронами орбиты каждый чётный электрон занимает противоположную узловую точку орбиты по отношению к предыдущему нечётному электрону, каждый нечётный электрон занимает свободную узловую точку орбиты, максимально удалённую от уже заполненных электронами узловых точек орбиты. Аналогично (45), движение электрона, по n-ной орбите можно описать уравнением:

Еkn∙2	Тn	=	n h	(49),
	2		2

где Е_kn = Е_k1/n² (так как V_n = V₁ /n) и Т_n /2 = n³∙Т₁ /2 .

ℓ_а

Рис. 15.

Сравним радиусы атома, вычисленные по формуле (39) (с учётом n, Z и σ) и с использованием экспериментальных макроскопических величин для молярного объёма. Монокристалл, состоящий из атомов только одного химического элемента, представляет собой гигантскую трёхмерную молекулу, образованную «кубиками» атомов с ребром 2r_п (r_п - «практический» радиус атома). Таким условиям удовлетворяет алмаз. Теоретический радиус (r_т) второй (внешней) орбиты атома углерода r_т = r_1(н)n²/(Z-σ)=5,29∙10^–11∙2²/(6-1)=4,232∙10^–11 м, откуда r_т³ = 7,5794∙10 ^–32 м³. Объём 1 моля алмаза равен 8r_n³ N_А = m / ρ,

где N_А –постоянная Авогадро, М – молярная масса, ρ - плотность. Отсюда

r_n³ = М/ 8ρN_А = 12 ∙10 ^–3 / 8∙3,5·10 ³·6·10 ²³ = 7,1428·10 ^–31 м³. Отношение этих радиусов

3 К =	rn^3	= 2,11 (50).
	rт^3

Это говорит о том, что при соединении двух одинаковых атомов в молекулу (обобщении их валентных электронов) расстояние между внешними орбитами атомов равно диаметру самого атома. Схема движения валентных электронов показана на рис. 16. Звёзды “белые карлики” представляют собой гигантский монокристалл железа, причем атомы железа лишены электронов на второй, третьей и четвёртой орбитах (валентными являются электроны первой орбиты). В результате “белые карлики” имеют плотность

ρ = М / 64 N_Аr_1т³_(Fe) = 56·10^–3 /64·6·10²³ · (5,29·10 ^–11 /26)³ =1,73·10 ⁸ кг/м^3.

Рис. 16.

1.15. КВАНТОВАНИЕ СКОРОСТИ.

Пусть электрон движется со скоростью

V = k·c (51)

(К-коэффициент пропорциональности, 0<k<1), его импульс р_е= m_еV (m_е- масса электрона). Сумма модулей импульсов фотонов, составляющих электрон, равна m_ес = n_еm_фc (m_ф – масса фотона, n_е – число фотонов, составляющих электрон). Тогда

р_е = k m_е с= k n_еm_ф c (52)

Можно представить, что каждый фотон “отдаёт” только часть (равную k) своего импульса на создание импульса электрона, или другими словами, что только некоторые фотоны (из составляющих электрон) участвуют в создании импульса электрона (их число n_ф, причем n_ф= k n_е). Тогда

р_е = n_фm_фc (53).

Кинетическая энергия электрона

Ек =	mеV^2	= k^2	mеc^2	= k^2 Eе (54)
	2		2

где E_е – полная энергия электрона. Так как n_ф не может по смыслу быть больше n_е, то у электрона (как и у всех других элементарных частиц) V ≤ с относительно любых других частиц, с которыми он способен взаимодействовать. Минимально возможное (не нуль) значение модуля скорости электрона будет при n_ф =1, т.е.

Vе min =

c nе

(55)

Для протона это значение в 1836,16 раза меньше (так как масса протона m_р = =1836,16 m_е, откуда число фотонов, составляющих протон, n_р = 1836,16 n_е)

Vр min =	c	(56)
	nр

Для тела массой m минимальное значение модуля скорости во столько же раз меньше с, сколько фотонов содержится в данном теле

V min =	c	(57)
	nф

Понятно, что любое возможное значение модуля скорости для любого тела в целое число раз больше V _min для этого тела:

V = n V_min (58),

где n – натуральное число – квантование скорости. Отсюда ясен физический смысл массы: масса – это показатель числа фотонов, составляющих данное тело, или другими словами, это коэффициент пропорциональности между скоростью тела и его импульсом.

1.16. ВКЛАД ФОТОНА В ИМПУЛЬС И ЭНЕРГИЮ ЭЛЕКТРОНА.

Вернёмся к электрону. Пусть под действием какой-то электрической силы данный электрон воспринял импульс ещё ∆n фотонов, его скорость возросла

до V+∆V (масса электрона не изменилась – см. выше), его импульс стал

n_е m_ф (V+∆V) = (n_ф+∆n) m_ф c, его кинетическая энергия стала

n_е m_ф (V+∆V) / 2 = ((n_ф+∆n)/n_е)² n_е m_ф c²/2.

Из законов сохранения импульса и энергии следует: изменение импульса

∆р = ∆n mф c, откуда ∆V =	∆n	c (59),
	ne

изменение кинетической энергии

∆Ек =	2nф∆n+∆n^2	*	mф c^2	(60),
	ne		2

т.е. каждый фотон, импульс которого воспринят, способствует проявлению части общей энергии электрона в виде его кинетической энергии, эта часть равна

2nф + 1	*	mф c^2	(61),
ne		2

где n_ф = n_e V/c, т.е. эта часть для каждого из воспринятых фотонов различна, так как зависит от уже достигнутой электроном скорости.

1.17. ЧИСЛО ФОТОНОВ В ЭЛЕКТРОНЕ.

При движении по первой орбите в атоме водорода за время t_ф электрон воспринимает импульс n фотонов, испущенных протоном. Так как скорость электрона при этом равна V₁ (43), что составляет V₁/с = 1/ 137,06≈1/137 часть скорости света, то n = n_e /137. Кинетическая энергия электрона в этом случае составляет 1/137² часть его полной энергии. Естественно предположить, что электрон содержит фотонов больше во столько же раз, со сколькими фотонами он взаимодействует за время t_ф при обращении по орбите вокруг протона. Поэтому электрон состоит из

n_e = 137² = 18769 (62)

фотонов. Так как нигде не обнаружено химических элементов 8-го периода, то значит их не существует. Отсюда следует, что разница в числе фотонов, чей импульс за время t_ф воспринимают электроны, обращающиеся по разным атомным орбитам, существуют только до седьмой орбиты включительно. Электроны могут двигаться по восьмой и более высоким атомным орбитам, но переход между седьмой и более высокими атомными орбитами не сопровождается изменением скорости (импульса, кинетической энергии) электрона. Поэтому не может существовать более 280 химических элементов, что соответствует полному заполнению электронами седьмой орбиты и всех нижележащих орбит.

Шаровая молния представляет собой атом обычного химического элемента 2-го или 3-его периода, у которого электронами заполнены все орбиты

до n ≈ 1,0 ∙ 10⁵. Общее число электронов в такой структуре равно около

n³/3 = 3,33∙10¹⁴, их общий заряд 5,33∙10 ^–5 Кл. Радиус шаровой молнии равен около n²r_1н/10 =10¹⁰∙5∙10 ^–11/10 = 5∙10 ^–2 м, диаметр - порядка 10 см. С поверхности шаровой молнии электроны совершают переходы на вакантные места на

2-6 орбитах окружающих атомов, что вызывает свечение шаровой молнии. При попадании заряда шаровой молнии в электрическое поле возникает один из видов разрядов, что сопровождается исчезновением шаровой молнии.

1.18. КОНСТАНТЫ.

Вычислим константы. Масса фотона m_ф меньше массы электрона m_е в n_e раз: m_ф = m_e /n_e =4,848∙10 ^–35 кг. Энергия фотона Е_ф = m_фc² /2 = 2,178∙10 ^–18 Дж, импульс фотона p_ф = m_ф c = 1,4534∙10 ^–26 кг ∙м/с. Из (1) находим

t_ф = n / 4E_ф = 7,599∙10 ^–17c. Период испускания виртуальных квантов

Т_о/2 =2 t_ф=1,5198∙10 ^–16с, что соответствует частоте 2υ_о = 1/0,5Т_о = 6,58∙10 ¹⁵ Гц. «Длина» кванта ℓ_о = сt_ф = =2,278 ∙ 10 ^–8 м, длина волны виртуального кванта

λ_о/2 = 2ℓ_о = 4,556 ∙10 ^–8 м (отсюда λ_о = 9,112 ∙10 ^–8 м = 91,12 нм, что находится на границе между ультрафиолетовым и рентгеновским излучением). (Почему берём Т_о /2, 2 υ_о , λ_о /2, а не Т_о, υ_о, λ_о – см выше).

Период испускания фотонов для гравитационного взаимодействия согласно (28) равен 2t_g = 1,885∙10 ²⁰ c = 5,972∙10¹² лет, «время жизни» протона согласно (29) равно t_v = 2,504∙10¹⁷ лет (что не означает распад протона - см. выше).

Электрон первой орбиты в атоме водорода за один t_ф поглощения (полупериод обращения) взаимодействует с 137 фотонами, испущенными протоном ядра. После этого в течение t_ф излучения электрон испускает фотоны, что на его движение влияния не оказывает. Движение электрона (сила его притяжения к протону ядра) определяется воспринятым импульсом 137 фотонов за время 2t_ф (период обращения). Тогда сила притяжения электрона к протону

F₁ = 137 p_ф /2 t_ф = 1,31∙10 ^–8 Н. Но по закону Кулона F₂= ke²/r_1н² = 8,24∙10 ^–8 Н, что в F₂/ F₁= 6,29 ≈ 6 раз больше. Это означает, что протон (электрон или любой элементарный заряд) за t_ф излучения по разным направлениям испускает

d=137∙6 = 822 (63)

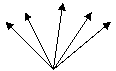
фотона (виртуальных кванта), и только 137 из них воспринимает электрон первой орбиты. Эти 137 фотонов летят в одной полуплоскости (рис. 17-а), все 822 фотона летят в трёх взаимно перпендикулярных плоскостях (рис. 17-б).

137 2

138 1

Рис. 17 а) б)

В следующий t_ф излучения ориентации плоскостей будут другими. Таким образом, закон Кулона носит статистический характер и применим только для вычисления силы взаимодействия макроскопических зарядов за время t >> t_ф , где сила взаимодействия определяется поверхностной концентрацией испущенных фотонов и величиной поглощающего их заряда. Теперь, зная d, вычислим константы электрического взаимодействия (из (5), (8) и (11)). Получаем:

а = 3,345∙10 ^–27В∙с∙м, b = 0,2319 м²·Кл^–1, N_o = 3,376∙10³⁷ с^–1 Кл^–1. Взаимодействие с силой 1 Н соответствует получению импульса 1/ р_ф = 6,9324∙10²⁵ фотонов

за 1 сек.

Минимальное изменение энергии и импульса элементарной частицы соответствует поглощению (излучению) одного фотона. Разделим обе части (1) на 2π, получим Е_ф· t_ф /π = ħ/2. Учитывая Е_ф = m_фc² /2 и ℓ_o =сt_ф , перепишем в виде

m_фc (ℓ_o /2 π) = ħ/2. Обозначая

Еф =∆E,	tф	= ∆t (64),
	π
mфc = ∆p,	ℓo	= ∆x (65),
	2 π

запишем ∆E∙∆t = ħ/2 и ∆p∙∆x = ħ/2 - соотношения неопределённостей. Из (64) и (65) следует, что ∆t и ∆х - константы, смысл которых в том, что при данных и меньших расстояниях и промежутках времени имеющее постоянную напряжённость электрическое поле в отношении данного тела перестаёт быть однородным – в данный момент времени в одних точках пространства фотоны поля есть, в других – нет (дистрофики не промокают под дождём потому, что они гуляют между каплями).

1.19. ЭФФЕКТ КОМПТОНА.

Если на электрон в стационарном состоянии в атоме падает реальный квант 1, состоящий из n₁ «-»-фотонов (модуль его импульса р₁ = n₁m_фс), то электрон за время t_ф поглощения поглотит квант 1 и в следующий t_ф излучения испустит реальный квант 2, состоящий из n₂ «-»-фотонов (n₂< <n₁) (модуль его импульса

р₂ = n₂ m_ф с), в направлении вектора скорости фотонов, составляющих электрон, в точке падения на электрон кванта 1 (рис. 18). При этом (n₁ - n₂) фотонов останутся на некоторое время в электроне, т.е. электрон приобретёт дополнительную энергию (n₁ - n₂)(m_фс²/2), которая проявится в виде его кинетической энергии направленного движения (n_е+n₁-n₂)(m_фV²/2) (дополнительной к его кинетической энергии на орбите в стационарном состоянии), где V– скорость направленного движения электрона после испускания кванта 2. Отсюда

(n₁ - n₂) (m_фс²/2) = (n_е + n₁ - n₂) (m_фV²/2) (66).

р₂ р₂ р_е р₂

р₁ φ р₁ £ φ

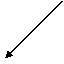£ р₁

р_е

р_е

_{Рис. 18 а) б) в)}

В стационарном состоянии на орбите среднее значение импульса электрона равно нулю (движение по окружности). После излучения кванта 2 электрон приобретает направленное движение и импульс, модуль которого р_е=(n_е+n₁ - n₂) m_фV Угол между р₁ и р₂ равен φ, угол между р₁ и р_е равен £. Из закона сохранения импульса следует р₁ = р₂ cos φ + р_е cos £, откуда cos£ = (р₁ - р₂ cosφ) /р_е, или (по теореме косинусов) cos£ = (р_е² + р₁² - р₂²)/ 2р_е р₁. Приравнивая выражения для cos£, приводя к общему знаменателю, приравнивая числители и перенося их в левую часть, получаем 2р₁²–2р₁р₂ cosφ-р_е² -р₁²+р₂²=0. Откуда р_е²=р₁²+р₂²-2р₁р₂ cosφ, или подставляя выражения для модулей импульсов, ( n_е + n₁ - n₂)² V² =

= (n₁²+n₂²-2n₁n₂ cos φ) с² . Откуда

V^2	=	n1^2+n2^2-2n1n2cos φ	(67).
с^2		(nе+n1- n2)^2

Вместе с тем из (66) следует

V^2	=	n1 - n2	(68).
с^2		nе+n1- n2

Приравнивая (67) и (68), приводя к общему знаменателю и приравнивая числители, получаем (n₁ - n₂)( n_е + n₁ - n₂) = n₁² + n₂² – 2 n₁n₂ cos φ . Откуда

(n₁ - n₂) n_е = 2n₁n₂ (1 - cos φ) и далее (1/ n₂) – (1/ n₁) = (2 / n_е)(1- cos φ). Умножив обе части на ℓ_o, получаем

ℓo	-	ℓo	=	2ℓo	(1- cos φ) (69).
n2		n1		nе

Здесь ℓ_o/n₁ и ℓ_o/ n₂ - расстояния между фотонами в квантах 1 и 2 соответственно, поэтому ℓ_o / n₁= λ₁/2 и ℓ_o / n₂= λ₁/2. Вместе с тем 2ℓ_o /n_е=2ℓ_е=с ·2t_e, где ℓ_е – длина орбиты, составляющей электрон, t_е – период обращения фотонов в электроне (см. ниже строение электрона). Учитывая h/2 = (n_е m_ф c²/2)∙2t_е (см. ниже), имеем

2ℓo	= 2ℓе =	h	= λсе (70) -
ne		me c

длина волны Комптона для электрона. Подставляя эти выражения в (69), получаем

λ2	-	λ1	= λсе (1 – cos φ) (71) -
2		2

формула Комптона.

1.20. ВОЛНА ДЕ БРОЙЛЯ.

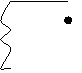
Пусть электроны вылетают со скоростью V = kc (51) из проводника П и попадают на экран Э (рис. 19,а) (проводник и экран в лабораторной системе отсчёта неподвижны).

V V

C B A

П

Э

Рис. 19. а) б)

Из уравнения h /2 = E_e· 2t_e (см. ниже строение электрона) следует

h	= Ek·	2te	(72),
2		K^2

где E_е = m_ec² / 2 - полная энергия электрона, t_е – период обращения фотонов в электроне, E_к = k ²Е_е = m_e V² / 2 (54) – кинетическая энергия электрона. Величину k²/2t_е обозначим 2υ_бе. Тогда из (72) следует

E_к =h·υ_бе (73)

Значит,

2 υБе =	k^2	=	nф^2	(74) -
	2 tе		ne 2tф

частота волны де Бройля для электрона (n_ф = k n_е – см. выше). Так как электрон движется со скоростью V, то и «вероятность его нахождения в пространстве» движется с той же скоростью – скорость волны де Бройля равна V. Отсюда

V = (λ_бе /2)·2 υ_бе, где λ_бе /2 – длина волны де Бройля, которая равна

λбе	=	V	=	k c·2 tе	=	2ℓе	=	2ℓo	(75),
2		2 υбе		k^2		k		nф

или учитывая (72),

λбе	=	V h	=	h	=	h	(76),
2		2 Eеk		me V		pe

где p_e – импульс электрона. Физический смысл: λ_бе/2 – расстояние между летящими друг за другом электронами по одному лучу, 2υ_бе – частота пролёта летящих по одному лучу электронов через данную точку на данном луче. Если скорость V электронов относительно экрана увеличится, то λ_бе/2 уменьшится (так как увеличатся n_ф, k и p_e). Как эта интерпретировать? Если увеличение V связано с увеличением напряжения (силы тока) в проводнике, то расстояние λ_бе/2 между слоями движущихся свободных электронов в проводнике (см. выше) уменьшится. Если же увеличение скорости электронов относительно экрана связано с движением экрана навстречу проводнику (и летящим электроном), то λ_бе/2 уменьшается вследствие того, что экран от момента времени с предыдущим электроном данного луча в точке А (см. рис. 19, б) до момента встречи с данным электроном в точке В пройдёт расстояние АВ и, следовательно, λ_бе/2 будет равна не СА, а СВ = СА – АВ, где С- точка нахождения данного электрона в момент встречи экрана с предыдущим электроном в точке А. Если V =0 (n_ф =0),

то λ_бе/2= ∞ - электрон не достигнет экрана. Если V = с (n_ф = n_е) ,

то λ_бе/2 = 2ℓ_е = h/m_е c = λ_се - длина волны Комптона для электрона.

1.21. СТЕПЕНИ СВОБОДЫ ФОТОНА.

Если рассматривать испускание виртуальных квантов как излучение с максимумом энергии, приходящимся на длину волны λ_о , то по закону смещения Вина это соответствует температуре Т = b/λ_o = 2,898∙ 10 ^–3 /9,112∙10 ^–8 = 31801 K. При такой температуре на 1 степень свободы приходится энергия Е = КТ/2 = =1,38∙10 ^–23 ∙ 31801/2 = 2,195∙10 ^–19Дж ( К – константа Больцмана). Сравнивая эту энергию с энергией фотона Е_ф, мы видим, что

Еф	= 9,92 ≈ 10 (77).
Е

Значит, фотон имеет 10 степеней свободы: одна степень – на движение по прямой в виде квантов, по три степени – на свободное движение в трёхмерном пространстве в составе элементарных частиц каждого из трёх принципиально существующих классов – лептоны, мезоны, барионы – итого: 1 + 3∙3 = 10.

1. ЧАСТИЦЫ.

2.1. ОБЩИЕ ПОЛОЖЕНИЯ.

При движении второго рода в круговой системе (см. выше) фотоны образуют элементарные частицы. При этом могут существовать одно -, двух – и трёхкольцевые структуры – лептоны, мезоны и барионы соответственно

(см. рис. 20).

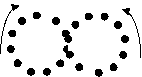
Рис. 20 а) лептон б) мезон в) барион

Образования со временем жизни меньше t_ф являются не элементарными частицами, а переходными состояниями, возникающими в процессе превращения элементарных частиц. Кольца (у мезонов и барионов) лежат в одной плоскости и имеют наружное касание, центры колец (у барионов) лежат на одной прямой. Фотоны двигаются по «восьмёркам» по всем кольцам (в мезоне или в барионе), по окружности (в лептоне) со скоростью с относительно центров колец данной элементарной частицы. Движение фотонов по кольцу (аналогично движению фотонов в виде квантов (1) или движению электрона по атомной орбите (45)) описывается уравнением:

Е ∙ 2t к =	h	(78),
	2

где Е = m_к с²/2 – полная энергия совокупности фотонов кольца, m_к – масса совокупности фотонов кольца, t _к – характерное время фотонов в кольце,

h – постоянная Планка.

Момент импульса совокупности фотонов кольца (спин кольца) равен

mк c rк =	ħ	(79),
	2

где r_к – радиус кольца. Из (78) и (79) следует, что

t к =	2π rk	(80) -
	с

период обращения фотонов в кольце, который (как и радиус кольца) обратно пропорционален полной энергии элементарной частицы (её массе). Все элементарные частицы состоят из электрической и гравитационной частей (хотя в гравитационном взаимодействии участвуют только нуклоны – см. выше), исключения – электрон (всё – электрическая часть) и нейтрино (всё – гравитационная часть). Электрическая часть состоит из n_е фотонов одного знака, располагающихся друг за другом и циркулирующих по кольцам как единое целое. Гравитационная часть состоит из чередующихся групп фотонов разного знака, каждая группа состоит из 137 фотонов одного знака (в нейтрино имеется по одной неполной группе – из 81 фотона – каждого знака).

2.2. ЭЛЕКТРОН

Электрон представляет собой однокольцевую структуру (рис. 20, а), состоящую из n_е «-»-фотонов. Из (79) следует, что радиус невозбуждённого электрона r_е = 1,93·10 ^-13 м, что в r_е/ r_1н = 274,1 раза меньше радиуса первой боровской орбиты в атоме водорода (что приблизительно равно 280 – порядковому номеру – заряду ядра – самого тяжёлого «последнего» теоретически существующего химического элемента – см. выше). Длина орбиты, составляющей электрон, ℓ_е= 2π r_е = 1,21·10^–12 м. Расстояние между фотонами, составляющими электрон, ℓ_ео = ℓ_е / n_е = 6,46·10^–17 м. Период обращения фотонов в электроне t_e = ℓ_e /c = 4,036·10 ^–21 с.

Расстояние между фотонами в гамма-кванте, образующемся при аннигиляции электрона, равно ℓ_eﻻ = ℓ_о/n_e = h/ n_e m_ф c = ℓ_e =1,21·10^–12 м (это следует из ℓ_о = с t_ф, (1), (79) и ℓ_e = 2 π r_e). Вообще, ℓ_e – предел, при котором прямолинейное движение фотонов переходит в круговое: если расстояние между фотонами больше или равно ℓ_e – то фотоны могут двигаться только прямолинейно, если расстояние между фотонами меньше ℓ_e – то фотоны могут иметь только круговое движение. В любом гамма-кванте расстояние между фотонами λ/2 ≥ℓ_e, поэтому число фотонов в реальном кванте 2 ≤ n ≤ n_e.

Орбитальный момент импульса электрона первой атомной орбиты

М₁ = m_e V₁ r₁ = ħ, орбитальный магнитный момент

μ₁ = IS = - eV₁r₁ /2 = - eħ /2m_e = μ_Б, где I = q/Т₁ = - eV₁/ 2π r₁- сила тока,

S = π r₁² – площадь орбиты, μ_Б – магнетон Бора.

Для n-ной атомной орбиты: М_n = m_e V_n r_n = n ħ = n M₁,

μ_n= - eV_nr_n/2= - e ħ n/2m_e= n μ_Б = n μ₁. Отсюда орбитальное гиромагнитное отношение:

μ	=	- e	(81).
M		2 me

При этом электрон создаёт магнитные явления только в периоды t_ф испускания, за эти периоды электрон пролетает половину длины данной атомной орбиты π r_n . При движении фотонов по орбите электрона ситуация другая: т.к. t_ф >> t_e (в n_e раз -см. (1) и (78)), то испускание фотонов может происходить при движении фотонов по обоим половинам орбиты электрона. Поэтому силу тока можно определить как

I =	-е	=	-е с	(82).
	tе /2		π rе

Отсюда спиновой магнитный момент

μ_S = IS = - e c r_e (83),

здесь S = π r_е² . Так как спиновой момент импульса M_S = m_e c r_e = ħ/2 (79), то

μS =	- eħ	= - μБ (84)
	2me

Отсюда спиновое гиромагнитное отношение

μS МS

=

- е me

(85)

(в два раза больше орбитального).

2.3. НЕЙТРИНО.

Масса нейтрино во столько же раз больше массы электрона, во сколько раз масса нейтрона больше массы протона

mυ =	mn	me =	1838,69 me	Me = 1,00138 me (86).
	mp		1836,16 me

Нейтрино является лептоном и состоит из

n_υ = m_υ / m_ф = 1,00138 n_e = 18794 (87)

фотонов (поровну – по 0,50069 n_e – фотонов обоих знаков, они все составляют – по 68 полных и одной неполной группе фотонов каждого знака - только гравитационную часть, электрической части нет). Подобно нейтрону нейтрино нестабильно. Так как масса нейтрино в 1836,16 раза меньше массы нейтрона, то радиус нейтрино больше радиуса кольца нейтрона (бариона) в 1836,16/3 = 612,053 раза, а расстояние между фотонами в нейтрино больше расстояния между фотонами в нейтроне в 612,053² раз. Поэтому время жизни (период полураспада) нейтрино в 612,053² раз больше, чем у свободного нейтрона ( ≈ 900 с), и равно 3,372∙10⁸ с ≈ 10 лет 8 мес 7 суток, нейтрино распадается на два гамма-кванта разного знака. Так как нейтрино не стабильно и в нём нет электрической части, то оно не участвует в гравитационном и электрическом взаимодействиях, поэтому нейтрино трудно обнаружить. Не существует разных видов нейтрино (электронное, мюонное и тау), это одна частица. Поэтому распад мюона выглядит как μ^– = е^– + υ + υ . Избыточные фотоны ≈ 204n_e (так как масса мюона ≈ 207m_e) – по 102 n_e фотонов каждого знака – распределяется хаотично между образующимися частицами, не нарушая их структуры (некоторая часть фотонов может сразу излучаться в виде гамма-квантов). Поэтому образующиеся частицы могут иметь разную кинетическую энергию – от 0 до 204 m_e c² /2, чаще – от 1/3 (204 m_e c² /2) = 68 m_e c²/2 до 1/2 (204m_e c²/2) = 102m_e c²/2 - для электронов. В дальнейшем избыточные (над основным состоянием частицы) фотоны излучаются в виде реальных квантов.

Законы сохранения лептонного (или барионного) зарядов заключаются в том, что при любых реакциях превращения элементарных частиц – если до реакции число лептонов (или барионов) (частиц или античастиц - не важно) было чётным (или нечётным), то и в результате реакции число лептонов (или барионов соответственно) останется также чётным (или нечётным соответственно) (ноль будем считать чётным числом). Выполнение этих законов обеспечивается стабильностью структуры расположения и движения фотонов по орбитам, составляющим самые лёгкие из данных классов частиц – электрон и протон. Рождение и аннигиляция частиц (лептонов или барионов) происходит парами, но парой не обязательно является античастица.

2.4. ПРИНЦИП ЗАПРЕТА.

У двух одинаковых фермионов (лептонов или барионов) с однонаправленными спинами направление движения фотонов в ближайших друг к другу участках этих частиц будет противоположным (рис. 21, а).

Рис. 21 а) однонаправленный спин б) противоположно направленный спин

Поэтому одинаковые фермионы с однонаправленными спинами не могут находиться рядом друг с другом (в одном квантово-механическом состоянии – принцип запрета Паули). При сближении такие частицы либо аннигилируют, либо изменят направление своей скорости и отдалятся друг от друга. У двух одинаковых фермионов с противоположно направленными спинами направление движения фотонов в ближайших друг к другу участках этих частиц будет совпадать (рис. 21, б), такие частицы могут находиться рядом друг с другом (быть спаренными). У данного мезона направление спина в одном из двух составляющих его колец всегда будет противоположным по отношению к направлению спина ближайшего кольца рядом расположенного другого мезона.

2.5. МЕЗОНЫ.

Мезоны имеют двухкольцевую структуру (рис. 20, б). Масса ( число) фотонов в одном кольце равна половине массы (числа) фотонов в мезоне. В заряженных мезонах число фотонов соответствующего знака на n_e больше числа фотонов противоположного знака, этот избыток n_e фотонов данного знака формирует электрическую часть, остальное – гравитационная часть. В нейтральных мезонах содержится поровну фотонов обоих знаков, имеются две электрические части противоположного знака, остальное – гравитационная часть; в нейтральном пионе электрические части циркулируют по противоположным орбитам, в нейтральном каоне электрические части циркулируют непосредственно друг за другом – отрицательная за положительной: этим объясняется нарушение комбинированной чётности при распаде нейтрального каона. Вследствие нестабильности мезоны в гравитационном взаимодействии не участвуют. Спин каждого кольца равен ħ/2 , но спины колец разнонаправлены, поэтому общий спин мезона равен нулю. Поэтому, если масса мезона в х раз больше массы электрона, то радиус кольца мезона (r_km ) в x/2 раз меньше радиуса электрона (r_е)

rkm =	2	re (88) -
	x

в соответствии с (79). Нейтральные пионы распадаются на несколько сотен гамма-квантов одного знака и столько же гамма-квантов противоположного знака, эти две группы гамма-квантов разлетаются в две противоположные стороны. Распад заряженного мезона и нейтрального каона идёт через стадию диссоциации орбит, каждая из которых сразу же после этого излучает определённое число фотонов обоих знаков в виде гамма-квантов с переходом оставшегося числа фотонов на орбиту большего радиуса – образуются два лептона.

2.6. ПРОТОН.

Протон имеет трёкольцевую структуру (рис. 20, в) и состоит из

n_p = 1836,16 n_e = 3,4463· 10⁷ (89)

фотонов обоих знаков. «+»-фотонов на n_e больше, чем «-» -фотонов, этот избыток «+» -фотонов формирует положительную электрическую часть, которая занимает на одном из колец дугу в 360·3/1836,16 = 0,588˚ = 0˚35΄16,8˝ , которая циркулирует по всем трём кольцам. Всё остальное – гравитационная часть. Спин каждого кольца равен ħ/2, спин соседних колец разнонаправленный, поэтому общий спин протона равен ħ/2 и имеет то же направление, что и спин боковых колец. Число (масса m_k = m_p/3) фотонов в каждом кольце одинаково и равно

nk =		= 612,053 ne (90).
	np 3

Радиус кольца, учитывая (79), равен

rk =	re	= 3,1533·10 ^–16 м (91).
	612,053

Длина протона

d_p = 6 r_k = 1,892·10 ^–15 м (92)

(что соответствует формуле для диаметра ядра атома d_я = 1,3·10 ^–15A^⅓ м ,

где А- массовое число ядра). Длина орбиты протона (длина трёх колец)

ℓ_p = 3∙2∙π r_k = 5,9438·10 ^–15 м (93).

Время пролёта фотонов по всем трём кольцам в протоне

tp =	ℓp	= 1,98·10 ^–23 c (94)
	c

(что совпадает с временем жизни резонансов). Расстояние между фотонами в протоне

ℓpo =	ℓp	=1,7247·10^–22м (95),
	np

т.е. в 612,053² = 374655 раз меньше, чем в электроне.

+ +

а) б)

Рис. 22.

Магнитный момент протона обусловлен циркуляцией его положительной электрической части. Если бы протон состоял из одного кольца, то его магнитный момент μ_S был бы равен μ_S = e ħ /2m_p = 1μ_я (μ_я -ядерный магнетон). Но μ_S = 2,79 μ_я. В тот период времени, когда электрическая часть циркулирует по одному из боковых колец (рис.22,а), μ_S = e ħ /2m_к = 3μ_я (так как m_к = m_p/3). В тот период времени, когда электрическая часть циркулирует по среднему кольцу (рис.22,б),

μ_S = -3μ_я (так как спин среднего кольца имеет противоположное направление). За большой промежуток времени (по сравнению с t_p ) электрическая часть 96,5% времени циркулирует по боковым кольцам, а 3,5% времени - по среднему кольцу. В результате среднее значение магнитного момента протона

μ_S = (0,965·3 – 0,035·3)μ_я = 2,79μ_я .

2.7. НЕЙТРОН.

Нейтрон также имеет трёхкольцевую структуру (рис. 20, в) и состоит из

n_n = 1838,69n_e = 3,451·10⁷ (96)

фотонов ( поровну обоих знаков). Размеры колец, расстояние между фотонами, время пролёта фотонов по кольцам - приблизительно равны соответствующим значениям в протоне (из-за приблизительного равенства масс протона и нейтрона). Спин боковых колец совпадает по направлению со спином нейтрона, а спин среднего кольца противоположен им, поэтому общий спин нейтрона равен ħ/2. Нейтрон имеет положительную и отрицательную электрические части, каждая из которых состоит из n_е фотонов соответствующего знака. Всё остальное – гравитационная часть. Отрицательная электрическая часть постоянно циркулирует по одному боковому кольцу. Положительная электрическая часть циркулирует по другому боковому и среднему кольцам, переходя через определённые промежутки времени с одного кольца по другое:

68	1	%	времени – по другому боковому кольцу (рис. 23, а)
	6
(при этом магнитный момент нейтрона равен нулю),				31	5	% времени -
					6

по среднему кольцу (рис. 23, б) (при этом магнитный момент нейтрона

равен – 6μ_я).

– + – +

а) б)

Рис. 23.

В результате среднее значение магнитного момента нейтрона равно

μS = 68	1	∙	0	– 31	5	∙	6	μя = –1,91 μя	В свободном нейтроне
	6		100		6		100

отрицательная электрическая часть через некоторое время ( ≈ 900 с ) вылетает из бокового кольца за пределы нейтрона, увлекая за собой по 0,765 n_e прилежащих фотонов каждого знака: вылетевшие фотоны организуются в электрон, нейтрино и гамма-кванты, оставшиеся в кольцах фотоны формируют протон – происходит β^– - распад. Боковые кольца протонов и нейтронов, имеющие противоположный спин, могут спариваться, образуются многокольцевые трёхмерные структуры – атомные ядра (рис. 24). При спаривании колец освобождаются «лишние» фотоны, что вызывает дефект массы ядра и большую энергию связи. Если боковое кольцо нейтрона с отрицательной электрической частью спарено с боковым кольцом протона – нейтрон стабилен, если не спарено – происходит β^- -распад (атомное ядро радиоактивно).

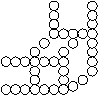
Рис. 24.

2.8. ОТСУТСТВИЕ ЧЁРНЫХ ДЫР.

Учитывая данное строение атомных ядер, вычислим плотность ядра

ρя ≈	3 mp	= 7,406 ∙10^17 кг/м^3 (97).
	dp^3

Нейтронные звёзды представляют собой гигантское атомное ядро, электронов внутри себя не содержат и атомных структур не образуют. Если Земля сожмётся до своего гравитационного радиуса r_g = 9 ∙10^{-3 м (масса Земли m = 6∙1024} кг), то она превратится в чёрную дыру, плотность которой

ρ =	m	= 2∙10^30 кг/м^3		Вычислим плотность фотона (в качестве
	4	π rg^3
	^3
радиуса фотона ориентировочно примем ℓpo/2 ≈ rф )
ρф =	mф		= 1∙10^31 кг/м^3.	Отсюда следует, что в чёрных дырах
	4 ^3		π rф^3

фотоны должны располагаться «вплотную» друг к другу и не могут образовывать ни квантов, ни элементарных частиц. С точки зрения данной теории это невозможно (см. выше), поэтому чёрные дыры в природе не существуют.

2.9. АНТИЧАСТИЦЫ.

Кольца в мезонах и барионах являются образованиями, которые было принято называть кварками или партонами, они не представляют собой отдельных частиц и не могут быть выделены в свободном состоянии. Отсюда также ясно, что пи-мезоны не являются носителями взаимодействия между нуклонами, и не существует носителей взаимодействия между кольцами – глюонов. Если в какой-либо элементарной частице одномоментно каждый из составляющих её фотонов заменить на фотон противоположного знака, не меняя направление его движения, то получится античастица по отношению к данной частице. Поэтому, позитрон состоит только из n_е положительных фотонов, антипротон имеет отрицательную электрическую часть, антинейтрон имеет циркуляцию положительной электрической части только по боковому кольцу и циркуляцию отрицательной электрической части по другому боковому и среднему кольцам, в нейтральном антикаоне положительная электрическая часть следует за отрицательной, а нейтрино и нейтральный пион античастиц не имеют. Законы сохранения лептонного и барионного зарядов (см. выше) отнюдь не требуют обязательного равенства частиц и античастиц во Вселенной.

2.10. КРАСНОЕ СМЕЩЕНИЕ.

Рассмотрим излучение с λ/2 > λ_о/2 от далёких источников – квазаров. Некоторые из фотонов в каждом луче будут поглощаться веществом межгалактической среды, которое представлено в основном атомами водорода (протон и связанный с ним электрон) и имеет плотность ρ = 1∙10^-28 кг/м³ . Пренебрегая массой электрона, получаем, что в 1 м³ пространства содержится ρ/m_ф = 0,0625 протона (точнее в 16 м³ содержатся 1 протон и 1 электрон). В прямоугольном параллилепипеде, две противоположные грани которого имеют площадь по 1 м² и перпендикулярны потоку фотонов (лучам), а расстояние между ними равно 1 мегапарсек (1 Мпк = 3,086 ∙10²² м ) (рис. 25), содержится

N = 0,0625∙3,086∙10²² =1,85∙10²¹ протонов (и столько же электронов).

Рис. 25.

Сумма площадей проекций этих протонов и электронов (точнее, сумма площадей орбит, составляющих их фотонов) на грань в 1 м² определяется суммой площадей проекций электронов (площадь проекции протона в r²_e /3r_pk² > 10⁵ раз меньше площади проекции электрона, поэтому площадью проекции протона мы пренебрегаем). Сумма площадей проекций всех электронов в этом параллелепипеде S = N π r_e² = 2,22∙10 ^–4 м² (так как плотность вещества очень мала, то проекции электронов не прикрывают друг друга). Значит, если плотность потока лучей одинакова на площади грани в 1 м² , то вероятность того, что данный луч встретит в данном параллелепипеде одну из находящихся в нём элементарных частиц (при этом поглотится один фотон из данного луча), составляет

Р = S/1 = 2,22∙10^–4. Следовательно, в каждом луче в среднем поглощается каждый из 1/Р = 4504,5 фотонов (2 фотона из 9009). Значит, если в одном луче в данный параллелепипед за 1 с влетает υ₁ фотонов, то вылетит из него в этом луче за 1с

υ₂ = (1– 2,22∙10^–4) υ₁ фотонов. Такое уменьшение частоты интерпретируется как увеличение длины волны – «красное смещение». С точки зрения эффекта Доплера это соответствует удалению источника излучения со скоростью V, которая находится из (1–2,22∙10^–4)υ₁ = (1–V/с)υ₁. Отсюда V = 6,65∙10⁴ м/c = 66,5 км/с, что находится в пределах принимаемых значений постоянной Хаббла

Н = 50 – 100 км/с∙Мпк. Поэтому, расширения Вселенной не происходит. После поглощения этих фотонов через некоторое время происходит их излучение, но, вследствие хаотичности движения атомов водорода в межгалактическом пространстве, равновероятно во всех направлениях, это формирует изотропное излучение одинаковой интенсивности во времени – реликтовое излучение.

2.11. СРЕДНЯЯ ПЛОТНОСТЬ ВСЕЛЕННОЙ.

Если рассматривать Вселенную как замкнутую систему, то следует принять, что её энтропия является постоянной величиной: если в одном месте энтропия понижается, то одновременно в другом месте энтропия повышается, и наоборот. Рождение и гибель звёзд и галактик являются флуктуациями.

Силы отталкивания повышают энтропию, а силы притяжения понижают её. Стационарность Вселенной обеспечивается равенством интенсивностей сил отталкивания и притяжения.

Рассмотрим силы, действующие между двумя атомами водорода в межгалактической среде. Сила притяжения между атомами (припишем ей знак «-» ) складывается из электрической силы между протоном одного и электроном другого атома и из гравитационной силы между протонами. Сила отталкивания между атомами (припишем ей знак « + » ) складывается из электрических сил между электронами и между протонами. Рассмотрим суммарную электрическую силу, действующую на данный атом со стороны другого атома,

Fe =	ke^2	. Вынесем за скобки ke^2и будем вычислять	1	суммарной электри -
	R^2		R^2

ческой силы, учитывая её знак. Исходя из плотности этой среды, среднее расстояние между атомами равно а = 2,5 м (расстояние между протонами). Расстояние между протоном и электроном в одном атоме равно b = 5,29·10^–11 м (радиус первой боровской орбиты в атоме водорода). Расстояние между электронами и расстояние между электроном одного и протоном другого атома меняются во времени (из-за движения электрона по орбите). Возможны несколько

«крайних» вариантов взаимного расположения электронов и протонов (см. рис.26)

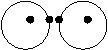
а) б) в) г) д)

Рис. 26

Рис. 26 в) включает 2 варианта (электроны слева и справа от протонов),

рис. 26 г) включает 4 варианта (электроны сверху и снизу - и аналогично ещё 2 варианта в горизонтальной плоскости), также 4 варианта включает рис. 26 д) – итого 12 вариантов.

В случае а)	1	=	1	+	1	-	2	≈	6 a^2 b^2+ 12 ab^3 + 4 b^4
	R^2		a^2		(a + 2b)^2		(a+ b)^2		a^6

В случае б)	1	=	1	+	1	-	2	≈	6 a^2 b^2+ 12 ab^3 + 4 b^4
	R^2		a^2		(a - 2b)^2		(a - b)^2		a^6

В случае в)	1	=	2	-	1	-	1	≈	- 6 a^2 b^2+ 2 b^4
	R^2		a^2		(a + b)^2		(a - b)^2		a^6

В случае г)	1	=	2	-	2	≈	2b^2	=	2 a^2 b^2
	R^2		a^2		а^2 + b^2		a^4		a^6

В случае д)	1	=	1	+	1	-	2	≈	- 2 a^2 b^2+ 4 b^4
	R^2		a^2		a^2 + 4b^2		a^2 + b^2		a^6

Среднее значение1/
	R^2

1	=	28b^4	=	7b^4	(98)
R^2		12a^6		3a^6

Итак, среднее значение силы электрического взаимодействия между «соседними» атомами водорода в межгалактической среде равно F_e= 1,726∙10^–71 Н, и имеет вид отталкивания.

Гравитационная сила между протонами соседних атомов в этой среде равна

Fg =	G m^2p	= 2,976 ∙ 10 ^– 65 Н, и имеет вид притяжения. В результате, силы
	a^2

притяжения между атомами водорода в межгалактической среде в

Fg	= 1,724∙10^6 раз больше сил отталкивания. Это приводит к конденсации ве-
Fe

щества и образованию галактик.

Вычислим среднее расстояние а между атомами водорода, при котором

силы притяжения равны силам отталкивания:		ke^2 ∙ 7b^4		=		G m^2p	.Отсюда
		3a^6				a^2
а = 6,9 ∙ 10^-2 м, что соответствует плотности в	2,5^3		=		47560 раз больше
	6,9^3 ∙ 10^-6

плотности межгалактической среды, а именно 4,726 ∙ 10⁴ ∙1∙10^-28 ≈ 4,8∙ 10^-24 кг/м³, которая является средней плотностью вещества во Вселенной, обеспечивающей её стационарность.

В системах, в которых среднее расстояние между атомами меньше 6,9∙10^-2м, силы отталкивания превышают силы притяжения, и начинает действовать второй закон термодинамики.

3. ЗАКЛЮЧЕНИЕ.

Данная теория соответствует физическим законам и фактам (на них имелись ссылки), но также даёт новую информацию. Например, кажущаяся независимость скорости света от скорости приёмника относительно источника света обусловлена не изменением качеств пространства и времени (которые сами являются качествами материи), а постоянством энергии и импульса фотона во всех инерциальных системах отсчёта. Также из данной теории следует отсутствие рождения Вселенной в результате «большого взрыва» и отсутствие «тепловой смерти» Вселенной.

Интересно, что данная теория имеет соответствия с разными древними философскими системами. Так, в индийской философии санкхья рассматривается первоматерия пракрити (фотоны), обладающая тремя гуннами (свойствами): саттва – гармония (круговое движение фотонов), раджас – источник движения (испускание квантов), тамас - препятствие движению (поглощение квантов). В Библии (Бытие, гл.1) говорится, что Бог сначала создал небо и землю (положительные и отрицательные фотоны), потом создал свет и отделил его от тьмы (создание квантов и элементарных частиц ), потом твердью (небом) разделил воды (создание звёзд и планет), а потом создал сушу и море. В средние века английский философ Роберт Гроссетест считал свет первоматерией и сводил все законы природы к геометрии.

То, что данная теория соответствует философским законам (единства и борьбы противоположностей, перехода количественных изменений в качественные, отрицания отрицания), мы думаем , ясно любому читателю.

Сухих Иван Николаевич,

Тульская обл., Щёкино.

Литература:

1. Советский энциклопедический словарь. М., «Советская энциклопедия», 1990.

2. Савельев И.В. Курс физики. М., «Наука», 1989. т.3.

3. Бедняков В.А. О происхождении химических элементов. ЭЧАЯ. т.33, вып.4, 2002, стр. 915-963.

4. Мамедов Т.Н., Стойков А.В., Горелкин В.Н. Исследование взаимодействий акцепторной примеси алюминия в решётке кремния μ^– - SR - методом. ЭЧАЯ. Т.33, вып. 4, 2002,

стр. 1005-1039