ЗОЛОТАЯ ПРОПОРЦИЯ, ФРАКТАЛЫ И ХАОС
В СВЯЗИ С НЕКОТОРЫМИ ПРЕДСТАВЛЕНИЯМИ
О МИРОЗДАНИИ
Сокольчук К.Ю., Остапович В.В. (Научно-технический центр «Булат НВР»,
г.Киев, Украина)
Определение. Фракталом будем называть структуру, состоящую из частей, которые в каком-то смысле подобны целому. Сам термин "фрактал" означает "дробный". Когда вы всматриваетесь во фрактальную форму, то видите одну и ту же структуру независимо от степени увеличения. Такое подобие можно увидеть в природе, рассматривая при разном приближении горы, облака, береговые линии и т.п. Его можно встретить, исследуя формы молекул или галактик. Фрактальность стремительно становится одной из самых емких метафор для объяснения и понимания мира.
Однако абсолютно точного определения фрактала не существует. Возможно, когда-нибудь оно будет найдено, но такого может и не случиться ввиду того, что фрактальная геометрия есть геометрия природы. Дефиниция фрактала стоит в одном ряду с дефиницией природы.
Концепция фрактальности мироздания и отдельных его элементов возникла во второй половине ХХ века в рамках новой научной парадигмы, объединяющей синергетику, кибернетику, информатику и другие теории, имеющие универсальное значение для любых явлений бытия. Фрактальная гипотеза базируется на представлениях теории хаоса и нелинейных динамических систем. В силу этого, а также некоторых других свойств (иерархичность структуры, обратная связь, чувствительность к начальным условиям и т.п.), фрактальные объекты обладают повышенной устойчивостью и приспособляемостью к внешним условиям по сравнению со статическими системами.
Математический алгоритм построения фракталов мироздания. Для математического моделирования построения фракталов, как нелинейных динамических систем, общепринято использовать рекуррентные формулы. Объекты, построенные с помощью рекурсии, обладают внутренним самоподобием и устойчивостью к ошибкам (случайным и систематическим). Кроме того, и это представляется важным, рекурсия – необходимое свойство автокреационных (т.е. строящих сами себя) систем. Нами в качестве алгоритма был выбран суммационный ряд Фибоначчи, т.к. в различных объектах природы (прежде всего, «живой») он проявляется слишком часто, что бы это было случайностью.
Результаты моделирования фрактальных объектов Фибоначчи.
Следуя работам проф. А.П.Стахова, обобщим формулу Бине (генерирующую ряд Фибоначчи) на множество всех действительных чисел. Полученную функцию:
F(x) =( φx-(-φ)-x)/√5
(1)
будем называть «программа Фибоначчи». Как и для ряда Фибоначчи, для нее на множестве действительных чисел выполняются соотношения:
F(x+1) = F(x)
+ F(x-1)
(2)
F(x+1)/F(x)
→ φ при х→
+∞, φ = (1+√5)/2 =
1,6180… (3)
F(x+1)/F(x) → -1/φ при х→ -
∞ (4)
Функция F(x) принадлежит области комплексных чисел, только в отдельных точках выходя в область действительных (при х целочисленном). Фазовый портрет программы Фибоначчи (в общем случае) – спираль и затухающая синусоида (рис.1) вдоль оси Х (действительной части комплексного числа).

![]()
![]()
![]()

а)
б)
Рис.1. Фазовый портрет
обобщенного ряда Фибоначчи на плоскости комплексных чисел (а) и положение спирали программы Фибоначчи в
пространстве (б).
Уравнение (2) , как функцию от начальных условий х0 , х1 и количества циклов х, представим в виде:
F(x+1, x0,
x1) = x1*F(x) + x0*F(x-1) (5)
Уравнение (5) описывает множество неких дискретных объектов, построенных по программе Фибоначчи, структура которых подобна, а отличие заключается лишь в масштабных (выбор начальных условий х0 и х1) и (или) временных (х – количество циклов) параметрах. Т.о., мы имеем дело с программой (обобщение формулы Бине), обеспечивающей рекуррентные соотношения в области комплексных чисел. Следуя представлениям, развитым Б.Мандельбротом, это необходимо и достаточно для образования фрактальных объектов в определенной области (х, х0, х1). Учтем, что подобие иерархических структур, выражаемое через золотое сечение φ, приближается к идеальному с ростом х (количества циклов), и выбор максимально отличных друг от друга начальных условий (на порядки) лишь несущественно увеличивает количество циклов для достижения требуемой точности оценки φ. Тогда весь пространственно-временной континуум можно представить как единый фрактальный объект, отдельные элементы которого являются аттракторами фракталов следующего, более низкого иерархического уровня.
Рассмотрим вопрос внутреннего подобия этой структуры более подробно. Развертка по времени (т.е. х0 и х1 – const) обеспечивает подобие соседних иерархических уровней, выражаемое как φ (что очевидно, в соответствии с формулой (3)). Не требует доказательства и то, что для уровней х и х-2 подобие выражается как φ2. В общем случае для уровней х и х-n, их отношение равно φn. В области отрицательных значений циклов х подобие в общем случае имеет вид: 1/(-φ)n. Развертку в пространстве рассмотрим на примере х и х1 – const, а переменной будет х0. При х0= 0 или 2 и х1 = 1 имеем, соответственно, тривиальные ряды Фибоначчи и Люка. Их отношение (что следует просто из формулы Бине) при одинаковом количестве циклов х равно √5 или, что тоже самое: φ + 1/φ. В случае х0 = 3 (т.е. ряд, следующий после Люка) отношение выражается как φ2 + 1/φ3=2,854… Дальше картина принципиально не изменяется. Подобие при пространственной развертке может быть записано с помощью только двух чисел – 1 и φ, а также элементарных математических операций с ними (+, -, *, : ). Вероятно, можно вывести и общую формулу. Таким образом, если «наш мир» построен по программе Фибоначчи, мы должны во всех многочисленных его проявлениях находить каким-то образом «золотое сечение» - φ. В действительности это наблюдается, главным образом, у материальных объектов, которые принято называть «живой» материей. Причина заключается, на наш взгляд, в том, что в большинстве случаев мы рассматриваем развертку объекта в сечении, где переменными являются все три параметра – х, х0, х1. Например, периодическая система элементов Менделеева. Все элементы образовывались на различных циклах (этапах) развития Вселенной и при различных начальных условиях (условно говоря – температура, масса, энтропия и др. характеристики аттракторов). Искать в их структуре какое-то регулярное подобие, выражаемое численно через φ и 1, дело бессмысленное. Аналогично, массы планет или их радиусы, или радиусы орбит вращения не удается описать через «золотую гармонию», несмотря на многочисленные попытки. С другой стороны, объекты «живой» материи, и человек в том числе, как целостные объекты с фиксированными начальными условиями и возможностью наблюдения их на всех циклах развития несут в морфологическом строении и функционировании гармонию, выражаемую через φ. (Фактические данные мы не приводим, они есть на сайте «Музей золотой гармонии», созданном проф. А.П.Стаховым).
Т.о., структура и топология нашей
Вселенной может быть закодирована с помощью только двух чисел – 1 и φ в
рамках описания развития, как выполнения программы Фибоначчи. Очевидно, эти
числа первичны, поскольку с их помощдвухью записана и выполняется программа.
Как появились они, в то время когда Творец еще только «писал» программу построения
Вселенной? Представим себе, что
программа в виде символов написана, структурирована или упакована (термины
могут быть любыми) как автокреационный объект, у которого каждый последующий
уровень есть функция двух предыдущих
(программа Фибоначчи). Выберем три соседних иерархических уровня.
Значение φ просто следует из отношения ближайших уровней. Отношение трех
соседних уровней фактически сводится к известному соотношению: φ2 = φ + 1 или φ2
– φ = 1. Таким образом, сама запись программы генерирует два первочисла
φ и 1. Как показано проф. Стаховым А.П., системы счисления и кодирования
информации с использованием φ имеют
преимущества перед другими (десятичная, двоичная и пр.) в части нахождения
ошибок, их дифференциации и исправления. Для корректного выполнения программы
развития эти свойства представляются исключительно важными.
Взаимодействие объектов программы Фибоначчи
и их графика.
Принимая концепцию (или гипотезу) глобального взаимодействия объектов Мироздания, на настоящем этапе исследования в качестве механизмов взаимодействия фракталов мы применяли элементарные алгебраические операции сложения, умножения и т.д. Для отображения получаемых структур использовалась компьютерная 3-D графика. Следует учитывать, что возникающие при взаимодействии фракталов структуры в общем случае n-мерны, поэтому получаемые изображения по сути являются трехмерными сечениями в «плоскости» циклов развития отдельных составляющих.
А) Счетчики циклов развития взаимодействующих объектов совпадают.
![]()
![]()
![]()
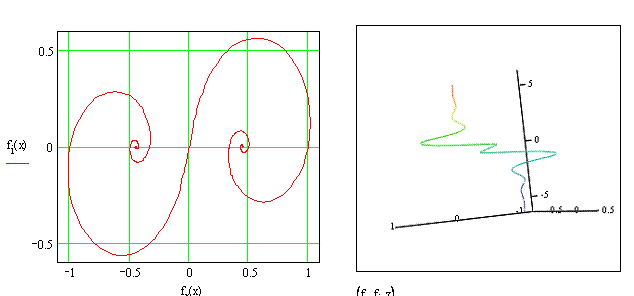
Рис.2а
Рис.2б
Рис.2 Фазовый портрет (2а) и вид в трехмерном
пространстве (2б) объекта, полученного из отношения объектов Фибоначчи и Люка
(начальные условия 0 и 1 ; 2 и 1, соответственно). Обозначения на рис.2б – оси Х и У –
действительная и мнимая часть объекта, ось Z – счетчик циклов (один для
Фибоначчи и Люка).
Фазовый портрет объекта (рис.2а) в целом очень похож на известное символьное изображение принципа Мироздания:

Очевидно, неслучайно, в некоторых работах ряды Фибоначчи и Люка рассматривают как мужское и женское начало (Инь и Ян). Не последнее место узор рисунка 2а занимает и в философско-художественных представлениях людей, проживавших на нашей земле.
Б) В случае, когда счетчики циклов взаимодействующих объектов не совпадают, вместо параметрических кривых (рис.1б и 2б) мы получаем трехмерные поверхности как сечения «плоскостью» циклов (времени).
![]()
![]()
![]()
![]()
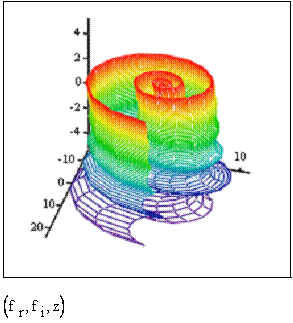
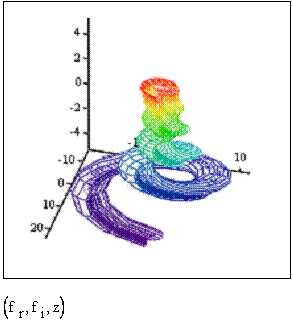
Рис.3.
Сложение фракталов Фибоначчи и Люка. Координатные оси в горизонтальной
плоскости – действительная и мнимая часть суммы. По вертикали – счетчик циклов
(слева – для фрактала Фибоначчи, справа – для Люка).
![]()
![]()
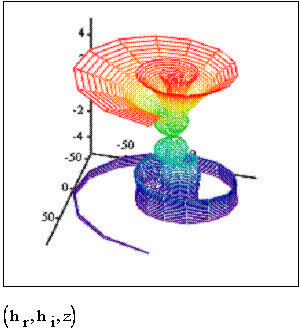

Рис.4. Произведение фракталов
Фибоначчи и Люка. Обозначения - как на рис.3
Представленные на рис.3 и 4 изображения с трудом поддаются интерпретации. Изменение начальных условий или секущей временной плоскости приводит к тем же спирально-вихревым структурам с некоторыми внешними отличиями. В этом направлении необходимы дальнейшие исследования. Гипотетически можно предполагать связь рассматриваемой модели с теорией поливихря Бугаева А.Ф. или торсионными полями Шипова Г.И. В этой связи необходимо учитывать следующее обстоятельство. В рамках теории комплексных переменных можно придумать очень много функций, генерирующих спиральные формы в фазовой плоскости. Такова природа этих чисел. В нашем случае нелинейной динамической модели (программа Фибоначчи) комплексные числа появляются естественным образом в рамках обобщения ряда Фибоначчи и формулы Бине, описывающих некоторые свойства чисел натуральных (1, 2, 3, 4, …). Случай в некотором смысле аналогичный квантово-механической теории в физике. Там при решении волнового уравнения Шредингера с необходимостью получаются функции комплексных переменных. Мнимая составляющая, по мнению некоторых эзотериков (например, Шнейдерман А.Г.), отражает непроявленную в нашем пространстве компоненту мироздания.
Фракталы программы Фибоначчи и Хаос.
Для сложных нелинейных динамических систем в рамках синэргетики важное значение имеет понятие точек бифуркации. Сущность явления заключается в том, что при определенных начальных условиях система из детерминированного состояния после некоторого количества циклов развития теряет устойчивость, разрушается и переходит в состояние хаоса. Существуют такие начальные условия и для нашей модели. Это оказались те самые первочисла –φ и 1 . При таких начальных условиях развитие объекта показано на рис.5.
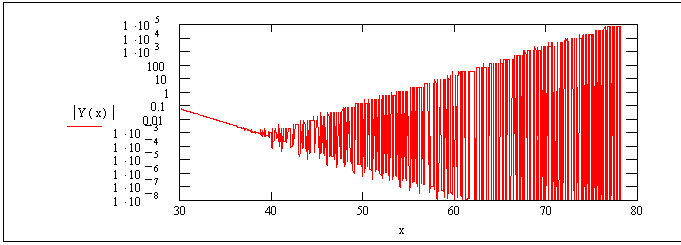
Рис.5. Бифуркационный переход объекта,
построенного по программе Фибоначчи. Y(x) рассчитывалось
по ур. (5) с использованием начальных условий:
х0 = -φ и х1 = 1.
Для возможно большего охвата количества циклов (по оси Х) значения состояния объекта (по оси Y) показаны в логарифмическом масштабе. Можно видеть, что точка перехода в состояние динамического хаоса находится при значениях 39-40 циклов. При анализе формулы (5) и полученных результатов было установлено, что поведение системы не изменяется при пропорциональном изменении начальных условий, т.е. для получения точки бифуркации в общем случае: х0 = -аφ и х1 = а (где а – любое действительное число, кроме, естественно, тривиального случая а=0). Это иллюстрирует рис.6, где в деталях показан участок бифуркационного перехода.
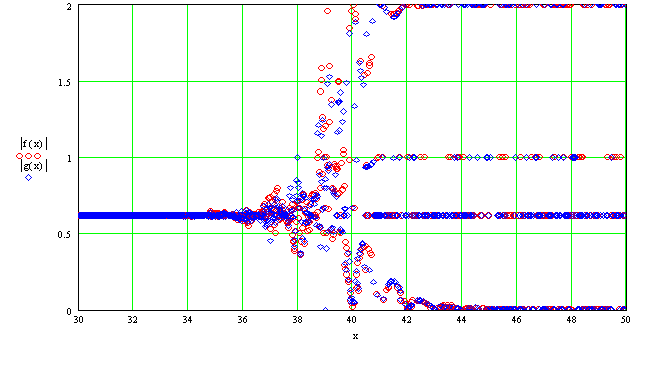
Рис.6. Область
бифуркационного перехода объектов, построенных по программе Фибоначчи.
В качестве критерия состояния объекта использовали модуль, вычисляемый стандартно, как для ряда Фибоначчи (формула (3)). Начальные условия кратны использованным на рис.5, а между собой отличаются в 1015 (красный цвет – а = 107, синий – а = 10-8). Можно видеть, что до 36-го цикла объекты развиваются детерминировано, модуль в обоих случаях равен 1/φ (0,61830….). Далее процесс разрушения лавинообразно нарастает и после 39-40 циклов наступает состояние динамического хаоса. Объекты как бы расщепляются и развиваются одновременно в нескольких состояниях (модули – 2, 1, 1/φ, 0). Положение точки бифуркации (39-40 циклов) имеет вероятно фундаментальный смысл в связи с эзотерическими знаниями. Отметим исключительную устойчивость точки бифуркации, т.к. изменение начальных условий на 15 порядков не сместило ее даже на один цикл. Результаты расчетов, представленные на рис.5 и 6, относятся к случаю а > 0. Если а < 0 (например, х0 = 1 и х1 = -1/φ), то картина становится зеркальной и точка бифуркации смещается к отрицательным значениям циклов -39-40. Возможно, этот случай представляет модель обратного перехода: «динамический хаос → детерминированная структура». В заключение на рис.7 показан вид бифуркационного перехода в динамический хаос с помощью 3-D графики для стороннего «далеко отстоящего» наблюдателя.
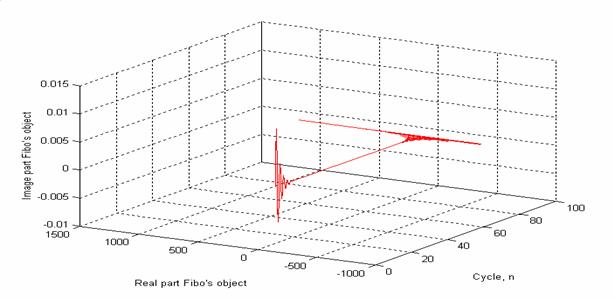
Рис.7. Переход «детерминированная структура – динамический хаос» для объекта, строящегося по программе Фибоначчи,
В рамках эзотерических представлений его можно назвать «крестовый разворот». Особенно наглядным это получается при изображении изменений фазового портрета объекта в динамике при использовании возможностей анимации программ Matcad или Matlab.
Заключение.
- Предложено понятие «программа Фибоначчи», как обобщение формулы Бине на область всех действительных чисел.
- Использование программы Фибоначчи позволяет с помощью рекуррентной формулы моделировать нелинейные динамические системы – спиралевидные фрактальные объекты на множестве комплексных чисел, несущие в своем строении «золотое сечение».
- Гипотетический математический алгоритм Мироздания - программа Фибоначчи позволяет объяснить некоторую часть эзотерических представлений.
- Существуют определенные начальные условия, при которых объект, созданный по программе Фибоначчи, через 39-40 циклов разрушается и переходит в состояние динамического хаоса.
- Человека можно представить целостным фрактальным объектом Мироздания, который находится в непрерывном циклическом развитии в рамках перехода „материальный мир (Ян) – духовное или информационное состояние (Инь)”.