Михаил РАЗЖИВИН. На полях созрели теоремы.

НА ПОЛЯХ

СОЗРЕЛИ

ТЕОРЕМЫ

Сегодня, когда интерес к таинственным рисункам-пиктограммам, периодически появляющимся на фермерских полях, несколько поутих и ореол сенсационности вокруг них померк, неплохо бы вернуться к опубликованным ранее материалам и спокойно порассуждать о природе и предназначении этих загадочных феноменов.

В качестве базового материала можно взять статью Людмилы Щекотовой в №11 журнала «Техника-молодежи» за 1993 год, вышедшую под заголовком «Евклидова жатва». Статья построена на обзоре широко популярных журналов «Science News» и «Bild der Wissenschaft» и речь в ней идет о находке американского астронома Джеральда Хоукинса, волею судьбы соприкоснувшегося с пиктограммами на английских полях.

Репутации как обоих журналов, так и известного во всем мире ученого, достаточно безупречны и это позволяет нам вполне серьезно отнестись к проблематике, изложенной в статье Л.Щекотовой. Расскажем вкратце, о чем там идет речь.

Некоторые закономерности, выявленные в характере построения пиктограмм, позволили Хоукинсу вывести ряд теорем, доселе неизвестных в евклидовой геометрии. Поначалу теорем оказалось четыре и так как все они обладают неординарной математической и даже эстетической красотой, то не лишним будет привести здесь их формулировки.

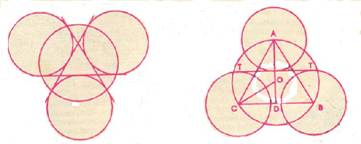
ТЕОРЕМА : отношение диаметра большого круга, описанного вокруг равностороннего треугольника, к диаметру малого круга, вписанного в этот треугольник, равно 4:3;

ТЕОРЕМА : для равностороннего треугольника отношение площадей описанного и вписанного кругов равно 4:1. Площадь кольца, образованного кругами, относится к площади вписанного круга как 3:1;

ТЕОРЕМА : для квадрата отношения площадей описанного и вписанного кругов равно 2:1. Если вписать второй квадрат внутрь вписанного круга, в него снова вписать круг и продолжать эту процедуру до m-го квадрата, тогда соотношение площадей внешнего описанного круга и наименьшего вписанного круга составит :1;

ТЕОРЕМА : для правильного шестиугольника отношения площадей описанного и вписанного кругов равно 4:3.

Далее в статье сказано: «Все четыре оригинальных теоремы Хоукинса оказались – в конечном счете – специальными случаями одной и той же, более общей теоремы» То есть, речь идет о ПЯТОЙ ТЕОРЕМЕ ХОУКИНСА (в дальнейшем, для удобства, - ПТХ). Эту свою теорему ученый публиковать не стал, а великодушно предложил попытать счастья как профессиональным, так и доморощенным математикам.

В течение первых полутора лет никто разгадать загадку Хоукинса не смог, да и сейчас ничего вразумительного по этому поводу не слышно. По крайней мере, на страницах «ТМ» об этой интригующей истории во всех последующих номерах не было напечатано ни слова. Следует ли это понимать так, что молчат и западные журналы – про то неведомо.

Как бы то ни было, но невольно напрашивается вывод о появлении в истории математики еще одной неразрешимой задачи, которая немногим уступает по части известности знаменитой Великой теореме Ферма. И что будет, если не дай бог, конечно, Джеральд Хоукинс унесет с собой эту тайну? Кроме того, он успел в свое время справедливо упрекнуть журналистов в том, что они оказались неспособны оценить по достоинству необычный талант создателя пиктограмм.

* * *

Все вышеперечисленные обстоятельства и заставили меня, журналиста, вспомнить азы математики, полученные когда-то в одном из электротехнических ВТУЗов . На разработку своей версии ПТХ у меня ушло времени значительно меньше полутора лет, я управился за час с четвертью. Позже я покажу, что и это очень огромный срок для решения такой простенькой задачи. Любой настоящий профессионал-математик управился бы с теоремой за полторы минуты, а то и меньше. Сразу надо признаться, что поиски закономерностей и последующее формулирование теоремы принесли вашему покорному слуге столько удовольствия, сколько порой не получишь за целый год обычной жизни. Бывает, случаются такие явления, происходящие на грани обычной творческой работы и некоего просветления. Поэтому легко было понять восторг, испытанный Хоукинсом, когда он успел впервые понять истинный смысл его находки. И так как зачастую бывает, что сам процесс поисков более поучителен, чем найденный результат, видимо иногда стоит показать поближе ход подобного процесса.

Что я имел в наличии пред решением задачи? Не так уж и много. Ну, во-первых, - отсутствие каких-либо ощутимых закономерностей. Во-вторых, - мельтешение перед глазами какой-то мистической четверки. В-третьих, довольно странный набор исследуемых фигур: треугольник, квадрат, шестиугольник.… Куда, скажем, подевался случай разбирательства с пятиугольником? А с семиугольником? Вопросы…вопросы.… Поэтому пришлось для начала набрать статистику и свести имеющиеся в наличии и вновь полученные данные воедино. Из этого материала скомпоновалась

ТАБЛИЦА 1

Число сторон (n)	Соотношение площадей описанных и вписанных кругов	Обратное соотношение этих площадей
3	4 : 1	1 : 4 = 0,25
4	4 : 2	2 : 4 = 0,5
5	4 : 2,618…	2,618… : 4 = 0,6545….
6	4 : 3	3 : 4 = 0,75
7	4 : 3,247…	3,247… : 4 = 0,812…

Третью колонку в этой таблице я заполнил просто так, по наитию. Дело в том, что с числами, меньшими единицы удобнее работать, если дело касается вычисления на микрокалькуляторе тригонометрических величин. А поскольку площади рассматриваемых фигур имеют зависимость от величин внутренних углов, то можно было заранее предвидеть: без тригонометрии не обойтись!

Пока еще особой пищи для размышлений не просматривается. Но в ситуации с пятиугольником внезапно выплыло на свет уникальное число, знакомое по давним работам с «золотым сечением» в области психологии. Это число 2,618033989…есть точный квадрат одной из двух констант «золотого сечения» - числа 1,618033989… Оно же является частным от деления этой константы на вторую константу:

1,618033989… : 0,618033989… = 2,618033989…

Этот случайный штрих мгновенно заставил посмотреть, что получится, если из чисел, выражающих соотношения площадей вписанных и описанных кругов, попробовать извлечь квадратные корни. И заодно посмотреть: не возникает ли при этом некая связь с тригонометрическими функциями?

Так оно и вышло. Полученные числа были квадратами косинусов углов вида = , где n>2 – натуральное число, обозначающее число сторон правильного многоугольника. В этом можно убедиться, взглянув на результаты вычислений, представленные как

ТАБЛИЦА 2

n	*Соотношение* *площадей вписанных* *и описанных кругов* *(с)*		arc cos	В радианах
3	*0,25*	*0,500*
4	*0,5*	*0,707…*
5	*0,6545…*	*0,809…*
6	*0,75*	*0,866…*
7	*0,812*	*0,901…*

Даже при беглом взгляде на эту таблицу становится понятным, что ПТФ в принципе уже доказана и можно приступить к ее окончательной формулировке. Если воспользоваться терминологией и речевыми оборотами самого Хоукинса, то на выходе получится примерно следующее:

ТЕОРЕМА : ДЛЯ ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА С ЧИСЛОМ СТОРОН n, ГДЕ n - НАТУРАЛЬНОЕ ЧИСЛО, n >2, ОТНОШЕНИЕ ПЛОЩАДЕЙ ВПИСАННОГО И ОПИСАННОГО КРУГОВ РАВНО : 1.

Площадь кольца, образованного кругами, относится к площади вписанного круга как : 1, а к площади описанного круга – как : 1.

Если внутрь вписанного круга вписать многоугольник с таким же числом сторон, в него снова вписать круг и продолжать эту процедуру до m-го многоугольника, тогда соотношение площадей наименьшего вписанного круга и и наибольшего описанного круга составит : 1.

Читатель может сам убедиться, что выводы, которые следуют из ПТХ, по-своему изящны и способны порадовать человека, понимающего красоту математики. Но тут важно шагнуть чуть дальше и не упустить из виду СЛЕДСТВИЕ, вытекающее из всего вышеизложенного, которое можно сформулировать примерно так:

ВСЕ ВЫВОДЫ, СЛЕДУЮЩИЕ ИЗ ПЯТОЙ ТЕОРЕМЫ ХОУКИНСА, В РАВНОЙ СТЕПЕНИ СПРАВЕДЛИВЫ ДЛЯ ФИГУР, ОБРАЗОВАННЫХ ПОСЛЕДОВАТЕЛЬНО ВПИСАННЫМИ В КРУГИ МНОГОУГОЛЬНИКАМИ.

Это, на первый взгляд, мало значащее добавление к ПТХ, способно значительно расширить наш угол зрения. Метод образования многоугольных фигур тот же. Берется любой правильный n-угольник, в который вписывается окружность. В эту окружность вписывается следующий n- угольник и так далее. Так вот, - соотношения между площадями каждой пары последовательно взятых многоугольников будут точно такими же, как и между площадями последовательной пары кругов.

На самом деле, никакого «ноу хау» в работе Джеральда Хоукинса, конечно , нет. Профессиональному математику не доставило бы труда протянуть руку к книжной полке, взять известный корновский «Справочник по математике» для научных работников и инженеров. М. «Наука», 1977 год и на стр. 47 найти формулы для радиусов описанной и вписанной окружностей для правильных многоугольников с числом сторон, равным n и длиной стороны, равной а. Вот что он увидит:

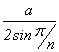R = ; r =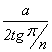

Далее, помня о том, что площади кругов не могут соотноситься иначе, как квадраты их радиусов, математик мгновенно обнаружил бы соотношение, вызвавшее у нас столь бурный восторг:

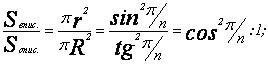
И все! Никаких мистических «золотых сечений», озарений и передачи инопланетной информации нам, землянам.

Но кое-что в этой истории наводит на размышления. Мы не зря упомянули вскользь в начале этой статьи о Великой теореме Ферма. Обратим внимание на общее условие в теоремах Хоукинса и Ферма: n обязательно должно быть натуральным числом, большим 2. Случайность? Вряд ли. Здесь подразумевается тот непреложный факт, что уже при n=3 приходится иметь дело с геометрическими фигурами, описать соотношения в которых можно только единственным способом: увязав их с окружностями, построение которых, как известно, немыслимо без использования трансцендентного числа . Неразрешимость в целых числах математического выражения, входящего в формулировку Великой теоремы Ферма как раз и объясняется этой трансцендентностью.

В заключение выскажу свое частное соображение о происхождении и характере знаменитых пиктограмм, появляющихся на полях с посевами.

Мне думается, что поле, засеянное монокультурой, представляет собой в период биологической активности, при цветении и колошении, своеобразную мощную приемную антенну-рефлектор, способную принимать и усиливать определенного рода информацию, раскодируя при этом тот или иной природный шифр. Еще Галилей подметил, что главный язык, на котором разговаривает с нами Природа – это язык математики. Стоит ли после этого удивляться рисункам на полях, содержащих в себе четкую математическую символику?

Михаил РАЗЖИВИН