Удк 57.017.6:51-7
Математическая теория старения в популярном изложении
(теория стопки монет)
©
В популярной форме излагаются основы
математической теории старения. Наглядно, на графиках, рассматриваются простейшие
математические модели роста. Устранены некоторые неточности, имевшие место в
ранних работах, и теперь теория имеет вполне завершённую логическую форму.
Предлагается план реального эксперимента по выявлению новых числовых
характеристик процессов роста и старения.
Ключевые слова: теория старения, математическая модель старения,
причина старения.
Для
краткости здесь мы не будем подробно останавливаться на разборе существующих
теорий старения. Читатель при желании может познакомиться с ними самостоятельно,
например, по пособию [1].
В
повседневной жизни мы не раз наблюдали, как зарастают царапины на коже. Также
мы видим, что листья на деревьях, опадая осенью, снова появляются весной. У нас
регулярно выпадают волосы, но также регулярно вырастают новые. В мире животных
известно такое явление, как регенерация. Например, морская звезда может
отрастить заново потерянный луч. Даже часть звезды, если она содержит желудок,
может регенерировать полную звезду. Некоторые виды ящериц могут отрастить
хвост. Кольчатый червь, будучи перерублен лопатой, из двух половинок образует
две самостоятельные особи. Перечень можно продолжать и продолжать. Все эти
примеры создают иллюзию того, что живой организм способен сам себя чинить и
обновляться, поэтому непонятно, по какой причине происходит старение.
Рассмотрим
в качестве модели плод черешни. Сначала размер плода очень мал, он зелёный,
затем наливается и спеет. Почему он спеет? Что, если мы будем считать, что
созревание плода черешни – это есть его старение? То есть, плод стареет как
орган, а само растение ещё продолжает вегетацию. Какова может быть причина
этого?
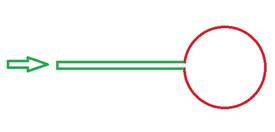
Рис. 1. Плод черешни схематично
Можно
предположить, что старение происходит в результате следующего процесса: сначала
в плод по плодоножке с ограниченным поперечным сечением поступают питательные
вещества, плод растёт. Однако со временем поступающих веществ не хватает, чтобы
обеспечить нормальное питание и жизнедеятельность всего объёма, ведь плод
увеличился, а размер плодоножки остался прежним. Может быть, любой другой живой
организм, проходя стадию роста, оказывается в подобной ситуации? Если наши
рассуждения верны, то теория старения должна учитывать динамику роста. Рост и
старение должны быть связаны. Рост должен создавать какую-то проблему, которая
скажется впоследствии. Как бы то ни было, данная модель послужила отправной
точкой в создании математической теории старения.
Чтобы
понять, какими фундаментальными проблемами сопровождается рост организма,
рассмотрим такой показательный пример из неживой природы, как рост городов.
Интересен исторический рост города, когда при его образовании изначально никем
не предполагалось, насколько большим окажется данный город в будущем. Каждый
город имеет определённую ширину улиц, которые вначале вполне удовлетворяют
транспортные потребности. Однако со временем город растёт в высоту,
увеличиваются плотность населения и количество приезжих, растут пригороды. Всё
больше транспорта устремляется из одного пригорода в другой по кратчайшему пути
– через центр. Через некоторое время оказывается, что пропускная способность
улиц в центре городов уже не способна обеспечить нормальное движение и требуется
расширение улиц. Чтобы добиться этого, требуется снести ряд зданий или даже
целых кварталов. Таким образом, дальнейший рост города невозможен без
разрушения уже имеющейся инфраструктуры. Чтобы обеспечить нормальное движение в
Париже, были снесены старые улицы и кварталы, а улицы шириной в 6 метров были
заменены на бульвары шириной в
Рост
живого организма также сопровождается постоянными переделками, должны
увеличиваться просвет сосудов, толщина стенок и т.д. Кроме того, в повседневной
жизни ткани организма и так постоянно подвергаются разрушающим воздействиям.
Так, при прохождении пищи по кишечнику, его стенки ежедневно получают травмы,
механические повреждения получают ткани при движении ног и рук в паху и
подмышках. Мы этого не замечаем, потому что в организме существует механизм
репарации и регенерации. Действие этого механизма начинает система свертывания
крови. Если где-то возникло повреждение, в этом месте образуется мельчайшая
заплата из тромбоцитов. Сначала организму надо заделать трещину, только затем
это место заполняется делящимися клетками данной ткани. Если нарушить работу
механизма свёртывания крови, то повреждения окажутся неустранимы. Есть яды, их
называют антикоагулянтами, которые применяют против мышей. Через 4 - 6 суток
после употребления яда у мыши нарушается механизм свёртывания крови, начинает
кровоточить кишечник, а под передними ногами (они несут наибольшую тяжесть)
образуются мешки из-за внутренних кровотечений, вскоре мышь гибнет.
Страшные
вещи происходят, когда в организме возникает рак. Мутировавшие клетки в
организме возникают регулярно, но система иммунитета организма их выявляет и
уничтожает. Но вот если происходит сбой, и иммунитет не воспринимает
мутировавшую клетку как опасность, тогда клетка начинает бесконтрольно
делиться. Вскоре образуется опухоль. Нормальная ткань, несущая определённую
функцию с сосудами, с нервами, с протоками, заменяется клетками одного вида,
без сосудов, без нервов. Те клетки раковой опухоли, что соприкасаются с
нормальной тканью, получают достаточное питание, а вот раковые клетки, которые
со временем оказываются внутри опухоли, из-за отсутствия инфраструктуры
перестают получать питание, гибнут и разлагаются. Образуется язва. Язва эта не
заживает, а распад клеток приводит к сильнейшей интоксикации организма, и
состояние больного резко ухудшается. При раке на слизистых оболочках язва
образуется очень быстро, практически без опухоли
После того, как вы получили
представление о проблемах, связанных с ростом, давайте рассмотрим задачу, при
решении которой будем полагаться на графический метод для упрощения. Клетки
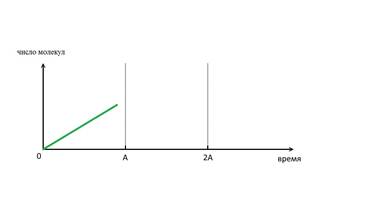
организма состоят из молекул. Попытаемся представить динамику роста и старения
молекул. Пусть это будут молекулы одного вида. Причём они непременно должны
быть не свободными, а встроенными в структуры клетки или ткани так, что их
извлечение, оттуда сопряжено с затратами энергии. Пусть в организме нарастание
количества данного вида молекул идёт во времени по линейной функции, т.е. по
прямой (рис. 2). За цвет прямой выберем зелёный.
|
|
Рис. 2. График роста числа
молекул одного вида
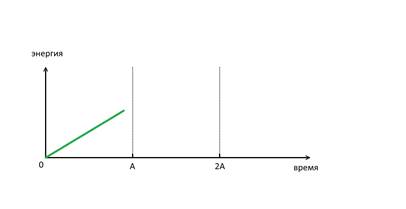
Если при этом считать, что на
производство 1 молекулы тратится 1 единица энергии, то получим тот же график,
только уже функцией здесь будет затраченная на рост энергия (рис. 3).
|
|
Рис. 3. График затрат энергии на
рост числа молекул одного вида
Пусть спустя некий период времени 
молекулы выходят из строя, ломаются и их надо
заменять. Чтобы заменить сломавшуюся молекулу, потребуется больше энергии, т.к.
надо эту молекулу произвести заново, т.е. затратить 1 единицу энергии, плюс
потратить значительную часть энергии, чтобы извлечь сломанную. Таким образом,
будем считать, что в сумме для ремонта 1 молекулы организм затратит уже 
единиц энергии, где 
. Спустя период времени 
, график энергии, затрачиваемой
на замену молекул, будет как бы
повторять наш предыдущий график, но только это будет более крутая прямая
из-за того, что . Обозначим её красным цветом.
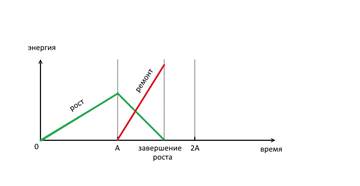
Начиная с момента времени , организм должен тратить энергию
не только на рост, но и на ремонт, поэтому начальная кривая роста пойдёт на
понижение. В какой-то момент времени рост прекратится, и вся энергия будет идти
только на ремонт (рис. 4).
|
|
Рис. 4. Динамика энергозатрат в начальный период
Таким
образом, как и в модели с черешней, здесь изначально заложено препятствие. Оно вводится тем условием, что на ремонт
(замену) молекулы тратится больше энергии. Давайте рассмотрим простой пример и
убедимся, что данное условие имеет под собою реальную основу. Возьмём несколько
монет и будем укладывать их стопкой одна на другую. Практически на укладку
каждой монеты мы тратим почти одну и ту же энергию. Вот у нас получилась стопка
монет (рис. 5). Если попытаться заменить монету из середины стопки, то ясно,
что мы потратим при этом куда больше энергии, чем тогда, когда просто клали
монетку в стопку.
|
|
Рис. 5. Стопка монет
Деление
клетки – это самый лучший способ решать проблемы ремонта. Концентрация старых молекул
при этом уменьшается в 2 раза. Если вернуться к нашему примеру, то ясно, что, когда
высота стопки уменьшается наполовину, процессы замены ускоряются.
С
графиком роста нам всё понятно, а как должен будет выглядеть график ремонта в
последующее время? Рассмотрим, например, период времени от 2А
до 3 А. Пусть это будет время 2А+ τ, где τ – строго фиксированный
малый промежуток времени, при этом τ < А. Значение энергии ремонта в
этой точке будет равно сумме значений
энергий роста в точках 0 + τ и А + τ, умноженной на . Действуя по
этому алгоритму, мы можем достроить график (рис. 6).
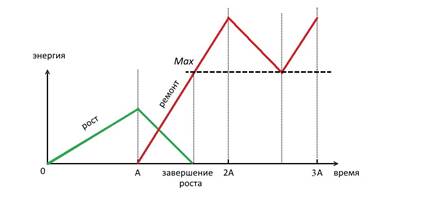
Рис. 6. Динамика энергозатрат на
конечном этапе. Красным цветом показано количество энергии, необходимой для
полноценной замены испорченных молекул в данный момент времени.
При анализе графика есть веские
основания полагать, что в точке завершения роста энергетические возможности
организма достигают максимально возможной величины и в дальнейшем этот максимум
не может быть превышен.
Теперь
сформулируем главный вопрос: хватит ли у организма энергии, чтобы после
остановки роста успешно заменять все выходящие из строя молекулы за период
времени ? Из рис. 5. становится ясно, что
нет. Этому
есть две причины.
Первая причина состоит в том, что для полной замены
потребуется энергия, равная всей энергии, затраченной на рост, умноженной на
число 
.
Количество
энергии равно площади под соответствующим графиком.
Вторая причина состоит в том, что промежуток времени А всегда меньше, чем время, затраченное на рост. Особенно
большая разница необходимого времени будет наблюдаться, если рост шёл по
второму варианту, как на рис. 7.
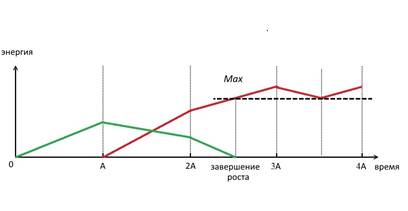
Рис. 7. Динамика энергозатрат при
росте по второму варианту
Вторая
причина указывает на энергетическую мощность: чтобы её найти, мы должны энергию
делить на промежуток времени.
Таким образом, для того, чтобы организм
мог восстановить все испорченные молекулы, ему необходимо потратить больше
энергии за меньшее время. В итоге мы приходим к важному выводу: после
прекращения активного роста организм не в состоянии обеспечить замену всех старых,
вышедших из строя молекул.
Если размышлять далее, то можно прийти
ещё к одному потрясающему выводу, который изложим в виде леммы: если
та доля молекул, которую организм не успевает заменять за период А, вызывает снижение энергетической способности организма,
пусть даже очень незначительное, то с каждым последующим периодом А доля
стареющих невосстанавливающихся молекул будет увеличиваться, и через
определённое количество периодов А наступит смерть организма. По-моему,
это вполне очевидно.
На тот случай, если кого-то смущает
слово «если» в данной лемме, то деваться некуда, приходится добавлять постулат:
«среди
всего многообразия молекул в организме старение, по крайней мере
одного вида молекул снижает его энергетическую мощность». Введение
данного постулата обосновано тем, что любой действующий механизм должен иметь в
своём составе хотя бы один структурный элемент.
При более глубокой разработке данной
математической модели следует учитывать, что
в общем случае функция энергетических затрат роста, обозначим её 
, может быть не линейной.
Величина затрат энергии на замену молекул может быть не постоянной
величиной, а лежать в некоторых пределах
в зависимости от места и времени замены. В
таком случае при моделировании процесса старения препятствие для вечной
молодости правильнее будет записать динамикой между значением определённого интеграла
от энергетической функции и двойным интегралом от 
функции энергии, потраченной на ремонт и
замену старых молекул. Если с возрастом меняется и величина средней
продолжительности жизни молекулы , то соответствующим тройным
интегралом от 
функции энергии, потраченной на ремонт и замену
старых молекул. Можно предполагать, что несмотря на
усложнения, более глубокие модели дадут тот же результат, а полученные графики
будут напоминать графики, представленные в данной статье с некоторыми
деформациями.
Зададимся вопросом: что, если не все
поломанные молекулы в организме заменяются? Например, в дереве большая часть
древесины – это мёртвые клетки. Будет ли дерево расти вечно? На поперечном
срезе дерева под корой находится слой живых клеток – камбий. Следовательно, при
росте дерева скорость деления клеток должна оставаться постоянной. Это значит,
что за равные промежутки времени длина окружности среза должна увеличиваться
каждый раз в два раза. Или площадь поверхности дерева для этого должна
увеличиваться в два раза за равные промежутки времени. Но известно, что этого
не происходит. Следовательно, клетки камбия тоже стареют.
Можно было бы придумать способ, когда
часть клеток погибает, а оставшиеся сохраняют необходимую скорость роста. Но, с
эволюционной точки зрения, к чему бы это привело? – К неизменности вида и, следовательно,
к проигрышу в эволюционном соревновании.
Есть ли способ проверить, все ли старые
молекулы определённого вида заменяются в организме животных? Мы можем
предложить следующий опыт.
Он должен проводиться с чистой линией
животных. Для создания чистой линии необходимо близкородственное
разведение животных на протяжении не менее 20-ти поколений. Это приводит к
такой же степени генетической однородности животных, как у однояйцовых
близнецов. Такие линии лабораторных животных используются в медицинских и
биологических экспериментах. Дополнительное
требование к чистой линии в нашем случае должно заключаться в том, чтобы
животные были одного пола, и чтобы животные одного возраста как можно меньше
различались по темпам роста. Тогда, забивая нескольких животных, мы можем
от разных особей получить разные данные и свести их в один процесс для
некоего среднестатистического животного. Например, что касается синтеза белка:
можно найти скорость общего синтеза белковых молекул в организме в данный
момент с помощью изотопов, найти синтезируемую долю интересующих нас молекул и
их количество. Повторяя опыты через равные промежутки времени, например, через
несколько дней, мы сможем построить график.
Пусть радиоактивная метка даётся за
короткий промежуток времени, тогда скорость синтеза данной молекулы:
Допустим, следующее измерение произойдёт
через время ∆t, тогда предполагаемый прирост массы
данных молекул будет
,
где 
– масса теоретическая.
Реальный прирост определяется прямым
взвешиванием всех молекул данного вида, выделенных из организма, и находится
как разность значений в соседние промежутки времени. Если реальный прирост 
окажется меньше, значит, часть молекул 
синтезировалась для ремонта:
,
,
где 
.
В отличие от
бактерий и простейших, в многоклеточном организме клетки не могут делиться,
когда им нужно, иначе это приведёт к хаосу и нарушит архитектуру и функции
организма. В этом плане в организме все строго контролируется. Кроме этого, в
организме имеется ещё один аварийный механизм на тот случай, если какая-то
соматическая клетка всё же решит делиться, не подчиняясь иерархическим
запретам. Это ограничение общего числа делений. О том, что такой механизм
должен быть, неожиданно выявилось в результате опытов Хэйфлика.
Оказалось, что культура клеток человека гибнет после того, как клетки совершат
около 50 –52 делений. Если при этом
брать для культивирования клетки из организма более пожилых людей, то число делений
ещё больше сокращается, а если брать клетки животных с малой продолжительностью
жизни, то количество делений оказывается ещё меньше. Дальнейшие исследования
выявили, что причина кроется в укорочении длины ДНК в соматических клетках при
каждом делении. Укорачиваются участки концевой ДНК, называемые теломерами. Теломеры препятствуют
соединению хромосом между собою. К старости, когда концы ДНК уже лишены теломер, концы хромосом становятся «липкими», и при делении
клетки хромосомы рвутся как попало, ДНК распределяется
по дочерним клеткам неравномерно, что приводит или к смерти клеток путем апоптоза, или к раковым заболеваниям. Раковые клетки
получают способность делиться неограниченно долго, потому что у них в
результате мутаций возобновляется способность удлинять теломеры.
Как бы то ни
было, для нас важно то, что в нормальном организме существуют, по крайней мере два механизма, препятствующие самопроизвольному делению
клетки. Поэтому, лишившись возможности делиться, клетка начинает стареть. Но
ограничение числа делений на основе теломерного
механизма нельзя считать начальной причиной старения, потому что к моменту,
когда этот механизм проявляет своё действие, организм уже находится в состоянии
глубокой старости.
Литература
1.
Чаплинская Е. В., Бутиловский В. Э.
Старение: теория и генетические аспекты.-Минск: БГМУ,
2014.
2.
ru.wikipedia.org›Пожары в Москве .
3. Прудников П. А. Математическая теория процесса старения. - Математическая
морфология. Электронный математический и медико-биологический журнал. - Т. 8. -
Вып. 1. - 2009. - URL: http://www.smolensk.ru/user/sgma/MMORPH/N-22-html/prudnikov/prudnikov.htm
4. Прудников П. А. Поиск алгоритмов старения. -
Математическая морфология. Электронный математический и медико-биологический
журнал. - Т. 11. - Вып. 4. - 2012. - URL: http://sgma.alpha-design.ru/MMORPH/N-36-html/prudnikov/prudnikov.htm
5. https://ru.wikipedia.org/wiki/Предел_Хейфлика
6. https://ru.wikipedia.org/wiki/Злокачественные_опухоли_полости_рта
7. https://ru.wikipedia.org/wiki/Заживление_ран
The mathematical theory of
ageing in the popular presentation
Prudnikov P. A.
The fundamentals of the mathematical theory of aging are presented in
a popular form. The simplest mathematical models of growth are considered
graphically. Some inaccuracies that took place in the early works have been fixed, the theory has a complete logical form and content
now. A plan of a real experiment to identify new numerical characteristics of
the processes of growth and aging is proposed.
Key words: mathematical model of ageing, the science of ageing, the ageing
reason, the theory of ageing, the ageing process, the growth.
Сведения об авторе:
Автор: Прудников Пётр Алексеевич,
Электронная почта: prpyotr@yandex.ru