Другие статьи

---

Поиск алгоритмов старения

П.А.Прудников,

2012г.

(prudnikov.doc, rar-архив)

УДК 51-76:57.017.6

Публикуется с разрешения автора

Исследуются различные варианты простейшей математической модели. Графики и программы прилагаются. Получены критерии, по которым можно указать, что в основе старения лежит именно причина, применяемая в модели. Предлагаются к изучению новые параметры реального эксперимента.

Ключевые слова: математическая модель старения, модель продолжительности жизни, причина старения, формула продолжительности жизни, теория старения.

Начнём с очевидного утверждения, что если живой организм успевает оставить плодовитое потомство до своей смерти по причине старения, то такой процесс будет повторяться и в будущем. Крайне сложной представляется задача, используя достижения математической и инженерной науки, сконструировать вечно живущий многоклеточный организм, подобный организму млекопитающего. Для этого он должен быть рассчитан на прочность, а каждая его деталь иметь возможность замены без вреда для его функциональности. Чтобы при этом не возникал транспортный и энергетический коллапс, чтобы все процессы обеспечивались надежным информационным аппаратом, чтобы при этом процесс жизнедеятельности не прекращался ни на секунду. Мы коснемся некоторых из этих моментов при дальнейшем изложении. Если будет доказано, что такую задачу не удаётся решить в отношении млекопитающих – это будет необходимым условием доказательства неизбежности старения.

Но зачем живой материи было решать эту задачу, если в силу вышеизложенного утверждения жизнь и так будет продолжаться? Мы знаем, что млекопитающие не осилили эту проблему, что, впрочем, не помешало им процветать на планете. Нам по этой причине представляется возможным найти достаточное условие того, что организм эту задачу не решил.

Обратимся к рассмотрению моделей роста и старения, изложенных в [1]. В основе их лежат два принципа. Первый: вся свободная энергия идёт на рост. Второй: затраты на поддержание структуры и функциональности больше, чем на рост. Суть же моделей сводится к рассмотрению динамики одного отдельно взятого вида молекул.

Примечание: для исследования могут браться любые молекулы, которые необходимы для поддержания архитектуры организма в широком понимании, и синтез которых продолжается на протяжении всей жизни организма. Это молекулы, которые не находятся в свободном плавании, а включены в состав мембран, сложных молекулярных комплексов, находятся в связанном состоянии в матриксе, т.е. в таких местах, откуда не могут быть извлечены без затрат энергии.

Примем, что синтезированная молекула спустя промежуток времени, равный А, полностью утрачивает свои функции и нуждается в замене. Синтез молекул для замены уже не входит в понятие роста.

Теперь дадим пояснения к рис.1.

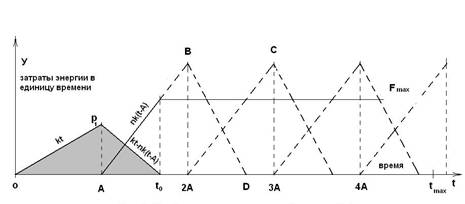
Рис. 1. Изображение процесса для варианта №2 по [1]. Энергетическое представление.

На оси ординат откладываются затраты энергии в единицу времени. На оси абсцисс – время. На оси абсцисс обозначены: интервалы, равные А, время максимальной продолжительности жизни и время прекращения активного роста .

Ордината на графике - это скорость производства молекул, умноженная на энергию её производства и внедрения. Когда используется затратный коэффициент n, то сюда приплюсовывается и несколько большая энергия извлечения старой молекулы.

В отличие от работы [1], коэффициент n имеет не абсолютное, а относительное значение. Значение энергии производства и внедрения молекул (этап, описываемый функцией kt) при росте принято за единицу.

При зарождении организма начальное число молекул незначительно. Этим числом в расчётах можно пренебречь. Поэтому на графике мы совместим начальное число молекул с точкой «ноль».

Нарастание числа молекул в процессе роста организма примем за линейную функцию kt . Спустя интервал времени, равный А, начинается процесс замены ранее синтезированных молекул. Он описывается энергетической функцией nk(t-A).

В организме в каждый конкретный момент времени имеется некоторое функциональное соответствие между уже имеющимся количеством молекул и способностью синтезировать молекулы с определённой скоростью в следующий малый промежуток времени. Обозначим эту функцию буквой F.

Начиная с точки t = A, рост замедляется, потому что часть энергии функции F теперь должна тратиться на замену старых молекул. Рост описывается уже функцией kt - nk(t-A). При этом существует определённая точка , в которой на восстановление молекул тратится всё значение функции F, и начальный рост останавливается. В этой точке функция F достигает своего максимального значения F = Max. Физический смысл точки - это время прекращения активного роста, включая эмбриональный период.

Так как скорость, умноженная на время, представляет собой количество, то площадь серой фигуры на данном рисунке - это количество исследуемых молекул в организме к моменту .

Процесс может происходить и так, как показано на рисунке № 2 из [1], но мы ограничимся первой моделью.

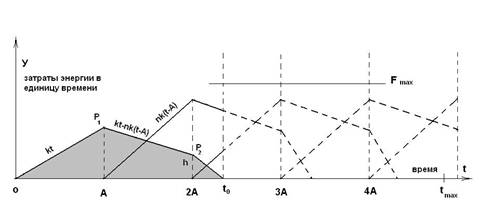
Рис. 2. Изображение процесса для варианта №2 по [1]. Энергетическое представление.

Покажем наглядно процесс старения по результатам работы [1]. Количество погибших от старости молекул на участке от 2A до 3A (рис.1.) равно площади треугольников 2ABD и 2AC3A, делённой на n, а число молекул, которые могут быть восстановлены (если принять, что функция F = Max остаётся на постоянном уровне), равно площади прямоугольника ниже линии F = Max, делённой на n.

Превышение числа погибших молекул до момента смерти организма показано оранжевым цветом на рис. 3. (если эту площадь разделить на n).

Понятно, что с увеличением времени максимальной продолжительности жизни это число увеличивается.

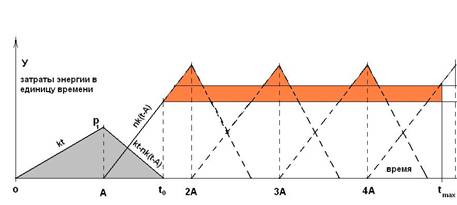
Рис. 3.

К моему удивлению, уже после публикации [1] я обнаружил, что в полученных решениях общее число таких молекул в организме после точки остановки активного роста тоже увеличивается. Получается, что в решениях [1] разработана одна из возможных моделей, когда после завершения активного роста идёт простое «латание», т.е. происходит уплотнение имеющихся молекул новыми молекулами без утилизации должного числа старых. Возможно наступление такого момента, когда уплотнение станет препятствием для внедрения, и синтез данных молекул для замены станет бесполезен. Для таких моделей процесс жизни условно можно разделить на два этапа. В начале старые молекулы заменяются полностью (причём в условиях постоянной перестройки многие молекулы, по-видимому, и не доживают до своей полной непригодности), а через некоторое время, после теперь уже условной остановки роста, идёт просто синтез и внедрение молекул без утилизации должного числа состарившихся молекул.

Но без ответа остался главный вопрос, которому была посвящена работа [1]: что будет в случае, если число молекул данного вида в организме достигнет определённого количества, и оно останется таким длительное время. Даже качественного рассмотрения тех же моделей хватает, чтобы прийти к догадке о том, что возникнет некоторое равновесие с функцией F, величина которой предполагалась неизменной. В самом деле, методы вычислительной математики позволяют нам получить такой, например, график:

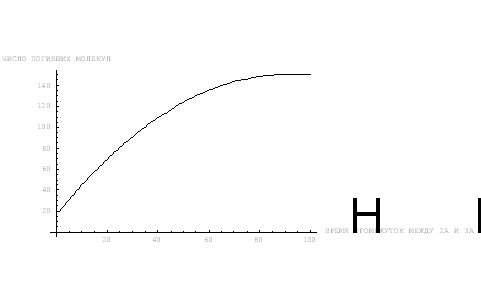
Рис. 4.

На графике представлены результаты того, что при изначальных данных, указанных в приложении №2, где приводится программа этого алгоритма, уже на временном интервале между 2А и 3А будет достигнуто равновесие. Соотношение старых молекул к общему количеству молекул данного вида будет поддерживаться на уровне 150 к 2850, это 5,26 %. Много это или мало? Не будем дискутировать по этому поводу: отметим, что здесь показано, что неизбежно образуется и присутствует некоторая доля старых молекул сразу после завершения активного роста.

Однако такой процесс, когда значение функции F остаётся неизменным, не является естественным. В работе [1] оговаривалось, что значение функции F в процессе жизни снижается. Покажем пример такого процесса. В самом деле, в организме 5,26 % буквально “мёртвых” молекул, а мы по-прежнему считаем, что функция F такая же, как если бы все молекулы были работоспособны.

Воспользуемся начальными данными графика на рис.1. Мы можем по ним найти функцию F на всём протяжении, вплоть до точки остановки активного роста, как это сделано в приложении №1. Затем, после точки остановки активного роста, зная число оставшихся в живых молекул, мы сможем вычислять значение функции F в дальнейшем.

Приведём график такого процесса:

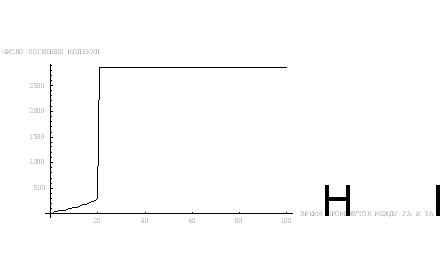
Рис. 5.

Как видим, при таких же изначальных данных (они указанны в приложении №3, где приводится программа этого алгоритма) уже на временном интервале между 2А и 3А будет достигнуто состояние, когда в организме не будет ни одной живой молекулы. Естественно, смерть организма наступает где-то раньше. Конечно, нельзя утверждать, что в реальном организме существует столь же симметричная зависимость функции F от числа живых молекул до и после точки , но какая-то, пусть и формальная, должна существовать. И даже при незначительном её убывании при постоянном числе молекул в организме будет наблюдаться необратимое старение. Модели с таким поведением назовём “модели угнетения”.

Чтобы построить настоящую модель, близкую к реальным процессам, необходимо располагать определёнными данными из опыта. Предположим, что мы ставим опыты с чистой линией животных. Основное требование к чистой линии заключается в том, чтобы животные были одного пола, и чтобы животные одного возраста как можно меньше различались по темпам роста. Тогда, забивая нескольких животных, мы можем от разных особей получить разные данные и свести их в один процесс для некоего среднестатистического животного. Например, что касается синтеза белка: можно найти скорость общего синтеза белковых молекул в организме в данный момент с помощью изотопов, найти синтезируемую долю интересующих нас молекул и их количество. При этом надо учесть и долю аминокислот, которые пошли на строительство после распада белка, ранее синтезированного в организме. Также можно найти (не вычислить, а измерить!) общее количество молекул данного вида в данный момент во всём организме. Повторяем опыты через равные промежутки времени, например, через несколько дней.

Из полученных данных мы можем построить график. В отличие от “энергетических ” графиков, как на рис.1 и рис.2, ординаты скорости ремонта будут ниже.

Пусть радиоактивная метка даётся за короткий промежуток времени, тогда скорость синтеза данной молекулы:

Допустим, следующее измерение произойдёт через ∆t, тогда предполагаемый прирост массы данных молекул будет

, где – масса теоретическая

Если реальный прирост окажется меньше, значит, часть молекул синтезировалась для ремонта:

,

, где

Заманчивой конечной целью получения данных служит построение с помощью программных методов полноценной динамичной картины до самого конца жизни животного. Безусловно, такой проект – весьма долгое, кропотливое и рискованное занятие, требующее дополнительной экспертной оценки, больших денежных средств и привлечения специалистов различного профиля. На данный же момент до конца не понятно, можно ли будет из опытных данных найти затратный (или затратные, если n меняется) коэффициент n, а также удастся ли установить подобие искомых функций. Тем не менее, используя выводы из рассмотренных моделей применительно к опытным данным, мы можем указать критерии того, что данная теория старения имеет право на существование.

Если из данных опыта следует, что общий синтез молекул данного вида уже не растёт, а масса (количество) этих молекул продолжается увеличиваться, то процесс старения идёт по “модели латаний” и неизбежно приводит к старению.

Если из данных опыта следует, что общий синтез молекул данного вида снижается, а масса (количество) этих молекул не увеличивается, то процесс старения идёт по ”модели угнетения”.

Пограничное условие: сочетание с теломерной теорией.

Из - за того, что всё изложенное выше может быть верно и в отношении молекул ДНК, возникает пограничное условие, когда не ясно, что в большей степени дальше управляет процессом старения. Трудность здесь состоит и в том, что если для целого организма в отношении ДНК проведение опыта представляется возможным, то для культуры одиночных не синхронизированных клеток млекопитающих, для того чтобы получить картину для одной клетки, это сделать сложно.

Выводы

Если исходить из изложенного представления о механизмах роста и старения, то можно заметить, что живые организмы могут избегать процесса старения в случае, например, с одноклеточными организмами, если их деление наступает до точки .

Либо, как в случае с древесными растениями, живые организмы продолжительное время могут избегать старения, если старые части не нуждаются в замене и могут выполнять несущие, транспортные и другие функции до той поры, пока рост и размеры не станут препятствием для функциональности.

P.S. В опыте лучше брать среднее значение скорости по двум соседним измерениям.

Приложение № 1

Уместно заметить, что значение в соответствии с моделью, изображённой на рис.1, должно лежать в пределах от точки А исключительно до точки 2А исключительно. Это возможно только при некоторых значениях n. Выражение для n находим из равенства в точке .

По данным графика, оказывается возможным найти вид функции F , а также зависимость значения функции F (скорости производства молекул данного вида) от количества молекул данного вида.

Для начала вычислим количество Z(A) дееспособных молекул в момент t = A.

Z(A) =

Любой промежуток времени на этом интервале

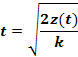
Таким образом, если количество дееспособных молекул в данном организме

≤ , то значение F =

Число дееспособных молекул , когда оно больше, чем Z(A), найдём из выражения:

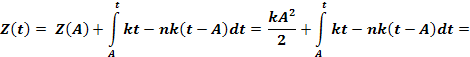
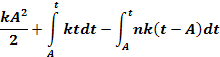
Кстати, используя подстановку

попутно найдём значение в точке окончания активного роста:

Из выражения для находим:

Мы выбираем именно этот корень, т.к. при этом решении с увеличением увеличивается .

Значение F на данном участке равно

Приложение №2

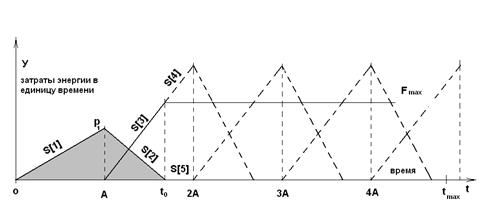
Рис. 6.

Программа №1 (на языке Mathematica 5)

Примечание

Несколько замечаний о программировании. Вычисления происходят в отдельной ячейке, в которой установлен курсор. Для этого нажимают Shift + Enter. Ячейка обозначается квадратной скобкой справа. После знака ; вычисления не выводятся на экран. Чтобы вывести, например, значение x, ставится просто x. Чтобы появилась нужная ячейка, можно в меню Cell выбрать Divide Cell. Цикл нельзя размещать в разных ячейках. Чтобы объединить ячейки, их выделяют, зажав клавишу Ctrl и, проводя курсором по квадратным скобкам справа, в меню Cell выбирают Merge Cells. Чтобы понять, что происходит в цикле, можно использовать команду Print[]. Чтобы узнать назначение какой-либо функции, её выделяют и нажимают F1.

K = 0.3; A = 100;= 1.9*A; n =; ∆t = 1; S[2] =Table[k*t-n*k(t-A),{t, A,}]; S[2] = Rest[S[2]]; S[3] = Table[n*k(t-A),{t, A,}]; S[3] = Rest[S[3]]; S[4] = Table[n*k(t-A),{t,}]; S[4] = Rest[S[4]]; w = Length[S[4]]; S[5] = Table[0, {w}]; z = ; q[0] = 0; L[1] = {1, 1}; Q[1] = {1, 1}; Do[ F = k*n(); q[j] = Part[S[4], j]+q[j-1] - F; Q[j+1]= Append[Q[j], q[j]]; L[j+1]= Append[L[j], F], {j, 1, w}]; L = Delete[L[w+1],{{1}, {2}}]; Q[w+1] = Delete[Q[w+1], {{1}, {2}}]; P = Join[S[3], L] + Join[S[2]*n, S[5]]; r=Length[P] ; q[0]=Part[Q[w+1],w];U[1]={1,1}; Do[ q[m] = Part[P, m]+q[m-1] - F; U[m+1] = Append[U[m], q[m]], {m, 1, r}]; U[r+1] = Delete[U[r+1], {{1}, {2}}]/n; P7=ListPlot[U[r+1], PlotJoined -> True, AxesOrigin -> {0, 0}, AxesLabel ->{“время (промежуток между 2A и 3A)”, “число погибших молекул”}];

Присваиваем значения; Формируем списки по рис.6, первые элементы отбрасываем; w – длина списка S[4] S[5] – достраиваем нулями z- число живых молекул; {1, 1} – затравочные списки; q[j]-часть молекул*n, которые не может восстановить F в цикле на промежутке от до 2А; удаление затравочных списков P – число молекул*n, нуждающихся в восстановлении (получаем общий список на промежуток 2А-3А); r - длина списка P; цикл на промежутке 2А-3А.

Приложение №3

Программа №2 (на языке Mathematica 5)

K = 0.3; A = 100;= 1.9*A; n =; ∆t = 1;

S[2] =Table[k*t-n*k(t-A),{t, A,}]; S[2] = Rest[S[2]];

S[3] = Table[n*k(t-A),{t, A,}]; S[3] = Rest[S[3]];

S[4] = Table[n*k(t-A),{t,}]; S[4] = Rest[S[4]];

w = Length[S[4]];

S[5] = Table[0, {w}];

z = ; q[0] = 0; L[1] = {1, 1}; Q[1] = {1, 1};

Do[If[z ≤ k*,

F = k*(n*k*A – )/(k*n-k)];

q[j] = Part[S[4], j]+q[j-1] - F; z = z – q[j]/n;

Q[j+1]= Append[Q[j], q[j]]; L[j+1]= Append[L[j], F], {j, 1, w}];

L = Delete[L[w+1],{{1}, {2}}]; Q[w+1] = Delete[Q[w+1], {{1}, {2}}];

P = Join[S[3], L] + Join[S[2]*n, S[5]];

r =Length[P] ;

q[0]=Part[Q[w+1],w];U[1]={1,1};G[1]={1,1};

Do[If[z ≤ 0, q[m] = ; Goto[tut], Print[z, “= ”, m] ];

If[z ≤ k*,

F = k*(n*k*A – )/(k*n-k)];

q[m] = Part[P, m]+q[m-1] - F; z = z – q[m]/n;

Label[tut]; U[m+1] = Append[U[m], q[m]];

G[m+1] = Append[G[m], F], {m, 1, r}];

P = Delete [G[r+1], {{1}, {2}}]; U[r+1] = Delete[U[r+1], {{1}, {2}}]/n;

P7=ListPlot[U[r+1], PlotJoined -> True, AxesOrigin -> {0, 0},

AxesLabel ->{“время (промежуток между 2A и 3A)”, “число погибших молекул”}];

Литература

1) Прудников П. А. Математическая теория процесса старения.

- Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 1. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/N-22-html/prudnikov/prudnikov.htm

2) Чигарев А.В., Кравчук А.И., Кравчук А.С. Основы системы Mathematica 4.0. Задачи и решения: Учебное пособие. – Минск:-150 с.

3) Бурзалова Т.В. Приемы решения задач по дискретной математике с

использованием компьютерной системы “Mathematica”. –

Улан-Удэ: Издательство Бурятского госуниверситета, 2002.-300с.

Сведения об авторе:

Автор: Прудников Пётр Алексеевич 1965 г.р., выпускник РГУ, специальность «биология».

Электронная почта: prpyotr@yandex.ru

Автор выражает признательность за помощь Сорокину Андрею и Сорокиной Анне.

Aging algorithm search

Prudnikov P.A.

Different options of prime mathematical model are investigated. Graphs and programs are attached. The criteria, indicating the fact that the reason used in the model underlies aging, are obtained. New characteristics of real-life experiment are suggested to research.

Keywords: mathematical model of ageing, model life length, the formula of life duration, the ageing reason, the theory of ageing, the ageing process, animal growth.