Математическая
теория процесса старения
П.А.Прудников,
Ключевые слова:
математическая модель старения, формула продолжительности жизни, продолжительность
жизни, рост, рост животных.
Аннотация:
на основании простой идеализированной модели, делается вывод, что процессы
роста и старения у организмов с ограниченным ростом могут происходить по двум
вариантам. Каждому варианту соответствует набор из трёх формул определения
максимальной продолжительности жизни. Рассматривается возможность приложения полученных формул к реальным объектам.
Keywords: mathematical model
of ageing, model life length, the formula of life duration, animal growth.
The summary: the model examined
two variants of processes of growth and ageing at organisms with the limited
growth. We have received three formulas of definition of the maximal life
duration for each variant.
Основные положения. Определения и термины.
Под ростом будем подразумевать нарастание числа новых молекул. Под процессом восстановления будем подразумевать только замену молекул. Производимые при этом в замен молекулы уже не будем считать участвующими в росте.
В этой статье под термином молекула понимается встраиваемая молекула.
Встраиваемые молекулы – молекулы, которые не находятся в свободном плавании, а включены в состав мембран, сложных молекулярных комплексов, находятся в связанном состоянии в матриксе, т.е. в таких местах, откуда не могут быть извлечены без затрат энергии.
Будем считать:
что на производство одной молекулы (или лучше одной пептидной связи, если молекула белковая) в среднем расходуется количество энергии равное m;
что через интервал времени, равный А молекула утрачивает свои биологические свойства и требуется её замена. При замене расходуется количество энергии (включая энергию обнаружения состарившейся молекулы, извлечения и т.д.), равное n, при этом n > m;
что в погоне за выживание, организм стремится, чтобы система, производящая молекулы - «конвейер» работал на пределе своих возможностей;
что в организме этот предел ограничен некоторой энергетической
функцией ответственной за подведение энергии к «конвейеру». Обозначим эту функцию буквой F.
Будем считать:
что максимального значения эта функция достигает в момент
окончания роста – в точке ![]() ;
;
что в этой точке значение F = Max;
что это значение
функции до конца жизни ![]() остаётся неизменным.
остаётся неизменным.
Введём ограничения для функции F. Будем
считать, что значение функции F в любой точке t не может быть больше, чем значение ![]() в этой точке.
в этой точке.
Очень трудно сделать функцию F зависимой от общего числа молекул (клеток). Потому как с ростом числа клеток, возникают различные транспортные и архитектурные проблемы, поэтому для продолжения роста требуется постоянная перестройка и переделка. На это тратится значительное количество энергии. В своей работе я исходил из самого простого принципа – что данная функция на отдельных участках линейна и, что чем больше молекул, тем большей должно быть значение функции F. Такое предположение в связи с изложенными проблемами роста кажется не столь уж невероятным.
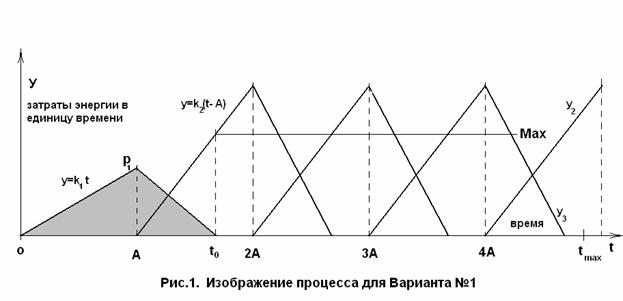
Теперь дадим пояснения к рис.1. По оси ординат откладываются
затраты энергии в единицу времени. По оси абсцисс – время. На оси абсцисс
обозначены: интервалы, равные А,
время максимальной продолжительности жизни ![]() и время прекращения
активного роста
и время прекращения
активного роста ![]() . Следует заметить, что время начинается с эмбрионального
периода, с момента образования зиготы.
. Следует заметить, что время начинается с эмбрионального
периода, с момента образования зиготы.
В начальный период масса, количество молекул и затрачиваемая
на их производство энергия малы по отношению к этим величинам у взрослого
организма, поэтому резонно начальную точку графика, изображённого на рис.1. расположить в ближайшей
окрестности точки «ноль», так что, если быть точным, то «ноль» на графике – на
самом деле «почти» ноль. Вертикальный «столбик» на графике (например, такой как
![]() ), равный
), равный ![]() – это количество производимых в этот момент времени молекул
умноженное на энергию m. Другими словами это скорость
производства молекул умноженная на энергию m.
– это количество производимых в этот момент времени молекул
умноженное на энергию m. Другими словами это скорость
производства молекул умноженная на энергию m.
Спустя интервал времени, равный А, начинается процесс замены
ранее синтезированных молекул. В каждый следующий интервал времени должно быть
восстановлено столько же молекул сколько их было синтезировано в предыдущем.
Получается, что функция ![]() как бы повторяется. Но
поскольку на восстановление молекул тратится больше энергии (n > m), то формула функции будет
как бы повторяется. Но
поскольку на восстановление молекул тратится больше энергии (n > m), то формула функции будет ![]() . Поэтому на графике изображён ряд прямых, параллельных
. Поэтому на графике изображён ряд прямых, параллельных ![]() , повторяющихся через интервал, равный А.
, повторяющихся через интервал, равный А.
Начиная с точки t = A, рост замедляется, потому, что часть
энергии функции F теперь должна тратиться на замену старых
молекул. В принципе, здесь возможны разные варианты. Мы не будем рассматривать
случай, когда неограниченный рост продолжается в течение жизни. Мы
будем исходить из предположения, что начиная с точки t = A, энергетические потребности
на восстановление молекул удовлетворяются в первую очередь, а на рост они
распределяются по остаточному
принципу. Такое предположение приводит нас к модели ограниченного
роста. При этом существует определённая точка ![]() , в которой на восстановление молекул тратится всё значение
функции F и на рост энергии не останется.
Физический смысл точки
, в которой на восстановление молекул тратится всё значение
функции F и на рост энергии не останется.
Физический смысл точки ![]() - это время прекращения интенсивного роста, включая
эмбриональный период.
- это время прекращения интенсивного роста, включая
эмбриональный период.
Если учесть, что для
встраиваемых молекул ![]() , то в силу введенных нами ограничений по функции F, точка
, то в силу введенных нами ограничений по функции F, точка ![]() может находится либо на интервале от А до 2А (первый
вариант), либо на интервале от 2А до 3А (второй вариант).
может находится либо на интервале от А до 2А (первый
вариант), либо на интервале от 2А до 3А (второй вариант).
Величины измеряются в следующих единицах:
A, t, ![]() ,
,![]() - (время),
- (время),
m, n – (энергия),
![]() ,
, ![]() -(энергия/
-(энергия/![]() ),
),
h – (энергия/время).
![]() ,
,![]() - реальные числа.
- реальные числа.
Вывод формул.
Рассмотрим вариант №
1.
При этом варианте точка ![]() расположена
между А и 2А.
расположена
между А и 2А.
Найдём, сколько было всего произведено молекул до окончания
времени интенсивного роста организма. Для
этого сначала найдём энергию W, затраченную на
производство молекул (интервал от 0 до ![]() , ограниченный сверху ломаной
, ограниченный сверху ломаной ![]() ), смотри рис. 1..
), смотри рис. 1..
Воспользуемся координатами точек из графика рис.1.: ![]()
![]()
Тогда ![]() ;
;
![]() .
.
W =  ;
;
W =![]() .
.
Соответственно, общее количество интересующих нас молекул Z, которые образуются при росте организма равно:
Z = ![]() , где m – это затрата энергии
на одну производимую во время роста молекулу.
, где m – это затрата энергии
на одну производимую во время роста молекулу.
Вернемся к рис.1.
Рассмотрим процесс восстановления молекул на участке между 2А и 3А. На этом
участке для исправного функционирования, организму потребуется воспроизвести
весь набор молекул, созданных за промежуток времени от 0 до ![]() . Таким образом, мы знаем, что на участке между 2А и 3 А,
т.е. на промежутке равном 1А, организм должен заменить Z =
. Таким образом, мы знаем, что на участке между 2А и 3 А,
т.е. на промежутке равном 1А, организм должен заменить Z = ![]() молекул. Это
потребует дополнительных расходов энергии. Энергия ограничена значением F = Max. Следовательно, часть старых
молекул останется без замены.
молекул. Это
потребует дополнительных расходов энергии. Энергия ограничена значением F = Max. Следовательно, часть старых
молекул останется без замены.
Мы можем записать следующее выражение:
![]() , где (1)
, где (1)
Q - это количество молекул, которые вышли из строя и не могут быть восстановлены в течение времени жизни.
Z - общее число молекул в организме.
![]() - такое соотношение старых, требующих замены молекул
(знаменатель) к общему числу молекул
(числитель), которое наблюдается в момент
- такое соотношение старых, требующих замены молекул
(знаменатель) к общему числу молекул
(числитель), которое наблюдается в момент ![]() , т.е. к концу жизни.
, т.е. к концу жизни.
Кроме того, в эту формулу должен быть включён ещё один
коэффициент. Обозначим его ![]() . Так как возникающий при старении дефицит энергии на
«конвейере» должен сказываться и на молекулах любого другого типа, которые на
нём производятся, то
. Так как возникающий при старении дефицит энергии на
«конвейере» должен сказываться и на молекулах любого другого типа, которые на
нём производятся, то ![]() - это энергетическая доля, которую занимает на этом конвейере
рассматриваемый нами пул молекул. Коэффициент
- это энергетическая доля, которую занимает на этом конвейере
рассматриваемый нами пул молекул. Коэффициент ![]() должен стоять перед всей левой частью приведённой формулы. Если
мы его из левой части перенесём в правую, то справа от знака равенства получим
выражение
должен стоять перед всей левой частью приведённой формулы. Если
мы его из левой части перенесём в правую, то справа от знака равенства получим
выражение ![]() . И выражение (1) примет вид:
. И выражение (1) примет вид:
![]() . (2)
. (2)
Значение функции F в
точке ![]() равно Max и
равно
равно Max и
равно ![]() .
.
Запишем выражение для определения того, какое количество
молекул Q в течение
жизни не может быть восстановлено, в зависимости от положения точки ![]() .
.
Вот это выражение:
Q = , где (3)
, где (3)
![]() ,
,
![]() ,
,
![]() ,
,
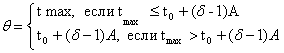
Найдём вид уравнений для![]() и
и ![]() .
.
![]() принадлежат точки с координатами:
принадлежат точки с координатами:![]() ,
,
![]() принадлежат точки с координатами:
принадлежат точки с координатами:![]() . Соответственно получаем:
. Соответственно получаем:
![]()
![]()
![]()
![]() ,
, ![]() ;
;
![]()
![]()
![]()
![]()
![]() . Подставляем полученные выражения в формулу (3):
. Подставляем полученные выражения в формулу (3):
Q =
 .
.
Теперь для удобства, разберём эту формулу на три:
1)
для случая t max ![]() 2A, получаем
2A, получаем
Q =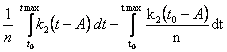 =
=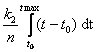 =
=![]() .
.
Примем во внимание, что ![]()
![]()
![]() .
.
Подставим полученные выражения в формулу (2). Получим:
![]() =
=![]() =
=![]() . Отсюда находим выражение для определения максимальной
продолжительности жизни. Так как обе части равенства по условию положительные,
оставляем одно решение:
. Отсюда находим выражение для определения максимальной
продолжительности жизни. Так как обе части равенства по условию положительные,
оставляем одно решение:
![]() .
.
2)
для случая 2A < t max ![]() , получаем
, получаем
Q =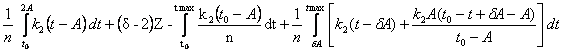 ,
,
Q=
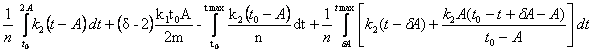 ,
,
= .
.
Поступая, как и в предыдущем случае, получаем (оставляя одно, устраивающее нас решение):
![]()
 .
.
3)
для случая 2A<![]() < t max, получаем
< t max, получаем
Q =

Поступая, как и в предыдущих случаях, получаем (оставляя одно, устраивающее нас решение):
![]() .
.
Формула работает при ![]() .
.
Вариант № 2: При
этом варианте точка ![]() расположена
между 2А и 3А.
расположена
между 2А и 3А.

Найдём, сколько было всего
произведено молекул до окончания времени интенсивного роста организма. Для этого сначала найдём энергию W, затраченную на производство молекул (интервал от 0 до ![]() , ограниченный сверху ломаной
, ограниченный сверху ломаной ![]() ), смотри рис. 2.
), смотри рис. 2.
Чтобы сделать это, необходимо на интервале от А до 2А знать
уравнение прямой ![]() . Это можно сделать двумя способами. В первом случае
уравнение прямой будет выражаться через величину h, во втором через коэффициент угла
наклона прямой. Мне кажется, что более удобно выразить уравнение прямой через h. Так и поступим.
. Это можно сделать двумя способами. В первом случае
уравнение прямой будет выражаться через величину h, во втором через коэффициент угла
наклона прямой. Мне кажется, что более удобно выразить уравнение прямой через h. Так и поступим.
Найдем уравнение прямой по двум точкам. Координаты первой
точки ![]() , координаты второй точки
, координаты второй точки ![]() . Составляем уравнение:
. Составляем уравнение:
![]()
![]() .
.
Уравнение прямой ![]() на интервале от 2A до
на интервале от 2A до ![]() также найдём по двум
точкам:
также найдём по двум
точкам: ![]() и
и ![]() . Составляем уравнение:
. Составляем уравнение:
![]()
![]() .
.
![]() .
.
Теперь можно приступить к вычислению энергии, затраченной на рост:
W=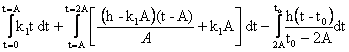 ;
;
W=![]() ,
,
![]() .
.
Из графика видим, что на участке между 3А и 4А, т.е. на
промежутке равном 1А, организм должен заменить как раз столько же молекул,
сколько их было произведено в процессе роста, т.е. Z= ![]() молекул.
молекул.
Запишем выражение для определения того, какое количество
молекул Q в течение жизни не может быть
восстановлено, в зависимости от положения точки ![]() .
.
Вот это выражение:
Q=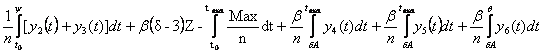 , где
, где
![]() ,
,
![]() ,
,
![]() ,
,
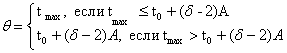
Найдём выражения для![]() ,
,![]() по точкам.
по точкам.
![]() принадлежат точки с координатами:
принадлежат точки с координатами:![]() , найдём соответствующее уравнение:
, найдём соответствующее уравнение:
![]() ;
;
![]() принадлежат точки с координатами:
принадлежат точки с координатами:![]() , найдём соответствующее уравнение:
, найдём соответствующее уравнение:
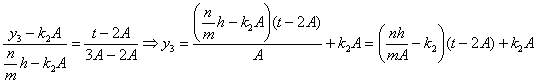 ;
;
![]() принадлежат точки с координатами:
принадлежат точки с координатами:![]() , найдём соответствующее уравнение:
, найдём соответствующее уравнение:
![]() ;
;
![]() принадлежат точки с
координатами:
принадлежат точки с
координатами: ![]() , найдём соответствующее уравнение:
, найдём соответствующее уравнение:
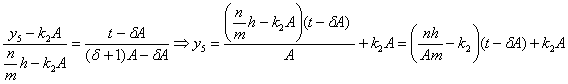 ;
;
![]() принадлежат точки с
координатами:
принадлежат точки с
координатами:![]() , найдём соответствующее уравнение:
, найдём соответствующее уравнение:
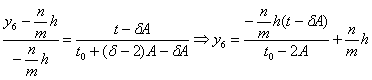 .
.
Для того чтобы найти значение F = Max в точке ![]() , надо решить уравнение
, надо решить уравнение
![]() . Решим его: найдём значение F в точке
. Решим его: найдём значение F в точке ![]() .
.
![]() ,
,
![]() = Max.
= Max.
Теперь для удобства, разобьём формулу
Q =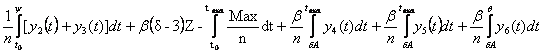
на три:
1)
для случая t max ![]() 3A, получаем
3A, получаем
Q = .
.
Сделаем необходимые подстановки: ![]() ;
;![]() ;
;![]() = Max; Z
=
= Max; Z
=![]() .
.
Примем во внимание, что ![]()
![]()
![]() .
.
Q =
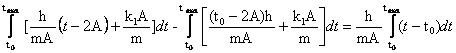 .
.
Таким образом:
Q =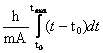 .
.
Подставим это выражение в формулу![]() , получим формулу для определения максимальной
продолжительности жизни. Так как обе части равенства всегда положительны, то
оставляем одно решение:
, получим формулу для определения максимальной
продолжительности жизни. Так как обе части равенства всегда положительны, то
оставляем одно решение:
![]() .
.
2)
для случая 3A< t max![]() , получаем
, получаем
Q =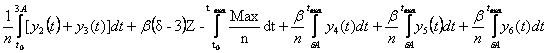 ,
,
сделаем необходимые подстановки: ![]() = Max; Z
=
= Max; Z
=![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;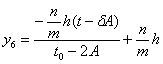 ;
; ![]() .
.
Q=
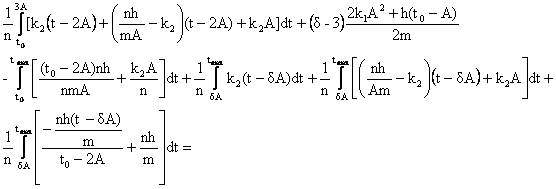

Поступаем как в предыдущих случаях, получаем, формулу для определения максимальной продолжительности жизни (оставляя одно устраивающее нас решение):
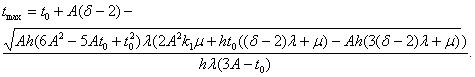
Формула работает при ![]() .
.
3)
для
случая 3 А <![]() < t max, получаем
< t max, получаем
Q = , сделаем необходимые подстановки:
, сделаем необходимые подстановки: ![]() = Max; Z
=
= Max; Z
=![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;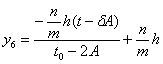 ;
; ![]() .
.
Q =
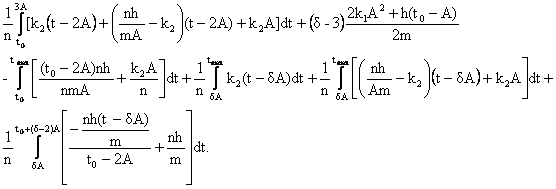
Q =

Поступая как в предыдущих случаях, получаем, формулу для определения максимальной продолжительности жизни (оставляя одно устраивающее нас решение):
![]()
Формула работает при ![]() .
.
Обсуждение результатов
В начале следует сделать одно
важное замечание: модель, и полученные на её основе формулы говорят о том, что
причина старения определяется энергетическим балансом. При этом в данной статье
не обсуждается от качественного соотношения пула, каких точно молекул наступает
смерть. Показатель ![]() констатирует только:
какое соотношение мы наблюдаем у встраиваемой молекулы в момент завершения
жизни.
констатирует только:
какое соотношение мы наблюдаем у встраиваемой молекулы в момент завершения
жизни.
***
Результаты данной работы показывают, насколько неперспективными могут быть поиски единой формулы старения для всех организмов.
При использовании метода к реальным живым объектам, необходимо учитывать ряд особенностей:
а) У
реального объекта зависимость ![]() от
от ![]() может отличаться от
вида
может отличаться от
вида![]() .
.
В частности из-за того, что доля в производстве встраиваемых молекул (например, коллагена) на ранних этапах роста может существенно отличаться от доли на поздних этапах. Это регулируется генами.
б) Острая вершина на графике может оказаться плоской или даже вогнутой из-за того, что на этот момент, как правило, приходится начало полового созревания. Вызванная этим перестройка организма забирает много энергии.
В связи с вышеперечисленным, реальный график, может сильно отличаться от используемого в моей модели. Но я надеюсь, что применённый метод, может быть творчески применён к особенностям каждого конкретного наблюдения и получаемых данных. Не берусь утверждать точно, но вполне вероятно, что график ежедневного прироста массы животного (с рядом оговорок) в какой-то мере будет грубым подобием графика, построенного для исследуемого пула молекул.