Другие статьи

НЕСТАНДАРТНЫЙ АНАЛИЗ НЕКЛАССИЧЕСКОГО ДВИЖЕНИЯ

П.В. Полуян

СОДЕРЖАНИЕ:

ЧИСЛА В ПРОСТРАНСТВЕ

I. ПРЕВРАЩЕНИЕ 4-МЕРНОГО ПРОСТРАНСТВА-ВРЕМЕНИ В КВАТЕРНИОННОЕ ВРЕМЯ-ПРОСТРАНСТВО.

II. ПРЕДЕЛЬНЫЙ ПЕРЕХОД МЕЖДУ ВРАЩЕНИЕМ И ПРЯМОЛИНЕЙНЫМ ДВИЖЕНИЕМ.

III. НЕПРЕРЫВНЫЙ КОНТИНУУМ И ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. БИПОЛЯРНОЕ ИСЧИСЛЕНИЕ.

ОТ АВТОРА: На прошедшей недавно международной математической конференции "Многомерный комплексный анализ" (International Conference "Multidimensional Complex Analysis", Krasnoyarsk, Russia, August 5-10, 2002) я представил внепрограммный доклад "Существуют ли гипердействительные числа в квантово-релятивистской вселенной?" Доклад был посвящен обширной теме "Нестандартный анализ неклассического движения", на первый план выдвигались математические и методологические аспекты проблемы, связанные с обоснованием нестандартной модели анализа А.Робинсона и расширением поля действительных чисел. Предлагаемая здесь работа адресована в первую очередь физикам, - математические аспекты вынесены за скобки, а физическое содержание конкретизировано. Автор рекомендует заинтересовавшимся читателям обратиться к электронным версиям "Нестандартный анализ неклассического движения. Существуют ли гипердействительные числа в квантово-релятивистской вселенной?", "Время и хронометрика. Ареальные множества", которые представлены на русском и английском языках в Интернете (на сервере Красноярского госуниверситета www.krasu.ru) - http://res.krasu.ru/non-standard и на сайте автора в США http://geocities.com/quantum_math_poluyan). Пользуясь случаем, автор благодарит математиков и физиков, высказавших в беседах и по e-mail свои критические комментарии к поставленной проблеме, а также друзей, которые помогают распространять его работы по Всемирной сети.

I

Один из научных текстов Вольфганга Паули начинается примечательной фразой: "Введем, как обычно, вещественные координаты X_k для пространства и мнимую координату X₄ = iCt для времени, и рассмотрим преобразования Лоренца..." (В.Паули. Труды по квантовой теории. М.: "Наука", 1977, в статье "К математической теории матриц Дирака", п.5 "Преобразование Лоренца волновых функций Дирака", с. 233.). Словесный оборот "как обычно" можно расценить в качестве особого рода интеллектуальной провокации, подразумевающей, что указанную процедуру можно сделать и "необычным" путем. Как? Не трудно сказать: мы попробуем для времени оставить вещественную координату, а 3 пространственные координаты представим как мнимые оси с размерностью времени. Тогда 4-мерный псевдоевклидовый континуум Минковского превратится в некое необычное многообразие, которое мы далее будем называть "кватернионное время-пространство".

Появление здесь термина "кватернион" понятно: четверку чисел, выражающих координаты, - одно вещественное и три мнимых - легко представить в качестве кватерниона. Однако кватернионы - это алгебраические числа, а 4-х мерное пространство-время Минковского - это континуум релятивистской физики, имеющий осмысленную физическую интерпретацию. Если так, то существуют ли достаточные основания для того, чтобы ставить их в соответствие? К этому вопросу мы вернемся несколько позже, а пока будем расценивать кватернионное время-пространство как некую чисто логическую конструкцию, - таковую можно рассмотреть в общем и проанализировать в частностях. Попутно отметим, что в современной науке термин "пространство" уже не связывается однозначно только с мерой расстояния [м], и ничто не мешает нам составить 4-мерное пространство, где на осях откладывается мера в размерности [t]. Но поскольку время - это физический параметр, отражающий важнейший аспект реальности, то нас в данной статье будет интересовать в первую очередь не формально-математические свойства полученной конструкции, а ее физический смысл.

То, что алгебра кватернионов не коммутативна - сразу же наводит на мысль: полученный таким образом абстрактный объект имеет прямое отношение к квантово-механическим особенностям физического мира. Однако мы не станем забегать вперед, будем рассматривать кватернионное время-пространство таким образом, как если бы мы ничего еще не знали о существовании квантовой механики. Иными словами, постараемся пока сохранить в неприкосновенности привычные представления о течении времени и протяженности пространства.

Итак, мы имеем перед собой 4-мерное многообразие, где вещественная ось - чистое время, а три другие - это пространственные координаты, превращенные в мнимые временные оси. Казалось бы ничего особенного не происходит, просто у 4-мерного пространства индекс 1 заменяется на индекс 3 и получается иная сигнатура метрики: (- - -+) вместо (+++-).

Однако всем известна физическая трактовка континуума Минковского, а для того, чтобы она имела смысл, требуется свести размерности осей к единой мере: поэтому все четыре координаты выражаются в одной мере [x], а достигается это с помощью умножения временной координаты на коэффициент C - скорость света [м/с]. В математическом смысле физические размерности не важны, однако без них невозможно обнаружить реальный прообраз ни для какой абстрактно-математической конструкции. Если мы для кватернионного время-пространства выбираем не меру [x], а меру [t], значит в итоге получается все-таки нечто иное, нежели просто другое представление для обычного физического пространства-времени.

Иногда считают, что для интерпретации континуума Минковского перевод t в x с помощью коэффициента C вообще не играет никакой роли - эта странная иллюзия, ведь время не может ФИЗИЧЕСКИ отождествляться с пространственным протяжением. Даже если C принять за единицу, размерности [t] и [x] от этого никуда не исчезнут. Равным образом, заявления о том, что "истинно значимым является только пространственно-временной интервал", "пространство и время едины по сути", "мы живем в четырехмерном пространстве, но сознание воспринимает его, как если бы время существовало" и т.п. - все это в большей мере философские утверждения, нежели физические. Поэтому крайне существенно, что мы в нашем кватернионном время-пространстве одноразмерность выбираем другую: мнимые пространственные координаты должны быть умножены на некий коэффициент S с размерностью [с/м]. И опять, может показаться, что ничего особенного не происходит - это ведь просто "обратная скорость света". Однако переворачивание коэффициента - не значимое математически - в физическом смысле ведет к очень значимым изменениям.

Обратная скорость света 1/C, как реальная физическая величина с размерностью [м/с] не может быть искомым коэффициентом, поскольку шкала обратных скоростей неравномерна. В классическом представлении скорость - это отношение, где в числителе отрезок расстояния, а в знаменателе период времени - времени как независимой переменной. Это - основа стандартного дифференцирования и алгоритм для классического сложения скоростей при переходе от одной системы отсчета к другой. С классической точки зрения для "обратной скорости", где числитель и знаменатель меняются местами, вместе с обращением размерности возникает и неравномерная шкала величин: 1[м/с] = 1[с/м], 2[м/с] = 1/2[с/м], 3[м/с] =1/3[с/м], 4[м/с] = 1/4[м/с] и т.п.

Стандартный математический анализ и псевдоевклидовость пространства не противоречат друг другу только потому, что у пространства как бы нет внутренней метрики (это подчеркивал Риман), иными словами единица может быть сколь угодно большой - она не задана как некоторая внутренняя мера величины расстояния. У нас же скорость света C, выступающая в качестве коэффициента при мнимой единице, - это вполне конкретная физическая константа, скорость электромагнитных волн. Мы можем ее мыслить в качестве некоторой единицы только условно. Для математических характеристик пространства-времени Минковского это не существенно, но в реальном мире единица C характеризует уникальный физический процесс, то есть ее "переворачивание" - математически безвредное - не может быть физически оправданным.

Но тогда создается впечатление, что по этой именно причине кватернионное время-пространство не имеет какого-либо физического смысла. Тогда предложенная автором конструкция - всего лишь искусственное построение, опирающееся на случайный факт: в кватернионе четыре числа и в континууме Минковского четыре измерения. Однако достаточно нам предположить, что коэффициент S[с/м] не является "обратной скоростью", и не имеет прямого отношения к скорости распространения электромагнитных волн, как все становится на свои места - S это просто некий коэффициент с размерностью [с/м].

Если же коэффициент C в псевдоевклидовом континууме Минковского - это вполне конкретная физическая величина, скорость света, имеющая в разных системах отсчета конкретное численное значение (но математически - это единица), то в нашем кватернионном время-пространстве коэффициент S также должен быть ни чем иным как некой физической величиной - константой, отличной по сути своей от скорости света, но имеющей размерность [с/м] - обратную размерности скорости. На роль такой константы можно выдвинуть комбинацию констант h/e², где h - постоянная Планка, а e - заряд электрона. Хорошо известно, что эта комбинация констант наряду с C входит в выражение безразмерной постоянной тонкой структуры 1/a = ħC/e² = 137,0306... (здесь ħ - это постоянная Планка, деленная на два "пи" - h/2p ). Я полагаю, что так оно и есть: квартернионное время-пространство - это математическое выражение реального аспекта микрофизической реальности, где константа S=h/e² с размерностью [с/м] столь же важна, как важна скорость света для глобального 4-мерного континуума Минковского.

Конечно, автора можно упрекнуть за некий произвол - ведь сконструировать размерность [с/м] из известных констант можно и другими способами. (Например, использовать гравитационную постоянную.) Единственный мотив, которым автор здесь руководствуется - это желание перекинуть логический мостик между квантовой и релятивистской физикой, задавая - пока только формально-математически - связь между глобальной пространственно-временной картиной мира и микрофизической квантовой реальностью, - поскольку именно эти константы принято использовать для выражения безразмерной постоянной тонкой структуры.

Ведь было бы крайне интересно, если бы постоянная тонкой структуры стала константой, показывающей соответствие между континуумом Минковского и кватернионным время-пространством. Я полагаю, что Вольфганг Паули, который настаивал на теоретическом обосновании физического статуса этого загадочного числа 137,0306..., имел в виду нечто подобное. Если же вести речь о нормировках, то гораздо естественнее именно это безразмерное число приводить к единице, нежели выбирать "естественные меры" в которых единицей становится скорость света.

Однако математических аргументов и эстетических оценок здесь не достаточно. Мы должны вскрыть и физическую суть обнаруженного соответствия, то есть увидеть логическую связь между граничной скоростью прямолинейного поступательного движения C и константой S, смысл которой пока не понятен. S=h/e² - это комбинация эмпирических констант с размерностью [с/м], мы включили ее в некую математическую структуру, но от этого смысл всего построения не стал яснее.

В классической физике скорость является количественной мерой поступательного движения, связывает между собой пространственные и временные параметры движения как прямолинейного поступательного перемещения. Если константа S включается нами в кватернионное время-пространство, значит, она также должна пониматься как граничное выражение какого-то аспекта движения, где пространственные и временные характеристики как-то связаны между собой. Более того, важнейшим свойством континуума Минковского являются преобразования Лоренца, приводящие к тому, что закон сложения скоростей при переходе от одной системы отсчета к другой дает предельное значение для прямолинейного поступательного перемещения. Логично предположить, что в кватернионном время-пространстве также обнаружится аналог преобразований Лоренца, который позволит трактовать константу S в качестве инварианта и предела в сложении каких-то величин. Так, по крайней мере, должно выглядеть дело в двумерном случае, где на комплексной плоскости псевдоевклидовым образом связываются одна временная и одна пространственная ось. Для континуума Минковского мнимой будет временная ось - iCt, а для кватернионного время-пространства - пространственная iSx. В двумерном случае дело облегчается тем, что мы оставляем за рамками рассмотрения некоммутативность (с другой стороны, обнаруживается, что некоммутативность связана напрямую с наличием еще двух мнимых пространственных координат).

Поскольку скорость света C - это неклассическое ограничение на максимальную скорость (скорость распространения сигнала между двумя точками пространства не может быть бесконечной), соответственно, константа S также не позволяет отношению D Dt/D Dx принимать бесконечные значения. Однако S - это предел для "обратной скорости", а увеличение D Dt/D Dx одновременно означает уменьшение отношения D Dx/D Dt, что позволяет предположить: в нашем реальном мире "нулевая скорость" столь же недостижима, как и бесконечная.

Тем не менее, и в случае упрощенного двумерного, комплексного представления кватернионного время-пространства, все-таки, остается пока непонятным: что за величины должны здесь складываться, и каков в данном случае физический смысл "системы отсчета"? На эти вопросы нам сейчас и предстоит ответить.

Поскольку S - это некий коэффициент пропорциональности между мерой времени t[с] и мерой расстояния x[м], то константа S как самостоятельная величина выражает некий аспект движения, но, поскольку для поступательного прямолинейного перемещения количественной мерой является классическое понятие скорости V[м/с] и ее неклассический предел C, эта новая константа S должна быть неклассическим пределом какой-то вполне классической меры движения, которая тем не менее не является поступательным перемещением. Мы предположим, что искомой формой движения является вращение.

Существуют микрофизические и математические соображения, для того, чтобы связать указанную величину именно с вращением.

Во-первых, в физике элементарных частиц экспериментально определено существование так называемых изотопических преобразований, которые полностью аналогичны обычным вращениям. Вернер Гейзенберг, перечисляя основные группы симметрии, рядом с группой Лоренца помещает особую группу - это "группа, исследованная Паули и Гюши, которая соответствует по своей структуре группе трехмерных пространственных вращений - она ей изоморфна, - и проявляет себя в появлении квантового числа, которое эмпирически было открыто у элементарных частиц и получило название "изоспин". ("Квантовая теория и строение материи", в кн. В.Гейзенберг, "Физика и философия. Часть и целое.", М.: "Наука", 1990, с. 103.) При этом, соотношения, следующие из изотопической инвариантности соблюдаются с точностью до поправок, величина которых определяется константой e²/hC. В учебной литературе отмечается, что "изотопическая инвариантность означает особую симметрию сильных взаимодействий, не связанную с общими свойствами пространства и времени. Хотя изотопическая инвариантность достаточно хорошо установлена экспериментально, связанные с нею свойства симметрии логически не вытекают из существующей теории и природа этих свойств симметрии пока не выяснена". ("Изотопический спин", в кн. "Физический энциклопедический словарь", М., 1962, т. 2, с. 143.)

Во-вторых, математически эрудированные читатели, видимо, уже поняли, что тот объект, который выступает здесь под именем кватернионного время-пространства, это структура известной алгебры Клиффорда для четырехмерного векторного пространства. Применимость алгебры Клиффорда в физике уже не раз показывалась, в том числе и для изоспинов. Однако обычное отношение к применению векторной алгебры в неклассической физике достаточно скептическое. То, что сделано в этом направлении во Франции (работы G.Casanova, C.R.Acad и др.) обычно рассматривается, как результат специфической интерпретации квантовой механики, а в России работы этого направления (В.В.Кассандров - "Алгебраическая структура пространства-времени и алгебродинамика" на сайте www.chronos.linia.ru, В.И.Елисеев - "Ввведение в методы теории функция пространственного комплексного переменного" http://www.maths.ru) большинством физиков воспринимаются как некие искусственные построения.

Таким образом, цель, которую автор здесь намечает - это обоснование фундаментальной значимости векторной алгебры для познания Универсума. Автор считает, что кватернионное время-пространство - это логически необходимое дополнение 4-мерного пространства-времени, которое замыкает пространственно-временную структуру Универсума, а раздвоение безразмерной единицы на две размерные константы определяет тот фрагмент Универсума, где имеют место и время физические явления. Автор стремится показать, что векторная алгебра не является всего лишь специфическим математическим языком для переоформления известных в физике результатов, напротив - она появляется столь же логично и естественно, как на базе классического декартова пространства строится псевдоевклидов континуум Минковского.

Автор утверждает, что стандартное определение вращения, используемое в физике, не отвечает новым задачам. Традиционное понятие вращения сформулировано в классической механике исключительно по отношению к инерциальным системам отсчета, что фиксируется в угловой скорости (относительно не вращающейся системы координат) и линейной мгновенной скорости (опять-таки относительно инерциальной системы отсчета). Мера вращения, соответственно, вводится тогда, как [м/с], поскольку для вращения в качестве независимой переменной заранее берется время. Но, в противоположность этому, можно вполне последовательно и непротиворечиво построить понятие вращения относительно вращения. Множество скоростей вращения и взаимоотношения на этом множестве получаются совершенно аналогичными множеству упорядоченных поступательных прямолинейных относительных скоростей, однако мерой скоростей вращательного движения становится [с/м], независимой переменной оказывается "длина дуги".

Таким образом, предлагаются новые логические и математические основания для понимания физическое реальности. С новых позиций вращение понимается уже не как некий аспект движения, редуцируемый к поступательному перемещению одной материальной точки по некоторой траектории (ее замкнутость - частный случай), а как фундаментальная характеристика движения, имеющая свою меру измерения [с/м] и свою независимую переменную - x[м].

Применимость названных подходов многими ставится под сомнение еще и потому, что этому мешает устоявшаяся привычка - стандартное понимание пределов и бесконечно малых. Автор считает, что поскольку работами Абрахама Робинсона доказана логическая непротиворечивость нестандартного анализа, где область действительных величин расширена за счет гипердействительных актуально бесконечно малых и бесконечно больших чисел, уже ничто не мешает нам переосмыслить стандартные представления о взаимоотношении бесконечно большого и бесконечно малого, и обнаружить их предельный взаимопереход друг в друга. Именно это и происходит, когда четырехмерное пространство-время замыкается с кватернионным время-пространством в единое целое. И это происходит РЕАЛЬНО.

II

Как читатель уже заметил, построение кватернионного время-пространства с новой константой S напоминает некое вольное конструирование математических моделей, снабженное искусственными привязками к тем или иным аспектам физического мира. Всем известно, что далеко не каждое математическое построение имеет отношение к реальности. Однако, напомню, - нами сделано конкретное предположение: кватернионное время-пространство должно иметь некий классический прообраз, где величина с размерностью [с/м] должна трактоваться как вращение.

То что континуум Минковского отражает реальные свойства Универсума - общепринято, но само это четырехмерное псевдоевклидово пространство-время возникло в результате более углубленного понимания классических представлений о стандартной декартовой координатной системе - обычном трехмерном евклидовом пространстве. Таким образом, кватернионное время-пространство также должно иметь какой-то классический прообраз. Однако среди теоретических представлений классической физики нет ничего, что можно было бы предложить на эту роль. Получается, что наше построение, в самом деле, - и произвольно и безосновательно.

Однако этот вывод ошибочен. Оказывается, прообраз (или, точнее, - пра-образ) кватернионного время-пространства имеется в науке, но в науке ДОКЛАССИЧЕСКОЙ. Классические декартовы координаты и время в качестве независимой переменной в свое время пришли на смену именно той теоретической модели, которая здесь именуется прообразом кватернионного время-пространства. Этим пра-образом является доклассическая, почти уже забытая, модель Вселенной в виде вращающихся небесных сфер. Если отвлечься от устаревшей натурфилософии, сопутствующей этой модели, то мы обнаружим нормальный математический подход: строится множество относительных вращений. Иными словами, если в декартовой системе координат, в трехмерном евклидовом пространстве определяется множество относительных поступательных скоростей, соизмеряемых в абсолютном времени, то в доклассической модели небесных сфер сравнивались и соизмерялись относительные вращения, а временные периоды при этом оказывались функцией от пространственной меры - независимой переменной (говоря современным языком).

Обычно считается, что от этой модели пришлось отказаться, когда "обнаружилось", что Земля не находится в центре мира. С этим мы спорить не будем, и требовать возвращения к средневековым представлениям смысла нет. Однако суть дела вот в чем: отказ от натурфилософской космологии не является ниспровержением теоретической модели. Иными словами, модель ОТНОСИТЕЛЬНЫХ ВРАЩЕНИЙ, которая использовалась для объяснения Солнечной системы, не утратила своего логического смысла от того, что обращение планет вокруг Солнца стали мыслить в декартовых координатах с помощью абсолютного времени, используя представления об ускорении и силе всемирного тяготения. (См. об этом работу автора "Новая научная парадигма физики и старая картина мира" в сб. "Взаимосвязь науки и практики", Братск, 1987, с. 60.)

Ниже мы постараемся перевести эту математическую модель относительных вращений на элементарный кинематический язык. Разумеется, вращения уже не будут связываться с орбитами небесных тел, а центр вращения будет появляться не потому, что "Земля находится в центре Вселенной", а потому что в центре системы отсчета помещается наблюдатель.

Математическая модель относительных вращений не исчезла вместе с геоцентрической астрономией. Соотношения, которые выводятся в алгебре для поворотов и длин дуг зафиксированы, например, в известной формуле для косинуса удвоенного угла cos2=(e²ⁱ+e^-2i)1/2Удвоение угла возникает в ходе предельного приравнивания центрального и вписанного углов в одной окружности при ее делении на нечетное количество бесконечно малых сторон. Здесь мы не будем касаться подробностей выведения этой формулы, отметим только один исторически важный момент. Для античных греческих математиков стало великим открытием обнаружение иррациональностей в виде несоизмеримости диагонали и стороны квадрата. Столь же великим достижением арабских алгебраистов было построение искривленного "квадрата", состоящего из дуг окружностей единичного и удвоенного радиусов (это их фундаментальное открытие воплотилось в сакральном символе полумесяца). Возникающее из такого построения соотношение поворотов позволило открыть методологию конструирования степенных рядов.

Напомню, что даже основополагающий для гелиоцентрической модели трактат Николая Коперника назывался "О вращениях небесных сфер", то есть, опирался на принцип сравнения вращений. Коперник поставил под сомнение "физический аргумент" Евдокса, Аристотеля, Птоломея о том, что "при вращении Земли все легкие предметы с ее поверхности улетели бы" и пересчитал вращения к новой системе отсчета. Интересно отметить, что есть разночтения в переводе названия его работы с латинского языка "De Revolutionibus": польское название - "Ob obrotach..." привело к русскому переводу "Об обращении...", которое потом пришлось изменять на "О вращении...", ссылаясь на то, что во времена Коперника в механике не различали вращательного движения тела вокруг оси, расположенной неподвижно, и кругового движения материальной точки вокруг центра (соответственно - "вращение" и "обращение"). Это действительно серьезно: ведь для великого польского астронома существенным оставалось понятие о "круговом импульсе", введенное средневековым философом и логиком Жаном Буриданом, благодаря чему вся Земля со всеми ее обитателями, водой и атмосферой может спокойно вращаться вокруг своей оси.

Автор хотел бы обратить внимание на то, что космогонические представления прошлого хоть и были предметом осмысления при формировании теоретической модели относительных вращений, но не являются ее единственной репрезентацией. Любая кинематическая модель - это установление логической связи между временными и пространственными мерами, физические аргументы по отношению к ней вторичны и нужны только для ее смысловых интерпретаций. Иными словами, соединение двух, вроде бы, альтернативных теоретических моделей в единую систему - это дело логики и математики, а физическая интерпретация полученного результата - это следствия и последующие выводы. Поэтому наша основная задача: показать, что кинематика сложения прямолинейных движений и кинематика соизмерения вращений РАВНОПРАВНЫ, - в равной мере логически обоснованы. Их равноправие предполагает создание обобщенной кинематической модели, а в рамках этой модели должны быть объединены четырехмерный континуум Минковского и кватернионное время-пространство. Вывод автора о том, что при этом происходит раздвоение безразмерной математической единицы на две размерные константы, определяющие масштабы реальной Вселенной - это уже некоторая физическая интерпретация, предполагающая установление связи между динамическими величинами типа "масса", "энергия", "импульс", "длина волны", "электрический заряд", "спин" и т.д.

Несколько предварительных замечаний.

Мы предположили, что специфической формой движения, которая в кватернионном время-пространстве будет вести себя аналогично обычной поступательной скорости, является именно скорость вращения, но с необычной мерой. В принципе, других логических вариантов у нас просто нет, ведь мы исследуем скорость движения как некое отношение между временным и пространственным параметрами, а таких отношений может быть только два: x/t и t/x.

В математике ПОВОРОТ в пространстве столь же фундаментальная операция как параллельный перенос. Уместно здесь упомянуть выдающегося французского математика Анри Пуанкаре, который указывал на наличие "скрытой аксиомы", которая замаскирована среди постулатов Евклида в виде алгоритма о прорисовке окружности циркулем. (А.Пуанкаре, "О науке", М.: "Наука", 1983.) То, что поворачиваемая полупрямая рано или поздно совпадает со своим продолжением логически не связано с аксиомами о статичных точках и прямых, Пуанкаре показывает, что устранение этой "аксиомы" может приводить к экзотическим теориям.

В то же время в классической механике Ньютона вращение - это нечто вторичное по отношению к прямолинейному поступательному движению, то есть вращение (движение по замкнутой траектории) редуцируется к бесконечно малым прямолинейным перемещениям материальной точки, поэтому скорость вращения традиционно измеряется в той же самой мере [м/с], выражаемой как число оборотов за секунду, то есть "угловая скорость" оказывается лишь условным выражением для обозначения истинной - линейной скорости. Окружность - замкнутая кривая, криволинейное движение - это перемещение в пространстве, замкнутость кривой - оборот - не играет существенной роли. При этом, время аксиоматически берется в качестве независимой переменной, ход времени в полном согласии с ньютоновским определением - равномерно и неотвратимо отсчитывает секунды (в заданной системе отсчета). Заметим, кстати, что в своей работе "Математические начала натуральной философии" Исаак Ньютон вводит абсолютное время при помощи достаточно подробных обоснований, призванных доказать, что мы должны постулировать ход времени сам по себе - без привязки как каким бы то ни было вращательным периодическим процессам, наблюдаемым в небе.

Так вращение было представлено как нечто, что легко можно свести к общим понятиям о прямолинейном перемещении, причем редукция выглядит сейчас вполне естественной и само собой разумеющейся. В исходных версиях классической механики для объяснения вращения вводились фиктивные силы, фиктивные потому, что явная инерция вращательного движения (материальная система может вращаться бесконечно долго, как бесконечно может двигаться в евклидовом пространстве материальная точка) не предполагает и не требует наличия "живой силы", связанной с затратами энергии. Особенно причудливый вид принимают фиктивные силы, когда рассматривается вращающееся колесо, свободно и равномерно катящееся относительно инерциального наблюдателя по прямой, - тогда материальная точка на ободе колеса прочерчивает циклоидальную траекторию.

Термин "циклоида" введен Галилеем. Независимо от него во Франции эту же кривую исследовал Мерсенн, он именовал такую траекторию "рулеттой". Возникла обширная литература о циклоидах - Торричелли, Вивиани, Роберваль, Ферма, Декарт. При построении касательных к циклоидам было введено специальное понятие - "мгновенный центр вращения". Механика циклоид сохранила свою значимость в инженерной науке, а из науки фундаментальной была вытеснена механикой Ньютона. Таким образом, в физике утвердилась только одна фундаментальная идеализация - "материальная точка". (Точка имеет точные координаты в плоском евклидовом пространстве, осуществляет движение по непрерывной траектории, а связь между производными по времени определяет динамические величины.)

Представление о чистом вращательном движении, которое неразложимо на перемещения отдельных точек, вернулось в классическую физику вместе с электромагнитной теорией. Результат известен: в конечном итоге трехмерное пространство мы вынуждены были превратить в четырехмерное пространство-время, - представление об абсолютном времени подверглось модификации. Сейчас, в свете неклассической релятивисткой физики, использование фразеологии, связанной с понятием "сила" выглядит архаическим и двусмысленным, а в квантовой механике фундаментальность вращения (то есть не сводимость его к движению точки по траектории) проявляется в таких феноменологически введенных понятиях, как спин, вращение плоскости поляризации и др.

Однако идейное наследие классической механики остается неприкосновенным, - оно зафиксировано в теоремах стандартного математического анализа и не подвергается пересмотру. Глубокое сочувствие вызывают старания теоретиков, доказывающих продуктивность использования в неклассической физике методов векторной алгебры - им приходится воевать на два фронта: против математиков, охраняющих классические принципы анализа, и против физиков, исповедующих идеологию "абстрактных пространств". Нельзя без боли читать беспомощный призыв в книге "Векторная алгебра" Гастона Казанова: "Обычное векторное исчисление очень полезно в геометрии, механике, гидродинамике и электродинамике... В то же время, и при изучении пространства-времени специальной теории относительности, а также в теории Дирака и в теории частиц не стоит отказываться от кватернионов". (Gaston Casanova, L`ALGEBRE VECTORIELLE, Presses Universitaires de France, 1976. Русское издание - Г.Казанова, "Векторная алгебра", М.: "Мир", 1979, с. 37.)

Почему же, все-таки, от подходов, основанных на алгебре Клиффорда большинство физиков отказывается? Да, потому что физическое вращение математически редуцируется к классическому движению точки по траектории, а такое понимание кажется настолько глубоко укорененным в человеческой логике, что другого, как бы, просто не может быть. Спрашивается, какая же тогда логика позволила У.Р.Гамильтону, Х.Грассману, У.К.Клиффорду, Дж.У.Гиббсу создавать аппарат векторного исчисления? Может быть алгебраические методы развивались сами собой? Но если мы используем в геометрии мнимую единицу, если мы принимаем, что основание натуральных логарифмов e=(1 + 1/n)ⁿ при n стремящемся к бесконечности, то все это должно иметь реальный смысл, должно что-то означать - не только абстрактно, но и конкретно. Настолько конкретно, что человеческая логика может это принять так же просто, как точки и прямые, как арифметически банальное "дважды два четыре". Если южноамериканские индейцы не пользовались колесом, это вовсе не значит, что понятие о круговом движении было выше их понимания. Рано или поздно все приходится начинать.

Поэтому, автор считает, что было бы вполне логичным попытаться посмотреть: как следует определять СКОРОСТЬ ВРАЩЕНИЯ последовательно кинематически, какая взаимосвязь возникает между координатами x и t, если вращение есть целостное интегральное движение. Если оно не является просто суммой бесконечно малых прямолинейных векторов-перемещений, и его скорость - это величина, которую надо определять именно для вращения, а не для движения точки на круговой траектории.

Сразу же отметим важную вещь: в алгебре Клиффорда в трехмерном пространстве о СКОРОСТИ вращения, понятно, речи не идет - это не физическое вращение, а поворот. А когда этот метод распространяется на четырехмерное пространство, то строится уже знакомое нам пространство индекса 1, понимаемое как векторный алгебраический аналог пространства-времени Минковского. То есть опять-таки, вращение оказывается чисто математическим поворотом, а не вращательным движением - конкретной фундаментальной формой со своей собственной мерой скорости.

Поэтому, для того, чтобы выявить истинное физическое содержание кватернионного время-пространства мы пойдем таким путем: сначала мы рассмотрим кинематику вращения и проследим как должно определяться при этом множество скоростей вращения, мы выясним какой параметр должен являться здесь независимой переменной. На этом этапе мы получим теоретическую модель, которая в свое время натурфилософски отождествлялась с моделью Вселенной, и которую потом сменила классическая механика с ее представлениями о бесконечном трехмерном пространстве и прямолинейном перемещении точек с разными равномерными или мгновенными скоростями. После этого станет совершенно ясно, что, точно также как континуум Минковского возник на основе классической модели, должно быть определено и кватернионное время-пространство, являющееся логическим продолжением альтернативной модели движения. Наконец, мы увидим, что объединение этих сопряженных пространств - континуального и алгебраического - требует от нас нового понимания взаимоотношений между бесконечностью и актуально бесконечно малым.

С самого начала в нашем рассмотрении появится некий конкретный образ - КОЛЕСО. Автор выражает надежду, что читатель отнесется к этому наглядному пособию как к некоторой условности - подобной тем "поездам", "падающим лифтам" и "световым часам", которые используются для уяснения сути дела в релятивистской физике.

* * *

Мы начнем с анализа смысла понятийного различения инерциальных и неинерциальных систем. Ясно, что вращающаяся система - не инерциальна, соответственно, выглядело бы бессмысленным - неоправданно сложным - определение параметров движущейся инерциальной системы по отношению к вращающейся. Поэтому обычная шкала относительных поступательных скоростей, возникает из рассмотрения множества исключительно инерциальных систем. С другой стороны, вращение традиционно понимается как нечто, что определимо только по отношению к системе, которая НЕ ВРАЩАЕТСЯ. В таком случае, возникает вопрос - можно ли отождествлять такую "не вращающуюся систему" с инерциальной? При внимательном рассмотрении выясняется, что такое отождествление как раз и происходит в логике классической механики. Математический вывод о том, что мерой вращения будет [м/с], а угловая скорость есть линейная на замкнутой траектории, - уже заранее заложен в предпосылки.

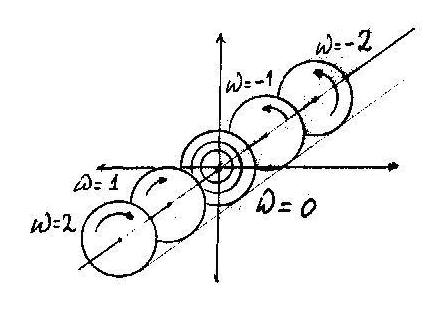
Давайте, уточним каков ход мысли, приводящий к стандартным выводам. Рассматривается множество вращающихся систем ("колес"), оси которых лежат вдоль одной прямой. Предположим, что в единицу времени они совершают некое кратное число оборотов, а расположим их так, что у двух соседних колес число оборотов отличается на единицу. Тогда можно принять одно из колес за неподвижную систему отсчета, - в обе стороны от него распределятся вращающиеся системы, направления вращений у которых противоположны, а переход от колеса к колесу в каждую из сторон будет приводить к равномерному возрастанию их скорости вращения относительно выбранной покоящейся системы отсчета. Понятно, также, что в качестве системы отсчета можно брать любое из колес - отношения между ними сохраняются.

Рис. 1.

Казалось бы, здесь определяется именно относительность вращений, ведь угловая скорость измеряется у одного колеса относительно другого. Если мы помещаем наблюдателя на одно из них, он кинематически может считать себя системой отсчета с нулевой угловой скоростью и фиксировать число оборотов измеряемой системы относительно собственной. Однако по сути дела здесь неявно присутствует кинематика прямолинейного движения, которая зафиксирована в том, как мыслится превращение угловой скорости в линейную. В классической механике вращение - это поступательное движение точки по криволинейной замкнутой траектории. Если эту точку "отпустить", она продолжит свое поступательное движение по прямой - угловая скорость перейдет в линейную.

Допустим, что в нарисованной системе колес, где, якобы, мы определяем относительность скоростей вращений, точки окружностей всех колес одновременно "отпущены на свободу". Оказывается НА САМОМ ДЕЛЕ система отсчета, задаваемая здесь, задается именно как инерциальная, а не просто как "условно не вращающаяся". У такого колеса точки никуда не должны улетать, их линейная скорость нулевая (как и угловая), и теперь относительно этой системы отсчета можно измерить все прямолинейные скорости улетающих точек.

Предположим иное, - что "условно покоящаяся" все-таки была вращающейся, и ее точки также должны "разлетаться", просто надо задействовать обычный принцип относительности для прямолинейных перемещений. Какая же получится картина в таком случае? Пусть наблюдатель находится в центре, тогда "отпущенные точки" начнут улетать от него. Однако, улетая, они все время остаются на окружности, то есть равными остаются расстояния от центра до любой из них. Если же наблюдатель в центре будет следить за поведением радиус-вектора, соединяющего центр и некоторую точку на этой расширяющейся окружности, он заметит: радиус вектор - поворачивается, как если бы расширяющаяся окружность продолжала вращаться. Радиус-вектор поворачивается с замедляющейся угловой скоростью, совершая четверть оборота за бесконечное время.

Но к этим выводам наблюдатель в центре может придти только в том случае, если он действительно покоится - то есть с ним связана не вращающаяся система декартовых координат с неизменной ориентацией осей, где и определяется бесконечно длящийся четверть-поворот радиус-вектора относительно фиксированного направления. Мы опять приходим к выводу, что неявно предполагается наличие инерциальной системы отсчета - не вращающейся системы пространственных координат. Мало того, здесь предполагается и наличие абсолютного времени: ведь расширение окружности - это процесс, происходящий сообразно отсчитыванию секунд.

Допустим, что обнаруженный факт не имеет особого значения: если инерциальная система и течение времени предполагаются - так тому и быть. Пусть вращение радиус-вектора - это иллюзия, возникающая от того, что разлетающиеся точки находятся на некоторой условной расширяющейся окружности, которая не является непрерывным континуумом, а "просто" состоит из точек. Но рассмотрение расширяющейся окружности, относительно неподвижного центра или же любой из ее "неподвижных" точек, приводит к нетривиальному вопросу: относительно какой меры расстояния это расширение фиксируется? Ведь все точки всех окружностей "разлетаются" с поступательными прямолинейными скоростями!

Данная проблема, действительно, нетривиальна, что обнаруживается уже в исходных понятиях, связанных с определением прямолинейной поступательной скорости.

Содержание принципа относительности изложить просто: абсолютного движения нет, то есть две точки могут двигаться только относительно друг друга. Если мы берем одну из них за точку отсчета, то полагаем ее покоящейся, а другая относительно нее оказывается прямолинейно двигающейся. Совершенно так же мы можем эту движущуюся принять за неподвижную точку отсчета и считать двигающейся другую. Представление о движении совершенно естественно и необходимо требует принципа относительности: изменение расстояния между точками со временем происходит МЕЖДУ НИМИ - увеличивается длина отрезка прямой, соединяющей эти точки. ("Координатная система, движущаяся равномерно и прямолинейно относительно инерциальной системы, сама является инерциальной. Каждый универсальный закон природы, который выполняется по отношению к некоторой системе отсчета С, должен также выполняться в любой другой системе С`, которая движется равномерно и прямолинейно относительно С". А.Эйнштейн. Собрание научных трудов. т. I, М.: "Наука", 1965 с. 679.)

Вот схема принцип относительности на примере двух точек:

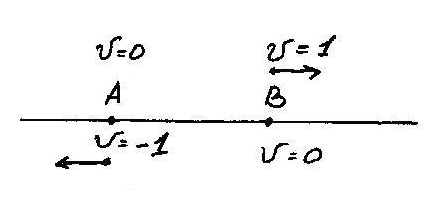Рис. 2.

принимаем одну за систему отсчета - вторая "движется относительно ее" и наоборот. Представим: в пустом пространстве находятся две точки (математически безразмерные), разделенные некоторым расстоянием. Теперь постараемся представить, как это расстояние изменяется... Но каким образом можно здесь зафиксировать изменение? Анри Пуанкаре однажды провел мысленный эксперимент - спросил: что было бы, если бы расстояния между всеми точками мира внезапно увеличились в два раза? И ответил: мир этого не заметил бы. Другими словами, для того, чтобы можно было определить изменение расстояния между двумя точками, надо представить себе наличие еще одной точки, которая относительно какой-либо из заданных неподвижна.

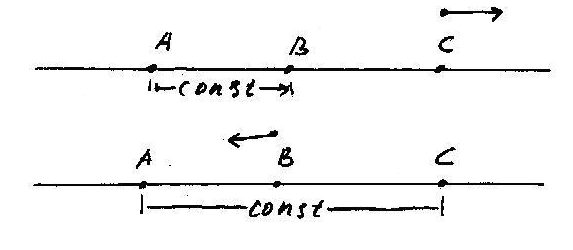Рис. 3.

Неподвижна - то есть находится все время от нее на одном и том же расстоянии: мы декларируем, что нам нужна не одинокая точка, а система отсчета с заданным эталоном длины. То есть мы должны задать неизменность расстояния между А и В, только тогда для точки С можно ввести равномерную скорость изменения расстояния относительно и А, и В, а затем - переходя в систему С - пользоваться этим же эталоном (продолжением градуированной прямой) для задания всего множества скоростей для всех последующих точек.

Но ведь мы начинали с двух точек, потом добавили третью и вроде как можем теперь говорить о движении, однако правомерно задать вопрос: как мы определим, что между точками А и В расстояние постоянно, а между А и С изменяется? Ведь с таким же успехом мы можем принять расстояние АС за эталон, а прежний эталон считать изменяющимся! В этих рассуждениях нет ничего нелогичного, наоборот, мы ввели третью точку и эталонное расстояние именно потому, что не могли определить ИЗМЕНЕНИЕ расстояния, но точно также мы не можем определить и неизменность его меры. Точнее можем определять его и так и эдак: то АВ берем за неизменный эталон и говорим, что точка С равномерно удаляется от А и от В, то берем за неизменность расстояние между А и С, тогда прежнее эталонное расстояние АВ должно полагаться изменяющимся.

Однако, если менять местами эталоны длины, получается странная картина. Мысленно представим, что "равномерно движущаяся" С как бы неподвижна и задает нам меру расстояния = const, тогда "реально неподвижная" относительно ЭТОЙ меры будет двигаться неравномерно: В приближается к А все время замедляясь и никогда не достигая ее.

Становится понятно, что подразумевал Ньютон под абсолютностью времени и пространства - это не только равномерный ход отсчитываемых секунд, но и аксиоматически заданная неизменность эталона длины, заданного в плоском евклидовом пространстве просто для того, чтобы оно могло считаться плоским.

Кроме того, чтобы определить плоское евклидово пространство, мало ввести неизменность эталона во времени - он должен быть неизменным и на расстоянии: 1 метр у начала координат неизменный "во веки веков", должен оставаться равным 1 метру и на любом расстоянии от точки отсчета. Если это не так, получится нечто вроде "статичной теории относительности" - где метр становится короче по мере своего удаления от начала отсчета. Можно даже ввести закон сложения эталонов длины, аналогичный закону сложения однонаправленных скоростей Лоренца: появится некоторое максимальное, константное для любого начала координат, расстояние. Получится как бы закон перспективы - по мере удаления от наблюдателя, линейные размеры тел сокращаются. Но это будет следствием не зрительной иллюзии, связанной с преломлением света в хрусталике глаза и уменьшением проекции единичной длины на его сетчатку, а существенным свойством самой геометрии прямой - она получается неевклидова.

Во избежание этого варианта, чтобы задать евклидовость пространства, в классической механике скорости должны складываться по арифметическому закону сложения. На схеме движущихся точек, мы располагаем их так, что за единицу времени каждая проходит расстояние на единицу эталона длины большее, нежели предыдущая. Если бы из начала координат одновременно вылетели точки, скорости которых отличаются на единицу в мере [м/с], то они расположились бы через единицу времени [с] по всей бесконечной прямой на равных расстояниях [м].

Таким образом, мы видим, что для определения равномерной скорости как таковой ("равномерное изменение расстояния между точками за единицу времени") приходится неявно предполагать наличие эталона длины - неизменного расстояния между двумя точками. А также предполагать плоское евклидово пространство и соответствующий ему арифметический закон сложения скоростей.

Классический способ построения множества равномерных прямолинейных скоростей дает нам образец для такого же построения множества скоростей вращения. Только вместо неизменного эталона длины, мы должны будем ввести нечто иное.

Попробуем это сделать.

Вернемся опять к классическому варианту и рассмотрим только одну точку в пустом пространстве. Что можно сказать о ее движении? Его просто нельзя определить. Это логически совершенно очевидно. (Интересно отметить, что Дж.В.Нарликар в теории конформной гравитации, рассматривая в совершенно пустой вселенной одинокую материальную точку - для нее отсутствует система отсчета, приходит к выводу, что ее состояние движения - это не нуль скорости, а неопределенность. (Дж.В.Нарликар, "Инерция и космология в теории относительности", в сб. "Астрофизика, кванты и теория относительности", М.: "Мир", 1982, с. 504. Это сборник статей к столетию А.Эйнштейна, выпущенный в Италии - "Astrofisica e cosmologia, gravitazione, quanti e relativita", Firenze, 1979.) Поэтому-то мы и вынуждены были вводить вторую точку: тогда определяется нулевая скорость - неизменность расстояния между точками с течением времени.

Для построения системы относительных скоростей вращения начнем с того же. Представим, что имеется вращающееся колесо. Что можно сказать о его скорости вращения? Она опять-таки совершенно неопределенна - о каком "числе оборотов в секунду" здесь можно говорить? Однако нашим следующим шагом должно быть не введение единичной угловой скорости, а введение какой-то особой системы отсчета для дальнейшего построения всего множества скоростей вращения. Введение второй точки В для построения множества поступательных скоростей в классическом варианте позволяет нам ввести неизменность расстояния, точно также введение второго вращения позволяет нам задать неизменное вращение - НО НЕ ЕГО СКОРОСТЬ!

Это делается просто: мы раздваиваем наше вращающееся колесо, разделяя центры вращения неким расстоянием.

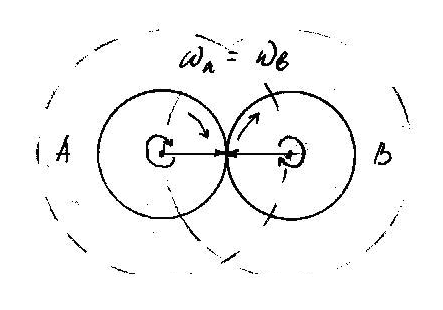Рис. 4.

Мы видим, что теперь имеются два радиус-вектора, которые вращаются вокруг двух центров так, что их концы периодически совпадают. О скорости вращения здесь речи нет, важность имеет только синхронность вращения. Она задает период времени, неизменный эталон - условную секунду. Все строится совершенно аналогично тому, что делалось для построения классического множества поступательных скоростей. Только вместо раздвоения точки и задания неизменного эталона расстояния - раздвоение "колеса" и задание неизменного эталона времени.

В классическом варианте точек А, В и С мы обязаны были аксиоматически задать неизменность расстояния между А и В, чтобы определить изменение расстояния между А и С - единичную скорость. Точно также и в случае вращений: мы ввели неизменное вращение, меру времени, можно теперь определять и относительные вращения. Для системы относительных скоростей вращения "абсолютно не вращающейся системы" нет, - это тоже самое, что для системы относительных поступательных скоростей какая-то воображаемая абсолютно неподвижная точка, покой которой задан сам по себе. (Тогда любая другая неподвижная точка будет иметь не относительное, а абсолютное расстояние от Центра Мира.)

Для системы точек А, В и С, мы должны аксиоматически задать неизменность расстояния только между А и В, а потом уже задавать для С изменение расстояния - скорость. Если же заявить: "Расстояние между С и А тоже можно принять за эталон - ведь все относительно!", тогда мы пытаемся описать неравномерное движение, не определив еще - что означает постоянство скорости. В свое время создатели классической механики избежали этого искушения "абсолютной относительности", - нам надо сделать так же - на каждом колесе точка конца радиус-вектор "закреплена" и каждый синхронизирован с противоположным, поэтому совпадение этих "меток" строго задает период. И только таким способом мы сможем осуществить градуировку времени - способом совершенно аналогичным тому, как градуировалась ось пространства при определении равномерной скорости прямолинейного перемещения.

Давайте, еще раз рассмотрим логические основания нашего определения. Что такое вращение В ПРИНЦИПЕ? Это возврат точки "на свое место" через обегание окружности - периодический процесс в чистом виде. Каждый оборот - это строгая фиксация периода времени, это "РАССТОЯНИЕ ВО ВРЕМЕНИ" между двумя тождественными событиями. И такое "расстояние" откладывается по оси времени в обе стороны. Что здесь может быть странного? Все так оно и есть, иначе просто невозможно и представить равномерность временной оси. Однако, согласитесь, здесь уже нет формального подхода: мы не берем тут некоторую прямую, на которой неизвестно почему уже заданы равные расстояния, и не говорим аксиоматически - "это и есть ось времени"! Иными словами, мы избегаем здесь "опространствливания времени" (как назвал эту искусственную операцию Анри Бергсон), а, наоборот, - мы конкретно определяем - ЧТО ЗНАЧИТ ГРАДУИРОВКА ВРЕМЕННОЙ ОСИ. Определяем с помощью совершенно понятной модели периодического процесса - вращения "колеса". И хотя точно также в классической механике на пространственной оси задается мера, которая может быть отложена в обе стороны, градуируя равномерно прямую, наш подход совершенно иной - предназначен только для времени.

Хочу обратить внимание на одну принципиально важную особенность нашего построения. Когда мы на пространственной оси откладываем равные отрезки, каждый из них характеризуется точкой начала и точкой конца. Есть две точки, между которыми заключен отрезок. А для градуировки времени - и это очень важно - началом и концом может быть только точка окружности вращения - она выступает началом вращения и окончанием периода вращения. Во времени - это два разных события, между ними "временное расстояние", но понимаются они как одна точка пространства, определяющая периодический процесс. Почему это очень важно осознать? Потому что может возникнуть иллюзия, что за единицу, градуирующую время, следует принять поворот на определенный угол - принять часть полного поворота. Достаточно немного вдуматься, и мы легко осознаем, что так делать нельзя. Для градуировки времени принципиально важна строгая периодичность процесса, а она может быть определена только единственным образом - если период полагается между двумя событиями - началом и окончанием полного поворота.

Как же так? Ведь если наше вращение проградуировало ось времени, то мы можем и дальше продолжать градуировку - разделяя это "временное расстояние" на части. Да, именно так, но определяя части уже определенного интервала, мы должны предполагать наличие другого периодического процесса - вращения - который задает эти периоды. Допустим, мы хотим разделить период на две равные части, - значит мы должны задать существование еще одного вращения, которое, начинаясь одновременно с уже определенным, отмеривает два своих периода и заканчивается в одной точке времени с окончанием единичного. Только тогда можно сказать: данный временной интервал разделен на два равных периода. (Автор полагает, что это само собой понятно, поэтому мы не станем здесь рисовать группу колес с совпадающими метками.)

Казалось бы, мы тем самым уже определили СКОРОСТИ вращения, но на самом деле этого пока не произошло. Просто задан принцип перехода от одной градуировки времени к другой. Таким же точно образом при градуировке пространственной прямой мы предполагаем, что начало единичного отрезка совпадает с началом его первой половины, а его конец с концом второй - единичный отрезок делится на два вполовину меньших.

Прежде чем мы пойдем дальше, автор позволит себе небольшую реминисценцию - один наглядный образ, осмыслить который будет полезно. Не так давно человечество отмечало начало нового тысячелетия, некоторые даже спорили: откуда начинать отсчет - с 2000 или с 2001 Нового года. А теперь представим себе огромный циферблат "Часы Вечности" на котором три стрелки - тысячелетняя, вековая и годичная. Тысячелетняя - самая медленная, она делает полный оборот за тысячу лет, поэтому для удобства наблюдателей циферблат разделен на тысячу делений. Самая быстрая - годовая, она успевает за 1000 лет сделать 1000 оборотов, а вековая - по скорости средняя, вращается она быстрее тысячелетней и медленнее годовой. В "начале времен" все три стрелки были в одном положении - вертикально вверх, и показывали они некую цифру 0. Через тысячу лет, когда тысячелетняя стрелка завершит свой круг, годовая и столетняя тоже придут в ту же точку - одновременно, минута в минуту. А теперь вопрос: через год после начала отсчета, годовая сделала один круг, а тысячелетняя передвинулась на одно деление - указывает на цифру 1 год. Где в этот момент находилась вековая стрелка? На какое деление циферблата она показывала? Вопрос, конечно, детский, но обдумывание его, позволит читателю глубже уяснить кое-что из только что изложенного. И мы еще вернемся к этой "занимательной физике" - она не столь проста, как кажется.

Перед нами стояла задачу: показать как для системы относительных скоростей вращения возникает мера скорости в [с/м]. В принципе, этот результат уже получен. Ведь если классическое множество поступательных скоростей возникало на основе введения неизменного расстояния - неизменного с течением времени, то у нас уже получена неизменная мера - единичный временной период. Но, во-первых, нам еще потребуется вникнуть в детали такого определения, а, во-вторых, автор подозревает, что у некоторых читателей уже появилось устойчивое мнение, что предложенный текст - пустопорожняя болтовня "вокруг да около", и что автор сам запутался и других путает.

Поэтому я решил не изображать из себя носителя "эзотерического знания" и раскрыть ТАЙНУЮ СУТЬ прямо здесь.

Поэтому я решил не изображать из себя носителя "эзотерического знания" и раскрыть ТАЙНУЮ СУТЬ прямо здесь.

СУТЬ СКРЫТОЙ АКСИОМЫ ПУАНКАРЕ

Анри Пуанакаре отмечал, что среди оснований евклидовой геометрии есть "скрытая аксиома" - полупрямую можно поворачивать, и при этом она рано или поздно совпадет со своим продолжением. Эта скрытая аксиома выражена в постулате о прорисовке окружности циркулем: он не только отмеряет равные расстояния в разные стороны, но может описать замкнутую кривую. Кроме того, давно уже выяснено, что для построения геометрической системы аксиом требуется только два вида исходных элементов, которые МОЖНО НАЗВАТЬ - "прямые" и "точки".

Мы не будем углубляться в проблематику построения формальных аксиоматик, таковых, как известно, много, а наборы исходных объектов и отношений в них варьируются. Иногда, место отрезка занимает угол, а иногда и "движение". Отметим только два важных результата: 1). отношения планиметрии можно изобразить на модели Кэли-Клейна, где бесконечная плоскость оказывается единичным кругом без границы; 2). отрезок, взятый как множество точек, оказывается - в соответствие с выводом Коэна - объектом не определяемым однозначно. Интересно, что автор любой системы аксиом таки или иначе открыто обращается к данным опыта. (Гильберт и Барнайс именуют эту процедуру "привязкой аксиоматической теории к фактам восприятия", -Гильберт Д., Барнайс П., "Основания математики. Логические исчисления и формализация арифметики", М., "Наука", 1979, с.30) Не избежал этого и Анри Пуанкаре, - любопытны его рассуждения о том, как понятие точки, психологически возникает из ощущения прикосновения к предмету, а понятие отрезка - от движения глаза...

Вообще говоря, формальный подход к основаниям геометрии выглядит в наше время странным: геометрия вроде бы заново изобретается, в то время как гораздо интереснее посмотреть: КАК и ЧТО изобрели ее настоящие авторы, математики прежних веков, коль скоро АБСОЛЮТНО ВСЕ, что ныне имеется в математике, - это развитие тех же самых исходных представлений.

Выше было коротко сказано, что начала математики отмечены двумя великими открытиями. Первое из них, сделанное античными пифагорейцами, хорошо известно - это открытие несоизмеримости длины стороны квадрата и его диагонали. Здесь - возникновение геометрии, как науки о протяженных в пространстве величинах. Второе великое открытие - несоизмеримость углов, это начало алгебры.

Квадрат с диагональю - привычная нам фигура, а вот полумесяц, состоящий из двух дуг, соответствующих центральному и вписанному углу, у большинства читателей вряд ли вызовет геометрические ассоциации. Для того, чтобы освежить в памяти некоторые элементарные навыки, вы можете посмотреть на приведенные здесь страницы из школьного математического справочника.

Определение "градусная мера дуги равна градусной мере центрального угла" - что может быть проще! Но взгляните на рисунок 24, где вписанный угол АВС опирается на диаметр, стягивающий полуокружность. Точка О отмечает вершину развернутого угла в 180° , а из теоремы выводится следствие: якобы, вписанный угол АВС равен 90° . Однако это не так. На самом деле прямой угол АВС и развернутый угол АОС несоизмеримы, а градусное равенство 2(90° )=180° равенством не является, поскольку нельзя приравнять градусы, измеряющие окружность радиуса 1, и градусы, измеряющие окружность радиуса = "корень из 2, деленный на 2".

Но ведь это абсурд! - ведь если угол АВС симметрично отразить через один из лучей (АВ или ВС), а потом перенести вершиной в точку О, мы получим разбиение полного угла АОС точно пополам, то есть равенство 2(90° )=180° для этих углов истинно и неопровержимо. Автор утверждает, что данное равенство для ЭТИХ УГЛОВ - и неистинно, и опровержимо.

На рисунке показаны дуги этих разных окружностей, проведенные между точками А и С. Конструкция из двух дуг, образующих полуокружность АВС и дуги АС являющейся четвертью окружности единичного радиуса, представляет собой алгебраический аналог квадрата с его диагональю. Если мы утверждаем, что угол АВС задан прямым, то есть является четвертью полного оборота единичного радиуса вокруг точки В, то мы должны признать, что "полный угол" АВС не является полным, то есть радиус-векторы ВО и ОС не лежат на одной прямой. Если радиус-вектор АО продолжить за точку О, другой радиус-вектор ОС составит с ней некоторый бесконечно малый угол. И наоборот: если продолжить за точку О радиус-вектор ОС, бесконечно малый угол образуется у этой прямой с радиус-вектором ОА.

Равенство 2(90° )=180° не является таковым, потому что по разные стороны знака равенства стоят "разные градусы" - градусы разных окружностей. Все эти выводы - прямое следствие определения, что градусная мера центрального угла является градусной мерой его дуги.

В только что приведенных рассуждениях нет никаких ошибок или мистификаций. Переход в радианную меру не изменяет факта: длины дуг у не соизмеримых углов - несоизмеримы. Все так оно и есть, более того: именно эта несоизмеримость углов приводит к построению, когда центральный угол оказывается на самом деле в два раза больше вписанного - когда они оба опираются на бесконечно малую дугу данной окружности, а само это соотношение выражается в формуле cos2=(e²ⁱ+e^-2i)1/2. Разумеется, не все углы не всех окружностей несоизмеримы, точно также и в прямоугольных треугольниках бывает соизмеримость катета и гипотенузы. Но в нашем построении, когда вписанный угол является центральным для другой окружности, а их радиусы связаны иррациональным числом "корень из двух пополам", несоизмеримость углов становится слишком явной, чтобы ее не заметили. Ее и заметили, и попытались "просчитать", - получилась формула, где трансцендентное число e оказалось в степени кратной мнимой единице... Впрочем, исторические экскурсы мало кого интересуют, тем более, что по широко распространенному среди современных ученых мнению, "древние все время заблуждались".

Рассмотрим "опровержение" элементарной геометрической теоремы более детально, чтобы суть проблемы оказалась логически очевидной.

Впишем в окружность равносторонние четырехугольник-квадрат и шестиугольник, совместив две их вершины. У такого шестиугольника стороны-хорды, как известно, равны радиусу данной окружности (примем радиус единичным). У четырехугольника сторона-хорда равна "корень из двух", то есть эти отрезки несоизмеримы. Напротив, сразу замечаем - дуги окружности соизмеримы, поскольку одна и та же единичная длина окружности составлена из 6 дуг с градусной мерой при центральных углах шестиугольника 60° , и из 4 дуг при центральных углах вписанного квадрата - по 90° .

Если мы начнем умножать число сторон вписанных многоугольников, деля эти дуги пополам, то "в пределе" все точки "сойдутся". Таким же образом мы можем делить континуум единичного прямого отрезка, начав с его разделения пополам и на 3 - точки с координатами (1/2)ⁿ и (1/3)n при устремлении n к бесконечности одновременно попадают в ноль, сливаются с началом отрезка. А сами эти меры 1/2 и 1/3, естественно, вполне рациональны, то есть соизмеримы.

Но с окружностью и центральными углами что-то не так, и это что-то всем очевидно. Вот, например, как это ЧТО-ТО экслицируется в научных текстах. "Для углов имеет место алгебра, аналогичная алгебре отрезков, основанная на сложении углов; разница лишь в том, что углы "ограничены" развернутым углом, тогда как отрезки не ограничены". "между отрезками и углами есть, однако, существенная разница: у отрезков нет геометрически выделенного масштаба, а для углов есть - это прямой угол (или развернутый)." (А.Д.Александров, "Основания геометрии", М.: "Наука", с. 80, с. 163.) Как видим, "скрытая аксиома" в изложении геометрии присутствует (хотя, обычно, только в примечаниях).

Если некоторый прямой отрезок L можно измерить в некоторой мере l, а их отношение выражается рациональным числом L/l=n, то мера и отрезок соизмеримы. Если мы возьмем меру k, которая несоизмерима с l, то есть их отношение иррационально, то, естественно, отрезок L в данной мере не может иметь рациональную длину. Правильно?

Но вот мы строим в окружности квадрат, который делит ее на четыре равные дуги, каждая хорда относится к единичному диаметру как "корень из двух пополам", ведь диагональ квадрата и его сторона несоизмеримы. Мы можем также разделить окружность на шесть частей, при этом каждая хорда соответствующей дуги будет равняться длине радиуса - половине единичного диаметра данной окружности (это известно из построения шестиугольника). Очевидно, что эта мера и мера, отмеряемая четырехугольником, несоизмеримы - их пропорция иррациональна. Однако наша окружность - единичная длина L - выражается в обеих мерах вполне рациональными числами - 6 и 4. Число 4 - это четно-четное число, а число 6 четно-нечетное (так их именовали в средневековой математике). Разумеется, можно взять сторону четырехугольника в качестве стороны некоторого иного равностороннего шестиугольника, но вписан он будет уже в другую окружность, большего диаметра.

В чем же дело? Ведь прямолинейный отрезок мы можем спокойно разделить на шесть частей, а потом сказать: вот его деление пополам, а вот его деление на три части, мера 1/6 - их общая, соизмеримая со всеми. Но, что за операцию мы проделали? Мы просто взяли единичный отрезок, деленный пополам, отложили его на прямой три раза и сказали - это единичный отрезок. А вот с окружностью эта "перенормировка" не проходит. Она вполне законченная единица. Мы можем отложить на ней, начиная с некоторой точки 0, некоторую единичную длину дуги и проделывать с ней операции, аналогичные тем, что только что совершили с отрезком, но рано или поздно таким "перенормировкам" придет конец, - когда длина единичной окружности закончится.

В отличие от окружности на бесконечной евклидовой числовой оси мы можем увеличивать единицу до любой величины, не заботясь о том, что бесконечный луч, начинающийся в точке 0, закончится и мы окажемся в начале отсчета с каким-то "остатком". Иными словами, отношения между дугами окружности строятся не так, как на бесконечной прямой, эти отношения не евклидовы. Они псевдоевклидовы, поскольку из любой точки 0, помимо "бесконечного луча", всегда отходит противоположно направленный вектор дуги - тот самый актуально бесконечно малый угол, который не позволяет двум радиусам окружности одновременно уложиться на прямую-диаметр.

Можно, конечно, считать центральный угол окружности 180° и вписанный 90° соизмеримыми, но тогда мы потеряем окружность, как ОКРУЖНОСТЬ. Многоугольники, которыми мы, вроде как, аппроксимируем окружность, в пределе, конечно, сойдутся и определят нам множество равноудаленных от центра точек, расстояние между которыми делается "сколь угодно малым", если его измерять по прямой на которой лежат эти, устремляемые друг к другу, точки. В евклидовой геометрии нет окружности, как непрерывной гладкой кривой. Мы просто мысленно подставляем окружность в качестве таковой линии, мысля ее как предел к которому, якобы, стремятся периметры описанного и вписанного многоугольников, когда число их сторон становится все больше. Любой многоугольник образует евклидову плоскость, а точка центра - это точка пересечения прямых, соединяющих противолежащие углы многоугольника, но эта точка не является центром вписанной окружности, поскольку центр окружности НЕ ПРИНАДЛЕЖИТ к евклидовой плоскости этого многоугольника.

В евклидовой геометрии нет никакого бесконечного деления континуума, есть только бесконечное прибавление отрезков друг к другу так, что любую сумму мы можем принимать за новую единицу и считать, что "дело сделано". Только с появлением не дифференцируемых линий, только в ходе анализа фракталов это, наконец, стало очевидным. А абстрактно, это всегда выражалось алгебраически - через бесконечные степенные ряды, через формулу Эйлера с мнимыми единицами, через странное число e - основание, так называемых, натуральных логарифмов. И вот, наконец, геометрия сомкнулась с алгеброй, когда был построен псевдоевклидовый континуум, где появилась абсолютная единица, которую нельзя превзойти с помощью сложения никаких меньших ее величин. Геометрическая аксиома Евдокса-Архимеда оказалась нарушена.

Есть "детский парадокс" - задачка, когда предлагается вообразить Земной шар и яблоко, обвязанные по окружности нитью. Затем говорится, что к ее длине добавлен один метр, а нить опять растянута до кривизны окружности. Мол, образуется "зазор" - у кого он больше: у яблока или Земного шара? Наивные дети отвечают: "Конечно у яблока, ведь для Земного шара этот "лишний метр" - ничего не значит!" Дети еще не поняли, что в геометрии Евклида L=2p R, а по этой формуле зазор R-r пропорционален "p ", а не отношению длины окружности и вставленному метру.

А ведь надо бы поверить детям, чье восприятие мира определяется его реальной геометрией, а не абстрактными построениями древних греков. Ведь единичная окружность, на которой осуществляются построения и выводится "пи", как отношение радиуса и ее длины, - это не "любая окружность", а абстрактная окружность принятая за единичную. Реальные окружности соотносятся своими радиусами и длинами дуг с помощью алгебраических отношений, а не геометрических. И трансцендентное число "пи" определяет не отношение длины всей окружности ко всему радиусу, а предельное отношение между актуально бесконечно малой частью прямого отрезка диаметра и дугой - актуально бесконечно малой частью единичной окружности. В свою очередь, трансцендентное число e является предельным отношением к которому стремятся бесконечно уменьшающиеся несоизмеримые дуги.

Что означают все эти голословные ничем не подкрепленные утверждения? Они означают, например, что если мы по бесконечной прямой начнем откладывать единичную длину некоторого отрезка и еще одну длину равную относительно этого отрезка e, то "где-то в бесконечности" эти точки сойдутся вместе. В этом месте окончится прямая, оказавшаяся бесконечно длинной окружностью.

Что касается подкрепления утверждений доказательствами, то здесь как раз тот случай, когда ничего доказывать не надо. Достаточно просто показать - на некоммутативные алгебры, на бесконечно изломанные фракталы, на псевдоевклидову геометрию. Ведь даже сама ОКРУЖНОСТЬ - это фигура, как следствие аксиом Евклида, а постулат построения - ее очерчивают циркулем, а рисуют по точкам и прямым.

Я полагаю, Николаю Лобачевскому, жившему в Казани среди российских мусульман, достаточно часто попадался на глаза алгебраический полумесяц. Не удивительно, что великий русский геометр усомнился в абсолютной плоскости евклидовой геометрии. Возможно, если бы он столь же внимательно всмотрелся в привычные шарообразные маковки православных церквей, увенчанные странным крестом - с двумя неравными перекладинами и одной наклоненной, то удалось бы ему построить и псевдоевклидово четырехмерие. Про индуистско-буддийские янь и инь - две окружности вписанные в круг - автор говорить здесь не будет, ими потом занимались коллеги Лобачевского по Казанскому университету, в том числе В.В.Васильев создавший "неевклидову логику", а ныне разработки многополярных логических систем, ведут философы В.В.Ленский и А.Г.Кочнев в Иркутске, А.Б.Григорьев в Красноярске. (Надеюсь, вы поняли, что последний абзац - это вольная реминисценция, не претендующая на научные обобщения.)

А сейчас вниманию читателей будет предложен вполне самостоятельный и законченный научный фрагмент, где суть дела излагается без исторических экскурсов и философских аргументов.

ЖОРДАНОВО ОПРЕДЕЛЕНИЕ ЛИНИИ И ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА

Определение линии, данное Камиллом Жорданом по многим причинам считается математически не строгим. Наиболее существенная из них очевидна уже из самого определения линии как траектории движущейся точки. То есть - это в большей мере физика, нежели математика. Однако соответствие между псевдоевклидовым абстрактным пространством индекса 3 и реальным 4-мерным пространством-временем - бесспорный факт современной науки, поэтому не должна казаться надуманной попытка переосмыслить жорданово определение линии.

Но прежде, чем это делать, следует, все-таки, разделить математический и физический аспекты проблемы.

Суть подхода Жордана к определению линии, по мнению автора, состоит в том, чтобы ввести в круг математических понятий ДВИЖЕНИЕ как таковое, то есть не как механическое перемещение, выражающее отношение пространственных величин и периодов ВРЕМЕНИ, а как некое отношение величин абстрактных, в которых утрачена какая бы то ни была конкретная специфика - и пространственная и временная.

Предложенная формулировка выглядит странно: ведь дифференциальное и интегральное исчисление без сомнения является результатом именно такого подхода и воочию демонстрирует его результаты. Начавшись в физике с выяснения связи между dx и dt в механическом движении, это исчисление давно уже оперирует с бесконечно малыми приращениями и отношениями величин абстрактных. Все так, но среди оснований классической физики не было релятивистского принципа относительности, поэтому есть веские причины подозревать, что его отсутствие в той или иной мере отразилось в методологии построения стандартного математического анализа.

Ставить под сомнение развитые в анализе методы вычислений и достоинства его аппарата было бы бессмысленно, однако не бессмысленно посмотреть - могут ли быть сделаны какие-то новые выводы, если принцип относительности изначально ввести в исходные представления математического анализа. Видимо, именно в этом и состоял замысел Камилла Жордана - дать определение линии, как траектории движущейся точки. Ведь в ином смысле такая постановка задачи выглядит изначально бесполезной - коль скоро в стандартном математическом анализе любой график функции по определению считать линией. (Так, кстати, и считалось до обнаружения не дифференцируемых, но непрерывных линий.)

С другой стороны, принцип относительности может быть расценен как чисто физическая логическая конструкция, ничего к математике не прибавляющая. Тогда как быть с псевдоевклидовым пространством - ведь это не физическая конструкция, а всецело математическая? И здесь можно сделать серьезное уточнение: представление псевдоевклидового пространства индекса 3 в качестве 4-мерного континуума пространства-времени - целиком и полностью следствие физической интерпретации данной математической конструкции. Для математического построения, обладающего своими собственными особенностями, не играют роли никакие физические представления о свойствах световых сигналов и инвариантности уравнений Максвелла. А тогда уже совсем иначе выглядит постановка нашей задачи: что если псевдоевклидовость метрики является следствием именно математически осмысленного использования принципа относительности? Ведь сам этот принцип, действительно, не связан ни с какими конкретными свойствами физических явлений, а представляет собой только особый способ сравнения систем координат.

Здесь опять возможно возражение: группа преобразований Галилея по общему мнению и является выражением принципа относительности, а специальный принцип относительности, использованный Эйнштейном, основывался опять-таки на чисто физической аксиоме - постулировании инвариантности скорости света для любой системы отсчета. Автор не согласен с такой оценкой, по его мнению - она отражает не логику теории, а лишь распространенное мнение, закрепившееся в популярной литературе по истории науки. Поэтому задача данной статьи в том, чтобы показать - как релятивистский принцип относительности реально вводится и работает в анализе абстрактного движения, понимаемого как особого рода взаимоотношения математической точки и линии, являющейся ее траекторией.

...........................................................................................................................................................................

Рассмотрим движение точки по окружности, которая в таком случае является линией в смысле Жордана. Окружность становится здесь не геометрическим местом точек, равноудаленных от центра, а некоторой траекторией единичной длины, которую точка проходит за некоторое единичное время. Обратимся теперь к принципу относительности, который стал отправным пунктом для создания релятивистской теории Эйнштейна и построения пространства-времени Минковского. Согласно этому принципу - нет покоящихся систем отсчета как таковых, есть только пары взаимоотносительных систем: если одна из них принята покоящейся, другая движется относительно ее, и наоборот. В таком случае, центр окружности, вокруг которого описана Жорданова линия, не должен являться неким неподвижным центром, он сам является только системой отсчета, которая в данном случае принята за покоящуюся. Иными словами, можно перевернуть определение линии, и рассмотреть движение центра относительно, как бы покоящейся, точки.

Обычно это понимают, как смену точек неподвижности - то есть движущийся конец циркуля как бы закрепляют, а другой приводят в движение: описывается еще одна окружность, центр которой сдвинут относительно первого. Действительно, это и есть в чистом виде принцип относительности в его математическом понимании, очищенном от физических представлений. Если на этом шаге остановиться, мы получим классические галилеевы преобразования для систем координат.

Однако, что означает в данном случае точка неподвижности и обегание конца циркуля по замкнутой траектории? Это по существу - неподвижность циркуля и поворачивание всей евклидовой плоскости вокруг одной из его точек. Но сущность относительности не только в этом, но и в том, что точек две и евклидова плоскость может поворачиваться вокруг любой из них. Тогда и только тогда можно говорить, что мы определили относительность движения точки по окружности вокруг центра, поскольку есть два относительных движения: точка по окружности вращается вокруг центра и центр по своей окружности вращается вокруг нее. Для двух неподвижных точек тем самым определяется два вращения евклидовой плоскости, причем одновременно. "Одновременность" здесь понимается не физически, а математически - как вращение двух евклидовых плоскостей, каждая вокруг своей неподвижной точки. "Неподвижность точки" здесь понимается не в смысле топологической неподвижной точки Пуанкаре, а как неизменность расстояния между двумя точками ("раствор циркуля"), причем это расстояние - некий отрезок, который, если так можно выразиться - составлен из точек не принадлежащих одновременно ни к одной из поворачиваемых евклидовых плоскостей. Отметим, что вращение здесь опять-таки не физическое механическое "перемещение в единицу времени", а обычный полный поворот.

В данной операции - поворачивание двух евклидовых плоскостей можно выделить две возможности: две плоскости поворачиваются в противоположные стороны, обе плоскости поворачиваются в одну сторону.

Рассмотрим первый вариант.

Он вроде бы прост: легко представить себе неподвижный циркуль, определяющий неизменное расстояние между двумя точками, и две плоскости, которые поворачиваются вокруг данных точек каждая в свою сторону. Две неподвижные точки определяют третью плоскость, которую можно связать с углом раствора циркуля или же представить соплоскостной вращающимся, но "абсолютно неподвижной" (если быть точным - то эта "абсолютно неподвижная" плоскость принадлежит пространству, в котором закреплен циркуль).

Тогда на вращающихся плоскостях очертятся две окружности - центр каждой совпадает с линией окружности другой. Однако, поскольку вращение определено именно для плоскостей в целом, то поворот каждой задает множество окружностей, очерчиваемых продолжением радиус-вектора. Иными словами, мы имеем на каждой из поворачиваемых плоскостей концентрические окружности, радиусы которых могут быть сколь угодно большими, относительно длины единичного радиус-вектора, задаваемого условиями.

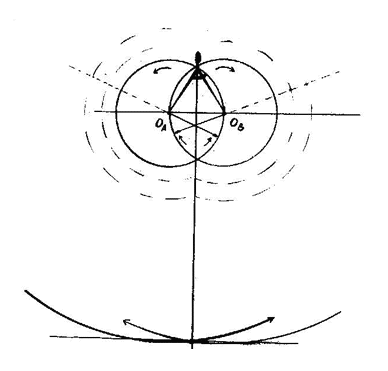Рис. 5

Предположим, что наблюдатель находится на "абсолютно неподвижной" плоскости, где раствор циркуля задает неподвижные точки и неподвижный отрезок между ними. По мере своего продвижения по перпендикуляру от центра этого отрезка, он может наблюдать окружности все большего радиуса, вращающиеся с постоянной "угловой скоростью". Что касается "линейной скорости", то движущиеся точки по этим окружностям мимо наблюдателя "проносятся" все быстрее и быстрее. Кроме того, возрастание радиуса кривизны каждой из последующей пары окружностей приводит к тому, что для наблюдателя эти окружности все больше уподобляются двум прямым, которые пересекаются в точке наблюдения под все меньшими углами. Можно представить наличие "предела", где эти окружности будут пересекаться под бесконечно малым углом, сливаясь с прямой, принадлежащей координатному пространству наблюдателя. В этой точке кривизну окружности можно считать нулевой, но тем не менее из общей картины ясно, что "прямая" образована все-таки двумя окружностями, пересекающимися в точке наблюдения под бесконечно малыми накрестлежащими углами.

Геометрия плоскостей евклидова, поэтому фактически на эту предельную прямую параллельно переносится и единичный отрезок, определяющий расстояния между центрами окружностей нулевой кривизны. А "бесконечно большой" радиус окружностей может быть определен в качестве такового только по отношению к этому единичному расстоянию. Аналогично мы можем определить и "бесконечно малый" предел, если относительно точки наблюдения считать уменьшающимся расстояние между центрами базовых окружностей. Однако эта операционная аналогичность все-таки не позволяет отождествить обе операции устремления к пределу, поскольку есть заданное движение - ЗАДАННАЯ ЛИНИЯ. Это легко видеть, поскольку в начальных условиях вращение циркуля никак не связано и не может быть связано с шириной его раствора, очерчивающего ЛИНИЮ.

Тогда предварительный вывод таков: на нашей "абсолютно неподвижной" плоскости любая прямая оказывается устроена так, что точка на ней может пониматься как пересечение двух окружностей с бесконечным радиусом, а в обе стороны от данной точки определяются два треугольника с бесконечно малыми углами при вершине, причем длина сторон треугольника принятая за действительную величину, однозначно связывается с бесконечной длиной радиуса: она является бесконечно малой относительно только этой бесконечности, а ни какой иной. Их соотношение равно соотношению некоторого перпендикуляра действительной длины, восставленного из данной точки и его бесконечно малой части. Эту странную пропорцию можно записать в виде 1/Dx = dx/1. Пропорция, в свою очередь, определяется для данного построения неизменностью "угловой скорости" вращающихся плоскостей. Иными словами, абсурдное в стандартном анализе пропорциональное отношение, связывающее бесконечно большое и бесконечно малое, возможно если и только если имеется некоторая константа - "угловая скорость", неизменная для любых отношений между единичным радиус-вектором вращающихся плоскостей и перпендикуляром к нему, который равен радиус-векторам концентрических окружностей лежащих в плоскостях, вращающихся относительно наблюдателя. Сам наблюдатель неизменно находится на "абсолютно неподвижной" плоскости - в координатной системе, в которой закреплен циркуль.

Эти необычные выводы являются необходимым следствием введения принципа относительности движения, который в данном построении логически самодостаточен, то есть, очевидно, не требует ни каких дополнительных физических гипотез. В построении заложено определенное соотношение между величинами, изменяющимися друг относительно друга. Реальный характер этих величин - вопрос интерпретации. Поэтому нас здесь не интересует - связана ли эта структура с физической специальной теорией относительности, где взаимозависимость временных и пространственных интервалов определены константой скорости электромагнитных волн, или же не связана. В принципе, она может быть моделью любой другой реальной структуры, где взаимозависимость элементов изоморфна отношениям, определенным в нашей конструкции.

Теперь обратимся к другой форме относительности между центром линии траектории образующей точки, образующей ее своим движением.

Вводится вращательное движение центра окружности вокруг самой движущейся вокруг него точки - оба вращения заданы в одном направлении. Для иллюстрации автор позволит себе использовать здесь наглядный образ. Представим себе колесо, закрепленное на кронштейне. Кронштейн по длине - радиус колеса. Кронштейн вращается и колесо вращается - с равными скоростями, в одну сторону. В начальный момент точка окружности колеса совпадает с центром вращения кронштейна, и после описания всей траектории опять приходит в нее. Получается циклоидальная траектория, похожая на обычную кардиоиду с петелькой.

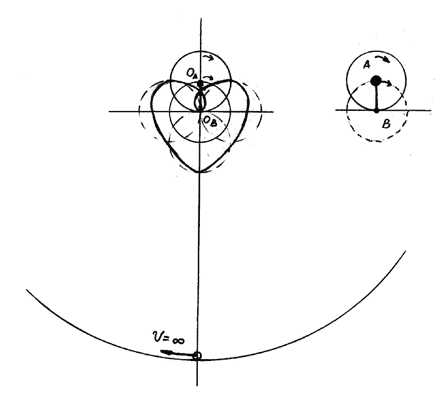Рис. 6.

Будем называть эту необычную кардиоиду нестандартной или неклассической. Классическая кардиоида - это алгебраическая кривая 4 порядка, получаемая как траектория движения точки окружности, катящейся по окружности того же радиуса - вращение колеса совпадает с направлением его движения. Вторая окружность - это нечто вроде абсолютно неподвижной системы отсчета, что становится совершенно очевидным, если мы вспомним об определении циклоиды. Циклоида - это траектория точки окружности колеса, которое катится по прямой - то есть вдоль оси абсолютно неподвижной системы декартовых координат. Если мы замкнем в окружность отрезок расстояния, проходимый колесом за один полный оборот, то циклоида превратится в кардиоиду. Теперь становится ясно, что получение нашей нестандартной кардиоиды с петелькой - это действительно применение именно неклассического принципа относительности, когда система отсчета понимается не как АБСОЛЮТНО НЕПОДВИЖНАЯ, а как имеющая ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ.

Неклассическая кардиоида - фигура, как очевидно, центрально несимметричная и задает выделенное направление, острие сердечка указывает во вполне определенную сторону. Мы исходили вроде бы из совершенно симметричного условия: точка окружность вращалась вокруг центра, а центр вращался вокруг нее. Вот на плоскости две одинаковые окружности: конец радиуса одной совмещен с центром другой. Они, как уже было отмечено, имеют одинаково направленные векторы скорости (на рисунке - "по часовой стрелке"). Мы вроде бы сможем построить две неклассические кардиоиды, симметричные относительно друг друга, если изменим направление вращения, однако этого не происходит. Задавая другое направление вращения мы всего лишь опишем ту же самую кривую, только в другую сторону. Единственный выход - это перевернуть лист, но такая операция в данном построении была бы искусственна. Мы продолжим наше рассмотрение и обнаружим, что в данном случае надо считать "точкой зрения наблюдателя".

Неклассическая кардиоида - это кривая описываемая в плоскости так, что неподвижная точка, вокруг которой накручена окружность, сама описывает окружность, вокруг точки, двигающейся относительно ее. Для данной окружности такая кривая - построение точное, не зависимое ни от каких параметров. Действительно, тут не важна скорость вращения: один полный оборот совершен за некоторую единицу времени, то есть - "временной интервал" не играет никакой роли, если оборот сделан полный и траектория завершена. Ни величину "петельки", ни длину кардиоиды нельзя изменить, если задан радиус производящей окружности и условие полного оборота (при неполном обороте будет получена только часть траектории).

Поэтому уместно задаться вопросом: что будет, если мы станем изменять радиус производящей окружности? Напомню: у нас нет другой окружности, относительно которой можно было бы задавать изменение радиуса, поскольку мы начинаем построение с одной окружности, по которой двигается точка, и применяем неклассический принцип относительности, полагая, что ее движение вокруг центра - это относительное движение центра вокруг нее в отсутствие какой бы то ни было неподвижной системы координат (евклидовой плоскости). Тем не менее, получается интересный результат: мы можем делать радиус окружности "сколь угодно малым", и неклассическая кардиоида будет уменьшаться вместе с самой производящей окружностью.

Обычно полагается, что геометрически процесс "стягивания окружности в точку" не сопровождается какими-либо осложнениями, но в нашем случае - когда окружность понимается не как геометрическое место точек, равноудаленных от центра, а как траектория движения - мы в точку устремляем именно жорданову линию, а не абстрактное множество неподвижных точек неподвижной окружности. Теперь вспомним: ориентация кардиоиды задает направление, тогда можно утверждать, что у отрезка присутствуют "начало" и "конец". А с помощью вращения теперь можно различить: что происходит во время стягивания такого отрезка в точку - начало устремлено к точке конца, или точка конца устремлена в начало.

Однако, уменьшение кардиоиды означает, что мы начинаем сжимать саму "неподвижную систему координат". Как это можно понять? Вспомним о наличие еще не определенной нами симметричной кардиоиды. Теперь становится понятно, что вместо двух неподвижных центров вращения, образующих систему координат (как было в нашем первом рассмотрении) у нас теперь задана неподвижная траектория только с одним неподвижным центром. Второй центр вращения только по видимости принадлежит к ней - на самом деле он лежит в иной плоскости, которая теперь нами приведена в движение в процессе стягивания отрезка. Точка к которой стягивается отрезок - это начало координат.

Выбор начала координат произволен, но мы можем зафиксировать результат: если, скажем, стягиваемый вектор, соединяющий центры симметричных окружностей А и В задается началом в точке А, то неклассическая кардиоида указывает "острием своего сердца" вниз, и наоборот - тогда главным будет "симметричное сердце", ориентированное в противоположную сторону. Но весь фокус в том, что плоскость, к которой принадлежит симметричная кардиоида, по отношению к нашей основной - той, что с неподвижной точкой (теперь ее уже можно с полным правом считать топологической "неподвижной точкой" Пуанкаре) и неподвижной кардиоидой, эта плоскость должна пониматься как вращающаяся С БЕСКОНЕЧНОЙ СКОРОСТЬЮ.

Это принципиально: оказывается по отношению к базовой плоскости следует определить другую плоскость, которая вращается с бесконечной скоростью. Что значит бесконечная скорость вращения? Легко уяснить, что эта не физическое вращение, а операция, которая мгновенно переводит все точки плоскости сами в себя, и вся плоскость тем самым остается тождественно неизменной. Однако в нашем построении относительные единичные скорости вращения выявляют неподвижную точку, а бесконечно быстро вращающаяся плоскость становится отличима - в ней определилась симметричная кардиоида, которая вращается бесконечно быстро относительно базовой, а ее центр вращения не совпадает с определенным для кардиоиды неподвижной.

Мы отметили, что неклассическая кардиоида получается для любой окружности и любой скорости движения точек. Последнее понятно, ведь меры времени у нас нет, точка может вращаться хоть со скоростью "один оборот в Вечность", главное, чтобы этот оборот завершался и Вечность замыкалась, а "реальная продолжительность" этой абстрактной Вечности может быть любой.

Радиус окружности также может быть любым, значение имеет только раздвоение окружности, когда вектор связывает центр и периферию и образуются как бы две окружности вращающиеся вокруг центров друг друга. Мы говорили, что "стягиваем" отрезок в точку (это позволило отличить базовую плоскость и тождественную к ней "бесконечно быструю"), но на самом деле отрезок все время является некоторой существенной длиной (мы пока не будем именовать ее действительной величиной), тогда что может означать это "стягивание", если в нашем построении не задана единичная мера длины, относительно которой радиус становится "бесконечно малым"?

Может показаться, что тут возможна привязка к скорости движения точки по траектории, но это не так. "Скорость вращения" здесь также неопределенна, да и не важна - ведь заданная окружность - ее центр и ее точки, делают один полный оборот вокруг друг друга - угловая скорость для всех точек, лежащих на радиус-векторе и его продолжении одна и та же. Но если радиус-вектор можно продолжать (а нет никаких причин этого не делать) открывается возможность разрешения ситуации. Итак, у радиус-вектора, начало которого - центр вращения, а конец совмещен с центром вращения тождественной окружности, есть нечто такое, чего мы пока в наше рассмотрение не включали. За точкой начала вектора лежит его продолжение, уходящее в бесконечность. Когда конец радиус-вектора описывает окружность, его противоположное неограниченное продолжение также описывает некоторую кривую. Почему мы берем в рассмотрение продолжение радиус-вектора за его началом, а не то, которое может быть продолжено в другую сторону - в сторону конца? Легко понять, что конец радиус-вектора, совмещается с центром тождественного вращения, любое его продолжение - это всегда точки, которые можно принимать за центры вращений, задавая единичную длину радиус-вектору. Другими словами - это и есть те радиусы, которые "стягиваются", могут быть сделаны "сколь угодно малыми".

Автор просит читателей внимательно всмотреться в ситуацию. Рассматривая первое построение, где относительные вращения полагались противоположными, мы с помощью продолжения радиус-вектора нарисовали концентрические окружности, а продолжать радиус-вектор можно было в любую сторону - он также очерчивал ту же самую окружность. Однако, когда мы задали однонаправленность относительных вращений, выявилась иная ситуация: теперь продолжать радиус-вектор можно только в сторону за точку центра его вращения, поскольку его противоположный конец очерчивает нестандартную кардиоиду. Ничего удивительного здесь нет, ведь исходные условия построения иные.

Итак, мы имеем вращающийся радиус-вектор, единичность которого определяется наличием относительных вращений. При этом обнаруживается наличие продолжения радиус-вектора за точкой принятой в качестве центра его вращения. Теперь на этом продолжении мы всегда можем задать расстояние, соотносимое с длиной единичного радиус-вектора (относительно которого радиус-вектор можно сделать бесконечно малым). При этом точка другого конца радиус-вектора также будет описывать некоторую траекторию, которую можно сравнить с исходной неклассической кардиоидой. Но существенно то, что у второго радиус-вектора направление противоположное, то есть их модули могут иметь количественное отношение (например, 1/dx), но сами векторы должны браться с обратными знаками.

Мы сразу же начнем с того, что зафиксируем длину единичного радиус-вектора, а его продолжение станем делать "сколь угодно большим". Легко понять, что увеличение второго радиус-вектора будет приводит к появлению фигуры все больше напоминающей окружность, с одним только отличием - "на краю" окружности имеется петелька, которая становится тем меньше, чем большую длину мы задаем для второго радиус-вектора.

В первом построении мы получали в пределе окружности сливающиеся с прямой. Теперь мы имеем окружность, у которой в точке предела находится "микропетелька", а вторая окружность вращается с бесконечной скоростью так, что ее "микропетелька" обегает бесконечность за мгновение. Но теперь можно уже понять, что это за мгновение - это бесконечно малая часть периода, который нами принят за единичный интервал поворота исходных относительных вращений.

Перевернем ситуацию. Пусть второй радиус-вектор имеет действительную длину, а единичный радиус-вектор относительно его становится бесконечно малым. Легко уяснить, что это означает: мы получаем как бы обычную окружность, но в ее центре находится бесконечно малая кардиоида, поскольку центр нашей действительной окружности вращается вокруг самого себя. Важное замечание: сердечко кардиоиды в плоскости, где существует действительная окружность не находится. Точнее оно находится в плоскости, которая совпадает с основной, но вращается относительно ее вместе с кардиоидой.

Читатель, видимо, уже понял, что все странности в данном построении появляются по одной простой причине: мы только что определили алгебраическую псевдоевклидовость, которая неявно присутствует в нашей конструкции.

У нас есть центр, относительно которого определены направления радиус-векторов, но если мы один из них берем с положительным знаком, длину второго должны брать с отрицательным. Однако это не обычная длина "в другую сторону". В самом деле, если мы возьмем в евклидовой плоскости некоторый отрезок и будем поворачивать его вокруг начала, то всегда в этой же плоскости можно задать равное ему по модулю продолжение - другой радиус-вектор, который будет обегать те же самые точки окружности. При этом никакой меры длины для отрезка задать нельзя - точнее, она может быть любой.

Если следовать логике нашего построения, ситуация выглядит сложнее. Получается, что у любого действительного радиус-вектора, который вращается очерчивая в евклидовой плоскости окружность, центр вращения не фиксирован, а описывает некоторую микроокружность, точки которой не принадлежат к данной плоскости, а являются движущимися относительно ее, но движутся они не относительно какой-либо неподвижной точки, а выразимся так: сами по себе. Если переходить на физический язык, где играет роль понятие скорости и времени перемещения, можно сказать так: пока действительный радиус-вектор описывает в евклидовой плоскости окружности за некоторое действительное время, его продолжение мнимой длины описывает микрокардиоиду, вращающуюся с бесконечно большой скоростью. (Может показаться, что жорданово определение линии в таком толковании справедливо только для окружностей - от нулевого радиуса до бесконечного, но как тогда быть со стандартными прямыми? Здесь мы не будем углубляться в данный вопрос, на рисунке показано как осуществляется переход от одной прямой траектории к другой - с помощью трех микровращений. Очевидно, что угол треугольника в такой кинематической геометрии - объект чисто условный.)

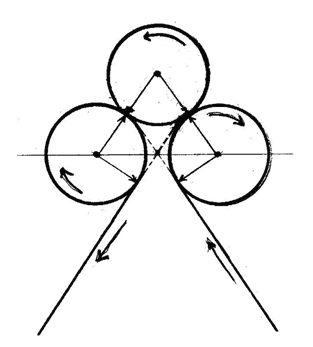Рис. 7

А что если на евклидовой плоскости задана окружность по которой нет никакого движения, то есть она не является траекторией точки в смысле Жордана? Дело выглядит следующим образом: мы считаем эту окружность линией потому, что по ней с бесконечной скоростью движется микропетелька, прочерчиваемая концом бесконечной прямой, на другом конце которой мнимый вектор, прочерчивающий в неевклидовой плоскости микрокардиоиду.

Наконец, есть и последний вариант: что если мы сделаем продолжение радиус-вектора бесконечно малым относительно его другого конца, очерчивающего кардиоиду? Автор утверждает, что в "поле зрения наблюдателя" окажется лишь часть этой бесконечно большой кардиоиды, являющаяся в его системе отсчета, в его масштабах в виде экспоненты. Появление числа e, основания натуральных логарифмов можно проследить аналитически, но здесь мы этого делать не будем.

Здесь мы ограничимся изложением - описанием сути дела понятными словами, а истинный математический смысл проделываемых операций выражается в том, что вся теория комплексных чисел оперирует мнимыми величинами, хотя реальный смысл псевдоевклидовости стал ясен только в рамках физики, интерпретировавшей псевдоевклидов континуум как 4-мерное пространство-время. Теперь математическая значимость принципа относительности релятивистской физики становится очевидной.

* * *

Вернемся к анализу кинематики вращений в ее классическом (точнее - доклассическом) варианте.

На рисунке представлены два колеса, соприкасающиеся своими окружностями, а их радиус-векторы составляют единый отрезок прямой и противоположно направлены: центр одного - это конец другого. Глядя на изображение, мы помещаем себя как бы в неподвижную, не вращающуюся систему отсчета, чтобы этого избежать поместим наблюдателя в систему отсчета колеса А, где он может следить за поворотами радиус-векторов. То что, колесо В будет вращаться по часовой стрелке - очевидно, но поскольку колесо А тоже вращается (вращается НА САМОМ ДЕЛЕ), то наблюдателю картина будет представляться так, будто центр вращения колеса В совершает вокруг него оборот против часовой стрелки.

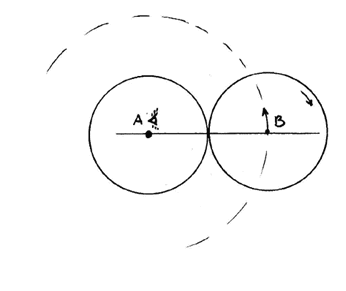Рис. 8.

Обратим внимание, что наше построение принципиально отличается от стандартного (Рис. 1). Если там мы задавали один оборот в секунду относительной скорости вращений, полагая одно из колес кинематически "покоящимся", и удовлетворялись фиксаций - "в другой системе увидят то же самое", то в нашем случае все выглядит несколько по иному: в кинематически покоящейся системе будет фиксироваться не скорость "один оборот в единицу времени", а наличие двух вращений - система вращается вокруг своей оси так, что центр ее вращения совершает обратный поворот вокруг нашей системы отсчета.

При этом линейные скорости точек на радиус-векторе не играют никакой роли: мы сравниваем вращения систем, а не скорости точек. (Равным образом, не играют здесь никакой роли и динамические характеристики - "силы" - которые мы привыкли связывать с вращением: ведь мы сравниваем колеса с одинаковой скоростью. Это одно и то же колесо, которое мы как бы раздвоили - разделили центры вращения некоторым расстоянием - и стали сравнивать вращение колеса самого с собой.) Наконец, не играет никакой роли и расстояние между центрами вращения, главное - чтобы оно БЫЛО. Тогда возникают противоположно направленные радиус-векторы вращений и всегда можно проследить как одно колесо вращается относительно другого.

А что будет, если мы в системе колеса В будем таким же образом рассматривать вращение колеса С? Очевидно, для него картина будет та же самая, но если мы вернемся в систему А, то наглядная картина вращения колес станет более сложной: получается, что центр вращения колеса В вращается вокруг А, но вокруг центра В осуществляется вращение колеса С, которое само вращается вокруг оси. Тем не менее, мы для колеса С можем осуществить ту же самую исходную операцию: совместим концы радиус векторов с центрами колес А и С и опять констатируем: колеса вращаются синхронно - то есть с одной и той же скоростью.

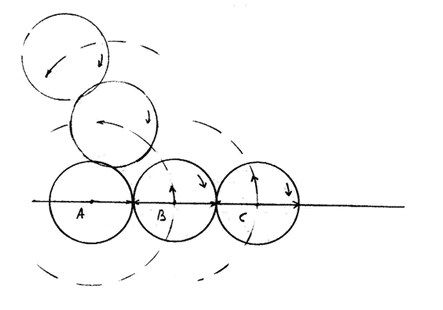Рис. 9.

Введение промежуточной системы В позволяет нам просто разложить радиус-вектор системы С на составные. Аналогично в схеме для поступательных прямолинейных скоростей складываются эталоны расстояния в одном направлении. Однако в нашем случае важно обратить внимание на то, что "одно направление" это не ось в некотором евклидовом пространстве, в котором крутятся наши модельные колеса, это некоторое расстояние, которое складывается из радиус-векторов. При соединении их всякий раз попарно можно синхронизировать вращения, но аналогом одновременности классической модели здесь будет одновременное совпадение всех концов и начал всех радиус-векторов. А ведь для колес А, В и С можно не меняя их единичного вращения построить схему, где колесо С находится не справа от колеса В, а, допустим, над ним. И, совершенно ясно, что в общем случае мы можем построит замкнутую цепочку колес. Тогда все они будут вращаться с одинаковой скоростью, но придется констатировать, что колесо H, которое расположится слева от исходного А, хоть и синхронизировано с ним, но отстает от него ровно на один оборот.

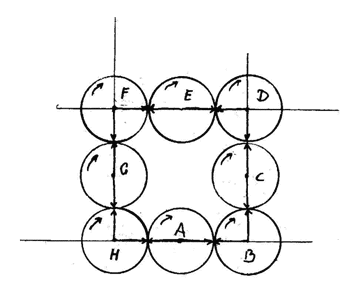Рис. 10.

Мы можем и дальше строить векторную алгебру вращений (поскольку здесь именно о ней речь), но лучше будет, если читатель сам обратится к литературе по данному вопросу, где все, сказанное здесь обычными словами, переведено на язык символов и математических операций. Смысл настоящей работы в другом: мы показываем КАКИЕ ИМЕННО ВЕКТОРА включаются в отношения, определяемые в алгебре Клиффорда (она начинается не со сложения векторов, а с определения их внутреннего и внешнего произведений), А главная цель автора - показать как самоочевидное: при сравнении вращений их скорость должна задаваться в мере [с/м].

Но прежде хотелось бы отметить важнейшую особенность логики сравнения вращений (она имеет отношение к предельному переходу между бесконечно большим и бесконечно малым). Сейчас мы поймем ЧТО ЗНАЧИТ введенная нами градуировка ВРЕМЕНИ.

Мы уже видели, что если построить замкнутый контур из радиус векторов, а синхронное совпадение их концов и начал считать за отсчет поворотов - единиц времени, то относительно колеса А левое колесо H будет как бы отставать на один оборот. При том, что скорости их вращений равны.

Это "отставание" напоминает эффекты специальной теории относительности, но есть пример более наглядный: случай, когда Магеллан и его команда, совершив кругосветное плавание, обнаружили, что в их календаре "пропал один день". (По легенде им пришлось приносить церковное покаяние за то, что они "не вовремя" справляли религиозные праздники.) Такой "эффект потерянного времени" понятен сейчас всем авиапассажирам, которые при дальних путешествиях пересекают много часовых поясов. (Что касается теории относительности, то, пользуясь случаем, хотел бы обратить внимание художников, иллюстрирующих книги по СТО: на циферблате часов движущейся системы, наблюдаемой из системы отсчета, стрелка, ориентированная по оси движения, не может быть прямой. Если стрелка - радиус-вектор - из центра циферблата выходит параллельно курсу, то конец стрелки тем не менее отклоняется в ту или другую сторону - так срабатывает эффект Не одновременности событий.)

Замкнутый контур можно составлять не только из радиус-векторов, сходящихся под определенными углами. На рисунке у нас 8 колес, все они вращаются с одной скоростью, но сложение вращений приводит к выводу, что колесо H отстает от колеса А на один оборот. Мы уже говорили, что для сравнения вращений реальная длина радиус-вектора не играет роли, главное - чтобы между центрами вращений было любое значимое расстояние. Иными словами, мы можем делать его сколь угодно малым. Например, сколь угодно малым относительно радиуса окружности, на которой эти центры помещены.

Рис. 11.

Если радиус-векторы бесконечно малы, то переход от одного вращения к другому осуществляется совершенно также, как это делается для колес А, В и С, синхронизация которых получается, когда их радиус-векторы составляют общий прямой отрезок. Значит на такой окружности, составленной из бесконечно малых радиус-векторов все колеса абсолютно синхронизированы. Этих колес бесконечно много, все они отсчитывают свои секунды одновременно, но мы вынуждены сделать поразительный вывод: по отношению к колесу А его бесконечно близкое соседнее колесо X_n (при n стремящемся к бесконечности) отстает на один оборот. Равным образом, колесо А отстает на один оборот от следующего колеса В.

Это не просто осознать. Рассмотрим ситуацию в макромасштабе: три колеса А, В и С абсолютно синхронизированы - когда их радиус-векторы совпадают своими началами и концами, они образуют прямой отрезок. То есть между ними нет значимых углов (можно сказать, что углы "бесконечно малы"). И вот теперь мы заявляем, что по отношению к колесу В, колесо А отстает на один оборот, а колесо С опережает его на один оборот. Но синхронизация колес означает, что каждое из них одновременно отсчитывает свою секунду! Тогда "отставание" и "опережение" означает, что колесо А отсчитывает ту секунду, которую колесо В уже отсчитало, а колесо С отсчитывает секунду, которую колесу В еще предстоит отсчитать!

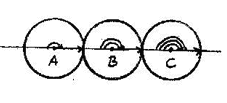Рис. 12.

Вот что означает градуировка времени: мы проградуировали актуально взятыми оборотами синхронных колес актуально взятую ось времени - с ее прошлым, настоящим и будущим. В принципе, этого и следовало ожидать. Как, в самом деле, можно иначе понимать градуировку оси времени? В кинематической модели прямолинейных скоростей мы градуировали пространственную ось и это не вызывало у нас какого бы то ни было протеста - пространство простирается перед нами актуально и присутствие в нем эталона расстояния "отсюда и дальше" не кажется чем-то необычным. Но ТОЧНО ТАКЖЕ градуировка оси времени означает, что мы задаем эталон времени "отсюда и в вечность", причем "вечность" эта, устремленная в будущее, приходит в точку настоящего в виде уже прошедшей секунды, уже отсчитанного оборота эталонного вращения. Так что ничего алогичного в таком выводе нет. Действительно, кинематическая модель сравнения вращений заставляет нас мыслить прошлое и будущее актуально существующими и замыкающимися через эталонную - бесконечно малую - секунду настоящего.

Нет никаких причин отвергать такую трактовку нашей модели. Ведь это только теоретическая МОДЕЛЬ, причем чисто классическая - построенная по той же схеме, по которой строилась модель множества поступательных прямолинейных скоростей. Последняя, как мы знаем, базировалась на понятиях бесконечного евклидового пространства и однонаправленного равномерно текущего времени. А эти представления в неклассической физике модифицировались в четырехмерный псевдоевклидовый континуум Минковского. Разумеется, странной выглядит для обыденного мышления недостижимая скорость света, при приближении к которой ход времени бесконечно замедляется, но с этим фактом уже ничего не поделаешь.

В чем особенность нашей модели, отличающая ее от стандартной? В последней редукция вращательной скорости к линейной приводит к однозначному выводу: точка центра вращения имеет бесконечно медленную линейную скорость - она покоится. В нашей модели центр вращения, даже понимаемый как математическая точка сохраняет свое вращение. Посмотрите, как раскладывается движение колеса, которое вращаясь двигается вокруг некоторого центра такого же: ведь точка конца радиус-вектора описывает вокруг некоторого центра окружность с удвоенным радиусом, но если мы рассматриваем эту систему из неподвижной координатной системы отсчета - такого вращения нет. Оно возникает в системе вращающегося наблюдателя только потому, что сам этот наблюдатель находятся в центре и вращается. Значит, основой всего нашего построения является аксиоматическое приписывание вращения математической точке.

Здесь мы построили модель относительных вращений, но ведь мы заранее подразумеваем, что в кватернионном время-пространстве ее основные параметры будут модифицированны, в частности, появится инвариантная для всех вращений скорость вращения - константа S, аналогичная пределу C для прямолинейных скоростей. Кроме того, мы знаем, что модель относительных вращений уже присутствовала в доклассической науке. Там, правда, вращения мыслились не абстрактно, как у нас, а связывались с вращениями вполне конкретных "небесных сфер", по которым астрономы отсчитывали ход времени. *

---------------------------------------

* Особенности этого теоретического подхода хорошо показаны в сочинениях Алексея Лосева, анализировавшего рассуждения раннехристианского ученого Плотина. Например, в кн. А.Ф.Лосев "Музыка как предмет логики", в главе "Время не есть движение и не есть мера движения". А.Ф.Лосев, Из ранних произведений, М.: "Правда", 1990, с. 300.

Мы просто выявили теперь ту специфическую, но строго математическую, логику, по которой древние осознавали структуру времени: для них не было однонаправленной "стрелы времени", будущие и прошлые мгновения существовали для них актуально, а поэтому можно было "по звездам" угадывать и будущие события. Этим и занимались все астрологи - от пресловутых халдеев, над которыми смеялся Цицерон, до прославленного Мишеля Нострадамуса, которому поклоняются даже наши современники. Становится также совершенно понятным, почему вращение стали редуцировать в классической механике к прямолинейным перемещениям точки по траектории: ведь однонаправленная стрела прямолинейного времени не могла непротиворечиво совместиться с моделью, основанной на сравнении скоростей вращения.

Автор предполагает, что и сейчас в мышлении читателей это противоречие возникает, вызывая скептическое отношение к изложенной здесь теории. Поэтому нелишне напомнить: доклассическая модель рассматривается нами как уже пройденный этап, нужный только для того, чтобы уяснить смысл представлений, которые лежат в основе алгебры кватернионного время-пространства. Никто не предлагает вернуться к средневековым представлениям, замкнутая окружность актуального времени - это такая же абстракция для сложения вращений, как однонаправленная ось абсолютного времени, нужная для сложения прямолинейных скоростей в евклидовом пространстве. И если в релятивистской физике классическая модель под напором фактов сменилась пространством-временем Минковского, то и на смену средневековой модели сложения вращений пришла алгебра кватернионного время-пространства, известная ныне как квантовая механика.

Анализ средневековой теоретической модели понадобился здесь только для того, чтобы уяснить суть дела: показать, что некоммутативный аппарат квантовой механики - это не просто условный язык для описания экспериментальных фактов, а вполне естественное продолжение теоретической модели, связывающей определенным образом время и пространство. Однако, связь эта такова, что вращение мыслится как фундаментальный вид движения, который не может математически редуцироваться к движению точки по круговой траектории. Соответственно, теоремы стандартного математического анализа оказываются здесь неприменимыми. Иными словами, элементарные частицы не могут двигаться по математическим траекториям с классическими параметрами, не из-за того, что они суть какие-то особые корпускулярно-волновые образования, а потому, что стандартный математический анализ - аппарат классической механики Ньютона - здесь не годится.

Каким должен быть математический анализ, объединяющий четырехмерное пространство-время и кватернионное время-пространство - это предмет особого разговора. Приведенный выше фрагмент о жордановой линии - это начала так называемого БИПОЛЯРНОГО ИСЧИСЛЕНИЯ, которое автор намеревается развернуто обосновать (и обоснованно развернуть) в отдельной статье. Что касается данной работы, здесь автор старательно избегает математических выкладок и символов. Во-первых, прежде чем писать ноты, надо сначала прочувствовать композицию, а, во-вторых, я не уверен, что всем читателям знакомы алгебра Клиффорда и ее применение в неклассической физике.

Читателям, привыкшим к математическому языку, рекомендую обратиться к вышеназванным книгам В.В.Кассандрова и В.И.Елисеева, а специально для тех, кто этот предмет хорошо знает, сделаю здесь важное пояснение. Конкретная "вращательной интерпретации" алгебры Клиффорда необходима нам для очень серьезного математического шага вперед. По мысли автора существенным недостатком в понимании алгебры Клиффорда является то, что она определена "как обычно" - над полем действительных чисел. Автор считает, что предлагаемая им интерпретация позволяет понять эту алгебру как определенную над полем чисел ГИПЕРДЕЙСТВИТЕЛЬНЫХ, которые вводятся в модели нестандартного анализа Абрахама Робинсона (одновременно показывается важнейшая значимость этой модели для математики и физики). Если принять такое понимание, то исходные вектора a, b, c, d..., произведения которых задают новые вектора A, B, C, D... (каждый из них есть сумма внутреннего и внешнего произведений исходных), должны определяться над гипердействительной частью робинсоновского поля гипердействительных чисел. В свою очередь, актуально бесконечно малые и актуально бесконечно большие числа перестают быть идеальными абстрактными объектами, а становятся актуально значимыми, существенными - и математически, и физически.

А для читателей, которым выражения "внутреннее произведение" и "внешнее произведение" покажутся какой-то искусственной математической абстракцией, хочу предложить иллюстрацию. Посмотрите на свои механические часы: в 1 часе - 60 минут, в 1 минуте - 60 секунд, значит, 1 оборот секундной стрелки - 1 минута, 1 оборот минутной стрелки - 1 час, 1 оборот часовой стрелки - ...? И это не особенность градуировки циферблата, просто минутная и секундная стрелки синхронизированы с "внутренним механизмом вращения" часов, а часовая стрелка - с "внешним механизмом вращения" планеты Земля, по поверхности которой скользит терминаторная линия дня и ночи. А все многочисленные шестеренки и балансиры наших часиков подобраны так, чтобы работала алгебра, связывающая градуировки этих вращений.

* * *

Вернемся к нашим колесам. Мы проградуировали время с помощью эталонного вращения, теперь наша задача - показать, как строится множество скоростей вращений с мерой [с/м].

У нас имеется - "колесо", которое раздвоено так, что противоположные, но равные, радиус-векторы образуют систему синхронизированных колес, отсчитывающих обороты. Скорость вращения изначально неопределенна, этого и не требуется - достаточно того, что могут фиксироваться совпадения концов радиус-векторов с центрами вращения. "Реально" наше колесо может крутиться с любой скоростью, но отсчет оборота это просто мера, а не количество мер. То же самое было и с введением эталонной длины, задающей градуированную ось x: ведь за эталон можно принимать любую реальную длину. Так и здесь: оборот - это градуировка временной оси и не более того. Колесо вращается с постоянной скоростью и задает нам разбиение оси времени на равные отрезки, а постоянство его скорости - гарантия того, что эта ось равномерна: такие же обороты отсчитывались раньше, они будут отсчитываться и впредь.

Важно осознать, что происходит здесь логически. Когда мы градуировали прямую в пространстве, мы опирались на очевидный факт: на самом деле есть она, эта прямая, и мы можем "пристыковывать" на ней эталонные метры один за другим, уходя все дальше и дальше. А в случае вращения мы так же опираемся на очевидное свойство времени: вращение - оборот - отсчитывает секунды одну за другой, и наше абстрактное колесо - это символ того, что эти обороты "простираются в вечность". Здесь становится явным то, что мы сделали: это вращающееся с неопределенной скоростью КОЛЕСО своими оборотами градуирует равномерную ось t, и эта градуировка отнюдь не является привычным отсчетом времени, как в случае прямолинейных скоростей, где движущаяся точка с каждой секундой проходит новый метр. Обороты абстрактного КОЛЕСА - это эталон градуированного времени, времени актуализированного, заданного вместе с прошлым и будущим.

Создается впечатление, что ничего особенного мы не получили. Если мы начнем отсчитывать обороты с некоторого момента, то и начнется отсчет стандартных секунд. Сколько оборотов наше колесо в секунду делает, столько долей секунды и будет отсчитываться. Но сколько же оборотов в секунду делает наше КОЛЕСО?

Давайте опять обратимся к построению множества прямолинейных скоростей. Допустим, делается такое утверждение: "Зачем нам задавать какой-то эталонный метр? Если есть единичная скорость в 1[м/с], то эталон сам и задается - за одну секунду точка как раз и пройдет один метр!" Достаточно вдуматься, чтобы понять - такое утверждение в классической кинематике недопустимо. Ведь в ньютоновской механике нет никакого эталона скорости, наоборот множество количественно различающихся скоростей строится на основе введения эталонного расстояния, а единичная скорость задается вместе с единичным временным интервалом, который требуется ей для прохождения этого эталона. А начинать с эталонного расстояния нам приходится потому, что мы ищем определения прямолинейной скорости - скорости точки, которая улетает от начала отсчета на все большее и большее расстояние. Величина преодолеваемого ею расстояния равномерно увеличивается потому, что евклидова прямая равномерно слагается из равных эталонных расстояний. Соответственно, закон сложения скоростей получается арифметическим: чем больше метров проходит точка за секунду (величина этой секунды определяется через ту скорость, которая принята за единичную) - тем больше скорость точки (по сравнению с той, что принята за единичную). Логика построения классического сложения скоростей совершенно очевидна и понятна.

Другое дело, что ее пришлось скорректировать в неклассической физике, где появляется инвариантность скорости С в любой системе отсчета. Но неклассические корректировки у нас еще впереди. Автор вновь напоминает, что мы строим кинематику вращений чисто классически - точно так, как ее строили математики прошлых веков, для которых никакой другой геометрии, кроме евклидовой, не существовало. (Хочу также принести читателям свои извинения за многочисленные повторы разными словами одного и того же - очень важно не сбиться с логического пути, ведь стандартная редукция вращения к "оборотам в секунду" крайне навязчива, и от нее трудно избавиться.)

Для двух синхронных колес нет заданной скорости - "обороты в секунду", поскольку абсолютного времени здесь нет, есть только фиксация периода - отрезка времени, разделяющего два момента, когда радиус-векторы колес совпали. Если бы мы ввели здесь абсолютное течение времени, то, конечно, не составило бы труда "засечь по секундомеру" - сколько "тиканий" прошло между этими двумя моментами. Но, понятно, что абсолютное время - это понятие из другой модели, а нам надо увидеть как будет выглядеть зависимость между отрезками расстояния и периодами времени при определении относительных скоростей вращения (как выглядит эта зависимость для относительных прямолинейных скоростей мы знаем из классической механики).

Исаак Ньютон в своем определении абсолютного времени предложил абстрагироваться от конкретных периодических процессов и ввел ход времени как таковой, - люди с помощью периодических процессов могут только фиксировать его с той или иной степенью точности. Это обстоятельство потом позволило Альберту Эйнштейну отвергнуть абстракцию абсолютного времени на основании того, что время без его измерения просто не мыслимо. Эталоном же для измерения времени оказался инвариант скорости света - вполне конкретной скорости, обладающей особым инвариантным свойством. Существенно то, что C - это именно поступательная прямолинейная скорость.

Однако в классических условиях нашей задачи нет подходящего конкретного эталона, типа "световых часов", зато есть периодический процесс как таковой, ведь вращение САМО ПО СЕБЕ - это периодический процесс в чистом виде, причем мерой времени является ОБОРОТ радиус-вектора по окружности.

Мы уже поняли, что наше КОЛЕСО - это градуировка оси времени. Не сложно было и осознать, как наша эталонная секунда может разбиваться на равные интервалы другими периодическими процессами. А как нам теперь с помощью эталонного вращения, отсчитывающего обороты-секунды определить СКОРОСТЬ вращения?

Начнем искомое построение. Допустим, у нас есть некоторое вращающееся колесо. С какой скоростью оно вертится? Смотрим на сколько оно повернулось за эталонную секунду - и определяем его скорость. Заметьте, мы здесь не число оборотов считаем в секунду, а измеряем "накручиваемую на колесо длину", ведь угол поворота для определенного радиуса задает и дугу пройденной окружности. И вот теперь ЭТУ, уже измеренную СКОРОСТЬ ВРАЩЕНИЯ, мы можем с полным правом принять за единичную. Точно таким же образом, на пространственной проградуированной прямой мы задаем единичную скорость поступательного прямолинейного перемещения - говорим: "Примем за единичную скорость точки, которая проходит эталонное расстояние за некоторое время, это интервал будет считаться единичным эталоном времени". Тогда, соответственно, те точки, которые за это же время "улетают" дальше по прямой задают своими координатами свои скорости - в данной, определенной уже нами, мере скорости, выраженной в [м/с]. Разве не так определяли мы все множество поступательных скоростей? Такое определение и позволило нам выстроить последовательность все увеличивающихся значений поступательных скоростей, которые можно складывать друг с другом арифметически, переходя от одной точки к другой. То есть, если мы выбираем точки, скорости которых отличаются друг от друга на 1[м/с], это означает:

• Вылетая из начала координат они все распределятся через секунду в точках с координатами 1[м], 2[м], 3[м], 4[м] и т.п.
• Движущаяся точка с координатой 1[м] через еще одну секунду окажется в точке пространства с координатой 2[м], а следующая - в точке с координатами 4[м] и т.п.

Соответственно, если мы перейдем в систему отсчета следующей точки, то наблюдатель в ней зафиксирует, что первая точка ОТСТАЛА от нее, иначе: движется от нее со скоростью -1[м/с], а последующая с такой же по модулю скоростью - удаляется от системы отсчета в противоположную сторону.

Для сравнения скоростей вращения также важно задать НАПРАВЛЕНИЯ вращений, что, конечно, не сложно. Но опять-таки - принципиальное отличие - для такого определения не существенно направление эталонного вращения (не важно в какую сторону вертится эталонное колесо, как не важны "начало" и "конец" для меры длины), оно задает только градуировку времени, а направление вращения определяется в зависимости от того, какой знак скорости вращения мы припишем колесу, скорость вращения которого измеряется. Иными словами, в нашей модели неопределенность направления вращения эталона - аналог нуля скорости точки отсчета классической модели.

Обратим внимание и на то, что выбор единичной скорости вращения полностью в нашей воле. Точно также, имея градуировку пространственной оси, мы любую скорость можем принять за единичную: "Пусть единичная скорость - это прохождение n или 1/n эталонных расстояний". Легко видеть, что при этом мы сохраняем арифметический закон сложения скоростей - большей скорости по-прежнему будет соответствовать большее число метров в секунду.

Теперь легко понять, как мы должны строить множество скоростей вращения. Мы просто скажем, что в эталонную единицу времени одно колесо накрутило угол - 1, другое - 2, третье - 3 и т.п. Аналогично, судя по всему, может определиться и множество с противоположно направленными скоростями: -1, -2, -3 и т.п. Пока мы не задаем здесь меру скорости, кажется ничего особенного не происходит. Вроде бы мы пришли опять к мере, измеряемой в числе оборотов в секунду. Но ведь это не так! Мы не исчисляем здесь обороты, а задаем углы или длины дуг, иными словами это и не углы вовсе, а нечто вроде длины нити, которая наматывается на катушку (или сматывается с нее). В чем же разница между этим определением и стандартным? Разница как раз в том, что для скорости вращения мы проградуировали время, а не пройденное точкой пространственное расстояние. То есть все перевернулось: скорость вращения это количество эталонных секунд, которые понадобятся тому или иному колесу, чтобы намотать или отмотать некоторую пространственную меру длины.

Теперь посмотрим, как определится здесь относительность вращений.

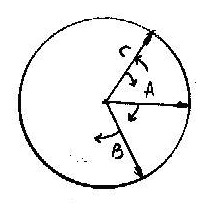Рис. 13.

Если уже задано направление скорости вращения, то для радиус-вектора А имеющего единичную скорость - поворот на единичный угол за условную секунду, определятся еще две скорости вращения: радиус-вектор В, который относительно А ушел вперед на такой же единичный угол, и радиус-вектор С, который отстал от А на это же угловое расстояние.

ВРАЩЕНИЯ ОТНОСИТЕЛЬНЫ. С этим утверждением трудно спорить. Но не просто осознать реальный смысл этой относительность. Мы привыкли, что секундная стрелка крутится "быстрее" минутной, но относительно секундной стрелки минутная отстает от нее с той же самой скоростью, однако ведь секундная стрелка НА САМОМ ДЕЛЕ крутится быстрее! Примерно такую же трудность пришлось преодолевать обыденному сознанию людей, узнавших о принципе относительности классической механики: "Как так? - мы ведь знаем, что ядро из пушки летит быстрее, чем едет карета! А вы говорите, что относительно ядра карета летит в обратную сторону с такой же скоростью. Полная чушь!"

Допустим, читатель и из уважения к автору, деликатно поглядел на часы, но все-таки признал правомерность принципа относительности для сравнения скоростей вращения: "Хорошо, пусть один радиус-вектор опережает другой на единичный угол - и означает это то же самое, что другой радиус-вектор отстает от него - как бы поворачивается в обратную сторону..." Подозреваю, что это согласие продлится не более одной минуты. Вот секундная стрелка обежала круг, догнала минутную и вновь ушла вперед на единичный угол. Разве это не свидетельствует о том, что она БЫСТРЕЕ?!

Видимо, чего-то существенного в нашей модели не хватает.

Во-первых, нам не хватает ТОЧКИ ОТСЧЕТА для вращения. Градуировка времени равными периодами - это только показатель евклидовости оси времени, а вот с какого момента нам надо начинать сравнивать вращения? Ведь только так, можно начать определение скорости.

А, во-вторых, открою тайну - ось времени псевдоевклидова (мнимость соседствует с действительностью) и мы с вами все это знаем. Последнее утверждение может вызвать недоумение. Проиллюстрируем его элементарным примером. Когда мы по ньютоновски сравниваем вращения колес на одной оси, можно одному из них "прибавить" оборот в секунду, - по "принципу относительности" система отсчета относительно его должна теперь иметь скорость на один оборот в секунду больше. Однако, мы уже построили истинную модель для сравнения вращений и видели, как раскладывается единичное вращение колеса в одну сторону - получается в системе наблюдателя два вращения: вокруг центра системы вращается другой центр вращения, причем вращения противоположно направлены. Допустим, мы решили у одного из вращений "убавить оборотов". Эталон времени уже задан, значит, исключение одного оборота дело возможное. Итак, в системе тождественных раздвоенных колес, между которыми полная относительность (в смысле относительности вращательных движений, а не поступательных), у одного из колес оборот отнят. Это означает, что в системе отсчета из двух вращений останется одно - то, которое вокруг центра системы. Иными словами, наблюдатель увидит колесо, которое вращается вокруг него, сохраняя ориентацию радиус вектора к центру. Эту картину мы можем наблюдать каждую ночь, глядя на Луну.

Здесь мы не будем обсуждать связь псевдоевклидовости с некоммутативностью, это тема отдельного разговора. По этой же причине автор избегает употреблять выражение "сложение вращений", чтобы не создавать иллюзию, что в нашей модели 1+(-1)=0.

Теперь, давайте, вспомним образ Часов Вечности - с их годовой, вековой и тысячелетней стрелкой. Читатели, конечно, уже поняли - где будет через год вековая стрелка: она укажет на цифру 10. Эта цифра для тысячелетней будет означать 10 лет, а для вековой стрелки заданная нормировка циферблата вообще не годится, - тут требуется иное толкование цифр. Один оборот вековая делает за 100 лет, в каждом столетии числа 10, 20, 30 и т.п. означают очередные годы. Первый год первого тысячелетия уже прошел, вот она и стоит на 10. А после истечения тысячи лет, когда все три стрелки сошлись, наши часы вообще уже ничего не показывают - наступила для них "проблема тысячелетнего года". Иными словами, надо бы нам на Часы Вечности навесить еще и Миллионнолетнюю стрелку, она в этот момент будет показывать на цифру 1 - что будет означать: одна тысяча лет из миллиона прошла. По истечении миллиона лет, придется вводить в оборот еще одну - еще более медленную - стрелку и т.п. А если нам понадобится отсчитывать внутри одного года какие-нибудь тысячные доли времени, то надо бы добавить и еще одну "быструю" стрелку, чтобы она делала один оборот, когда годовая прошла одно деление.

Но, постойте, если годовая указывает на одно деление, то быстрая стрелка нам уже не нужна! В самом деле, мы теперь можем проградуировать циферблат с какой угодно частотой делений (благо пространственный континуум принято делить до бесконечности), тогда на нашем циферблате по годовой стрелке в течение одного ее оборота можно определять "внутригодовые" интервалы времени с какой угодно степенью точности.

Что это все означает? Это означает, для того, чтобы отмерять более длительные периоды - нам нужны особые вращения, которые будут поворачиваться на определенные углы, сообразно тому сколько оборотов накрутило эталонное вращение.

Причем этих медленных "стрелок" - каждая со своей скоростью вращения - нам понадобится бесконечно много, ведь единичный угол поворота каждой очередной - когда-нибудь сложится в полный поворот: наступит полная синхронизация всех вращений - как бы конец времен. Всегда нужна стрелка, которая к этому моменту свой поворот не завершила. А как нам измерять скорость этой стрелки? Очень просто. Единичный угол задан, есть эталонное вращение. Значит, скорость любой стрелки можно измерить по числу оборотов стрелки эталонной. Тысячелетняя, например, поворачивается на единичный угол ровно за 1 оборот годовой, а свой интервал отмеряет за 1000 эталонных периодов.

Вот и все. Мы проградуировали ось времени и задали принцип определения скорости бесконечного множества вращений.

Выше мы говорили, что измерение "отрезка времени" требует задания его конца и начала - полного периода вращения. Значит, для всего множества стрелок надо задавать не угол поворота, а полный оборот. Тогда эталонное вращение будет отсчитывать число пройденных эталонных периодов, требуемых для завершения оборота той или иной стрелкой. Таким образом, угол превращается в расстояние, для данного циферблата - эта длина ее окружности. Каждая из стрелок будет проходить эту длину за свое, строго определенное число эталонных периодов, а мерой станет [с/м]. То есть независимой переменной оказывается пространственное протяжение - нить, накручиваемая на колесо в течение его одного оборота. Конечно, колесам можно приписывать разные радиусы - точно также и в модели прямолинейных перемещений мы с помощью независимой переменной t можем выбирать для скорости любую меру - метры в секунду, километры в час, или километры в секунду, метры в час.

А как быть с самой медленной стрелкой, которая не сможет завершить свой оборот ни за какое счетной число эталонных периодов? Придется с этим смириться, как смирился Ньютон с существованием непонятной бесконечной скорости, приняв ее в качестве выражения для мгновенного действия на расстояние. (Если поискать аналогичный "пра-образ" для нашей модели, то это - не удивляйтесь! - это Конец Времен, когда все-все стрелки сойдутся на Часах Вечности в момент Конца Света.)

С эталонным интервалом времени все ясно. Пора, наконец, более точно описать - что значит ЕДИНИЧНАЯ СКОРОСТЬ. Для того, чтобы отличать единичную скорость от единичного эталона времени достаточно вспомнить, про обратное направление вращения и принцип относительности. Действительно, если мы зададим единичную скорость вращения в 1 оборот за 1 эталонный период, то основная стрелка на наших часах как бы "потеряет скорость". Не ясно, что она на самом деле делает - градуирует ось времени или задает единичную скорость. Разобраться в этом вопросе не сложно.

Надо задать "точку отсчета" для вращения - направление вектора, относительно которого будут совершаться ВСЕ повороты. На Часах Вечности мы совершенно произвольно задавали вертикальное положение, в котором синхронизируются все стрелки. Но это направление можно задать вполне обоснованно. У нас есть раздвоенное колесо: два колеса, которые вращаются в одну сторону. И это действительно эталон времени, поскольку его можно, скажем так, "параллельно" переносить по оси времени, прикладывая к началу любого периодического процесса. Это эталон времени. А вот единичная скорость вращения - это нечто иное. Мы возьмем эти же два синхронизированных колеса и одно из них "отразим в зеркале": то есть зададим ему такую же, но противоположно направленную скорость вращения. Синхронизация колес, как ясно, от этого не измениться. Теперь посмотрим, как будет выглядеть дело в системе отсчета наблюдателя. Он будет наблюдать вращение вокруг своего центра некоторого другого центра вращения, и оба вращения будут осуществляться в одну сторону.

Выше автор делал небольшой исторический экскурс на тему циклоид-рулетт. Хорошо известно, что колесо, которое катится по ободу другого, равного диаметра, прочерчивает точкой конца радиуса эпициклоиду, называемую кардиоидой. Точка излома этого "сердечка" ("мгновенный центр вращения" в теории циклоид) отмечает на окружности вполне определенную точку, задающую направление радиус-вектора - неизменное для данных синхронизированных вращений. Так мы получаем в системе вращений направление отсчета - в этой точке времени и будут синхронизироваться все скорости сравниваемых нами вращений. Это точка, относительно которой можно нашим эталоном градуировать ось времен.

Для классического построения модели сравнения вращений не суть важно как трактовать кардиоиду - стандартно или не стандартно, важно, что эта фигура центрально несимметрична - то есть задает определенное направление.

Вот стрелка, которая описывает свой оборот и приходит вновь к цифре 0. Мы добавляем "зеркальную" стрелку, которая крутится с той же скоростью, но в обратную сторону: в 0 они приходят одновременно. Так вот, эталонную меру времени и точку отсчета на оси времен задает та стрелка, которая отсчитывает эталонные обороты, вращаясь в сторону, противоположную той, в которую крутятся все остальные стрелки, измеряемые по скоростям вращения. Тогда базовая, которой мы отводили функцию отсчитывания эталонов времени, будет вращаться с единичной скоростью - один эталонный период на один пробег окружности, ее Л=+1 [с/м], определяя и все кратные ей: 2[с/м], 3[с/м], 4[с/м], 5[с/м] и т.п. - в условных "секундах" и "метрах". А как нам измерить скорости вращения, направленные в другую сторону? Точно также, но теперь эталон времени будет отсчитывать та стрелка, которой мы приписывали только что единичную скорость. Теперь уже она вертится вокруг новой системы отсчета, задавая точку излома кардиоиды и тот же самый момент на общей оси времен. Точно как и в классической модели, мы переносим систему отсчета в ту вращательную систему, относительно которой измеряется скорость вращения.

Теперь проанализируем, как будет поворачиваться стрелка, которая описывает один оборот за два эталонных периода: она относительно стрелки, имеющей единичную скорость, все время отстает - пока та опишет две окружности за два интервала времени, наша стрелка опишет только одну. Поэтому в нашей мере ее относительная скорость по сравнению с единичной = 1[с/м]. Значит, сложение скоростей будет идти арифметически. Но самое интересное, что в системе отсчета эталонной стрелки она как раз и будет описывать две окружности за один ее оборот - ведь она "убегает" от нее. Выше мы уже отмечали, что секундная стрелка часов "убегает" от минутной с той же скоростью, с которой минутная отстает от нее. Здесь мы применяем этот же принцип относительности для вращающихся систем.

Итак, еще раз рассмотрим распределение ролей среди множества стрелок скорости, которых различаются кратно единичной. Напомню, что здесь уже не Часы Вечности с вековыми и годичными стрелками, а просто некий воображаемый циферблат, где в обе стороны относительно его вращаются стрелки. На этом циферблате начало отсчета - общая синхронизация всех возможных стрелок - они стоят на цифре 0, которую задает эпициклоида обратного единичного вращения, - поскольку одновременно в противоположных направлениях начинают вращаться две эталонные стрелки, а их скорости относительно друг друга единичны. Для построения остального множества скоростей мы в качестве единичной, принимаем ту, которая вращается в ту же сторону, что и все измеряемые. Скоростям стрелок приписываются значения в мере [с/м] - то есть сколько эталонных интервалов времени проходит к моменту, когда измеряемая стрелка обегает единичную окружность. В этот момент эталонная стрелка сходится с измеряемой на цифре 0. Отметим, что эта точка циферблата не произвольно выбрана - ее задают синхронные совпадения эталонной стрелки, измеряющей время, и противоположно направленной стрелки с единичной скоростью. Иными словами, о "неподвижном циферблате" можно уже не говорить, поскольку важна не "неподвижность" как таковая, а то, что стрелки с равными, но противоположными скоростями всегда будут однозначно задавать момент отсчета и полную окружность за полный оборот, а все остальные стрелки в определенном направлении будут замыкать равные окружности именно на этой точке. (Тем не менее, на роль "циферблата" мы еще найдем актера.)

Кстати, в средние века часто на городских ратушах устанавливались не те, привычные нам, часы с неподвижным циферблатом, а часы, где стрелка и циферблат вращались в противоположные стороны - этим как бы фиксировалась абсолютная эталонность обегаемой ими окружности. Затем циферблат закрепили, зато часовой стрелке предписано делать два круга в течение суток, встречаясь с цифрой XII два раза. Понятно, почему это так - ведь циферблат, не смотря на всю его "неподвижность", это вращающаяся система отсчета - он "относительным образом" движется навстречу часовой стрелке, и полный круг совершается после двух встреч. (Другими словами, два связанных, синхронизированных противоположно направленных единичных вращения - это гарантия для того, чтобы исключить любые другие вращения, в которых может участвовать наблюдатель, сам не замечая этого.)

Вернемся к "распределению ролей". Если мы решим измерить скорости в противоположном направлении, то надо будет за эталон периода брать ту, которая вращается с единичной скоростью в противоположную сторону, а единичную скорость приписывать прежней эталонной. Мы поступаем точно также, как в классическом принципе относительности, когда утверждаем, что точка отсчета удаляется относительно той, которой в данной системе приписывалось единичная скорость. У инерциальных систем нет единой, абсолютной, общей для всех системы координат, система отсчета может быть связана с каждой из них. Нет неподвижного центра мира, относительно которого определяются скорости. Точно также для вращающихся систем нет неподвижной - абсолютно не вращающейся системы отсчета. Мы можем задавать вращения, только связывая систему отсчета с вращающейся.

Автор считает, что здесь есть принципиальный момент, который следует акцентировать. На примере построения вращающихся систем отсчета мы можем выделить логически важное обстоятельство, которое в классической модели прямолинейных перемещений часто остается не выясненным. Действительно, зачастую прямолинейные перемещения определяются нами так, как если бы евклидовость пространства была уже задана. Как будто есть уже плоское пространство, в котором можно задавать в одном направлении линейные меры, неизменные на расстоянии. Для ньютоновской кинематики это было естественно, но сейчас есть причины усомниться в этой аксиоме.

Мы, конечно, можем за единицу принимать любую длину, но почему эта единица как бы сама собой откладывается все дальше и дальше в бесконечность? Теория относительности Эйнштейна выдвинула на первый план иной логический подход. Мы поняли, что мера расстояния может задаваться только через скорость. Только если есть единичная прямолинейная скорость, можно теперь говорить о том, что за равные промежутки времени некоторая точка пролетает в данной системе отсчета равные расстояния. При этом, та же самая точка может быть принята за систему отсчета, и тогда вся наша система координат придет в движение - с той же единичной скоростью, но противоположно направленной. Это, вроде бы совсем не значимое, уточнение приводит к существенным выводам.

Допустим, из начала координат одновременно вылетают точки с разными скоростями в одном направлении. В это утверждении уже есть неточность. Что значит - "из начала координат"? Никаких "координат" еще нет. Для того, чтобы они появились, мы должны одной из точек приписать единичную скорость, а тому расстоянию, которое она УЖЕ прошла за НЕКОТОРЫЙ интервал времени можно теперь приписать единичную пространственную меру. Что же из этого следует? Что НЕЛЬЗЯ говорить: из начала координат в противоположных направлениях одновременно вылетели две точки с единичными скоростями. Не правда ли странное заявление? Как это - "нельзя говорить"? А так: единичная скорость - это та скорость, которая задает для точки отсчета единичное расстояние и меру времени. И "противоположно направленной" единичной скоростью обладает сама система отсчета, относительно единичной скорости. Переходя в эту систему отсчета, мы должны сделать координатное преобразование и для времени: для нее секунду назад произошло событие - вылет некоторой точки с единичной скоростью в противоположном направлении. Но это если и только если направления - вправо и влево - заданы строго для обоих наблюдателей. В противном случае придется вести речь о повороте начала координат: каждый наблюдатель поступает симметрично - приписывает положительное направления тому, в котором точка улетает от него, ведь направление из настоящего в будущее у наблюдателей должны быть одинаковы.

Мы условились, ничего пока не говорить о псевдоевклидовости, поэтому автор здесь должен остановиться (отсылаю заинтересованных читателей к книге В.И.Елисеева "Введение в методы теории функций пространственного комплексного переменного" http://www.maths.ru, где развит математический аппарат, учитывающий, что в четырехмерном пространстве-времени Минковского оси координат не могут все выходить из одной точки.)

Отмеченное свойство перехода из одной системы отсчета в другую, не столь явное для классической модели прямолинейных поступательных скоростей, для вращающихся систем отсчета выдвигается на первый план УЖЕ В СТАНДАРТНОЙ КИНЕМАТИКЕ - ведь градуировка временной оси требует вращения, полного оборота раздвоенного колеса, синхронизированного с самим собой, и полного поворота двух стрелок, обегающих воображаемый циферблат в противоположных направлениях.

Попробуем теперь нарисовать на чертеже множество наших скоростей вращения, выраженных в мере [с/м].

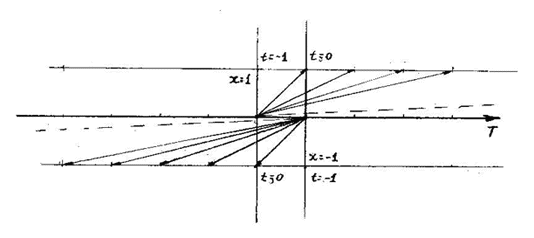Рис. 14.

Мы строим все множество скоростей в момент, когда все стрелки синхронизированы, то есть лежат на выделенном направлении - направлении, которое фиксировано для наблюдателя. Это начало координат. Относительно наблюдателя в этот момент интервал времени уже задан, его задали своими оборотами синхронные единичные стрелки. Мы, соответственно, рисуем вектор для единичной скорости. Ее вращение началось период назад и пройдена ею полная окружность. Начало радиус-вектора в t=-1 конец вектора - в t=0 на единичном расстоянии. Радиус-вектора остальных стрелок будут иметь концы на все более удаляющихся интервалах времени, кратных эталонному периоду. Картина, в общем-то, совершенно тождественная той, как если бы мы рисовали вектора прямолинейных скоростей, выходящие из начала координат: чем выше поступательная скорость - тем круче ее наклон к оси t, наибольшая скорость прямолинейного поступательного движения - бесконечна. У нас наоборот, скорости вращательных движений арифметически идут к бесконечно медленному вращению. Но есть важная особенность, мы ведь еще не построили множество противоположно направленных скоростей вращения. Для них наша стрелка с единичной скоростью вращения становится эталонной, то есть уже не наматывает длину окружности, а отматывает ее. Поэтому здесь мы должны задать координату x с обратным знаком. Но мало этого, не совпадают и точки отсчета времени. "Зеркальность" противоположной скорости означает, что "отматывание" - это наматывание, обращенное по времени. Это, действительно, так - в этом легко удостовериться, проверяя как будет осуществляться переход из единичной системы отсчета вращения в противоположную. Надо только не забывать, что у нас, в соответствие с принципом относительности, нет нулевой не вращающейся системы. Система с единичным вращением в одну сторону, становится единичной, но противоположно направленной. Нулевая скорость (отсчетная система) - не между ними, а каждая является нулевой (отсчетной системой) для противоположной. Потому и наступает "перекрытие" временных циклов: начало одного оказывается концом другого.

С "нулевой" скоростью вращения вроде бы все ясно, а вот как быть с бесконечной?

Получается, что после начала синхронизации в бесконечном будущем какая-то бесконечно медленная стрелка завершит полный поворот. Но ведь она вращается бесконечно медленно. Как это понимать?

Выше мы подбирали актера на роль "циферблата" - он перед вами. Действительно, циферблат - это некая проградуированная шкала, которой мы приписываем неподвижность, по его делениям можно в любой момент определить угол поворота, поскольку относительно выделенного направления, задаваемого вращением единичных стрелок, циферблат неподвижен. Теперь выяснилось, что неподвижность - это бесконечно медленное вращение, полный поворот за бесконечность. Однако, если это не абсолютный покой, если все-таки вращение имеется, мы должны тогда признать, что за единичный эталонный период происходит сдвиг циферблата на бесконечно малый угол - эта "неподвижная" стрелка успевает описать бесконечно малую дугу окружности. Но фиксация направления задана абсолютно - единичные стрелки +1 и -1 задают точку - мгновенный центр вращения, излом кардиоиды, который никуда сдвигаться не должен. Теперь выясняется, что относительно циферблата за каждый оборот это направление сдвигается на бесконечно малый угол.

Более того, относительность этих вращений приводит нас к еще более интересному выводу: этот угол изменяется с каждым оборотом. Мы задали, что в начале отсчета 0 циферблата и начало эталонной окружности, пробегаемой стрелкой за период совпадают. После первого круга между ними образуется бесконечно малый угол - бесконечно малая дуга. Дуга какой окружности? Ясно, что окружности заданной. Обозначим ее длину за единицу. Теперь к 1 прибавим 1/¥ . Существенно, что это не некий предел dx, который мы делаем "сколь угодно малым", а самая натуральная актуально бесконечно малая часть единицы. Она появилась у нас, когда мы определили бесконечно медленный поворот, который описывает стрелка по окружности за бесконечное время. И мы не можем здесь отговориться, что это просто абстракция - идеальный объект, вроде бесконечно удаленной точки в проективной геометрии. Ведь у нас задано условие синхронизации: бесконечно медленный поворот уже завершился по крайней мере один раз - поскольку задано совпадение всех стрелок в начале отсчета. Опять повторим: наше рассмотрение классическое, здесь бесконечная медленность стрелки возникает также естественно, как бесконечная скорость прямолинейного перемещения в стандартной модели поступательных скоростей (и как ортогональность осей X и Y в стандартном математическом анализе).

Что же получается? За один эталонный оборот единичная стрелка пришла не в точку 0, а сдвинулась относительно ее на некоторую бесконечно малую долю, она "накрутила", получается, чуть больше длины, нежели ей отмерено. Образно выражаясь, за один оборот "капитал" возрос на некоторый бесконечно малый "процент". * А далее начинается нарастание "процентов на проценты", то есть единичная длина будет раз от разу возрастать так, что отношение длин окружностей, которые обегаются в двух соседних циклах, вроде почти единично = (1 + 1/¥ ), но ведь число периодов, отмеренных за вечность также бесконечно. То есть образуется геометрическая прогрессия с множителем 1 + 1/N, и если длина первой окружности нами принята за единицу, то происходит нарастание длин таким образом, что длина "последней единичной окружности" оказывается (1 + 1/n)ⁿ. Не трудно заметить, что эта длина - e.

Можно подумать, что автор получил здесь основание натуральных логарифмов в результате некоторого шулерского приема - вроде извлечения числа "пи" из египетской пирамиды. Однако все концы свяжутся, если мы попробуем их связать. Что мы, в самом деле, тут получили? Получили вывод, что некая единичная окружность описываемая за эталонное время когда-нибудь через бесконечное время оказывается длиннее исходной. Так вроде бы быть не должно. Но еще в самом начале мы для нашей кинематики получили не менее поразительный вывод: здесь будущее должно смыкаться с настоящим, приходя из прошлого. А коли так, то наша противоположно направленная единичная скорость - это радиус-вектор который должен описать не длину единичной окружности, а какую-то более длинную окружность. Но этого не может быть!

Тем не менее, это как раз и происходит. И эту "более длинную окружность" не надо искать где-то в будущем, ведь к моменту синхронизации вечность уже прошла. Вспомним, как мы сравнивали относительные, но противоположно направленные единичные вращения. Мы помещали наблюдателя в систему отсчета, вокруг которой вращалось противоположно направленное эталонное колесо. Точка на конце его радиус вектора прочерчивала кардиоиду, задающую точку на окружности - направление относительно которого потом отсчитывались полные повороты. Как вы думаете: относительно наблюдателя - какова длина этой кардиоиды? Она равняется 2,71... со всеми требуемыми знаками после запятой.

Автор просит читателей, проверить это расчетами, но при этом длину кардиоиды подсчитывать точно, но приравнивая бесконечно малые дуги кардиоиды и окружности. Соответственно, на этом месте мы прервем анализ псевдоевклидового время-пространства, поскольку задача настоящей работы - не изложение математического аппарата, а обоснование логики, которая к нему приводит.

-------------------------------------------

* Известно, что и Коперник, и Ньютон занимались проблемами денежного оборота. Это были, судя по всему, не случайные превратности судьбы, а вполне осознанный научный интерес. А то, что "денежный континуум" псевдоевклидов, можно предположить по наличию "отрицательных денег" (мнимых денег) - долговых расписок, векселей и пр. Необходимость научного понятия "отрицательные деньги" обоснована красноярским экономистом Е.В.Вальковым.

* * *

В дополнение к этому краткому очерку классической кинематики вращений, следует привести еще один текст, образующий, опять-таки, "вполне самостоятельный и законченный фрагмент, где суть дела излагается без исторических экскурсов и философских аргументов".

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА И МАТЕМАТИЧЕСКАЯ КИНЕМАТИКА ДВИЖЕНИЯ

Что такое специальная теория относительности? Это механика движущихся часов. Но есть одно принципиальное условие: все эти часы, которые мы сравниваем в теории относительности, отсчитывают время В ОДНУ СТОРОНУ. Что это значит? Что интервалы времени, отсчитываемые ими идут от точки общего настоящего в будущее. Будем считать "точкой общего настоящего" момент синхронизации, когда все часы совмещены в начале системы отсчета и синхронизированы - все стрелки показывают на цифру XII. Поскольку все часы одинаковы, то ничего особенного не случится, если мы предположим, что их часовые стрелки вращаются в одну сторону. Однако все часы, кроме покоящихся в нашей системе отсчета, еще и прямолинейно поступательно перемещаются - зададим им общее направление движения, допустим - вправо, "по часовой стрелке" - то есть туда же, куда направлены все мгновенные линейные скорости концов их стрелок.

А теперь - принципиальный вопрос: вот в точке общего настоящего размещаются одинаковые часы, которым приписываются разные поступательные скорости, одинаковы ли угловые скорости вращения их стрелок? В теории относительности сделано неявное физическое предположение, что у одинаковых часов угловые скорости вращения стрелок одинаковы, а при медленном ускорении - реальном переходе из системы в систему - угловая скорость часов не должна меняться. (Легко вообразить, как наши часы очень медленно поступательно ускоряются - что особенного может произойти с угловой скоростью? Даже если предположить, что в точках XII и VI на стрелку воздействуют некие силы, то в одну сторону эти силы будут ускорять, а в другую замедлять стрелки - то есть не повлияют в среднем.) Так вот, если все так, то мы получаем множество часов, стрелки которых имеют одинаковую угловую скорость, но сами часы относительно нас движутся с разными прямолинейными и поступательными скоростями.

Как вы думаете, если мы захотим теперь сравнивать показания часов в разных системах отсчета, что мы увидим? Перейдя в систему отсчета, которая удаляется от нас, мы увидим, что оттуда вращение стрелки наших часов идет в сторону, которая противоположна скорости движения - "удаления от нас". Могут возразить, что в специальной теории относительности нет никаких механических часов и стрелок, а есть только "световые часы". Согласен. Но легко сделать из световых часов с двумя зеркалами часы и с тремя зеркалами, и с большим числом зеркал, расположенных касательно к окружности так, чтобы луч света бегал, отражаясь от них, совершая оборот по окружности.

Когда появляются часы из трех зеркал, появляется движение света по кругу. И не просто по кругу, а по определенному направлению - по часовой стрелке или против. И не надо особого остроумия, чтобы повернуть такие часы в плоскость перпендикулярную оси движения, где нет Лоренцева сокращения, а затем вообразить вращение самой системы зеркал навстречу лучу, или от него, да вместо трех зеркал поставить 6, 9 и т.п., чтобы новое зеркало успевало подойти на нужное место, пока луч идет по одной стороне, своей треугольной траектории. (Нечто вроде опыта Физо, но вывернутого наизнанку.)

Поскольку наше рассмотрение кинематическое, то ни на каком рассеянии света речи нет - мы должны рассматривать только мгновенные отражения под геометрически точными углами. Тогда вращение системы зеркал в движущейся от нас системе отсчета медленнее, нежели у нас (мы смотрим вслед движущейся системе - система вращается вкруг оси зрения). Это понятно, ведь в нашей системе координат луч пролетает до новой встречи с очередным зеркалом большее расстояние, поэтому зеркальные часы вращаются в удаляющейся системе отсчета медленнее наших. Разве это не замедление времени в движущихся системах? Причем - чем быстрее движение, тем медленнее относительно нас крутится их зеркальное колесо. Но вот что интересно, если мы доведем число зеркал до бесконечности, а угол отражения до нуля, то получим сам свет летящий по окружности, находящийся все время в точке своего отражения - то есть мгновенная линейная скорость поворота стрелки - это и есть сам свет, летящий по круговой траектории.

Повернем опять наши часы в плоскость движения, забудем, что вращение стрелки мы только что отождествляли с беганием луча света, и рассмотрим из своей системы отсчета все часы, однажды уже синхронизированные в ней. Если угловая скорость везде одинакова, то и направление ее, разумеется, одно. Это накладывает дополнительное условие. Если покоящиеся часы имеют единичную угловую скорость, то на наших часах конец стрелки имеет некоторую линейную скорость. Поэтому, МЫ ОБЯЗАНЫ СЧИТАТЬ, что поступательные скорости всех часов относительно нас не превышают мгновенную линейную скорость точки на конце стрелки наших часов (в тот момент, когда она показывает на цифру XII). А как быть с противоположно направленным движением часов? А для этого множества вращающихся стрелок, можно ввести противоположное направление вращения. Время течет из настоящего в будущее - пусть на этих часах угловая скорость стрелок противоположного направления, все равно отсчет времени идет не в прошлое, а в будущее.

Итак, мы определили некоторое множество поступательных скоростей, с которыми двигаются наши часы, но с некоторым граничным условием. У всех движущихся инерциальных систем значение их скорости в нашей системе отсчета не превышает скорость, с которой двигается конец стрелки на наших покоящихся часах. А поскольку все угловые скорости в каждой из систем отсчета одинаковы, то в любой из систем отсчета мгновенная линейная скорость конца стрелки их часов всегда одна и так же, - для наблюдателя, сидящего в центре циферблата этих движущихся часов.

Теперь, полагаю, читателю уже ясно - ЧТО мы получим, если начнем следить за ходом часов движущейся системы отсчета из нашей - покоящейся. Если угловая скорость вращения стрелок везде одинакова, то линейная скорость стрелки на цифрах XII и VI, получается, относительной. Относительность эта такова, как будто дифференциал dx, лежащий параллельно курсу движения, изменил свои размеры. Не будем говорить - как и почему, а просто проследим за траекторией конца стрелки движущихся часов. Если их угловая скорость та же, что и у нас, то мы заметим, как в движущейся системе передвижение стрелки относительно нас меньше, а у той, что движется с линейной скоростью, равной скорости конца нашей стрелки, вообще не произойдет ни одного "тиканья" - стрелка просто не может сдвинуться с места. Как же так? Ведь вращение есть! Конечно, но все дело в том, что циферблата нет - он превратился в отрезок. Вместо совершения углового поворота конец самой быстрой стрелки превратится в точку, прыгающую по этому отрезку с частотой, соответствующей нашей угловой скорости.

При этом, конечно, нет никаких оснований, считать, что сами эти движущиеся часы "сжались", просто ТАК дело выглядит, если смотреть на них из нашей покоящейся системы отсчета. Наши часы, относительно любых движущихся, будут выглядеть так же, как они выглядят относительно нас. Понятно, что количество движущихся часов можно делать любым, помещая между любыми двумя новые - так, чтобы сохранялось относительное равенство скоростей. А сложение относительных поступательных скоростей будет идти по специальному закону, чтобы заданная единичная скорость была их пределом. Вот и вся логика построения псевдоевклидового континуума Минковского: инвариантность угловой скорости задана аксиоматически, а все множество поступательных скоростей построено так, чтобы сложение скоростей давало в пределе значение мгновенной линейной скорости, которое связано с инвариантной угловой, принятой за единичную. *

----------------------------------

* Автор подчеркивает: наше рассмотрение полностью адекватно кинематике специальной теории относительности, ни один из ее выводов не утратил свою силу. Однако мы ввели в рассмотрение вращение стрелок, а это позволило увидеть внутреннюю схему кинематики СТО, получается, что свет - это не просто сигнал из точки в точку, а форма, в которой теория относительности представляет вращение. Единичная линейная скорость конца стрелки - вот тот предел, к которому выстроена кинематика сложения скоростей, а свет как таковой - это физический процесс, задающий поступательное перемещение равное константе, уже заложенной в логике этой чисто математической кинематики.

Вращение удалено из релятивистской кинематики, в системах отсчета его нет, оно перенесено в поворот координатных систем относительно друг друга в общем пространстве-времени Минковского. Поворот для одной системы координат не мыслим, что, в частности, проявляется в дискуссиях вокруг "парадокса близнецов", где их встреча может быть обеспечена только, после поворота и возврата назад. И очень показательно, что в этом "парадоксе" разлученных близнецов всегда двое. Если предположить близнецов-тройняшек, один из которых остается на Земле, а двое других разлетаются в противоположных направлениях, чтобы потом вернуться назад, круговое движение придется включить в рассмотрение в одной системе координат, а этого в рамках кинематики СТО не получается. (Оригинальная идея о близнецах-тройняшках принадлежит красноярскому физику А.Полтавцеву.)

Построенная в данной статье кинематика, включающая вращения, вовсе не является какой-либо физической концепцией, альтернативной специальной теории относительности. Наша задача была показать: как строится кинематика, основанная на принципе относительности без каких либо физических аксиом - инвариантность скорости света (факт как бы физический) оказывается константой для угловой скорости вращения. Это логическая предпосылка данной кинематики, а не "постулат", который якобы введен по экспериментальным причинам. Специальная теория относительности Эйнштейна непротиворечива и отражает важнейшую сторону более общей кинематики.

Да, физическая интерпретация возникает, когда инвариантная угловая скорость связывается с конкретным процессом - с электромагнитными волнами, с природой света. Кинематическая схема соответствует физическому факту, но логика построения этой схемы не зависит от того, что за инвариантную угловую скорость мы выбрали за единичную. Для любой единичной угловой скорости, однозначно задающей мгновенную линейную скорость в направлении поступательного прямолинейного движения, геометрическая кинематическая модель получится такая же. А то "бесконечное замедление" времени, которое мы наблюдаем на удаляющихся от нас часах, в пределе образует предельное замедление скорости вращения - это и есть та самая бесконечная медленность, которая возникает в алгебраической модели ТОЙ ЖЕ САМОЙ КИНЕМАТИКИ. Математически - и геометрическая, и алгебраическая модели приводят к одинаковым, согласующимся выводам.

Но эта тождественность возникает не из-за перевода - мол, "одно и то же, но на разных математических языках". Существует важнейшее условие, позволяющее делать этот перевод: мы должны ввести в математический язык "бесконечно большие величины". Точно также, как мы вводили "бесконечно малые", понимаемые как бесконечно малые относительно единицы (относительно любого, сколь угодно малого числа e , являющегося долей данной действительной единицы), так и здесь мы вводим "бесконечно большие" величины - остающиеся бОльшими, чем любое наперед заданное число 1/e - выражающее любое количество заданных единиц. Понятно, что дифференциальное отношение dy/dx превращается тем самым в конкретное отношение бесконечно больших (1/dx деленное на 1/dy). Алгебраист Мишель Ролль, яростно критиковавший Ньютона, Лейбница, Декарта, Лопиталля и всех других пионеров дифференциального исчисления, может спокойно сосуществовать с ними в мире ином: "немыслимые" бесконечно малые в соединении со столь же "немыслимыми" бесконечно большими образуют нормальные количества, которые можно сочетать алгебраически.

Но нас здесь не интересует извечный конфликт математиков-конструктивистов и математиков-интуитивистов, ведь реально, физически, ЕДИНИЦА - это не та абстрактная величина, которую можно и делить, и умножать, меняя нормировки и гоняя ее по числовой оси между двумя полярными точками - в нуле и в бесконечности. Физически "единичная мгновенная скорость" оказывается не произвольно задаваемой, а вполне конкретной. Эта единица имеет размерность и отождествляется с конкретным физическим процессом - инвариантной скоростью электромагнитных волн. Аналогично, и бесконечная медленность - построенная на основе этой единицы (математически говоря - бесконечно большая относительно ее) оказывается не бесконечностью, а другой ЕДИНИЦЕЙ, которая также предстает как вполне конкретная физическая константа.

Подведем теперь, если позволено так выразиться, - предваряющий философский итог.

В основании логики рационального понимания пространства и времени лежат представления о нуле и бесконечности: точка и бесконечная протяженность, мгновение и бесконечная длительность. Математически это приводит к сочетанию двух логических схем:

1. Вечное движение по траектории, приводящее к представлению о постоянной угловой скорости, что позволяет связывать постоянную угловую скорость и получать вектор мгновенной линейной.

2. Бесконечная угловая скорость вращения, которая для циклического движения по траектории, оказывается абсолютным покоем, что позволяет понимать равномерную скорость, состоящей из мгновенных вращений, - фиксирующих точки траектории в плоском пространстве.

Первый подход воплотился в стандартном математическом анализе, второй подход, неявно присутствовал, а в конечном итоге привел к некоммутативной алгебре, которая оказалась другим выражением псевдоевклидовых пространственных построений. Если же эквивалентность обоих подходов признать, то над полем гипердействительных чисел надо ввести биполярное исчисление, включающее и бесконечно малые, и бесконечно большие. Тогда теория функций комплексного переменного может быть переосмыслена как аппарат, описывающий отношения таких величин, а вместо стандартных траекторий мы получаем бесконечно изломанные фрактальные линии, частным случаем которых являются те линии, которые мы обычно называем гладкими. Но эта тема - уже из другой математики.

III

Итак, автор постарался показать, как квартернионное время-пространстве появляется в анализе естественных процессов вращения, в которых объективно существует особая связь между временными и пространственными параметрами. Предложенный метод построения представляется автору совершенно понятным, внутренне последовательным и логичным. Однако так же, совершенно понятно, что многие читатели предпочтут охарактеризовать все это другими эпитетами. Поэтому я посчитал нужным, завершить работу неким кратким очерком, призванным показать место данного подхода в общем русле движения науки.

Еще в XIX веке Уильям Гамильтон сформулировал перспективную задачу: если есть геометрия как наука о пустом пространстве, то - просто по аналогии - можно представить некую науку о "чистом времени". Более того, он предположил, что алгебра - это и есть такая наука, просто мы не улавливаем в ней скрытую временную специфику, не понимаем - как НА САМОМ ДЕЛЕ в алгебраических уравнениях воплощаются внутренние свойства ВРЕМЕНИ. Открытие некоммутативной алгебры Гамильтоном произошло в результате его попыток смоделировать время в "Теории алгебраических пар чисел", и остается только поражаться интуиции этого великого математика. Программу Гамильтона ныне продолжает русский физик-теоретик В.В.Кассандров в своей книге "Алгебраическая структура пространства-времени и алгебродинамика", опубликованной на сайте сетевого Института проблем времени (www.chronos.linia.ru).

Тем не менее, переход к рядам чисел от привычных непрерывных континуумов выглядит проблематично. Здесь подспудно присутствует и некая философская парадогма: если геометрические отношения воспринимаются как нечто объективно заданное метрикой окружающего Универсума, то числа трактуются как некий продукт нашего ума, склонного к абстракциям и комбинаторике. (По известному афоризму Л.Кронекера: "Натуральные числа создал Бог, а остальные - дело рук человеческих".) Если для физиков квантовая прерывность обоснована ссылками на результаты экспериментов, то для математики никаких "числовых квантов" не существует - любая значимая величина бесконечно делима. Числовая дискретность редуцируется к непрерывности, бесконечно малое обращается в нуль.

Странная ситуация сложилась: классический математический анализ формировался на основе классической механики, в современной физике таковая уже является делом прошлого, однако мы все еще строим математические модели на базе представлений стандартного математического анализа и стандартного понимания предела.

Ричард Фейнман в своей книге "Характер физических законов" пишет: "Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны." (Richard Feynman, The Character of Physical Law. Русский перевод: Р.Фейнман. Характер физических законов. М.: Мир, 1968, стр. 184).

А вот какое примечательное суждение высказано в известной книге Д.Гильберта и П.Бернайса: "На самом деле мы вовсе не обязаны считать, что математическое пространственно-временное представление о движении является физически осмысленным также и в случаях произвольно малых пространственных и временных интервалов. Более того, у нас имеются все основания предполагать, что, стремясь иметь дело с достаточно простыми понятиями, эта математическая модель экстраполирует факты, взятые из определенной области опыта, а именно из области движений в пределах того порядка величин, который еще доступен нашему наблюдению." (Гильберт Д., Барнайс П., "Основания математики. Логические исчисления и формализация арифметики", М., "Наука", 1979, с. 41, первое издание книги - 1934 г.).

Прошу прощения за столь обширное цитирование, оно понадобилось, чтобы обрисовать предпосылки важной проблемы:

1. Существует принципиальное расхождение между современными физическими представлениями о движении и классическими понятиями анализа.

2. Допустима мысль о "математической модели", подходящей для описания микродвижения в пределах "недоступного наблюдению порядка величин".

Однако - НА САМОМ ДЕЛЕ - речь надо вести не о МОДЕЛИ, и не о ПОСТРОЕНИИ. Речь идет о том, чтобы внутри самой логики классической математики найти основания для дальнейшего развития теории.

Сейчас принята идеология, которую можно назвать модельным конструктивизмом: математика рассматривается как поставщик абстрактных конструкций для теоретического моделирования результатов физических наблюдений. Как выразился Бертран Рассел: "Математическая концепция дает абстрактную логическую схему, под которую можно подогнать подходящими манипуляциями эмпирический материал..." (Б.Рассел "Введение в математическую философию", М.: "Гнозис", 1996.с. 101). Теперь математика - это не язык Логоса, Объективного Духа, а символический язык науки для описания реальности. Сообразно этому, конструируются все более и более абстрактные схемы, математические концепции физиков-теоретиков уходят все дальше и дальше от очевидной логичности, свойственной "математическим началам натуральной философии". Создается впечатление, что абстрактные объекты выступают ныне в роли допотопных слонов и черепах, с помощью которых древние "моделировали" Вселенную...

Но реальное развитие науки идет иначе - я бы назвал этот путь ЛОГОГЕНЕЗОМ. То есть новые сущности "не измышляются", а в естественной логике теории отыскиваются основания, способные развиться в полноценную математическую науку, претендующую на ИСТИННОСТЬ. Если принять этот философский подход, то следует согласиться с Фейнманом - классический анализ НЕ СООТВЕТСТВУЕТ РЕАЛЬНОСТИ, но не потому, что он неверен, а потому, что в его основаниях пока не выявлены логические возможности, позволяющие привести математическую теорию в соответствие с физическими данными.

Однако можно ли перекинуть логический мостик между континуумом и числом? Автор не является профессиональным математиком, и не претендует на то, что он ДОКАЗАЛ необходимость дополнения классического анализа, созданного Ньютоном и Лейбницем, принципами нестандартного анализа, в котором используются гипердействительные актуально бесконечно малые и большие числа. Логическую правомерность нестандартной модели анализа показал в 60-е годы прошлого века Абрахам Робинсон, но до сих пор остается вопросом: "Существуют ли гипердействительные числа в квантово-релятивистской Вселенной?" Иными словами, можем ли мы расширить поле действительных чисел только потому, что придумали новые абстрактные объекты, или надо поискать для этого какие-то предметные основания?

Мы только что рассмотрели квартернионное время-пространство, составляющее дополнительную пару с 4-мерным псевдоевклидовым континуумом. Автор утверждает, что безразмерная единица, связывающая вещественную и мнимую ось, расщепляется на две размерные константы, - однако подлинный смысл такого расщепления остается совершенно непонятным. Является ли это отражением свойств Универсума или это только особенность произвольного формального построения? А если это отражение свойств нашей Вселенной, то как мы должны их понимать: как мгновенное выворачивание всего пространства-времени через каждую из своих точек или как-то более естественно?

Математически произошла странная вещь: обычная числовая ось нами стандартно мыслится как нечто, где на одном конце ноль, а на другом - бесконечность. Где-то "возле" нуля маячит единица. Теперь вдруг единица как-то раздвинулась, освободив место для размерных величин, при этом бесконечность и нуль сомкнулись. Последнее следует пояснить.

Для фиксации движения мы можем использовать только два фундаментальных параметра - единицы времени t[с] и пространства x[м]. При этом очевидно, что их отношение имеет точное количественное выражение в любом случае: если мы соотносим x/t или t/x. Стандартное определение покоя - это 0[м/с], но одновременно и ¥ [с/м], что обычно не учитывается из-за непонятности и ненужности такого количественного выражения. Однако еще Готфрид Лейбниц при создании математического анализа неоднократно размышлял над этим вопросом. Он писал: "Покой может рассматриваться как бесконечно малая скорость или как бесконечно большая медленность" (Г.В.Лейбниц. Сочинения в четырех томах. Т. 1. М.: "Мысль" с. 205. См. также т. 3, с. 199.).

У Лейбница есть еще одно примечательное рассуждение: он отождествляет нулевую скорость движения по окружности с бесконечной скоростью, когда "каждая точка окружности должна всегда находиться в одном и том же месте" (Т. 3, с. 290). То есть логически отождествляются не только 0[м/с] и ¥ [с/м] (соответственно ¥ [м/с] и 0[с/м]), но также 0[с/м] и ¥ [с/м] при циклическом движении. То есть шкала величин, на которой лежат значения скорости вращений оказывается столь же замкнутой, как круговая траектория - ноль и бесконечность смыкаются.

Относительно бесконечно медленной скорости вращения любое единичное вращение - бесконечно быстро. Когда мы отсчитываем скорости, различающиеся по числу оборотов, мы фактически от бесконечности отнимаем действительные числа. Иными словами, уменьшение частоты оборотов следует отсчитывать от бесконечности. Получается, что мы говорим здесь о прибавлении единиц к ¥ ... Точнее, наоборот: -1 предстает перед нами не просто как "нечто влево от нуля", а как единица, которую вычли из бесконечного множества...

Впрочем, философствовать на эту тему можно долго (автор только о Гегеле здесь еще не упоминал, хотя вспомнить о нем было бы более чем уместно). А простейший методологический вывод из этой теоретической ситуации таков: следует признать, что числовые соотношения - это не просто символический язык для описания пространственных отношений, возникающий из-за введения условных мер и мысленных операций над ними, а столь же фундаментальная объективная сущность, как и само пространство - протяженный континуум. Числа существуют не потому, что мы их придумали для упорядочивания данных опыта, полученного с помощью технологии измерения, а потому, что мы их открыли - так же, как открыли в свое время простейшие соотношения между точками и прямыми.

В заключение своей статьи я опишу некоторые математические объекты, в которых воплощается то, вокруг чего накручивается эта проблематика.

Если мы на числовой прямой будем отмечать точки, соответствующие ряду Фибоначчи, где каждое последующее является суммой двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21 ...), то в пределе - при устремлении в область все больших и больших чисел - отношение "двух последних" чисел Фибоначчи, как известно, дает j . Это знаменитое иррациональное число 1,61803... , задающее "золотую пропорцию" - сечение, при котором меньший отрезок относится к большему, как больший к их сумме. Можно заявить, что двигаясь так по числовой прямой мы и получаем в трансфинитной области два актуально бесконечно больших "отрезка", отношение между которыми выражается конечным иррациональным числом j .

И наоборот, можно в сторону убывания длин построить "в наших масштабах" ряд отрезков, соответствующих "золотому сечению":

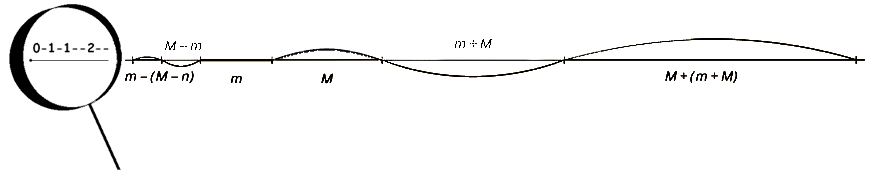
Поскольку отношение большего отрезка к соседнему меньшему = 1,6... - то есть больше единицы, их общая длина в сторону убывания будет иметь на прямой вполне определенную предельную точку окончания. В ее окрестности и будут "скучиваться" уменьшающиеся отрезки, которые - в полном соответствии с бесконечной делимостью непрерывного континуума - никогда не перестанут делиться.

Важно только не упускать из виду, что здесь строится последовательность отрезков, где единичным является любой из них: в сторону увеличения - у правого - длина увеличена в 1,61... раза, в сторону уменьшения - у левого - уменьшена 1/1,61... То есть не исходная величина делится на пропорциональные части - типа 1=1/2+1/4+1/8..., - а от исходной единицы строится пропорциональное отношение в обе стороны. Например, последовательность для рационального деления пополам - в численном выражении: ... 1/16, 1/8, 1/4, 1/2, 1, 2, 4, 8, 16 ... (Или для иррационального "корень из 2" - построение на основе прямоугольного равностороннего треугольника, где исходная гипотенуза становится катетом большего, а исходный единичный катет представляется как гипотенуза меньшего треугольника, и т.д.)

В нашем построении последовательности отрезков, относящихся попарно в "золотой пропорции" в сторону уменьшения их величин, реальная предельная точка никогда и не будет достигнута, однако можно утверждать, что в этой актуально бесконечно малой окрестности возле предельной точки происходит удивительная вещь: вместо непрерывного континуума образуются ЧИСЛА, которые будут идти к предельной точке как уменьшающиеся числа Фибоначчи. А поскольку ряд Фибоначчи начинается 1, 1, 2, 3 ... , то эти числа (и соответствующие им актуально бесконечно малые гипердействительные длины) благополучно придут в точку предела.

Очевидно, здесь предельный переход понимается несколько иначе, нежели в классическом анализе. А, кроме того, меры на пространственной оси вводятся без "точки отсчета" (в полном соответствии с принципом относительности, лежащим в основе теории Альберта Эйнштейна). Но самое главное - мы остаемся все-таки в рамках теоретических представлений, мы не подгоняем математику под результаты эксперимента, а просто расширяем границы того, что считается в математике допустимым.

Могут быть предложены и теоретико-множественные аргументы, показывающие связь континуальности и дискретности. В классической теории множеств два первых уровня в иерархии бесконечностей - это счетная числовая и непрерывно-континуальная. Если посмотреть, как строится множество мощности континуума, то можно заметить, что оно возникает за счет дополнения счетного множества рациональных чисел за счет всех подмножеств этого множества. Множество всех бесконечных подмножеств бесконечного счетного множества образует ареальное множество - по терминологии автора (этому вопросу посвящена статья "Хронометрика. Ареальные множества"), а континуум полупрямой, представляемый как числовая ось, является ареальным множеством, объединяющим все бесконечные варианты нормировок числовой оси. И обратно, - континуум легко преобразуется к числовым дискретностям с помощью исключения из него континуальных подмножеств: например, известные построения вроде "ковра Серпинского" и пр.

Особое место среди подобного рода построений занимает бесконечно ломанная фигура Ван дер Вардена: в равностороннем треугольнике начинают делить стороны на три и надстраивать в середине по треугольнику, сначала получается Звезда Давида, потом "снежинки" со все возрастающим числом отростков. В пределе получается бесконечно ломанная с бесконечной длинной "сторон", с периметром бесконечной длинны. То есть мы конечную площадь ограничиваем бесконечно длинную замкнутую ломанную линию.

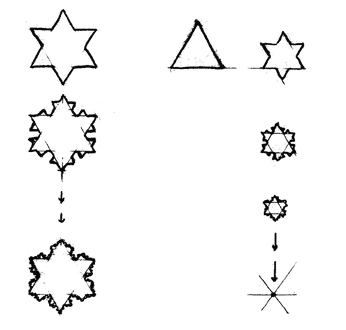Рис. 16.

"В работе "Существуют ли гипердействительный числа в квантово-релятивистской вселенной?" автор предлагает иное построение - обратный вариант, когда в исходном треугольнике единичного периметра стороны делятся на четыре части, а срединные складываются в треугольную "крышу". То есть периметр не меняется, а треугольник от такого складывания уменьшается. Понятно, что в пределе он "сжимается в точку". В отличие от "стягивания в точку" обычных окружностей, здесь у нас фигура Ван дер Вардена "сжимается в точку", укладывая в нее свой единичный периметр. А ведь в наших масштабах фигура Ван дер Вардена имеет вполне действительную площадь, поэтому в процессе стягивания в точку, вписанной в нее окружности, мы можем посмотреть какая площадь получится у микрофигуры: конечно же ее площадь - это актуально бесконечно малая по отношению к той, что ограничивалась фигурой Ван дер Вардена. Если мнимые выражения читателей не пугают, а треугольник с нулевыми углами из геометрии Лобачевского не страшит, можно заняться выведением соответствующих отношений между единицами, нулями и бесконечностями - для данного построения.

Так легко показывается реальное существование "e -окрестности" математической точки, - относительно этой окрестности область действительных масштабов с ее единичными длинами становится тем же, чем для нашей фигуры Ван дер Вардена бесконечная - относительно нас - окружность, к длине которой стремится периметр ломанной Ван дер Вардена "у нас".

Впрочем, мнимую площадь легко увидеть и в обычном круге. В самом деле, что за площадь получается из обычной S=p R², если один из корней этого уравнения берется как -1? Не трудно сказать: это площадь круга, с радиусом, противоположным заданному - то есть та же самая площадь, повернутая на 180 градусов. Но деление полной окружности на градусы может быть двояким - на четное их число и нечетное, причем каждый из вариантов имеет соответствующее геометрическое построение, и приводит к разным выводам - евклидово-геометрическим и псевдоевклидово-алгебраическим.

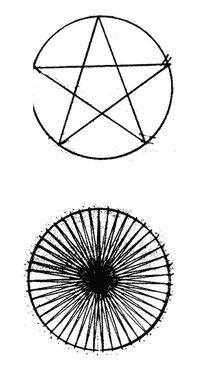Рис. 17.

Вот, например, сакральная фигура - звезда в круге. Площадь круга равна площади этой звезды + площадь оставшихся секторов. Если количество лучей замкнутого контура звезды неограниченно увеличивать, то площадь этой "тонкой звезды" будет сокращаться, а вершины сектров будут неограниченно приближаться к центру круга. В пределе мы получим стандартную площадь круга S=p R² с вещественным R + мнимую площадь звезды с бесконечным концом лучей и маленькой серединкой, в которую концы секторов вещественного круга так и не попадут. Или кто-то решит, все-таки, что можно доказать обратное, нарисовав стандартную аппроксимацию площади круга бесконечносторонним многоугольником?..

...Как не верти, - точка центра круга не принадлежит его площади, а является точкой перехода в мнимую область или, если угодно - на его обратную сторону. Подобную по сути подхода трактовку предлагал выдающийся русский ученый Павел Флоренский в своей работе "О мнимостях в геометрии" еще в 20-е годы прошлого века.

В конце 50-х начале 60-х годов Абрахам Робинсон доказал (и это признано) методами математической логики, что можно на основе представления об актуально бесконечно малых гипердействительных числах построить нестандартную модель анализа, где, конечно же, для актуально бесконечно малых нарушается аксиома Евдокса-Архимеда. Более того: он показал, что аппарат дифференцирования и интегрирования может быть даже проще, чем стандартный. Именно эту актуально бесконечно малую "e -окрестность" по сути дела кладет в основу своей концепции Владимир Елисеев в работе "Введение в методы теории функций пространственного комплексного переменного" (www.maths.ru). Грубо говоря, в актуально бесконечно малой окрестности любой точки умещается целое псевдоевклидово пространство.

Ситуацию можно охарактеризовать так: Николай Лобачевский полагал, что евклидовость - это бесконечно малый передел его Пангеометрии, но оказалось все наоборот - в актуально бесконечно малой окрестности евклидовой точки размещается геометрия Лобачевского. То есть, в чисто евклидовой плоскости нет никаких окружностей - как непрерывных линий, подобных отрезкам прямых, а есть только геометрическое место равноудаленных точек. Зато из точки-центра, как в геометрии Лобачевского, можно протянуть стороны нулевого угла - так, что основанием его будет отрезок. Из этих-то отрезков и состоят бесконечно малые стороны многоугольника с бесконечным четным числом сторон, которыми мы стандартным образом привыкли аппроксимировать окружность.

Автор считает необходимым отметить, что попытку соединить в едином построении точки геометрии Лобачевского и точки геометрии Евклида предпринимал украинский математик А.А.Вотяков. К сожалению, эта попытка привела его не к научным выводам, а к своеобразной натурфилософской мифологии (А.А.Вотяков, Логос и магия, Киев, 1996). С другой стороны похожее направление поисков обозначил московский философ Виталий Ковалев (глава "Парадигма времени", в кн. В.И.Ковалев, Философия пост-истории, Москва, 1992), но его "логарифмические спирали" не выходили за пределы классической модели, а философские выводы имели экзистенциальный характер. Надо сказать, что проблематика, рассматриваемая в настоящей работе, постоянно заводит ищущих теоретиков в философские дебри иррационализма, где можно фантазировать что угодно и рассказывать интересные сказки. Зато на другом полюсе господствует столь же иррациональный, но скучный, позитивизм, когда в Универсуме остается одинокий наблюдатель и его математически систематизированные ощущения. Последний вариант околонаучной философии наиболее распространен, потому что одинокого наблюдателя легко мыслить не вращающимся.

Людям пришлось развивать геометрический и алгебраический аппарат до самой крайней степени абстракции, понадобилось обнаружить предел скорости света (отношение двух отрезков не может превзойти какую-то константу, в то время как в классическом анализе ничего подобного и быть не может), понадобилось увидеть, как в микромире точки "не хотят" двигаться по математически непрерывным траекториям, - и только ТЕПЕРЬ возникла мысль: а может мы должны переделать сами исходные представления? И ведь было уже такое: считали предметы, получили натуральный ряд, стали измерять гипотенузы прямоугольников - нашли иррациональности. Так что А.Робинсон совершенно правильно претендовал на то, чтобы расширить поле действительных чисел за счет актуально бесконечно малых и актуально бесконечно больших (отсюда термин "гипердействительные"). Однако существование их доказать невозможно, мы можем их только УВИДЕТЬ.

Раздвоение псевдоевклидова четерхмерия на сопряженные пространство-время Минковского и кватернионное время-пространство кажется математически несущественным - ведь единица не имеет физической меры и ее можно переворачивать: прямая и обратная единицы тождественны.

Но в физическом смысле, в реальности, оси псевдоевклидвого пространства размерны. И время - это другая сущность, нежели расстояние. Это что-то другое, это ЧТО-ТО как-то связано с движением, которого, как правильно полагали античные математики, в геометрию допускать нельзя. Но мы его допустили - и в результате развития математики получилось представление о псевдоевклидовых пространствах. Мы волей-неволей должны заниматься интерпретацией - переводить математические построения на язык реального мира. Поэтому не надо забывать, что реальный мир - это не пустое пространство геометрий. В математическом пространстве никаких МАТЕРИАЛЬНЫХ точек нет, нет там ни планет, ни электромагнитных волн, ни машин, ни людей... А в реальном Универсуме все это есть. Значит, чем-то отличается реальный мир от этих псевдоевклидовых геометрических и алгебраических пространств. Чем? А тем, что в реальном мире безразмерная единица раздвоена на размерные константы. Образно выражаясь, мы живем "внутри единицы". Ведь если собрать вместе С[м/с] и S[с/м] и нормировать подходящим образом - мы соединим сопряженные псевдоевклидовы пространства, - получим тот математический образ пустого Универсума, в котором нет ничего, кроме непрерывных осей и алгебраических соотношений. Но мы - люди - ЕСТЬ, мы существуем, существуем среди атомов, частиц и полей, а значит нельзя отождествлять Универсум с неким пустым математическим пространством, наоборот, надо признать, что реальный мир - это раздвоение сопряженных псевдоевклидовых пространств, где безразмерная единица раздваивается на размерные константы, которые определяют границы микро и макромасштабов нашей области существования.

ЗАКЛЮЧЕНИЕ

Кватернионное время-пространство не является произвольным формально-математическим построением, о котором автор рассказал, чтобы поговорить на отвлеченные темы. Изменение сигнатуры метрики пространства-времени - (- - -+) вместо (+++-) - использует, например, помянутый выше Дж.В.Нарликар, чтобы доказать в теории конформно-инвариантной гравитации положительный знак константы связи c =8p G/C⁴ (G - гравитационная постоянная). Самым существенным моментом моей работы является попытка объединения числового и пространственного аспектов 4-мерного многообразия. В статье нет математических выкладок, - сейчас важно изменение точки зрения, глядя из которой мы можем собрать потом в новую систему известные уже формальные символы. Прежде чем писать уравнения, надо представить - что мы хотим ими выразить.

Автор написал эту статью не для пропаганды "своих идей", а для тех физиков и математиков, кто ВСЕ ЭТО почти уже знает или ВСЕ ЭТО предчувствует. И совершенно понятно, что предложенная точка зрения и изложенный подход - суть отправные пункты для очень длительного поступательного движения. Те, кому предложенный маршрут не нравится, могут вращаться по привычным абстрактным траекториям сколь угодно долго.

Трудно вообразить кватернионное время-пространство - некий непрерывный континуум, но не геометрических точек, а вращательных моментов. Причудливо выглядят фрактально-броуновские метания точки, которая должна двигаться по непрерывной траектории, "натыкаясь" в каждое мгновение времени на вращательный момент (см. об этом в статье "Существуют ли гипердействительные числа в квантово-релятивистской Вселенной?" в главе "Движение с неопределенной скоростью"). Обращает на себя внимание и такое физически важное следствие: константа S, определяющая минимальный предел t/x, должна, при формальном объединении сопряженных 4-мерных многообразий, каким-то образом переходить через предельный 0-¥ переход и превращаться в C. Но ведь C - это скорость электромагнитных волн, значит, речь идет о каком-то конкретном физическом процессе. А если окажется, что спин - "внутреннее вращение" - может превращаться в электромагнитную энергию? Короче говоря, автор сейчас может только в общих чертах представлять, к каким результатам приведет развитие предлагаемого подхода...

Вводя квант действия h, Макс Планк трагически переживал, что приходится модифицировать формулы со ссылками на эксперимент. Может быть его переживания были небеспочвенны, и квантование можно вывести теоретически - исходя из логических оснований? Я полагаю, что дело обстоит именно так. Мысль Альберта Эйнштейна о том, что реальный мир можно понять чисто математическим путем не кажется мне чрезмерно смелой.

Существуют ли гипердействительные числа

в квантово-релятивистской вселенной?

Автор благодарен оргкомитету международной конференции "Многомерный комплексный анализ" (август 2002, Красноярск) за возможность представить данный материал вне программы конференции в качестве стендового доклада. Особенно хочу поблагодарить глубоко уважаемых мной красноярских математиков А.К.Циха и В.А.Степаненко за проявленный к моей работе интерес, а также участников конференции, высказавших свои замечания и дополнения. Я таже благодарю всех, кто в посланиях по e-mail высказал свое мнение, особенно профессора С.С.Кутателадзе, указавшего на ряд существенных недоработок, но одобрившего направление поиска. Пользуясь случаем, выражаю свою признательность за организационную поддержку Олегу Коледову, помощнику депутата Государственной Думы В.А.Демина (Комитет по высоким технологиям, промышленности и строительству), компьютерщикам Борису Чигишеву и Александру Ульверту, а также сотрудникам школы иностранных языков "О'key" за помощь в редактировании английского текста

ОТ АВТОРА: Гипердействительные числа появляются в нестандартной модели анализа Абрахама Робинсона в результате расширения поля действительных чисел, если допускается нарушение аксиомы Евдокса-Архимеда. Иными словами, гипердействительные числа - это искусственно созданный абстрактный математический объект, а если так, то вопрос, вынесенный в заголовок данной статьи, звучит по крайней мере странно.

В связи с этим, следует пояснить о каком <существовании> я веду речь, и почему столь важны квантово-релятивистские характеристики объективного мира. Поэтому статья начнется с философского вступления, которое читатели не склонные к вопросам философии и методологии могут пропустить. После вступления материал статьи располагается так:

I. Обоснование логически необходимой связи между действительными и гипердействительными числами. Появление гипердействительных чисел в некоторых конкретных случаях. Предельный переход для расходящегося ряда: числа Фибоначчи и <золотая пропорция>, гармонический ряд и число e. Сжатие функции Дирихле.

II. Нестандартное перемещение. Фрактальная траектория, движение с неопределенной скоростью - общие определения. Обратная скорость. Неархимедово сложение и скорость света.

III. Деструкция линейного континуума временного порядка, хронометрика. Понятие ареального множества и приложение его к анализу времени. Множество нормировок.

IV. Бесконечные ряды как ареальные множества. Гипердействительность. Нестандартный подход к псевдоевклидовому континууму. Неархимедово сложение и скорость света. Обратная скорость как инвариант.

V. Некоторые общетеоретические выводы. Многообразие геометрий и единственность эмпирического пространства.

Должен также отметить, что по мере изложения материала у читателей будут возникать мысли о переходе к смежным темам, таким как p-адический анализ, теория множеств, к техническим вопросам, связанным с математическим аппаратом современной физики и пр. Однако мы не будем заниматься этими проблемами - для экономии времени и места. В целом, данная статья является лишь тезисным изложением обширной темы, которую я именую <Нестандартный анализ неклассического движения>. Возможно, заявленная тема кому-то покажется слишком претенциозной, а выбранная форма изложения, напоминающая философское эссе, - вызовет болезненное раздражение. Я признаю, что не смог должным образом обеспечить соответствие текста принятым научным стандартам, и прошу читателей миролюбиво относиться к вынужденным скороговоркам, нечетким определениям и эмоциональной риторике. Выражаю надежду, что излагаемый подход по сути своей направленности позволит исследователям творчески развивать его, применительно к широкому кругу вопросов.

ФИЛОСОФСКОЕ ВСТУПЛЕНИЕ

Мы знаем, что физика как точная наука началась с основополагающего труда Исаака Ньютона <Математические начала натуральной философии>, основополагающего не только для теоретической физики, но и для классического математического анализа. До сих пор в учебниках понятие производной объясняется учащимся на примере физических представлений о механическом перемещении материальной точки и мгновенной скорости. Однако в современной неклассической физике ньютоновские представления о скорости и перемещении существенно модифицированы. В релятивистской физике не всякое отношение dx/dt допустимо - задан верхний предел скорости С, а в квантовой механике траектория движения частицы, где жестко связаны момент времени и координата, заменена квантово-волновыми представлениями с известным соотношением неопределенности Гейзенберга.

Таким образом, оказалась нарушенной определенная гармония между физическими и математическими представлениями, которая существовала в классической науке. Если бы в позапрошлом веке, кто-либо задал вопрос: <Существует ли во Вселенной дифференцируемые функции?>, то определить смысл слова <существование> в такой формулировке вопроса не составило бы труда. Многие полагали, что <Бог говорит математическим языком> - математика раскрывает нам сущность Мироздания, даже если мы этого не понимаем. Интересна в этом смысле идея Гамильтона о том, что подобно тому, как геометрия является теорией пространства, алгебра по сути дела является теорией времени. Столь же примечательны попытки Гаусса и Лобачевского экспериментальным путем определить - является ли неевклидова геометрия адекватной реальности.

Сейчас господствует иная идеология: математика рассматривается как поставщик абстрактных конструкций для теоретического моделирования результатов физических наблюдений. Как выразился Бертран Рассел: <Математическая концепция дает абстрактную логическую схему, под которую можно подогнать подходящими манипуляциями эмпирический материал...> (Б.Рассел <Введение в математическую философию>, М.: <Гнозис>, 1996, с. 101). Теперь математика - это не язык Логоса, Объективного Духа, а символический язык науки для описания реальности. Сообразно этому, создаются все более и более абстрактные схемы, а математические концепции, используемые физиками-теоретиками, уходят все дальше и дальше от очевидной простоты, свойственной <математическим началам натуральной философии>. Создается впечатление, что абстрактные объекты ныне выступают в роли допотопных слонов и черепах, с помощью которых древние <моделировали> Вселенную...

Еще с древнегреческих времен прослеживаются две линии: классическая философия, озабоченная поисками ИСТИНЫ, и софистика, занятая выработкой внутренне логичных схем для доказательства всего, чего угодно. В настоящее время этот последний - идеологический подход - доминирует [см. об этом в книге Н.М. Чуринова "Совершенство и свобода", Изд-во Красноярской аэрокосмической академии, 2001, в главе "Два проекта науки"]. Полагают, что любое внутренне непротиворечивое, абстрактное математическое построение можно попробовать применить в физике. Именно поэтому расхождение неклассических представлений о механическом движении и исходных оснований классического анализа не считается серьезной проблемой. Что за беда! - для моделирования есть математические аппараты иного типа, и для каждого случая найдется более-менее приемлемая интерпретация.

Может ли такое положение дел рассматриваться как единственно возможный вариант познания, а оправдывающая его идеология - как единственно правильная? Мой ответ - отрицательный. Более того, есть основания полагать, что этот вердикт не просто мнение философа-идеалиста, а отражение определенных интенций, свойственных многим. Приведу две цитаты.

Ричард Фейнман в своей книге <Характер физических законов> пишет: <Теория, согласно которой пространство непрерывно, мне кажется неверной, потому что она приводит к бесконечно большим величинам и другим трудностям. Кроме того, она не дает ответа на вопрос о том, чем определяются размеры всех частиц. Я сильно подозреваю, что простые представления геометрии, распространенные на очень маленькие участки пространства, неверны. Говоря это, я, конечно, всего лишь пробиваю брешь в общем здании физики, ничего не говоря о том, как ее заделать.> (Richard Feynman, The Character of Physical Law. Русский перевод: Р.Фейнман. Характер физических законов. М.: Мир, 1968, с. 184).

А вот какое примечательное суждение высказано в известной книге Д.Гильберта и П.Бернайса: <На самом деле мы вовсе не обязаны считать, что математическое пространственно-временное представление о движении является физически осмысленным также и в случаях произвольно малых пространственных и временных интервалов. Более того, у нас имеются все основания предполагать, что, стремясь иметь дело с достаточно простыми понятиями, эта математическая модель экстраполирует факты, взятые из определенной области опыта, а именно из области движений в пределах того порядка величин, который еще доступен нашему наблюдению... Подобно тому, как при неограниченном пространственном дроблении вода перестает быть водой, при неограниченном дроблении движения также возникает нечто такое, что едва ли может быть охарактеризовано как движение> (Гильберт Д., Барнайс П., <Основания математики. Логические исчисления и формализация арифметики>, М., <Наука>, 1979, с. 41, первое издание книги - 1934 г.).

Прошу прощения за столь обширное цитирование, оно понадобилось, чтобы обосновать основные предпосылки важной проблемы:

1. Существует принципиальное расхождение между современными физическими представлениями о движении и классическими понятиями анализа.

2. Возможно построение <математической модели>, которая подойдет для описания микро-движения в пределах <недоступного наблюдению порядка величин>.

Однако на самом деле речь надо вести не о МОДЕЛИ, и не о ПОСТРОЕНИИ. Задача в том, чтобы внутри самой логики классической математики найти основания для дальнейшего развития теории.

Сейчас принята идеология, которую можно назвать модельным конструктивизмом, но реальное развитие науки идет иначе - я бы назвал этот путь ЛОГОГЕНЕЗОМ. То есть новые сущности <не измышляются>, а в естественной логике теории отыскиваются основания - <гены>, способные развиться в полноценную математическую науку, претендующую на ИСТИННОСТЬ. Если принять этот философский подход, то следует согласиться с Фейнманом - классический анализ НЕ СООТВЕТСТВУЕТ РЕАЛЬНОСТИ, но не потому, что он ошибочен, а потому, что в его логике пока не выявлены логические возможности, позволяющие привести математическую теорию в соответствие с физическими представлениями. Вводя квант действия h, Макс Планк трагически переживал, что приходится модифицировать формулы со ссылками на эксперимент. Может быть, его переживания были небеспочвенны, а квантование вместе с релятивистскими закономерностями можно вывести теоретически - исходя из логических оснований, пока еще скрытых и не выявленных? Я полагаю, что дело обстоит именно так.

Однако было бы слишком опрометчиво заявлять, что нужную теоретическую модель дает нам, упомянутый в начале статьи, нестандартный анализ, а гипердействительные числа - как раз тот абстрактный объект, который позволит моделировать квантово-механическую дискретность. Рассуждая так, мы остаемся в рамках модельного конструктивизма. Неархимедов анализ в его современном виде - это искусственная модель, основанная на прямом отрицании аксиомы Евдокса-Архимеда, и нет пока никаких серьезных причин расширять поле действительных чисел. В самом деле: что это за числа такие, сколь угодно большая сумма которых не может превзойти единицу, а обратные им оказываются за знаком бесконечности? Их введение - это произвольное допущение, а модель анализа, сконструированная на их основе, - остается экзотическим построением, не имеющим отношения ни к эмпирической реальности, ни к теоретической физике.

Правда, в последнем случае, мы можем обнаружить некоторые интересные особенности.

В теории относительности Альберта Эйнштейна, как известно, используется релятивистское правило сложения скоростей, когда прибавление единиц не приводит к бесконечному возрастанию суммы - она ограничена верхним пределом скорости света. Однако и в этом случае суть дела не в нарушении аксиомы Евдокса-Архимеда, а в особенностях преобразований Лоренца, действенных для псевдоевклидова континуума пространства-времени. Разумеется, можно допустить, что аналогичное правило сложения может работать и для простых величин, типа длин или временных отрезков, но, опять-таки, совершенно не ясно почему мы должны ограничивать бесконечное пространство неким заданным радиусом, к которому будет стремиться сумма складываемых единичных длин. Закон перспективы существует, но ведь мы понимаем, что уменьшение размеров с расстоянием - это зрительная иллюзия, а не свойство пространственной метрики.

Теперь обратимся к квантовой механике. Известно, что так называемая <ультрафиолетовая катастрофа> была прямым следствием из формул классического математического анализа - для равновесного излучения в области высоких частот получались бесконечные значения энергии. Однако выход был найден не в модификации математических принципов, а в осмыслении экспериментальных данных: гипотеза Макса Планка положила предел бесконечному дроблению энергии - E=hn оказался неделимым. И сейчас классические формулы анализа продолжают использоваться, а все мешающие бесконечности современные физики-теоретики научились, как выразился Ричард Фейнман, - <заметать под ковер>.

Таким образом, теоретическую ситуацию можно охарактеризовать так. С одной стороны, классический анализ оказался недостаточен для физики, хотя его исходные представления выглядят интуитивно очевидными и столь естественными. С другой стороны, нестандартный анализ кажется для физики подходящим: актуально бесконечно малые как бы <квантуют> континуум в микромасштабах, а гипердействительность (выражение Мартина Девиса из его книги <Прикладной нестандартный анализ>) разбивается на <микромир>, мир <действительных масштабов> и мир <космической> бесконечности. Однако неархимедов анализ - это все-таки искусственное построение, эта <неархимедовость> противоречит бесконечной делимости и классическому понятию предела. Таким образом, единственным выходом может быть только логическое соединение нестандартной модели анализа с анализом классическим, обнаружение их необходимой связи, если угодно, - их дополнительности. Появление иррациональных чисел не отменило числа рациональные, точно также введение гипердействительных чисел должно быть не декларативным модельным построением, а естественным выведением их из логики классического анализа. Я собираюсь показать, что такая постановка задачи правомерна.

I. АКТУАЛЬНАЯ БЕСКОНЕЧНОСТЬ В СОБСТВЕННОМ СМЫСЛЕ СЛОВА

<Анализ - это исчисление бесконечно малых, а основное понятие анализа - понятие действительного числа>, - данное утверждение в книге Гильберта и Бернайса дополняется уточнением, - <Понятие бесконечно большого и бесконечно малого теорией действительных чисел в собственном смысле слова из рассмотрения исключаются>. (Ук. изд., гл. 2, п. 4 <Нефинитные методы в анализе>, с. 64-65).

Нестандартный анализ, наоборот, включает в рассмотрение бесконечно малые и бесконечно большие в собственном смысле слова, отсюда и возникает представление о гипердействительных числах. Поэтому, если в микромасштабе при неограниченном дроблении мы в самом деле рассчитываем получить разрыв непрерывности континуума (как ожидал Р.Фейнман) и открыть <нечто такое, что едва ли может быть охарактеризовано как движение> (как предсказывали Д.Гильберт и П.Бернайс), то это должно быть связано с бесконечно малым масштабом - с чем-то вполне актуальным. Однако Георг Кантор в <Учении о множествах> специально оговаривал неуместность таких представлений. Он риторически спрашивал: <Нельзя ли продолжить числа не только в область бесконечно больших, но и в область бесконечно малых?> И эмоционально возражал: такие попытки - <насильственны>, у них <шаткий фундамент>, они, вообще, <беспочвенны> и пр. (Г.Кантор. Учение о множествах. Русское издание - в кн. <Новые идеи в математике>, сб. 6, СПб, 1914, с. 15.)

Кантор сформулировал прямой запрет: <Не существует отличных от нуля линейных числовых величин (числовых величин, представимых в образе ограниченных непрерывных прямолинейных отрезков), которые были бы меньше сколь угодно малой конечной числовой величины, то есть такие величины противоречат понятию линейной числовой величины> (Г.Кантор. Труды по теории множеств, М.: <Наука>, 1985, с. 294). Доказательство этого положения у Кантора основано на аксиоме Евдокса-Архимеда и его убежденности в <противоестественности> любых попыток введения актуально бесконечно малых (по его мнению - такие построения <остаются только на бумаге>).

Но на этой же странице Кантор сопоставляет свою теорию трансфинитов с гипотезой бесконечно больших и бесконечно малых чисел, высказанной в свое время Фонтенелем, и отмечает: <Нельзя сказать, что растущие конечные числа приближаются сколь угодно близко к w, скорее всякое сколь угодно большое число n остается столь же далеким от w, как и наименьше число. Мое наименьшее трансфинитное число w, и, следовательно, все большие порядковые числа ВСЕЦЕЛО расположены ВНЕ бесконечного числового ряда 1, 2, 3, ... Несчастной ошибкой Фонтенеля было то, что он искал трансфинитное ВНУТРИ числового ряда 1, 2, 3, ... n ... , хотя некоторым образом в конце его (между тем как такового не существует). После того как он ввел таким образом наперед неразрешимое противоречие в свои бесконечные числа, судьба его бесплодной теории была решена. Но если критики, соблазненные крушением фонтенелевских бесконечных чисел, думают вынести приговор актуально бесконечным числам вообще, они ОПРОВЕРГНУТЫ фактом моей радикально отличной от фонтенелевской и вполне непротиворечивой теории>. (Ук. изд., с. 294).

Критикуя Фонтенеля за поиски бесконечно больших чисел ВНУТРИ расходящегося числового ряда, Кантор сам помещает актуально бесконечно малые <в конец> сходящегося ряда и успешно доказывает, что их там нет. Но ведь актуально бесконечно малые могут быть помещены ВНЕ числового ряда действительных чисел, и тогда приговор Кантора окажется несостоятельным. Характерно, что в примечаниях к цитируемому сборнику его трудов научный редактор Колмогоров А.Н. пишет: <Возможно, небезынтересно было бы прочесть книгу Фонтенеля с точки зрения нестандартного анализа> (Ук. изд. с. 408).

Однако следует сделать одно существенное уточнение. В уже упомянутой книге Мартина Девиса <Прикладной нестандартный анализ> (Martin Davis, Applied Nonstsndard Analysis, N.Y., 1977) гипердействительные числа трактуются в качестве ИДЕАЛЬНЫХ ЭЛЕМЕНТОВ - типа бесконечно удаленных точек в проективной геометрии, то есть акцентируется искусственность их появления в математике. Правда, сам создатель нестандартного анализа Абрахом Робинсон придерживался на этот счет иного мнения, а если вспомнить известный афоризм Л.Кронекера, мол, натуральные числа придумал Творец, а все остальное - дело человеческих рук, то вопрос об искусственности и естественности оказывается вопросом вкуса и идеологической ориентации.

Более того, история взаимоотношений физики и математики дает нам показательный пример: один из создателей классического анализа Г.Лейбниц утверждал, что дифференциалы dx и dy - это идеальные математические объекты, условные знаки вычислений, подобные мнимой единице i, однако для другого основоположника дифференцирования И.Ньютона эти "флюксии" и "флюэнты" были выражением объективных физических свойств мира. Как известно, последний концептуальный подход и стал движущим мотивом, заставившим математиков признать дифференциалы в качестве полноправных математических объектов - сейчас мы даже не вспоминаем, что некогда этот вопрос был дискуссионным. Ныне можно утверждать, что вопрос о статусе гипердействительных чисел в наше время будет решен также вне математики, а в динамичном процессе использования нестандартного анализа для моделирования неклассического движения. Ведь абстрактное разделение математических объектов на "реальные" и "идеальные" - само по себе искусственно.

В принципе, единственным критерием остается способность данного подхода необходимым образом войти в систему науки. Канторовы трансфиниты открыли перед нами обширную область приложения творческих усилий, дают ли такую же возможность гипердействительные числа?

Давайте посмотрим, на какой идейный базис опирается традиционное представление о бесконечном делении непрерывного континуума.

Вот деление единичного отрезка пополам, обычный сходящийся ряд 1/2 + 1/4 + 1/8 + ..., который в сумме образует единицу. Мы видим как точки деления <сгущаются> у начала отрезка - у точки О, которая остается недостижимой, поскольку любую точку деления от нуля всегда отделяет отрезок значимой длины.

Рис. 1

Операция деления пополам является одновременно операцией удвоения, то есть исходный единичный отрезок - это такой же отрезок, как и любая его часть, и полная картина получается только, если мы продолжим ряд отрезков в сторону их увеличения: ... 1/8, 1/4, 1/2, 1, 2, 4, 8, ...

Рис. 2

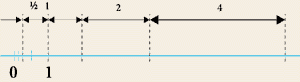
При этом бесконечность (обозначим ее символом [) оказывается также недостижимой, как и О. Правда, О <у нас перед глазами>, а [ <находится> где-то далеко-далеко за краем экрана дисплея.

То, что единица задает нам меру, относительно которой происходит увеличение или уменьшение - понятно. Сдвиг этой меры не меняет отношение соседних величин, но именно возможность этого сдвига определяет бесконечность деления: любой, сколь угодно малый, оставшийся до О, отрезок, может полагаться единичным. Точка О <у нас перед глазами> потому, что она является концом выбранного единичного отрезка, в отличие от <точки бесконечности> - [, которая концом не является просто по определению. Однако насколько правомерно понимание точки О в качестве КОНЦА? Ясно, что это определение связано с выделением ОТРЕЗКА, но ведь его деление - это одно, а построение последовательности отрезков - иное. Откладывая увеличивающиеся отрезки вправо, мы никогда не достигаем <точки> бесконечности (эту точку <поставил> Георг Кантор, когда сделал бесконечность актуальной). Точно также, откладывая влево уменьшающиеся, мы не сможем завершить построение в какой бы то ни было точке. Это вроде бы нас не должно смущать, ведь точка О уже задана на прямой и для данного построения задан предел. Однако построение на прямой - это расположение точек в определенной последовательности, дело существенно меняется, когда ПОСТРОЕНИЕ становится реальным.

Допустим, отрезок 1/2 строится как перпендикуляр к единичному, а 1/4 - как перпендикуляр к 1/2 и т.п.

Рис. 3

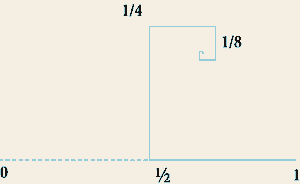
В этой закручивающейся улитке тоже пока нет ничего примечательного, мы можем построить ряды дающие координаты точки, в которую должен попасть конец ломанной. Но вот вопрос: с какой стороны в эту точку попадает эта ломанная - <сверху>, <снизу>, <справа>, <слева>? Ведь данное построение задает, в отличие от традиционного, сразу 4 направления. Вопрос не бессмысленный. Если, скажем, по обычной прямой происходит равномерное движение точки, которая последовательно проходит половину расстояния, затем четверть и т.п., то как мы должны трактовать такое равномерное движение в случае прямоугольной спирали? Если мы предположим, что по этой ломанной движется точка, проходя за одинаковые промежутки времени равные отрезки, то ее попадание в центр <улитки> оказывается таким, что нельзя указать направление вектора ее скорости в этой точке. Может показаться, что здесь нет ничего странного - ведь и в любой точке излома траектории у движущейся точки появляются два взаимоперпендикулярных вектора скорости, но ведь точка предела - не может быть точкой излома! Чтобы сказанное стало более ясным, вообразим, что улитка состоит не только из отрезка траектории от 1 до О, но также и ее продолжения от О до -1:

Рис. 4

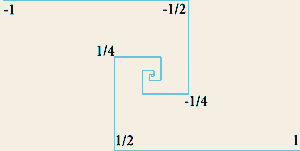
Точка О оказывается таким <местом> изломанной траектории, где направление вектора ее движения становится неопределенным, а ее движение в этой точке, в самом деле, уже трудно <охарактеризовать как движение>. При этом, мы ни на одном из этапов не попадаем в какую-либо область <микромасштабов>, сложности появляются только в точке О. Можем ли мы сказать, что такая особенность присуща точке О и в том случае, когда движение задано по прямой, а не по ломанной? Нет, до тех пор, пока само это движение связывается с движением по отрезку. Но, если мы начинаем вести речь о мгновенной скорости, о скорости в точке - вопросы появляются снова. Фактически, возникает проблема: с какой стороны мы должны стягивать отрезок, устремляемый к О, - как должно выглядеть в данном случае отношение дифференциалов?

И опять может показаться, что проблемы нет: ведь если точка по прямой движется от 1 к -1 через О, то заключая от общего к частному, мы должны придти к выводу, что и в любой точке траектории (и в О) направление ее движения остается таким же. Ведь, если предположить, что в О направление ее движения неопределенно, то, заключая от частного к общему, придется говорить о неопределенности направления ее движения в целом по отрезку, а это противоречит заданному вектору скорости. Однако правомерна ли такая логика в нефинитном рассуждении?

Проблема становится еще острее, когда в положении недифференцируемого О оказываются все точки траектории. Рассмотрим фигуру Ван-дер-Вардена, получаемую из равностороннего треугольника, когда каждая сторона его делится на три части, к которым добавляется еще одна, образуя на каждой из сторон новый треугольник:

Рис. 5

...и так далее - до бесконечности. Как известно, в пределе мы получаем фигуру, в каждой точке которой <имеется излом>, а общая длина этой бесконечно изломанной линии стремится к бесконечной величине 3(4/3)ⁿ при n стремящейся к бесконечности. Когда мы задаем движение точки по единичному отрезку, нас не смущает, что он является частью бесконечной прямой, можем ли мы и в случае фигуры Ван-дер-Вардена говорить о движении точки по такой траектории?

Фактически здесь возникает очень серьезная проблема. Как известно, первое строгое определение линии Камилл Жордан давал со ссылкой на представление траектории движущейся точки. Затем оказалось, что математически непрерывными линиями являются также и "бесконечно ломанные" - типа фигуры Ван-дер-Вардена: тем самым представление о движении механической точки по траектории исключалось, выносилось за скобки математических определений. Но, давайте, вернемся в исходную теоретическую ситуацию и поставим вопрос: "КАК точка может двигаться по ТАКОЙ траектории?"

Н.Винер показал, что броуновское движение частицы, массой которой можно пренебречь, совершается по такой линии, не имеющей касательной. Но введение этой условности, предполагает, что РЕАЛЬНО материальная точка все-таки двигается по дифференцируемой траектории. А почему, собственно? Ведь гораздо естественнее было бы утверждать, что материальная точка НА САМОМ ДЕЛЕ МОЖЕТ двигаться по такой вот "бесконечно изломанной" линии, а, приняв это, затем проследить - какими свойствами должно обладать ТАКОЕ механическое движение. Пусть классический анализ для описания такого движения не подходит - это же самое интересное! Ведь здесь открывается никем неизведанный путь - траектория для движения исследовательской мысли.

Итак, точки, составляющие фигуру Ван-дер-Вардена, - все <у нас перед глазами>, однако парадокс в том, что между любыми двумя (даже сколь угодно близкими) лежит расстояние бесконечно большое. <Выпрямим> ломанную между двумя такими точками - это станет очевидным. А если считать фигуру Ван-дер-Вардена актуально заданной со всеми ее изгибами, то выпрямление ее даст <в пределе> бесконечно большой треугольник. Попробуем в обратную сторону: можно заданный треугольник с единичными сторонами превратить в бесконечно изломанную фигуру, если делить его стороны не на 3 части, а на 4, складывая две центральные как стороны треугольника. В итоге мы получим фигуру:

Рис. 6

*

где звездочка - это бесконечно ломанная конечной длины, <втиснутая> в область нулевого размера. Если существует точка, которая преодолевает обычный отрезок (единичную сторону треугольника) за конечное время, то она как-то должна двигаться и по траектории Ван-дер-Вардена, возникающей на основе так сжатого треугольника. О том, каково направление движения точки, преодолевающей такое конечное расстояние за конечное время, предоставляю судить читателям. Может быть, так двигающаяся точка находится вообще в состоянии покоя, коль скоро она не удаляется от своего места ни на какое расстояние, выражаемое действительным числом?

Впрочем, даже стандартный единичный треугольник НА САМОМ ДЕЛЕ не столь прост, как обычно считается. Есть детский парадокс, когда <доказывается>, что 2 = 1, так как сумма двух сторон треугольника равна третьей. Эти две стороны начинают <ломать> (при этом сумма сторон, составляющих ломанную, не меняется), и утверждают, что <в пределе> получается ломанная совпадающая с основанием треугольника.

Рис. 7

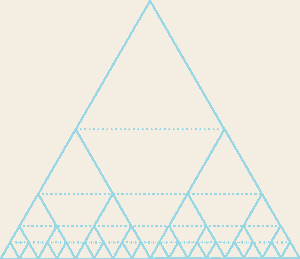
Этот парадокс, как известно, мнимый, но его можно сделать и более серьезным. Предположим, что мы <выпрямили> эту бесконечную ломаную заданной конечной длины, но ведь нам ничто не мешает сказать, что полученные две стороны треугольника сами суть такие же ломанные, которые можно <распрямить>, образовав на сторонах этого треугольника еще два. И так далее.

Рис. 8

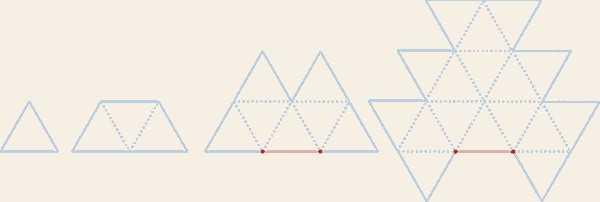
Иными словами, отрезок прямой, образующий единичное основание треугольника будет приравнен не к длине = 2, а к длине = 2ⁿ, где n устремлено к бесконечности. Фактически мы проделываем следующую операцию: утверждаем, что вплотную к единичному основанию треугольника располагается бесконечный ряд микротреугольников, которые можно последовательно <распрямлять>, выкладывая странную линию бесконечной длины.

Если дробя отрезки мы пытались нащупать область, где располагаются актуально бесконечно малые величины, то в последних случаях у нас появились бесконечно большие числа - (4/3)ⁿ и 2ⁿ выражающие бесконечно большое число единичных длин при n устремленном к бесконечности. Обычно считается, что основание степени не играет особой роли, коль скоро степень устремляется ко все большим и большим порядкам (см. например, эссе Дж.Литлвуда <Большие числа> в кн. J.E.Litlewood. A Mathematiclan`s Miscellany, London, 1957. - Правда, английский математик, приравнивая <большие числа>, все-таки берет слово <равенство> в кавычки. - Русское издание: Дж.Литлвуд. Математическая смесь, М.: <Наука>, 1978, с. 108). На самом деле наши оценки определяются тем, что сравнение бесконечных длин немыслимо. Попробуем сделать построение, в котором бесконечная длина оказывается <перед глазами>.

Если бесконечная десятичная дробь (для простоты возьмем дробь периодическую) 1,11111111.... представляет собой сходящийся ряд 1 + 1/10 + 1/100 + 1/1000 + ..., то расходящийся ряд 1 + 10 + 100 + 1000 + ... можно условно записать в виде числа 111111..., где первая цифра означает число единиц, вторая - число десятков и т.п. Можно построить <бесконечное дерево>, граф, длина которого равна этому числу. От единичного отрезка отходит 20 ветвей с длиной в 1/2, сумма которых дает длину 10, от каждой веточки отходит еще по 20 отростков с длинами 1/4 и т.п. Если некий жучок будет ползти все время вверх, то за конечное время он приползет на верхушку, поскольку его путь 1 + (1/2 + 1/4 + 1/8 + ...) = 2. Каково число жучков, сидящих на <кончиках> этой <ведьминой метелки>?

Рис. 9

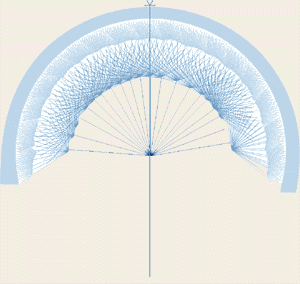
Создается впечатление, что для гипердействительных чисел реально имеются некие <экологические ниши>. Можно ли каким-то образом <прозондировать> эти <заколдованные места>? Что происходит в области нуля, куда бесконечно делящиеся действительные величины попасть не могут? И что может происходить с числами в трансфинитной области, куда не может попасть ни одно, сколь угодно большое действительное число?

Если мы на числовой прямой будем отмечать точки, соответствующие ряду Фибоначчи, где каждое последующее является суммой двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21 ...), то в пределе - при устремлении в область все больших и больших чисел - отношение двух последних чисел Фибоначчии, как известно, дает j -. знаменитое иррациональное число 1,61803... Оно задает <золотую пропорцию> - сечение отрезка, при котором меньшая часть относится к большей, как большая к их общей длине. Можно заявить, что двигаясь вдоль числовой прямой, "шагая" числами Фибоначчи, мы обнаружим в трансфинитной области актуально бесконечно большие <отрезки>, отношение между которыми выражается конечным иррациональным числом j.

И наоборот, можно в действительной области построить ряд отрезков, соответствующих <золотому сечению>:

Рис. 10

Поскольку отношение большего отрезка к соседнему меньшему = 1,61903..., их общая длина в левую сторону прямой будет иметь вполне определенную предельную точку окончания. В ее окрестности и будут <скучиваться> уменьшающиеся отрезки, которые - в полном соответствии с бесконечной делимостью непрерывного континуума - никогда не перестанут делиться. В этом построении предельная точка никогда и не будет достигнута, однако можно утверждать, что в этой бесконечно малой окрестности возле предельной точки происходит удивительная вещь: вместо непрерывного континуума образуются ЧИСЛА, которые будут идти к предельной точке как уменьшающиеся числа Фибоначчи. А поскольку ряд Фибоначчи начинается 1, 1, 2, 3 ... , то эти числа (и соответствующие им актуально бесконечно малые гипердействительные длины) благополучно придут в точку предела.

Здесь можно было бы пока поставить точку, но хочется наметить некоторые пути развития предлагаемого подхода. Например, интересно представить - как будет выглядеть функция Дирихле, если ее единичное значение будет устремлено к нулю и перейдет в гипердействительную область актуально бесконечно малых?

К интересным результатам приводит и рассмотрение под этим углом зрения гармонического ряда целых чисел 1, 2, 3, 4, 5, ... Очевидным образом, в бесконечно большом пределе образуется отношение бесконечно больших (N+1)/N, а в трансфинитной области эти числа переходят в отношение актуально бесконечных отрезков равной длины. Казалось бы, здесь перевернуть операцию невозможно: в действительной области ряд единичных длин не дает нам предельную точку, возле которой в гипердействительной окрестности выстроится гармонический ряд чисел. К счастью, тут обнаруживается свойство иного рода. Хотя мы и <не видим> область, где находятся актуально бесконечно малые длины, образующие гармонический ряд чисел, но мы видим бесконечную прямую на которой отложены равные единичные отрезки и можем, начиная с любого рассмотреть бесконечную полупрямую. На ней соседние отрезки относятся друг к другу как (N+1)/N, где N - бесконечно большое число, выражающее сумму актуально малых длин. То есть образуется геометрическая прогрессия с множителем (1 + 1/N), и если длина первого отрезка нами принята за единицу, то происходит нарастание длин таким образом, что длина <последнего единичного отрезка> на этой бесконечной полупрямой оказывается (1 + 1/N)^N. Не трудно заметить, что эта длина - иррациональное число e.

Попробуем интерпретировать данный результат.

Допустим, из начала координат вылетает бесконечное число точек, скорость первой - единица, а расстояния, проходимые ими за единицу времени, последовательно отличаются друг от друга на актуально бесконечно малые единичные величины. И на каком же отрезке расположатся эти точки через единичный период времени?

Поставив это вопрос, я сделал одно упущение: не сказал, что всем векторам скорости надо задать одно общее направление - вдоль прямой. Но можно ли это единое направление действительно задать?

II. ДВИЖЕНИЕ С НЕОПРЕДЕЛЕННОЙ СКОРОСТЬЮ.

В изложенных только что построениях ДВИЖЕНИЕ - перемещение точки по траектории с некоторой скоростью - играло по большей мере вспомогательную, иллюстративную роль. Теперь мы попробуем осмыслить ДВИЖЕНИЕ по существу.

Механика начинается с понятия равномерной постоянной скорости, но для постоянной скорости устремление соотносимых интервалов расстояния и времени к бесконечно малому теряет смысл - все интервалы подобны. И хотя мы устремляем к нулю интервалы DХ и DТ, всегда подразумевается, что имеются две точки и два момента времени, переход между которыми непрерывен. Математически все конечные отрезки прямой равноправны, чем же мотивировано представление о <бесконечной малости>? Ведь не можем же мы определять <бесконечно малое приращение> относительно каких-либо своих, человеческих масштабов! Тем не менее, это настолько хорошо увязывается с обыденной практикой, что и сомнений не вызывает. Однако можно перевернуть логическую связку, сказав, что именно обыденная практика предопределила математическую концепцию, с помощью которой она моделируется.

Разумеется, можно развести реальное движение и его математическую модель, но поставив под сомнение адекватность последней, надо, по крайней мере, предложить иной способ теоретического моделирования. И при этом, все-таки, придется исходить из тех же самых элементарных предпосылок: любые виды механического движения суть перемещения точки в проcтранстве (она, грубо говоря, в разные моменты времени находится в разных местах), точки нахождения всегда разделены неким расстоянием, а моменты нахождений задают интервалы времени. Самое интересное, что эти же исходные предпосылки позволяют сформировать совершенно иное представление о движении, противоположное традиционному.

Итак, даны две точки пространства Ха и Хв, в которых материальная точка находится в два разных момента времени Та и Тв. Эти два, будем говорить - <нахождения>, позволяют ввести отношение отрезка расстояния и интервала времени, которое нами именуется <скорость>. Если мы остаемся в рамках первого закона Ньютона-Галилея, то движение равномерно и прямолинейно. Значит для заданной постоянной скорости все такие отрезки между <нахождениями> - строго подобны. Тем не менее, мы считаем нужным ввести понятие мгновенной скорости, устремляя интервалы к нулю, где в пределе каким-то странным образом появляются <бесконечно малые>. Здесь неявно присутствуют и отождествляются два умозаключения:

1. Если скорость постоянна на всем интервале - она присуща материальной точке в любой точечный момент времени, в любой точке траектории.

2. Если в любой момент в любой точке пути скорость одна и та же, она присуща материальной точке и в течение всего времени движения по всей траектории.

Очевидно, эти утверждения обосновывают друг друга, образуя логический круг.

Здесь можно было бы вспомнить апорию Зенона <Стрела>. Древнегреческий философ хотел заострить внимание теоретиков на парадоксальности движения-перемещения: если для определения скорости надо обязательно иметь в виду ДВА местоположения и ДВА момента времени, то каким образом мы заключаем о наличии скорости в один - данный - момент, в данном месте? Понятно, что введением мгновенной скорости мы скрыли эту парадоксальность. Однако, если dx и dt <очень малы> они тем не менее остаются <отрезками> и <интервалами>. <Стремиться к точке> - не значит <пребывать в точке>.

Считается, что еще аристотелевская физика преодолела Зеноновский парадокс. Ясно ведь, что философ ошибался, когда утверждал, что в мгновение в точке <движенья нет>. Мы приняли, что, если движение есть ВООБЩЕ (на множестве мгновений и мест), то оно есть и В ЧАСТНОСТИ - в каждое отдельное мгновение. Понятное дело: если есть движение - значит есть скорость, раз уж движение есть вообще, оно есть и в частности, и значит мы обязаны приписать точке скорость в каждом мгновении, в каждом месте. Иного, кажется, просто не может быть.

Сейчас мы рассмотрим модель движения, где эти логические обязательства с нас снимаются. То есть - в каждое мгновение, в каждой точке ДВИЖЕНИЕ ЕСТЬ, а СКОРОСТИ НЕТ.

Пусть скорость - это отношение отрезка (Ха, Хв) и интервала времени (Та ,Тв).

Рис. 11

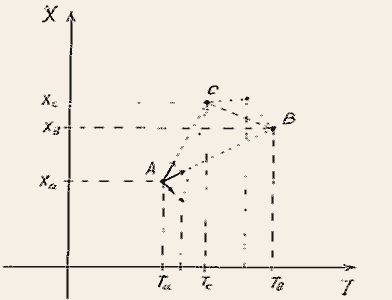
Зафиксировав это отношение, возьмем мгновение времени Тс , находящееся между Та и Тв. В этот момент точка находилась в некоем Хс, и, соответственно, мы получаем уже два новых отрезка, два новых интервала. Говоря о постоянстве скорости, мы неявно предполагаем, что отношения новых отрезков и интервалов дадут нам то же самое значение скоростей. Мы делаем логический выбор: ведь есть два варианта - либо Vав = Vас = Vсв, либо они не равны. Казалось бы, выбор этот предопределен. Действительно, если мы уже задали скорость Vав, она предполагает наличие этой скорости и в точке А и в точке В, а если Vас не равна Vсв, то и значения скоростей в точках А и В получаются иными - в противоречие уже найденному первоначально значению. Но мы введем следующее абсолютное правило: независимо от того, каким было исходное отношение, <новые> скорости (Ха,Хс)/(Та,Тс) и (Хс,Хв)/(Тс,Тв) в общем случае могут быть ЛЮБЫМИ.

Иными словами, мы декларируем, что всякий раз получаются новые значения отношения DХ_ij/DТ_ij, которые в общем случае не обязательно соответствуют предыдущим и не обязательно связаны с ними какой-то закономерностью. Это правило должно быть справедливым для всякого <сколь угодно малого> дробления исходного интервала времени. И естественно, в общем случае, соответствующие точки нахождения в пространстве могут и не лежать на одной прямой, хотя всякий раз они будут задавать конечные отрезки расстояний. В свою очередь, частным случаем ТАК определенного движения будет стандартное равномерное движение по прямой с неизменной скоростью (если <любые>, то, возможно, и <равные> при равенстве соответствующих интервалов времени).

Выбрав точку и мгновение Хс, и Тс, мы не исчерпали точки пространства и мгновения времени. Если продолжить выбор мгновений времени мы будем получать от точки к точке иные значения скоростей и можно предположить, что все они дадут нам значения скорости не равные друг другу. Иными словами, для исходной позиции Ха, и Та (и в конечной позиции Хв и Тв) мы будем получать все новые и новые значения скорости. То есть значение скорости <в точке в данное мгновение> - в общем случае надо считать НЕОПРЕДЕЛЕННЫМ.

Таким образом, для любых двух моментов времени имеются два нахождения точки в пространстве, чем и задается значение скорости ИМЕННО ДЛЯ ЭТИХ ДВУХ МОМЕНТОВ. Но при этом любое нахождение точки, соответствующее моменту времени, находящемуся между двумя первоначально выбранными, позволяет найти уже иные отношения интервалов пути и времени. В целом - для каждого одиночного момента времени имеется вполне определенные координаты нахождения и совершенно неопределенная скорость (определенность появляется, если, и только если, мы выбираем еще один момент-нахождение). Разумеется, все варианты неравномерного движения также оказываются частными случаями движения с неопределенной скоростью.

В только что изложенном построении нет ничего противоестественного, чуждого исходным предпосылкам понимания механического движения-перемещения и принципам его теоретического воспроизведения, а если такой подход логически допустим, то мы не имеем права им пренебрегать, его не рассматривать. А самое-самое главное: этот логический вариант является более ОБЩИМ, ведь <равенство> величин - это частный случай всех возможных их взаимоотношений. Поэтому наша модель априори более общая, поскольку охватывает стандартное представление о скорости.

Не спорю, такая нестандартная модель движения материальной точки в пространстве чрезвычайно экзотична, более того, предлагаемый вариант полностью противоположен классическому: при стандартном подходе постоянная скорость берется за основу и уже из нее конструируются любые частные случаи неравномерных движений - с ускорением, с искривленными траекториями. У нас все наоборот: за основу берется модель, которую можно охарактеризовать как некое абсолютно неравномерное движение, лишь в отдельных случаях совпадающее с равномерным, равноускоренным и пр.

Главная черта данной модели движения: ни в одной точке нет определенной скорости. Эта неопределенность заложена в модель: между сколь угодно близкими моментами времени всегда найдется мгновение, которому соответствуют новые нахождение точки в пространстве с новыми значениями скорости.

Такая последовательность операций определения значений скорости принципиально бесконечна, ни о каком стандартном дифференцировании, ни о какой мгновенной скорости тут речи быть не может. Траектория такого "абсолютно броуновского" движения здесь подобна математической фрактальной кривой, хаотически изгибающейся на любом, сколь угодно малом своем участке. (А так называемая "прямая" оказывается частным случаем фрактального построения.) В каждый момент материальная точка находится в определенном месте, все нахождения лежат на определенной (фрактальной) траектории. Хаотически разбросанные нахождения - суть точки, из которых <собирается> такая по-своему все-таки непрерывная траектория. Пусть - в частном случае - это может быть прямая с постоянным значением всех возможных (<любых>) скоростей, но тогда - это прямая принципиально иного типа: для нее операция дифференцирования, приводящая к мгновенной скорости теряет смысл просто потому, что траектория движения и время движения изначально заданы поточечно - совершенно разрывно, прерывно, дискретно. Такое движение абсолютно дробно, но оно дробится на бесконечное множество отрезков DХ и интервалов DТ не потому, что непрерывный отрезок прямой делим до бесконечности, а потому, что точки деления сами его и образуют.

Так становится очевидной и причина альтернативности нашего построения: традиционное понимание основано на понятии отрезка (который и задает точки его ограничивающие), а наше, нетрадиционное понимание, наоборот, основывается на точках и моментах нахождений, любая пара которых задает отрезки-интервалы, обнаруживаемые между ними. Общим для обоих альтернативных вариантов остается то, что последовательность прохождения точек (нахождений в пространстве) сообразна последовательности мгновений времени, которые им соответствуют.

Замечу, что в предложенной модели движения материальной точки элементарное понятие скорости не исчезает - скорость номинально определима для любых интервалов Х и Т, однако невозможно приписать это значение скорости отдельным точкам-моментам, образующим эти интервалы. Таким образом, понятие скорости необходимо для нашей модели, но становится лишь элементом описания процесса, перестает быть его прямым отображением.

Я отдаю себе отчет, насколько необычной кажется предложенная модель движения, но хочу еще раз подчеркнуть: она сконструирована из тех же основополагающих представлений, что и традиционная (точки нахождения в пространстве, моменты времени и пр.). Она является логически альтернативой последней, и как таковая теоретически с ней равноправна. Пока мы не касаемся ее физического смысла, ее эмпирической адекватности, не ведем разговора об уравнениях движения, о квантованности-дискретности или о соотношениях неопределенности. Подобно тому, как классическая динамика интерпретирует различные варианты движения, а стандартный математический анализ позволяет их описать, введенное только что движение с неопределенной скоростью также потребует потом введения неких динамических характеристик. Пусть точки-нахождения хаотически, поточечно разбросаны по пространству - будто рассыпавшиеся бусы, но все-таки должна быть ниточка, которая их свяжет!

Важным является не то, какая причина делает движение "абсолютно броуновским" - будь то воздействие физического вакуума или спонтанные колебания пространства-времени, - важно то, что этот тип механического движения логически не менее обоснован, нежели классическое движение материальной точки в плоском евклидовом пространстве. Более того, домысливание физических причин - это так или иначе "измышление сущностей", аналогичное "теплородной материи" или "светоносному эфиру", мы придумываем физические причины, когда еще не ясна ЛОГИКА. В данном случае ЛОГИКА движения с неопределенной скоростью в точном смысле слова - очевидна.

Как читатель уже почувствовал, главное затруднение на предлагаемом пути - это идеология классического математического анализа. Получается, что его мощный, хорошо разработанный аппарат для наших целей не годится. Позвольте мне процитировать слова Абрахама Робинсона: <Мы собираемся показать, что в настоящих рамках можно развить исчисление бесконечно малых и бесконечно больших величин. Это дает нам возможность заново сформулировать многие известные результаты теории функций на языке бесконечно малых так, как это было предсказано в неопределенной форме еще Лейбницем>. (<Введение в теорию моделей и мета-математику алгебры>, М.: <Наука>, 1967, с. 325.) И еще: <Нестандартное дифференциальное исчисление может конкурировать в простоте с самым ортодоксальным подходом>. (Там же, с. 340.) Об интегрировании: <Наше ограничение разбиениями на интервалы одинаковой длины слишком искусственно. Мы построим аппарат, который позволит нам рассмотреть более общие разбиения>. (Там же, с. 341).

Наличие нестандартной модели анализа в современной математике свидетельствует, что никаких принципиальных, логических запретов на избранном нами пути не существует. Пусть новые представления о движении кажутся, если не абсурдными и безумными, то надуманными и бесполезными. Они, просто-напросто, необычны и непривычны, но точно также НЕПРОТИВОРЕЧИВЫ.

В 1963 году Лео Мозер показал, что если луч света падает под углом на две сложенные вместе стеклянные пластинки, то в зависимости от числа отражений, которые он испытывает, получается разное число возможных путей. При больших значениях числа отражений числа возможных путей образуют ряд Фибоначчи. (Пример Мартина Гарднера из Scientific American. Русский перевод: М.Гарднер. Математические новеллы. М.:<Мир>, 1974, с. 398.) Предлагаемый нестандартный подход, очевидно, может оказаться продуктивным для интерпретации квантово-механических явлений, однако данная модель движения не согласуется с выводами теории относительности, где варианты отношений dx/dt ограниченны верхней границей C - скоростью света. В то же время, релятивистский закон сложения скоростей, как уже отмечалось, нарушает аксиому Евдокса-Архимеда. И хотя сам этот закон является следствием преобразований Лоренца для 4-х мерного псевдоевклидового простраства-времени, нестандартный подход позволяет взглянуть на суть дело несколько по иному.

Ничто не мешает нам перевернуть логику следования и сказать, что неархимедово сложение величин является первопричиной, а псевдоевклидово пространство - моделью, которая отражает это более фундаментальное отношение. Иными словами, для любой величины, изменяющейся по линейному закону от нуля до бесконечности, мы можем ввести мнимую дополнительную координатную ось и коэффициент перевода этой величины в ее мнимую меру. Тем самым мы зададим закон преобразований, по которому линейное прибавление единичных величин будет осуществляться по неархимедовому закону сложения. Возникает вопрос: если скорость - это отношение расстояния и периода времени, то каким образом мы должны определять скорость изменения абстрактной величины по отношению к самой себе? А главное: коэффициент C - это эмпирическая константа, и было бы слишком самонадеянно искать математические основания для ее введения.

Тем не менее, мы попытаемся рассмотреть этот вопрос подробнее. Но прежде чем вести разговор о пространстве-времени, следует осмыслить важнейшую составляющую этого 4-х мерного континуума. Предметом нашего исследования будет ВРЕМЯ.

III. ХРОНОМЕТРИКА. АРЕАЛЬНЫЕ МНОЖЕСТВА.

К сожалению, метрические свойства времени, в отличие от его направленности и текучести, привлекают внимание теоретиков в последнюю очередь. Есть важная причина: именно здесь время как таковое легко отождествляется с пространством - с одномерным линейным континуумом, поэтому ничего специфически временного здесь как бы не обнаруживается.

Да, и можно ли вообще вести речь о "метрических свойствах" времени, если его теоретической репрезентацией является прямая? Ведь метрические свойства - это атрибуты многомерного пространства, где появляются линейно независимые векторы. Если же мы рассматриваем "чистое время", - числовую ось, где откладываются отрезки, конгруэнтность которых обосновывается ссылками на периодичность каких-либо естественных процессов, то ничего кроме линейных операций с временными отрезками проделать нельзя. В связи с этим, надо внести уточнение: метрическими я называю здесь такие свойства "чистого времени", которые не могут быть сведены к особенностям одномерного линейного континуума вещественных чисел. Иными словами, мы заранее предположим, что время является более сложным объектом, нежели ординарная прямая числовая ось.

Хочу напомнить, что еще в XIX веке Уильям Гамильтон сформулировал перспективную задачу: если есть геометрия как наука о пустом пространстве, то - просто по аналогии - можно представить некую науку о "чистом времени". Более того, он предположил, что алгебра - это и есть такая наука, просто мы не улавливаем в ней скрытую временную специфику, не понимаем - как в алгебраических уравнениях воплощаются внутренние свойства ВРЕМЕНИ. И далеко не случаен тот факт, что открытие некоммутативной алгебры Гамильтоном произошло в результате его попыток смоделировать время в "Теории алгебраических пар чисел".

В 1959 году (J.L.Syng, "The New Scientist" 19th February, 1959, p. 410.) Синг предложил создать особую науку о чистом времени под названием "хронометрия" - по аналогии с геометрией. Но в русском языке такой термин однозначно ассоциируется с процедурой измерения времени, поэтому я ввожу здесь другое название "хронометрика", в этом наименовании зафиксировано наличие особых - метрических - свойств.

Известны попытки дать логическое обоснование тому, что временная ось является именно линейным континуумом подобным континууму вещественных чисел. Наиболее детально это сделано Бертраном Расселом. Мне представляется существенным замечание высказанное по этому поводу английским космологом Дж.Уитроу в его великолепной книге <Естественная философия времени> (G.J.Whitrow, London and Edinburgh, 1961, русское издание - М.: <Прогресс>, 1964), он совершенно правильно указывает, что в математике существуют упорядоченные множества и более сложного типа.

Уитроу замечает: <Рассел ОПРЕДЕЛЯЕТ мгновение как такое множество событий, любые два события из которого одновременны, и не существует другого события (то есть события, не содержащегося в множестве), одновременного со всеми этими событиями. Предполагается, что мгновения, определенные таким образом, СУЩЕСТВУЮТ> (Дж.Уитроу, Естественная философия времени, с. 207.)

Мы оказываемся в замкнутом круге: собираясь предпринять логическое исследование времени мы неизбежно начинаем опираться на <эмпирические данные опыта>, и в результате получается наукообразный перевод наших субъективных установок на язык логических терминов.

Тем не менее, отметим важность поставленного вопроса: является ли континуум времени тождественным континууму вещественных чисел или он имеет некую иную, более сложную, структуру? Ответ на этот вопрос может составить основу науки под названием <ХРОНОМЕТРИКА>.

Таким образом, нас в первую очередь будут интересовать метрические отношения, характерные для временного континуума. И здесь открывается еще один принципиальный аспект - конгруэнтность. Если для определения конгруэнтности пространственных отрезков более-менее подходят ссылки на сравнимость отрезков при их параллельном переносе, то для сравнимости временных периодов даже эта возможность исчезает. Вольно или невольно мы приписываем времени свойства, которые считаются присущими пространственным отношениям.

Проблеме конгруэнтности пространственных и временных отрезков посвящена книга Адольфа Грюнбаума <Философские проблемы пространства и времени> (Adolf Grunbaum, Philosophical Problem of Space and Time. N.Y., 1963, русское издание - М.: <Прогресс>, 1969.) Суть дилеммы: существует ли основание для приписывания пространству (и времени) внутренней метрики, согласно которому совпадение только устанавливает равенство отдельных интервалов, обусловленное внутренне присущим им количеством? Грюнбаум защищает в своей книге позицию Римана-Пуанкаре, согласно которой определение конгруэнтности конвенционально. То есть у пространства и времени нет внутренне присущей им метрики. Также как и у линейного континуума вещественных чисел, где за единицу измерения может быть принято любое число: начав с 1, мы прибавляем к ней еще одну и получаем 2, одновременно получая и 1/2, при условии, что полученная двойка будет считаться единичной мерой.

Однако, как и следовало ожидать, в анализе проблемы конгруэнтности у Грюнбаума чаще всего рассматриваются пространственные отношения, которые потом переносятся на временной порядок. А специфика временного порядка опять-таки появляется только в анализе анизотропии (направленности) времени и экзотических вариантов замкнутого, циклического временного порядка.

Итак, основной проблемой хронометрики является поиск ответа на вопрос: тождественны ли континуум временного порядка и континуум вещественных чисел? Возможных ответов выявляется три: оба континуума тождественны, а если не тождественны, то - либо упорядоченный временной ряд более прост, либо он более сложен. В свою очередь, простота времени может выражаться в том, что он является счетным множеством: тождественен натуральному ряду чисел - имеет атомарную структуру и теряет континуальность, либо тождественен множеству рациональных чисел - все интервалы соизмеримы. В случае его <большей сложности> вариантов снова два: либо какая-либо известная нам <сложность>, либо некая особая специфика - множество какого-то особого типа.

Когда Рассел писал в 1914 году свое исследование, он традиционным образом переносил на временной порядок уже известные из математики методы, а сам временной порядок представлял исходя из данных нашего чувственного опыта. Вообще-то другого пути у нас нет: все наши представления о времени - это данные нашего опыта. Но опираться надо все-таки на представления о ВРЕМЕНИ, а не о его ИЗМЕРЕНИИ. Это очень важная оговорка.

Дело в том, что ИЗМЕРЕНИЕ времени - операция совершенно идентичная построению шкалы для любой измеримой величины. Однако, когда мы строим шкалу температур, мы не утверждаем, что температура - это линейный континуум. Здесь мы отдаем себе отчет, что мы именно ТАК упорядочиваем данные измерения, для того, чтобы было удобно сравнивать разные температуры одного тела в разных ситуациях или разных тел в одной ситуации. А вот со временем - иначе. Мы неявно предполагаем, что наша процедура измерения - откладывание последовательно неких длительностей, определенных по <тик-так> какого-либо периодического процесса - это и есть ВРЕМЯ. То, что время нами измеряется, конечно, отражает особенности этой сущности, однако эта сущность - ВРЕМЯ - ими отнюдь не исчерпывается. Иными словами, в наших представлениях о времени надо поискать такое его свойство, которое с <измеримостью> не связано, то есть отражает какое-то другое специфическое качество времени.

Мы возьмем за основу такое всем понятное свойство времени, как его разделение на ПРОШЛОЕ, НАСТОЯЩЕЕ и БУДУЩЕЕ. Ясно, что к измерению времени это разделение не относится, но вот к анизотропии, к направленности времени оно явно имеет прямое отношение. Новизна моего подхода состоит в том, что я предлагаю именно от этой <явности> и абстрагироваться. То есть для нашего анализа пока совсем не важно, что время <течет из прошлого - через настоящее - в будущее>. Важно то, что единое множество мгновений времени каким-то образом делится на части (подмножества).

Итак, мы начнем с очевидного для всех разделения <единого потока времени> на ПРОШЛОЕ - НАСТОЯЩЕЕ - БУДУЩЕЕ. Понятно, что, если мы хотим хоть немного продвинуться в научном понимании сущности времени, надо раз и навсегда отбросить психологические интерпретации и признать: разделение ПРОШЛОЕ - НАСТОЯЩЕЕ - БУДУЩЕЕ - это объективное свойство ВРЕМЕНИ, присущее ему независимо от того, кто воспринимает его или участвует в этом процессе - человек-мыслитель, собака-сторож или спонтанно распадающаяся элементарная частица.

Если мы абстрагируемся от субъективности, то ВРЕМЯ предстанет перед вами как предмет вполне пригодный для аналитики и мы заметим одну фундаментальную его особенность.

Здесь, в знак уважения к прошлому, я хочу воспроизвести постулат из работы <Учение о Пространстве и Времени> оригинального русского философа Александра Васильевича Сухово-Кобылина, работы написанной еще в конце XIX века. Это Учение - часть так до сих пор и не изданной книги <Всемир>, где философ пытался смоделировать Универсум с помощью биномиального разложения многочлена бесконечной степени. А.В.Сухово-Кобылина у нас знают больше как литератора, а его научные труды мне пришлось изучать в 1990 году в архиве ЦГАЛИ СССР, где хранятся неопубликованные рукописи этого замечательного мыслителя. Сходящиеся ряды у автора <Всемира> предстают символом процессирования Абсолютной Идеи, тут же разворачивается <Философия спирали>, от бесконечности отнимаются конечные числа и пр. Так вот, у Сухово-Кобылина, как некий рефрен, повторяется: <Время, разделено на три времени - настоящее, прошедшее и будущее... Прошедшее прошло, его нет. Будущее еще будет, его нет. ЕСТЬ только настоящее>.

В логическом смысле представляет интерес деструкция, рассечение этого <потока мгновений> на три части (три подмножества). Причем, только одно подмножество ЕСТЬ, а двух других подмножеств, оказывается, НЕТ. Будущего-прошлого НЕТ потому, что разделяющая их связка - настоящее - снабжено <предикатом> ЕСТЬ. Так появляются абстрактные объекты, к которым можно попробовать применить традиционные для математики методы.

Итак. Будем считать ВРЕМЯ - множеством мгновений. Или иначе:

1. Есть некое множество, которое мы именуем <время>.

2. Состоит это множество из бесконечного числа индивидных элементов, которые мы именуем <мгновения>.

3. Элементам ЭТОГО множества будет приписано оригинальное качество: если один элемент этого множетсва ЕСТЬ, то остальных элементов этого множества НЕТ.

Чтобы не путаться в чувственных ассоциациях, связанных со словами ЕСТЬ и НЕТ, определим это оригинальное свойство поточнее, а определение дадим пошире. Скажем так. Все элементы данного множества обладают такой особенностью: если один (или несколько) элементов являются РЕАЛЬНЫМИ, то все другие элементы множества являются НЕРЕАЛЬНЫМИ. А множества такого типа будем именовать - АРЕАЛЬНЫЕ МНОЖЕСТВА. Термин <ареальность> воплощает два смысла: это соединение отрицательной приставки <а> со словом <реальность>, и отсылка к биологическому термину <ареал> (место обитания определенного вида существ). Отношение АРЕАЛЬНОСТИ предлагаю обозначать символом

Что мы получили в результате такого определения?

Во-первых, констатируем, что ВРЕМЯ, как таковое, подходит под это определение - если мгновение настоящего считать одним единственно реальным, то все другие мгновения в самом точном смысле, - нереальны: прошлые мгновения уже были реальными, будущим эта роль еще предстоит. Во-вторых, задав ОБЩЕЕ определение, мы подразумеваем, что помимо времени есть и другие прообразы, которые временем совсем не являются. Если мы определили некое небывалое множество, то правомерность определения может быть подтверждена только в том случае, если помимо ВРЕМЕНИ, удастся найти другие денотаты для этой номинации.

Но прежде чем заниматься этими поисками, надо сделать одно важное замечание. (На необходимость этого уточнения автору указал профессор С.С.Кутателадзе.) Введенное только что определение ареального множества явным образом создает некий специфический объект, который отличается от того множества, понятие которого сформировалось в классической теории множеств. Ведь объединение неких элементов в единое целое - множество - подразумевает завершенный акт, отсюда представление об актуальной бесконечности. В нашем же случае сделано существенное уточнение: -множество также является актуально данной совокупностью элементов, однако элементы его являются таковыми благодаря тому, что некие другие элементы не являются элементами данного множества. Иными словами, для данного -множества существенной становится наличие ВОЗМОЖНОСТИ того, что его элементами МОГУТ стать и некие другие элементы (при условии, что другие элементы его исключаются из его состава).

Я не думаю, что такое определение идет в разрез с логикой, по которой формировалось понятие множества. Напротив, представляется, что мы здесь находим точку зрения, откуда традиционные представления о множестве могут быть рассмотрены более детально. А главным критерием, которым я руководствуюсь здесь: конструктивность подхода - построение модели, которая позволяет продвинуться в теоретическом осмыслении реальности.

Итак, какие же примеры ареальности можно еще найти? Мы сразу же вынесем за скобки различные эмпирические случаи, которые могут рассматриваться в качестве ареальных отношений. (Это, например, случаи из биологии популяций - доминирование определенного фенотипа в данных условиях, обусловленное наличием других возможностей, заложенных в генотипе этого вида.) Мы сосредоточим свое внимание на математических объектах - как наиболее абстрактных и пригодных для точного анализа.

Так, например, ареальность хорошо улавливается в процессе введения меры на оси действительных чисел. В самоме деле, для заданной оси естественным образом предполагается, что возможна перенормировка: взяв 2 за новую единицу, мы старую единицу превращаем в 1/2 и т.п. Иными словами, вся совокупность возможных мер-нормировок является типичным -множеством: если взята - стала реальна - одна из мер, все другие остаются нереализованными - так сказать <пребывают в нереальности>. При всей непривычности таких оценок, использование определения <ареальное множество> здесь оказывается правомерным.

Но самое примечательное, что простейшее ареальное отношение - это ни что иное, как логический закон противоречия: либо - А, либо не-А, третьего не дано. То есть, если А - реально, то не-А - нереально. Оно ведь не исчезает это не-А, без него ведь само это А просто немыслимо, но мы, как само собой разумеющееся, полагаем: если А существует, то не-А - именно что не существует! То есть, оно существует - мыслимо - но существует как-то - <нереально>. Короче говоря, А и не-А вместе образуют ареальное множество из двух элементов.

Аристотель, а за ним и все логики, постоянно подчеркивали, формулируя закон противоречия: не может быть и А и не-А в одном и том же отношении, в одно и то же ВРЕМЯ. Сейчас важно переставить акценты: мы формулируем ЛОГИЧЕСКОЕ ОТНОШЕНИЕ, с помощью которого моделируем время, а не эмпирическое время используем для подкрепления логической очевидности.

Введя принцип АРЕАЛЬНОСТИ, мы неожиданно обнаруживаем в самом эмпирическом времени особое свойство.

Попробуем отождествить ВРЕМЯ, как -множество, с только что введенной ареальностью множества нормировок линейного континуума действительных чисел. Если временной континуум отождествить с таким же ареальным множеством нормировок числовой оси, то надо сделать странное заключение: временной порядок осуществляется так, что реализация одной из нормировок происходит только в том случае, если реализовалось - стала мгновением - лишь ОДНА ее точка. Реализация конкретной нормировки может происходить во времени только через реализацию одной ее точки - иначе реальным должно становиться все множество точек, соответствующих данной нормировке. Иными словами, в данной системе отсчета любой РЕАЛЬНО ПРОТЕКШИЙ отрезок времени образован точками, каждая из которых является точкой только одной определенной уникальной нормировки из бесконечного множества таковых. Если <стрела времени> линейна, то только потому, что в нереальность выводится с каждым мгновением бесконечное множество других мгновений, образующих вместе с данным ординарный линейный континуум вещественных чисел.

Напомню, мы рассматриваем здесь свойства "чистого времени" - множество мгновений, которые не отождествляются тут с какими-либо событиями. И вот обнаруживается, что любое мгновение - это не просто точка на оси, а определенная заданная нормировка, а его реальность - это реализация множества точек, которые относительно данной уходят в "прошлое" и "будущее". Но особенность в том, что все эти точки уже стали "реальными" и никогда в будущем ни одна из них уже не станет мгновением и не была таковым ранее.

Это уже следующий шаг в понимании времени, понятие ареальности приводит, как видим, к необходимости дальнейшего анализа, но здесь мы ограничимся сказанным. На данном этапе построения ХРОНОМЕТРИКИ элементарного качественного описания, полагаю, достаточно.

До сих пор в определении -множества я старался держаться в рамках общепринятых понятий. Все вышеизложенные построения осуществлялись на основе обычных, хорошо известных представлений, - что может быть обыденнее разделения времени на ПРОШЛОЕ-НАСТОЯЩЕЕ-БУДУЩЕЕ! Полагаю, критически настроенный читатель мог счесть изложенное неким бесполезным мудрствованием, но, не думаю, что понятие ареальности могло вызвать у него активный протест. Сейчас я попробую использовать ареальность для уточнения некоторых моментов, касающихся основ математики - здесь позиция автора окажется более уязвимой. Тем не менее, рискну изложить ее.

Чтобы хоть как-то обосновать свой подход, я должен уточнить исходную теоретическую позицию.

Как уже было сказано, нестандартный неархимедов анализ в его современном виде - это искусственная модель, основанная на прямом отрицании аксиомы Евдокса-Архимеда, и нет пока никаких серьезных причин расширять поле действительных чисел. Сейчас принято говорить об "идеальном расширении", но, мне представляется, что этот прием имеет чисто риторический характер, вроде самоназвания подхода Лобачевского - "воображаемая геометрия" (она и оставалась таковой до того момента, когда была понята ее значимость для физики).

С другой стороны, эта "неархимедовость" логически не сочетаться с принципом бесконечной делимости и противоречит классическому понятию предела. Таким образом, единственным выходом может быть только логически естественное соединение нестандартнй модели анализа с анализом классическим, обнаружение их необходимой связи, если угодно, - их дополнительности. Появление иррациональных чисел не отменило числа рациональные, точно также введение гипердействительных чисел должно быть не декларативным модельным построением, а естественным выведением их из логики классического анализа. Я хочу показать, что такая постановка задачи правомерна.

Представление времени в качестве ареального множества - это первый шаг. Он демонстрирует, что МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ как таковое не может прямо и точно воспроизводиться в классическом понятии производной dx/dt, поскольку моменты времени - это не точки на оси T, а элементы некоторого множества, имеющего иную структуру, нежели ординарный линейный континуум. С другой стороны, введение отношения ареальности позволяет взглянуть иначе на такой континуум и обнаружить там некоторые неожиданные свойства.

Мы начнем с простейшего, можно сказать - стандартного утверждения: "Сходящийся ряд чисел имеет конечную сумму, но не имеет последнего члена". Если мы рассмотрим это утверждение как некоторое логическое высказывание, то увидим в нем признаки ареального определения. Множество чисел - членов сходящегося ряда - образуется при условии, что у последовательности последнего члена НЕТ. В самом деле, конечность суммы - это актуализация множества, мы начинаем складывать числа, начиная с первого, наибольшего. Общее число слагаемых - бесконечно. Мы можем говорить об актуальной счетной бесконечности этого множества, но это не отменяет важного признака элементов этого множества: они ЕСТЬ, они выстраиваются в определенном порядке, если мы ПОЛАГАЕМ, что последнего члена у последовательности слагаемых этого ряда - НЕТ. Иными словами, сходящаяся последовательность членов ряда может рассматриваться как ареальное множество, когда обычная счетная бесконечность элементов этого множества дополняется неким НЕРЕАЛЬНЫМ элементом - тем самым "последним членом", которого НЕТ.

Это странное рассуждение, казалось бы, ничего содержательного не прибавляет - служит просто каким-то искусственным домыслом. Но попробуем посмотреть: что будет, если мы примем АРЕАЛЬНОЕ отношение за основу? Первый вывод. Этот исключенный из последовательности "последний член", хотя и не является элементом множества, но тем не менее он ЕСТЬ. То есть, продолжив ареальную логику, мы должны сказать, что ТАКАЯ сходящаяся последовательность членов ряда может предстать перед нами и в ином виде. Действительно, должно быть осмысленным тогда и такое представление о данном множестве, когда "последний член" ЕСТЬ, но в нереальность переходят все остальные - те, которые заведомо больше его. Что же это такое? Это ни что иное, как область гипердействительных чисел в смысле нестандартного анализа.

Таким образом, в рамках логики ареальных отношений, мы определили взаимную дополнительность области действительных чисел (где располагаются члены сходящегося ряда) и область гипердействительных чисел, которые все меньше "наименьшего". Для гипердействительных чисел не действует аксиома Евдокса-Архимеда ПОТОМУ, что она действует для остальных - действительных - элементов этого ареального множества.

Второй вывод. Если ареальное множество - это нечто единое, то мы не можем просто так "пристыковывать" гипердействительные числа к действительным, ведь у нас была задана некая вполне определенная сходящаяся последовательность действительных чисел. Иными словами, в этом ареальном множестве, взятом как целое, должно каким-то образом сохраняться общее для всей этой последовательности ОТНОШЕНИЕ элементов. Совершенно непонятно - каким образом закон сходимости (отношение элементов N_i и N_i+1) должен продолжаться в гипердействительной области!

Сейчас мы попробуем понять КАК ЭТО ПРОИСХОДИТ, рассматривая конкретные случаи последовательностей. Возможно, наше рассмотрение будет выглядеть неким произвольным измышлением, но, если ЛОГИКА АРЕАЛЬНОСТИ принята, то эти выводы будут получаться с необходимостью. Однако прежде чем это сделать, следует кое-что уточнить.

Понятно, что любая сходящаяся последовательность - это искусственно извлеченный фрагмент ряда чисел, связанных порядковым отношением между N_i-1, N_i, N_i+1. То есть, у такого ряда нет не только последнего члена, но и "первого", точнее - мы можем начать с некоторого N и выстроить бесконечный сходящийся ряд с конечной суммой членов, но то же самое отношение, продолженное в сторону увеличения, разумеется, не будет давать нам конечной суммы, а величина каждого очередного члена ряда будет неограниченно возрастать. Иными словами, отношение ареальность для такого ряда - это вытеснение в нереальность обеих областей определения гипердействительных чисел: актуально бесконечно малых и актуально бесконечно больших. Строго говоря, начиная свои рассуждения с фразы "нет последнего члена", я просто использовал обычное "школьное" определение, для иллюстрации ареального подхода. Тем не менее, это было необходимо - ведь вся суть в том, что говоря о сходящемся ряде, мы не можем описать его иначе, нежели словами: "У этой суммы нет последнего слагаемого".

Сейчас нам поможет другое "школьное" определение: ряды, где величина членов ряда последовательно возрастает, а "последнего" члена ряда опять-таки НЕТ. И типичным примером такого ряда будут как раз те самые числа Фибоначчи, которые мы уже рассмотрели ранее. Вспомним, как мы на числовой прямой отмечали точки, соответствующие ряду Фибоначчи, где каждое последующее является суммой двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21 ...), а в пределе - при устремлении в область все больших и больших чисел получили "золотую пропорцию" - знаменитое иррациональное число 1,61803... Иными словами, ряд чисел в трансфинитной области превратился в последовательность актуально бесконечно больших "отрезков", отношение между которыми выражается конечным иррациональным числом j.

И наоборот, ряд отрезков, отложенных на действительной числовой оси в сторону уменьшения соответственно "золотому сечению", скучивается у некоей предельной точки, которая никогда не будет достигнута. И здесь предельный переход в гипердействительную область актуально бесконечно малых превращает непрерывные отрезки в ЧИСЛА, которые будут идти к предельной точке как уменьшающиеся числа Фибоначчи. А поскольку ряд Фибоначчи начинается 1, 1, 2, 3 ... , то эти числа (и соответствующие им актуально бесконечно малые гипердействительные длины) благополучно придут в точку предела.

Я понимаю, что предлагая для серьезного обсуждения такую "нестандартную" интерпертацию связи между действительными и гипердействительными числами, вызываю тем самым вполне естественную отрицательную реакцию. Перечитывая текст, сам постоянно ловил себя на ощущении неудобства, - будто в приличном обществе опозорился, допустив бестактность. И, конечно, могу представить отношение критически настроенных читателей: произвольные манипуляции с математическими понятиями наводят на мысль, что у автора "не все в порядке", а выводы похожи на некое дилетантское фокусничанье - вроде извлечения числа "p" из египетской пирамиды. Что ж, попробуйте воспринять их как любопытный курьез, годный в качестве повода для философских и методологических дискуссий. А, может быть, найдутся читатели, которым предложенный ход рассуждений покажется перспективным?

Важным критерием научности подхода, является его способность давать выводы, позволяющие увидеть ранее не видимые связи между привычными явлениями и понятиями. Полагаю, что решающее слово здесь будет не за математиками, а за физиками.

IV. НЕСТАНДАРТНЫЙ ПОДХОД И РЕЛЯТИВИСТСКИЕ ИНВАРИАНТЫ

Сейчас мы обратимся к физике, я попробую продемонстрировать, как нестандартный подход позволяет связать области, между которыми ранее связь не прослеживалась.

Выше было отмечено, что в теории относительности Альберта Эйнштейна используется релятивистское правило сложения скоростей, когда прибавление единиц не приводит к бесконечному возрастанию суммы - она ограничена верхним пределом скорости света. Это формально напоминает сложение гипердействительных чисел по неархимедову принципу, когда сумма равных слагаемых не может превзойти единицу. Однако отличие физики от математики в том, что физические величины размерны, и ЕДИНИЦА в теории относительности измеряется в единицах скорости [м/с].

В 4-х мерном псевдоевклидовом континууме реального пространства-времени периоды времени и отрезки пространства связаны коэффициентом пропорциональности, который в физике интерпретируется как скорость света умноженная на миную единицу. В классической физике верхний предел скорости был неограничен, теперь роль бесконечности стала исполнять скорость света. Иными словами, все забесконечные значения скорости оказались вытеснены в нереальность, а это наводит на определенные мысли. Что если попытаться применить здесь технику, уже опробованную нами на бесконечных последовательностях?

Особенно интересно было бы посмотреть, что происходит в малом - это область квантовой механики, а превращение непрерывности в ряд чисел указывает на определенное сходство результатов.

Что касается релятивистского сложения скоростей, то нестандартный подход приводит к гипотезе, что точно также, как в сторону увеличения скорости обнаруживается предельное значение С - скорость света, в сторону уменьшения может обнаружиться некий предел. Однако, такая гипотеза о "скорости темноты" выглядит экзотично, а главное не совпадает с теми выводами, которые можно сделать на основе формального подхода и его физической интерпретации. Полученные на этом пути результаты представляются мне интересными и физически осмысленными.

Начнем опять-таки с основополагающего для механики представления - с принципа относительности.

Содержание классического принципа относительности Галилея изложить легко: абсолютного движения нет, то есть две точки могут двигаться только относительно друг друга. Если мы берем одну из них за точку отсчета, то полагаем ее покоящейся, а другая относительно нее оказывается двигающейся. Совершенно так же мы можем эту движущуюся принять за неподвижную точку отсчета и считать двигающейся другую. Представление о движении совершенно естественно и необходимо требует принципа относительности - ведь изменение расстояния между точками со временем происходит МЕЖДУ НИМИ.

[Поскольку принцип относительности имеет и более замысловатые интерпретации, а это вызывает недопонимание (рецензент "Научной сети", например, счел мою трактовку ошибочной), привожу здесь цитату из работы Альберта Эйнштейна "Что такое теория относительности?": "Координатная система, движущаяся равномерно и прямолинейно относительно инерциальной системы, сама является инерциальной. Специальный принцип относительности представляет собой обобщение этого утверждения на все процессы природы: каждый универсальный закон природы, который выполняется по отношению к некоторой системе отсчета С, должен также выполняться в любой другой системе С`, которая движется равномерно и прямолинейно относительно С". (А.Эйнштейн. Собрание научных трудов. т. I, М.: "Наука", 1965 с. 679.)]

Схематически принцип относительности поясняется на примере двух точек:

Рис. 12

принимаем одну за систему отсчета - вторая <движется относительно ее> и наоборот. Представим: в пустом пространстве находятся две точки (математически безразмерные), разделенные некоторым расстоянием. Теперь постараемся представить, что это расстояние изменяется... Но каким таким образом можно здесь зафиксировать <изменение>? Анри Пуанкаре, иллюстрируя этот казус, провел мысленный эксперимент - спросил: что было бы, если бы расстояния между всеми точками мира внезапно увеличились в два раза? И ответил: мир этого не заметил бы. Думаю, все понятно. Для того, чтобы можно было говорить об изменении расстояния между двумя точками, надо представить себе наличие еще одной точки, которая относительно какой-либо из заданных неподвижна.

Рис. 13

Неподвижна - то есть находится все время от нее на одном и том же расстоянии. Тут пока никаких сложностей нет: просто мы декларируем, что нам нужна не точка, а система отсчета с заданным эталоном длины АВ. Но ведь мы начинали с двух точек, потом добавили третью и вроде как можем теперь говорить о движении, однако правомерно задать вопрос: как мы определим, что между точками А и В расстояние постоянно, а между А и С изменяется? Ведь с таким же успехом мы можем принять расстояние ВС за эталон, а прежний эталон считать изменяющимся! В этих рассуждениях нет ничего нелогичного, наоборот, мы ввели третью точку и эталонное расстояние именно потому, что не могли определить изменение расстояния, но точно также мы не можем определить и неизменность его меры. Точнее можем определять его и так и так: то АВ берем за неизменный эталон и говорим, что точка С равномерно удаляется от А и от В, то берем за неизменность расстояние между А и С, тогда прежнее эталонное расстояние АВ должно полагаться изменяющимся.

Рис. 14

Но ведь, если менять местами эталоны длины, получится странная картина. Мысленно представим, что <равномерно движущаяся> С как бы неподвижна и задает нам меру расстояния АС = const, тогда <реально неподвижная> относительно ЭТОЙ меры будет двигаться неравномерно: В приближается к А все время замедляясь. В самом абсурдном варианте (если рассмотрение начать с более раннего момента) она ускоряется от нуля до бесконечности, потом <прилетает> из бесконечности с другой стороны и начинает опять замедляться до нуля - всю оставшуюся в запасе вечность.

Вышеописанный вывод кажется настолько диким, что первое желание - отбросить его за ненадобностью. Проблема в том, что если мы в принципе относительности Галилея-Ньютона открываем для себя взаимоэквивалентность двух точек именно в процессе их мысленной замены, то почему в логически необходимой системе из трех точек вдруг должны отвергнуть взаимозамену совершенно такую же? Логические возможности возникают не для того, чтобы мы их просто отбрасывали, надо все-таки попытаться понять, что обнаруживается в этой странной ситуации. Может быть, все дело в неправильной интерпретации полученных результатов?

Что мы вообще хотим сказать, когда говорим: "Данная материальная точка имеет заданную скорость?"

Стандартный вариант, если внимательнее присмотреться, тоже не очень-то прост. Если у нас задана только одна единственная равномерная постоянная скорость, то ее количественное выражение может быть двояким. Скорость - как отношение отрезка пути к заданной единичной мере времени [м/с], и - совершенно эквивалентное - отношение периода времени, затраченного для прохождения единичного отрезка расстояния [с/м].

Зададимся простым вопросом: почему в обычном понимании движения исключена альтернативная размерность, почему мы не выражаем скорость как количество секунд, затрачиваемых на прохождение единицы расстояния - ведь это отношение логически допустимо, а математически вполне индивидуально для каждой конкретной скорости?

Разве нас удивляет, что на стадионе спортивный результат судьи выражают не в численном значении скорости бегуна, а в количестве времени, затраченном на прохождение дистанции? Это ведь уникальный факт: движение измеряется не метрами за секунду, а временем, которое потребовалось для преодоления заданного расстояния! Тем не менее, в физике данная мера движения с размерностью [с/м] отвергается. Почему?

На этот <детский> вопрос можно дать вполне серьезный ответ. Множество всевозможных скоростей люди упорядочивают по принципу <медленнее-быстрее>, и, сообразно этому, выстраивают по вектору <меньше-больше>: чем быстрее скорость, тем она численно больше, - большее количество метров преодолевается за единицу времени. Взяв же иную меру, мы столкнемся с обратным соотношением: большей быстрости вынуждены будем приписывать меньшее число, - чем быстрее движется материальная точка, тем меньшее количество секунд ей требуется для прохождения единичного расстояния.

Традиционный спектр скоростей начинается с нуля (покой) и количественно возрастает по мере увеличения-убыстрения скорости (в классической механике верхний предел скорости неограничен). <Самая быстрая>, бесконечно большая скорость - это бесконечное количество метров за единицу времени. А вот с альтернативной размерностью [с/м] все выглядит точно наоборот: покой - это бесконечное количество секунд, затрачиваемых на <прохождение> единичного расстояния, так сказать, бесконечно большая медленность. Согласитесь, считать от бесконечности к нулю, по крайней мере, не удобно.

Может показаться, что наши рассуждения - мудрствования на пустом месте. Однако это не так. Достаточно сказать, что Готфрид Лейбниц при создании математического анализа неоднократно размышлял над этим вопросом. Он писал: <Покой может рассматриваться как бесконечно малая скорость или как бесконечно большая медленность> (Г.В.Лейбниц. Сочинения в четырех томах. Т. 1. М.: <Мысль> с. 205. См. также т. 3, с. 199.).

У Лейбница есть еще одно примечательное рассуждение: он отождествляет нулевую скорость движения по окружности с бесконечной скоростью, когда <каждая точка окружности должна всегда находиться в одном и том же месте> (Т. 3, с. 290). То есть логически отождествляются не только О м/с и [ с/м (соответственно [ м/с и О с/м), но также О м/с и [ м/с при циклическом движении. Это последнее отождествление открывает перед нами выход из запутанной ситуации.

Почему не удобно отсчитывать увеличение скорости движения в мере [с/м]? Потому, что приписывая системе отсчета бесконечную медленность и вводя для движущейся точки некую единичную медленность 1[с/м], мы не получим равномерную шкалу величин, где можно арифметически складывать А[с/м] + В[с/м] = (А + В)[с/м]. То есть такое сложение будет противоречить нормальному представлению о том, как оцениваются скорости числом переходов от одной системы отсчета к другой. Но дело коренным образом измениться, если мы воспользуемся, так сказать, преобразованием Лейбница.

В самом деле, когда мы в классическом принципе относительности выявили необходимость введения третьей точки, задающей неизменную меру расстояния, именно эта третья точка и служила прообразом покоя - за любой период времени она <могла пройти> только нулевое расстояние. Если мы, вслед за Лейбницем, отождествим покой и бесконечную скорость циклического движения, то обнаружим удивительную вещь: приписав такой покоящейся точке бесконечную скорость, мы вместе с мерой длины вводим и меру круговой траектории, длина которой определяется мерой длины как радиусом. Тогда оказывается, что в мере медленности [с/м] эта скорость будет уже обладать не бесконечной, а нулевой медленностью: для обегания этого радиуса ей требуется ноль секунд. Теперь мы уже можем вести нормальное сложение медленностей, начинаем с покоящейся системы отсчета, а единичной медленностью будет считаться 1 секунда, требуемая для обегания единичной круговой траектории. Соответственно, обегание этой траектории за 2 секунды дает другую величину скорости движения - более медленную и т.п. При этом относительность в таком круговом движении полностью сохраняется, а <медленности> можно складывать арифметически. Иными словами, теперь для величин медленности строится нормальная ось, где отсчет идет от нуля до бесконечности. Правда, к бесконечной медленности - к полному покою - устремлены не скорости линейного перемещения по прямой, а скорости передвижения по единичной круговой траектории.

А теперь самое интересное. Если для такой величины как медленность также должен действовать неархимедов закон сложения, то до бесконечной медленности нам не добраться. Должна существовать верхняя грань - предел медленности, столь же недостижимый, как скорость света. Мерой этого предела будет, естественно, [с/м] - то есть величина обратная мере скорости. И если эмпирическая предельная скорость C реально существует и измеряется в [м/с], то должна существовать некая эмпирическая константа, измеряемая в [с/м]. Требуемая константа в физике известна - она образуется из соотношения e²/h где e - заряд электрона, а h - постоянная Планка. А отношение скорости света к данной комбинации эмпирических констант дает нам безразмерную величину, именуемую постоянной тонкой структуры. Ее величина округленно равна 137, и до сих пор не прекращаются попытки выразить это число через комбинацию математических констант p и e. Теперь можно утверждать, что эти попытки не лишены оснований.

Подведем итог. Известно, что в псевдоевклидовом 4-мерном пространственно-временном континууме Минковского на осях откладывается единая мера, соответствующая пространственному протяжению х [м], а преобразование меры t [с] осуществляется с помощью коэффициента пропорциональности С [м/с] - скорости света и мнимой единицы i.(В случае движения по прямой он превращается в обычную комплексную плоскость.) Мы показали, что связь между x и t таким же образом может быть использована для построения псевдоевклидового континуума (комплексной плоскости), где на осях будет откладываться единая мера, соответствующая временным периодам t [с], а преобразование меры x [м] будет осуществляться с помощью коэффициента преобразования 1/v [с/м] и мнимой единицы i. В такого рода построении нет ничего "ошибочного", хотя подход достаточно формальный. Однако попробовать было интересно, ведь такого псевдоевклидового континуума применительно к физическим величинам никто не пытался строить.

Создав его, мы сталкиваемся с проблемой интерпретации, поскольку "обратная скорость света" имеет меру [с/м] и не может являться скоростью в обычном понимании этого слова. Эту странную величину на основе традиционного принципа относительности можно интерпретировать как "скорость" вращения по единичной орбите, а коэффициент 1/v для нового типа континуума оказывается константой, которой в физике соответствует комбинация констант e²/h. Вряд ли это является совпадением. Напротив, поскольку в математических построениях, относящихся к многомерному комплексному анализу, все величины безразмерны, а в физике они связаны с конкретными физическими параметрами, отмеченная двойственность псевдоевклидова континуума пространства-времени имеет нетривиальный смысл. По крайней мере, этот формальный подход показывает определенного рода взаимосвязь между понятиями и представлениями теории относительности и квантово-механическими параметрами.

Можно задаться вопросом: значит ли все вышеизложенное, что для абстрактного континуума существуют естественная метрика и реальный закон, упорядочивающий возрастание величины в области действительных чисел, располагающихся между недостижимыми точками О и [? Я полагаю, что - да. Правда, для того чтобы это четко показать надо точно уяснить: что он из себя представляет - этот линейный континуум? Если для пространства суть дела более-менее уяснена, то в отношении времени дело выглядит не столь ясным.

Однако возникает вопрос: почему в физике математическая безразмерная ЕДИНИЦА как бы расщепилась, образовав некоторую область с неархимедовым сложением скоростей (скорость оказывается здесь всего лишь коэффициентом пропорциональности между осями псевдоевклидового континуума)? Поскольку в наших построениях не фигурировали никакие динамические физические величины, то понятно, что на подобные вопросы ответов пока нет. Однако у меня нет сомнения - развивая далее предложенный подход, отмеченные неясности можно будет объяснить математически корректно и физически осмысленно.

Последнее требует пояснения: что означает "физически осмысленно"? Принцип интерпретации, когда определенным математическим структурам находится физический аналог сомнений не вызывает, наоборот - именно эта гармония логического и эмпирического мне представляется главным результатом и целью познания. Но ведь для того, чтобы связь математических выводов и физических представлений стала очевидной, требуется, кроме всего прочего, еще и определенное понимание самой физической реальности. Если мы рассматриваем ее через некий "теоретический прибор", свойства этого прибора в определенной мере так или иначе искажают "картину мира".

Кроме математических аксиом и логики, есть еще некие также мировоззренческие принципы, главным из которых является принцип детерминизма: мы усматриваем связь между явлениями ТАК, как ОН того требует. То понимание детерминизма, которое ныне общепринято, привело, например, к своеобразным мировоззренческим выводам: в научном истеблишменте укрепилось мнение о близком завершении фундаментальной науки. Поскольку это мнение мне представляется одним из проявлений господствующей идеологии, а публикуемая работа направлена против нее, этому вопросу посвящена отдельная статья "Игра в шахматы и квантовая механика", с которой читатели, заинтересовавшиеся "Нестандартным анализом неклассического движения", также могут ознакомиться.

Понятно, что принцип детерминизма, как бы он не понимался, - это прибор из арсенала физики, а не математики. Мы привыкли считать, что математика - это область чистых абстракций, не связанных напрямую с эмпирической реальностью. Однако есть одна область математики, в которой реальность была запечатлена изначально. Это - геометрия.

V. ЭМПИРИЧЕСКОЕ ПРОСТРАНСТВО. СИНКРЕТИЧЕСКАЯ ГЕОМЕТРИЯ.

Считается, что геометрия - это первая наука созданная человеком последовательно и логически. Именно геометрия с ее постулатами, аксиомами и теоремами стала парадигмальным образцом, на который ориентировались все ученые - и физики, и математики, и даже философы. Честно говоря, остается не ясным - может ли мысль, претендующая на звание научной, воплощаться в какой-либо иной форме.

Когда Декарт воображал три взаимоперпендикулярные прямые, пересекающиеся в одной точке, он мыслил перед собой всю объемлющую нас пустоту, в которой двигаются мириады разнообразных и разноразмерных материальных тел. Они прочерчивают в трехмерном пространстве свои траектории, меняя в каждый момент времени свои координаты, создавая абстракцию линии (по определению Камилла Жордана). Это представление о соотношении геометрической (мыслимой) теории и реального (эмпирического) пространства было долгое время бесспорным.

Если Николая Лобачевского еще волновал вопрос: соответствует ли реальное пространство его <воображаемой геометрии>, то продолжатели неевклидовости пришли к однозначному выводу: пространство - это только формальная модель, математическая структура. Так в истории науки выстроилась интересная цепочка идеологем: сначала описывают как бы реальное окружающее пространство, потом понимают, что <пространство> - это нечто более общее (пространство как математическая структура), и получается, что окружающее нас <реальное пространство> - лишь частный случай, описываемый этой моделью.

Давайте вдумаемся в смысл последнего утверждения. Оказывается, что аксиоматическая математическая структура, которая нами именуется <пространство> - это только МОДЕЛЬ, которая может описывать много разных ситуаций, в том числе - и ту реальную пустоту, которая нас окружает. Таким образом, геометрия перестала быть наукой об <эмпирическом пространстве>: описывая пространство мы пользуемся МОДЕЛЬЮ, которая сама по себе ТАКАЯ, а вовсе не потому, что пространство таково. Широкая применимость пространственных моделей выявила явным образом разделение модели и ее прообраза. Иными словами: то НЕЧТО, которое вокруг нас - это отнюдь не то же самое, что мы привыкли выражать в геометрической модели 3-х взаимоперпендикулярных осей. Может быть, реальное <эмпирическое пространство> - то, окружающее нас, пространственноподобное НЕЧТО на самом деле - по сути своей - гораздо сложнее?

Я здесь не о потусторонних <тонких мирах> говорю, и не о физическом вакууме или каком-либо воображаемом эфире. Как писал Оккам: не следует измышлять сущностей сверх необходимости. Нужно просто в старых <сущностях> увидеть то, что по сути возможно и сейчас необходимо. Надо выработать новое фундаментальное логическое понимание, фундаментальное не в меньшей мере, нежели евклидовы точки и прямые. Тысячу лет назад Евклид сформировал представление о том, что аксиоматическая система взаимоотношений таких точек и прямых - это и есть пространство. Сейчас мы должны найти такую же <простую идею> - фиксирующую суть того НЕЧТО, что нас окружает.

Когда Ричард Фейнман заявлял: <Теория, согласно которой пространство непрерывно, мне кажется неверной>, он восставал не против геометрии, а против отождествления геометрических моделей и эмпирического пространства. Стало быть, речь идет о том, чтобы использовать имеющиеся геометрические, математические и метаматематические модели для создания единой теории, более адекватно описывающей окружающее нас НЕЧТО.

В принципе, единственным "недостатком" стандартной геометрии является то, что идея непрерывно делимого континуума в ней доминирует, а привычная для физики квантованность не вписывается в систему. Для модельных конструкций это приемлемо, а для науки о реальном пространстве - нет. Возможно, нестандартная "гипердействительность" позволит исправить положение дел.

О такой "натуральной" геометрии говорили многие, хотелось бы упомянуть здесь выдающегося философа и ученого Павла Александровича Флоренского (расстрелян 8 декабря 1937 г.), написавшего в начале прошлого века такие важные работы как "Идея прерывности как элемент миросозерцания" (см. "Историко-математические исследования", вып. 30, М. 1986), "Некоторые понятия из учения о бесконечности", "Иррациональности в математике и догмат", "Понятие тождества в математической логике" (М. 1914), "О мнимостях в геометрии" (М. 1924). Неархимедовы геометрические построения предлагали Гильберт и Веронезе, а <натуралистические> поправки к геометрии делал еще Анри Пуанкаре. Он указывал на так называемую <скрытую аксиому> - эмпирический факт, который замаскирован среди аксиом Евклида в виде постулата о прорисовке окружности циркулем. То, что поворачиваемая полупрямая рано или поздно совпадает со своим продолжением логически не увязывается с аксиомами о статичных точках и прямых, не следует из них, не подразумевается ими. А сам этот <эмпирический факт> выражается в конкретном иррациональном числе p - метрическом "кванте", который связан с линейным "квантом" е - основанием натурального логарифма. Такие <эмпирические константы> в математике - это знаки, указывающие нам путь к единой синкретической геометрии.

ЗАКЛЮЧЕНИЕ.

Мысль Альберта Эйнштейна о том, что можно понять мир чисто умозрительным путем не кажется мне чересчур смелой.

У 2002 Павел Полуян