4. Задача поиска в обучаемых системах управления

 

Почти все действия объектов с обучаемыми системами управления, выражающиеся в движениях приводов и исполнительных механизмов, преследуют такие цели, при достижении которых указанные движения приостанавливаются: есть цель — есть движение, цель достигнута — нет движений. Продолжительные, сложные работы представляют собой, как правило, череду преследуемых целей и череду соответ­ствующих им действий.

Допустим, робот с обучаемой системой управления обслуживает станок; его работа также представляет собой последовательность отдельных действий. Начнём с поиска тары, в которой перевозят заготовки; для этого система управления должна включить в работу те приводы, которые обеспечивают её поиск. Как только она будет найдена, все эти приводы остановятся, и робот перейдёт к выбору требуемой заготовки внутри тары. Может быть при этом включатся в работу те же приводы, но возможно также, что они будут допол­нены другими, так как роботу придётся приблизиться к таре и даже углубиться в неё. Распознавание заготовки завершится тогда, когда схват правильно сориентируется относительно неё и зависнет над ней. Последующим действием робота будет захват заготовки; при этом сработают соответствующие приводы: раскрытия схвата, прибли­жения его к заготовке и её захвата; выполнив всё это, приводы снова остановятся. Затем робот должен отыскать то станочное при­способление, на которое устанавливается заготовка. Найдя его, он должен отключить приводы поиска и включить приводы установки за­готовки на приспособление. И так далее, и каждый раз любое дей­ствие завершается остановкой приводов.

Потом робот должен найти пневматический кран, осуществить поворот ручки крана и таким образом зажать заготовку; затем должен отыскать кнопку пуска, включить станок в работу и отойти в безопасное место. По окончание обработки деталь нужно снять с при­способления и уложить в тару. Сделав это последнее дело, робот может успокоиться, но едва ли ему дадут отдохнуть; скорее всего, его снова и снова будут заставлять повторять все эти движения. В результате за один цикл робот должен выполнить все перечислен­ные шестнадцать видов действий, не считая таких, как выходы в безопасную зону.

Обратим наше внимание в данном примере на следующие моменты в поведении робота: на начало каждого действия и на его завер­шение (само действие выполняется как навык и сейчас нас не инте­ресует). Механизм начала заключается в переключении внимания обучаемой системы управления; оно рассмотрено выше: каждый раз для перехода на очередную работу система управления подаёт изме­нённое напряжение питания на соответствующую группу рецепторных участков. Признаком, побуждающим такое переключение, является завершение предыдущего действия.

Но в чём физически выражается этот признак? Как система управ­ления догадывается, что действие закончено? Здесь возможны, по крайней мере, два подхода. По первому — признаком завершения пре­дыдущего действия является его последняя ситуация. Вид разыски­ваемой заготовки в сочетании с определённым распределением напря­жения питания по рецепторным участкам может явиться признаком завершения поиска этой заготовки. Образ данной ситуации неповто­рим; он-то и переключает внимание системы управления, заставляя робот переходить к захвату заготовки. Этот первый способ харак­терен для животных.

По второму — признаком завершения любого действия является также последняя ситуация, но в совокупности с нулевыми сигналами управления приводов, участвовавших в этом действии. Такой подход требует того, чтобы в образе были учтены сигналы управления, то есть чтобы они были введены в мозг как возбуждения рецепторов; а для этого внутри мозга должны существовать рецепторы самого мозга. Соединение мотонейронов с этими рецепторами образуют внут­ренние обратные связи, которые можно характеризовать как основу мыслительного процесса, происходящего параллельно действиям ис­полнительных органов или вообще без этих действий /1.38/. Такое свойственно, пожалуй, только человеку.

И по первому подходу, и по второму завершение действий можно расценивать как распознавание образа, но только это — такое рас­познавание, какое происходит в результате действий, а точнее — по их окончанию, но не предшествует им. Не вдаваясь в более глу­бокий разбор явления распознавания, отметим лишь, что у человека оно значительно сложнее, чем у животных; в частности, признаком распознавания может быть не образ текущей ситуации с учётом ин­формации рецепторов мозга, другими словами — не моментальный образ, а образ, растянутый во времени, создаваемый внешней ситуа­цией в купе с мыслительным процессом.

Приблизительно также, как робот, вёл бы себя тот же прокат­ный стан, будь он оснащён обучаемой системой управления, или станок, или какой-то транспортный объект. Во время прокатки также сменяют друг друга пели: приведение стана в состояние захвата сляба, сам захват, многочисленные коррекции режимов прокатки, подготовка выхода полосы и приведение в норму холостых клетей. И также, как у робота, завершение каждой операции знаменуется прекращением движений приводов этой операции, У станка, например сверлильного, выход на позицию сверления должны обеспечивать два, а может быть даже три привода, и после выхода все они должны остановиться. То же самое — и у транспортного средства, и у дру­гих объектов, если они оснащены обучаемыми системами управления.

Итак, любое действие — это движение приводов, а успешное завершение действия — их остановка. И самым характерным действием среди всех прочих, пожалуй, является поиск: поиск предмета, поиск положения, поиск состояния или, в общем случае, поиск ситуации; одним словом — поиск; им и займёмся.

Поиск, как операция, особенно выразителен у животных. При­смотритесь к птицам: к грачам, к синицам, к воробьям, — к домаш­ним животным: к корове, к овце, к курице, к собаке, — или к ди­ким животным, если у вас есть такая возможность, и вы обнару­жите, что они живут в постоянном поиске; другое что-то в их жиз­ни даже трудно выявить, если не относить сюда бездействие и всё то, что связано с переработкой пищи.

В действиях человека поиск занимает тоже значительное место, чуть ли не довлеющее. Сели мы, например, за обеденный стол, и начались поиски один за другим: ищем ложку, хлеб, тарелку, ищем собственный рот, чтобы поднести к нему ложку, ищем соль, чашку, сахар и так далее. Поиск может быть не только зрительным; он может быть слуховым при нахождении, например, любимой песни среди звуковых записей, — осязательным, когда мы поправляем наощупь шапку на голове; вестибулярным, поддерживающим наше вертикаль­ное положение; обонятельным, когда мы по аромату духов определя­ем их хозяйку, и каким угодно другим. И всё это — поиск.

Чтобы упростить себе задачу, выберем в качестве объекта робот со зрением; и пусть он находит заданный предмет, свободно рас­положенный на столе. Будем считать такой поиск классическим, то есть обычным и наиболее характерным. Робот пусть будет тоже обыч­ный: с одной рукой и с глазом на охвате руки. Впрочем, выражение «глаз на схвате руки» звучит несколько необычно; нужна какая-то коррекция терминологий; уделим ей внимание.

По расположению глаз роботы можно разделить на две группы: на скотоподобные (да простят роботы такое сравнение) и на чело­векоподобные. У роботов первой группы глаза совмещены со схватом, что напоминает голову животных, таких как корова, лошадь, собака; эти и почти все другие животные не способны захватить предмет иначе как своей пастью — их ноги и лапы для этого не предназна­чены. Для обеспечения приемлемой резкости видимых захватываемых предметов глаза у большинства животных отодвинуты от схватываю­щей части пасти на определённое расстояние; этим объясняются их вытянутые морды. Уместно, может быть, по подобию то звено скотоподобного робота, которое принято именовать рукою, называть теперь шеей, схват — пастью, а схват с глазами и техническим мозгом — головой.

У человекоподобных (антропоморфных) роботов глаза устанавли­ваются не на охвате и даже не на руке, а где-то в некотором уда­лении от них; поэтому рука такого робота действительно соответ­ствует функционально руке человека, а примитивный охват, будь он усложнён, — кисти руки с пальцами. Человекоподобный робот может иметь не обязательно одну руку, но и две, не только один глаз, но и два, а может быть и больше.

Определимся и со способами поисков, выделив из них два наи­более характерных: это — продольно-поперечный  поиск и поиск свысока. Стратегия первого способа отроится на том, что глаз скользит вдоль некоторой полосы, а при попадании в его поле зре­ния искомого предмета смещается поперёк полосы до совмещения о ним. Для поиска этим способом глаз должен иметь три привода, обеспечивающих перемещения: x вдоль полосы, y поперёк по­лосы и поворот a вокруг своей оптической оси. Все три привода — независимые и действуют одновременно. По завершении удачного поиска глаз должен остановиться напротив искомого предмета, то есть должны остановиться все три его привода.

Стратегия поиска свысока — несколько иная. Отдалённый глаз обозревает некоторое поле. При появлении на этом поле предмета глаз приближается к нему на определённое расстояние и, если предмет — искомый, зависает над ним. Для поиска свысока глаз должен иметь столько приводов, сколько нужно для приближения к предмету, и ещё один — для поворота глаза вокруг своей опти­ческой оси. Приближение к предмету может быть оптическим, если глаз оборудован телескопической оптикой с соответствующим при­водом. Все приводы также независимы друг от друга и должны оста­навливаться при совмещении глаза с искомым предметом.

Продольно-поперечный поиск представляется более простым; он требует меньшего количества приводов и очень простого набора ситуаций в обучаемую выборку; его и рассмотрим более подробно. Он хорош ещё и тем, что удачно сочетается с конструктивными особенностями скотоподобных роботов, которые сами по себе проще человекоподобных.

 

 

4.1. Поперечные перемещения поиска

 

Итак, представим себе робот, у которого голова со схватом (пастью) и одним глазом (что поделаешь? — у животных тоже иногда остаётся один глаз) закреплена на подвижной длинной шее; заста­вим этот робот выполнять продольно-поперечный поиск заданной детали, и начнём с поперечного перемещения. Выберем статичес­кое обучение (есть ещё динамическое), как наиболее простое и займёмся обучаемой выборкой; введём в неё наименьшее число си­туаций, а именно: одну целевую и три дополнительных. За целевую примем такую ситуацию, в которой искомый предмет расположен в центре поля зрения глаза и сориентирован определённым образом. В этой ситуации привод поперечного перемещения должен остано­виться, то есть обучаемая система управления должна выдать на него нулевой сигнал управления:  = 0. Таким же нулевым дол­жен быть сигнал управления и в том случае, когда в поле зрения глаза ничего нет — только однообразный фон; это — первая допол­нительная ситуация, и в ней  = 0. В двух остальных дополнительных ситуациях искомый предмет располагается справа или слева от центра поля зрения по ходу продольного перемещения, и приводы обязаны смещать глаз соответствующим образом до совме­щения центра поля зрения с этим предметом; сигналы управления в этих ситуациях должны иметь разные знаки: если >0, то  < 0.

Принятая наипростейшая обучаемая выборка ситуаций обеспечи­вает в принципе отслеживание предметов, однако при этом могут появиться некоторые трудности: при больших значениях  и  могут возникнуть поперечные автоколебания головы робота, а при уменьшении этих сигналов глаз может не успеть сместиться в по­перечном направлении и проскочит искомый предмет; на практике приходится постоянно сталкиваться с этим. Попытаемся разобрать­ся в этом и предложить общие рекомендации.

Для исследований и расчётов привода поперечного смещения го­ловы робота можно воспользоваться с некоторыми оговорками тео­рией автоматического управления. Оговорки касаются того, что обратная связь осуществляется с помощью зрения, а закон измене­ния сигнала управления, формируемый в процессе обучения авто­матически, носит явно нелинейный характер и может быть выявлен только опытным путём после завершения обучения.

Функциональная схема системы управления робота представлена на рис. 3.11,а. Механизм робота М, он же — манипулятор, вклю­чает силовой шкаф, привод и исполнительную часть. После незна­чительной трансформации, в результате которой множество инфор­мационных каналов между глазом и мозгом заменены одним каналом обратной связи, функциональную схему (рис. 3.11,а) можно пред­ставить в виде привычной структурной схемы с отрицательной об­ратной связью (рис. 3.11,б); на этой схеме: Е — сигнал управле­ния,   формируемый обучаемой системой управления (ОСУ); у — смещение глаза;  расположение цели;  — рассогласование.

 

 

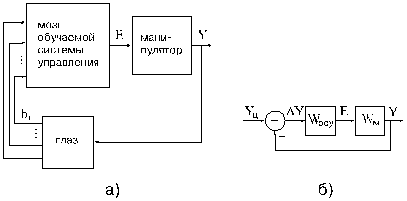
Рис.3.11. Функциональная схема обучаемой системы управления
робота со зрением а) и соответствующая ей структурная схема
автоматической системы с отрицательной обратной связью б)

 

Передаточную функцию обучаемой системы управления можно представить в виде апериодического (инерционного) звена первого порядка:

 

,

 

где  — коэффициент передачи, отражающий линейность зависимости  ; такое можно допустить, если рассматривать отклонения в узком интервале;  — постоянная времени, определяемая в основном быстродействием фоторецепторов глаза.

Манипулятор может быть отображен как интегрирующее колебательное звено:

 

,

 

где  — коэффициент передачи;  — постоянная времени мани­пулятора, определяемая инерционностью механизма;  — коэф­фициент демпфирования или динамического сопротивления.

В передаточной функции манипулятора  все статические ра­бочие характеристики также приняты линейными. Структурная схема (рис. 3.11,6) с принятыми передаточными функциями позволяет про­вести динамический анализ робота; но будем помнить, что такое представление объекта с обучаемой системой управления слишком упрощенное, чтобы полагаться на достоверность его анализа.

Поперечные перемещения при поиске в образном представлении. Углубимся в исследования и начнём с обучаемой системы управле­ния. Все математические выкладки для удобства договоримся пред­ставлять физически; с этой целью воспользуемся оптическим вари­антом обучаемой системы, описанным выше. Напомним, что в этой системе мозг представляет собой диапозитив или, точнее, набор диапозитивов — по два на каждый привод. Видимая сцена, собран­ная оптикой, пропускается через указанные диапозитивы; потоки света, проходящие через них, определяют сигналы управления. Один из парных диапозитивов (плюс-) определяет положительную составляющую , а другой (минус-) - отрицательную ; сигнал управления Е  получается как разность (-). Удобство та­кого физического представления состоит в том, что и сама ситуа­ция как видимая глазом сцена, и состояние мозга как рисунки диа­позитивов представлены в нём в одном виде — виде оптических изображений; поэтому их можно сравнивать принятыми методами те­ории обучаемых систем управления, то есть с помощью коэффициен­тов приведения и степени сходства. Так коэффициент приведения изображения диапозитива с к изображению ситуации  в обычном виде можно представить как

 

,

 

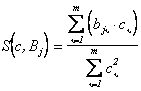где  — i-ый пиксель диапозитива;  — соответствующий ему пиксель изображения j-ой ситуации; m — число пикселей; все эти величины можно истолковать как обычные:  — возбуждение i-го рецептора;  — проводимость соответствующего синапса.

С учетом того что , получим

 

.

 

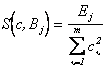В действительности единого образа с не существует; он состоит из двух образов:  и . В электрическом мозгу им соответствуют проводимости синапсов  плюс- и минусмотонейронов, а в оптическом — изображения плюс- и минусдиапозитивов. Также разделяется сигнал управления Е на  и . В результате вместо одного коэффициента приведения  получим два:

 

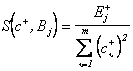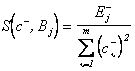;        .         (3.52)

 

Встречные коэффициенты определятся как

 

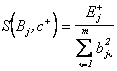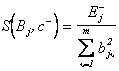;           ,         (3.53)

 

а степени сходства примут вид

 

;

 

.

 

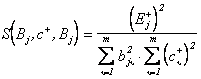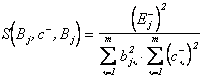И коэффициент приведения, и степени сходства позволяют находить количественные соотношения между образами. Эти соотношения становятся более зримыми, то есть упрощается их физическое пред­ставление, если принимать образы как оптические. Так коэффици­ент  можно истолковать как отношение потоков света, про­ходящих один в виде изображения ситуации через плюс-диапозитив, а второй в виде рассеянного света через два спаренных плюс-диа­позитива. Если изображение ситуации, собранное оптикой, предста­вить также в виде диапозитива, то получится так, что в числителе коэффициента будут стоять спаренные диапозитивы этого изображения и мозга, а в знаменателе — два дубля диапозитива мозга. В таком представлении есть некоторая приблизительность, но в общем оно отражает физическую сторону коэффициента приведения.

Разделим на плюсовые и минусовые составляющие все сигналы управления и определим их соотношения:

· в целевой ситуации: =;

· в ситуации с однообразным фоном: =;

· в ситуации, когда цель — в поле зрения справа при движении вдоль полосы: >;

· в ситуации, когда цель — слева: <.

Из равенства парных сигналов управления в целевой, ситуации и в ситуации с однообразным фоном с учётом (3.52) следует

 

.                 (3.54)

 

Кроме того равенство парных составляющих сигнала управления в ситуации с однообразным фоном даёт

 

.

 

Допуская, что все  в этой ситуации равны между собой, по­лучим

 

,

 

то есть суммарные проводимости (прозрачности) плюс- и минус-диапозитивов мозга одинаковы. Правда, на этом основании нельзя ут­верждать, что также одинаковы сами изображения диапозитивов и что . Последнее справедливо только при абсолютной световой симметрии изображения искомого предмета; а это — мало вероятно.

На основании (3.52) и с учётом (3.54) можно получить следу­ющие соотношения коэффициентов приведения для двух последних дополнительных ситуаций обучаемой выборки:

 

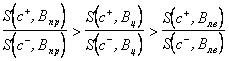.                (3.55)

 

Из условия (3.55) следует вывод, который в приложении к опти­ческой обучаемой системе звучит так: если искомый предмет ярче фона, то плюс-диапозитив после обучения будет более прозрачным с той стороны, на которую падает свет от правой половины поля зрения глаза при движении вдоль полосы, а минус-диапозитив, на­оборот, — более прозрачным с другой стороны. Указанные просвет­ления накладываются на сложные изображения обученных диапози­тивов. Эта асимметрия взятых в отдельности плюс- и минус-диа­позитивов согласуется в то же время с некоторой симметрией их между собой, точнее говоря, — с их зеркальностью: на сколько у плюс-диапозитива одна сторона (правая или левая) прозрачнее дру­гой, на столько у минус-диапозитива всё наоборот; это следует из условия (3.54).

Выражения (3.53) позволяют выявить связь между результирую­щими сигналами управления и коэффициентами приведения; так в ситуации  получим

 

,

 

а в ситуации  абсолютная величина сигнала управления будет равна

 

.

 

Из этого следует:

 

;

 

,

 

и тем самым подтверждаются приведённые выше выводы об асимметрии и симметрии плюс- и минус-диапозитивов мозга.

Переход из состояния  в состояние  и из состояния  в состояние , и далее через  до  или навстречу осущест­вляется плавно; эта плавность характерна для обучаемых систем управления. Следовательно, также плавно в данных переходах будут изменяться сигналы управления. Стоит только появиться предмету на краю поля зрения глаза, как начнёт расти от нуля сигнал управ­ления, заставляющий глаз смещаться в сторону предмета. В некото­ром смещённом положении предмета сигнал достигает своего наиболь­шего значения, а по мере приближения изображения предмета к центру поля зрения начнёт снова уменьшаться и дойдёт до нуля в центре.

Если в общем такой характер изменения сигнала управления нас устраивает, то в некоторых позициях — не совсем. Для того, чтобы глаз быстрее начал движение в сторону предмета при появлении его на краю поля зрения, — а это очень важно, иначе глаз может успеть сместиться в продольном направлении и проскочить мимо предмета, — необходимо, очевидно, увеличить крутизну нарастания сигнала Е. Сделать это можно путём резкого перехода образа  в образ  (или ); оценить переход можно по изменению степени сходства этих образов  и  в зависимости от смещения глаза у. Усиления резкости перехода можно добиться, например, подсветкой, связанной с глазом и направленной на края его поля зрения, или с помощью той же подсветки, но дающей на краях поля зрения резкие тени от предмета, или выбором контрастно­го по отношению к предмету фона и другими методами.

Не менее важно определить характер изменения сигнала управле­ния привода поперечного перемещения при нахождении предмета вблизи от центра поля зрения, то есть в ситуациях , , . Сохраняя прежнее требование — быстродействие смещения глаза, — нужно побеспокоиться о том, чтобы оно не привело к автоколеба­ниям в центре. Для этого необходимо, чтобы сигнал управления имел в ближайших окрестностях центра самые малые значения, а при большем смещении от центра нарастал бы по крутой зависимости. В переложении на степень сходства образов , ,  это означает обратное: в окрестностях центра она должна быть наи­большей и близкой единице, а далее к краям — резко бы уменьша­лась. Достичь этого можно опять же соответствующей подсветкой или расширением обучаемой выборки — введением дополнительных двух ситуаций с предметом по обе стороны (вправо, влево) от цент­ра вблизи него с уменьшенными или даже нулевыми сигналами управ­ления. Говоря о подсветке, мы имеем в виду, что она должна быть постоянной и не требовать изменения в зависимости от ситуаций; было бы нелепо держать для этих целей человека, который подсве­чивал бы фонариком то тут, то там.

Динамика механизма поперечного перемещения при поиске. Исследо­вания процесса поперечного перемещения головы робота при поиске заданного предмета не могут замыкаться только на системе управ­ления: она значит многое, но не всё; ещё есть динамика всего ро­бота — и она не менее важна. Представлять дело так, что её ана­лиз может быть ограничен передаточными функциями линеаризован­ной системы, означало бы чрезмерное упрощение. Во-первых, робот на самом деле является сугубо нелинейной системой, некоторые нелинейности которой, может быть даже, недопустимо линеаризиро­вать, например такие как сухое трение или наличие предела тяго­вого усилия привода, а во-вторых, практика обучения робота поис­кам предметов убеждает нас в высокой нестабильности процессов, и теория линейных автоматических систем бессильна помочь в этом.

Проведём для наглядности физическое отображение процесса вы­ведения робота на цель. Но прежде перечислим все факторы, влияю­щие на процесс; к ним относятся: активная сила привода , динамическое сопротивление , сухое трение R, инерция механизма и запаздывание системы управления. Характеристика ак­тивной силы  (рис.3.12,а) формируется, как уже говорилось, в процессе обучения и имеет явно не теоретический вид; её другой особенностью является ограничение по величине силы  Е — это та­кая особенность, которая не поддаётся линеаризации. Проинтегри­руем активную силу по перемещению у и получим кривую (рис. 3.12,б) напоминающую впадину со склонами. Такое сравнение не случайно: интеграл силы равноценен потенциальной энергии Н. Инерцию манипулятора можно отобразить в виде шарика, перекатывающегося со склона на склон. Сухое трение R механизма изменит форму впадины так, что уклон главного склона (по которому скатывается шарик) уменьшится — он станет более пологим, а уклон противооклона увеличится — он станет более крутым; при этом произойдёт сме­щение нижней точки впадины назад по направлению движения шарика на величину  (рис. 3.12,в). В результате форма впадины определится таким отображающим выражением:

 

.

 

Динамическое сопротивление механизма можно представить в виде вязкой жидкости, заполнившей впадину. И сухое трение, и динами­ческое сопротивление, очевидно, будут тормозить шарик, гася его колебания относительно положения цели  .

Фактором, способствующим неустойчивости шарика, кроме его инер­ции, будет так называемое апериодическое запаздывание системы управления, характеризуемое постоянной времени . В нашем физическом отображении это запаздывание приводит к тому, что кри­вая впадины смещается вперёд по ходу движения шарика на величину  (рис. 3.12,г), и самая нижняя точка впадины — точка равно­весия — может оказаться на противоположной стороне от положения цели (если >). Учитывая то, что смещение впадины отно­сительно положения цели, вызываемое апериодическим запаздыванием системы управления, происходит только во время движения шарика (нет движения — нет смещения), то, остановившись в нижней точке, шарик в тот же момент оказывается на противосклоне (так как впа­дина сместилась назад), и он вынужден катиться в обратную сторону. Величина смещения впадины вперёд по ходу движения шарика опреде­ляется двумя параметрами: скоростью шарика и постоянной времени системы, причём в прямой зависимости. Поэтому всякое уменьшение скорости шарика и, особенно, постоянной времени  будет способ­ствовать стабилизации процесса, а при =0 колебания могут прекратиться вовсе.

 

 

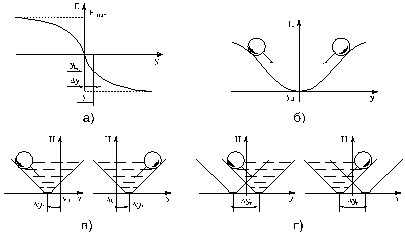
Рис. 3.12. Физическое отображение динамики привода поперечного перемещения

 

Но об этом можно только мечтать. Реальность такова, что инер­ционность современных фоторезисторов, определяемая живучестью выбитых светом электронов, достаточно велика, и не приходится говорить о их нулевом апериодическом запаздывании. Напомним ещё раз, что постоянная времени  обучаемой системы управления оп­ределяется в основном инерционностью фоторезисторов.

Фазовые методы исследований и расчётов поперечного перемеще­ния. Более точные по сравнению с теорией линейных автоматических систем исследования можно провести фазовыми методами /32/. Их достоинство в том, что они позволяют проводить конкретные исследования и расчёты на относительно простом инженерном уровне прак­тически любых нелинейных систем без линеаризации. Обычным для них является использование экспериментальных рабочих характеристик, форма которых сильно отличается от аналитических кривых. Принци­пиальной особенностью фазовых методов является то, что они прово­дятся не во временном пространстве, а в разовом, сочетающем любые параметры между собой, кроме времени. Впрочем, время может быть также введено в оборот, но только наравне со всеми другими пара­метрами без предоставления ему статуса фона, на котором развора­чиваются события. Такое отношение ко времени сродни обучаемым системам управления, в которых, говоря принятым языком, действуют исключительно фазовые соотношения.

Примем за основу плоскость, осью абсцисс которой является по­перечное перемещение , а осью ординат — скорость того же пе­ремещения  (рис. З.13); такая плоскость наиболее распростра­нена в фазовых методах. Изобразим на ней вое силовые характеристики, приведённые к конечной точке робота — к смещающемуся глазу, так что:  представляет собой активную силу привода;  — сила динамического сопротивления;  — сухое трение. Все эти силы могут быть получены без особого труда опытным путём, причём активная сила есть не что иное как сигнал управления обучаемой системы после завершения обучения. Экспериментальный характер кривых обязывает учитывать масштабы их изображений; более того, предполагая проведение исследований графическими методами, мы должны придать масштабированию особо важное значение, но об этом — чуть ниже. Аналитические кривые, если такие появятся, также могут быть использованы в фазовых расчётах и исследованиях, но на общих правах о экспериментальными.

Фазовая траектория в плоскости  представляет собой кри­вую, оборачивающуюся вокруг начала координат по часовой стрелке. В основу методики графического построения траектории положим уравнение

 

,                                     (3.56)

 

где m — масса всех движущихся частей робота, приведённая к его голове (инерция);  — ускорение головы.

 

 

Рис. 3.13. Построение фазовой траектории

 

Возьмём произвольную точку траектории в квадранте (,) фазовой плоскости и обозначим её цифрой 1; определим положе­ние траектории в окрестностях этой точки. Для этого уравнение (3.56) приведём к виду

 

.

 

Если допустить, что приведённая масса m робота постоянна, то отношения сил к ней можно воспринимать как сами силы в иной размерности или в определённом масштабе изображения на фазовой плоскости; отобразим это чертой над ними:

 

.

 

Разделим правую и левую части уравнения на скорость :

 

.

 

Представим ускорение и скорость в виде:

 

;      ,

 

и подставим их в полученное выражение; после сокращения на  получим

 

.                                           (3.57)

 

Выражение (3.57) является уравнением фазовой траектории и его можно отобразить на фазовой плоскости графически. В точке 1 (рис. 3.13) оно примет вид

 

.                                    (3.58)

 

Для дальнейших рассуждений произведём некоторые графические построения. Опустим из точки 1 перпендикуляр на ось у; полу­чим проекцию точки . Отложим по ходу оси у (вправо) величину ; получим точку . Будем утверждать, что точка  является мгновенным центром кривизны фазовой траек­тории в точке 1. На этом основании отрезок прямой (1-2), проведённый перпендикулярно радиусу (-1), есть не что иное, как кусочек самой траектории. Являясь прямым, этот отрезок, ес­тественно, отклоняется от действительной кривой траектории, и чем он длиннее, тем — больше отклонение. Допустим такую погрешность в построении фазовой траектории. Её можно несколько уменьшить, если изобразить отрезок (1-2) в виде дуги окружности с цент­ром в точке  и само собой разумеется: чем короче отрезок (1-2), тем он меньше отклоняется от траектории. Повторив все построения относительно точки 2, получим следующий отре­зок фазовой траектории (2-3), и так далее.

Вернёмся к доказательству нашего утверждения. Линия (А-2), проведённая перпендикулярно мгновенному радиусу кривизны (-1) образует с осью у угол b, тангенс которого, как известно, равен производной:

 

(1).

 

С другой стороны из подобия треугольников () и () следует, что угол () также равен b; тангенс этого угла определится как

 

.

 

Приравняв оба тангенса между собой, получим выражение (З.58); следовательно, оно справедливо.

При построении отрезка фазовой траектории (1-2), находяще­гося в четверти плоскости (;), мы откладывали активную силу  вправо от проекции , то есть по ходу оси у, а силы сопротивления  и  влево, то есть вычитали из ак­тивной силы. Определимся с направлениями сил в других четвер­тях. Для этого воспользуемся проведённым выше отображением. Дви­жение изображающей точки, образующей фазовую траекторию, в чет­верти (;) соответствует скатыванию шарика с левого склона (рис. 3.14); активная сила в этом случае разгоняет его, а силы F и R тормозят: . Переход изображающей точки через ось  означает, что шарик в этот момент находится в ниж­ней точке впадины; активная сила Е равна нулю, а силы сопро­тивления F и R направлены в противоположную сторону от век­тора движения, то есть влево: ; мгновенный центр кривизны траектории лежит на оси у слева от начала координат, поэтому траектория при переходе оси   всегда имеет отрицательный наклон.

В следующей четверти (;) движение изображающей точки тра­ектории соответствует подъёму шарика на правый склон. В этом слу­чае все силы, и в том числе активная, будут тормозить шарик: ; а это означает, что при построении их следует откладывать влево от проекции на ось у очередной точки траек­тории. В своей самой верхней точке на правом склоне шарик поте­ряет скорость (=0), динамическое сопротивление и сухое трение исчезнут, а активная сила достигнет своего максимума и будет на­правлена влево: . Фазовая траектория в этом случае будет всегда переходить ось у перпендикулярно ей.

Четверть (;) соответствует скатыванию шарика с правого склона впадины; активная сила  разгоняет шарик и будет нап­равлена влево, а силы сопротивления  и  тормозят и должны быть отложены при построении траектории вправо: . В самой нижней точке впадины скорость достигает своего максимального значения, но активная сила при этом исчезает; поэтому на оси : , и любая траектория будет пересекать ось у под отрицательным наклоном.

В последней четверти (;) движение изображающей точки отражает подъём шарика на левый склон. В этом случае , то есть все три силы тормозят шарик, поэтому на фазовой плоскос­ти их необходимо откладывать вправо. В крайней левой точке тра­ектории, соответствующей самому верхнему положению шарика, ско­рость  уменьшается до нуля, силы сопротивления  и  исчезают и ; траектория пересекает ось у по перпен­дикуляру к ней. Далее всё повторяется.

Таков порядок графического построения фазовой траектории  поперечного перемещения головы робота при поиске. Построение можно ускорить, если воспользоваться средствами вычислительной техники.

Выше мы говорили о том, что графическое построение требует определённого согласованного масштабирования всех параметров; если масштабы окажутся несогласованными, то результаты будут ошибочными. Начнём с оси абсцисс (рис. 3.13); по ней откладыва­ем смещение у головы робота. Это смещение может в действитель­ности измеряться тысячами миллиметров, но на оси у оно должно умещаться в пределах обычного листа. Нужен масштаб изображения смещения; обозначим его через ; в результате каждому сме­щению головы робота у будет соответствовать на оси абсцисс отрезок изображения . Также каждой скорости смещения  будет соответствовать на оси ординат отрезок , где  — масштаб скорости. И, наконец, каждая из учитываемых сил ,  и  должна быть ото­бражена на соответствующей оси фазовой плоскости в масштабе :

 

; ;

;

 

Размерности масштабов:

 

; ; .

 

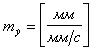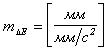Согласование масштабов начнём с выражения (3.58); изобразим его в малых приращениях:

 

.

 

Приращение  представляет собой на фазовой плоскости отрезок (2-В), а приращение — отрезок (1-В); в результате получим

 

.

 

Все указанные отрезки соответствуют определённым величинам, отложенным на плоскости в своих масштабах:

 

.

 

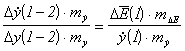Отсюда:

 

.

 

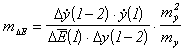Из геометрии построения следует:

 

;  .

 

В результате получим:

 

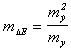.                                          (3.59)

 

Таково соотношение масштабов изображения всех величин; масштаб  в равной степени относится как к , так и ко всем другим силам, и справедлив при откладывании этих сил по обеим осям  и  .

Выбранная нами фазовая плоскость  исключила из оборота время, однако его можно восстановить косвенным путем; это иногда необходимо делать, например для учета апериодического запаздывания процесса, для построения привычных временных характеристик или для иных целей.

Для восстановления времени воспользуемся снова выражением (3.56) и представим его в виде .

Отсюда:

 

.

 

В приращениях отрезка траектории (1-2) (рис.3.13) это выражение предстанет как

 

.

 

Из подобия треугольников () и () получим:

 

.

 

Следовательно, отрезок времени , за который изобра­жающая точка проходит по фазовой траектории на плоскости  при выбранных масштабах отрезок (1-2), равен тангенсу угла отклонения мгновенного радиуса кривизны траектории:

 

.                               (3.60)

 

Зависимость (3.60) позволяет определить время прохождения изображающей точкой любой части фазовой траектории или, что одно и то же, головой робота — любого соответствующего участка дей­ствительной траектории; это время определяется простым сумми­рованием составляющих отрезков времени. Таким же образом можно определить период поперечных колебаний головы робота и их час­тоту, как обратную величину.

Следует, однако, иметь в виду, что подставлять в выражение (3.60) транспортирный угол g очень рискованно; более правиль­ным является представление тангенса угла g в виде отношения величин  и  в абсолютных значениях, проверяя при этом, чтобы отношение размерностей этих величин давало размер­ность времени, то есть секунды.

По виду фазовых траекторий при некотором навыке можно судить о поведении объекта с обучаемой системой управления, в нашем случае — робота. На рис. 3.14 приведены типовые траектории; их определяющим параметром является рабочая характеристика актив­ной силы ; если она достаточно крутая (рис. 3.14,а), то фазовая траектория включает много оборотов и слабо стремится к началу координат, то есть к положению цели. В переложении на физическое отображение (3.14) это означает, что шарик будет со­вершать слабозатухающие колебания, перекатываясь со склона на склон, а применительно к роботу, совершающему поиск, можно ска­зать так: раскачиваясь из стороны в сторону в поперечном направ­лении, робот едва ли сможет зафиксировать цель и проскочит мимо неё, двигаясь вдоль полосы поиска. Силы сопротивления в данном примере (рис. 3.14, а) приняты такими: сухое трение составляет 5% от максимального значения активной силы, а динамическое сопро­тивление принята квадратичным в зависимости от скорости смещения с коэффициентом 0,01. В действительности силы сопротивления могут оказаться ещё слабее, и в таком случае процесс станет более неус­тойчивым, ведь его успокоение полностью зависит от этих сил.

На рис. 3.14,6 активная сила  более пологая, сухое трение составляет уже 6 % от её наибольшего значения, а коэффициент квадратичности динамического сопротивления увеличен по сравнению с предыдущим случаем в четыре раза и составляет 0,04. В резуль­тате фазовая траектория более выражение стремится к началу коор­динат, но говорить об удовлетворительном поиске всё равно ещё не приходится: поперечные колебания головы робота сох­ранились, и они не позволят «схватить» цель.

 

 

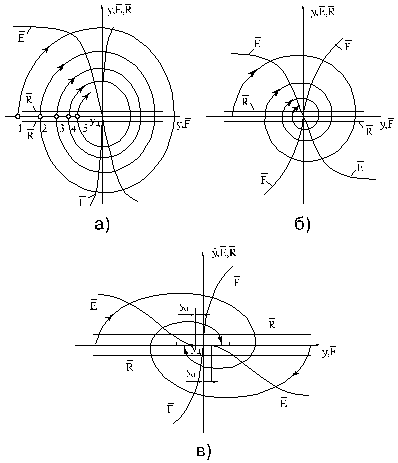
Рис.3.14. Фазовые траектории поперечного перемещения при поиске: а) слабое затухание; б) более ускоренное затухание колебаний;
в) сильное затухание колебаний

 

Более приемлемыми выглядят фазовые траектории на рис. 3.14, в: все они ограничиваются одним оборотом. Достигнуто это за счёт целого ряда мер. Во-первых, активная сила принята ещё более по­логой, сухое трение доведено до 15 %, а коэффициент квадратичности динамического сопротивления принят равным 0,05. Во-вторых, искусственно расширена нулевая область активной силы; зона ос­тановки, таким образом, оказалась довольно широкой — на рис. 3.14, в она выделена жирной линией.

Как всего этого можно достичь на практике? Что касается уве­личения сил сопротивления, то здесь способы — обычные: чтобы тормозить, напрмер, трением, особой изобретательности не требу­ется. Сложнее — с рабочей характеристикой . Если расши­рение нулевой области активной силы — дело, в общем-то, не очень трудное, то с уменьшением наклона характеристики не всё так просто

Начнём с нулевой области. Введём в обучаемую выборку ещё две целевых ситуации со смещением положения искомого предмета на величину  в обе стороны от целевой позиции ; сигналы управления в них должны быть также нулевыми. Тогда зона остановки определится тем, что в ней сухое трение — больше или, по крайней мере, равно активной силе: . Всё, казалось бы, хорошо, но одно плохо: при этом усложняется захват искомого предмета — та процедура, ради которой и осуществляется поиск. В самом деле: схват робота (пасть головы) может остановиться в такой точке над предметом, что не сможет его потом захватить. Другими словами, расширение зоны остановки снижает точность позиционирования, хотя, с другой стороны, способствует стабилизации поперечного привода.

Что же касается наклона рабочей характеристики в окрестностях целевой позиции, то следует помнить, что он формируется автома­тически в процессе обучения, и регулировать его не очень просто. К тому же при этом возникает трудноразрешимое противоречие: чтобы ускорить поперечное перемещение и повысить надежность поиска, желательно увеличить наклон, а для того, чтобы стабилизировать процесс — нужно уменьшить. Если же всё-таки будет принято решение об уменьшении наклона рабочей характеристики активной силы, то достичь этого можно, во-первых, определённой подсветкой иско­мого предмета в процессе обучения, такой, которая размывала бы образ предмета, а во-вторых, введением постоянных колебаний глаза с малой амплитудой — так называемого тремора. Более подробно эти колебания и их влияние на поиск будут рассмотрены ниже, а пока мы говорим только о том, что о их помощью можно также существенно размыть образ и уменьшить активные силы на подходе к цели.

Апериодическое запаздывание поперечного привода. Возможны и иные способы стабилизации привода поперечного перемещения головы робота при поиске, и некоторые из них хорошо представлены в той же линейной теории автоматического управления, но прежде чем при­ступить к стабилизации, стоило бы хорошенько изучить дестабили­зирующие факторы. Одним из таких факторов является апериодическое запаздывание; оно отражено в передаточной функции  структурной схемы обучаемой системы управления робота со зрением (рис. 3.11,6) и характеризуется по­стоянной времени . Выше уже  говорилось о том, что аперио­дичность обучаемой системы  возникает, в основном, по вине фото­резисторов; совсем незначительно она усиливается за счёт инерци­онности усилителей, стоящих на выходе из мозга; сам же мозг дей­ствует в этом смысле безукоризненно — практически мгновенно. Зная, что апериодическое запаздывание обучаемой системы — может быть, самая главная причина нестабильности поперечных перемещений, предлагаем отнестись к нему более внимательно.

Чтобы оценить влияние апериодического запаздывания на процесс, учтём его при построении фазовых траекторий, но сначала уточним сам порядок построения. Каждой точке фазовой плоскости, отражаю­щей текущий момент, соответствует своя координата у и своё зна­чение активной силы , снятое с силовой характеристики, но действительное значение силы    в указанной точке будет нес­колько иным. Дело в том, что сигнал управления обучаемой системы изменяет свою величину не мгновенно, а по апериодическому закону или, как иногда говорят, по экспоненте; поэтому изменение дейст­вительной силы  не будет успевать за ростом или падением текущей силы , и всё время  будет отставать. Если на каком-то участке фазовой траектории текущее значение  посто­янно или изменяется совсем незначительно, то указанного запазды­вания не будет, и =. Но там, где кривая характеристики  имеет наклон, там действительная сила  будет прини­мать какое-то значение, располагающееся в интервале между неким предыдущим и текущим; и чем круче окажется наклон, тем сильнее будут разниться величины  и .

Для того, чтобы определить порядок построения фазовой траекто­рии с учётом сказанного, произведём следующие рассуждения. Вер­нёмся от текущего момента назад на некоторый отрезок времени, равный  и будем считать, что в начале этого отрезка дейст­вительное значение активной силы было равно ; это — пре­дыдущая сила. В конце отрезка времени  сила должна была бы равняться соответствующему значению , но из-за апериодич­ности  не сможет измениться до  и достигнет только ка­кого-то значения . Мы знаем, что изменение силы будет происходить по экспоненте; следовательно, за время  её изме­нение составит только часть, определяемую выражением

 

,

 

где ; в абсолютном значении это будет равно

 

.

 

Здесь рассматривается спуск шарика с левого склона; ему соот­ветствует постоянное уменьшение активной силы. В результате пре­дыдущая сила  уменьшится на указанную величину, так что дей­ствительная сила  текущего момента определится как

 

.

 

Это выражение можно изобразить в более компактном виде:

 

.                        (3.61)

 

Полученная действительная сила для последующего отрезка вре­мени, очевидно, окажется предыдущей. Так, переходя от одного от­резка к другому, можно постепенно определить соответствующие им значения действительной силы. Если при построении фазовой траек­тории принимать временной шаг  всегда одним и тем же, то вели­чина  окажется постоянным простым числом меньше единицы.

Графически при построении фазовой траектории неизменному шагу  будет соответствовать неизменный угол g (рис. 3.13).

Для того, чтобы убедиться в справедливости выражения (3.61), проверим его в крайних состояниях. Начнём с =0, при этом  окажется равной , то есть сила никак не успеет изме­ниться; это естественно. Если же =¥, то действительная сила окажется равной текущей; и это понятно: апериодический про­цесс за такое время закончится полностью, и никакого запаздывания сил не будет. Конечно, принятое значение =¥ — несколько утрировано; известно, что экспонента почти полностью выходит на свой предел уже при соотношениях .

Последний вывод не должен вводить нас в заблуждение относи­тельно того, что достаточно выбрать при построении фазовой тра­ектории угол g относительно большим, и можно исключить апериоди­ческое запаздывание и всё то негативное, что связано с ним в ре­альном процессе; к сожалению, реальность никак не отреагирует на наши графические построения. Ошибка подобного заключения сос­тоит в том, что таким образом допускается недопустимое увеличе­ние шага построения, то есть угла g; этим самым реальный про­цесс искажается на столько, что можно ожидать в результате чего угодно.

Крайние состояния выражения (3.61) не очень характерны; пос­мотрим, что даёт оно в приемлемых условиях. Допустим, сетчатка глаза робота собрана из фоторезисторов типа СФЗ-1, постоянная времени которых Т =0,06 сек. Приблизительно такой же будет постоянная времени всей обучаемой системы управления. Пусть час­тота поперечных колебаний головы робота составляет 5 Гц; ей соот­ветствует период колебаний 0,2 сек. За это время траектория на фазовой плоскости совершит полный оборот. Если период разбить на 20 одинаковых по времени участков ( g = 360°/20 == 18°), то каждый из них окажется равным  = 0,2/20 = 0,01 сек. При выбранных значениях получим:

 

.

 

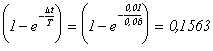Это говорит о том. что предыдущая сила , за время  = 0,01с успеет измениться только приблизительно на одну шестую перепада сил, возникшего на данном отрезке, то есть будет наблюдаться явно выраженное запаздывание действительной силы.

Выражение (3.61) закольцовано: предыдущая сила текущего отрезка времени является действительной силой предыдущего отрезка времени является действительной силой предыдущего отрезка; и, как будто, у этого процесса нет начала, в котором действитель­ная сила равнялась бы текущей. Это так, и тем не менее за начало можно принять очередную крайнюю точку положения, в которой фазо­вая траектория пересекает ось у; в этих точках голова робота задерживается дольше всего (они соответствуют крайним верхним положениям шарика на склонах, где он останавливается), и с некото­рым допущением в них можно принять =.

После того, как мы определили порядок построения фазовых тра­екторий о учётом апериодического запаздывания, продемонстрируем его — этот порядок — на конкретном примере. Примем исходные дан­ные такими же, как в случае с фазовой траекторией, изображённой на рис. 3.16,6, то есть ту же рабочую характеристику активной си­лы , то же динамическое сопротивление  с коэффициентом квадратичности 0,04 и то же сухое трение , составляющее 6 % от наибольшего значения активной силы. Кроме того примем постоян­ную времена системы   Т = 0,06 сек, и временной шаг построения  = 0,025 сек; при этих условиях получим , а выражение (3,61) примет вид

 

.

 

Строя шаг за шагом фазовую траекторию и откладывая одновремен­но соответствующие значения действительной активной силы, получим в результате фазовый портрет рассматриваемого примера (рис. 3.15), Сравнивая его с рис. 3.14,б, видим, что, если на прежней фазовая траектория, худо-бедно, стремилась к центру, и можно было ожидать постепенного затухания колебаний, то на полученном портрете фазо­вая траектория раскручивается до некоторого предельного цикла (предельным циклом принято называть замкнутую траекторию), и ожи­дать затухания не приходится. Кривая действительной активной силы  существенно отличается от статической рабочей характеристики  и её отличие состоит в основном в том, что она имеет явно выраженный гистерезисный вид; кривой предельного цикла соответствует замкнутая петля гистерезиса. Суммируя время отрез­ков , можно получить период колебаний; в рассмотренном при­мере он равен 0,5 сек, а зная масштаб , можно определить размах колебаний и амплитуду предельного цикла. По отдельным от­резкам фазовой траектории есть возможность восстановить колебания в привычном временном виде:  (рис. 3.15, справа внизу).

 

 

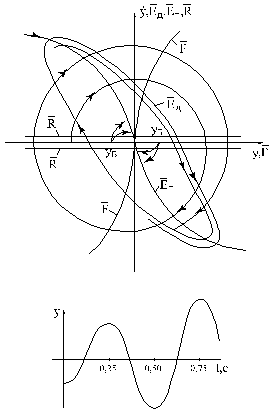
Рис.3.15. Фазовая траектория поперечного перемещения при поиске с учетом апериодического запаздывания

 

Полученный фазовый портрет отражает действительный процесс, можно сказать, без искажений: все параметры приняты такими, какие они есть на самом деле. Погрешности могли возникнуть только от неточности графического построения; в частности, от выбора увели­ченных отрезков  (вспомним, что, чем меньше отрезки, тем точнее построение), или ещё от того, что была принята постоянной инерция робота, то есть приведённая масса m; в действитель­ности она может изменяться в зависимости от положения робота. Последнюю погрешность, если она существует, можно уменьшить или даже устранить совсем, произведя корректировку силовых характе­ристик; для этого необходимо разобраться в кинематике робота и рассчитать величину коррекции в зависимости от смещения у; по отношению к характеристикам  и  сделать это нетруд­но, а динамическое сопротивление  придётся сохранить в преж­нем виде. Впрочем, указанные корректировки не могут привести к серьёзным изменениям фазовых траекторий, и поэтому их лучше не производить.

Анализ фазового портрета (рис. 3.15) позволяет выявить общие закономерности колебаний поперечного перемещения головы робота при поиске. Очевидно, большим отклонениям у будут соответство­вать ограничение по величине активной силы (та нелинейность, ко­торую нельзя устранить) и резкое квадратичное возрастание динамического сопротивления; в результате колебания с большим размахом склонны будут затухать до выхода на тот же предельный цикл. С дру­гой стороны при малых отклонениях у в той области, где актив­ная сила  соизмерима с сухим трением , будет наблюдать­ся отчётливое затухание колебаний вплоть до полной остановки.

В натуре это выглядит следующим образом. Если предает оказался на дальнем краю поля зрения, то голова робота с глазом устремля­ется к нему, набирает скорость, проскакивает его и начинает ко­лебаться вправо-влево относительно цели с некоторой постоянной амплитудой, меньшей первоначального отклонения. Если же предмет окажется недалеко от центра поля зрения глаза, то всё равно воз­никнут те же самые колебания с той же амплитудой, но в этот раз она будет больше начального отклонения. И только тогда, когда предмет возникнет в поле зрения совсем рядом с центром, смещения будут носить хотя и колебательный, но центростремительный затухающий характер.

Итак, обратим наше внимание на то, что любые первоначальные отклонения предмета от центра поля зрения, кроме самых малых, при­водят к автоколебаниям головы робота, причём амплитуда этих коле­баний всегда постоянна; это — главный вывод. (Автоколебаниями называют такие колебания, которые поддерживаются за счёт их под­питки внешней энергией, в нашем случае — активной силой.) Основной причиной незатухающих колебаний является апериодическое запазды­вание системы управления; его влияние хорошо видно на примере по­строения фазовой траектории (рис. 3.15). Интересным моментом яв­ляется то, что существует такое граничное отклонение , исходя из которого фазовая траектория может пойти с равной вероятностью по одному из двух направлений: либо на раскручивание до предель­ного цикла, либо на затухание до нуля; такое раздвоение траекто­рии называется бифуркацией.

Точечный преобразования. Завершим рассмотрение фазовых методов расчета и исследований так называемыми точечными преобразованиями; они применяются, как правило, для геометрической интерпретации состояний исследуемых систем, но иногда и для непосредственных расчётов. Суть точечных преобразований заключается в следующем. Если взять произвольную линию и пересечь ею закручивающиеся спирали фазовой траектории, то можно подучить последовательность точек, каждая из которых яв­ляется последующей к некоторой предыдущей и предыдущей к следую­щей; удобнее всего в качестве такой секущей линии принимать одну из полуосей фазовой плоскости. Зависимость координат последую­щих точек от координат предыдущих отражает в полной мере исследу­емый процесс и называется функцией исследования; эту функцию мож­но изобразить на графике исследования.

Рассмотрим конкретный пример. Примем в качестве секущей линии на фазовой плоскости рис. 3.14,а полуось (-) и обозначим по­следовательность пересечений этой линии фазовой траекторией цифрами 1,2,3,4,5 и так далее. Функцию последования отразим на плоскости с осями: абсцисса — координата предыдущей точки  ордината — координата последующей точки . Замерим коор­динаты всех отмеченных на рис. 3.14,а точек и построим саму функцию (рис. 3.16, а). Ступенчатая траектория, ограниченная функцией последования и биссектрисой координатного угла, отобра­жает в итерационном виде фазовую траекторию; в нашем примере (рис. 3.16,а) ступенчатая траектория устремляется к началу коор­динат и свидетельствует о затухании колебаний головы робота.

 

 

Рис. 3.16. Графики точечных преобразований

 

Более сложный график точечных преобразований представлен на рис. 3.16.б; он отражает тот же процесс, но с учётом апериоди­ческого запаздывания. Функция последования представляет собой сложную кривую, дважды пересекающую биссектрису координатного угла. Первое пересечение с абсциссой  образует аттрактор, к которому устремляются ступенчатые траектории с обеих сторон; это — предельный цикл, а  — его амплитуда. Второе пересече­ние с абсциссой  образует бифуркацию; ступенчатые траекто­рии от него, наоборот, разбегаются.

Выше было сказано, что функции последования извлекаются из фа­зовых траекторий; в общем это правильно, но в принципе их можно получить также иными способами, в частности путём снятия экспери­ментальных характеристик. В нашем примере с роботом последний путь, пожалуй, даже проще. Так или иначе эксперименты проводить надо, хотя бы для того, чтобы снять действительные силовые харак­теристики, чтобы на их основе построить семейство фазовых траек­торий. А можно, минуя этот процесс, заснять сразу же сами функции последования, задавая для этого различные исходные положения пред­метов в поле зрения и фиксируя последовательные отклонения головы робота. Так, пожалуй, даже проще.

На этом исследования поперечных перемещений поиска закончим. Отметим лишь, что поворот головы робота вокруг оптической оси глаза до совмещения с определённым положением искомого предмета в плане его динамики ничем от поперечного перемещения не отлича­ется; все рассмотренные выше методы применимы к нему в полной мере.

 

 

4.2. Продольные перемещения поиска

 

Продольное перемещение происхо­дит вдоль оси х; осуществляет его отдельный привод. Простей­шая обучаемая выборка продольного перемещения состоят всего из трёх ситуаций: в целевой, когда искомый предмет расположен в цен­тре поля зрения глаза и определённо сориентирован, сигнал управ­ления должен равняться нулю: =0; в двух других дополнитель­ных, в одной из которых в поле зрения — чистый однообразный фон, а в другой — любой предмет (лучше — похожий на искомый), сигналы управления должны быть больше нуля и всегда положительными: >0; >0. Желательно, чтобы сигнал управления в фоновой ситуации был несколько больше: >.

Такая обучаемая выборка в принципе обеспечивает поиск, но не гарантирует его безотказность. Стоит только в борьбе с попереч­ными колебаниями снизить скорость поперечного перемещения, так сразу возникает проскакивание цели, особенно в случаях, когда искомый предмет оказывается на самом краю поля зрения; об этом уже говорилось. Пока нарастает сигнал управления привода попереч­ного перемещения, пока привод набирает свою скорость и пока он смещает глаз к предмету, привод продольного перемещения успевает сместить глаз дальше предмета, то есть проскакивает, и поиск не состоится.

Для устранения этого дефекта можно предложить более тщатель­ный подбор соотношения величин сигналов обоих приводов: скорость поперечного перемещения увеличить до предела, а скорость продоль­ного — снизить до гарантированного поиска. Такое решение можно было бы считать наиболее удачным, если бы не то обстоятельство, что продольные и поперечные перемещения нужны роботу не только для поиска, но и для других целей, и тогда установленное соотноше­ние скоростей приводов может оказаться неприемлемым. По той же самой причине нельзя считать выходом из положения согласование сигналов приводов в движении, то есть при росте сигнала попереч­ного привода уменьшать сигнал продольного, может быть даже вплоть до полной остановки: а вдруг в какой-то ситуации потребуется, чтобы оба сигнала были максимальными.

Другим неприятным моментом при поиске является так называемое сползание глаза с цели, когда он, хотя и притормаживает на ней, но не до нуля, и, перевалив через неё, уходит дальше. Так обычно ведёт себя глаз при приближении к постороннему предмету, и, чем больше тот похож на искомый, тем сильнее притормаживание; и всё-таки совсем глаз в этом случае не останавливается. И это — хоро­шо, но только не по отношению к искомому предмету.

Прежде, чем принимать какие-либо решения по устранению указан­ных нежелательных явлений, попытаемся поглубже разобраться в са­мом процессе продольного перемещения при поиске. Представим сиг­налы управления привода во всех ситуациях обучаемой выборки в разделённом виде:

·       в целевой ситуации: =;

·       в ситуации с однообразным фоном: >;

·       в ситуации, когда в поле зрения — любой посторонний предмет: >.

Если по-прежнему считать, что в ситуации с однообразным фоном все возбуждения рецепторов  равны между собой (или близки к этому), то из самого определения слагаемых сигнала управления

 

;

 

, —

 

следует, что  может быть больше  только при условии

 

.                                      (3.62)

 

А это в приложении к оптической обучаемой системе управления означает, что плюс-диапозитив, управляющий продольным перемещением головы робота, всегда светлее минус-диапозитива; одного этого достаточно, чтобы обеспечить такое перемещение.

Представим соотношение сигналов управления во всех ситуациях обучаемой выборки, оговоренные в начале, в разделенном виде:

 

.

 

Выражая слагаемые сигналов управления через коэффициенты приведения  в соответствии с (3.52), получим

 

 

Третья разность, равная нулю дает

 

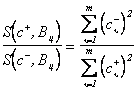.                             (3.63)

 

Вторая разность больше нуля:

 

, —

 

из нее следует

 

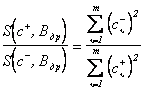.                         (3.64)

 

Первая разность больше второй, следовательно:

 

, —

 

и тогда:

 

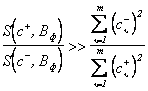.                             (3.65)

 

Сводя условия (3.63), (3.64) и (3.65) вместе, получим

 

.                  (3.66)

 

Соотношения коэффициентов приведения, представленные в условиях (3.66), отражают работоспособность привода продольного перемещения в принципе, но не затрагивают качественную сторону его работы.

Преломляя все полученные условия к оптической системе, можно сделать такие умозаключения. Из условия (3.63) с учетом (3.62) следует, что, несмотря на то, что плюс-диапозитив в общем и целом прозрачнее минус-диапозитива, центр его, то есть та зона, которую занимает искомый предмет, несколько темнее, чем центр ми­нус-диапозитива при условии. что искомый предмет ярче фона. Усло­вие (3.64) уточняет предыдущее заключение: центр плюс-диапозитива не просто темнее, а избирательно темнее, то есть избирательно только к более ярким пятнам образа искомого предмета. Результиру­ющее условие (3.66) сводит все эти умозаключения воедино.

Динамика продольного перемещения. При продольном перемещении действует тот же самый набор сил, что и при поперечном, но только это — свои силы:  — активная сила привода продольного переме­щения;  — динамическое сопротивление;  — сухое трение; m — инерция, то есть приведённая к голове робота масса движу­щихся в продольном направлении частей. И снова допускаем, что все они получены экспериментальным путём и не выглядят как теорети­ческие.

В фоновой ситуации скорость продольного перемещения, очевидно, должна быть постоянной; следовательно, активная сила привода в ней должна уравновешиваться силами сопротивления:

 

.

 

На силовой характеристике (рис. 3.17,а) участки с фоновыми активными силами  выглядят как прямые, параллельные оси х; величина положительного смещения этих сил соизмерима с величиной отрицательного смещения сухого трения . При размещении иско­мого предмета вблизи центра поля зрения активная сила уменьшает­ся и достигает нудя при совмещении предмета с центром. Посторон­ние предметы также вызывают уменьшение активной силы, но не до нуля.

Представим сначала динамику продольного перемещения в виде физического отображения и воспользуемся для этого отображающим преобразованием, которое было применено при поперечном переме­щении; в данном случае оно примет вид

 

.

 

 

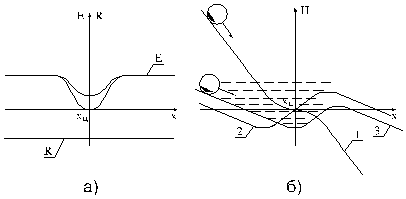
Рис. 3.17. Физическое отображение динамики привода про­дольного перемещения.

 

Согласно этому отображению продольное перемещение выглядит как склон одного направления с выровненной площадкой в центре, по которому скатывается шарик (рис. 3.17,б). При отсутствии су­хого трения уклон склона — очень крутой, а площадка в центре поля зрения (х=0) — горизонтальная (кривая 1). Скатывающийся шарик, очевидно, легко преодолеет эту площадку и укатится дальше, то есть глаз не задержится на искомом предмете и проскочит его. Сухое трение, соизмеримое с активной силой, резко уменьшает уклон скло­на и создаёт противоуклон центральной площадки (кривая 2); пре­одолеть этот противосклон шарику не так-то просто, но это возмож­но. Если же добавить к сухому трению ещё динамическое сопротив­ление в виде вязкой жидкости, то остановка шарика в центре ста­новится более вероятной; и всё будет зависеть от инерции этого шарика (от его массы): если инерция окажется большой, то шарик перевалит через противосклон и укатится дальше; если инерции на это не хватит, то шарик остановится. В последнем случае колеба­ния шарика относительно центра невозможны, так как противосклон будет менять свою ориентацию в зависимости от направления дви­жения шарика. Апериодическое запаздывание, игравшее решающую роль в поперечных перемещениях, в данном случае влияет на динамику не столь активно; тем не менее оно также влияет на процесс отри­цательно, уменьшая уклон противосклона (кривая 3).

Все эти рассуждения переложимы к продольным перемещениям го­ловы робота. Если она, приближаясь к искомому предмету, имела от­носительно небольшую скорость, то вполне возможно, что задержит­ся в положении пели; но есть вероятность того, что притормаживание при приближении к искомому предмету будет неполным, и тогда достаточно глазу в силу инерции механизма продвинуться чуть даль­ше, как снова начнёт нарастать скорость, и он окончательно поки­нет цель; поиск не состоится. Тем более он не состоится в том случае, если образ искомого предмета будет искажён или вместо него окажется посторонний предмет.

Процесс притормаживания продольного движения на цели хорошо отображается с помощью фазовых траекторий на плоскости (;) (рис. 3.18). Здесь учтена все те параметры, что и при поперечном перемещении, но только применительно к приводу продольного. Так  — силовая характеристика этого привода;  — его дина­мическое сопротивление;  — его сухое трение. Черта над пара­метрами означает деление на приведённую массу головы робота при продольном перемещений. Все силовые  характеристики могут быть полностью экспериментальными. Координата , — положение цели — искомого предмета. Координатами  отмечены конечные точки бифуркационных траекторий, выделенных на рисунках штриховкой; в по­ложении  активные силы равны силам сопротивления. Бифурка­ционная фазовая траектория характерна тем, что она с равной веро­ятностью может завершиться либо полной остановкой, либо сползани­ем с цели. Все траектории, располагающиеся ниже неё, гарантируют остановку, то есть успешный поиск; все траектории выше неё после притормаживания на цели уходят дальше — поиск провалился.

 

 

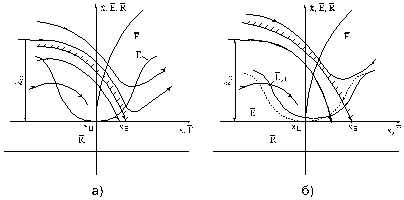
Рис. 3.18. Фазовые траектории продольного перемещения

 

На рис. З.18,а выбрана более крутая силовая характеристика  по сравнению с той же характеристикой на рисунке б); другими сло­вами можно сказать, что на рис. 3.18,б цель более размыта и зани­мает большее пространство, чем на рисунке а). (Размывание зритель­ного образа — явление положительное и будет рассмотрено особо.) Все другие силовые характеристики на обоих рисунках одинаковы. Размером  выделены фазовые траектории, имевшие на подходе к цели постоянную скорость — назовём её фоновой; на однообразном фоне скорость продольного перемещения глаза в конце концов стаби­лизируется — ей соответствует равенство активной силы и сил соп­ротивления: .  Так вот, во втором случае (рис.3.18,б) фазовая траектория с фоновой начальной скоростью завершается пол­ной остановкой, в то время как на рисунке а) она притормаживает на цели не до нудя и в конце концов уходит дальше, увеличиваясь снова в скорости. Считая фоновую скорость на подходе к цели наи­более вероятной, можно сделать вывод о том, что силовая характе­ристика на рис. 3.18, а выбрана неудачно. Следовательно, при обучении робота поиску нужно хорошо продумать все моменты, такие как положение искомого предмета в целевой ситуации, распределение освещения поля зрения, уровень фонового сигнала управления  и может быть даже придётся изменить состав ситуаций в обучаемой выборке. На первых порах было бы целесообразным совмещение экс­периментов обучения с построением и анализом фазовых траекторий, благо что при некотором навыке это не отнимает много времени.

Фазовые траектории второго случая (рис. 3.18, б) выглядят бо­лее предпочтительными, несмотря даже на то, что при их постро­ении было учтено апериодическое запаздывание системы управления. В основу расчётного определения действительной активной силы  при графическом построении фазовых траекторий с учётом аперио­дического запаздывания было положено выражение (3.61), которое в равной мере применимо как в случае поперечных перемещений, так и при продольном. Исходными параметрами были приняты: фоновая скорость   = 200 мм/сек; габарит искомого предмета L = 200 мм; постоянная времени  Т = 0,06 сек. Время прохождения глазом всего предмета на скорости  определится в одну секунду; действительное время из-за притормаживанвя окажется большим. Исходя из всего этого, примем временной отрезок постро­ения фазовых траекторий равным  = 0,06 сек. Тогда выраже­ние (3.61) примет вид

 

.

 

Напомним, что  — текущее значение активной силы, снятое со статической характеристики;  — предыдущее значение  ак­тивной силы, равное действительному значению , посчитан­ному на предыдущем шаге построения.

В общем и целом апериодическое запаздывание ухудшает процесс поиска как при поперечном перемещении, так и при продольном, только при продольном ухудшение, может быть, не столь заметно. Апериодическое запаздывание сдвигает все фазовые траектории (рис. 3.18) вправо, то есть по ходу движения робота; а это озна­чает, что располагавшиеся до бифуркационной границы траектории на самом деле (с учётом апериодичности) проходят уже за ней, при­тормаживают не до конца и уходят дальше с увеличением скорости, свидетельствуя о несостоявшемся поиске.

За основные мы приняли фазовые траектории, начинавшиеся с фоновой скорости . Другие траектории начинаются с иных скорос­тей, возникновение которых объяснять едва ли стоит: реальный про­цесс поиска может быть усложнён самыми непредвиденными обстоятельствами настолько, что возникнут скорости и больше, и меньше .

Если рассматривать только те фазовые траектории, которые заканчи­ваются на оси абсцисс, то есть полной остановкой головы робота, то, как видно из рис. З.18, все они, как правило, выходят на ось х правее центра , что свидетельствует о том, что глаз ро­бота останавливается не над серединой искомого предмета, а чуть проскакивает её. Объяснять это едва ли стоит — и без того понятно, — но учитывать такое явление очень желательно. Если схват робота (его пасть), совмещённый с глазом, зависнет не над серединой предмета, а вектором смещении, то захватить его будет нелегко. Луч­ше, очевидно, было бы располагать схват чуть позади глаза, но только в том случае, если направление продольного перемещения не меняет­ся на обратное. Впрочем, обстоятельства поиска могут быть разными, и торопиться с принятием однозначных решений не стоит.

Противоуклон продольного перемещения. Выше мы уже говорили о противоуклоне, создаваемом сухим трением; он способствует торможе­нию шарика в физическом отображении динамики привода продольного перемещения (рис.3.17,б). Там же указывалось, что противосклон меняет свою ориентацию в зависимости от направления движения. По­ясним: противосклон от сухого трения виртуален (есть такой термин в эфирной физике): он как бы есть и его как бы нету; пока глаз движется в продольном направлении, он возникает; стоит только глазу остановиться, и он исчезает. Поэтому в обратном направле­нии шарик под действием такого виртуального противоуклона смещать­ся не может, а надо бы.

Желательность противосклона объясняется тем, что искомые пред­меты могут зрительно отличаться друг от друга, и это отличие де­лает их неузнаваемыми. Если даже в процессе обучения в целевой ситуации использовать наиболее характерный предмет или даже нес­колько различающихся предметов, то и тогда найдутся в действитель­ности такие, которые всё же будут отличаться ещё больше. Обучен­ная система, очевидно, будет выдавать нулевой сигнал привода про­дольного перемещения только в том случае, если образ искомого предмета будет абсолютно схож с эталонным, использованным при са­мом обучении; во всех иных случаях сигнал управления будет больше нуля, а это — такая помеха при поиске, которая делает его безре­зультатным. Нужна лунка, да такая, в которой, образно говоря, мог бы застрять любой искомый предмет (в самом деле застревает глаз).

Рассмотрим одно из предложений: введём в обучаемую выборку еще одну сопредельную с целевой ситуацию о искомым предметом, смещён­ным от центра поля зрения по ходу на расстояние , и с сигна­лом управления, небольшим по величине, но обратным по знаку по отношению к :  < 0. Сформировавшаяся в процессе обучения силовая характеристика будет иметь в принципе такой вид, который представлен на рис. 3.19,a. Воспользовавшись простейшим отобража­ющим преобразованием:

 

, —

 

получим физический склон (рис. 3.19,б). За физическое отображение головы робота, как обычно, примем шарик. В отображающем преобра­зовании на этот раз не учтено сухое трение; это сделано для того, чтобы получить склон, так сказать, в натуральном виде, без всяких виртуальных уклонов, а сухое трение и динамическое сопротивление будем иметь в виду, зная, что то и другое тормозят движение.

Полученный склон (рис.3.19,б) образует в районе цели () лунку, как место притяжения шарика. Нетрудно предположить, как он будет вести себя в этой лунке. Варианты такие: 1) по инерции ша­рик переваливает через край лунки и скатывается дальше по склону; 2) шарик совершает в лунке незатухающие колебания (автоколебания); 3) постепенно колебания шарика в лунке затухают; 4) шарик останав­ливается в лунке без колебаний; последний вариант — самый предпо­чтительный. Очевидно, поведение шарика в лунке определится соотно­шением таких факторов: с одной стороны — активной силой, инерцией самого шарика и его скоростью на подходе к лунке, а с другой сто­роны — силами сопротивления.

 

 

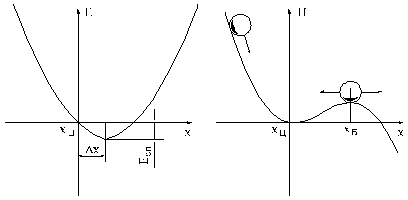
Рис. 3.19. Физическое отображение динамики привода продольного перемещения с противосклоном

 

Координатой  обозначена на рис. 3.19,б позиция бифурка­ции: оказавшись в этой точке без скорости, шарик с равной вероятностью может либо вернуться назад в лунку, либо скатиться дальше по склону.

Дальнейшие наши исследования сведём к выбору величин введён­ных дополнительных параметров  и . Сигнал управления  следует выбирать, очевидно, из тех соображений, что глаз, с одной стороны, не должен проходить мимо искомых предметов, если они даже несколько различаются между собой по внешнему виду, а с дру­гой стороны, не должен останавливаться у посторонних предметов, пусть даже похожих на искомые.

Выберем среди искомых предметов два, в наибольшей мере разли­чающихся между собой; и пусть их степень сходства равна . А среди посторонних предметов найдём такой, какой более всего похож на идеальный искомый; и пусть степень сходства его о ним равна . Нормальным условием, очевидно, следует считать, что >. В противном случае обучаемая система не справится с задачей сортировки предметов на искомые и посторонние. Впрочем, в такой ситуации человек тоже будет ошибаться. И будем рассуждать следующим образом. Идеальный искомый предмет (пронумеруем его цифрой 1), породит согласно обучению сигнал управления = -; любому другому предмету будет соответствовать сигнал больше . Только, всё равно, договоримся считать, что любые искомые пред­меты будут порождать сигналы управления меньше нуля, и в крайнем случае — нулевыми, а посторонние — больше; так что второй выбран­ный нами искомый предмет должен дать <0, а выбранный посто­ронний (№3) — должен дать >0. Следовательно, условия пра­вильной сортировки предметов примут вид

 

;   .

 

С другой стороны разность сигналов управления (-) и (-) можно выразить через степень сходства  и . Для этого применим те же рассуждения, что и при формировании выражения (3.48). Тогда мы анализировали потенциальные возможности системы и опре­деляли роль степени усиления сигнала управления; продолжим эту мысль.

Пусть система уже обучена и коэффициент усиления уже выбран. Если теперь предъявить системе предмет, абсолютно похожий на тот идеальный, что применён в обучении, то, надо полагать, сигналы управления, порождаемые ими, будут неразличимыми; другими словами: если степень сходства равна единице, то разность сигналов равна нулю. Предъявив же предмет №3, имеющий некоторое отличие от предмета №1 (>1), получим явно не нулевую разность (-) эта разность будет коррелироваться с величиной (1-), то есть со степенью различия предметов.

В общем случае, в пределах того, о чём мы ведём речь, явно просматривается прямая связь разности сигналов управления в двух ситуациях со степенью различия образов этих ситуаций:

 

,                                      (3.67)

 

где k — коэффициент передачи, учитывающий усиление на выходе из мозга.

Согласимся, что говорить о полной линейности выражения (3.67) никак нельзя, но в узком интервале и в схожих обстоятельствах она искажается незначительно; что же касается прямой пропорции выражения (3.67), то сомнения в ней едва ли могут возникнуть. Поэтому в нашем случае можно записать:

 

;  .

 

И условия правильной сортировки предметов приобретут следую­щий вид

 

;   .             (3.68)

 

Эти условия можно представить в несколько ином виде, если за­менить в них степень сходства S на степень различия Р, опираясь на соотношение

 

.

 

В результате получим:

 

;  ,

 

где  — наибольшая степень различия образов любых двух иско­мых предметов;  — наименьшая степень различия образов иско­мого и постороннего предметов.

Таким образом, условия (3.68) позволяют выбрать величину сигнала управления , которую необходимо задать в дополнительной сопредельной ситуации, чтобы обеспечить надёжный поиск различа­ющихся искомых предметов. Любому постороннему предмету, как бы он не был похож на искомый, будет соответствовать такой сигнал управления, который будет приводить к надёжному сползанию глаза.

Смещение , определяющее положение искомого предмета в до­полнительной сопредельной ситуации, следует выбирать из сообра­жений динамики системы. Увеличение смещения  будет способ­ствовать повышению надёжности «захвата» глазом искомого предме­та, но приведёт к некоторой неустойчивости привода: в положении, близком к цели, могут появиться колебания и даже автоколебания. Уменьшение смещения  может породить проскакиваете цели. Бо­лее конкретные рекомендации могут быть получены в результате построения фазовых траекторий с учётом действительных характе­ристик.

На рис. 3.20 представлены два случая с различными смещениями . В первом случае а) смещение относительно большое, и все возможные (почти все) фазовые траектории устремляются в положению цели , при этом наиболее характерная траектория, начинаю­щаяся с фоновой скорости , приходит к центру с возвратом, то есть сначала голова робота проскакивает искомый предмет, а затем возвращается к нему. Фазовая траектория со штриховкой является бифуркационной, то есть граничной; как видно из рис.3.20 проскакивание цели маловероятно.

 

 

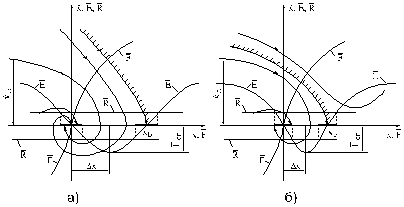
Рис. 3.20. Фазовые траектории продольного перемещения
с противосклоном

 

Во втором случае (рис. 3.20, б) смещение  при всех прочих равных условиях меньше предыдущего, и это отразилось на фазовых траекториях. Бифуркационная траектория (со штриховкой) выглядит теперь далеко не крайней, а это говорит о том, что вероятность проскакивания цели явно увеличилась; хотя траектория с начальной фоновой скоростью  по-прежнему возвращается к цели.

Положение бифуркации  на оси  в обоих случаях сов­падает с вершиной гребня противосклона в физическом отображении; и можно было бы, казалось, говорить о завершении движения в этих точках, тем более о учётом сухого трения, которое растягивает указанные точки до участков (на рис. 3.20 выделены жирными от­резками), однако такая приостановка — ненадежная: под воздей­ствием любого, даже самого слабого сотрясения голова робота будет оползать либо в ту, либо в другую сторону. Таким образом, если позиция , притягивает траектории и может рассматривать­ся как аттрактор, то позиция  отталкивает их и является типичной бифуркацией.

Увеличение смещения сопредельной ситуации относительно целевой, способствующее надёжности поиска, может оказаться, к сожалению, причиной «неразберихи», если искомые и посторонние предметы будут располагаться на расстоянии друг от друга, менее ; поэтому окончательные решения и по стратегии обучения, и по обучаемой выборке, и по конкретным параметрам можно принимать лишь в резуль­тате подробных исследований, совмещая их с практикой обучения. Самый простой путь — дообучение робота: если он проскакивает ис­комые предметы, — заставлять его останавливаться; если же его глаз зависает на посторонних предметах, — подталкиванием прогонять его дальше.

На этом рассмотрение процедуры продольно-поперечного поиска закончим. В заключение ещё раз отметим, что поиск — не самоцель; он всегда предшествует последующим действиям, которые могут начаться только после того, как будет переключено внимание объекта. Итак, допустим, робот нашёл тот предмет, который искал, и требуется его захватить. Пере­ключение внимания на захват может осуществить образ найденного предмета — это самое простое решение: видит глаз определённый пред­мет — происходит переключение питания рецепторных участков; про­изошло переключение — включается в работу захват. Очевидно, все эти процедуры должны быть предусмотрены в обучаемой выборке, и робот должен быть обучен всему этому. Переключение внимания с учётом нулевых сигналов управления приводов поиска возможно только с под­ключением так называемого мыслительного блока, в котором входные сигналы заведены обратными связями как рецепторы самого мозга; в этом случае процедура распознавания несколько сложнее.

 

 

4.3. Колебания глаза

 

Сходство функциональных назначений технического глаза обучае­мой системы управления и глаза животных, в том числе человека, побуждает к осмысленному переложению особенностей живого зрения, приспособленного к поиску, на техническое. Одной из таких особенностей являются колебания глаза. Различают несколько типов этих колебаний; наиболее ярко выражены скачки, благодаря которым глаз перескакивает с точки на точку сво­его внимания. Определён термин таких скачков — саккады. Скачки — саккады не носят регулярного характера и постороннему наблюдате­лю кажутся хаотичными. Есть дрейф — плавное смещение глаза в одном каком-либо направлении, и есть тремор — регулярные колебания глаза с определённой частотой и почти неизменной амплитудой. Колебания — тремор ещё называют микросаккадами, но по виду своему они нисколь­ко не похожи на саккады. Вое эта колебания своих глаз человек, как правило, не замечает; они ему не мешают. Более того, как показали эксперименты, устранение этих колебаний создаёт человеку опреде­лённые неудобства. Следовательно, колебания не есть нежела­тельная неустойчивость приводов глаз, вытекающая из самой природы автоматического наведения, а является положительным свойством /3.I3/. Сосредоточим свое внимание на треморе и попытаемся, исходя из теории обучаемых систем управления, обосновать целесообразность введения его в техническое зрение.

Уточним параметры тремора глаз человека. Амплитуда тремора сос­тавляет у разных людей от нескольких десятков угловых секунд до 1,2 угловой минуты; частота колеблется от 30 до 100 Гц /3.1/. По другим источникам /1.41/ колебания совершаются несколько раз в се­кунду на величину I...2 угловых минуты. Расхождения в параметрах у разных источников — несущественные. Что интересно, амплитуда тре­мора соизмерима с наименьшим расстоянием между двумя точками, которые способен различать человек; она равна приблизительно 0,5 угловых минуты. Приведём ещё такие данные из нейробиологии: одно волокно зрительного нерва охватывает примерно 125 рецепторов глаза; одна ганглиозная клетка сетчатки, объединявшая несколько рецепторов, охватывает своим рецепторным полем примерно 3 угло­вых градуса всего поля зрения или около одного миллиметра на сет­чатке; рецептивные поля ганглиозных клеток накладываются друг на друга с некоторым смещением.

Нэйрофизиологи, говоря о треморе, обычно отмечают такие поло­жительные моменты его влияния: он, прежде всего, устраняет адап­тацию рецепторов, как нежелательное явление; без колебаний глаз неподвижные предметы в поле зрения через несколько секунд стано­вились бы невидимыми; во-вторых, было замечено, что тремор обостряет остроту зрения; тонкие линии он делает более различимыми.

Объектом нашего внимания является технический глаз обучаемой системы управления, рецепторами которого являются обычные фоторе­зисторы, например из германия, из кремния или из соединений кад­мия с серой, селеном, теллуром /З.З/. Фоторезисторы имеют хорошую, близкую к линейной чувствительность, но страдают такими недостат­ками, как малое быстродействие и относительно большие габариты. Постоянная времени фоторезисторов , характеризующая их быст­родействие, колеблется в пределах 0,03...0,08 секунды, а габариты фоточувствительной площадки измеряются миллиметрами. В качестве рецепторов глаза могут быть использованы фотодиоды или лавинные фотодиоды, но у них имеются свои недостатки. У всех перечисленных технических фоторецепторов отсутствует адаптация, характерная для рецепторов живого глаза. Говоря техническим языком, адаптация есть регулирование по реально-дифференцирующему закону. Можно, разуме­ется, в каждый рецептор встроить электрическую схему с таким зако­ном регулирования, но в данном случае будем рассматривать простые фоторецепторы без подобных схем.

При использовании в качестве оптики технического глаза объек­тивов типа Гелиос с углом зрения 28 градусов и диаметром изобра­жения не более 50 мм можно расположить в этой зоне сетчатку с 2000 фоторезисторов, то есть до 50 штук по диаметру. Таким об­разом, один рецептор будет охватывать приблизительно 0,5 угловых градуса поля зрения или 1 мм сетчатки.

Охарактеризуем возбуждения рецепторов сетчатки. В силу нелинейностей фоторезисторных свойств рецепторов и оптических искажений поле возбуждений рецепторов будет, очевидно, отличаться от изображения на сетчатке, а это изображение — от видимой сцены. Но в данном случае эти отличия нас не интересуют, и поэтому обобщим и то, и другое, и третье одним понятием — образ. Элементами об­раза, как известно, являются пятна, границы или контуры пятен, линии, точки и полутоновые участки. Напомним, что пятно есть участок рецепторного поля с равными возбуждениями рецепторов, причём при смещении изображения на величину не более, чем на один рецептор, возбуждения сохраняются неизменными. Пятна могут быть светлыми, тёмными или серыми. Рецепторы света, возбуждающиеся на свету, будут иметь соответственно наибольшее, наименьшее или частичное возбуждение. Рецепторы же темноты, возбуждающиеся в темноте, наоборот, — соответственно наименьшее, наибольшее или частичное обратное возбуждение. Граница пятна или контур включа­ет только те рецепторы, возбуждение которых изменяется при сме­щении изображения по сетчатке на один рецептор. Линия есть тот же контур, но без пятна; при смещении изображения поперёк линии на один рецептор возбуждения всех рецепторов изменяются. Точка охватывает только один или несколько, но малое число рецепторов, и при смещении в любом направлении возбуждения их изменяются. Полутоновые участки характерны тем, что рецепторы их хотя и слабо, но изменяют своё возбуждение при любом смещении изображений.

Влияние колебаний глаза на зрительный образ. Прежде чем выдать рекомендации по введению колебаний технического глаза (тремора), посмотрим, как эти колебания отразятся на образе, то есть на изо­бражении сетчатки. Из всех элементов образа важнейшими являются линии и точки; только у них при малых смещениях изображений по сет­чатке глаза происходят существенные изменения возбуждений рецепто­ров, и только эти изменения могут обеспечить требуемые изменения сигналов управления обучаемых систем. Рецепторы полутоновых участ­ков и, тем более, пятен в изменении сигналов управления участия практически не принимают. Тонкие линии, ширина которых соизмерима с размерами оптических окон рецепторов или даже меньше их, могут оказаться незамеченными глазом.

Введём колебания глаза. Амплитуда этих колебаний, скорее всего, должна быть соизмеримой с размерами рецепторов, а частота — с по­стоянной времени рецепторов , то есть со временем запаздыва­ния срабатывания фоторецепторов. Более точные параметры колебаний определим дальше. Колебания, о которых идёт речь, не должны распро­страняться на остов: если глаз закреплён на охвате робота, то при­воды колебаний должны смещать глаз относительно охвата; причём же­лательно заставлять колебаться глаз в двух направлениях в плоскос­ти, перпендикулярной оптической оси глаза.

Сосредоточим своё внимание на некоторой линии образа, изобразим её в виде полосы шириной а (рис. 3.21) и заставим колебаться в поперечном направлении по синусоидальному закону с амплитудой А и частотой w:

 

.

 

Считаем, что линия (полоса) ярко выделяется на общем фоне и за­свечивает фоторецепторы сетчатки глаза. На самом деле линия может быть тёмной на светлом фоне, но, учитывая, что сетчатка включает кроме так называемых рецепторов света, ещё и рецепторы темноты, тём­ные линии можно приравнять к светлым, и также можно говорить о яркости тёмных линий.

Во время колебаний зона засветки оказывается шире полосы на ве­личину двух амплитуд. Однако вследствие колебаний рецепторы будут освещены не всегда, а только в момент выхода на них полосы. Те из них, которые освещены постоянно, или почти постоянно, будут возбуждены максимально, но а те, на которые свет падает кратковремен­но, окажутся возбуждёнными лишь частично. Определим степень зас­ветки рецепторов в зависимости от смещения их от центрального поло­жения. Обозначим через х — смещение края полосы в поперечном на­правлении и заменим в синусоидальном законе частоту w на период Т:

 

,

 

где  — время начала засветки.

 

 

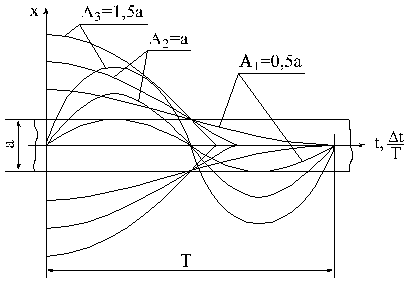
Рис.3.21. Зависимость засветки рецепторов от колебаний глаза

 

Полное время засветки за один период колебаний Т определится как

 

,

 

а с учётом синусоиды получим:

 

.                       (3.69)

 

На рис. 3.21 изображены: полоса шириной а, три синусоиды с амплитудами: ; ; , — и кривые зависимости продолжительности засветки рецепторов в течение одного периода Т от удалённости рецепторов х. Как видно из графика, рецепторы, расположенные на оси t, будут освещены полосой по­стоянно, если амплитуда колебаний полосы А окажется меньше поло­вины ширины а. При А=а те же рецепторы будут освещены только 2/3 времени периода Т, а при  — ещё меньше: . Но при любой амплитуде колебаний полосы время освещения ею указан­ных рецепторов не будет меньше половины периода Т. Рецепторы, расположенные не по центру полосы, будут освещены меньше; чем даль­ше от центра, те ещё меньше. Координата крайней освещённой точки определяется как , а общая ширина освещаемой зоны будет равна .

Теперь посмотрим, как будут возбуждаться рецепторы под воздей­ствием мелькающего света. Закон роста возбуждения (проводимости) фоторезистора в этом случае может быть представлен в виде экспо­ненты:

 

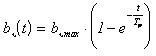,                            (3.70)

 

где  — наибольшее возбуждение фоторезистора при непрерывном освещении его полосой.

Примем за время отсчёта начало засветки фоторезистора; тогда в конце засветки возбуждение возрастёт до такой величины:

 

,

 

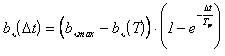где  — остаточное возбуждение от засветки в предыдущем периоде.

После засветки рецептор погружается в темноту, и возбуждение его начинает спадать по тому же закону экспоненты:

 

.                               (3.71)

 

В конце затемнения возбуждение фоторезисторов снизится согласно (3.71) до значения

 

.

 

В результате можно определить высшее возбуждение фоторезистора в конце засветки:

 

,

 

и его низшее возбуждение в конце затемнения:

 

.

 

На рис.3.22 представлена кривая изменения возбуждения фоторезистора во времени t при условии, что . Среднее возбуждение  фоторезистора можно определить по кривой (рис.3.22) путем интегрирования выражений (3.70) и (3.71) и деления суммарной величины на период Т. Однако, учитывая то, что экспонента спадания возбуждения (3.71) по своим параметрам повторяет экспоненту роста (3.70), а также то, что начальные и конечные точки этих экспонент совпадают, на этом основании можно утверждать, что

 

.                                (3.72)

 

 

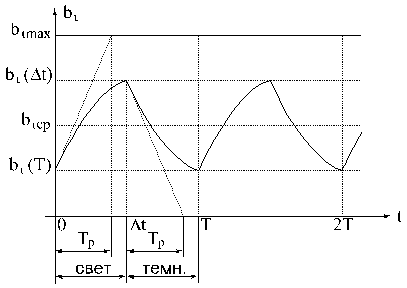
Рис. 3.22. График возбуждения фоторецептора
при мелькающей освещении.

 

Если же учесть, что ионизация токопроводящего слоя обычных, упомянутых выше фоторезисторов порождается исключительно светом и не носит лавинный характер, как у лавинных фотодиодов, то до­пустимо считать, что среднее возбуждение  каждого фоторе­зистора будет пропорционально засветке :

 

.

 

С учётом (3.69) последнее выражение примет вид:

 

.         (3.73)

 

И выражение (3.72), и выражение (3.73) в общем случае дают раз­мытое изображение линии на сетчатке глаза с увеличением её ширины. Хорошо ли это или плохо? То, что все видимые линии становятся тол­ще, — это ещё не значит, что они становятся более видимыми. Если уширение линии осуществить без полутонов, ступенчато, то такая линия становится пятном, и решающим фактором изменения сигнала управления становится лишь край этой уширенной линии. Другое дело — полутоновое, размытое к краям изображении линии на сетчатке гла­за: любое смещение изображения приводит к изменению возбуждений рецепторов, охваченных этой линией. И чем шире размыта линия, тем больше рецепторов фиксируют её. В этом смысле размывание линий действительно способствует обострению остроты зрения (хотя понятие остроты зрения требует особого толкования).

Однако такой вывод справедлив лишь в отношении отдельной линии. При наличии нескольких рядом расположенных линий размывание их может привести к стиранию границ между ними, то есть к потере ост­роты зрения. Другими словами, отдельно расположенные линии при ко­лебаниях глаза будут фиксироваться большим количеством рецепторов и тем самым ярче выделяться, но плотно расположенные линии будут сливаться в общее пятно. Именно так видит человеческий глаз: до определённого момента он отчётливо различает тонкие линии и мелкие точки, а дальше — при сближении их — изображения линий и точек сливаются. Граница различимого-неразличимого человеческого глаза известна, и она удачно используется в телевизорах, где пятьсот строк сканирования при определённых размерах экрана обеспечивают восприятие изображения как непрерывного. С учётом указанных осо­бенностей человеческого глаза сформировалась также точечная поли­графия.

Острота зрения как следствие обучения.  А теперь — об инженер­ном толковании остроты зрения (уточним: технического зрения) с по­зиции обучаемых систем. Очевидно, какой бы рельефной (контрастной) ни была видимая сцена, глаз не задержит своего внимания ни на чём в этой сцене, если он не обучен этому; и говорить в этом случае об остроте зрения бессмысленно. Вот если обучаемая система управле­ния со зрением обучена отыскивать вокруг себя заданные предметы, зрительно выделяющиеся на общем фоне, или любые изображения (для глаза предметы — тоже изображения), то тогда и возникает острота зрения.

Из чего она складывается?

Изменение любого образа В, как известно, порождает соответствующее изменение сигнала управления:

 

;   .

 

Величина  становится определённой только в том случае, когда она выделяется из общего «шума», то есть когда , где  — уровень «шума» (или допустимое отклонение). Такой порог чувствительности и определяет остроту зрения. Он порождается соот­ветствующим изменением  образа при соответствующем состоя­нии мозга:

 

;  .

 

Обострить остроту зрения, то есть усилить изменение образа до граничного значения , можно различными способами, напри­мер дополнительной подсветкой обозреваемой сцены, или наведением оптики на большую резкость, или увеличением напряжения питания технического глаза. Но можно обострить, оказывается, с помощью колебаний глаза.

Чтобы объяснить это, рассмотрим более подробно техническое зре­ние. В конечном счёте острота зрения проявляется не в простом из­менении сигнала управления на величину, больше чем  (хотя в общем случае это справедливо), а в сосредоточении внимания на заданном объекте или, говоря иными словами, в надёжном поиске. Если глаз реагирует на изменение образа и с помощью технического мозга заставляет привод смещать схват в сторону выделенного пред­мета, то, следовательно, этот глаз в данном случае имеет необхо­димую остроту зрения. Её можно считать достаточной и в том случае, если схват притормаживает при выходе на посторонний, но схожий по виду предмет и притормаживает ровно на столько, на сколько необходимо для надёжного обозревания предмета. Значит, кроме зри­тельного выделения на общем фоне искомых и похожих на них пред­метов, должен сформироваться соответствующим образом в процессе обучения сам технический мозг, то есть образ С. А так как про­водимости технических синапсов, как известно, в процессе обучения изменяются под воздействием возбуждений соответствующих рецепто­ров, то, очевидно, наибольшие изменения претерпят только те си­напсы, рецепторы которых окажутся наиболее возбуждёнными. Это оз­начает, что при обучении в целевых ситуациях яркие пятна, линии и точки образов этих ситуаций оставят в мозгу наибольший след. Если говорить об отдельной линии образа целевой ситуации, то ей будет соответствовать некоторое проявление в мозгу, которое «ска­жет своё слово» в момент выхода в процессе работы на эту же целе­вую ситуацию. Так во время поиска заданного предмета при прибли­жении к нему линии (контуры) его изображения на сетчатке глаза постепенно будут надвигаться на проявления этих же линий в мозгу, и, как только они сольются, схват остановится — предмет найден.

Образно говоря, рельеф состояния мозга С напоминает рельефы образов ситуаций В обучаемой выборки, и в том числе — целевых с нулевыми сигналами управления, а посему в момент выхода глаза на любую целевую ситуацию, то есть в момент нахождения заданного предмета, оба стыкующихся рельефа (образа ситуации В и образа состояния мозга С) находят, как бы, наиболее плотное прилега­ние друг к другу с наименьшей потенциальной энергией, точнее го­воря — с нулевой, так что дальше глаз перемещаться уже не сможет: предмет найден. Продолжая это же образное сравнение, можно ска­зать, что в прочих нецелевых ситуациях указанные рельефы не име­ют плотного прилегания и скользят друг по другу, как скользит шарик по неровной поверхности в поисках лунки. В этом смысле В, С и Е отражают, образно говоря, штамп:  В — пуансон, С — матрица, а Е — зазор между ними.

Возвращаясь к исследуемым линиям образов ситуаций, можно пред­ставить их в виде выступающих рёбер рельефа, а их проявления в мозгу — в виде желобов (соответственно: точка — бугорок, а прояв­ление точки в мозгу — лунка), и при сближении рёбер и желобов они стыкуются. Нельзя забывать при этом, что проявление зрительных элементов в мозгу никоим образом не является простым их отпечатком. При наложении в процессе обучения одних ситуаций на другие и при многократном повторе картина проводимостей синапсов в мозгу ока­жется очень сложной и далеко не однозначной по отношению к кон­кретному зрительному образу. Тем не менее след от отдельных си­туаций всё же в мозгу останется; точнее говоря, это — уже даже и не след, а некоторое искажённое проявление его.

Сравним в образном представлении линии без колебаний и с коле­баниями глаза. Без колебаний — линии будут выглядеть как узкие рёбра с отвесными краями, а их проявления в мозгу — как такой же ширины щели. Хотя очертания этих рёбер и этих щелей полностью сов­падают и они могут плотно прилегать друг к другу, но находить друг друга рёбра и щели будут с трудом: достаточно иметь самое малое смещение, и стыковка невозможна. Даже стремясь друг к другу, они легко будут проскакивать позицию совпадения. Отсюда следует, что схват с глазом обречён на неустойчивость, которая усугубляется инерцией головы робота и запаздыванием срабатывания фоторецепто-ров.

Другое дело — при треморе, то есть при колебаниях глаза относи­тельно схвата. Линию теперь можно представить уже в виде выступа­ющего широкого ребра с пологими сторонами, а проявления линии в мозгу — в виде такой же ширины жёлоба также с пологими краями. И нахождение, и стыковка этих рёбер и желобов могут осуществляться без каких-либо трудностей. Достаточно попасть пологой стороне ребра на край жёлоба, и начнётся естественное «скольжение» к полному совпадению, к стыковке данных ребра и жёлоба, то есть к выходу схвата с глазом на искомый предмет. Пологие профили рё­бер и желобов предотвращают неустойчивость приводов головы робо­та в нулевой позиции, снижая влияние инерции головы и апериоди­ческого запаздывания системы. Скольжение ребра по склону жёлоба можно назвать проявлением остроты зрения.

С другой стороны, пологие склоны рёбер и желобов таят в себе некоторую опасность «зависания» на них: чем положе склон, тем ме­нее проявляется стремление двигаться под действием его уклона. Так детские санки на слабом склоне горки могут не скользить вниз. Причиной «зависания», как обычно, может быть сухое трение приво­да и механизма, которое преодолевается только тогда, когда сигнал управления Е привода достигает своего порогового значения. Вы­ход из положения связан опять же с тремором: колебания глаза при­водят к пульсированию сигнала управления, и в позиции, близкой к целевой, такое пульсирующее подталкивание приведёт к дальней­шему скольжению по склону вплоть до почти нулевой отметки. Прав­да, в других позициях, далёких от целевых, пульсирование сигнала управления не позволяет стабилизироваться любому положению схвата робота, и схват с глазом смещается даже в том случае, когда нет для этого видимых причин. Это и есть тот дрейф, то есть бес­цельное плавное блуждание, который отмечен у человеческого глаза.

Выбор параметров колебаний глаза. Итак, колебания-тремор тех­нического глаза способствуют выделению искомых предметов, поиску их, быстрейшему выходу на них и стабилизации положения после на­хождения. Другими словами, колебания-тремор обостряют зрение или, проще, улучшают его. И такое улучшение наблюдается почти на всём пространстве зрительных возможностей за исключением только того, что очень мелкие детали зрительного поля, напротив, сливаются и глазом не выделяются. Но и это можно расценить как улучшение зрения: благодаря такой способности глаза можно, оказывается, линей­ные или точечные, то есть дискретные изображения воспринимать непре­рывными, монолитными.

Если целесообразность введения в техническое зрение колебаний-тремора считать очевидной, то возникает вопрос выбора параметров этих колебаний: какими они должны быть? Практика, разумеется, даст свой ответ на поставленный вопрос, а пока приходится руководствова­ться логическими соображениями.

И одним из этих соображений может быть необходимость. Колебания глаза должны быть такими, чтобы различать вполне определённые по раз­мерам мелкие предметы или детали этих предметов. Допустим, робот предназначен для монтажа электрических плат. Самыми мелкими деталями плат являются отверстия в этих платах и ножки устанавливаемых в них микросхем. Значит, глаз должен их различать с расстояния, допустим, 0,5 метра. Достаточно пересчитать размеры указанных мелких деталей в масштаб сетчатки глаза, чтобы определить их угол зрения. Пусть их размер окажется равным полградусу угла зрения объектива; тогда ампли­туда колебаний глаза может составлять порядка 0,25...0,50 угловых градуса. Такой вывод следует из анализа кривых зависимости продолжи­тельности засветки от соотношения ширины линии и амплитуды колеба­ний (рис. 3.21). Что же касается выбора частоты колебаний, то, исхо­дя из тех же соображений необходимости, можно рекомендовать как мож­но большую частоту.

Другим соображением при выборе параметров колебаний-тремора может быть соотношение их с параметрами глаза, в частности с размерами и с постоянной времени рецепторов. Пусть амплитуда колебаний будет рав­на половине угла зрения одного рецептора, то есть 0,25 угловых гра­дуса. При равных размерах амплитуда и ширины полосы (А=а) полу­чается, что глаз окажется способным различать предметы с размерами, соответствующими приблизительно 0,75 угловых градуса. Более мелкие детали поля зрения будут сливаться. Частоту колебаний следует выби­рать с учётом того, что период колебаний Т должен быть больше по­стоянной времени  рецептора, но обязательно меньше постоянной времени привода робота: . Если известные фоторезисторы имеют = 0,03...0,08 сек, то период можно принять равным Т = 0,05...0,10 сек при условии, что  = 0,20 сек.

Ещё одним соображением при выборе параметров колебаний-тремора глаза может быть реальная возможность. Приведённые выше параметры фоторезисторов не очень удачные для технического зрения. Желательно было бы иметь такие фоторецепторы, размеры оптических окон которых не превышали бы сотых или даже тысячных долей миллиметра, а посто­янная времени — измерялась бы тысячными и менее долями секунды. Тог­да при обычной оптике типа объективов фотоаппаратов можно было бы довести число рецепторов в сетчатке глаза до десятков и сотен ты­сяч, а быстродействие робота, оснащённого техническим зрением, — до быстродействия широко известных робототехнических, станочных и иных приводов.

И, наконец, можно принять за эталон известные параметры колебаний человеческого глаза.

 

 

Примеры и задачи

 

Пример 3.1. Расчетное обучение принятию решений в двух ситуациях при квадратичном законе саморегулирования синапсов.

Исходные данные: в таблице 3.1. Исходные данные приняты такими, как в примере 1.2; это позволит сравнить результаты.

Таблица 3.1.

Исходные данные

Ситуации	Возбуждения рецепторов				Требуемые решения	Допустимые погрешности
А	1	2	1	2	1	0,1
В	2	1	2	1	2	0,1

Первоначальные проводимости синапсов равны нулю.

Требуется: вычислить пошаговые погрешности  и проводимости синапсов  методом расчетного обучения по алгоритму: (1.12), (1.13), (1.14), (3.7), (1.16), — и сравнить результаты с обучением при линейном законе саморегулирования синапсов.

Выполнение:

Цикл 1-ый, шаг 1-ый, ситуация А:

Фактическое решение: .

Погрешность: .

По формуле (3.7) вычисляем поправки проводимостей синапсов:

 

;   ;

 

; 

 

Проводимости синапсов:

 

;            ;

 

;          

 

Цикл 1-ый, шаг 2-ой, ситуация В:

 

;

;

;

;

;

.

 

И так далее. Обучение продолжим до тех пор, пока абсолютное значение погрешностей  в обеих ситуациях не окажется меньше 0,1. Результаты обучения представлены в таблице 3.2.

Таблица 3.2.

Результаты обучения

Цикл	Ситуации	Погрешность	Проводимости синапсов
0		0,0	0,0	0,0
1   2   3   4   5	А В А В А В А В А В	1,0 1,33... -0,844 0,6 -0,4 0,27 -0,177 0,12 -0,079 0,0528	0,055... 0,35 0,3 0,433 0,411 0,47 0,46 0,4868 0,4824	0,22... 0,296 0,1 0,133 0,044 0,059 0,01966 0,02637 0,008796

 

Изобразим в виде графика изменения абсолютных погрешностей по циклам обучения и сравним с таким же графиком при линейном законе саморегулирования синапсов (рис.3.23).

 

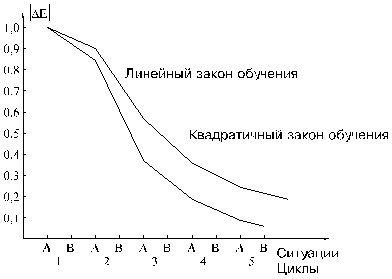
Рис. 3.23. Изменение погрешностей численных значений решений в процессе обучения при квадратичном и линейном законах
саморегулирования (обучения синапсов)

 

Пример 3.2. Расчетное жесткое обучение принятию решений в двух ситуациях с переменным перерегулированием.

Исходные данные: те же, что и в примере 3.1. Исходные проводимости синапсов равны: 0,3967; 0,2048, — что соответствует предварительному обучению по нормальному алгоритму в двух циклах. Жесткость обучения: h=0,5.

Требуется: Вычислить пошаговые погрешности  и проводимости синапсов  методом расчетного обучения по алгоритму: (1.12), (1,13), (3.23), (3.15), (1.14), (3.24), (1.16), — и сравнить результаты с результатами примера 1.2.

Выполнение:

Цикл 3-ий, шаг 1-ый, ситуация А:

 

;

;

;

;

;

.

 

Цикл 3-ий, шаг 2-ой, ситуация В:

 

;

;

;

;

;

.

 

Цикл 4-ый, шаг 1-ый, ситуация А:

 

;                                           ;

;                  ;

;                            .

 

Цикл 4-ый, шаг 2-ый, ситуация В:

 

;                                        ;

;                     ;

;                         .

 

Цикл 5-ый, шаг 1-ый, ситуация А:

 

;                                     ;

;;

;                       .

 

Цикл 5-ый, шаг 2-ый, ситуация В:

 

;                    .

 

Погрешность  меньше допустимой d=0,1. Определим погрешность  в ситуации А:

 

;

, — также меньше 0,1.

На этом расчётное обучение прекращаем. Результаты обучения представлены в виде графиков на рис. 3.24, с наложением их на графики рис. 1.17.

 

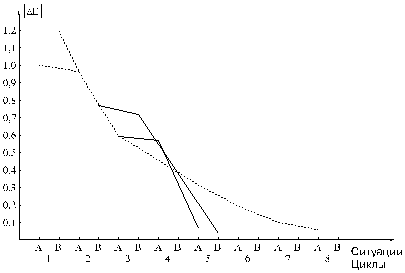
Рис. 3.24. Изменение абсолютных значений погрешностей в зависимости от продолжительности в циклах при жестком обучении с переменным перерегулированием (h=0,5). Штриховыми линиями выделены те же зависимости при нормальном обучении

 

Вывод: Жёсткое обучение с переменным перерегулированием при h=0,5 сокращает продолжительность обучения.

 

Пример 3.3. Разделение очувствления на рецепторные участки с целью переключения внимания системы с решения одних задач на другие.

Исходные данные: система может различать ситуации, степень сходства образов которых не превышает 0,94; допустимый коэффици­ент увеличения напряжения питания рецепторов u = 2; напряжение питания рецепторов может иметь только два уровня: нормальный и повышенный, — то есть градация g = 2.

Требуется: определить максимальное количество участков, на ко­торое можно разбить очувствление; определить число решаемых задач; вычислить продолжительность обучения при требуемых сигналах управ­ления:  = +5;  = -5, — и при допустимом отклонении d = 0,01.

Выполнение:

Подставим в выражение (3,46) степень сходства = 0,94 и коэффициент увеличения напряжения u = 2:

 

.

 

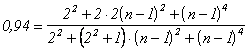Решим его относительно n; получим     n = 4,36; округляем в меньшую сторону: n = 4. Следовательно, очувствление можно разбить максимально на 4 рецепторных участка.

По формуле  определим число задач, которые требуют пере­ключения внимания системы:

 

.

 

Столько независимых задач может решить система, имеющая 4 рецепторных участка.

По формуле (2.21) определим продолжительность обучения при ус­ловии, что степень сходства образов наиболее схожих ситуаций при­нята предельно допустимой: =0,94, а коэффициенты приведения этих образов — прямой и встречный — равны между собой:

 

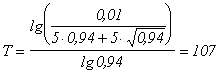циклов.

 

Пример 3.4. Суждение о сходстве образов ситуаций с образами мозга.

Исходные данные: три ситуации с сигналами управления в них: в первой — нулевой; во второй — максимально положительный; в третьей — максимально отрицательный.

Требуется: охарактеризовать образы мозга  и , на основе сравнения их с образами указанных трёх ситуаций.

Выполнение:

Очевидно:

· в первой ситуации: ;

· во второй ситуации: ;

· в третьей ситуации: .

Рассмотрим первую ситуацию; согласно выражений (3.53) получим:

 

;    .

 

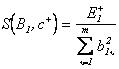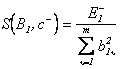А так как , то:

 

.

 

Из этого можно вывести только одно заключение: образ ситуации одинаково соотносится с образами мозга  и . Применительно к оптической обучаемой системе это означает, что оптическое изо­бражение ситуации , пропущенное через диапозитивы мозга  и , образует на фотоэлектрических экранах приблизительно оди­наковые рисунки (если выражаться точнее — одинаковую освещённость экранов). То же самое можно сказать и про соотношения резисторного поля очувствления с резисторными полями плюс- и минус-столб­цов мозга электрической обучаемой системы.

Образ второй ситуации более похож на образ  и мало похож на образ .Это говорит о том, что светлые и тёмные пятна оп­тического изображения второй ситуации совпадают с почти такими же по форме светлыми и тёмными пятнами диапозитива мозга  и не совпадают с подобными пятнами диапозитива ; в последнем слу­чае, может быть даже, реализуется перекрёстное совмещение светлых пятен с тёмными. Образ третьей ситуации, наоборот, более похож на  и не похож на .

 

Пример 3.5. Выбор противоуклона продольного перемещения при поиске.

Исходные данные: наименьшая степень сходства любых двух иско­мых предметов = 0,990; наибольшая степень сходства искомого предмета с посторонним = 0,988; коэффициент передачи мозга, учитывающий усиление на выходе, k = 100.

Требуется; выбрать величину сигнала управления  в допол­нительной сопредельной ситуации, образующей противоуклон продоль­ного перемещения.

Выполнение:

Воспользуемся выражениями (3.68).

 

;       .

 

Получим:

 

.

 

Выбираем: =1,1

Знак сигнала  принимаем обратным по отношению к сигналу управления  в фоновой ситуации.

 

Задача 3.1. Расчётное обучение принятию решений в двух ситуациях при нелинейных законах работы и обучения.

Исходные данные: см. табл. 3.1. Исходные проводимости синапсов равны нулю.

Требуется:

Вычислить проводимости синапсов методом расчётного обучения по алгоритму: (3.1), (1.13), (1.14), (3.7), (1.16).

Построить график изменения погрешностей численных значений ре­шений и сравнить его с графиками рис. 1.17 и рис. 3.23.

 

Задача 3.2. Построение графика функции последования при жёст­ком обучении в двух ситуациях с постоянным перерегулированием.

Исходные данные: степень сходства образов ситуаций = 0,85; допустимое отклонение = 10 мм; постоянное перерегулирование =50 мм.

Требуется: Построить координатную плоскость функции последо­вания (типа рис. 3.3); принимая исходную погрешность, равной = 100 мм, построить ступенчатую траекторию, отражающую процесс обучения; определить число циклов обучения.

 

Задача 3.3. Выявление предельного цикла графика функции последования при жёстком обучении в двух ситуаци­ях с постоянным перерегулированием.

Исходные данные: степень сходства образов ситуаций = 0,5774; постоянное перерегулирование = 60 мм.

Требуется: Построить график функции последования, выявить пре­дельный цикл и определить размах его колебаний.

 

Задача 3.4. Расчётное обучение принятию решений в двух ситуаци­ях с переменным перерегулированием.

Исходные данные: те же, что и в примере 3.2 при жесткостях обу­чения: h = 0,2; 0,8; 1,5.

Требуется: Вычислить пошаговые погрешности  и проводимости синапсов  методом расчётного обучения по алгоритму: (1.12), (1.13), (3.23), (3.15), (1.14), (3.24), (1.16) — и сравнить результаты с результатами примера 3.2.

 

Задача 3.5. Определение количества рецепторных участков, на которое необходимо разбить всё очувствление, и продолжительность обучения в двух ситуациях, если известно число решаемых задач и ограничено напряжение питания рецепторов.

Исходные данные: число решаемых задач N = 64; нормальное на­пряжение питания U = 15 В, предельное напряжение питания =30 В; напряжение может быть только двуступенчатым.

Требуется: Рассчитать количество рецепторных участков n.

Определить продолжительность обучения Т в двух ситуациях; сигналы управления в ситуациях, их допустимые отклонения и соот­ношение коэффициентов приведения образов ситуаций выбрать по сво­ему усмотрению.

 

Задача 3.6. Определение предельных значений степени сходства искомых и посторонних предметов, то есть определение  и  из условий гарантированной остановки продольного перемещения при поиске.

Исходные данные: сигнал управления в дополнительной сопредель­ной ситуации = 2; коэффициент передачи мозга, учитывающий уси­ление на выходе, k = 200.

Требуется: Определить предельные значения степени сходства искомых предметов между собой  и искомого предмета с посто­ронним .

 

Задача 3.7. Суждение о сходстве образов ситуаций с образами мозга.

Исходные данные: три ситуации с сигналами управления в них: в первой — максимальный; во второй — средний; в третьей — нулевой.

Требуется: Охарактеризовать образы мозга  и  на основе срав­нения их с образами указанных трёх ситуаций.