КАК СОЗДАТЬ  «ВЕЧНЫЙ» ДВИГАТЕЛЬ

П.Д.Нагорный

 

Выдвинута гипотеза о том, что возможны материальные системы (плазма совместно с проводниками в гравитационном поле, полупроводники в электрическом поле), в которых невозможно одновременное установление термодинамического и электростатического равновесий, в связи с чем вопрос о возможности создания «вечного» двигателя остается открытым.

 

Введение

Под «вечным» двигателем понимается двигатель, источником энергии которого является тепловая (точнее, внутренняя) энергия окружающей его равновесной среды. Этот источник энергии можно рассматривать как «вечный» источник энергии.

Создание этого двигателя имело бы огромное значение, т.к. высокоразвитая земная цивилизация невозможна (!) без потребления энергии, а земные энергоносители (нефть, газ, уголь, уран) в недалеком будущем неизбежно (!) исчерпаются, что может привести к катастрофическим (!) последствиям для людей (если энергетическая проблема не будет решена). К тому же, использование этих энергоносителей приводит к ухудшению (!) экологии на земле (химическое и радиационное загрязнение окружающей природной среды, глобальное потепление).

Цель данной работы: теоретически показать, что в принципе «вечный» двигатель может быть создан. Экспериментальная проверка этого принципа может быть следующим этапом исследований в этом направлении. Если этот принцип будет подтвержден, то совершенствование конструкции этого двигателя будет очередным этапом исследований.

Без надежного фундамента (а энергетика является таковым) все рано или поздно рухнет: перестанет функционировать экономика и транспорт, нормальный быт людей (особенно в городах) станет невозможным… В настоящее время этот фундамент не является надежным. Поэтому поиск решения энергетической проблемы, актуальность которой с каждым годом возрастает, должен быть приоритетным. Не исключено, что экспериментальные исследования, целесообразность которых обосновывается в данной работе, помогут решить эту проблему.

 

Плазма и проводники в гравитационном поле

Вначале рассмотрим систему, показанную на рис. 1. Она представляет собой два одинаковых полых металлических шара А и В, соединенных диэлектрической трубкой С, а также металлического стержня D (его металл такой же, как у шаров). Система находится в гравитационном поле с ускорением свободного падения g, направленного от шара А к шару В. Расстояние между центрами шаров равно h. В шарах А, В и трубке С находится плазма какого-нибудь газа. Это значит, что температура данной системы порядка 1500 К.

Из-за гравитационного поля концентрация молекул газа, его ионов и электронов в шаре А будет меньше, чем в шаре В. Эта разность концентраций определяется формулой Больцмана (барометрической формулой). Причем из-за того, что масса электрона намного меньше массы иона, шар А будет заряжен отрицательно, а шар В – положительно (мы предполагаем, что в плазме нет отрицательных ионов). При этом отрицательный заряд шара А будет расположен на внешней его поверхности (как известно, в заряженном проводнике заряд располагается на его внешней поверхности). Ионы не могут проходить сквозь стенки шара В. Но они могут отбирать электроны у металла, рекомбинировать и в итоге положительный заряд шара В также будет расположен на внешней его поверхности. В стержне D будет наоборот: верхняя его часть будет заряжена положительно, а нижняя –  отрицательно, т.к. в нем свободно могут перемещаться электроны, а ионы не могут. При этом если нет контакта стержня D с шарами А и В, то данная система будет находиться в равновесном состоянии как в термодинамическом (тепловом), так и в электростатическом (электрическом) смыслах.

Если стержень D привести в контакт с шарами А и В, то электроны будут переходить от шара А к стержню D и от стержня D к шару В (выравнивание потенциалов). При этом в стержне D из-за сил электрического поля, создаваемого заряженными шарами А и В, электроны будут перемещаться сверху вниз. Если электрическое сопротивление стержня намного меньше, чем плазмы в трубке С, то из-за короткого замыкания произойдет разряд шаров А и В. Но при этом нарушится термодинамическое равновесие в плазме. Поэтому электроны по трубке С будут переходить от шара В к шару А. В итоге в данной системе будет неубывающий во времени постоянный электрический ток. Энергия этого тока может быть превращена в механическую работу и тем самым в принципе может быть создан «вечный» двигатель.

 

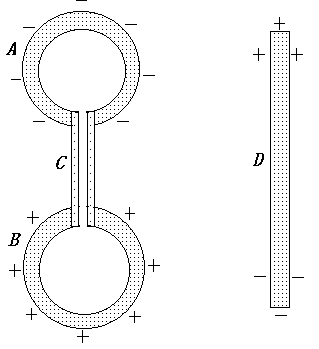
                                    Рис.1.

 

Прохождение тока по стержню D означает, что он будет нагреваться и температура его будет повышаться. Адиабатическое перемещение (поднятие) электронов в трубке С в поле гравитационных сил и в поле сил электрического поля создаваемых при этом зарядами шаров означает, что трубка С будет охлаждаться и ее температура будет понижаться. Поэтому теплота будет переходить от стержня к трубке, чтобы выравнять их температуры.  Эти процессы, приводящие к неубывающему току в цепи, являются следствием невозможности одновременного установления термодинамического и электростатического равновесий. В данной системе будет динамическое равновесие, которое является более общим, чем термодинамическое и электростатическое равновесия.

Вышеописанные процессы (явления) можно назвать термоэлектрическими явлениями во внешних потенциальных полях (конечно, если эти явления имеют место в действительности), а возникающую при этом разность потенциалов условно можно назвать внешнеполевой разностью потенциалов. Поскольку в вышеописанной системе (цепи) может быть неубывающий во времени электрический ток, то эта разность потенциалов является внешнеполевой электродвижущей силой.

Если нет контакта стержня D с шарами А и В и не учитывать влияния зарядов стержня D на заряды шаров А и В, то для случая, когда радиусы шаров намного меньше высоты h (в этом случае можно пренебречь изменением концентрации частиц внутри шаров), формулы Больцмана для ионов и электронов плазмы имеют вид:

n_+А = n_+В exp (- U₊ / kT ),                                                                        (1)

n _-А = n _-В exp (- U_- / kT ),                                                                         (2)

где Т – абсолютная температура,  n_+А , n_+В , n _-А , n _–В –  концентрации ионов (+) и электронов (-) в плазме шаров А и В,   U₊ , U_- -- разности потенциальных энергий ионов и электронов в шарах А и В соответственно.

Так как заряды располагаются на внешних поверхностях шаров, то в них плазма электронейтральна. Поэтому

n_+А = n _–А ;    n_+В = n _–В .                                                                          (3)

Из (1), (2) и (3) следует:

U₊ = U_- .                                                                                                   (4)

Очевидно:

U₊ = m₊ g h – eφ ,                                                                                    (5)

U_- = m _- g h + eφ ,                                                                                     (6)

где m₊ , m _- -- массы иона и електрона, e – заряд электрона (иона), φ – внешнеполевая разность потенциалов шаров А и В. Первые слагаемые в (5) и (6) показывают величину разности в шарах А и В потенциальной энергии ионов и электронов в гравитационном поле, а вторые слагаемые, равные eφ, -- в электрическом поле, создаваемом заряженными шарами.

Подставляя (5) и (6) в (4) и пренебрегая массой электрона по сравнению с массой иона, находим:

φ = m₊ g h / 2 е.                                                                                         (7)

Форма системы может быть не обязательно такой, как показано на рис. 1. Она может быть такой, как показано на рис. 2. Эта система представляет собой окруженный адиабатической оболочкой О герметичный сосуд (например, цилиндрической формы), в котором находится плазма и который находится в гравитационном поле. Нижняя и верхняя стенки сосуда (основания цилиндра) металлические, а боковые – диэлектрические. При разомкнутом ключе К в системе будет разность потенциалов нижней и верхней стенок сосуда, определяемая формулой (7) (при выводе этой формулы не делалось никаких предположений о форме сосуда). При замкнутом ключе К в электрической цепи будет протекать неубывающий во времени ток, энергия которого может быть превращена в работу, т.е. можно было бы создать «вечный» двигатель.

 

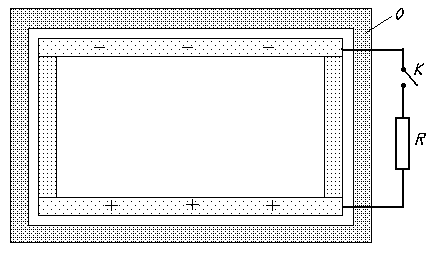
                                         Рис. 2.                           

 

Этот двигатель можно создать, в частности, следующим образом. Если сопротивление R является обмоткой электродвигателя, то в идеале всю электрическую энергию тока можно преобразовать в механическую работу. Часть этой работы нужно затратить на перевод теплоты из окружающей среды (ее температура около 20 ^оС) в сосуд для подогрева плазмы с помощью теплового насоса, а остальную часть этой работы для выполнения полезной механической работы. При этом окружающая среда будет охлаждаться. Но после выполнения работы энергия в виде теплоты возвратится (например, за счет трения) назад в окружающую среду и температура ее станет прежней. При этом энергия не исчезает и не возникает, а имеет место ее круговорот, закон сохранения энергии не нарушается. Мы не учитываем паразитные потери энергии за счет теплопроводности и трения. Но нам важен принцип, т.к. если он правильный, то эту идею создания «вечного» двигателя можно развивать.

Если в цепи сопротивление R намного больше сопротивления плазмы, то она будет источником электрического напряжения и сила тока в цепи определяется формулой:

I = φ / R = m₊ g h /(2 е R),                                                                          (8)

где h – высота сосуда.

При этом выделяемая на сопротивлении R мощность будет:

W = I² R = (m₊ g h)² / (4 е² R).                                                                   (9)

Оценим численные значения величин.   Пусть  m₊ = 1,7·10^-27 кг (такая масса протона), g = 10 м/с² (такое земное ускорение), h = 0,2 м, R = 0,001 Ом, как известно, е = 1,6·10^-19 Кл. Тогда по формулам (7), (8) и (9) находим: φ = 1· 10^-8 В,  I = 1· 10^-5 А,  W = 1· 10^-13 Вт.

Как видим, эти величины малые. Но они не равны нулю. Как видно из (7), (8) и (9), их можно увеличить путем увеличения величин m₊ , g ,  а также путем увеличения объема системы (мощность двух систем, показанных на рис. 2, в два раза больше, чем одной). Заменив массу протона на массу иона определенного вещества, величины φ и I можно увеличить приблизительно на 2 порядка, а величину W – на 4 порядка. Также заменив земные гравитационные силы на центробежные (во вращающейся плазме), величины φ и I можно увеличить приблизительно на 4 порядка, а величину W – на 8 порядков. В итоге величины φ и I можно увеличить приблизительно на 6 порядков, а величину W – на 12 порядков. Но и в этом случае эти величины будут малые: φ = 1· 10^-2 В,  I = 10 А,  W = 0,1Вт.

Мощность «вечного» двигателя можно намного увеличить путем замены слабых земных гравитационных и несколько больших центробежных сил на большие электрические силы, а также путем замены плазмы на полупроводник. Между последними имеется некоторое сходство: в них (в отличие от металлов) удельное электрическое сопротивление повышается при понижении температуры. При этом, как мы увидим ниже, можно намного упростить конструкцию этого двигателя (в частности, не нужно высоких температур и вращения системы).

В земном гравитационном поле сила, действующая на протон,  m₊g = 1,7· 10^-26 Н. В электрическом поле сила, действующая на элементарный заряд е, т.е. на электрон (или на протон):

F = e E = e φ / d,

где E – напряженность электрического поля, например, между обкладками плоского конденсатора, φ – разность потенциалов обкладок, d – расстояние между обкладками. Например, если φ = 10 В и d = 0,01 м, то F = 1,6·10^-16 Н. Эта сила на 10 порядков больше силы m₊g.

 

Полупроводники в электрическом поле

Рассмотрим систему, показанную на рис. 3. Она имеет некоторое сходство с системой, показанной на рис. 1. В этой системе гравитационное поле заменено электрическим полем между обкладками А и В заряженного плоского конденсатора. Шары А и В с плазмой (рис.1) заменены полупроводниковыми обкладками С и D. Размеры этих обкладок (их площадь) такие же, как и размеры (площадь) обкладок А и В. Трубка С с плазмой (рис. 1) заменена полупроводниковым стержнем Е, материал которого такой же, как и материал обкладок С и D. Стержень D (рис.1) заменен стержнем F, материал которого может быть либо полупроводниковым (но не таким, как стержня Е), либо металлическим. Электрическое поле конденсатора АВ посредством стержней Е и F будет наводить заряды на обкладках С и D. Величина этих зарядов приблизительно такая же, как и на обкладках конденсатора АВ. Температура системы равна или меньше комнатной.

Одно из различий систем, показанных на рис. 1 и рис.3, следующее: если в системе (рис. 1) заряды шара А и верхней части стержня D (а также шара В и нижней части стержня D) имеют разные (противоположные) знаки, то этого нет в системе (рис. 3). Но и в этом случае, как показывается ниже, в системе (рис. 3) может быть вышеописанное термоэлектрическое явление во внешнем потенциальном поле, т.е. может быть неубываемый во времени электрический ток.

Как известно, в полупроводниках имеют место электронная и дырочная проводимости, а также возможны их собственная и примесная проводимости. Для упрощения выкладок мы будем рассматривать полупроводники лишь с электронной проводимостью. Будем полагать, что стержни Е и F являются полупроводниками одного и того же химического элемента (например, кремния). Причем в стержне Е (и обкладках С и D) имеет место собственная, а в стержне F – примесная  проводимость. При этом в стержне F удельная проводимость может быть намного больше (например, на 4 порядка), чем в стержне Е. Концентрация носителей заряда (электронов) в стержне F во столько же раз больше, чем в стержне Е.

Известно, что из-за малости в полупроводниках концентрации электронов, проводящих ток, к ним применима классическая статистика Больцмана. Это означает, что в равновесии для стержня Е (также и для стержня F) справедлива формула Больцмана:

n_h = n_o exp[- e(φ_o – φ₁) / kT],                                                                      (10)

где n_o, n_h – концентрации электронов проводимости в стержне Е (или стержне F) в местах с координатами z = 0 и z = h соответственно (см. рис. 3), е – заряд электрона, k – постоянная Больцмана, Т – абсолютная температура, φ_o – абсолютная величина разности потенциалов между плоскостями с координатами z = 0 и z = h, обусловленная зарядами конденсатора АВ,  φ₁ – абсолютная величина разности потенциалов между теми же плоскостями, обусловленная зарядами на обкладках С и D.

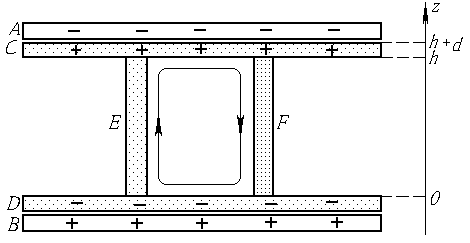
                                                Рис. 3.

 

Потенциальная электрическая энергия системы (рис. 3) стремится к своему минимальному значению, т.е. идет процесс к установлению разности φ_o – φ₁, равной нулю. Однако кинетическая энергия теплового движения электронов стремится выравнять  концентрации электронов обкладок С и D, т.е. идет процесс к установлению разности φ_o – φ₁, равной φ_o. В результате действия этих двух противоборствующих процессов в равновесии будет нечто среднее: разность φ_o – φ₁ будет не равна нулю, но она будет меньше величины φ_o. Найдем равновесную разность φ_o – φ₁ для каждого стержня Е и F в отдельности.

Отличие стержней Е и F по отношению к обкладкам С и D состоит в том, что в отличие от стержня Е в местах контакта стержня F с обкладками С и D из-за их разнородности может быть контактная разность потенциалов. Однако в свете вышеизложенного рассмотрения системы (рис. 1) мы будем предполагать, что внешнеполевая разность потенциалов обкладок С и D не зависит от контактной разности потенциалов, т.е. мы будем предполагать, что нижеприводимый расчет величины φ_o – φ₁ для стержня Е такой же и для стержня F.

Предполагая, что стержень F отсутствует, из (10) следует, что в стержне Е

.                                                                                  (11)

Абсолютные величины зарядов на обкладках С и D одинаковы. Поэтому

 ,                                                                                            (12)

где n – концентрация электронов проводимости в электронейтральном полупроводнике стержня Е (или обкладок С и D), Δn – величина различия концентраций электронов проводимости в заряженных и электронейтральных обкладках С и D в равновесном состоянии.

Очевидно:

,                                                                                  (13)

где N –  число электронов на обкладке С (или D), создающих ее заряд q, е – заряд электрона, V – объем обкладки, S – ее площадь, d – ее толщина (см. рис. 3).

Если Δn << n, то учитывая (12) и (13), имеем:

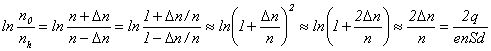    _.   (14)

Как известно, разность потенциалов обкладок плоского конденсатора (в данном случае конденсатора СD, без учета поля конденсатора АВ) определяется равенством:

 ,                                                                                                 (15)

где h – расстояние между обкладками конденсатора СD, ε – относительная диэлектрическая проницаемость среды между его обкладками.

Из (15) находим величину q и подставляя ее в (14) находим величину ln(n_o/n_h). При этом равенство (11) перепишется:

φ_o – φ₁ = А φ₁,                                                                                              (16)

где .

Из уравнения (16) несложно найти φ₁, а также если А << 1, несложно найти искомую величину:

,                                                                                            (17)

где мы ввели обозначение S = φ_o – φ₁.

Из (17) видно, что величина S не равна нулю, если величина φ_o не равна нулю. Также видно, что величина S обратно пропорциональна концентрации n. Например, если в стержне F величина n на 4 порядка больше, чем в стержне Е, то в нем величина S будет меньше на столько же порядков. Отметим, что если бы формула (17) была справедлива и для металлов, то величина S была бы очень малой; намного меньше, чем в полупроводниках (напомним, что, например, для серебра n = 6·10²⁸ м^-3).

Приведем численную оценку. В чистом (без примесей) кремнии при Т = 300 К концентрация n ≈ 1·10¹⁶ м^-3 [1, с.46]. Пусть h = 0,05 м, d = 0,001 м, φ_o = 10 В. Напомним, что ε_о = 8,85·10^-12 Ф/м, k = 1,4·10^-23 Дж/К, е = 1,6·10^-19 Кл. Тогда (если ε = 1) из (17) находим: S = 6·10^-5 В. Как видно из (17), эта величина может быть увеличена путем уменьшения величин h и d, что приводит к компактности (положительный момент) системы (рис. 3), а также путем увеличения величины φ_o.

Чтобы электроны могли переходить от обкладки D к обкладке С, электрическая энергия электрона еS должна быть сравнимой (или меньшей) с его тепловой энергией kT. Если эти энергии равны, то

S = kT/e.                                                                                                         (18)

Например, при Т = 300 К, как следует из (18), S = 0,026 В.

В системе (рис. 3) посредством  стержня Е идет процесс установления равновесной разности потенциалов обкладок С и D, равной S_Е. В то же время, посредством стержня F идет процесс установления другой равновесной разности потенциалов обкладок С и D, равной S_F. Эти разности потенциалов оцениваются по формуле (17). Поскольку в стержне F величина n намного больше, чем в стержне Е, то S_F << S_E, т.е. между обкладками С и D посредством стержня Е устанавливается некоторая напряженность электрического поля, а посредством стержня F напряженность этого поля уменьшается. Поэтому в цепи, образованной из стержней Е и F и обкладок С и D, будет неубывающий во времени электрический ток (на рис. 3 линией со стрелками показана циркуляция электронов). В стержне F электроны перемещаются от обкладки С к обкладке D. Этот ток разогревает стержень F, т.к. при этом электрическая потенциальная энергия всей системы (с учетом конденсатора АВ) уменьшается. В стержне Е электроны перемещаются от обкладки D к обкладке С. Этот ток охлаждает стержень Е, т.к. при этом потенциальная энергия системы увеличивается. Этот ток приводит к появлению между обкладками С и D электрического поля. Адиабатическое перемещение электронов в этом поле и приводит к охлаждению стержня Е. То есть, вообще говоря, теплота сама собой может переходить от менее нагретого тела (стержня Е) к более нагретому (стержню F).

Отметим, что разность потенциалов S_E (точнее, разность S_E – S_F) является внешнеполевой электродвижущей силой в цепи, т.е. «силой», приводящей к неубывающему во времени электрическому току в цепи.

Из-за малости в полупроводниках (по сравнению с металлами) концентрации n в электрическом поле они (стержни Е и F) не являются электронейтральными по их объему. Поэтому величина S (формула (17)) не равна нулю и поле от зарядов на обкладках С и D не компенсирует полностью поля конденсатора АВ. Полная компенсация была бы в случае большой величины n, как это имеет место в металлах. В заряженном проводнике (металле) заряды располагаются на его внешней поверхности, а в полупроводнике – по его объему (если величина n достаточно малая). Если в находящихся во внешнем электрическом поле диэлектриках электрическое поле имеет место, в металлах его нет, то в полупроводниках имеет место нечто среднее. В то же время, сильно легированные полупроводники (в них имеет место большая концентрация примесных атомов и, следовательно, большая концентрация n) проявляют металлические свойства [1, с. 38].

В системе (рис. 3) стержень F имеет контакты с обкладками С и D. Из-за разнородности этого стержня и обкладок в местах этих контактов могут быть контактные разности потенциалов, которые могли бы скомпенсировать величину S_E – S_F так, что в цепи не было бы неубывающего во времени электрического тока. Однако из-за того, что эти контакты одинаковые, но противоположные по знаку (в смысле потенциального барьера для протекающего тока), они компенсируют друг друга и ток должен быть. В то же время, на обкладках С и D имеются заряды разных знаков, т.е. различие обкладок имеется. Поэтому протекание тока не очевидное.

Для доказательства того, что такой ток может быть, рассмотрим систему, показанную на рис. 4. В электрическом поле заряженного конденсатора АВ находятся полупроводниковые шары 1 и 2, соединенные таким же полупроводником (стержнем) Е и полупроводниковые шары 3 и 4, соединенные таким же полупроводником (стержнем) F. Пусть полупроводник Е имеет собственную проводимость, а полупроводник F – примесную, т.е. легирован (или сильно легирован). Шары 1 и 2 окружены оболочками из материала, который совпадает с материалом стержня F. В электрическом поле конденсатора АВ на шарах будут наводиться электрические заряды, показанные на рис. 4, вследствие чего вне шаров от них будут внешние электрические поля.

В местах контакта оболочек с шарами 1 и 2 возможна контактная разность потенциалов. При этом электрическое поле будет сосредоточено в тонком сферическом слое, оно не будет выходить за пределы шаров, от зарядов в этом слое не будет внешнего (за пределами шаров) электрического поля.

В случае хорошей проводимости полупроводника F (в том числе оболочек шаров 1 и 2) наведенные на всех шарах заряды будут располагаться если не на поверхностях шаров, то вблизи их. Если расстояние между центрами шаров намного больше радиуса r шара, то разность потенциалов между шарами 1 и 2 в поле конденсатора АВ и в поле самих шаров 1 и 2 (без учета поля шаров 3 и 4) можно оценить по формуле:

.                                                                                            (19)

Формула (19) имеет сходство с формулой (17). В этих формулах обозначения величин одинаковы. Формула (19) такая же и для шаров 3 и 4 (без учета поля от шаров 1 и 2). Вывод формулы (19) аналогичен выводу формулы (17). При выводе этой формулы учитывалось, что потенціал поля вне заряженного шара на расстоянии L от него определяется известной формулой:

Φ = q / (4π ε_o ε L).

Как и в формуле (17), в формуле (19) величина S обратно пропорциональна концентрации n. Поэтому разность потенциалов шаров 1 и 2 будет больше, чем шаров 3 и 4. Это означает, что заряды шаров 3 и 4 будут больше, чем заряды шаров 1 и 2, т.е. полупроводник F лучше компенсирует поле конденсатора АВ, чем полупроводник Е. Из-за различного количества зарядов на шарах 1 и 3 (на шарах 2 и 4) между ними будет разность потенциалов. Поэтому если замкнуть ключи К₁ и К₂, то по проводам электроны будут переходить от шара 1 к шару 3 (и от шара 4 к шару 2) до тех пор, пока потенциалы (заряды) их не выравняются. Но при этом нарушится термодинамическое равновесие в полупроводниках в поле конденсатора АВ. Поэтому электроны будут переходить от шара 2 к шару 1 и от шара 3 к шару 4. В итоге в цепи возникнет неубывающий во времени электрический ток. Это и требовалось показать. Если этот ток имеет место в системе (рис. 4), то нет гарантий того, что в других аналогичных системах его нет.

 

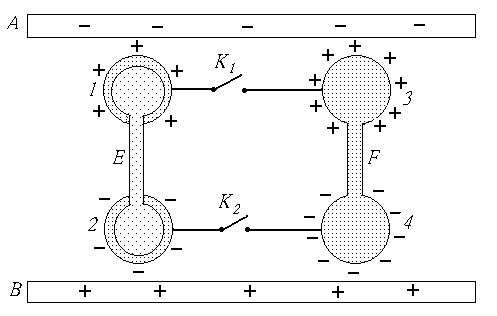
                                                             Рис.4.                                          

 

Развитие вышеизложенных соображений приводит к системе, показанной на рис. 5. В электрическом поле плоского конденсатора АВ  находится полупроводник Р, имеющий собственную проводимость. К нему примыкают обкладки С и D. Они могут быть из того же полупроводника, но легированного. В принципе они могут быть металлическими. Обкладки С и D предназначены для снятия электрических зарядов с полупроводника Р, т.к. полупроводники без примесей имеют, как правило, плохую электропроводимость. Ток этих зарядов через ключ К подается на нагрузочное сопротивление R_н (им может быть входное сопротивление электроизмерительного прибора).

В свете вышеизложенного, если ключ К разомкнут, то части полупроводника Р не будут электронейтральными (в данном случае верхняя его часть заряжена положительно, а нижняя – отрицательно) и будет разность потенциалов S_E нижней и верхней его плоскостей, а также, следовательно, обкладок С и D. Из-за этого если ключ К замкнут, то по сопротивлению R_н будет протекать неубывающий во времени электрический ток. По сути полупроводник Р играет роль стержня Е, а сопротивление R_н с проводами – роль стержня F системы (рис. 3).

Если обкладки С и D металлические, то при замыкании ключа К индуцированные заряды на них будут размещаться на внешних поверхностях в очень тонких слоях толщиной порядка десяти атомных размеров. Поэтому такой толщины должна быть и толщина металлических обкладок. С другой стороны, поле от зарядов на металлических обкладках может полностью скомпенсировать поле конденсатора АВ и в полупроводнике Р не будет электрического поля, т.е. по всему объему он будет электронейтрален (никакой разницы: есть он или его нет), разность потенциалов  S_E будет равна нулю и в цепи не будет тока. Этот недостаток, по-видимому, можно устранить путем размещения металлических обкладок С и D (в виде сеток) в полупроводнике Р в непосредственной близости от его поверхностей.

 

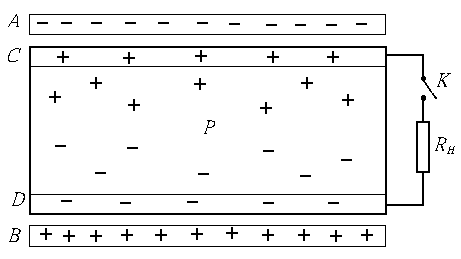
                                                 Рис. 5.

 

Известно, что удельная электропроводность проводника электричества (в том числе полупроводника)

σ = е μ n ,                                                                                                  (20)

где е – заряд носителя (электрона) тока, μ – подвижность носителей (электронов) тока, n – концентрация носителей (электронов) тока.

Известно также, что

σ = σ_о exp(-ΔW / 2kT),                                                                              (21)

где σ_о – некоторая постоянная,  ΔW – ширина запрещенной зоны в полупроводнике [2, с. 256].

При некоторой температуре Т₁ (например, Т₁ = 300 К) из (21) имеем:

σ₁ = σ_о exp(-ΔW / 2kT₁),                                                                            (22)

где σ₁ -- величина σ при температуре Т₁.

Из (22) находим:

σ_о = σ₁ exp(ΔW / 2kT₁),                                                                              (23)

Из (20) и (21) имеем:

n = (σ_о / е μ)  exp(-ΔW / 2kT),                                                                    (24)

Подставляя (24) в (17), находим:

                                                                   (25)

Формула (25) применима для системы (рис. 3), а не для системы (рис. 5). Но для оценок мы будем предполагать, что формула (25) применима и для системы (рис. 5). При этом по сути предполагается, что стержень Е  имеет большую площадь поперечного сечения, что заряды полупроводника Р сосредоточены в некоторых приповерхностных (нижней и верхней) его областях. Мы будем предполагать, что величина d равна одной десятой величины h.

Протекаемый в цепи системы (рис. 5) ток определяется формулой:

I = S_E / (R_p + R_н),                                                                                        (26)

где R_p – сопротивление полупроводника Р.

Как известно, наибольший коэффициент полезного действия источника тока (он равен отношению полезной мощности, выделяемой в сопротивлении R_н , ко всей мощности, развиваемой электродвижущей силой в цепи) имеет место в случае, когда сопротивление нагрузки равно сопротивлению источника тока [2, с. 121]. Поэтому в (26) мы положим, что

R_н = R_р.                                                                                                        (27)

По закону Ома

R_р = h / (σ S),                                                                                               (28)

где S – площадь поперечного сечения полупроводника Р.

Подставляя (21) в (28), имеем:

R_p = h /(S σ_o) exp(ΔW / 2kT).                                                                      (29)

Подставляя (25) и (29) в (26) и учитывая (27), находим:

                                                                                     (30)

Мощность, развиваемая источником тока, равна произведению электродвижущей силы и тока, т.е.

W = S_E I.                                                                                                      (31)

Подставляя (25) и (30) в (31), находим:

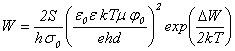.                                                         (32)

Объем V системы (рис. 5) в основном (или такого порядка) определяется объемом полупроводника Р, который равен Sh. Поэтому из (32) следует, что мощность от единицы объема системы (рис. 5) будет порядка:

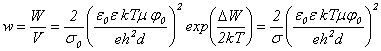.                    (33)

Приведем численные оценки величин. Пусть полупроводником Р является кремний без примесей. Для него ΔW = 1,1 эВ = 1,8·10^-19 Дж. При Т = 300 К = Т₁ величина σ =4,3·10^-4 Ом^-1м^-1 = σ₁. Из (23) находим: σ_о = 5,6·10⁵ Ом^-1м^-1. Для кремния μ ≈ 0,1 м²/(В·с). Пусть h = 0,01 м, d = 0,001м, φ_о = 10 В, S = 0,01 м², ε = 1. Тогда по формулам (25), (30) и (33) находим: S_E = 8·10^-5 В, I = 2·10^-8 А, w = 4·10^-8 Вт/м³. С понижением температуры величины S_E и w  возрастают. При Т = 250 К будет: S_E = 5·10^-3 В, I = 2·10^-8 А, w = 2·10^-6 Вт/м³. Формулы (25), (30) и (33) справедливы при выполнении вышеприводимых условий: Δn << n и А << 1. Поэтому для более низких температур эти формулы должны быть уточнены (изменены).

Как видим, величина w очень малая и достаточно мощный «вечный» двигатель должен иметь очень большие размеры. Однако, как видно из (33), величина w может быть намного увеличена путем уменьшения величин h, d, величины σ, а также увеличения величины φ_о. Величины S_E и I могут быть измерены в эксперименте и тем самым вышеизложенная теория (идея) может быть проверена экспериментально.

Отметим следующее. Величина w увеличивается с уменьшением величины σ, т.е. с увеличением удельного сопротивления ρ полупроводника (ρ = 1/σ). Это имеет место при понижении температуры. Поэтому величина w в принципе может быть большой при низких температурах (при этом, по-видимому, полупроводник должен быть легирован).

 

1. В.Л.Бонч-Бруевич, С.Г.Калашников, Физика полупроводников. Москва: Наука, 1977.

2. И.В.Савельев, Курс общей физики, т. 2. Москва: Наука, 1973.