Основания
рекуррентной математики
Г.С. Мельников (
Настоящая монография была задумана в период
становления понятий фрактальной оптики, но полного завершения не получила.
Многие разделы, такие как Главы 1, 2…4 вошли в последующие публикации, в частности,
в Препринт (сборник статей по конференции «Однородные вычислительные среды и
систолические структуры» - http://soi.srv.pu.ru/r_1251/investigations/fractal_opt/data5/mono/mono1.pdf )
Ряд
разделов так и не нашел своих публикаций.
Ниже
приводится восстановленные разделы – раздел 1.1.-1.5
Оглавление
Введение
1. Дискретные индексные
пространства
1.1.
Основные определения
1.2.
Дискретные индексные метрические числовые пространства
1.2.1. Дискретные индексные
метрические пространства целых чисел
1) Линейные индексные
метрические пространства
2) Аддитивные нелинейные
индексные метрические пространства
3) Мультипликативные нелинейные
индексные метрические пространства
Заключения по разделу 1.2.1
1.2.2. Классификация одномерных
рекуррентных индексных последовательностей по порядку рекуррентности
1.2.3. Топологическая модель
рекуррентных индексных последовательностей (основные определения)
1.3.
Рекуррентный нуль
1.4.
Введение в теорию симметрии
1.5.
Многослойное тело Мебиуса
2. Дискретные
тригонометрические функции
2.1.
Карденово движение. Связь гиперболической, круговой и
дискретной тригонометрии
2.2.
Некруговые тригонометрические функции
2.2.1. Знаковые тригонометрические
функции
2.2.2. Тригонометрические
преобразования в знаковой тригонометрии
3. Числовые системы и античисла
3.1.
Позитивные системы счисления
3.2.
Античисла
3.2.1. Графоаналитическая связь
числовых и античисловых последовательностей
3.3.
Симметрические числа
3.4.
Катенаны числовых последовательностей
4. Многомерные индексные
пространства
4.1.
Однородные вычислительные среды и систолические структуры
4.2.
Трехмерные индексные тела действительных чисел
4.2.1. Возможные информационные
связи в трехмерных систолических структурах рекуррентных тел действительных
чисел
4.2.2. Линейные рекуррентные тела
действительных чисел
4.2.3. Аддитивные нелинейные
рекуррентные тела действительных тел
4.2.4. Мультипликативные нелинейные
рекуррентные тела действительных чисел
4.3.
Трехмерные индексные тела комплексных чисел
4.4.
Трехмерное тело Паскаля
5. Рекуррентные методы
систолических вычислений
5.1.
Алгоритмы систолических вычислений на линейных телах
5.2.
Алгоритмы систолических вычислений на аддитивных телах
5.3.
Алгоритмы систолического дифференцирования и интегрирования
5.4.
Рекуррентные алгоритмы автоматизации анализа, сжатия и синтеза цифровой
информации на систолических структурах
6. Технические приложения
6.1.
Пространственно инвариантные преобразования на цифровых мониторах
видеоинформации
6.2.
Структурные схемы вычислительных ячеек СБИС для реализации рекуррентных
алгоритмов вычисления.
6.3.
Оптические методы дискретных тригонометрических преобразований
6.3.1. Растровые явления внепараксиальной оптики
6.3.2. Возможности передачи
изображений по одиночному волокну
7. Основные направления
дальнейшего развития рекуррентной теории чисел и ее приложений
1.
ДИСКРЕТНЫЕ
ИНДЕКСНЫЕ ПРОСТРАНСТВА
В
этой главе мы рассмотрим с новых позиций считающуюся к настоящему времени
законченной простой и ясной, маленькой математической теорией [1] - теорию
дискретных возвратных последовательностей, составляющую основу исчисления
конечных разностей.
Новизна
позиций заключается в различии возвратных и рекуррентных (фр. Recurente - возвращающихся к началу)
последовательностей, что к настоящему времени, пока, считается в математике
синонимами, а также с новых позиций рассматривается область существования
возвратных последовательностей.
Существующая
теория возвратных последовательностей оперирует с последовательностями вида:
U1, U2, U3, ...,
или коротко {Uk}, где k = 1, 2, 3, .....; k ®¥
Мы
же будем обращаться к последовательности вида
..., U-3, U-2, U-1,
...,
или коротко {U±k},
где k = Î [-¥ , ... , 0 , ... , +¥].
1.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
В
общем случае все алгебраические и групповые операции, рассматриваемые в
настоящей монографии, применимы вплоть до гиперкомплексных числовых
пространств, однако, не нарушая общности мы будем
обращаться к числовым системам с делением, т.е. к таким системам, в которых
числа можно складывать, вычитать, умножать и делить.
При
этом предполагается, что сложение и умножение в этих системах коммутативно и
ассоциативно [2¸4]:
a + b = b + a; (a + b) + g = a + (b + g) (1.1.1)
a × b = b × a; (a × b) × g = a × (b × g) (1.1.2)
а умножение - дистрибутивно относительно сложения:
a × (b + g) = a × b + a × g (1.1.3)
здесь a, b, g - произвольные числа
системы.
Во
всякой выбранной числовой системе, кроме того, будем рассматривать
отрицательные числа не как удобную математическую символику, а как
самостоятельные числа - противоположные положительным числам. При этом для
всякого произвольного числа системы имеется и притом единственное положительное
ему число. [5]
Во
множестве выбранной числовой системы должно содержаться особое число,
являющееся нулем, т.е. такое число, сумма которого с любым выбранным числом
системы равна самому этому числу, причем нуль этот должен быть единственным.
Существование числа (чисел) противоположных нулю обсуждается в разделе 1.3.2.
Кроме того, в этом же разделе мы покажем и последовательно выведем свойства
особых последовательностей, т.е. мы придем к тому, что для всех возрастающих и
убывающих последовательностей непременно существует антипоследовательности.
Т.е.
мы введем понятие античисел. Это один из удивительнейших случаев, когда
экспериментаторы физики свободно оперируют с понятием античастиц, изучают их
свойства из наблюдаемых фактов эксперимента, в то время как надежного
математического аппарата, выявляющего гносеологические основания и
симметрические свойства антиэлементов, не существует. С разработкой этих понятий: античисла,
антипоследовательности и антинуля (рекуррентного нуля) можно надеяться на
сокращение или полное устранение отмеченного разрыва.
Для
любых двух последовательностей чисел {Uk} и {Vk} будет называться суммой
(разностью, произведением, частным) последовательность вида
{Uk + Vk}, {Uk - Vk}, {Uk ×Vk}, {Uk /Vk}
при этом деление на Vk = 0 будет оговариваться особо.
Определение
1.1
Рекуррентными
последовательностями будем называть неразрывные дискретные последовательности
вида (1.2).
..., U-3, U-2, U-1,
...,
Или коротко {U±k}
такие, для которых существует натуральное число m и числа a1, a2, ... am (действительные или мнимые,
причем, конечное число am ¹ 0), что для любого члена
последовательности существует однозначное соответствие.
где ( k ³ m ³ 1).
При
этом последовательность (1.2) будем называть рекуррентной последовательностью
порядка m, а отношение (1.1.4) -
рекуррентным уравнением порядка m.
Определение
1.2.
Возвратными
будем называть последовательности вида
U0, U1, U2, U3, U4, ....,
или коротко {U+k},
а также
U-¥.,...,
или коротко {U-k},
такие, для которых существует натуральное число m и числа a1, a2, ... am (действительные или мнимые,
причем, конечное число am ¹ 0), что, начиная с
некоторого номера i и для всех следующих номеров,
существует однозначное соответствие.
где ( |k| ³ |m| ³ 0).
При
этом последовательность (1.1.5) будем называть правосторонней возвратной, а
последовательность (1.1.6) - левосторонней возвратной последовательностью
порядка m.
Здесь
знаки перед m и k в выражении (1.1.7)
записываются по схеме: верхние - для правосторонних последовательностей
(1.1.5), нижние - для левосторонних последовательностей (1.1.6).
Названия
для возвратных последовательностей мы дали не только от мнемонического правила
возвращения к нулевому члену последовательности справа или слева,
соответственно, а еще и по тому, что, как будет показано в разделе 1.2 и далее
по тексту, правосторонние и левосторонние последовательности лежат в основе
математического аппарата сдвиговой суперпозиции. И, в свою очередь, могут быть синтезированы с помощью операций правостороннего
(левостороннего) матричного сдвига или правосторонних (левосторонних)
бесконечностей.
1.1.1. АРИФМЕТИЧЕСКИЙ КОНТИНУУМ
В
[6] арифметический континуум определяется как числовая
прямая. Континуум (от лат. Continuus - непрерывный, сплошной) - непрерывное многообразие, например
совокупность всех точек прямой или какого-либо ее отрезка, множество всех
действительных чисел, заключенных между двумя какими-либо действительными
числами, например между 0 и 1 [7].
Мы
же арифметическим континуумом предлагаем считать более широкое понятие:
Определение
1.3.
Арифметический
континуум это непрерывное многообразие числовых пространств, в общем случае,
гиперкомплексных чисел.
В
таких пространствах числовая прямая составит лишь одну
из возможных координатных осей.
В свою очередь, как числовую прямую, так и гиперпространство чисел
в целом считать континуальным можно лишь условно, так как непрерывность сама по
себе, как будет показано ниже, является порождением бесконечного числа упаковок
(вложений) структурно упорядоченных дискретных числовых решеток, [11] или сеточных полей друг в друга [9,18].
Задача
настоящей монографии показать фундаментальные основы построения этих
правильных, структурно-упорядоченных, дискретных систем. Основным аппаратом,
который позволит выполнить эту задачу, послужить введенная выше классификация
возвратных и рекуррентных последовательностей.
Известное
высказывание Леопольда Кронекера (1823 - 1891) [8], «Бог создал натуральное
число, все прочее - дело рук человека» не вполне точно определяет тот
фундамент, на котором строится здание математики.
Наша задача показать, что
этим фундаментом является не только натуральные числа, а в более общем смысле,
дуальная возвратная последовательность, составленная из целых чисел, т.е.
натуральных чисел, противоположных им
отрицательных чисел и нуля, склеенная на особых элементах - рекуррентных нулях
с антипоследовательностью, состоящей из античисел и антинуля.
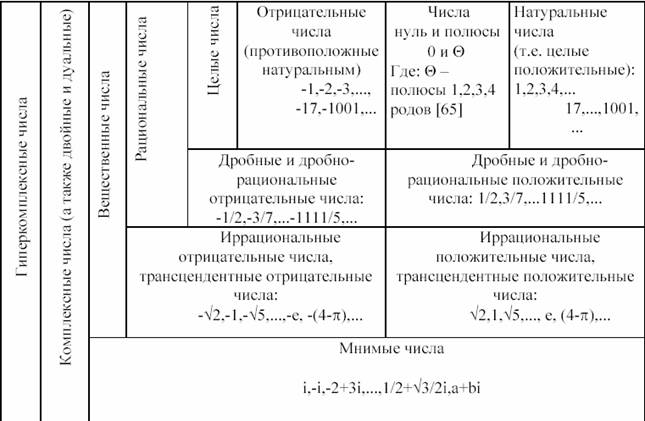
Следуя
[2], а также дополняя данными [3-5] приведем здесь
классификацию числовых пространств по множествам (см. табл. 1.1.).
Определения
для чисел разбитых на множества (табл..1.1.) можно найти в целом ряде
монографий и учебников, например [2, 5]. В силу
этого останавливается на детальном изложении известных положений мы не будем,
а, путем последовательного введения в рассмотрение все более сложных числовых
колец и полей [2, 5], из которых будут
строиться возвратные и рекуррентные последовательности, покажем способы их
структурного упорядочения и выведем методы параллельного анализа, кодирования и
синтеза числовых последовательностей более общего класса.
Таблица 1.1.
|
|
|
|
1.2. ДИСКРЕТНЫЕ ИНДЕКСНЫЕ
МЕТРИЧЕСКИЕ ЧИСЛОВЫЕ ПРОСТРАНСТВА
В теории функций и
функциональном анализе вводится понятие метрического пространства [12], путем
обобщения представлений о действительных числах как о множестве, в котором
введено расстояние между элементами.
Согласно [12] метрическим
пространством называется пара (x, r) состоящая из некоторого множества (пространства) x элементов (точек) и
расстояния, т.е. однозначной, неотрицательной действительной функции r(x, y),
определенной для любых x и y из x удовлетворяющей трем
условиям:
1)
r(x, y) = 0 тогда и только тогда, когда x = y (1.2.1)
2)
(аксиома
симметрии): r(x, y)= r(y, x) (1.2.2)
3)
(аксиома
треугольника): r(x, z) £ r(x, y) + r(y, z) (1.2.3)
Само метрическое пространство,
т.е. пару (X,r)
обозначают одной буквой
R = (X,r) [12, стр. 46] (1.2.4)
Указанное определение
метрических пространств вводится для реализации
важнейшей операции анализа - предельного перехода. В основе
этой операции лежит тот факт, что на числовой прямой определено расстояние от
одной точки до другой. Например множество
действительных чисел с расстоянием r(x, y) = ½x - y½ образует метрическое
пространство R1 и обобщая, множество упорядоченных групп
действительных чисел x = (x1, x2, x3, ... xn) с расстоянием
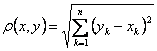(1.2.5)
называется n-мерным арифметическим
эвклидовым пространством Rn. Для Rn аксиомы 1 и 2 очевидны, а аксиомы
треугольника принимают вид, для x = (x1, x2, ..., xn), y = (y1,y2,...,yn) и z = (z1, z2, ..., zn) аксиомы 3 записывается
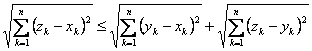(1.2.6)
Следует подчеркнуть, что
метрическое пространство (1.2.4) носит геометрический, точечный характер, в
силу того, что z, y и x могут принимать не только
целочисленные значения, а такие рациональные, иррациональные, трансцендентные.
Введем интегральное понятие
метрических дискретных пространств - пространство индексных элементов.
В реальных
физических системах таких, например, как экраны индикаторов цифровых
телевизионных и тепловизионных систем с дискретными
линейками (матрицами) чувствительных элементов, однородные и систолические
вычислительные структуры, биологические объекты типа клетка, или, в физики
микромира, с дискретными элементами - элементарными частицами и т.д., приходится иметь дело не с математической
точкой, а с конечным отрезком, площадкой, трехмерным элементом конечного
объема, - частицей, которые удобнее описывать не однозначной функцией расстояния r(x, y),
а индексным элементом, положение которого в пространстве (времени) определяется
позиционным набором целочисленных индексов x, y, z... А само значение
индексной функции положения rx,y,z... описывается усредненными
интегральными характеристиками по конечному отрезку, площади, объему и гиперобъему индексного элемента.
Широко известным в
дискретной математике примером двумерного пространства индексных элементов
являются таблицы и матрицы.
Матрицей называется совокупность вещественных или комплексных чисел ai,j, расположенных в виде
прямоугольной таблицы [13, 14].
Числа ai,j
называются элементами матрицы. Индексы i,j обозначают, что элемент ai,j
расположен на пересечении i-й строки и j-ого столбца матрицы.
Понятие матрицы можно расширить увеличивая число базисных индексных координат.
Определение 1.4.
Пространственной гиперматрицей будем называть совокупность вещественных или
комплексных чисел rk,n,l,p,m , расположенных в гиперкубических
прямоугольных элементах числовых пространств.
В таких пространствах
позиционное положение элемента осуществляется индексами k, l, m, ..., n, p, ... .
Верхние индексы (такие как n, p, ...) будем называть в том
случае, когда метрика координатного положения элемента по осям n, p,
выбранного числового пространства будет логарифмической, т.е. она будет
определять порядковую (размерностную) характеристику числовых последовательностей
Un, Vp, расположенных по строке
(столбцу) пространственной гиперматрицы.
В случае чисто линейных
пространств используем только нижние индексы, например rx,y. Если нам необходимо задать само индексное числовое
пространство (гиперматрицу), будем пользоваться
заглавными буквами, например: Nk,n,l или Mk,l.
В первом случае Nk,n,l будет обозначать бесконечную трехмерную матрицу с
линейными индексными координатами k и l и логарифмической индексной
координатой n; Mk,l
- обычная двумерная бесконечная матрица. В ряде случаев, где это не будет
вызывать сомнения, все или часть индексов будем опускать. В общем случае,
метрика, задаваемая по индексным координатам k, l, ..., n
может быть разная.
Однако,
в дальнейшем мы будем преимущественно оперировать с пространствами и матрицами
равной метрики, т.е. с такими пространствами и матрицами, для которых
расстояние по индексным координатам между двумя соседними элементами будут
равны, при этом, как правило будем оперировать с пространствами и матрицами у
которых:
(1.2.7)
т.е.
(1.2.8)
Кроме
того, как мы условились в начале этой главы, мы будем преимущественно
интересоваться возвратными и рекуррентными последовательностями, дискретные
значения которых составляют элементы интересующих нас пространств и матриц. Для
них индексные координаты занимают всю числовую ось от
-¥ до +¥ в своих дискретных
целочисленных значениях.
Другими
словами, мы будем интересоваться обобщенными бесконечными матрицами.
Как
известно [14] сложение и умножение бесконечных матриц, рассматривавшихся до
настоящего времени, определяется соотношениями:
A +B = (ai,j
+ bi,j) (1.2.9)
lA =
(lai,j) (1.2.10)
где l любое действительное или
комплексное число (скаляр).
(1.2.11)
Таким образом. Если A×B=(Ci,j),
то
(1.2.12)
только в том случае, когда сумма (1.2.12)
существует.
Подчеркнем
существенную разницу в понимании бесконечных матриц, излагаемых в
фундаментальной монографии Р. Кука [14] с предлагаемой ниже трактовкой.
Так
в [14] рассматриваются матрицы с элементами от 1 до ¥. Мы же рассматриваем
фрагменты обобщенных матриц, локализованные относительно центрального элемента rо,о,о,..., но при этом сами элементы
матриц уходят в обе стороны от нулевого элемента по всем индексным координатам
от -¥ до +¥ т.е. наши обобщенные
матрицы являются дуальными бесконечными матрицами по каждой базисной
координате. Этим матрицам, так же как обычным бесконечным матрицам присущи
отличия от конечных [14] в следующем:
1) В теории конечных матриц
основную роль играют определители; в теории бесконечных матриц их роль в
значительной степени теряется.
2) В теории бесконечных матриц
часто встречаются проблемы существования, которые не имеют аналога в теории
конечных матриц.
Например,
если даны две бесконечных матрицы A и B, то их произведение A×B может
не существовать, так как ряды
(1.2.13)
могут расходиться для всех или нескольких значений i и j.
Для
обобщенных дуальнобесконечных матриц, построенных из
рекуррентных последовательностей, ряды всегда расходятся в одну из сторон
индексных осей.
Следовательно,
выражение (1.2.13) для таких матриц не имеет смысла. Поэтому введем для них
операцию, заменяющую векторное умножение (1.2.13) конечных и обычных бесконечных
матриц, на метрическое скалярное или поэлементное умножение.
Определение 1.5.
Скалярным
или поэлементным матричным умножением будем считать следующую операцию
умножения:
обозначаем ее , такую
C = A B (1.2.14)
что
Ci,j = ai,j
× bi,j (1.2.15)
3) Поэлементное умножение еще в
большей степени уводит теорию бесконечных матриц в раздел анализа по сравнению
с теорией конечных матриц, являющихся частью алгебры. Так, например, как будет показано ниже теория обобщенных дуальнобесконечных
матриц позволит нам с успехом использовать ее в задачах синтеза и сжатия
информации.
4) Другими словами, типы
проблем, решаемых при помощи бесконечных матриц, имеют совершенно другой
характер, чем проблемы, решаемые с помощью конечных матриц.
Учитывая
вышесказанное, мы в плотную подошли к определению
дискретных индексных метрических пространств - предмету изложения настоящего
раздела.
По
аналогии с непрерывными метрическими пространствами (1.2.4) дадим определение
дискретным индексным метрическим пространствам.
Определение
1.6.
Дискретным
индексным метрическим пространством будем называть совокупность чисел (x, y, z, ..., r), записываемую в виде
r x, y, z, ... (1.2.16)
из некоторого множества (пространства) индексных
элементов x (в общем случае гиперкубических элементов), в которых введено расстояние l между индексными элементами
l(xi+1-xi)
= 1 (1.2.17)
и самого числа r, записываемого
(индуцируемого) или хранящегося в этом гиперкубическом
элементе.
Под
определение 1.6. подпадают все возможные физические дискретные системы, для
которых индексное положение элемента определяется индексами x - номер строки, y - номер столбца, z - номер слоя и т.д. Сам же элемент r
характеризуется числом (например, яркостью свечения элемента экрана), а также
числовыми измерениями во всевозможных матрицах (таблицах) в математике, и
элементах однородных вычислительных структур, для которых задана метрика по
координатам x,y,z,... При этом конечные матрицы можно рассматривать, как
локальные фрагменты дискретных индексных метрических пространств на плоскости x,y.
В
последние годы в процессе разработки конвейерно-векторных вычислительных систем
5-го и 6-го поколений интенсивно развиваются техника и алгоритмы параллельных
вычислений на однородных вычислительных средах и систолических структурах.
Как
будет показано ниже на эти сеточные вычислительные структуры и ориентирован
развиваемый нами аппарат дискретных метрических пространств.
В
общем случае значения индексов x,y,z,...
могут лежать на интервалах
[-¥,
+¥],
но не принимают они, по определению, целочисленные значения.
Таким
образом, рекуррентная последовательность типа (1.2) является одномерным
дискретным индексным метрическим пространством {U±x},
где x ®[-¥, +¥], при ее записи в виде
однородной таблицы.
На
примере последовательности целых чисел покажем разницу между непрерывными
метрическими пространствами (1.2.4) и индексным дискретным пространством
(1.2.16).
Согласно
(1.2.4) последовательность действительных чисел в виде r(x) º r(x,xo)
может быть представлена на рис.2.
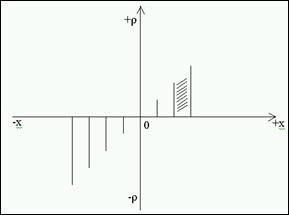
Рисунок 2.
Последовательность
же целых чисел представленная в дискретном индексном метрическом пространстве
(1.2.16) есть rx (см. рис.3) *.
|
–ОÙ |
–∞ |
… |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
… |
+∞ |
+ ОÙ |
Рисунок 3.
В
соответствии с определением 1.6. дискретное индексное одномерное метрическое
пространство правильнее было бы представить в виде оцифрованных отрезков
числовой оси (рис. 4),
|
–ОÙ |
–∞ |
… |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
… |
+∞ |
+ ОÙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4
начало и конец которых
определяются соответственно выражениями:
и 
(1.2.18)
Однако, учитывая, что
элементы строки и столбца в физических системах имеют длину и ширину, в
дальнейшем и для одномерного случая будем пользоваться представлением вида
Рис.3.
* - Функцию и свойства особого числа 
введем в разделе 1.3.
1.2.1. ДИСКРЕТНЫЕ ИНДЕКСНЫЕ
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА ЦЕЛЫХ ЧИСЕЛ.
Очевидно, что дискретных
индексных метрических пространств мы можем образовать бесконечное множество. Но в зависимости от линейности или нелинейности пространств, а
также от числа и последовательности поэлементных и групповых арифметических
(алгебраических, а в равной мере и пространственных (позиционных) операций),
определяющих взаимную функциональную зависимость между элементами, с учетом
особых свойств числовых пространств, построенных на рекуррентных
последовательностях, в этом бесконечном многообразии пространств можно
установить структурную упорядоченность, т.е. разделить их на счетные множества.
Введем первую классификацию возможных
дискретных индексных метрических пространств.
Определение 1.7.
Дискретные индексные
метрические пространства могут быть представлены в виде одного из четырех
типов:
1) - линейные индексные
метрические пространства;
2) - аддитивные нелинейные
индексные метрические пространства;
3) - мультипликативные
нелинейные индексные метрические пространства;
4) - случайные индексные
метрические пространства.
Различаются эти пространства
соответствием поэлементных и групповых операций данному состоянию дискретного
числового пространства.
При этом поэлементные и
групповые операции в качестве аргументов используют значения индексов.
Прежде чем перейти к
рассмотрению структуры множества индексных метрических пространств и методов их
синтеза, определим два особых индексных метрических пространств целых чисел.
Определение 1.8.
Дискретное числовое
пространство называется пустым или нулевым, если во всех его элементах,
позиционное положение которых определяется индексами x, y, z; n, p, ..., значение самого числа
rx,n,y,p,z =
0 (1.2.19)
Определение 1.9.
Дискретное числовое
пространство называется единичным, если во всех его элементах значение самого
числа rx,n,y,p,z = 1 (1.2.20)
Как будет показано ниже,
состояния дискретных числовых пространств (1.2.19) и (1.2.20) сохраняют их метричность и являются особыми фундаментальными состояниями
порождающими соответственно:
·
(1.2.19) - линейные и аддитивные нелинейные индексные метрические
пространства;
·
(1.2.20) - мультипликативные нелинейные индексные метрические
пространства;
Линейные индексные
метрические пространства
Определение 1.10.
Линейными
индексными дискретными метрическими пространствами целых чисел будем называть
числовые пространства, для которых в совокупности rx, y, z выполняются операции
поэлементного сложения и вычитания, параллельного переноса столбцов либо
параллельного сдвигового переноса строк (столбцов), таких, для которых
справедливы условия 1,2 и 3 (см. ниже), а также обобщенные операции переноса -
параллельного матричного переноса.
Условие 1.
1)
rx, y, z
= x+y+z+... = ...+z+y+x (коммутативность) (1.2.21)
2)
rx, y,
z = x+(y+z+...) = (x+y)+z+... (ассоциативность) (1.2.22)
3)
В
X существует такой элемент 0,
что
x+y+z+...+0 = x+y+z+... = rx, y, z...0 (1.2.23)
4)
Для
каждого элемента xÎX (1.2.24)
Условие
2.
Любое
число соответствующего элемента rx, y, z, ... может быть представлено посредством умножения одного из индексов, либо
их суммы на произвольное число a т.е.
1) rx, y, z,… = a(x+y+z+...) = ax + ay + az... (1.2.25)
при этом
2) I×x = x
Объединяя условие 1 и 2, в общем виде можем записать
определение 1.8 в следующей форме.
Определение
1.11.
Линейными
индексными метрическими пространствами будут являться такие числовые
пространства, для которых выполняется обобщенное условие
rx, y, z,… = a(x+y+z+...) + (x0 + y0 +
z0...) (1.2.26)
Из рассмотрения выражения
(1.2.26) нетрудно видеть, что при равенстве a=1 или х0, у0, z0=0
мы приходим снова к условиям 1 и 2.
Еще раз подчеркнем, что для обозначения элементов
линейных индексных метрических
пространств мы будем
пользоваться только нижними
индексами rх, у, z,…
Рассмотрим структуру
индексных линейных метрических пространств.
По определению (1.11), в общем случае, к линейным индексным метрическим
пространствам необходимо отнести (в одномерном варианте) возвратные и
рекуррентные последовательности целых чисел, образуемых арифметическими
прогрессиями, т.е.
rх = aX (1.2.27)
Начнем рассмотрение со
случая, когда, как a, так и X
являются целыми числами -¥, …,-3, -2, -1, 0, 1, 2, 3,
…, +¥
Для рекуррентной
последовательности (1.2.27) можно в соответствии с (1.1.4) найти возвратное
уравнение.
Известно, что для
арифметических прогрессий
rk+1 = rk + d (1.2.28)
где d - разность арифметической
прогрессии.
Соотношение (I.2.28) еще не
имеет вид (1.1.4). Для этого рассмотрим два соотношения, написанные для двух
соседних значений k.
rk+2 = rk+1 + d и rk+1 = rk + d (1.2.28*)
Далее, путем почленного вычитания получаем
rk+2 -rk+1 = rk+1 -rk
или
rk+2 = 2rk+1 - d (1.2.29)
для всех целочисленных значений k на
интервале от –¥ до
+¥ соотношение (1.2.29) это
уже уравнение вида (1.1.4), откуда находим, что m=2; a1=2; a2 =–1, т.е. арифметическая
прогрессия является возвратной последовательностью второго порядка.
Перепишем уравнение (1.2.29)
в следующем виде:
(1.2.30)
или в общем виде
(1.2.31)
где k - целые числа, c - натуральные числа;
Условие 3
Выражение
(1.2.30) и (1.2.31) показывают, что любой элемент линейных индексных
метрических пространств может быть выражен через среднеарифметическое двух соседних
элементов (слева и
справа от выбранного элемента) или
любых, сколь угодно удаленных, от искомого элемента на равные индексные
расстояния.
Пример 1
Покажем, что
линейная сдвиговая суперпозиция
простейшей арифметической прогрессии с разностью d=1 - последовательности целых
чисел, представленной в одномерном дискретном индексном метрическом,
пространстве 1.2.16 и удовлетворяющей Условию 3 (1.2.29…1.2.31), при
поэлементном суммировании и вычитании порождает новые линейные одномерные
индексные последовательности, которые, в свою очередь, так же удовлетворяют
Условию 3 (см. табл. 1.2)
Таблица 1.2
|
k |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Rk |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Rk+4 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Sk |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
|
Dk |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
Как видно из табл. 1.2,
поэлементное суммирование исходной арифметической прогрессии с разностью d=1 т.е. Rk с последовательностью Rk+1,
т.е. той же арифметической прогрессией, сдвинутой влево относительно исходной
на четыре индексных элемента, при поэлементном суммировании (Sk)
приводит к образованию четной арифметической прогрессии с разностью d=2 , а поэлементное вычитание Dk = – 4
, т.е. к константе Constk = – 4.
Не представляет труда убедиться,
что Условие 3 - условие линейности справедливо и для вновь образованных,
дуально бесконечных арифметических прогрессий. Характерно, что при сдвиговой
суперпозиции на нечетное число элементов, поэлементное суммирование приводит к
образованию нечетной дуально-бесконечной арифметической прогрессии с разностью d=2
…, -7, -5, -3, -1, 1, 3, 5,
7, 9, 11, …
а поэлементное вычитание (Dk)
приводит к образованию вырожденной арифметической прогрессии, имеющей разность d=0 и
являющейся константой.
Аддитивные нелинейные индексные метрические пространства
Определение 1.12.
Аддитивными
нелинейными индексными метрическими пространствами целых чисел будем
называть числовые пространства,
для которых в совокупности чисел rx,y,z, так же выполняются операции параллельного
переноса столбцов, строк,
слоев, и обобщенная операция параллельного матричного
переноса с поэлементным
сложением и вычитанием, при сохранении порядка рекуррентности, но не
выполняется Условие 3 (условие линейности), при этом числа rx,y,z хотя бы от одной из индексных
координат находятся в аддитивной
зависимости (т.е. подчиняется обычным рекуррентным уравнениям выше второго
порядка).
Пример 2
Простейшим примером
аддитивных нелинейных индексных метрических пространств могут быть названы
пространства, основанные на одномерной возвратной последовательности Фибоначчи (
).
Это известная
последовательность
f1=1; f2=1; f3=2; f4=3; f5=5;
f6=8… (1.2.32)
для которой, начиная с
элемента с индексом
k=3, справедливо рекуррентное уравнение
fk+2= fk+1+ fk (1.2.33)
Рекуррентная форма
последовательности (1.2.32) получается путем распространения рекуррентного
уравнения (1.2.33) на всю числовую (индексную) ось, для чего перепишем его в
виде
fk-1= fk+1 - fk (1.2.33*)
и достроим последовательность для отрицательных
чисел, т, е. в табл. 1.3.
|
(1.2.34) |
Простыми преобразованиями
можно убедиться в справедливости определения 1.12.
Действительно:
Условие 3 - условие
линейности не выполняется т.к. уравнение 1.2.33, будучи переписанным, в форме
1.2.30 показывает
fk= fk+1 - fk-1 (1.2.35)
т.е. отличается от условия
линейности 1.2.30.
Пример 3
Операции параллельного
переноса исходной строки (1.2.34) вправо (или влево) с поэлементным
суммированием или вычитанием приводит к следующему (например, при сдвиге вправо
на 3 элемента, см. табл. 1.4, или вправо на 4 элемента, см. табл. 1.5).
Таблица 1.4.
|
K |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
f±k |
5 |
-3 |
2 |
-1 |
1 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
f±k-3 |
-21 |
13 |
-8 |
5 |
-3 |
2 |
-1 |
1 |
0 |
1 |
1 |
2 |
|
Sk |
-16 |
10 |
-6 |
4 |
-2 |
2 |
0 |
2 |
2 |
4 |
6 |
16 |
|
Dk |
26 |
-16 |
10 |
-6 |
4 |
-2 |
2 |
0 |
2 |
2 |
4 |
6 |
Таблица 1.5.
|
K |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
f±k |
5 |
-3 |
2 |
-1 |
1 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
f±k-4 |
34 |
-21 |
13 |
-8 |
5 |
-3 |
2 |
-1 |
1 |
0 |
1 |
1 |
|
Sk |
39 |
-24 |
15 |
-9 |
6 |
-3 |
3 |
0 |
3 |
3 |
6 |
9 |
|
Dk |
-29 |
18 |
-11 |
7 |
-4 |
3 |
-1 |
2 |
1 |
3 |
4 |
7 |
Как видно из анализа
последовательностей и операций аддитивной сдвиговой суперпозиции, приведенных в
табл. 1.4. и табл. 1.5., сдвиг исходной рекуррентной последовательности F±(k-3) на три индексных элемента
вправо, т.е. F±(k-3) выполнение операций
поэлементного суммирования
(1.2.36)
и поэлементного вычитания
(1.2.37)
приводит в первом случае к последовательности 2Fk-1 т.е.
fk+fk-3=2fk-1 (1.2.38)
т.е. исходной последовательности сдвинутой вправо на один элемент с поэлементным удвоением.
Примечание: Характерно сравнение
рекуррентного уравнения (1.2.38) для последовательности F±k и рекуррентного уравнения.
(1.2.29) для линейной последовательности R±k. Это сравнение
показывает, что в
индексной последовательности Фибоначчи линейность нарушается. При этом
происходит сжатие последовательности в сторону возрастания индексов k.
При поэлементном вычитании Dk, получаем
fk - fk-3=2fk-2 (1.2.39)
Сдвиговая суперпозиция при
сдвиге на 4 элемента (см. табл. 1.5) приводит к следующему
(1.2.40)
а разность
(1.2.41)
приводит к новой последовательности типа Фибоначчи (
), сдвинутой относительно нулевого индексного элемента
на 3 шага.*
* - Эта последовательность известна под названием –
Последовательность чисел Люка [Стахов А.О. Коды золотой пропорции., М., Радио и связь, 1984г.]
Методами
аддитивной сдвиговой суперпозиции можно получить бесконечное число индексных
последовательностей типа Фибоначчи, например …9,-5,4,-1,3,2,5,7,12,…получается
с помощью Dk при сдвиге вправо на 5 элементов.
Анализу
многомерных индексных тел и способам параллельных вычислений в дискретных
индексных пространствах Фибоначчи посвящены разделы 4.2.3 и 5.2 настоящей
монографии.
Мультипликативные
нелинейные индексные метрические пространства.
Определение 1.13
Мультипликативными
нелинейными индексными метрическими пространствами можно назвать такие числовые
пространства, для которых операции параллельного переноса столбцов, строк и
слоев и обобщенная операция матричного переноса в совокупности чисел rх, у, z
выполняется с мультипликативными аналогами операций поэлементного сложения и
вычитания, т.е. умножения (Пk) и деления (%k).
При этом рекуррентные уравнения являются уравнениями первого порядка, а на
логарифмическом уровне последовательностей, образующих эти пространства, могут
быть уравнения выше 2-го порядка.
Пример 4
Для пояснения этого
определения представим рекуррентную одномерную последовательность (М±k)
– геометрическую прогрессию с основанием q = 2 (см. табл. 1.6).
Таблица 1.6
|
k |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
М±k |
2-5 |
2-4 |
2-3 |
2-2 |
2-1 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
М(k-2) |
2-7 |
2-6 |
2-5 |
2-4 |
2-3 |
2-2 |
2-1 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
Пk |
2-12 |
2-10 |
2-8 |
2-6 |
2-4 |
2-2 |
20 |
22 |
24 |
26 |
28 |
210 |
212 |
214 |
|
%k |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
Геометрические
прогресии описываются рекуррентными уравнениями первого порядка [1]
μk+1=qμk (1.2.42)
в нашем случае q = 2, т.е.
μk+1=2μk (1.2.43)
Как видно из
табл. 1.6, в которой в строке М±k, приведена исходная
дуально-бесконечная геометрическая последовательность с основанием 2. Для этой
рекуррентной последовательности индексные элементы с положительными числами
являются возрастающей геометрической
прогрессией целых чисел, а индексные элементы с отрицательными индексами -
геометрическая регрессия дробных чисел с основанием 2.
Сдвиговая суперпозиция
исходной последовательности М±k на два элемента вправо т.е.
М±(k-2)
с выполнением поэлементных операций умножения Пk=(Мk·Мk-2)
и поэлементного деления %k=(Мk/Мk-2)
приводят :
·
в первом случае к построению дуально-бесконечной геометрической
прогрессии с основанием 4=22,
·
во втором случае последовательность обращается в индексную константу Сk=4.
Детальному анализу свойств мультипликативных индексных метрических пространств будет посвящен раздел 4.2.4 настоящей монографии.
Обобщая определения,
введенные в настоящем разделе, и первые опыты обращения к операциям сдвиговой
суперпозиции следует добавить, что простыми признаками аддитивности
или мулътипликативности является проверка на наличие
индексного элемента равного нулю.
Если однородное индексное
метрическое пространство содержит в себе хотя бы один элемент равный нулю, то это или случайное или аддитивное пространство.
С другой стороны
порядок рекуррентности
последовательностей, образующих пространство, в
свою очередь определяет тип
пространства.
Пространства, образованные
последовательностями нулевого порядка рекуррентности -
случайные пространства -
Пространства с первым порядком рекуррентных уравнений - мультипликативные
пространства. Пространства,
составленные из последовательностей, описываемых рекуррентными уравнениями
второго и выше
порядков - аддитивные пространства.
При этом
пространства, составленные из
последовательностей, описываемых
рекуррентными уравнениями второго
порядка и удовлетворяющих условию
3 - аддитивные
линейные пространства.
Полученные выводы можно представить в виде
классификационной таблицы индексных метрических пространств, табл. 1.7.
Таблица
1.7.
|
Типы характеристик |
Вид пространств |
|||||
|
|
Индексные метрические пространства |
|||||
|
Тип сдвиговой суперпозиции |
Мультипликатывные |
Случайные |
Аддитивные |
|||
|
Тип линейности |
Мультипликатывные нелинейные |
|
Линейные |
Аддитивные нелинейные |
||
|
Тип порядка рекуррентного
уравнения |
Первого порядка |
Нулевого порядка |
Второго порядка |
Второго и выше порядка |
||
1.2.2. КЛАССИФИКАЦИЯ ОДНОМЕРНЫХ
РЕКУРРЕНТНЫХ ИНДЕКСНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ ПО ПОРЯДКУ РЕКУРРЕНТНОСТИ.
Используя математические приемы
для отыскания рекуррентных уравнений, описывающих свойства основных возвратных последовательностей, изложенные
в [1] (см., например, вывод уравнения 1.2.29) и, распространяя далее полученные
рекуррентные уравнения на всю индексную ось, можно по аналогии с приведенными
выше примерами построить наиболее часто
встречающиеся рекуррентные индексные метрические последовательности.
Задаваясь целью
навести структурную упорядоченность в основных рекуррентных последовательностях, разместим
наиболее характерные
последовательности в табл.
1.8 по степени
возрастания порядка
рекуррентности.
Таблица 1.8
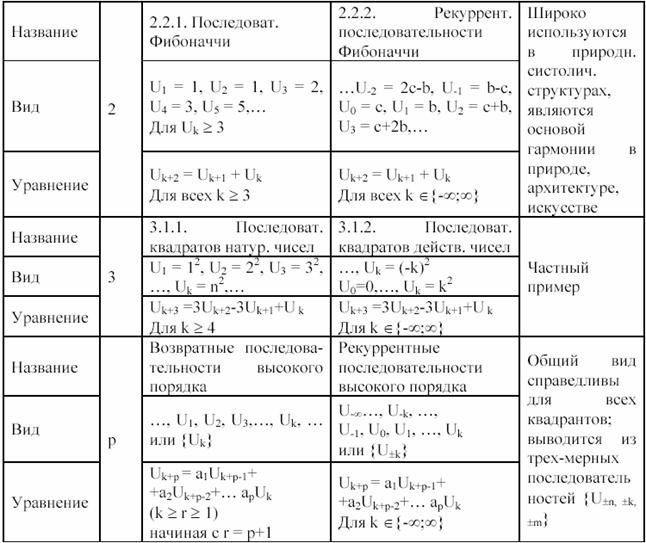
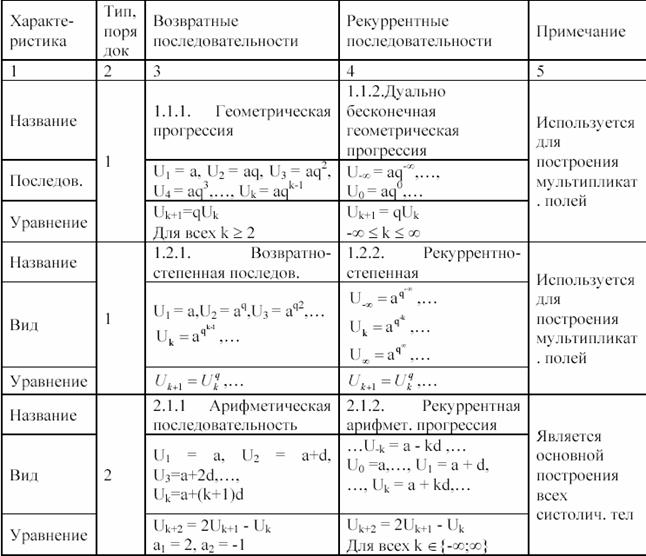
Разумеется, что в табл. 1.8
приведены только основные примеры возвратных
и рекуррентных
последовательностей. Например, виды рекуррентных последовательностей второго порядка никак не
ограничиваются арифметическими
прогрессиями и последовательностями Фибоначчи (или типа
Фибоначчи). Этих видов бесконечное множество в зависимости от выбора
коэффициентов а1 и а2, а
множество самих
последовательностей, кроме того определяется начальными величинами а, b, c
и α.
Каким образом из одномерных
индексных метрических последовательностей образуются многомерные пространства?
Какую роль при их формировании играют операции сдвиговой суперпозиции? Этим и
другим, более сложным вопросам, будут посвящены следующие главы.
1.2.3. Топологическая модель
рекуррентных индексных последовательностей (основные определения).
Как же связываются числовые
последовательности (1.2.27) ... (1.2.42) в кольца целых чисел.
В соответствии с [5]
"во множестве целых чисел определены две основные операции: сложение и
умножение, а также отношение "больше", Сложение и
умножение коммутативны,
ассоциативны и умножение дистрибутивно относительно сложения. В отличие от
натурального ряда во множестве
целых чисел всегда
осуществляется операция, обратная сложению, - вычитание. Так, что
множество целых чисел представляет собой упорядоченное кольцо, которое
называется кольцом целых чисел и обозначается буквой z" [5. стр.54].
Принятое определение кольца
целых чисел только по ассоциации может быть названо кольцом.
Введем понятие истинного
кольца целых чисел или катенаны (от латинского catena - цепь).
Определение 1.14.
Истинным кольцом целых чисел
- катенаной назовем дуальное кольцо целых
чисел и античисел состоящее из индексных последовательностей ρ±k, внутрисвязных с
антипоследовательностями 
, в которых определены две операции: сложение и умножение,
отношение "больше", операция обратная сложению - вычитание, а также
существует элемент противоположный нулю - так называемый рекуррентный нуль.
На элементе рекуррентный
нуль производится "склеивание" индексных последовательностей ρ±k
в ленту Мебиуса, в общем случае - в многослойное тело Мебиуса.
Термин катенана
ранее был введен
в химии для
обозначения антихимических монстров, т.е. соединений в которых молекулы
держатся друг за друга без всяких химических связей [15].
В математике он еще не
использовался.
Я преднамеренно не применяю
для обозначения истинного кольца целых чисел русский аналог определения
катенаны - цепь, и вот почему:
- Наше определение катенаны
почти сходно с определением тела в теории множеств. Как
известно [22], кольца,
в которых для всех отличных от
нуля элементов существуют обратные, называются телами. Тела не содержат
делителей нуля. Это определение мультипликативно
связных тел.
Мы же определением 1.14.
подразумеваем аддитивный аналог, как бы двойного тела, связанного с двойным
антителом, в которых для каждого элемента существует противоположный элемент, включая элементы
противоположные нулю.
- С другой стороны, как будет
показано в этом разделе простейшее истинное
кольцо целых чисел
- катенана первого
порядка - есть однозвенная цепь (с точки зрения
топологической интерпретации).
Кроме того, будет показано,
что катенана первого порядка может быть разбита на многозвенные цепи, т.е.
цепи, состоящие из нескольких колец, именно колец, а не тел.
В то время, как в
теоретико-множественных построениях цепью называется подмножество, в
котором любые два элемента сравнимы между, собой (в смысле частичной
упорядоченности) [12]. Т.е. цепь в теории множеств стоит
на более низком иерархическом уровне связанности, чем вводимая нами катенана.
Для получения большей
наглядности топологической модели катенаны подойдем к рассмотрению трехмерного
листа Мебиуса.
"Вселенная, изображаемая теорией относительности Эйнштейна,
подобна раздувающемуся мыльному пузырю.
Она - не его внутренность, а пленка. Поверхность пузыря двумерна, а пузырь
вселенной имеет четыре измерения: три
пространственных и одно – временное". Этими словами английского физика
Джеймса Джинса можно с большой степенью
приближения охарактеризовать гносеологическую основу
не только вселенной теории относительности Эйнштейна, но и, в целом,
всех индексных метрических пространств. Они
- эти пространства - сотовые,
составлены из двумерных пленок - сот (см. цепей ), а
сам пузырь - индексных метрических пространств - катенана, может иметь
неограниченное число измерений.
Еще более точная интуитивная
догадка выражена в [15].
"Форма, геометрические
свойства играют в нашем мире удивительную роль. В нем царит таинственная ассиметрия, а вовсе
не прозрачная симметрия, и поэтому идея Вселенной в виде трехмерного листа
Мебиуса имеет кое-какие шансы оказаться жизненной".
Что же такое трехмерный лист
Мебиуса в числовых пространствах последовательностей, равно
как и в их топологических наглядных моделях?
Прежде всего, покажем
сходства и коренные различия противоположных элементов (0) и рекуррентный нуль (Θ).
1.3. РЕКУРРЕНТНЫЙ НУЛЬ.
В метрических пространствах
(1.2.4) аналогами рекуррентных нулей являются
точки, не принадлежащие области определения рациональной функции S,
называемые полюсами [16]. Это в
точности корни многочлена F из несократимой записи
функции S. Кратностью
(или порядком) полюса называется его кратность как корня многочлена F.
Таким образом, если S = G / F - несократимая
запись рациональной функции S и если
F = (x – xo)nF0 , где F0 ≠ 0, то х0 -это полюс, a v~ его кратность.
Известна лемма [[16], стр.
49]
«Точка xo тогда и только тогда является полюсом кратности v
рациональной функции S, когда
lim
(x-x0)m S(x)= 
(1.2.44)
При этом число A0 = lim(x-x0)v S(x) отлично от нуля и является
главным коэффициентом функции S в полюсе x0.
По определению, если x0 – полюс рациональной
функции S, то
limS(x)=∞ (1.2.45)
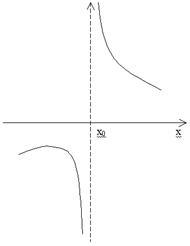
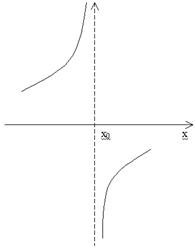
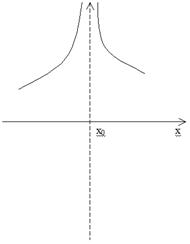
Различаются следующие типы
полюсов в зависимости от поведения функции S в окрестности точки x0.
|
|
|
|
Тип 1 |
Тип 2 |
|
|
|
|
Тип 3 |
Тип 4 |
Рис 5.
Каждый из типов можно
определить:
Тип 1 характеризуется тем, что
при x, близких к xΘ, но меньших чем xΘ, функция S
отрицательна, а при x, больших, чем xΘ – положительна. Можно
сказать, что в таком полюсе функция скачком переходит от
-∞ к +∞.
Тип 2 характеризуется положительным
поведением: при x<xΘ функция положительна, а при
x>xΘ – отрицательна. В полюсе этого типа функция скачком
переходит от +∞ к -∞.
В
обоих случаях при переходе через полюс функция меняет знак.
Остальные два типа
(Тип 3 и Тип 4) характеризуются тем, что при переходе через них функция знак не
меняет:
-
в случае полюса Тип 3 она остается положительной,
-
в случае полюса Тип 4 она остается отрицательной.
С помощью «односторонних»
пределов
S(x0-0)=limS(x) (1.2.46)
и
S(x0+0)=limS(x)
(1.2.47)
эту классификацию полюсов
можно свести в следующую таблицу
Таблица 1.9
|
Тип |
S(x–0) |
S(x+0) |
|
1 |
– ∞ |
+ ∞ |
|
2 |
+ ∞ |
– ∞ |
|
3 |
+ ∞ |
+ ∞ |
|
4 |
– ∞ |
– ∞ |
Пусть v
– кратность
полюса xΘ, число (x-x0)v S(x)
имеет тот
же знак, что и число A0, следовательно, справедливо
следующее предложение.
Предложение
Полюс имеет:
|
Тип
1 |
|
тогда,
A0>0 и n нечетно |
(1.2.48) |
|
Тип
2 |
и
только A0<0 и n нечетно |
||
|
Тип
3 |
тогда,
A0>0 и n четно |
||
|
Тип
4 |
и
только A0<0 и n четно |
Определение 1.15
Индексом рациональной
функции S в полюсе x называется число ind x0S,
определяемое формулой
|
|
|
+1 |
,
если n нечетно и A0>0 |
(1.2.49) |
|
-1 |
,если
n нечетно и A0<0 |
|||
|
0 |
,если
n четно |
Таким образом
В индексных метрических
пространствах скачкообразного перехода дискретных функций не происходит, а этот
переход осуществляется на одном из элементов пространства Θ, в силу того, что индексные координаты
целочисленные.
Определение 1.16.
Таким образом, рекуррентным
нулём Θ будем называть элемент индексного пространства, на
котором дискретная функция имеет полюсы или склейки.
Как будет показано ниже, эти склейки (сплайны) могут быть более
разнообразны, чем выше перечисленные 4 типа полюсов.
Общим для
всех рекуррентных нулей
является сингулярность индексного
пространства на этом элементе, т.е. это особые "точки" пространства,
переводящие какую либо из характеристик последовательностей лежащих слева и
справа от рекуррентного нуля на диаметрально
противоположную.
Например, если
арифметическая последовательность слева от нуля возрастает (прогрессия), то
справа она будет убывать (регрессия), и наоборот; если
для элементов или
строк (столбцов) может
быть поставлена
в соответствие поэлементная или групповая пространственная или алгебраическая
операция, то на элементе рекуррентный нуль эта операция сменяется на противоположную.
Сложение заменяется на
вычитание, правосторонняя сдвиговая суперпозиция заменяется на левостороннюю и т.д.
1.4. ВВЕДЕНИЕ
В ТЕОРИЮ СИММЕТРИИ
Существует одна важная
область математики - учение о симметрии. Элементарное знакомство с ним
позволяет глубоко вникнуть в существо важнейших положений физики [23]. Вызывает
удивление, что это учение в большинстве случаев не является обязательным курсом
ни в средней школе, ни в высших учебных заведениях.
Основания учению о симметрии
положены кристаллографом Браве О. В его «Memoire sur les polyedres der forme symetrique» и других работах, которые
впоследствии, уже после его смерти собраны под именем «Studes cristallographiques» (
Существенное развитие этих
основ и исправление ряда ошибок Браве, а также
разработка аналитического учения о симметрии выполнена в работах русского
математика и кристаллографа Е.С. Фёдорова: «Симметрия конечных фигур»,
«Симметрия правильных систем фигур», «Сопоставление кристаллографических
результатов г-на Шёнфлиса с моими» и др. [18].
В математику и физику
Федоровское учение о симметрии вошло из кристаллографии практически без
изменений вплоть до настоящего времени.
Е.С. Федоров так определил
симметричные фигуры:
«Симметрическою фигурой
называется такая, которая непосредственно может быть совмещена с самой собой в
разных положениях, или же совмещение в разных положениях может быть
произведено, если мы заменим ее другою, которая относится к ней, как
изображение в зеркале к изображаемому предмету».
На вопрос, какие виды и элементы
симметрии можно вывести из основного определения, Е.С. Федоров строго отвечает,
что «... их существует всего три
1) Фигура путем вращения вокруг
некоторой оси совмещается сама с собой. Это случай оси симметрии.
2) Фигуру можно совместить саму
с собой посредством отражения в плоскости. Это случай плоскости симметрии.
3) Совмещения не удается
достигнуть путем операции 1), ни путем операции 2), если они берутся в
отдельности, но оно наступает при одновременном использовании обеих операций,
т.е. когда мы вращаем фигуру вокруг некоторой оси и отражаем ее в плоскости.
Это случай сложной симметрии.
Соответственную
ось и плоскость я называю осью и плоскостью сложной симметрии. Известно, что
они должны быть взаимно перпендикулярны». И далее «центром симметрии» Е.С. Федоров
считает точку пересечения всех элементов симметрии данной фигуры. [18, стр. 261
- 262].
Кроме
элементов симметрии конечных фигур Е.С. Федоров различает еще элементы
симметрии правильных систем (т.е. пространственных групп). Он пишет, что «...
системы обладают еще следующими элементами симметрии:
1) винтовыми осями (этот
элемент симметрии был введен еще Зонке),
2) плоскостями скользящего
отражения и трансляции, параллельной этой плоскости.
Под этими словами мы
понимаем такой элемент симметрии, который состоит одновременно из плоскости
симметрии и трансляции, параллельной этой плоскости.
Каждый возможный вид
симметрии представляет собой лишь комбинацию элементов симметрии, и ближайшей
задачей учения о симметрии является полный вывод всех этих комбинаций» [18, стр.
263 - 264].
Отмеченные Е.С. Федоровым
утверждения в математике нашли доказательства в виде
теорем Шаля возможных преобразований для плоскости:
- «Всякое перемещение
плоскости является параллельным переносов, поворотом или скользящей
симметрией».
и для пространства:
- «Всякое перемещение
пространства является либо винтовым перемещением, либо скользящей симметрией,
либо поворотной симметрией». [19]
«Физика,
и в особенности физика микромира строилась до 1956 года как симметричное
здание, до тех пор, пока оно не стало сильно проседать на один угол, когда в
1956 году было обнаружено несохранение
пространственной четности. То есть оказалось, что законы физики меняются при
замене левого на правое. Такое преобразование
происходит при отражении в зеркале и называется р-преобразование,
от английского слова parity - четность.
До
1956 года существовала молчаливая уверенность в том, что все физические
процессы как в нашем мире, так и в «зазеркалье» (т.е. будучи отраженными
в зеркале) идут одинаково. Так при зеркальном отражении левая перчатка
превращается в правую. Эту уверенность в симметрии
относительно р-преобразования иногда выражаем в
утверждении, что в микромире правое и левое неотличимо. Однако обнаружилось,
что существуют такие процессы, для которых это утверждение несправедливо.
...
Одновременно с открытием несохранения
пространственной четности было найдено, что законы физики не инвариантны
относительно преобразования с-четности, которое
состоит в том, что все частицы заменяются на античастицы» [20].
Я позволил себе пространственное цитирование работ [18 - 20] только
для того, чтобы наглядно показать, что хорошо продуманное и высказанное в [18]
утверждение Е.С. Федорова о «симметрических фигурах», а соответственно, и о
симметрии физических законов, равно симметрии между элементами и антиэлементами фундаментальна, и его необходимо только
правильно применять для устранения возникающих парадоксов, а также для
логического введения нашего определения антипоследовательностей
и античисел.
Поможет
нам это сделать ускользающий в перечислениях, но явно прослеживаемый в
определении симметрических фигур Е.С. Федорова, еще один простой вид симметрии
- линзовая симметрия.
Прежде
чем перейти к определению линзовой симметрии, рассмотрим один из
фундаментальных фактов, приведших к возникновению мнения физиков о нарушении
зеркальной симметрии в процессах слабого взаимодействия [21]. Этот эксперимент
был предсказан китайскими физиками-теоретиками Янгом и Ли
в 1956 году.
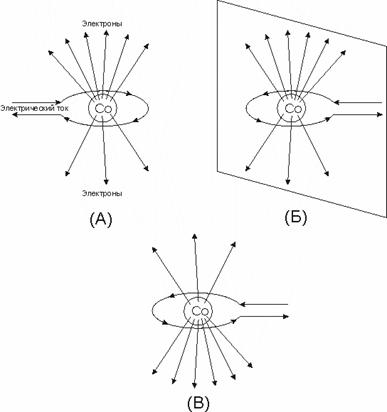
Принцип
этого эксперимента иллюстрируется рисунком (рис. 6) заимствованным из [21].
|
|
Рисунок 6.
Иллюстрация к эксперименту с кобальтом-60.
«В
этом эксперименте проводилось наблюдение за электронами, излучавшимися в
процессе радиоактивного распада кобальта-60 (60Со).
Образец
кобальта, охлажденный до очень низких температур, был помещен внутрь катушки,
по которой протекал электрический ток (его направление указано стрелками).
Было
обнаружено, что если эксперимент поставить так, как показано на рис. 6 (а), то
вверх излучается больше электронов, чем вниз.
Поскольку
гравитация к этому эксперименту не имеет ни малейшего отношения, правильнее
было сказать так: большее число электронов излучается в направлении того торца
катушки, с которого ток представляется текущим по виткам катушки по часовой
стрелке.
Справа
на рисунке рис. 6 (б) изображено зеркальное отражение описанного
эксперимента, а внизу рис. 6 (в) действительный, так называемый
«зеркальный эксперимент» [21]. Последний состоит в том, что экспериментальная
установка такая же, как при зеркальном отражении исходного эксперимента, а
именно: ток в катушке имеет то же направление. При этом в зеркальном отражении
эксперимента большинство электронов также излучается «вверх», тогда как в
«зеркальном эксперименте» большинство их излучается «вниз» [21].
На
основании описанных экспериментальных фактов и появилось мнение о нарушении
законов симметрии в микрофизике слабого взаимодействия.
В
действительности о нарушениях законов симметрии этот эксперимент не говорит, он
только констатирует, что эксперимент с кобальтом-60 не подчиняется зеркальной
симметрии. Это ясно видно из рис. 6.
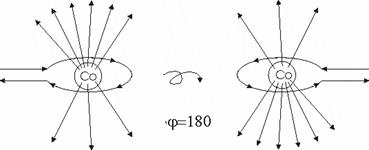
С
другой стороны, если этот эксперимент схематически трактовать рисунком (рис.
7), все становится на свои места и здание симметрии сохраняется незыблемым.
Схема
рис. 7 показывает, что пространственный эксперимент процесса радиоактивного
распада ядра кобальта-60 подчиняется не зеркальной симметрии, а может быть
интерпретирован Федоровской винтовой симметрией с поворотом на 180°.
|
|
Рисунок 7.
Интерпретация эксперимента с кобальтом-60 Фодоровской
винтовой симметрии с поворотом на 180°.
Наличие
винтовой симметрии в правостороннем варианте и аналога - поворотной симметрии в
плоскостном варианте скрывало от глаз исследователей их «двухцветную» трактовку
на плоскости и в пространстве.
Объединить
«одноцветную» и «двухцветную» поворотную и винтовую симметрию можно одной
элементарной операцией симметрии - зеркально-линзовой симметрией.
На
мой взгляд, зеркально-линзовую симметрию необходимо вводить в учение о
симметрии как самостоятельную элементарную операцию наравне с зеркальной
симметрией, несмотря на то, что зеркально-линзовая симметрия очень схожа со
случаем двойной винтовой симметрии, т.е. пространственно-винтового поворота на
180°. А по сути дела линзовая симметрия - это
последовательная двойная винтовая симметрия.
Определение 1.17.
Линзовой симметрией назовем инвариантное преобразование пространства, переводящее все его точки на диаметрально противоположные относительно выбранной винтовой оси. Кроме того, при рассмотрении симметрических фигур, подчиняющихся линзовой симметрии с одной и другой стороны относительно линзовой плоскости, перпендикулярной винтовой оси, происходит на только замена «верха» на «низ», но и «лицевой» и «изнаночной» сторон (лицо - спина; негатив - позитив; противоположные и отрицательные последовательности), т.е. то, что мы называем «двухцветностью».
Это название симметрия не только по аналогии с оптической терминологией
- «зеркальная симметрия», но также в силу возможности изучения симметрических
свойств на модели известной с древних времен - двояковыпуклой собирающей линзе,
вращательно симметричной относительно винтовой оси.
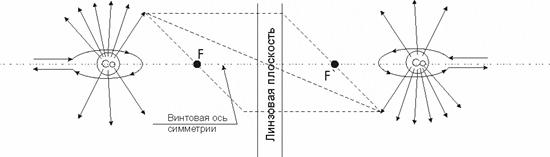
Наглядно пояснить
определение 1.17 можно на примере того же «зеркального» эксперимента процесса
радиоактивного распада ядра кобальта-60. (см. рис. 8).
|
|
Рисунок 8. Схематическое
изображение преобразования линзовой симметрии в прямом и «зеркальном» опыте
ядра кобальта-60.
Действительно, если образец кобальта-60, помещенного в катушку с
направлением тока, соответствующим прямому эксперименту, расположить
схематически в пространстве предметов указанной «линзы», а установку,
схематически соответствующую зеркальному эксперименту в пространство
изображений, то эти схемы могут быть взаимно-инвариантными при построении хода
лучей в геометрической оптике.
Для пояснения второй части определения 1.17, воспользуемся схемой рис.
9.
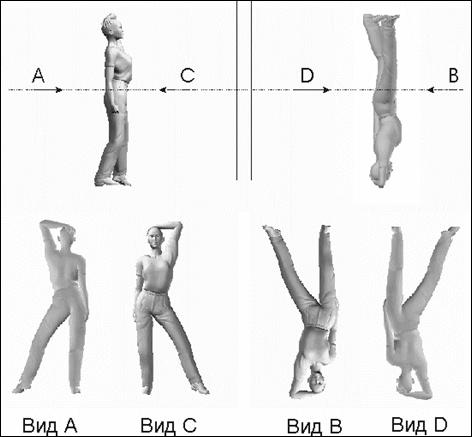
Рисунок 9. Схема поясняющая свойства линзовой симметрии при
рассмотрении инвариантности этого преобразования с одной и другой сторон от
линзовой плоскости.
Вид А
- вид со стороны «пространства предметов»;
Вид В
- вид со стороны «пространства изображения», а также вид на симметрические
фигуры со стороны линзовой плоскости;
Вид С
- вид на фигуру в пространстве предметов со стороны линзовой плоскости;
Вид D - вид на фигуру в пространстве
изображений со стороны линзовой плоскости.
В реальной линзовой системе
Вид D не правомерен, т.к. обычная линза не позволяет заглянуть на тыльную
сторону изображения предмета. К этой возможности приближаются лишь специальные
методы трехмерной голографии.
Схематическое изображение
Рис. 9 показывает, что элементарная операция линзовой симметрии, равно как и ее
обобщение винтовой симметрии обладает релятивистскими свойствами. Это значит,
что в координатах элемента пространства, в процессе указанных симметричных
преобразований никакие изменения «лево»-«право»,
«верх»-«низ» не происходит. А все эти изменения могут быть замечены лишь
внешним наблюдателем, зафиксированным во внешней координатной системе.
Точки зрения Вид А и Вид В правомерны для внешнего наблюдателя в случае,
если рассматриваемая система подчиняется линзовой симметрии - однослойная (т.е.
внутренняя линзовая симметрия).
В случае, если система
позволяет произвести расслоение по линзовой плоскости, то правомерны парные
точки зрения Вид А - Вид С, Вид В - Вид D, Вид В
- Вид В, Вид С - Вид D.
Не трудно видеть, что первые
из указанных пар перестают подчиняться линзовой симметрии, в то время, как вторые сохраняют линзовую симметрию.
Первые пары подчиняются
негативной («двухцветной») зеркальной симметрии, вторые образуют позитивную и
негативную пары линзовой симметрии.
Дальнейшему изучению
математических свойств этих видов элементарной операции симметрии мы еще уделим
внимание ниже. Однако уже здесь напрашивается физическая интерпретация
отмеченных закономерностей.
Есть все
основания предполагать, что физические законы, описывающие системы с линзовой и
зеркальной симметриями будут обладать аналогичными свойствами, как преломляемые
и отражаемые лучи в их оптических моделях.
Поэтому эти симметрии, следуя
разделению оптики с Герона Александрийского на диоптрику, т.е. науку о
преломлениях, и катоптрику, т.е. науку об отражениях, также следовало бы назвать диоптрической и
катоптрической симметрией, соответственно.
На основании сказанного, вероятно, интерпретация физического
эксперимента по взаимодействию магнитных моментов ядер кобальта с внешним
магнитным полем должна осуществляться не из отыскивания их отклонений от
катоптрических свойств, а, весьма возможно, что для сил слабого взаимодействия
необходимо искать диоптрические свойства описывающих их законов.
1.5. МНОГОСЛОЙНОЕ ТЕЛО
МЁБИУСА
Здесь
мы последовательно подойдем к определению и детально рассмотрим свойства
многомерного тела Мёбиуса.
1.5.1. Двойственные свойства
ленты Мёбиуса
а) Поставим перед собой
задачу:
– заготовку для ленты Мёбиуса, т.е. узкую
длинную полоску, раскрасить с двух сторон в семь цветов радуги, как это сделано
на рис. 10.
На
рис. 10 видно, что раскрашивание заготовки мы произвели исходя из
предположения, что заготовка подчиняется законам зеркальной симметрии (здесь
плоскость зеркальной симметрии мы считаем саму плоскость заготовки).
Проверим
закономерность зеркальной симметрии на односторонней поверхности, к тому же
имеющей один край – поверхность Мёбиуса. После положенного поворота на 108
градусов и склеивания концов заготовки мы убеждаемся, что одноцветной будет
только зеленая центральная дорожка, остальные будут раскрашены в два
чередующихся цвета:
красный – фиолетовый, оранжевый – синий, желтый –
голубой, соответственно.
Из
этого опыта мы убеждаемся, что сквозной или двухсторонней зеркальной симметрии
лист Мёбиуса на периферии не подчиняется.
б) Предположив для ленты
Мёбиуса правомерность линзовой симметрии, считая линзовой плоскостью плоскость
заготовки, а винтовую ось ориентируя по осевой линии к
зеленой дорожке, как это сделано на рис. 10) мы, после положенного
пространственного поворота на 180 градусов относительно осевой линии и
склеивания концов заготовки, убеждаемся, что все семь дорожек будут
одноцветными вдоль всего пути и замкнутыми.
Рис. 10.
Но
вот, интересный факт, описанный, например, в [15]:
– после разрезания дорожек
по их пограничным линиям, убеждаемся, что получаем фигуру, состоящую из 4-х
колец, перевивающих друг друга (см. рис. 11. Для большей наглядности рассматривается
разрезание не по семи полосам , а по трем)
|
|
|
Рис. 11.
Центральное
кольцо короткое, оно так же как и в случае а)
выкрашено в один цвет – зеленый, три других, удвоенной длины, все так же имеют
цвета: красный – фиолетовый, оранжевый – синий, желтый – голубой, но с разных
сторон получившихся колец, при этом один цвет непрерывен, замкнут по стороне.
Это происходит из-за односторонности центральной зеленой дорожки и
двусторонности периферийных дорожек (после разрезания). Другими словами,
центральная дорожка 3.- лист Мёбиуса, все остальные – дважды перекрученные
двусторонние кольца.
в) Если мы раскрасим
заготовку на четное количество цветов, то после разрезания односторонних
поверхностей вообще не будет. Другими словами – лист Мёбиуса не терпит
четности. В этом случае он превращается в цепь, состоящую из обычных
двусторонних колец, дважды перекрученных вдоль своей оси [15] и перевивающих
друг друга. Длина каждого из образовавшихся колец будет равна удвоенной длине
заготовки.
г) Если раскрасить заготовку
на дорожки цветами, зеркально симметричными относительно центральной дорожки,
либо центральной линии – линии раздела, то после разрезания все дорожки с обеих
сторон будут одноцветными. Но это только иллюзия односторонности колец. На самом
деле двусторонними будут все периферийные дорожки, и лишь одна центральная (при
нечетном числе дорожек) останется лентой Мёбиуса.
д) А теперь попытаемся
представить себе многослойный «лист» –
«тело» Мёбиуса, состоящим, например, из семислойной ленты. При этом
каждый слой ленты окрасим с двух сторон в соответствующий цвет радуги по
принципам, описанным в п. б). После разрезания ленты
по плоскостям склейки слоев вдоль всего «тела» мы убеждаемся, что описанные
выше в п.п. а), б), в), г) явления сохраняются и для плоскостной разрезки
«тела» Мебиуса.
В
этом легко убедится, сделав нужное число заготовок (слоев) и склеив каждое
начало и конец ленты с соответствующим слоем после поворота второго конца
«тела» на 180 градусов.
|
|
|
|
|
|
Рис 12. В этом примере, так же для простоты усвоения многослойное тело
строилось из трех слоев.
Обобщая
дуальные свойства первого топологического объекта – ленты Мёбиуса, можно придти
к следующим заключениям:
- лента Мёбиуса – уникальный топологический объект –
одностороннее геометрическое тело, имеющее один край и обладающее свойством двусвязности;
- если к этому объекту применить нетопологические
операции продольного разреза или расслоения, то указанное тело распадается в
многозвенную цепь (см. катенану), звенья которой
могут быть геометрическими объектами, имеющими две стороны, два края и
обладающими каждое свойствами двусвязности ( о двусвязности см., например
[15]).
Другими
словами: Лист Мёбиуса может быть представлен как пространственная суперпозиция
звеньев катенаны, соответствующим образом уложенных
одно относительно другого как по ширине, т.е. по плоскости листа, так и по его
толщине (многослойная структура).
1.5.2. Преобразование Р-,
С- и СР- четности на «теле» Мёбиуса.
Для
того чтобы не усложнять и без того непривычную в первом прочтении
топологическую модель полного кольца целых чисел – катенаны,
начнем рассмотрение с «тела» Мёбиуса, состоящего всего из двух слоев, т.е.
приступим к построению катенаны первого порядка.
Другими словами, будем рассматривать два состояния ленты Мёбиуса:
- 1-е состояние – обычный, классический лист Мёбиуса
– двусвязный, односторонний и имеющий один край.
- 2-е состояние – кольцо удвоенной длины, дважды
перекрученное вдоль своей оси, двустороннее, имеющее два края и также
двусвязное [15].
На этих
лентах разместим последовательности индексных
элементов, соответствующих арифметическим прогрессиям. И, далее, докажем, что
наше размещение удовлетворяет всем свойствам линзовой симметрии, а также
позволяет выполнить более глубокий анализ свойств преобразований р-, с-,
ср- и срт- четности, по сравнению с принятыми в
настоящее время представлениями.
Для
этого еще раз обратимся к [20] и
воспользуемся принятым в настоящее время схематическим представлением
(рис. ) преобразований р-, с-, и
ср- четности [20, рис. 41].
Рис.
Схематическое изображение преобразований р-, с-, ср- четности.
(Рисунки, пока, не
восстановлены)
С-преобразование
осуществляет замену «частицы» на «античастицу», но не меняет левое на правое. Р-преобразование
эквивалентно отражению в зеркале (двуцветное зеркальное отображение; редакция
наша). СР-преобразование были Л.Д. Ландау и американскими теоретиками
китайского происхождения Т. Ли и Ч. Янгом, которые заключалось в том, что
одновременно меняются левое на правое и «частицы» на «античастицы».
В микрофизике оперируют
также СРТ-преобразованием, которое
заключается в одновременной тройственной замене:
«частица» - «античастица»,
Правое – левое
прямой ход времени –
обратный ход времени.
Установлено, что только СРТ- преобразование не меняет законы физики, т.е. установлен
принцип СРТ-инвариантности. Относительно с-четности, р-четности и
ср-преобразований найдены нарушения в ряде физических процессов.
Ниже мы постараемся по новому проиллюстрировать метафизические свойства всех
названных преобразований четности на основной топологической модели – листе
Мёбиуса. Для чего нам и понадобится введенная выше элементарная операция
симметрии – линзовая симметрия.
(Вот, пока, все что удалось
восстановить из заброшенной в текучке дел монографии, которая планировалась к
изданию еще в 1984 году)
Литература
1.
А.И. Маркушевич. Возвратные
последовательности. М. «Наука» 1983г.
2.
Е.С. Ляпин, А.Е. Евсеев. Алгебра и теория
чисел. М. «Просвещение» ч.1, 1974г., ч.2, 1975г.
3.
И.И. Привалов. Введение в теорию функций комплексного
переменного. М. «Наука» 1977г.
4.
И.Л. Кантор, А.С. Солодовников. Гиперкомплексные числа. М. «Наука»
1977г.
5.
А.Ш. Блох. Числовые системы. Минск, «Высшая школа», 1982г.
6.
Математическая энциклопедия. М. «Советская энциклопедия»; т.1, А-Г, 1977г.; т.2,
Д-КОО, 1979г.; т.3., КОО-ОД, 1982г.; т.4, ОК-СЛО, 1984г.
7.
Словарь иностранных слов. М., ОГИЗ РСФСР, 1937г.
8.
Р. Курант, Г. Роббинс. Что такое математика., М.-Л., ОГИЗ, 1947г.
9.
Г.И. Марчук. Методы вычислительной математики. М. «Наука», 1977г.
10. Г.И. Марчук, В.И. Агошков. Введение в проекционно-сеточные методы. М.
«Наука», 1981г.
11. Д. Гилберт, С. Кон-Фоссен. Наглядная геометрия. М. «Наука», 1981г.
12. А.Н. Колмогоров, С.В. Фомин.
Элементы теории функций и функционального анализа. М. «Наука», 1968г.
13. В.В. Воеводин, Ю.А.
Кузнецов. Матрицы и вычисления. М. «Наука», 1984г.
14. Р. Кук. Бесконечные матрицы
и пространства последовательностей. М., ГФМЛ, 1960г.
15. К.Е. Левитин. Геометрическая
рапсодия. М., «Знание», 1984г.
16. М.М. Постников. Устойчивые
многочлены. М., «наука», 1981г.
17. О. Браве.
Избранные научные труды. Кристаллографические этюды. М., «Наука», 1974г.
18. Е.С. Федоров. Симметрия и
структура кристаллов. Основные работы. М., из-во
Академии наук СССР, 1949г.
19. В.В. Никулин, И.Р.
Шафаревич. Геометрии и группы. М., «Наука», 1983г.
20. М. Сапожников.
Антимир-реальность? М., «Знание», 1983г.
21. Крис Льюэллен-Смит.
Явные и скрытые симметрии. В сб. под ред. Дж. Малви. Фундаментальная структура материи. М., «Мир», 1984г.
22. Э. Фрид.
Элементарное введение в абстрактную алгебру. М., «Мир», 1979г.
23. А.С. Компанец.
Симметрия в микро- и макромире. М., «Наука», 1987г., стр.205.