Волна в фокусе и функции Бесселя

Кулигин В.А., Кулигина Г.А., Корнева М.В.

 (Исследовательская группа АНАЛИЗ;  http://kuligin.mylivepage.ru/file/index/)

Аннотация.  Показано, что вопреки сложившемуся мнению фаза волны не меняется при касании лучом каустики или при прохождении волной фокуса. Анализируются вопросы интерпретации решений с использованием функций Ганкеля.

1.     Постановка задачи

Эта задача появилась благодаря желанию разобраться в процессах, происходящих при прохождении волной фокуса. В геометрической оптике пучки параллельных лучей, проходя тонкую круглую линзу, сходятся в точку, именуемую фокусом, как показано на рис. 1. 

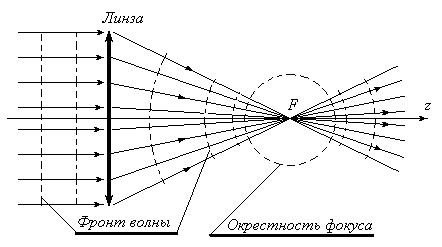
Рис. 1. Фокус как точка, где сходятся лучи.

Геометрическая оптика это предел волновой оптики. А что же происходит «на самом деле» в этой точке, т.е. в окрестности фокуса? Анализ показывает, что при конечной длине волны такой точки не существует. Волновая оптика свидетельствует, что волна, имеющая после прохождения линзы сферический фронт, по мере приближения к фокусу преобразуется. В окрестности фокуса она превращается в «трубку», где форма фронта становится плоской, как показано на рис. 2 [1]. 

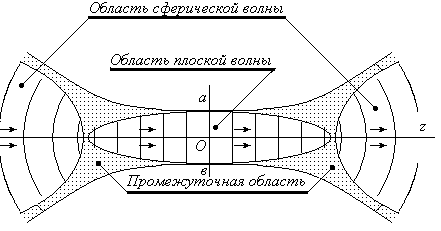
Рис. 2. Характер фронтов волны в окрестности фокуса

Между областями плоской и сферической волн появляется промежуточная (дифракционная) область, где происходят амплитудные и фазовые преобразования сферической волны в плоскую и обратно. Пример распределения интенсивности светового потока в фокальной плоскости приведен на рис. 3.

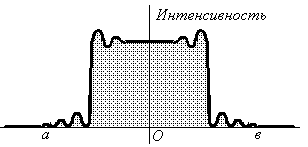
Рис. 3. Распределение интенсивности по сечению луча в фокальной плоскости

Все это согласуется с представлениями, сложившимися в волновой теории света и в теории электромагнитных колебаний. Например, в теории синфазных антенн (рупорные или зеркальные антенны) плоскость а-О-в (фокальная плоскость) рассматривается как излучающая поверхность синфазной антенны. А область, простирающаяся от фокальной плоскости до перехода плоской волны в сферическую, является зоной формирования главного луча антенны.

Однако при детальном рассмотрении есть аспект в существующих представлениях, который вызывает сомнения с физической точки зрения. Речь идет о «скачке фазы» волны при прохождении волной фокальной плоскости. Как утверждается в современной теории (см., например, [2]), волна, проходя фокальную плоскость (фокус) изменяет свою фазу на угол 180^о, как показано на рис. 4.

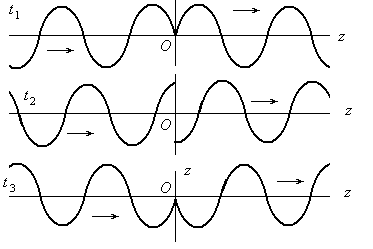
Рис. 4. Скачок фазы при прохождении волной фокуса

Хотя эти «скачки фазы» следуют как из приближенных, так и из точных математических решений уравнений волновой электродинамики, они вызывают сомнение в своей «физичности». В природе таких резких скачков не существует.

2.     Переопределение областей изменения аргумента

Уравнение Гельмгольца для потенциала u,

              (2.1)

распространяющегося вдоль оси z и сходящегося в фокус в начале координат сферической системы, приводит к следующему решению

          (2.2)

где a_mn и b_mn постоянные, которые определяются из условий задачи; P^m _n – шаровые функции;  J_n+1/2 (kr) – функция Бесселя; m, n = 0, 1, 2, … .

По условию задачи угол раствора конуса сходящейся в фокус волны должен быть ограничен величиной 0 < q < p / 2.

Расположим ось z вертикально, как показано на рис. 5.

Рис. 5

В современной теории область определения независимых переменных в сферических координатах определяется следующим образом: r (0 ¸ ¥);  q (0 ¸ p); j (0 ¸ 2p). Однако мы можем изменить ее, приняв, например, следующие:

 r (- ¥ ¸ ¥); q (0 ¸ p); j (0 ¸ p),    или     r (- ¥ ¸ ¥); q (0 ¸ p/2); j (0 ¸ 2p) и др.

Конечно, здесь могут возникнуть возражения, касающиеся цилиндрической системы координат. Этот вопрос будет рассмотрен позже.

Итак, сделаем очевидную замену переменных r ® - r; q ® p - q и j® j  + p в выражении  (2.2). При такой замене точка А сохраняет неизменным свое положение в пространстве.

 

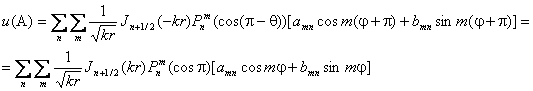
Как мы видим, выражение сохранило прежний вид, что подтверждает наше допущение о возможности использовать функцию r в области ее отрицательных значений. А это, в свою очередь позволяет анализировать различные представления функций Бесселя и записывать математические результаты в удобно интерпретируемой форме.

В последующем мы будем использовать следующие известные соотношения [3]

              (2.3)

                 (2.4)

                  (2.5)

                  (2.6)

Вернемся к выражению (2.2) и представим функцию Бесселя в виде суммы функций Ганкеля первого и второго рода

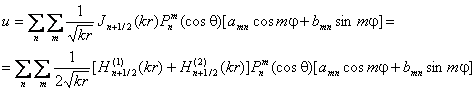
В силу обозначенных ранее условий для сходящейся в фокус волны, решение может выражаться через функцию Ганкеля второго рода. По этой причине мы преобразуем первый член суммы функций Ганкеля в скобках, используя область отрицательных значений r (см. рис. 5). Сделаем очевидную замену переменных в функции Ганкеля первого рода r ® - r; q ® p - q и j® j  + p и воспользуемся выражением (2.5). При такой замене, как уже говорилось, точка А сохраняет свое положение в пространстве неизменным.

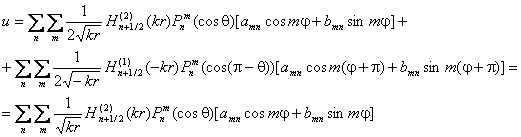                       (2.7)

Выражения (2.2) или (2.7) для той же задачи мы можем преобразовать и к другой форме

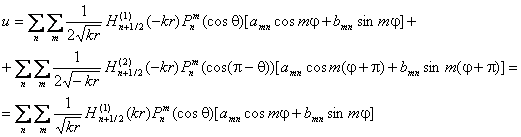                (2.8)

Хотя мы провели все выкладки формально корректно, результат получился неожиданным (можно сказать: фантастическим). Его необходимо каким-то образом объяснить, поскольку выражения (2.2), (2.7), (2.8) несопоставимы с физической точки зрения. Заключение о том, что нельзя использовать область отрицательных значений радиуса, мы отбросим, как некорректное.

3.     «Скрытые» источники потенциала

Итак, попытаемся выяснить причины получения противоречивых результатов. Обратимся к закону сохранения энергии [4] и запишем интегралы для потоков.

, где u^* - комплексно сопряженное значение потенциала.

Интегрирование будем вести по поверхности сферы постоянного радиуса R с областью определения переменных: r (- ¥ ¸ ¥); q (0 ¸ p/2); j (0 ¸ 2p)

Рассмотрим для сравнения один и тот же член суммы в выражениях (2.2), (2.7), (2.8), например, с индексами m и n.

Выражение (2.2)

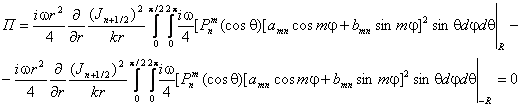
Мы получили нуль, поскольку меняется направление вектора плотности потока по отношению к внешней нормали поверхности сферы n⁰.

Выражения (2.7) и (2.8). Здесь для оценки выберем достаточно большой радиус R, чтобы воспользоваться асимптотическими формулами для функций Ганкеля.

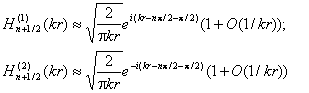
Нетрудно видеть, что при больших R имеем для (2.8)

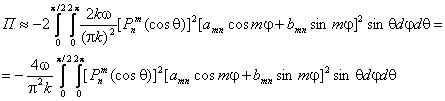                  (3.1)

и для (2.7)

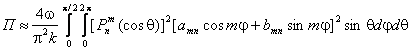               (3.2)

Здесь мы учли, что интегралы для R и для -R одинаковы.  

Поскольку в свободном пространстве нет источников, поток направлен от центра системы координат (2.7) или к центру (2.8). Исходя из физических соображений, можно сказать, что это может быть только в том случае, если в начале координат существует излучающий источник (2.7) или источник, поглощающий энергию (2.8). Сингулярность при r = 0 в уравнении Бесселя приводит к появлению «скрытых» источников, что фактически равнозначно неоднородному уравнению Бесселя с мультипольными источниками типа d - функций в начале координат (см. рис. 6).

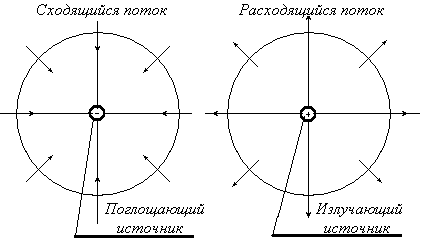
Рис. 6 Иллюстрация к функциям Ганкеля

С этой физической точки зрения использовать функции N_n и H_n  следует осмотрительно. Все волновые решения в свободном пространстве всегда могут быть выражены формулой

Эту формулу можно рассматривать как суперпозицию полей, создаваемых излучающими и поглощающими мультипольными источниками, когда эти источники одной природы как бы взаимно уничтожают («гасят») друг друга, но их поля, распространяющиеся в противоположных направлениях, сохраняются.

4.     Поведение волны в окрестности фокуса

Теперь мы можем вернуться к первому параграфу «Постановка задачи».

Пусть мы имеем волновой поток, сходящийся в фокус в начале координат (2.2). Не ограничивая общности рассуждений, будем считать его симметричным, независимым от угла j. Окружим начало координат сферической поверхностью радикса R. Будем также считать, что внутренняя поверхность тонкой линзы также сферическая, и выбранная нами сфера касается этой поверхности. Дифракционные явления на краях линзы мы рассматривать не будем. Нас будет интересовать потенциал внутри сферы.

Общее поле внутри сферы можно представить в виде суммы полей, бегущих к центру (к «скрытым» поглощающим мультипольным источникам) и суммы полей, убегающих от центра (от «скрытых» излучающих мультипольных источников).  Опираясь на принцип суперпозиции, рассмотрим волну, идущую к центру (к поглощающим источникам).

Распределение амплитуды синфазного потенциала на поверхности линзы определяется выражением

где U₀ (q) – комплексная амплитуда потенциала. Она отлична от нуля на внутренней поверхности линзы и равна нулю на остальной поверхности.

Найдем коэффициенты a_n в этом выражении. Опираясь на ортогональность полиномов Лежандра, можно записать

Итак, для волны, идущей к началу координат мы имеем

                  (4.1)

Теперь запишем волну, уходящую из начала координат. Ее можно получить, заменив r на –r , а q ® p - q  и преобразуя полученное выражение.

 

Теперь осталось записать суммарное решение

              (4.2)

Как можно заметить, потенциал u непрерывен вместе со своей первой производной, а каких-то скачков фазы нет и быть не может. Характер изменения потенциала иллюстрируется рис. 1.

В частности, если мы рассмотрим плоскую волну в сферической системе, то при сколь угодно большом радиусе сферы (R ® ¥)  потенциал можно записать как u = U₀ exp(ikz) =  = U₀ exp(ikrcosq). Следуя приведенной выше методике, можно получить хорошо известное выражение для плоской волны, бегущей против оси z.

5.     Вронскиан функции Бесселя

Как мы обещали, перейдем теперь к цилиндрической системе. Однако прежде сделаем небольшое замечание. Как известно, фундаментальное решение уравнения Бесселя индекса n

       (1)

есть

где J_n (z) и N_n (z) – функция Бесселя и функция Неймана. 

Запишем определитель Вронского [5] для этого уравнения (1)

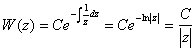
где С некоторая константа, которая выбирается из определенных соображений.

Итак, мы показали, что W (z) есть четная функция независимой переменной. В то же время, в современной математической литературе [3] вронскиан уравнения Бесселя также не зависит от индекса n, но оказывается пропорциональным не , а 1/z, т.е. является нечетной функцией z. Для положительных значений аргумента z вещественной оси такое представление не имеет значения. Однако для отрицательных значений вещественной оси (равно как и для комплексных) это весьма принципиально.

6.     В каких случаях вронскиан является четной функцией?

Рассмотрим общий случай, т.е. линейное дифференциальное уравнение второго порядка, сохраняющее свой симметричный вид относительно замены положительного аргумента на отрицательный аргумент. Такое уравнение имеет вид

                       (3.1)

В силу выбранного нами типа уравнений, коэффициент p есть нечетная функция, а q  четная функция переменной z.

Рассмотрим теперь случаи, в каких случаях вронскиан уравнения (3.1) является четной, а в каких - нечетной функцией. Для этого запишем определитель Вронского в следующей форме

        (3.2)

где функции y₁(z) и  y₂(z) образуют фундаментальную систему решений уравнения (3.1).

Выберем в качестве y₁(z) и  y₂(z) такие функции, которые были бы четными (нечетными) относительно знака z. Это следует из четности уравнения (3.1).

Здесь возможны два варианта:

1.      Функции y₁(z) и  y₂(z) являются одновременно четными или же нечетными.

2.      Одна из функций (y₁(z) или  y₂(z)) является четной, а вторая – нечетной.

Нетрудно видеть, что в первом случае отношение y₂(z) / y₁(z) является четной функцией. Следовательно, определитель Вронского будет нечетной функцией z. Во втором случае это отношение будет нечетной функцией z. По этой причине вронскиан останется четной функцией.

Итак, чтобы определитель Вронского был бы четной функцией z,  необходимо и достаточно, чтобы фундаментальная система решений могла быть представлена в виде четной и нечетной функций. Общее решение уравнения (3.1), составленное из такой фундаментальной системы, мы назовем физическим решением.

7.     Физическое решение

Запишем уравнение Бесселя для цилиндрической системы отсчета

Из уравнения следует, что в начале координат имеет место особенность (сингулярность).

Для положительных значений r общее решение уравнения Бесселя имеет вид

Функция Бесселя J_n(r) является четной функцией для четных значений n (n = 0, 2, 4, …)  и нечетной для нечетных значений n.

Теперь нам необходимо «построить» второе фундаментальное решение так, чтобы оно было нечетным для четных значений n и четным для нечетных значений. Иными словами, нам необходимо заново определить N_n (r)  для отрицательных значений аргумента.

Мы поступим следующим образом. Поскольку функция N_n (r) имеет сингулярность в нуле, мы пока исключим из рассмотрения точку 0 и доопределим эту функцию для отрицательных значений r следующим образом.

Пусть N_n (- r) = N_n (r) для нечетных значений n (четная функция) и  N_n (- r) = - N_n (r) для четных значений (нечетная функция). Вблизи нуля нечетная функция N_n (r)  обращается в ± ¥. Несмотря на это, в точке 0 нечетная функция N_n (r) должна принимать значение 0.

 Заметим, что при таком определении N_n (r) будет соблюдаться правильное чередование нулей функций J_n(r) и N_n (r) на всей действительной оси в полном соответствии с теоремой Штурма [4]. Мы не будем вводить специальные обозначения для нового определения функции N_n (r).

Мы изложили схему построения физического решения. Обоснование ее должно опираться на теорию обобщенных функций, что выходит за рамки нашей статьи.

Соотношения для бесселевых функций целого индекса (физические решения) при изменении знака аргумента приведены ниже.

 J_n (- r)  = (- 1)ⁿ J_n (r);      N_n (- r) = (- 1)^{n+ 1} N_n (r);

H⁽¹⁾_n (- r) =  H⁽²⁾_n (r);        H⁽²⁾_n (- r) =  H⁽¹⁾_n (r)

В этой связи мы можем использовать не только традиционные области определения переменных в цилиндрической системе координат: z (- ¥ ¸ ¥); r (0 ¸ ¥);  j (0 ¸ 2p), но и, например, такие: z (- ¥ ¸ ¥); r (- ¥ ¸ ¥);  j (0 ¸ p).

Рассмотрим цилиндрическую волну, сходящуюся в начале координат плоскости (r; j) и расходящуюся после прохождения начала. Как и в случае сферических волн никаких скачков фазы при прохождении волной начала координат не образуется. Это можно показать тем же способом, что и для сферической волны.

Замечание. Аналогичным образом можно построить фундаментальную систему из четной и нечетной функций и для мнимых значений r. Здесь имеется возможность продолжить в некотором смысле аналогию с тригонометрическими и гиперболическими функциями.

8.     Скачки фазы в каустиках и фокусе

Из дифференциальной геометрии известно, что всякая поверхность имеет для каждого  своего бесконечно малого элемента два, в общем случае, различных радиуса кривизны. Как показано на рис. 7, линии aОc и bОd есть главные круги кривизны с радиусами кривизны R₁ и R₂ , центры кривизны которых расположены в точках О₁ и О₂.

С точки зрения геометрической оптики интенсивность волнового потока будет обращаться в бесконечность в центрах кривизны О₁ и О₂. Отталкиваясь от элемента поверхности и переходя ко всей волновой поверхности, можно утверждать, что интенсивность волнового потока будет бесконечно возрастать, вообще говоря, на двух поверхностях, которые являются геометрическим местом кривизны волновой поверхности. Эти поверхности носят название каустик. В частном случае, когда поверхность имеет сферический фронт, обе каустики сливаются в точку, которая именуется фокусом. В случае цилиндрического волнового фронта каустики вырождается в линию.

 

Рис. 7

Конечно, бесконечное возрастание интенсивности при прохождении каустики или при прохождении фокуса есть «огрех» геометрической оптики как предела волновой. На самом деле плотность потока в этих случаях действительно сильно возрастает, но, как мы убедились, не до бесконечности.

Рассмотрим более важный для нас вопрос о скачках фазы. Обратимся к доказательству, приведенному в монографии [6]. Цитируем:

«Если плоскости XY и XZ выбраны совпадающими с главными плоскостями кривизны волновой поверхности в точке О, то вблизи этой точки уравнение поверхности есть

где R₁ и R₂  - главные радиусы кривизны. Расстояние же R от точки волновой поверхности с координатами X, y, z  до точки Р с координатами x, 0, 0 есть

Вдоль волновой поверхности поле u можно считать постоянным; то же касается множителя 1 / R. Поскольку мы интересуемся только изменением фазы волны, то коэффициент опускаем и пишем просто

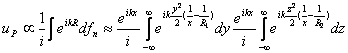                   (59,3)

Центры кривизны волновой поверхности лежат на рассматриваемом луче в точках x = R₁  и x = R₂ ; это и есть точки касания лучом каустик. Пусть R₂ < R₁. При x < R₂ коэффициенты при i в показателях подынтегральных выражений в обоих интегралах (по dy и dz) положительны, и каждый из этих интегралов пропорционален (1+ i). Поэтому на каждом участке луча до касания первой каустики имеем u_P µ e^ikx. При R₂ < x < R₁, т.е. на отрезке луча между двумя точками касания, интеграл по dy пропорционален (1+ i), а интеграл по dz пропорционален (1- i), так что их произведение не содержит i. Таким образом имеем здесь u_P µ - i e^ikx, т.е. при прохождении луча вблизи первой каустики фаза дополнительно меняется на - p / 2. Наконец, при x > R₁ имеем u_P µ - e^ikx  =  e^{ikx + p}, т.е. при прохождении луча вблизи второй каустики фаза еще раз меняется на - p / 2.».

Покажем теперь ошибку.

Величина  всегда положительна. Поэтому приближенное выражение в отличие от цитированного выше должно иметь следующий вид

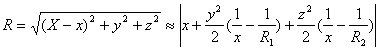
По этой причине интеграл (59,3) не может изменять фазу скачком на - p / 2 при касании каустики. По той же причине волна не может испытывать скачок фазы на - p  при прохождении фокуса даже в рамках геометрической оптики.

Заключение

В физике существуют не только гносеологические проблемы [7] (проблемы правильной интерпретации физических явлений), но и проблемы математического характера, также ведущие к некорректной интерпретации явлений в физике. Одну из них мы рассмотрели в этой статье. Перечислим полученные результаты.

1.      Решения, выражаемые через функции Ганкеля, содержат «скрытые» источники поля. Последние возникают благодаря наличию сингулярностей в однородных уравнениях Бесселя или в уравнениях сводимым к ним. По этой причине требуется корректное (физически интерпретируемое, а не формальное) использование этих функций.

2.      Учет «скрытых» источников однородных уравнений (возникающих из-за сингулярностей в коэффициентах уравнений) позволяет дать физически ясное объяснение волновым процессам и упростить в некоторых случаях постановку задачи и ее решение.

3.      Помимо этого, показана возможность построения решений для области отрицательных значений радиуса как в цилиндрической, так и в сферической системах координат.

4.      Дан анализ причины, по которой определитель Вронского для уравнения Бесселя  считается нечетной функцией аргумента. Рассматривается возможность построения такой фундаментальной системы, в которой этот определитель становится четным, что важно для построения решений в цилиндрической системе координат.

5.      Полученные результаты позволяют изучать особенности потенциала волны в окрестности фокуса (каустики). Анализ поведения волны в окрестности фокуса (каустик) показал, что  при прохождении фокуса (или касания лучом каустики) волна не испытывает скачка фаз. Решение в этой области непрерывно вместе со своей первой производной. Утверждения типа: «волна при прохождении фокуса изменяет фазу на - p» - некорректны как с физической точки зрения, так и с математической (т.е. ошибочны).

Источники информации

1.        Кулигин В.А. Поведение волны в окрестности фокуса. // Вопросы рассеяния и оптимального приема радиоволн.ВГУ, Воронеж. 1975.

2.        Каценеленбаум Б.З. Высокочастотная электродинамика. Наука. М. 1966.

3.        Ватсон Г.Н. Теория бесселевых функций. Перев. с англ., М., ИЛ. 1949.

4.        Кулигин В.А., Кулигина Г.А., Корнева М.В. Ревизия теоретических основ релятивистской электродинамики. http://www.n-t.org/tp/ns/rt.htm  25.06.2006.

5.        Степанов В.В. Курс дифференциальных уравнений. ГИФФМЛ. М. 1958.

6.        Ландау Л.Д., Лифшиц Е.М. Теория поля. ГИФФМЛ. М. 1960.

7.        Кулигин В.А., Кулигина Г.А., Корнева М.В. «Конвективный потенциал» и философия. http://www.inauka.ru/blogs/article66754.html , 01.09.2006.