Варианты формулы Кирхгофа
Кулигин В.А., Кулигина Г.А., Корнева М.В.
Аннотация.
Рассмотрен физический смысл задачи по определению потенциала внутри замкнутого объема по заданному потенциалу и его нормальной производной на поверхности, ограничивающей объем. Рассмотрена подробно задача для сферической поверхности. Показано, что формула Кирхгофа имеет несколько вариантов, физический смысл которых рассматривается.
Введение
Нами была опубликована работа «Волна в фокусе и функции Бесселя» [1] в популярной форме. Статья вызвала отклики. Отвечая на них, мы продолжили изложение этого вопроса в качестве дополнения к указанной статье.
1. Определение потенциала поля внутри сферы
Плоский случай. Рассмотрим бесконечно малый элемент поверхности. Его можно считать плоским. Пусть на поверхности задан потенциал и задана нормальная производная этого потенциала. Поскольку поверхность элемента мала, потенциал и его производную можно считать постоянными, а поле вблизи этой поверхности можно представить как сумму двух плоских волн, распространяющихся в противоположных направлениях колинеарно нормали. Потенциал удовлетворяет уравнению Du = 0.
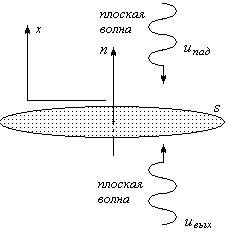
Рис. 1
Потенциал падающей волны uпeikx, а выходящей волны uвe-ikx . При малых расстояниях и размерах амплитуды этих постоянны, но имеют комплексную форму. На поверхности S (при х = Х) будем иметь следующие выражения для потенциала на поверхности и его производной:
![]() (1.1)
(1.1)
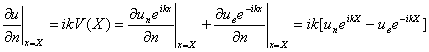 (1.2)
(1.2)
Комбинируя (1.1) и (1.2) можно найти амплитуды падающей и выходящей волн.
![]() (1.3)
(1.3)
Таким образом, задача решена, т.е. найдены комплексные амплитуды падающей и выходящей волн.
Косое падение волны. Тот же подход возможен при подходе волны под углом p - j к поверхности y = 0.
Пусть волна описывается потенциалом
![]()
На поверхности y = 0 потенциал будет равен
![]() , (1.4)
, (1.4)
где y(х) можно
рассматривать как фазу волны в точке х.
Нормальная производная при y = 0 равна (нормаль совпадает по направлению с осью у)
![]() (1.5)
(1.5)
Нам необходимо, пользуясь этими значениями, записать волны, переносящие энергию. Но необходимо записать их так, чтобы эти волны удовлетворяли специфическому волновому уравнению в окрестности бесконечно малой площадки поверхности.
![]()
Иными словами, это волны, идущие коллинеарно нормали. С этой точки зрения выражения (1.4) и (1.5) мы формально можем представить в виде суммы двух волн с волновым вектором k, идущих нормально к поверхности, но в противоположных направлениях.
![]()
![]()
Отсюда можно найти
![]()
![]()
Такова, на наш взгляд, интерпретация этой задачи.
Сферическая поверхность. Задача определения потенциала внутри сферы, ограничивающей некоторый объем, по заданной величине потенциала и его нормальной производной на поверхности решается аналогично.
Пусть имеется сферическая поверхность, на которой задан потенциал и его нормальная производная. Пусть потенциал внутри сферы, включая ее границы (поверхность) описывается уравнением Гельмгольца Du = 0. Источники, создающие потенциал, находятся вне этой сферы. Необходимо определить потенциал внутри сферы.
Это обычная (классическая) задача, с которой сталкиваются в теории дифракции, теории антенн и т.д. Ее решение сводится к решению предыдущей задачи.
Потенциал на поверхности сферы радиуса R определяется суммой волн, которые распространяются как внутрь сферы, так и из этой сферы. Можно сказать, что потенциал на поверхности и вблизи нее в каждом бесконечно малом элементе поверхности складывается из потенциала уходящей из сферы волны и потенциала входящей в сферу волны
U(R,q;j)
= uп(q;j) eikR + uв(q;j) e-ikR, (1.4)
где q;j – координаты поверхности сферы радиуса R. Амплитуды uп(q;j) и uв(q;j) являются, вообще говоря,
комплексными.
Будем считать, что потенциал и его нормальная производная непрерывны вблизи поверхности сферы и имеют следующий вид на сколь угодно малом расстоянии от нее
U(r,q;j) =
uп(q;j) eikr + uв(q;j)
e-ikr,
R + e > r > R - e;
где e - сколь угодно малая величина.
Нормальная производная на поверхности R = const также будет складываться из производных по нормали от потенциалов этих волн, как и в предыдущем случае
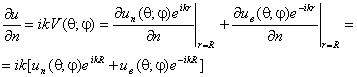 (1.5)
(1.5)
Комбинируя выражения (1.4) и (1.5) можно определить амплитуды uп(s) и uв(s) на поверхности сферы.
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
Теперь, зная амплитуды падающей и выходящей волн, можно определить потенциалы внутри сферы. Для этого запишем выражения для каждой из этих волн в виде ряда.
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
где amn и bmn – неизвестные коэффициенты, H(kr) – функции Ганкеля первого и второго рода, Ynm – шаровые (сферические) функции.
Приравняем выражения (1.6) и (1.8), а также (1.7) и (1.9) попарно при r = R. Теперь, раскладывая выражения (1.6) и (1.7) в ряд по шаровым функциям, можно определить неизвестные коэффициенты amn и bmn.
Здесь следует обратить внимание на тот факт, что выражения (1.8) и (1.9) имеют особенность в начале координат («скрытые» источники). Об этом мы писали в статье [1].
В решении, которое определяется суммой выражений (1.8) и (1.9), таких источников не будет. Покажем это.
Пусть потенциал внутри сферы определяется суммой выражений (1.8) и (1.9).
![]() (1.10)
(1.10)
Сделаем замену переменных в этом выражении: r ® - r; q ® p - q; j ® p + j . Как следует из [1], мы используем тождественное преобразование, когда каждая точка возвращается на свое место (не меняет своего положения).
Выражение (1.10) примет вид
 (1.11)
(1.11)
Сравнивая (1.10) и (1.11), можно заметить, что оба выражения совпадут, если коэффициенты amn и bmn будут тождественно равны друг другу. В этом случае мы получаем окончательное выражение для потенциала внутри сферы и на ее поверхности
![]()
Это есть решение поставленной задачи.
2. Разные варианты формулы Кирхгофа
Как известно, потенциал u волнового поля внутри объема Т, ограниченного замкнутой поверхностью S, можно найти с помощью формулы Кирхгофа. Для вычисления потенциала в любой точке М внутри объема Т достаточно знать потенциал u(Р) и нормальную производную потенциала на этой поверхности ¶u(Р) / ¶n [2], где Р – точка, принадлежащая поверхности S (см. [2]).
![]() (2.1),
(2.1),
где r –
расстояние между точками М и Р.
Результаты работы [1] позволяют записать несколько эквивалентных формулировок уравнения Кирхгофа (см. формулы (2.2), (2.7) и (2.8) в [1]), которые приводят к одному и тому же решению.
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
Однако есть и отличие. Поясним причину такого утверждения. Сама логика доказательства формулы Кирхгофа корректна. Однако есть один момент, который допускает определенный произвол.
В качестве функции v в формуле Грина [2] мы могли бы выбрать любую другую функцию, удовлетворяющую однородному уравнению Гельмгольца
Du +k2u = 0,
а не только функцию e-ikr / r.
Любое решение этого уравнения, которое мы выберем в качестве функции v, позволяет однозначно дать решение задачи по нахождению потенциала внутри объема.
Действительно, потенциал на замкнутой поверхности S (равно его производная по нормали на поверхности) определяет не только волны, проникающие внутрь объема, но и волны, которые движутся изнутри объема к его поверхности и выходят из него.
По этой причине в объеме Т в окрестности точки М обязательно будут существовать не только поля, сходящиеся к этой точке (типа e-ikr / r), но также поля, уходящие от нее (типа eikr / r). Потенциал и нормальная производная на поверхности S полностью определяют искомый потенциал u. В первом параграфе мы уже об этом говорили.
Хотя все три формулы дают одинаковый результат, между ними имеется одно отличие. Попробуем ответить на вопрос: получим ли мы равенство u(M) = u(Р), если мы точку М совместим с точкой Р, лежащей на поверхности S? Логика подсказывает, опираясь на непрерывность потенциала и его нормальной производной, что в пределе мы должны иметь это равенство при М = Р.
u(M) = u(Р) (2.4).
Оказывается, что такое равенство не всегда возможно. Оно возможно лишь в том случае, если только в качестве функции v выбрана функция sin (kr) / r. Если же мы выберем функцию eikr / r или же е-ikr / r, то в пределе мы получим бесконечное значение величины u(M) , т.е. u(M) ¹ u(Р), если M = Р. Это обусловлено появлением на поверхности S «скрытых» источников потенциала, обусловленных выбором функции v.
Источники информации:
1. Кулигин В.А., Кулигина Г.А., Корнева М.В.. Волна в фокусе и функции Бесселя. http://kuligin.mylivepage.ru/file/index , 2006.
2. Тихонов А.Н., Самарский А.А. Уравнения математической физики. ГИТТЛ, М. 1953.