Взаимодействие с волной как диссипативный процесс

Кулигин В.А., Кулигина Г.А., Корнева М.В.

(Исследовательская группа АНАЛИЗ;  http://kuligin.mylivepage.ru/file/index/)

Аннотация.  На основе механико-математической модели исследуется процесс взаимодействия частицы с волной. Вскрывается диссипативный характер этого взаимодействия.

Введение

Эта работа является продолжением статьи: «КАКАЯ ТЕОРИЯ ЗАМЕНИТ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ?» [1], в которой была поставлена задача анализа различных теорий, претендующих на роль СТО. В этой статье мы проанализируем механизм взаимодействия волны и частицы на основе механико-математической модели.

1.     Диссипативный характер излучения

Рассмотрим маленький шарик массой m (материальная точка), который закреплен на бесконечной натянутой струне. Этому шарику с помощью молоточка сообщается импульс p. Начальная скорость шарика равна V₀. От удара шарик начнет движение, и вместе с ним будут  распространяться две поперечные волны, бегущие по оси x в разные стороны от шарика, как показано на рис. 1.

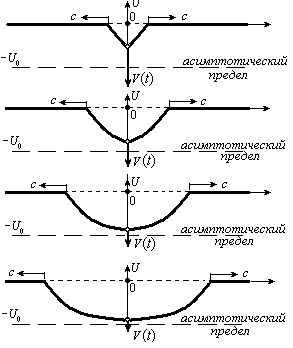
Рис 1. Распространение волн при движении шарика.

Для смещения струны от положения равновесия необходима энергия. Кинетическая энергия шарика постепенно расходуется на изменение положения элементов струны, скорость шарика уменьшается, и он постепенно останавливается. При этом струна стремится к своему асимптотическому пределу.

Запишем процесс математически.

Уравнение движения шарика:

,

где U – смещение шарика; V = ¶U /¶t – скорость шарика; F – сила, действующая на шарик со стороны струны.

Здесь нет необходимости использовать полную производную, которая совпадает с частной производной (см. Приложение 1).

Уравнение движения струны [2]:

,

где: Т₀ – натяжение струны;  ρ – линейная плотность массы струны.

Уравнение движения струны можно привести к виду

,

где: c² = T₀ / ρ -  квадрат скорости распространения волны;  f = F / ρ – плотность силы, отнесенная к плотности массы струны. По аналогии с теорией длинных линий параметр (T₀ ρ) ^{- ½} можно назвать «волновым сопротивлением» струны.

Можно решить эти уравнения «в лоб» (см. [2], Задача  № 9, стр. 80). Мы будем исходить из закона сохранения энергии, поскольку это нагляднее.

1. Шарик. Изменение скорости шарика происходит по экспоненциальному закону, поэтому можно предположить, что сила F пропорциональна скорости движения заряда.

,

где λ – некоторая постоянная.

Решение для вертикальной координаты шарика имеет вид

   (1.1)

Начальная скорость, импульс и кинетическая энергия шарика соответственно равны

                        

2. Струна. Рассмотрим теперь энергетические соотношения для струны и определим параметр λ. Мы будем исходить из того, что точка соприкосновения шарика со струной изменяет свое положение U в соответствии с выражением (1.1). Соответственно, соседние точки (х ≠ 0) будут определяться следующими выражениями

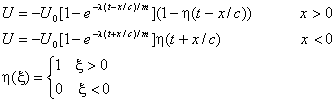
Подсчитаем энергию струны, учитывая симметричность ее распределения

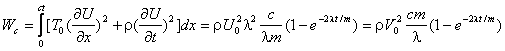
Сложим энергии струны и шарика. Учитывая закон сохранения энергии, найдем величину параметра λ.

Здесь мы подобрали λ так, чтобы энергия не зависела от времени. Проверим теперь закон сохранения импульса. Суммарный импульс шарика и возбужденных элементов струны не должен зависеть от времени. Действительно

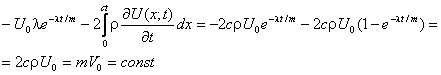
Величина силы зависит только от параметров струны и скорость шарика

Итак, кинетическая энергия механического движения шарика преобразуется в волновую энергию струны, распространяющуюся от шарика.

2.     Воздействие волны на шарик

Рассмотрим теперь другую ситуацию. Пусть шарик закреплен на струне (х = 0). Вдоль струны распространяется бегущая волна, описываемая потенциалом , которая начинает воздействовать на этот шарик при t ³ 0.

Какими будут колебания струны?

Сначала рассмотрим качественную картину физического процесса распространения волны. При  t < 0 она только подходит к шарику. При t ³ 0 волна начинает взаимодействовать с шариком. Она сообщает ему ускорение, отдавая часть своей энергии. В свою очередь шарик сам воздействует на волну. Это проявляется в том, что он возбуждает в струне вторичные колебания (переотраженные волны). Эти колебания распространяются симметрично от шарика вдоль струны в противоположных направлениях.

Будем называть исходный невозмущенный потенциал U₀ (x - ct) «первичной волной», две переотраженные волны будем именовать «возмущенной прямой» u₊ и «возмущенной обратной» u_- волнами (см. рис. 2).

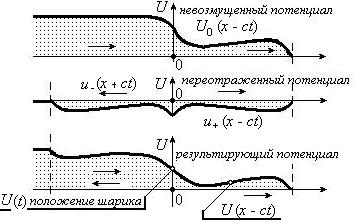
Рис. 2. Обозначения: U₀(x - ct) – невозмущенная волна; U(t) – положение шарика;  u₊(x - ct)  - возмущенная волна, распространяющаяся вдоль оси х;  u_-(x + ct)  - возмущенная волна, распространяющаяся против оси х.

Запишем уравнение движения шарика

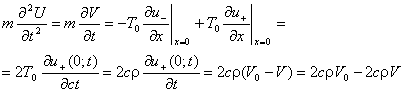     (2.1)

Первый член в правой части (2.1) 2cρV₀ представляет собой внешнее воздействие на шарик со стороны невозмущенной волны, а второй – является диссипативным членом, обуславливающим появление переотраженных волн.

Заметим, что первый член в правой части можно записать в стандартной форме как  при х = 0.

Умножим (2.1) на ¶U(t) / ¶t = V  (V – скорость шарика)

(2.2)

Соотношение (2.2) представляет собой баланс мощностей. Изменение кинетической энергии шарика равно работе (в единицу времени) произведенной невозмущенной волной над шариком, без мощности, затраченной на создание двух возмущенных волн:  u₊(ct - x) и  u_-(ct + x). Последнее слагаемое как раз и обуславливает диссипативный характер взаимодействия волны, распространяющейся вдоль струны и взаимодействующей с шариком. Следует заметить, что последнее слагаемое соответствует диссипативному члену Релея, вводимому в классической механике в функцию Лагранжа для описания потерь энергии.

Рассмотрим теперь энергетические соотношения для волн, распространяющихся по струне. Волны описываются уравнением

   (2.3)

Значения ранее найденных потенциалов волн соответствуют х = 0, т.е. определяют характеристики шарика.

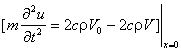
Решением уравнения (2.2) при нулевых начальных условиях являются выражения

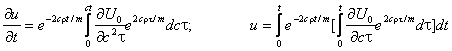
Таким образом, мы определили изменение потенциала (колебания струны и шарика)  в начале координат (х = 0). Теперь запишем колебания струны в остальных точках.

Но решать уравнение (2.3) нет необходимости, поскольку известен потенциал падающей волны и потенциал в точке, где колеблется шарик. Запишем сразу решение для трех областей (см. рис. 2):

или

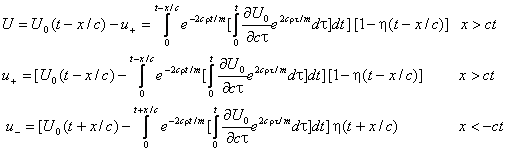
Для проверки мы воспользуемся законом сохранения энергии и составим баланс энергий для интервала времени от 0 до ct. Энергия первичной волны W разделяется на  три части:

1. W_-  энергия возмущенного потенциала u_- .
2. W₁ энергия прошедшей волны U₁ .
3.  W_k кинетическая энергия шарика.

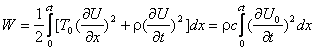
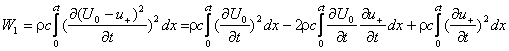
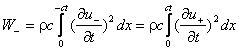
Отсюда можно найти кинетическую энергию шарика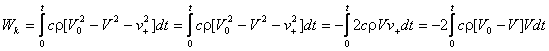

где: V₀ = ¶U₀ /¶t; V = ¶U /¶t;  v₊ = ¶u₊ /¶t .

Нетрудно видеть, что это выражение эквивалентно выражению (2.2).

Таким образом, решение корректно. Нам необходимо обсудить принципы построения уравнений при взаимодействии частицы с волной. Несмотря на диссипативный характер взаимодействия закон сохранения энергии, как мы убедились, не нарушается. Общая схема взаимодействия волны и частицы приведена ниже.

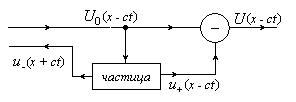
Рис. 3. Схема взаимодействия волны и частицы.

Потенциал невозмущенной волны воздействует на частицу, изменяя ее кинетическую энергию. Часть этой энергии «теряется» на создание двух волн возмущения, одна из которых бежит против оси х, другая изменяет потенциал невозмущенной волны после того, как невозмущенная волна начнет уходить от частицы вдоль оси х.

В соответствии с этой схемой мы должны записывать уравнения для волны и для частицы раздельно. 

Заключение

У «специалистов» после прочтения предыдущих параграфов возникнет сомнение: следует ли «городить огород», когда решение простых задач, рассмотренных выше, можно найти достаточно просто? Искусство научного поиска в том и состоит, что из «обыденных» фактов можно получить весьма важные выводы. Главный вывод касается диссипативного характера взаимодействия частицы с волной. Нам удалось вскрыть один из многих возможных механизмов диссипации энергии и уйти от феноменологичекого описания этого процесса.

1.      Еще раз отметим, что взаимодействие шарика и неограниченной струны носит диссипативный характер. В научной литературе обсуждений этого явления мы не обнаружили.

2.      Величина параметра диссипации λ не зависит от амплитуды колебаний струны.

3.      Опираясь на результаты работы [3], можно записать в общем виде закон сохранения энергии для колебаний неограниченной струны U для области вне источника: . Плотность энергии равна  и плотность потока, соответственно, .  Отсюда следует, что поток энергии распространяется вдоль оси х, а механический импульс шарика р = mv «выпадает» из закона сохранения. Аналогичная ситуация имеет место и для закона сохранения плотности потока [3]: . Механический импульс вновь не входит в закон. Эта проблема требует осмысления.

4.      Аналогичные явления должны иметь место при взаимодействии заряда с электромагнитной волной, например, в ускорителях элементарных частиц бегущей волны, в приборах вакуумной электроники СВЧ (генераторы, усилители) и т.д. Эти вопросы мы рассмотрим в другой статье.

Интересным может оказаться приложение диссипативного эффекта к термодинамике. Обратимся, например, к кинетической теории газовой среды. Рассмотрим газ в замкнутом термостате, находящийся в стационарном состоянии (температура газа, его давление и объем внутри термостата постоянны). Пусть число молекул газа N, и каждая молекула имеет 3 степени свободы (для простоты). Пусть молекулы, взаимодействуя друг с другом, испытывают только взаимное расталкивание (консервативные силы), величина которого уменьшается при увеличении расстояния. Обычно считается, что соударение молекулы со стенкой термостата носит абсолютно упругий характер, и мы имеем дело с консервативной системой.

Система уравнений при упомянутых выше граничных условиях имеет следующий вид

, где f_nk – сила взаимодействия между частицами с номерами n и k.

Подобную линейную систему можно привести к диагональному виду с числом уравнений второго порядка равным 3N. Это означает, что:

·        спектр имеет дискретный характер (3N – собственных частот или спектральных линий);

·        интенсивность спектральных линий будет зависеть от начальных условий;

·        максвелловского распределения молекул по скоростям не будет даже при t ® ∞.

Следовательно, максвелловское распределение по скоростям имеет другой механизм образования, который не связан с взаимодействиями молекул газа между собой (с их упругими столкновениями). Можно предположить, что хотя газ и термостат находятся в термодинамическом равновесии, взаимодействие молекул со стенками не является абсолютно упругим. Молекулы взаимодействуют со стенкой подобно взаимодействию шарика с волной. Колебательно-волновой характер этого взаимодействия определяет специфический обмен энергией с молекулами газа, при котором часть молекул уменьшает свою скорость (отдает энергию стенке), а другая увеличивает (забирая энергию у стенки). Именно стенки задают и определяют характер максвелловского распределения молекул газа по скоростям, непрерывность спектра и его независимость от начальных условий.

Быть может, распределение молекул по скоростям описывается другой формулой, которая напоминает по структуре формулу Планка для излучения абсолютно черного тела?

Приложение 1

Некоторые читатели предыдущих статей просили объяснить, в каких случаях полную производную по времени можно заменить частной производной. Покажем это на примерах.

Обратимся к рис. 4. Рассмотрим удар клюшкой по шайбе.

Рис. 4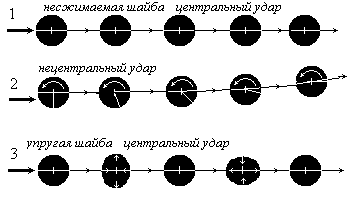

1. Если шайба несжимаемая, а удар центральный, то из-за сил трения шайба будет двигаться замедленно. Все точки шайбы имеют одинаковые скорости и ускорения, а шайбу можно рассматривать как материальную точку. В этом случае полную производную можно заменить частной.
2. Если мы по несжимаемой шайбе наносим удар не по центру, шайба будет перемещаться по дуге, вращаясь, как показано на рис. 4 (2). Здесь каждая точка шайбы будет иметь свою скорость, и мы уже не сможем описать движение шайбы как материальной точки. Мы должны учитывать энергию вращательного движения. А это можно сделать только с помощью полной производной.
3. То же положение имеет место при центральном ударе по упругой шайбе. Она будет двигаться с замедлением, обусловленным трением, одновременно совершая упругие колебания (периодически сжимаясь в одном направлении и растягиваясь в другом), как показано на рис. 4 (3).

Итак, в тех случаях, когда материальный объект можно заменить материальной точкой, мы должны использовать частную производную. Это касается также потока материальных частиц, между которыми отсутствует взаимодействие или по условиям задачи таким взаимодействием можно пренебречь. Когда же мы рассматриваем непрерывную среду, точки которой связаны между собой взаимодействием, мы обязаны использовать полную производную по времени.

Источники информации

1.        Кулигин В.А., Кулигина Г.А., Корнева М.В. Какая теория заменит теорию относительности? http://kuligin.mylivepage.ru/file/index/

2.        Тихонов А.Н., Самарский А.А. Уравнения математической физики. ГИТТЛ, М., 1953.

3.        Кулигин В.А., Кулигина Г.А., Корнева М.В. Ревизия теоретических основ релятивистской электродинамики. http://kuligin.mylivepage.ru/file/index/