MDX –
язык запросов к многомерным базам данных
ЗОЛОТЫЕ ИНВАРИАНТЫ ГАРМОНИЧЕСКИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Косинов Н.В.
E-mail: kosinov@unitron.com.ua
Аннотация
Показано,
что основное золотое сечение φ=0,618033… вляется одним из
представителей большого семейства золотых сечений. Приведены примеры построения
некоторых золотых сечений. Рассмотрены нецелочисленные последовательности,
образованные золотой пропорцией. Для таких нецелочисленных последовательностей
справедлива рекуррентная формула вида: a(n)=a(n-1)+a(n-2). Эта рекуррентная
формула обобщена на семейство числовых гармонических последовательностей.
Обобщенное соотношение имеет вид:
a(n)=±k a(n-1)±a(n-2). Золотая пропорция
является одним из представителей большого семейства числовых инвариантов
гармонических последовательностей и является корнем уравнения X-1/X=± k при k
=1. При других значениях k уравнения X±1/X=± k дают семейство золотых
инвариантов, которые проявляют такие же свойства, как и золотая пропорция.
Золотые инварианты являются константами гармонических последовательностей.
Представителями этого класса последовательностей являются числа Фибоначчи и
числа Люка.
1. Семейство золотых сечений.
Кроме основного золотого сечения
φ=0,618033 известно второе золотое сечение [1,2]. Второе золотое сечение
вытекает из основного золотого сечения и имеет отношение 44/56. Эта пропорция
обнаружена в архитектуре, а также имеет место при построении композиций картин
удлиненного горизонтального формата [1]. Очевидно первое и второе золотые
сечения не исчерпывают всех проявлений золотого сечения. Существует целое
семейство золотых сечений. Для получения значений золотых сечений рассмотрим
соотношение:
![]() (1)
(1)
В этой формуле Ф =1,61803… При
отрицательных n получим семейство чисел: 0,61803, 0,78615, 0,8517 и т.д. Первое
из них – основное золотое сечение, другие являются степенными функциями
основного золотого сечения. На рис.1 приведено семейство золотых сечений и
обратные им числа для n= ±1, ±2, ±3, ±4.
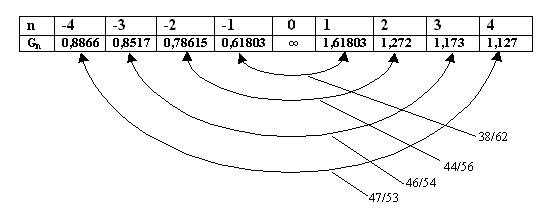
Рис.1. Семейство золотых сечений.
Первое золотое сечение представлено отношением
38/62. Его значение φ=0,618033… Значение золотой пропорции Ф1 =1,61803…
Второе золотое сечение представлено отношением 44/56 [2]. Его значение φ2
= 0,78615… Значение второй золотой пропорции Ф2 =1,272…Третье
золотое сечение представлено отношением 46/54. Его значение φ3
=0,8517… Значение третьей золотой пропорции Ф3 =1,173…Четвертое
золотое сечение представлено отношением 47/53. Его значение φ4
=0,8866… Значение четвертой золотой пропорции Ф4 =1,127… и т. д.
Таким образом формула (1) дает семейство золотых сечений при отрицательных n и
семейство золотых пропорций при положительных n.
На рис.2 приведен пример построения некоторых
золотых сечений.
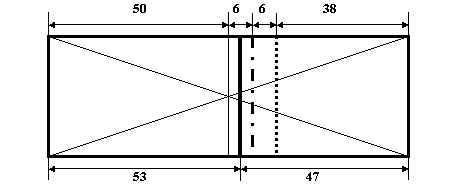
Рис.2. Деление прямоугольника линиями
первого, второго и четвертого золотых сечений.
На рис.2 положение линии первого золотого
сечения показано пунктиром. Линия второго золотого сечения находится посередине
между средней линией прямоугольника и линией первого золотого сечения. Она
показана штрих-пунктирной линией. Положение линии четвертого золотого сечения
показано жирной сплошной линией. Она находится посередине между средней линией
прямоугольника и линией второго золотого сечения. Линия третьего золотого
сечения будет находиться в промежутке между линией четвертого золотого сечения
и линией второго золотого сечения и разделит этот промежуток так, что его части
будут иметь отношение 1:2. В пределе n-ое золотое сечение стремится к числу
1,0000.
Формула с использованием второго золотого
сечения
![]()
при m=∞ позволяет получить
нецелочисленную последовательность Gn. В этой формуле Ф2 =1,272…,
φ2 = 0,78615… Фрагмент последовательности Gn
приведен в таблице1.

Эта последовательность стремится к
целочисленной последовательности, которая представляет собой числа: 4, 5, 7, 9,
11, 14, 18, 23, 29, 37,… Эта последовательность представляет собой комбинацию
двух последовательностей. Четные члены являются числами Люка. Нечетные члены -
есть числа 4, 5, 9,14,…, представляющие собой обобщенные числа Фибоначчи. Для
этой последовательности справедлива рекуррентная формула:
![]() .
.
2. Нецелочисленные последовательности.
Рассмотрим
формулу вида:
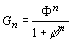 (2)
(2)
В формула (2) Ф =1,61803…,
φ=0,618033… έта формула порождает нецелочисленную последовательность.
Для этой последовательности справедлива рекуррентная формула:
![]()
Из формулы (2) при m=0 получим числа,
представленные в таблице 2.

Эта
последовательность стремится к целочисленной последовательности a(n): 3, 6, 9,
15, 24 … В этом ряду чисел Gn число 0,5 относится к обобщенной
золотой пропорции [3,4]. На число 1,309 обратил внимание С.В. Петухов [5]. Он
установил, что двойное отношение длин трехзвенных конечностей млекопитающих,
птиц и насекомых приближается к величине 1,309. С.В. Петухов назвал величину
1,309 золотым вурфом [5].
При m=1 получим числа, приведенные в табл.3.

Эта последовательность стремится к
целочисленной последовательности, которая представляет собой смещенную на один
шаг последовательность Люка: 2, 1, 3, 4, 7, 11 …
При m=2 получим числа, приведенные в табл.4.

Эта последовательность стремится к
целочисленной последовательности, которая представляет собой числа Фибоначчи:
1, 1, 2, 3, 5, 8,13,…
Из таблицы3 и таблицы 4 следует, что между
соответствующими членами нецелочисленных последовательностей, порождающих числа
Фибоначчи и Люка существует связь посредством константы:
![]()
Отношение соответствующих членов последовательности
Фибоначчи и смещенной последовательности Люка по мере удаления от начала также
стремится к величине 1,170820393...
![]()
Отношение (n+1)-го члена смещенной
последовательности Люка к n-му члену последовательности Фибоначчи по мере
удаления от начала стремится к величине 1,381966...
![]()
При m=∞ из формулы (2) получим числа, приведенные
в табл.5.

Эта последовательность стремится к
целочисленной последовательности, которая представляет собой числа Люка: 2, 1,
3, 4, 7, 11 … Нечетные члены нецелочисленных последовательностей 4,23606…,
11,0901…, 29,0344… и т.д. переходят в обратные им значения 0,23606…, 0,0901…,
0,0344… и т.д. при вычитании целой части. Нечетные члены последовательности
4,23606…, 11,0901…, 29,0344… и т.д. дают ближайшие целые числа 4, 11, 29 и т.
д. при вычитании от них обратных значений. Таким же свойством обладает золотая
пропорция. Нечетные члены последовательности Gn являются числовыми
инвариантами целочисленных последовательностей с рекуррентными свойствами вида:
a(n) = ka(n-1) + a(n-2). Эти числовые инварианты являются корнями уравнений
X-1/X=k, где k=1, 4, 11, 29,…
Четные члены последовательности 1,000…,
2,61803…, 6,8541… и т.д. дают ближайшие целые числа при добавлении к ним
обратных значений. Четные члены 1,000…, 2,61803…, 6,8541… и т.д. переходят в
обратные им значения 1,000…, 0,381966…, 0,145898… и т.д. при вычитании их от
ближайшего целого числа. Четные члены последовательности являются числовыми
инвариантами целочисленных последовательностей с рекуррентными свойствами вида:
a(n) = ka(n-1) - a(n-2). Они являются корнями уравнений X+1/X=k, где k=2, 3, 7,
18,…
Числа Gnu, приведенные в табл.5,
определяются по формуле (2) или по рекуррентной формуле Gn = Gn-1
+ Gn-2 и являются членами нецелочисленной последовательности. Эти
числа Gn одновременно являются числовыми инвариантами
последовательностей a(n)= k a(n-1)±a(n-2), где k = Gn ± 1/Gn.
Отношение соседних членов числовых последовательностей по мере удаления от
начала стремится к определенным константам. Эти константы являются числовыми
инвариантами соответствующих последовательностей. Например, для
последовательности 2,3,7,18… справедлива рекуррентная формула a(n)=
3a(n-1)-a(n-2) при a(0)=2 и a(1)=3. Отношение соседних членов этой
последовательности по мере удаления от начала стремится к величине 2,61803…
Числовой инвариант 2,61803… является корнем уравнения X+1/X=3. Для другой
последовательности 2,2,2,2… числовым инвариантом выступает 1,0000, которое
является корнем уравнения X+1/X=2. Рекуррентной формулой для этой
последовательностиявляется соотношение a(n)= 2a(n-1)-a(n-2) при a(0)=2 и
a(1)=2.
В таблице 6 в первом столбце приведены члены
нецелочисленной последовательности Gn, взятые из таблицы 5. В
таблице приведены, формулы, порождающие константы Gn, а также соответствующие
им целочисленные последовательности и их рекуррентные формулы. В последнем
столбце табл.6 приведены номера, под которыми последовательности
зарегистрированы в энциклопедии Нейла Слоуна [6].
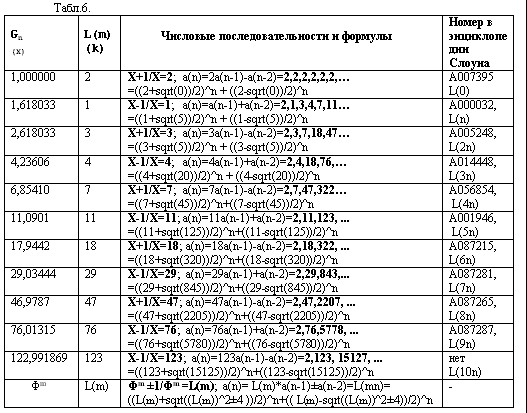
Все константы Gn, приведенные в
таблице 6, являются степенными функциями золотой пропорции. Константы Gn
- это числовые инварианты последовательностей, которые являются прореженными
последовательностями Люка: L(2n) –A005248, L(3n) – A014448, L(4n) –A056854,
L(5n) – A001946, L(6n) - A087215,
L(7n) - A087281,
L(8n) - A087265 ,
L(9n) - A087287 , и
т.д. [7,8].
3. Класс гармонических последовательностей
и золотые инварианты.
Числовые инварианты последовательностей с
рекуррентными свойствами a(n)= ±k a(n-1)±a(n-2) не ограничиваются числами Gn,
приведенными в таблицах 5 и 6. Уравнения X±1/X=±k дают большое количество
других числовых инвариантов (констант) при k=0, ±1, ±2, ±3,…[7]. Числовыми
инвариантами для последовательностей с рекуррентным свойством a(n)= ±k a(n-1)±a(n-2)
являются константы, полученные по формуле:
![]() .
.
Эти же константы являются корнями уравнений
X±1/X=±k [7]. Они обладают замечательными свойствами. Одни из них переходят в
обратные им значения при вычитании целой части. Таким же свойством обладает золотая
пропорция Ф=1,618033…. (Ф-1=1/Ф). Другие числовые инварианты переходят в
обратные им значения при вычитании их от ближайшего целого числа. Таким же
свойством обладает золотая пропорция в квадрате Ф2 =2,618033…. (3-Ф2
=1/Ф2). Назовем эти инварианты золотыми инвариантами или золотыми
константами числовых последовательностей. Золотые инварианты являются
константами числовых последовательностей с рекуррентными свойствами a(n)= ±k
a(n-1)±a(n-2). К классу последовательностей с рекуррентными свойствами a(n)= ±k
a(n-1)±a(n-2) относятся числа Фибоначчи и числа Люка. Будем называть этот класс
последовательностей гармоническими последовательностями. В таблице 7 приведены
золотые инварианты, гармонические последовательности и формулы для определения
золотых инвариантов и членов гармонических последовательностей для
положительных значений k. В последнем столбце табл.7 приведены номера, под
которыми последовательности зарегистрированы в энциклопедии Нейла Слоуна.
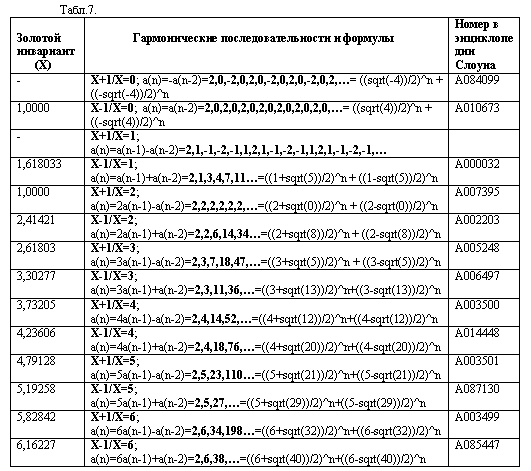
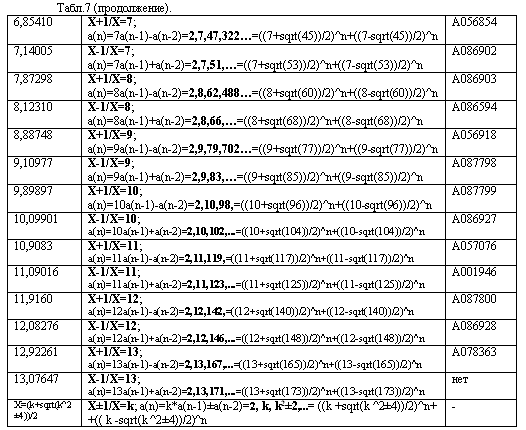
Общая формула для определения значений
золотых инвариантов для положительных k имеет вид: X=(k+sqrt(k^2±4))/2. Общая
формула для определения членов гармонических последовательностей имеет вид:
a(n)=((k+sqrt(k^2±4))/2)^n+((k-sqrt(k^2±4))/2)^n.
Более подробные сведения о
последовательностях, например при k = 7 – 13, можно найти в энциклопедии Нейла
Слоуна (A086902, A086903, A086594, A056918 , A087799, A086927, A057076, A001946, A087800, A086928, A078363
[6,8].
В таблице 8 приведены золотые инварианты,
гармонические последовательности и формулы для определения золотых инвариантов
и членов гармонических последовательностей при отрицательных значениях k.
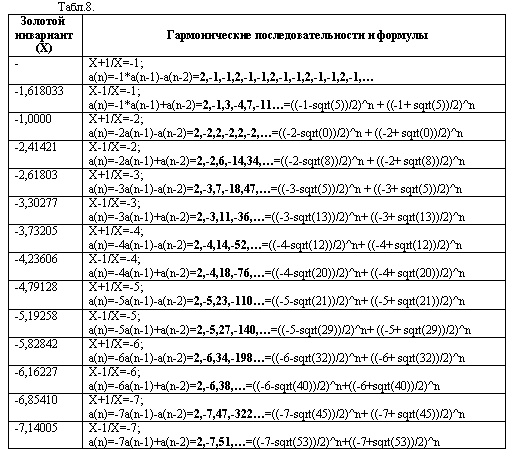

Общая формула для определения значений
золотых инвариантов для отрицательных k имеет вид: X=(-k-sqrt(k^2±4))/2. Общая
формула для определения членов гармонических последовательностей в этом случае
имеет вид: a(n)=((-k-sqrt(k^2±4))/2)^n+((-k+sqrt(k^2±4))/2)^n.
Золотые константы гармонических
последовательностей располагаются попарно вблизи целочисленных коэфициентов k.
На рис.3, в качестве примера, показаны семейства гармонических
последовательностей, золотые инварианты последовательностей и их попарная
(дублетная) группировка вблизи коэфициентов k, для k=±3, ±4, ±5. Расположение
золотых инвариантов на числовой оси на рис.3 показано жирными точками. Рядом с
золотыми инвариантами показаны соответствующие рекуррентные формулы
гармонических последовательностей.
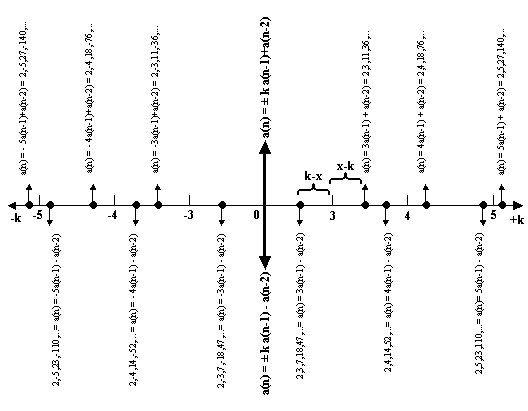
Рис.3. Дублетное расположение золотых
инвариантов гармонических последовательностей вблизи коэффициентов k.
По
мере увеличения значения k расстояние между золотыми инвариантами
последовательностей и коэффициентом k (ΔXi =Xi – ki
) уменьшается. При этом произведение золотого инварианта на разность
между золотым инвариантом и коэффициентом k всегда равно единице для всех
последовательностей данного класса: ΔXi Xi =1.
Таким образом, выявлен класс гармонических
последовательностей, которые построены по единому принципу. Класс гармонических
последовательностей представлен четырьмя подклассами. Подклассы располагаются в
соответствующих квадрантах на рис.3. Числа Люка и числа Фибоначчи являются
одними из представителей большого класса гармонических последовательностей. Для
всего класса гармонических последовательностей, в том числе и для
последовательностей Фибоначчи и Люка, справедливо уравнение: ΔXi Xi=1.
Для гармонических последовательностей выявлено семейство золотых инвариантов,
которые проявляют такие же свойства, как и золотая пропорция.
Источники информации
1. Ковалев Ф.В. Золотое сечение в живописи.
К.: Выща школа, 1989. – 143с.
2. Цеков-Карандаш Ц. О втором золотом
сечении. Журнал “Отечество”, N10, 1983.- София.
3. Стахов А.П. Коды золотой пропорции.
Москва: Радио и связь, 1984.
4. Альберт Тимашев. Обобщенное золотой сечение и теория времени. http://www.astrologer.ru/article/ggstt/ggstt.html
5. Цит. по Цветкову В.Д. Сердце, "золотое
сечение" и симметрия. Пущино: ПНЦ РАН, 1997.
6. Neil J.A.Sloane http://www.research.att.com/~njas/sequences/
7. Косинов Н.В. Константы гармонических
последовательностей. http://filosof.net/disput/kosinov/kgp.htm
8. Nikolay
V. Kosinov. Sequences: A087215, A087281, A087265 , A087287 ,A086902, A086903, A086594, A087799, A086927, A087800, A086928.

Демографические пенсии