Комментарии к специальной теории относительности
Кочетков Виктор Николаевич,
главный специалист ФГУП «Центр эксплуатации
объектов наземной космической инфраструктуры»
(ФГУП «ЦЭНКИ»)
В данной
статье делается попытка установить, являются ли в специальной теории
относительности преобразования Лоренца единственно возможной связью между
координатами и временем в инерциальных системах отсчета, а также соответствуют
ли выводы специальной теории относительности требованиям, накладываемым
условием симметрии пространства и времени.
1. Введение
В
настоящее время в журналах и Интернете публикуется большое количество статей,
посвященных критике специальной теории относительности. Складывается впечатление,
что только ленивый ее не критикует.
В
тоже время не удается увидеть ни одной статьи, защищающей специальную теорию относительности. Возможно,
ее защитники считают ниже своего достоинства вступать в полемику с критиками
или они забыли, в чем же она заключается.
Также
можно отметить, что критические замечания в отношении специальной теории
относительности в основном состоят из описания логического несоответствия ее выводов
реальному представлению пространства и времени.
Но
ведь специальная теория относительности – это идеализированная математическая
модель, построенная в рамках определенных условий, и поэтому результаты ее не
могут быть в обязательном порядке распространены вне рамок, установленных для
нее условий.
По-моему,
если уж и критиковать специальную теорию относительности, то критику надо было
бы начать с ее математической модели.
Может,
было бы полезно еще раз рассмотреть математическую модель специальной теории
относительности, а выводы ее проверить на выполнение условий, закладываемых при
ее создании.
1.1. Краткая история
создания специальной теории
относительности
На
рубеже XIX-XX веков стараниями крупнейших физиков мира была создана специальная теория
относительности.
В
конце XIX столетия между двумя важнейшими разделами физики - механикой и
электродинамикой - возникли серьезные противоречия.
В
механике утвердился принцип относительности Галилея - полное равноправие систем
отсчета, движущихся относительно друг друга прямолинейно и равномерно.
В
электродинамике основополагающее место заняла идея эфира - среды, заполняющей
мировое пространство, и в которой происходят все физические процессы, в т.ч.
электромагнитные колебания. При этом движение частиц и поля следовало описывать
в координатах, жестко связанных с эфиром - абсолютной системой отсчета.
В
1881, 1886÷1887 годах А. Майкельсону и Э. Моли в ходе экспериментов не
удалось зарегистрировать "эфирный ветер". В результате эфирная теория
света, казалось бы надежно подтвержденная опытами, не согласовывалась с
классической механикой.
В
1889 году ирландский физик Д. Фицджеральд предложил принять, что при движении
тела со скоростью V относительно эфира его продольный размер l´ испытывает сокращение по закону:
l´ = l
· [1 – (V2 / c2)]1/2 ( 1
)
где: c - скорость света,
l - длина неподвижного в отношении
эфира тела.
В
1892 году нидерландский физик Х. Лоренц дополнил гипотезу Д. Фицджеральда идеей
"местного" времени t´, связанного с
"истинным" универсальным
временем t преобразованием:
t´ =
t –
[(x · v) / c2]
( 2 )
где: v - скорость движения тела при прохождении точки
пространства с координатой x.
Также
Х. Лоренц видоизменил преобразования Галилея на случай больших скоростей:
x1 =
β · ( x2
– V · t2
)
( 3 )
y1 =
y2
( 4 )
z1
= z2 ( 5 )
t1 =
β · { t2
– [(x · V) / c2]} ( 6 )
путем введения
"релятивистского" множителя β :
β = 1 / {[1 –
(V2 / c2)]1/2} (
7 )
Формулы
(3)÷(6) перехода между инерциальными системами отсчета получили
наименование "преобразования
Лоренца".
Еще в
1881 году английский физик Д. Томсон предположил, что масса М тела,
движущегося со скоростью v, будет больше, чем масса Мо
в состоянии покоя, причем величина М равна:
М =
Мо / {[1 – (v2 / c2)]1/2} ( 8 )
1.2. Специальная теория
относительности
В
1905 году А. Эйнштейн взял за основу фундаментальные принципы, в сжатом виде
передающие суть двух классических физических теорий: из механики - принцип
равноправия всех инерциальных систем отсчета (принцип относительности), из
электродинамики - принцип постоянства скорости света.
Принцип
относительности: в любых инерциальных системах отсчета все физические
явления при одних и тех же условиях протекают одинаково, т.е. физические
законы независимы (инвариантны) по отношению к выбору инерциальной
системы отсчета - уравнения, выражающие эти законы, имеют одинаковую форму во
всех инерциальных системах отсчета.
Принцип
инвариантности скорости света: скорость света в вакууме не зависит от
движения источника света, т.е. скорость света одинакова во всех
направлениях и во всех инерциальных системах отсчета.
Используя
принцип относительности и принцип постоянства скорости света, А. Эйнштейн вывел
преобразования Лоренца, однако придал им иной физический смысл:
x1 =
[x2 + (V · t2)] / [1 –
(V2 / c2)]1/2 ( 9 )
x2 = [x1
– (V · t1)] / [1
– (V2 / c2)]1/2 ( 10 )
y1 =
y2 ( 11 )
z1 = z2
( 12 )
где: x1, y1, z1
–
координаты точки А в момент времени t1 в неподвижной инерциальной системе
отсчета O1x1y1z1;
x2, y2, z2 – координаты точки А в момент времени t2 в подвижной инерциальной системе
отсчета O2x2y2z2 (как показано на рис. 1).
t1
= {t2
+ [( V · x2) / c2]} / [(1 – V2/ c2)1/2] ( 13 )
t2 = {t1
– [( V · x1) / c2]}/ [(1 – V2 / c2)1/2] ( 14 )
Исходя
из формул (9)÷(14), связь между проекциями vx2, vy2 и vz2 скорости движения точки А в подвижной системе
отсчета O2x2y2z2 на оси декартовых координат и
аналогичными проекциями
vx1, vy1 и vz1 скорости той же точки А в
неподвижной системе отсчета O1x1y1z1 определена в виде:
vx1
= (vx2
+ V) / {1 + [(V · vx2)/ c2)]}
( 15 )
vx2
= (vx1
– V) / {1 – [(V · vx1)/ c2)]}
( 16 )
vy1
= {vy2 · [1
– (V2 / c2)]1/2} / {1 + [(V · vx2)/ c2)]} ( 17 )
vy2
= {vy1
· [1
– (V2 / c2)]1/2} / {1 – [(V · vx1)/ c2)]} ( 18 )
vz1
= {vz2 · [1
– (V2 / c2)]1/2} / {1 + [(V · vx2)/ c2)]} ( 19 )
vz2
= {vz1
· [1
– (V2 / c2)]1/2} / {1 – [(V · vx1)/ c2)]} ( 20 )
В
специальной теории относительности зависимости массы М(V) , импульса Р(V) и кинетической энергии Ек(V) материальной точки, движущейся со скоростью V, выражаются формулами:
М(V) =
Мо / [1 – (V2 / c2)]1/2 ( 21 )
Р(V) =
( Мо · V ) / [1 – (V2 / c2)]1/2 ( 22 )
Ек(V) = Мо · c2 · {{1 / [1 +
(V2 / c2)]1/2} – 1} ( 23 )
где: Мо - масса этой материальной точки в состоянии
покоя.
В
заключение можно отметить, что специальная теория относительности была создана
в первую очередь для объяснения результатов экспериментов (А. Майкельсона и
др.), приведших к рассмотрению вопроса о постоянстве скорости света (а точнее к
объяснению постоянства скорости света).
2. Кинематика
2.1. "Специальная теория
относительности в общем виде"
Чтобы не путаться в наименованиях, предполагаемую ниже идею
назовем "специальная теория относительности в общем виде".
Предположим,
что пространство однородно и изотропно, а время
однородно (т.е. имеется симметрия пространства и времени).
При
рассмотрении будем использовать принцип относительности: в любых
инерциальных системах отсчета все физические явления при одних и тех же
условиях протекают одинаково.
В
связи с отсутствием необходимости не будем применять принцип инвариантности
скорости света (т.е. применим менее жесткие условия).
Предположим,
что имеются две инерциальные системы отсчета: неподвижная O1x1y1z1 и подвижная O2x2y2z2, изображенные на рис. 1 и у которых:
- сходные оси декартовых координат
систем O1x1y1z1 и O2x2y2z2 попарно параллельны и одинаково
направлены;
- система O2x2y2z2 движется относительно системы O1x1y1z1 с постоянной скоростью V2 относительно оси Ox1;
- в качестве начала отсчета времени (t1=0
и t2=0) в обеих системах выбран тот момент,
когда начала координат O1 и O2 этих систем совпадают.
Исходя из симметрии пространства и времени
(однородности и изотропности пространства и однородности времени), соотношения
между координатами и временем одного и того же события в двух инерциальных
системах отсчета неподвижной O1x1y1z1 и подвижной O2x2y2z2 могут быть записаны следующим
образом:
x1 = β1 · ( x2 + V1 · t2 )
( 24 )
x2 = β2 · ( x1 +
V2 · t1 ) ( 25 )
y1 = β3 · y2
( 26 )
y2 = β4 · y1
(
27 )
z1 = β5 · z2
( 28 )
z2 = β6 · z1 (
29 )
где: x1, y1, z1
и x2, y2, z2 – координаты точки А в
системах отсчета O1x1y1z1
и O2x2y2z2,соответственно;
t1
и t2 -
значения времени в системах отсчета O1x1y1z1
и O2x2y2z2, соответственно;
β1, β2, β3, β4, β5
и β6
- коэффициенты перехода;
V1 - скорость движения системы O1x1y1z1 относительно системы O2x2y2z2.
y1
t2 О2 x1 x2 y2 О1
≡ О2 x1 x2 y2 y1 t1
V
![]()
· А
![]()
![]()
![]()
V
· А
![]()
![]()
![]()
![]()
![]()
![]()
![]()
t1 =
t2 = 0
О1
Рис.
1
Использование
принципа относительности и симметрии пространства и времени позволяет получить:
V1 =
– V2 = V
( 30 )
β1 =
β2 = β
( 31 )
β3 =
β4 = 1
( 32 )
β5 =
β6 = 1
( 33 )
При
этом система уравнений (24)÷(29) упростится и примет вид:
x1 = β · ( x2 + V · t2 )
( 34 )
x2 = β · ( x1 –
V · t1 )
( 35 )
y1 = y2 (
36 )
z1 = z2
( 37 )
Причем
коэффициент перехода β не зависит от значений координат x1, y1, z1, x2, y2, z2 и времени t1 и t2, а предположительно может являться
функцией скорости V перемещения систем отсчета O1x1y1z1
и O2x2y2z2 относительно друг друга.
Из
формул (34) и (35) можно записать зависимость для значений времен t1
и t2 :
t1 = {[(β2
– 1) · x2] / (β · V)} +
(β · t2) ( 38 )
t2 = {[(1 –
β2 ) · x1] / (β · V)} +
(β · t1) ( 39 )
Про
коэффициент перехода β в формулах (34) и (35) можно сказать
следующее:
-
исходя из принципа относительности, симметрии пространства и времени
коэффициент перехода β может быть только действительной величиной;
-
коэффициент
перехода β будет равен 1 при V = 0 (граничное условие);
-
коэффициент
перехода β будет равен 1, если коэффициент перехода β не будет зависеть от величины
скорости V;
- при принятом направлении оси декартовых
координат систем O1x1y1z1 и O2x2y2z2 коэффициент перехода β будет больше 0 , так как отрицательные значения
коэффициент перехода β будет иметь при разной
направленности осей O1x1 и O2x2;
- при значении коэффициента перехода β > 1 линейный размер тела,
движущегося относительно инерциальной системы отсчета, уменьшается в
направлении движения и ход времени часов, движущихся относительно инерциальной
системы отсчета, замедляется;
- при значении коэффициента перехода 0
< β < 1 линейный размер тела, движущегося относительно
инерциальной системы отсчета, увеличивается в направлении движения и ход
времени часов, движущихся относительно инерциальной системы отсчета,
ускоряется;
-
принцип
относительности и симметрия пространства и времени определяют также, что в
случае зависимости коэффициента перехода β от величины скорости V величина коэффициента перехода β однозначно зависит от величины скорости
V (т.е. одному
конкретному значению скорости V может соответствовать только одно конкретное значение
коэффициента перехода β).
Формулы
(24)÷(29) однозначно определяют связь между координатами x1, y1 и z1 точки А и временем t1 в неподвижной системе O1x1y1z1 и координатами x2, y2 и z2 этой же точки А и временем
t2 в подвижной системе O2x2y2z2.
Используя
формулы (24)÷(39), можно получить однозначную связь между проекциями vx2, vy2 и vz2 скорости движения точки А в подвижной системе O2x2y2z2 на оси декартовых координат и
аналогичными проекциями
vx1, vy1 и vz1
скорости
этой точки А в неподвижной системе O1x1y1z1 :
vx1 =
(vx2 +
V) / {{[(β2
– 1) · vx2] / (β2
· V)} + 1} ( 40 )
vx2 =
(vx1 –
V) / {{[(1 – β2) · vx1] / (β2
· V)} + 1} ( 41 )
vy1 = vy2 / {{[(β2
– 1) · vx2] / (β
· V)} + β} ( 42 )
vy2 =
vy1 / {{[(1 – β2) · vx1] / (β
· V)} + β} ( 43 )
vz1 =
vz2 / {{[(β2
– 1) · vx2] / (β
· V)} + β} ( 44 )
vz2 =
vz1 / {{[(1 – β2) · vx1] / (β
· V)} + β} ( 45 )
Рассматривая
формулу (40) для случая, когда коэффициент перехода β > 1 при действительных значениях V, vx1, vx2, можно отметить, что:
- при
положительных значениях vx2:
vx1
≤ (vx2 +
V) ( 46 )
- при
отрицательных значениях vx2:
vx1
≥ (vx2
+ V) ( 47 )
Неравенства
(46) и (47) не исключают, что при β > 1 возможно существование такого
действительного значения скорости vx1 движения точки в неподвижной
инерциальной системе отсчета O1x1y1z1, которое было бы равно значению
скорости vx2 движения этой же точки в подвижной
инерциальной системе отсчета O2x2y2z2.
Исследуя
формулу (40) для случая, когда коэффициент перехода 0 < β < 1 при действительных значениях V, vx1, vx2, можно отметить, что:
- при
положительных значениях vx2:
vx1
≥ (vx2
+ V) ( 48 )
или при V ≠ 0 : vx1
> vx2
( 49 )
- при
отрицательных значениях vx2:
vx1
≤ (vx2
+ V) ( 50 )
Неравенства
(48)÷(50) показывают, что при 0 < β < 1 не может существовать такое действительное
значение скорости vx1 движения точки в неподвижной
инерциальной системе отсчета O1x1y1z1, которое было бы равно значению
скорости vx2 движения этой же точки в подвижной
инерциальной системе отсчета O2x2y2z2.
Из
формул (38)÷(45) может быть получена однозначная связь между
проекциями ax2, ay2 и az2 ускорения точки А в подвижной системе O2x2y2z2 на оси декартовых координат и
аналогичными проекциями
ax1, ay1 и az1 ускорения этой точки А в
неподвижной системе O1x1y1z1 :
ax1
= (ax2 · β-3) / {{[(β2
– 1) · vx2] / (β2
· V)} + 1}3 ( 51 )
ax2
= (ax1 · β-3) / {{[(1 –
β2)
· vx1] / (β2
· V)} + 1}3
( 52 )
(ay2 · {{[(β2 –
1) · vx2] / (β · V)} + β}) – {[(β2 –
1) · vy2 · ax2] / (β · V)}
ay1 = ———————————————————————————– ( 53 )
{{[(β2 –
1) · vx2] / (β
· V)} + β}3
(ay1 · {{[(1 –
β2) · vx1] / (β · V)} + β}) – {[(1 –
β2) · vy1 · ax1]
/ (β · V)}
ay2 = ———————————————————————————– ( 54 )
{{[(1 –
β2) · vx1] / (β · V)} + β}3
(az2 · {{[(β2 – 1) · vx2] / (β · V)} + β}) –
{[(β2 – 1) ·
vz2 · ax2] / (β · V)}
az1 = ———————————————————————————– ( 55 )
{{[(β2 –
1) · vx2] / (β
· V)} + β}3
(az1 · {{[(1 –
β2) · vx1] / (β · V)} + β}) – {[(1 –
β2) · vz1 · ax1]
/ (β · V)}
az2 = ———————————————————————————– ( 56 )
{{[(1 –
β2) · vx1] / (β · V)} + β}3
2.2. Определение особой скорости
Допустим,
что существует такое значение Vxкр проекции vx1 скорости движения точки А в
неподвижной системе отсчета O1x1y1z1, которому бы соответствовало
значение проекции vx2 скорости движения точки А в
подвижной системе отсчета O2x2y2z2, равное Vxкр, т.е. когда:
vx1 =
vx2 = Vxкр
( 57 )
Подставив
значение (57) в формулу (40) или (41), получим:
Vxкр2 =
(β2 · V2) / ( β2
– 1 ) ( 58 )
Из
формулы (58) следует зависимость Vxкр от величины скорости V и
коэффициента перехода β для любого возможного значения
скорости V:
Vxкр =
± (β · V) / ( β2
– 1 )1/2 ( 59 )
В
случае, если коэффициент перехода β имеет значение β ≥ 1 , получим, что Vxкр будет иметь действительное значение
(что находится в соответствии с условиями (46) и (47)) и ее для дальнейшего
рассмотрения запишем как :
Vxкр =
vxкр1 =
± (β · V) / ( β2
– 1 )1/2 ( 60 )
где: vxкр1 - действительная величина, имеющая размерность
скорости.
А в
случае, если коэффициент перехода β имеет значение 0 < β ≤ 1 , получим, что Vxкр будет иметь мнимое значение (что
находится в соответствии с условиями (48)÷(50), т.к. скорость движения
точки в неподвижной системе отсчета всегда выше скорости этой же точки в
подвижной инерциальной системе отсчета при 0 < β ≤ 1) и которую для дальнейшего
рассмотрения запишем как :
Vxкр =
ί · vxкр2 =
± (ί · β · V) / (1 – β2 )1/2 ( 61 )
где: vxкр2 - действительная величина, имеющая размерность
скорости,
а ί
равно:
ί =( – 1 )1/2
( 62 )
Из
формулы (58) можно получить зависимость коэффициента перехода β от величины скорости V для любого возможного значения
скорости V :
β2 = 1 / [1 –
(V2 / Vxкр2)] ( 63 )
Тогда
из формулы (63) с учетом формулы (60) для коэффициента перехода β, имеющего значения β ≥ 1 и который обозначим как β>, можно записать:
β> 2 = 1 / [1 –
(V2 / vxкр12)] ( 64 )
А из
формулы (63) с учетом формулы (61) для коэффициента перехода β, имеющего значения 0<β≤ 1 и который обозначим как β< , можно записать:
β< 2 =
1 / [1 + (V2 / vxкр22)] ( 65 )
2.3. Уравнение связи для
коэффициентов перехода
Рассмотрим
три инерциальные системы отсчета: неподвижную O1x1y1z1 и подвижные O2x2y2z2 и O3x3y3z3, показанные на рис. 2 и у которых:
- сходные оси декартовых координат
систем O1x1y1z1 , O2x2y2z2 и O3x3y3z3
попарно
параллельны и одинаково направлены;
- система O2x2y2z2 движется относительно системы O1x1y1z1 с постоянной скоростью V2 относительно оси Ox1 ;
- система O3x3y3z3 движется относительно системы O1x1y1z1 с постоянной скоростью V3 относительно оси Ox1 ;
- в качестве начала отсчета времени (t1=0 , t2=0 и t3=0) в этих трех системах выбран тот
момент, когда их начала координат O1 , O2 и O3 совпадают.
t3 V3 t2 t1 y3 y2 y1 О3 О2 О1 x3 x2 x1 t1 = t2 = t3 = 0 V3 О1
≡ О2≡ О3 x3 x2 x1 y3 y2 y1
![]()
V2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
V2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис.
2
Опираясь
на формулу (41), можно определить значение скорости V23 движения точки O3 относительно точки O2:
V23
= (V3
– V2) / {{[(1 –
β22) · V3] / (β22
· V2)} + 1} ( 66 )
и значение скорости V32 движения точки O2 относительно точки O3:
V32
= (V2
– V3) / {{[(1 –
β32 ) · V2] / (β32
· V3)} + 1} ( 67 )
где: β2 и β3
- коэффициенты перехода для инерциальных систем отсчета, движущихся
относительно неподвижной системы отсчета со скоростью V2 и V3, соответственно.
Используя
принцип относительности, согласно которому точка O3 будет удаляться относительно точки O2 со скоростью, равной по абсолютной
величине и противоположно направленной скорости, с которой точка O2 удаляется относительно точки O3 , т.е.:
V32
= – V23
( 68 )
Подставив
уравнение (68) в формулы (66) и (67), получим:
{[(1 – β22) · V3] / (β22
· V2)} + 1 = {[(1
– β32) · V2] / (β32
· V3)} + 1 (69
)
Отсюда
уравнение для коэффициентов перехода β2 и β3 запишется следующим образом:
β32
= (β22
· V2) /
[V32 – (β22
· V3) + (β22
· V2)] ( 70 )
2.4. Получение зависимости для
коэффициента перехода β
Из
уравнения (69) можно получить формулу:
(β22
– 1) / (β22
· V22) = (β32
– 1 ) / (β32
· V32)
( 71 )
Так
как величины коэффициентов перехода β2 и β3 не зависят друг от друга, а зависят только от величин
скоростей V2 и
V3, соответственно, и
величины скоростей V2 и V3 задавались произвольно (также не зависят друг от
друга), то можно сказать, что:
(β22 –
1) / (β22 · V22) = (β32 –
1 ) / (β32 · V32) = К = Const ( 72 )
т.е.
получается в общем виде, что:
(β2
– 1) / (β2
· V2) =
К = Const
(
73 )
где: К -
постоянная величина, независящая от величины скорости V (V2 и V3) и величины коэффициента перехода β (β2 и β3) и имеющая размерность, обратную
квадрату скорости.
Как
видно из формулы (73), в зависимости от величины константы К коэффициент
перехода β может иметь следующие значения:
- при
К = 0 коэффициент перехода β будет равен 1,
-
если константа К имеет действительное положительное значение, то
коэффициент перехода β будет больше или равен 1, т.е. β ≥ 1,
-
если константа К имеет действительное отрицательное значение, то
коэффициент перехода β будет меньше или равен 1, т.е. 0
< β ≤ 1.
Но
так как константа К не зависит от
величины скорости V и величины коэффициента перехода β, то для любого конкретного значения
величины скорости V получается, что константа К не
может быть одновременно величиной положительной величиной и отрицательной, т.е.
для всех возможных значений скорости V значения коэффициента перехода β могут находиться только в диапазоне
β ≥ 1 или
только в диапазоне 0 <
β ≤ 1.
Одним
словом, β ≥ 1 и 0 < β ≤ 1 являются двумя взаимоисключающими
диапазонами коэффициента перехода β, т.е. все значения коэффициента
перехода β в зависимости от величины скорости V находятся только в диапазоне β ≥ 1 или в диапазоне 0 < β ≤ 1.
Основная
задача заключается в выборе одного из этих двух диапазонов, в котором будет в
действительности определяться величина коэффициента перехода β в зависимости от величины скорости V (если β зависит от V).
Из
уравнения (73) можно получить формулу для коэффициента перехода β:
β 2
= 1 / [1 – (К · V2)] ( 74
)
Если
вернуться к формуле (63):
β2 = 1 / [1 –
(V2 / Vxкр2)] ( 63 )
и
сравнить ее с формулой (74), то можно отметить, что:
К = 1 / Vxкр2 ( 75
)
т.е. Vxкр2
будет являться постоянной величиной, не зависящей от значений скорости V и коэффициента перехода β.
Опираясь
на формулы (74) и (75), можно сказать, что в случае, когда коэффициент перехода
β не равен 1,
должна существовать такая величина скорости Vxкр (действительная или мнимая) движения
точки, которая была бы инвариантна во всех направлениях и во всех инерциальных
системах отсчета.
Исходя
из формулы (74), в формулах для коэффициента перехода β:
- при β ≥ 1:
β> 2 = 1 / [1 –
(V2 / vxкр12)] ( 64 )
- при
0<β≤ 1:
β< 2 =
1 / [1 + (V2 / vxкр22)] ( 65 )
величины vxкр1 и vxкр2 будут постоянными величинами, не
зависящими от величины скорости V и коэффициента перехода β, т.е.:
vxкр1 =
Const
( 76 )
vxкр2 =
Const ( 77 )
Граничное
условие (при значении скорости V, равной 0, коэффициент
перехода β равен 1) устанавливает, что при стремлении величины скорости V к 0 коэффициент перехода β стремится к
1, а это, согласно формулам (64) и (65), позволяет отметить, что:
vxкр1 ≠ 0
( 78 )
vxкр2
≠ 0
( 79 )
А в
случае, когда коэффициент перехода β не зависит от
величины скорости V (т.е. при значении коэффициента
перехода β = Const = 1), то:
vxкр1 =
∞
( 80 )
vxкр2
= ∞
( 81 )
2.5. Основные кинематические уравнения
«специальной теории относительности в общем виде»
Подставив
формулу (63) в уравнения (34), (35), (38)÷(39), (40)÷(45) и (51)÷(56),
получим следующую систему уравнений:
x1 = [x2
+ (V · t2)] / [1 – (V2 / Vxкр2)]1/2 (82 )
x2 =
[x1 – (V · t1>)] / [1 –
(V2 / Vxкр2)]1/2 (83)
t1
= {t2
+ [( V · x2) / Vxкр2]} / [(1 – V2/ Vxкр2)1/2] (84)
t2 = {t1
– [( V · x1) / Vxкр2 ]}/ [(1 – V2/ Vxкр2)1/2] ( 85 )
vx1
= (vx2
+ V) / {1 + [(V · vx2)/ Vxкр2)]}
( 86 )
vx2
= (vx1
– V) / {1 – [(V · vx1)/ Vxкр2)]} ( 87 )
vy1
= {vy2 · [1
– (V2 / Vxкр2)]1/2} / {1 + [(V · vx2)/ Vxкр2)]} ( 88
)
vy2
= {vy1
· [1
– (V2 / Vxкр2)]1/2} / {1 – [(V · vx1)/ Vxкр2)]} ( 89
)
vz1
= {vz2 · [1
– (V2 / Vxкр2)]1/2} / {1 + [(V · vx2)/ Vxкр2)]} (90)
vz2
= {vz1
· [1
– (V2 / Vxкр2)]1/2} / {1 – [(V · vx1)/ Vxкр2)]} (91)
ax1
= {ax2
· [1
– (V2 / Vxкр2)]3/2}/ {1 + [(V · vx2)/ Vxкр2)]}3 (92)
ax2
= {ax1
· [1
– (V2 / Vxкр2)]3/2}/ {1 – [(V · vx1)/ Vxкр2)]}3 (93)
[{{1+[(V·vx2)/ Vxкр2)]}·ay2}}
–[(V·vy2 ·ax2)/ Vxкр2]] · [1 – (V2/ Vxкр2)]
ay1 =
———————————————————————————— (94)
{1 + [(V · vx2)/ Vxкр2)]}3
[{{1–[(V·vx1)/ Vxкр2)]}·ay1}}
+[(V·vy1 ·ax1)/ Vxкр2]] · [1 – (V2/ Vxкр2)]
ay2 =
———————————————————————————— (95)
{1 – [(V · vx1)/ Vxкр2)]}3
[{{1+[(V·vx2)/ Vxкр2)]}·az2}}
–[(V·vz2 ·ax2)/ Vxкр2]] · [1 – (V2/v Vxкр2)]
az1 =
———————————————————————————— (96)
{1 + [(V · vx2)/ Vxкр2)]}3
[{{1–[(V·vx1)/ Vxкр2)]}·az1}}
+[(V·vz1 ·ax1)/ Vxкр2]] · [1 – (V2/ Vxкр2)]
az2 =
———————————————————————————— (97)
{1 – [(V · vx1)/ Vxкр2)]}3
2.6. Основные кинематические
уравнения при коэффициенте перехода β ≥ 1
Подставив
формулу (64) в уравнения (34), (35), (38)÷(39), (40)÷(45) и (51)÷(56),
получим следующую систему уравнений при коэффициенте перехода β= β>:
x1> = [x2>
+ (V · t2>)] / [1 –
(V2 / vxкр12)]1/2 ( 98 )
x2> =
[x1> – (V · t1>)] / [1 –
(V2 / vxкр12)]1/2 ( 99 )
t1> = {t2>
+ [( V · x2>) / vxкр12]} / [(1 – V2/vxкр12)1/2] ( 100 )
t2> =
{t1> – [( V · x1>) / vxкр12 ]}/ [(1 – V2/vxкр12)1/2] ( 101)
vx1> = (vx2> + V) / {1 + [(V · vx2>)/ vxкр12)]}
( 102 )
vx2> = (vx1> – V) / {1 – [(V · vx1>)/ vxкр12)]} ( 103 )
vy1> = {vy2> · [1
– (V2 / vxкр12)]1/2} / {1 + [(V · vx2>)/ vxкр12)]} ( 104
)
vy2> = {vy1>
· [1
– (V2 / vxкр12)]1/2} / {1 – [(V · vx1>)/ vxкр12)]} ( 105
)
vz1> = {vz2> · [1
– (V2 / vxкр12)]1/2} / {1 + [(V · vx2>)/ vxкр12)]} ( 106
)
vz2> = {vz1>
· [1
– (V2 / vxкр12)]1/2} / {1 – [(V · vx1>)/ vxкр12)]} ( 107
)
ax1> = {ax2> · [1 –
(V2 / vxкр12)]3/2}/ {1 + [(V · vx2>)/ vxкр12)]}3 ( 108 )
ax2> = {ax1> · [1 –
(V2 / vxкр12)]3/2}/ {1 – [(V · vx1>)/ vxкр12)]}3 ( 109 )
[{{1+[(V·vx2>)/vxкр12)]}·ay2>}}
–[(V·vy2> ·ax2>)/vxкр12]] · [1 – (V2/vxкр12)]
ay1> = ———————————————————————————— (110)
{1 + [(V
· vx2>)/ vxкр12)]}3
[{{1–[(V·vx1>)/vxкр12)]}·ay1>}}
+[(V·vy1> ·ax1>)/vxкр12]] ·
[1 – (V2/vxкр12)]
ay2> =
———————————————————————————— (111)
{1 – [(V · vx1>)/ vxкр12)]}3
[{{1+[(V·vx2>)/vxкр12)]}·az2>}}
–[(V·vz2> ·ax2>)/vxкр12]] ·
[1 – (V2/vxкр12)]
az1> =
———————————————————————————— (112)
{1 + [(V
· vx2>)/ vxкр12)]}3
[{{1–[(V·vx1>)/vxкр12)]}·az1>}}
+[(V·vz1> ·ax1>)/vxкр12]] ·
[1 – (V2/vxкр12)]
az2> =
———————————————————————————— (113)
{1 – [(V
· vx1>)/ vxкр12)]}3
2.7. Основные кинематические
уравнения при коэффициенте перехода 0
< β < 1
Подставив
формулу (65) в уравнения (34), (35), (38)÷(39), (40)÷(45) и (51)÷(56),
получим систему уравнений для случая, когда коэффициент перехода β = β<:
x1< = [x2<
+ (V · t2<)] / [1 + (V2 / vxкр22)]1/2 ( 114 )
x2< =
[x1< – (V · t1<)] / [1 +
(V2 / vxкр22)]1/2 ( 115 )
t1< = {t2< – [( V · x2<) / vxкр22]} / [(1 +
V2/vxкр22)1/2] ( 116 )
t2< = {t1<
+ [( V · x1<) / vxкр22 ]}/ [(1 + V2/vxкр22)1/2] ( 117 )
vx1< =
(vx2< +
V) / {1 – [(V · vx2<)/ vxкр22)]} ( 118 )
vx2< =
(vx1< –
V) / {1 + [(V · vx1<)/ vxкр22)]} ( 119 )
vy1< =
{vy2< · [1 +
(V2 / vxкр22)]1/2} / {1 – [(V · vx2<)/ vxкр22)]} ( 120
)
vy2< =
{vy1< · [1
+ (V2 / vxкр22)]1/2} / {1 + [(V · vx1<)/ vxкр22)]} ( 121
)
vz1< =
{vz2< · [1 +
(V2 / vxкр22)]1/2} / {1 – [(V · vx2<)/ vxкр22)]} ( 122
)
vz2< =
{vz1< · [1
+ (V2 / vxкр22)]1/2} / {1 + [(V · vx1<)/ vxкр22)]} ( 123
)
ax1< = {ax2< · [1 +
(V2 / vxкр22)]3/2}/ {1 – [(V · vx2<)/ vxкр22)]}3
( 124 )
ax2< = {ax1< · [1 +
(V2 / vxкр22)]3/2}/ {1 + [(V · vx1<)/ vxкр22)]}3
( 125 )
[{{1–[(V·vx2<)/vxкр22)]}·ay2<}}+[(V·vy2<
·ax2<)/vxкр22]] ·
[1 + (V2/vxкр22)]
ay1< =
———————————————————————————— (126)
{1 – [(V · vx2<)/ vxкр22)]}3
[{{1+[(V·vx1<)/vxкр22)]}·ay1<}}–[(V·vy1<
·ax1<)/vxкр22]] ·
[1 + (V2/vxкр22)]
ay2< =
———————————————————————————— (127)
{1 + [(V
· vx1<)/ vxкр22)]}3
[{{1–[(V·vx2<)/vxкр22)]}·az2<}}+[(V·vz2<
·ax2<)/vxкр22]] ·
[1 + (V2/vxкр22)]
az1< =
———————————————————————————— (128)
{1 – [(V
· vx2<)/ vxкр22)]}3
[{{1+[(V·vx1<)/vxкр22)]}·az1<}}–[(V·vz1<
·ax1<)/vxкр22]] ·
[1 + (V2/vxкр22)]
az2< =
———————————————————————————— (129)
{1 + [(V · vx1<)/ vxкр22)]}3
К сожалению,
из кинематических уравнений связи определить значение постоянной величины Vxкр (vxкр1 или vxкр2) невозможно, поэтому придется обратиться за помощью к динамике.
3. Динамика
Для
установления зависимости массы движущегося тела от скорости воспользуемся - с
одной стороны - принципом относительности, утверждающим, что физические законы
инвариантны по отношению к выбору инерциальной системы отсчета, т.е. уравнения,
выражающие эти законы, имеют одинаковую форму во всех инерциальных системах
отсчета.
С
другой стороны - постараемся опереться на ограничительные условия к
пространству и времени, которые устанавливаются в специальной теории
относительности.
Этими
условиями являются однородность и изотропность пространства и однородность
времени, т.е. симметрия пространства и времени.
Согласно
теореме Эммы Нетер симметрии действия соответствует закон сохранения этого
действия.
Теорема
Эммы Нетер позволяет установить, что:
-
закон сохранения механической энергии связан со свойством симметрии времени –
однородностью времени (это свойство времени проявляется в том, что законы
движения замкнутой системы не зависят от выбора начала отсчета времени);
-
закон сохранения импульса связан со свойством симметрии пространства –
однородностью пространства (это свойство проявляется в том, что физические
свойства замкнутой системы и законы ее движения не зависят от выбора положения
начала координат инерциальной системы отсчета, т.е. не изменяются при
параллельном переносе в пространстве замкнутой системы как целого);
-
закон сохранения момента импульса связан со свойством симметрии пространства –
изотропностью пространства (это свойство пространства проявляется в том, что
физические свойства и законы движения замкнутой системы не зависят от выбора
направления осей координат инерциальной системы отсчета, т.е. не изменяются при
повороте в пространстве замкнутой системы как целого на любой угол).
3.1. Системы
уравнений для определения зависимости
массы движущегося тела от скорости
Для
определения зависимости массы движущегося тела от его скорости перемещения
воспользуемся:
- законом сохранения импульса: импульс
замкнутой механической системы тел (на
которую не действуют внешние силы) для любого момента времени является
величиной постоянной;
- законом сохранения механической
энергии: механическая энергия
консервативной механической системы тел (у которой все внутренние силы
потенциальны, а внешние силы потенциальны и стационарны) для любого момента времени является величиной постоянной,
который для замкнутых механических систем принимает вид: механическая энергия замкнутой механической системы не изменяется с
течением времени, если все внутренние силы, действующие в этой системе,
потенциальны, а точнее - его частным случаем, когда у тел, составляющих
замкнутую механическую систему, не происходит изменение потенциальной энергии
(в том числе, когда тела, составляющие замкнутую механическую систему,
испытывают только абсолютно упругие взаимодействия): кинетическая энергия
замкнутой механической системы тел для любого момента времени является
величиной постоянной.
Допустим,
что зависимость массы тела от скорости его движения не меняется при изменении
потенциальной энергии тела.
Предположим,
что масса М(V) материальной точки, движущейся со скоростью V,
равна:
М(V)
= Мо ·
f (V)
( 130 )
где: Мо – масса рассматриваемой
материальной точки в состоянии покоя;
f(V) – функция, предположительно зависящая от величины
скорости V.
Исходя
из формулы (130), импульс Р(V) материальной точки, движущейся со скоростью V, равен:
Р(V) =
Мо · f (V) ·
V
( 131 )
А
формула (131) позволяет записать следующее уравнение для кинетической энергии Ек(V) материальной точки, движущейся со скоростью V:
v
Ек(V) = Мо
· ∫ {[ f (V) · V ] + [ f′ (V) · V2]} ·dV ( 132 )
0
где: f′
(V) – производная функции f (V) .
Постараемся
установить зависимость массы (функции f (V)) движущегося тела от скорости его
перемещения, рассмотрев взаимодействия (а точнее результаты взаимодействия) тел
(материальных точек), составляющих замкнутую механическую систему и
перемещающихся в пространстве только линейно.
С
целью написания системы уравнений, позволяющих определить значение функции f
(V),
рассмотрим два простейших примера.
3.1.1. Пример № 1
Допустим,
что имеются две инерциальные системы отсчета, аналогичные системам отсчета,
изображенным на рис. 1, - неподвижная O1x1y1z1 и подвижная O2x2y2z2 , которая движется со скоростью V параллельно оси O1x1 относительно системы O1x1y1z1.
Предположим,
что имеется замкнутая механическая система тел, состоящая из тела 1 и тела 2 (как
показано на рис. 3) имеющих массы в состоянии покоя, равные Мо1
и Мо2 соответственно.
t2
> t2c
v22хк 2 V x1 x2 y2 y1 О2 О1 t2
< t2c v22хн 2 1 О2 О1 y2 x2 x1 y1 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
v21хн
![]()
![]()
V
![]()
![]()
![]()
![]()
![]()
v21хк
Рис.
3
В
подвижной системе отсчета O2x2y2z2 тело 1 и тело 2 до некоторого
момента времени t2с двигались параллельно оси O2x2 по одной линии с постоянными по
величине скоростями v21xн и v22xн соответственно.
В
какой-то момент времени t2с между телами 1 и 2 произошло
абсолютно упругое прямое центральное столкновение.
Далее
после столкновения в момент времени больший t2с тела 1 и 2 стали двигаться
параллельно оси O2x2 по одной линии с постоянными по
величине скоростями v21xк и v22xк соответственно.
Учитывая,
что между телами 1 и 2 имело место прямое центральное столкновение, и
рассматривая их как материальные точки, запишем закон сохранения импульса для
замкнутой механической системы тел 1 и 2 в подвижной системе отсчета O2x2y2z2 для моментов времени меньшего и
большего, чем t2с :
[Мо1 · f (V= v21xн) · v21xн] + [Мо2 · f (V= v22xн) · v22xн] = [Мо1 · f (V= v21xк) · v21xк] + [Мо2 · f (V= v22xк) · v22xк]
( 133 )
А операясь
на то, что столкновение тел 1 и 2 носило абсолютно упругий характер, можно
записать закон сохранения механической энергии для замкнутой механической
системы тел 1 и 2 в подвижной системе отсчета O2x2y2z2 для моментов времени меньшего и
большего, чем t2с, предполагая, что величины потенциальных энергий тел 1 и 2
остаются неизменными до и после столкновения:
v21xн v22xн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0 0
v21xк v22xк
{ Мо1·
∫ {[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫ {[f (V)·V] +[f′ (V)·V2]}·dV} (134)
0
0
Все
ранее сказанное о движении тел 1 и 2 в подвижной системе отсчета O2x2y2z2 можно сказать и о движении тел 1 и 2
в неподвижной системе отчета O1x1y1z1, за исключением того, что:
-
столкновение между телами 1 и 2 происходит в момент времени t1с, соответствующий моменту времени t2с в системе O2x2y2z2,
- тело
1 имеет соответственно до и после столкновения скорости v11xн и v11xк , соответствующие скоростям v21xн и v21xк,
- тело
2 имеет соответственно до и после столкновения скорости v12xн и v12xк , соответствующие скоростям v22xн и v22xк.
Аналогично
формулам (133) и (134) можно записать закон сохранения импульса и закон
сохранения механической энергии для замкнутой механической системы тел 1 и 2 в
неподвижной системе отсчета O1x1y1z1 для моментов времени меньшего и
большего, чем t1с, также предполагая, что величины потенциальных энергий тел 1 и 2
остаются неизменными до и после столкновения:
[Мо1 · f (V= v11xн) · v11xн] + [Мо2 · f (V= v12xн) · v12xн] = [Мо1 · f (V= v11xк) · v11xк] + [Мо2 · f (V= v12xк) · v12xк]
( 135 )
v11xн v12xн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
v11xк v12xк
{ Мо1·
∫ {[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫ {[f (V)·V] +[f′ (V)·V2]}·dV} (136)
0
0
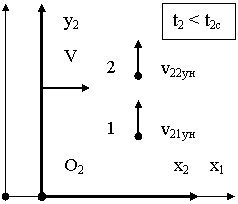
3.1.2. Пример № 2
Пример
№ 2 подобен примеру № 1 и отличается от него только тем, что в подвижной системе отсчета O2x2y2z2 тела 1 и тела 2 двигаются не
параллельно оси O2x2, а параллельно оси O2y2, как показано на рис. 4.
В подвижной системе отсчета O2x2y2z2 тела 1 и тела 2 до некоторого
момента времени t2с двигались параллельно оси O2y2 по одной линии с постоянными по
величине скоростями v21yн и v22yн соответственно.
О1
y1 Рис.
4

После
столкновения в момент времени больший t2с тела 1 и 2 стали двигаться параллельно
оси O2y2 по одной линии с постоянными по
величине скоростями v21yк и v22yк соответственно.
Тогда
можно записать закон сохранения импульса и закон сохранения механической
энергии для замкнутой механической системы тел 1 и 2 в подвижной системе
отсчета O2x2y2z2 для моментов времени меньшего и
большего, чем t2с, предполагая, что величины потенциальных энергий тел 1 и 2
остаются неизменными до и после столкновения:
[Мо1 · f (V= v21yн) · v21yн] + [Мо2 · f (V= v22yн) · v22yн] = [Мо1 · f (V= v21yк) · v21yк] + [Мо2 · f (V= v22yк) · v22yк]
( 137 )
v21yн v22yн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0 0
v21yк v22yк
{ Мо1·
∫ {[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫ {[f (V)·V] +[f′ (V)·V2]}·dV} (138)
0
0
Аналогично
можно записать закон сохранения импульса (два уравнения для проекций импульса
на оси O1x1 и O1y1) и закон сохранения механической
энергии для замкнутой механической системы тел 1 и 2 в неподвижной системе
отсчета O1x1y1z1 для моментов времени меньшего и
большего, чем t1с, предполагая, что величины потенциальных энергий тел 1 и 2
остаются неизменными до и после столкновения:
{Мо1 · f [V = (v11yн2+ V2)1/2] · V } + {Мо2 · f [V = (v12yн2+ V2)1/2] · V } =
{Мо1 · f [V = (v11yк2+ V2)1/2] · V } + {Мо2 · f [V = (v12yк2+ V2)1/2] · V } ( 139 )
{Мо1 · f [V = (v11yн2+ V2)1/2] · v11yн} + {Мо2 · f [V = (v12yн2+ V2)1/2] · v12yн} =
{Мо1 · f [V = (v11yк2+ V2)1/2] · v11yк} + {Мо2 · f [V = (v12yк2+ V2)1/2] · v12yк} ( 140 )
(v11yн2+ V2)1/2 (v12yн2+ V2)1/2
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
(v11yк2+ V2)1/2 (v12yк2+ V2)1/2
{ Мо1·
∫{[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫{[f (V)·V] +[f′ (V)·V2]}·dV} ( 141)
0
0
3.1.3. Зависимость массы движущегося
тела от скорости
С
целью определения зависимости для массы движущегося тела составим следующую
систему уравнений:
[Мо1 · f (V= v21xн) · v21xн] + [Мо2 · f (V= v22xн) · v22xн] = [Мо1 · f (V= v21xк) · v21xк] + [Мо2 · f (V= v22xк) · v22xк]
( 133 )
v21xн v22xн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
v21xк v22xк
{ Мо1·
∫{[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫{[f (V)·V] +[f′ (V)·V2]}·dV} ( 134)
0
0
[Мо1 · f (V= v11xн) · v11xн] + [Мо2 · f (V= v12xн) · v12xн] = [Мо1 · f (V= v11xк) · v11xк] + [Мо2 · f (V= v12xк) · v12xк]
( 135 )
v11xн v12xн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
v11xк v12xк
{ Мо1·
∫{[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫{[f (V)·V] +[f′ (V)·V2]}·dV} ( 136)
0
0
[Мо1 · f (V= v21yн) · v21yн] + [Мо2 · f (V= v22yн) · v22yн] = [Мо1 · f (V= v21yк) · v21yк] + [Мо2 · f (V= v22yк) · v22yк] (
137 )
v21yн v22yн
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
v21yк v22yк
{ Мо1·
∫{[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫{[f (V)·V] +[f′ (V)·V2]}·dV} (138)
0
0
{Мо1 · f [V = (v11yн2+ V2)1/2] · V } + {Мо2 · f [V = (v12yн2+ V2)1/2] · V } =
{Мо1 · f [V = (v11yк2+ V2)1/2] · V } + {Мо2 · f [V = (v12yк2+ V2)1/2] · V } ( 139 )
{Мо1 · f [V = (v11yн2+ V2)1/2] · v11yн} + {Мо2 · f [V = (v12yн2+ V2)1/2] · v12yн} =
{Мо1 · f [V = (v11yк2+ V2)1/2] · v11yк} + {Мо2 · f [V = (v12yк2+ V2)1/2] · v12yк} ( 140 )
(v11yн2+ V2)1/2 (v12yн2+ V2)1/2
{ Мо1
· ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо2 · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
(v11yк2+ V2)1/2
(v12yк2+ V2)1/2
{ Мо1·
∫{[f (V)·V] +[f′ (V)·V2]}·dV} + {
Мо2 · ∫{[f (V)·V] +[f′ (V)·V2]}·dV} ( 141)
0
0
В эту
систему уравнений нужно также добавить уравнения связи между проекциями
скоростей тел 1 и 2 в подвижной O2x2y2z2 и неподвижной O1x1y1z1 системах отсчета, записанные исходя
из формул (86) и (88):
v11xн
= (v21xн
+ V ) / {1 + [(V · v21xн) / Vxкр2)]}
( 142 )
v12xн
= (v22xн
+ V ) / {1 + [(V · v22xн) / Vxкр2)]}
( 143 )
v11xк
= (v21xк
+ V ) / {1 + [(V · v21xк) / Vxкр2)]}
( 144 )
v12xк
= (v22xк
+ V ) / {1 + [(V · v22xк) / Vxкр2)]}
( 145 )
v11yн
= v21yн · [1
– (V2 / Vxкр2)]1/2
( 146 )
v12yн
= v22yн · [1
– (V2 / Vxкр2)]1/2 (
147 )
v11yк
= v21yк · [1
– (V2 / Vxкр2)]1/2 (
148 )
v12yк
= v22yк · [1
– (V2 / Vxкр2)]1/2 (
149 )
И
так, имеется 17 уравнений, 12 неизвестных значений и одна неизвестная функция.
Единственной
функцией f(V), способной
удовлетворить всем требованиям 17 уравнений, является:
f (V) = 1 / [1
– (V2 / Vxкр2)]1/2 ( 150 )
Тогда,
с учетом уравнений (130)÷(132), можно записать зависимости для массы М(V), импульса Р(V)
и
кинетической энергии Ек(V)
движущегося
тела со скоростью V:
М(V) =
Мо / [1 – (V2 / Vкр2)]1/2 ( 151 )
Р(V) =
( Мо · V ) / [1 –
(V2 / Vxкр2)]1/2 ( 152 )
Ек(V) = Мо · vxкр12 ·
{{1 / [1 – (V2 / Vxкр2)]1/2}
– 1} ( 153
)
3.1.4. Зависимость массы движущегося
тела от скорости при коэффициенте
перехода β>1
В случае, когда значение коэффициента
перехода β находится в диапазоне β>1 , то исходя из формул (150)÷(153) с учетом уравнения (60)
зависимости для функции f(V)>, массы М(V)>, импульса Р(V)>, кинетической энергии Ек(V)>
движущегося
тела со скоростью V, можно записать:
f (V)> = 1 / [1
– (V2 / vxкр12)]1/2 ( 154 )
М(V)> =
Мо / [1 – (V2 / vxкр12)]1/2 ( 155 )
Р(V)> =
( Мо · V ) / [1 –
(V2 / vxкр12)]1/2 ( 156 )
Ек(V)> = Мо · vxкр12 ·
{{1 / [1 – (V2 / vxкр12)]1/2}
– 1} ( 157
)
3.1.4.1. Проверка правильности выбора
формулы (150) при β>1
(для примеров № 1 и № 2)
Сначала
перепишем формулы (133)÷(141) с учетом формул (60) и (154)÷(157):
{(Мо1 · v21xн) / [1 – (v21xн2 / vxкр12)]1/2} + {(Мо2 · v22xн) / [1 – (v22xн2 / vxкр12)]1/2} = {(Мо1 · v21xк) / [1 – (v21xк2/vxкр12)]1/2} + {(Мо2 · v22xк) / [1 – (v22xк2/vxкр12) ]1/2} (158)
{Мо1 / [1
– (v21xн2 / vxкр12)]1/2} + {Мо2 / [1
– (v22xн2 / vxкр12)]1/2} = {Мо1 / [1 – (v21xк2 / vxкр12)]1/2} + {Мо2 / [1
– (v22xк2 / vxкр12)]1/2} ( 159 )
{(Мо1 · v11xн) / [1 – (v11xн2 / vxкр12)]1/2} + {(Мо2 · v12xн) / [1 –
(v12xн2 / vxкр12)]1/2} = {(Мо1 · v11xк)/[1 – (v21xк2/vxкр12)]1/2} + {(Мо2 · v12xк)/[1 – (v12xк2/vxкр12)]1/2}
( 160 )
{Мо1 / [1
– (v11xн2 / vxкр12)]1/2} + {Мо2 / [1 – (v12xн2 / vxкр12)]1/2} = {Мо1
/ [1 – (v21xк2 / vxкр12)]1/2} + {Мо2 / [1 – (v12xк2 / vxкр12)]1/2} ( 161 )
{(Мо1 · v21yн) / [1 – (v21yн2 / vxкр12)]1/2} + {(Мо2 · v22yн) / [1 – (v22yн2 / vxкр12)]1/2} = {(Мо1 · v21yк) / [1 – (v21yк2/vxкр12)]1/2} + {(Мо2 · v22yк) / [1 – (v22yк2/vxкр12)]1/2}
(162)
{Мо1 / [1
– (v21yн2 / vxкр12)]1/2} + {Мо2 / [1
– (v22yн2 / vxкр12)]1/2} =
{Мо1 / [1 – (v21yк2 / vxкр12)]1/2} + {Мо2 / [1
– (v22yк2 / vxкр12)]1/2} ( 163 )
{(Мо1 · V)/{1 – [(v11yн2+V2)/vxкр12]}1/2}
+ {(Мо2 · V)/{1 – [(v12yн2+V2)/vxкр12]}1/2}
= {(Мо1·V)/{1 – [(v11yк2+V2)/vxкр12]}1/2}+
{(Мо2·V)/{1 – [(v12yк2+V2)/vxкр12]}1/2}
(164)
{(Мо1·v11yн)/{1–[(v11yн2+V2)/vxкр12]}1/2}+{(Мо2·v12yн)/{1 – [(v12yн2+V2)/vxкр12]}1/2}
=
{(Мо1·v11yк)/{1–[(v11yк2+V2)/vxкр12]}1/2}+{(Мо2·v12yк)/{1–[(v12yк2+V2)/vxкр12]}1/2}(165)
{Мо1 /{1 –
[(v11yн2 + V2 )/ vxкр12]}1/2} + {Мо2
/{1 – [(v12yн2+ V2)/ vxкр12]}1/2} =
{Мо1 / {1 – [(v11yк2+V2)/ vxкр12]}1/2} + {Мо2
/{1 – [ (v12yк2+V2)/ vxкр12]}1/2} ( 166 )
Где, исходя из формул (60) и (142)÷(149):
v11xн
= (v21xн
+
V )
/ {1 + [(V · v21xн) / vxкр12)]}
( 167 )
v12xн
= (v22xн
+ V ) / {1 + [(V · v22xн) / vxкр12)]}
( 168 )
v11xк
= (v21xк
+ V ) / {1 + [(V · v21xк) / vxкр12)]}
( 169 )
v12xк
= (v22xк
+
V )
/ {1 + [(V · v22xк) / vxкр12)]}
( 170 )
v11yн
= v21yн · [1
– (V2 / vxкр12)]1/2
( 171 )
v12yн
= v22yн · [1
– (V2 / vxкр12)]1/2 ( 172 )
v11yк
= v21yк · [1
– (V2 / vxкр12)]1/2 (
173 )
v12yк
= v22yк · [1
– (V2 / vxкр12)]1/2 ( 174 )
Предположим,
что Мо1 = 1 , Мо2 = 0,5 , V / vxкр1 = 0,5 , v21xн
/ vxкр1
= = v21yн
/ vxкр1
= 0,9 ,
v22xн
/ vx кр1
= v22yн
/ vxкр1
= 0,6 .
Тогда
числовые расчеты дают следующие результаты для примера № 1:
1) тело 1 имело:
а) до столкновения
скорость v21xн
/ vxкр1 = 0,9 , массу М21н
= 2,294157338706, импульс Р21н / vxкр1 = 2,064741604835, кинетическую
энергию Ек21н /
vxкр12 = 1,294157338706;
б) после столкновения v21xк / vxкр1 = 0,7360143377, М21к
= 1,477179174242, Р21к / vxкр1 = 1,087225051595, Ек21к /
vxкр12 = 0,477179174242;
2) тело 2 имело:
а) до столкновения v22xн / vxкр1 = 0,6 , М22н =
0,625 , Р22н / vxкр1 = 0,375, Ек22н / vxкр12 = 0,125;
б) после столкновения v22xк / vxкр1 = 0,937959108239, М22к
= 1,441978164463, Р22к / vxкр1 = 1,35251655324, Ек22к /
vxкр12 = 0,941978164463;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М21н + М22н) = 2,919157338706 ,
импульс (Р21н + Р22н)
/ vxкр1 = 2,439741604835, кинетическую
энергию (Ек21н
+ Ек22н) /vxкр12 = 1,419157338706;
б) после столкновения
массу (М21к + М22к) = 2,919157338706 ,
импульс (Р21к + Р22к)
/ vxкр1 = 2,439741604835, кинетическую энергию (Ек21к
+ Ек22к) / vxкр12 = 1,419157338706;
II. В неподвижной системе отсчета O1x1y1z1 :
1) тело 1 имело:
а) до столкновения v11xн / vxкр1 = 0,965517241379 , массу М11н
= 3,841143835489, импульс Р11н / vxкр1 = 3,708690599782, кинетическую энергию
Ек11н / vxкр12 = 2,841143835489;
б) после столкновения v11xк / vxкр1 = 0,903514517939, М11к
= 2,333409263988, Р11к / vxкр1 = 2,108269146306, Ек11к /
vxкр12 = 1,333409263988;
2) тело 2 имело:
а) до столкновения v12xн / vxкр1 = 0,846153846154 , М12н
= 0,938194187433 , Р12н / vxкр1 = 0,793856620136, Ек12н / vxкр12 = 0,438194187433;
б) после столкновения v12xк / vxкр1= 0,978882996844, М12к
= 2,445928758933, Р12к / vxкр1 = 2,394278073612, Ек12к /
vxкр12 = 1,945928758933;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М11н + М12н) = 4,779338022922 ,
импульс (Р11н + Р12н)
/ vxкр1 = 4,502547219918, кинетическую энергию (Ек11н + Ек12н)
/ vxкр12= 3,279338022922 ;
б) после столкновения
массу (М11к + М12к) = 4,779338022922 ,
импульс (Р11к + Р12к)
/ vxкр1 = 4,502547219918, кинетическую энергию (Ек11к + Ек12к)
/ vxкр12 = 3,279338022922.
Для
примера № 2 числовые расчеты дают следующие результаты:
1) тело 1 имело:
а) до столкновения
скорость v21yн
/ vxкр1= 0,9 , массу М21н
= 2,294157338706, импульс Р21н / vxкр1 = 2,064741604835, кинетическую
энергию Ек21н /
vxкр12 = 1,294157338706;
б) после столкновения v21yк / vxкр1 = 0,7360143377, М21к
= 1,477179174242, Р21к / vxкр1 = 1,087225051595, Ек21к /
vxкр12
=
0,477179174242;
2) тело 2 имело:
а) до столкновения v22yн / vxкр1 = 0,6 , М22н =
0,625 , Р22н / vxкр1 = 0,375, Ек22н/ vxкр12 = 0,125;
б) после столкновения v22yк / vxкр1= 0,937959108239, М22к
= 1,441978164463, Р22к / vxкр1 = 1,35251655324, Ек22к /
vxкр12 = 0,941978164463;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М21н + М22н) = 2,919157338706 ,
импульс (Р21н + Р22н)
/ vxкр1 = 2,439741604835, кинетическую энергию (Ек21н + Ек22н)
/ vxкр12= 1,419157338706;
б) после столкновения
массу (М21к + М22к) = 2,919157338706 ,
импульс (Р21к + Р22к)
/ vxкр1 = 2,439741604835, кинетическую энергию (Ек21к + Ек22к)
/ vxкр12 = 1,419157338706;
II. В неподвижной системе отсчета O1x1y1z1 :
1) тело 1 имело:
а) до столкновения проекции
скорости v11xн / vxкр1 = 0,5 и v11yн / vxкр1= 0,779422863406 , массу М11н
= 2,64906471413 , проекции импульса Р11xн / vxкр1 = 1,324532357065 и Р11yн / vxкр1 = 2,064741604835, кинетическую
энергию Ек11н / vxкр12 = 1,64906471413;
б) после столкновения v11xк / vxкр1 = 0,5 , v11yк / vxкр1 = 0,637407113998 , М11к = 1,70569958778
, Р11xк / vxкр1 = 0,85284979389 , Р11yк / vxкр1 = 1,087225051595 , Ек11к /
vxкр12 = 0,70569958778;
2) тело 2 имело:
а) до столкновения v12xн / vxкр1 = 0,5 , v12yн / vxкр1 = 0,519615242271 , М12н =
0,721687836487 , Р12xн / vxкр1 = 0,360843918244 , Р12yн /vxкр1 = 0,375 , Ек12н / vxкр12 = 0,221687836487;
б) после столкновения v12xк / vxкр1= 0,5, v12yк / vxкр1= 0,812296415446, М12к =
1,665052962837, Р12xк /vxкр1 = 0,832526481418 , Р12yк /vxкр1 = 1,35251655324 , Ек12к/
vxкр12 = 1,165052962837;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М11н + М12н) = 3,370752550617 , проекции
импульса (Р11xн + Р12xн) / vxкр1 = 1,685376275309 и (Р11yн + Р12yн) / vxкр1 = 2,439741604835 , кинетическую энергию (Ек11н + Ек12н)
/ vxкр12 = 1,870752550617;
б) после столкновения
массу (М11к + М12к) = 3,370752550617 ,
проекции импульса (Р11xк + Р12xк) / vxкр1 = 1,685376275309 и (Р11yк + Р12yк) / vxкр1 = 2,439741604835 , кинетическую энергию (Ек11к + Ек12к)
/ vxкр12 = 1,870752550617.
По результатам расчета можно сделать следующий вывод: в
примерах № 1 и № 2 в подвижной O2x2y2z2 и неподвижной O1x1y1z1 системах отсчета до и после
столкновения масса, импульс и кинетическая энергия механической системы тел 1 и
2 остаются неизменными.
Следовательно, формулы (150)÷(153) в случае, когда
коэффициент перехода β > 1, удовлетворяют требованиям
системы уравнений (133)÷(141).
3.1.5. Зависимость массы движущегося
тела от скорости при коэффициенте
перехода 0 < β < 1
В случае, когда значение коэффициента
перехода β находится в диапазоне 0 < β < 1 , то, исходя из формул (150)÷(153) с учетом уравнения (61) зависимости
для функции f(V)<, массы М(V)<, импульса Р(V)<, кинетической энергии Ек(V)<
движущегося
тела со скоростью V, можно записать:
f (V)< = 1 / [1
+ (V2 / vxкр22)]1/2 ( 175
)
М(V)< =
Мо / [1 + (V2 / vxкр22)]1/2 ( 176 )
Р(V)< =
( Мо · V ) / [1 +
(V2 / vxкр22)]1/2 ( 177 )
Ек(V)< = Мо · vxкр22 · { 1 – {1 / [1
+ (V2 / vxкр22)]1/2}} ( 178 )
3.1.5.1. Проверка правильности выбора
формулы (150) при 0 < β < 1
(для примеров № 1 и № 2)
Сначала
перепишем формулы (133)÷(141) с учетом формул (61) и (175)÷(178):
{(Мо1 · v21xн) / [1 + (v21xн2 / vxкр22)]1/2} + {(Мо2 · v22xн) / [1 + (v22xн2 / vxкр22)]1/2} = {(Мо1 · v21xк)/[1 + (v21xк2/vxкр22)]1/2} + {(Мо2 · v22xк)/[1 + (v22xк2/vxкр22) ]1/2}
( 179 )
{Мо1 / [1
+ (v21xн2 / vxкр22)]1/2} + {Мо2 / [1
+ (v22xн2 / vxкр22)]1/2} = {Мо1 / [1 + (v21xк2 / vxкр22)]1/2} + {Мо2 / [1
+ (v22xк2 / vxкр22)]1/2} ( 180 )
{(Мо1 · v11xн) / [1 + (v11xн2 / vxкр22)]1/2} + {(Мо2 · v12xн) / [1 +
(v12xн2 / vxкр22)]1/2} = {(Мо1 · v11xк)/[1 + (v21xк2/vxкр22)]1/2} + {(Мо2 · v12xк)/[1 + (v12xк2/vxкр22)]1/2}
( 181 )
{Мо1 / [1 + (v11xн2 / vxкр22)]1/2} + {Мо2 / [1 + (v12xн2 / vxкр22)]1/2} = {Мо1 / [1 + (v21xк2 / vxкр22)]1/2} + {Мо2 / [1 + (v12xк2 / vxкр22)]1/2} ( 182 )
{(Мо1 · v21yн) / [1 + (v21yн2 / vxкр22)]1/2} + {(Мо2 · v22yн) / [1 + (v22yн2 / vxкр22)]1/2} = {(Мо1 · v21yк) / [1 + (v21yк2/vxкр22)]1/2} + {(Мо2 · v22yк) / [1 + (v22yк2/vxкр22)]1/2}
(183)
{Мо1 / [1
+ (v21yн2 / vxкр22)]1/2} + {Мо2 / [1
+ (v22yн2 / vxкр22)]1/2} =
{Мо1 / [1 + (v21yк2 / vxкр22)]1/2} + {Мо2 / [1
+ (v22yк2 / vxкр22)]1/2} ( 184 )
{(Мо1 · V)/{1 + [(v11yн2+V2)/vxкр22]}1/2}
+ {(Мо2 · V)/{1 + [(v12yн2+V2)/vxкр22]}1/2}
= {(Мо1·V)/{1 + [(v11yк2+V2)/vxкр22]}1/2}+
{(Мо2·V)/{1 + [(v12yк2+V2)/vxкр22]}1/2}
(185)
{(Мо1·v11yн)/{1+[(v11yн2+V2)/vxкр22]}1/2}+{(Мо2·v12yн)/{1+ [(v12yн2+V2)/vxкр22]}1/2}
=
{(Мо1·v11yк)/{1+[(v11yк2+V2)/vxкр22]}1/2}+{(Мо2·v12yк)/{1+[(v12yк2+V2)/vxкр22]}1/2}(186)
{Мо1 /{1 +
[(v11yн2 + V2 )/ vxкр22]}1/2} + {Мо2
/{1 + [(v12yн2+ V2)/ vxкр22]}1/2} =
{Мо1 / {1 + [(v11yк2+V2)/ vxкр22]}1/2} + {Мо2
/{1 + [ (v12yк2+V2)/ vxкр22]}1/2} ( 187 )
Где,
исходя из формул (61) и (142)÷(149):
v11xн
= (v21xн
+ V ) / {1 – [(V · v21xн) / vxкр22)]}
( 188 )
v12xн
= (v22xн
+ V ) / {1 – [(V · v22xн) / vxкр22)]}
( 189 )
v11xк
= (v21xк
+ V ) / {1 – [(V · v21xк) / vxкр22)]}
( 190 )
v12xк
= (v22xк
+ V ) / {1 – [(V · v22xк) / vxкр22)]}
( 191 )
v11yн
= v21yн · [1
+ (V2 / vxкр22)]1/2 ( 192 )
v12yн
= v22yн · [1
+ (V2 / vxкр22)]1/2 (
193 )
v11yк
= v21yк · [1
+ (V2 / vxкр22)]1/2 (
194 )
v12yк
= v22yк · [1
+ (V2 / vxкр22)]1/2 (
195 )
Предположим,
что Мо1 = 1 , Мо2 = 0,5 , V / vxкр2 = 0,5 , v21xн / vxкр2
= = v21yн / vxкр2
= 0,9 ,
v22xн / vxкр2
= v22yн
/ vxкр2
= 0,6 .
Тогда
числовые расчеты дают следующие результаты для примера № 1:
1) тело 1 имело:
а) до столкновения
скорость v21xн / vxкр2= 0,9 , массу М21н
= 0,743294146247 , импульс Р21н /
vxкр2 = 0,668964731622 , кинетическую
энергию Ек21н /
vxкр22 = 0,256705853753;
б) после столкновения v21xк / vxкр2 = 0,691099932748, М21к
= 0,822656908881, Р21к / vxкр2 = 0,568538134403, Ек21к /
vxкр22 = 0,177343091119;
2) тело 2 имело:
а) до столкновения v22xн / vxкр2 = 0,6 , М22н =
0,428746462856 , Р22н
/ vxкр2 = 0,257247877714, Ек22н / vxкр22 = 0,071253537144;
б) после столкновения v22xк / vxкр2= 1,023729712365, М22к
= 0,349383700222 , Р22к / vxкр2 = 0,357674474934 , Ек22к /
vxкр22 = 0,150616299778;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М21н + М22н) = 1,172040609103 ,
импульс (Р21н + Р22н)
/ vxкр2 = 0,926212609336 , кинетическую энергию (Ек21н + Ек22н)
/ vxкр22 = 0,327959390897;
б) после столкновения
массу (М21к + М22к) = 1,172040609103 ,
импульс (Р21к + Р22к)
/ vxкр2 = 0,926212609336 , кинетическую энергию (Ек21к + Ек22к)
/ vxкр22 = 0,327959390897;
II. В неподвижной системе отсчета O1x1y1z1 :
1) тело 1 имело:
а) до столкновения скорость
v11xн / vxкр2= 2,545454545455 , массу М11н
= 0,365652372423 , импульс Р11н / vxкр2 = 0,93075149344 , кинетическую
энергию Ек11н / vxкр22 = 0,634347627577;
б) после столкновения v11xк / vxкр2 = 1,820001331727 , М11к
=0,481548724902, Р11к /vxкр2 = 0,876419320614 , Ек11к /
vxкр22 = 0,518451275098;
2) тело 2 имело:
а) до столкновения v12xн / vxкр2 = 1,571428571429 , М12н
= 0,268437746097 , Р12н / vxкр2 = 0,421830743866 , Ек12н / vxкр22 = 0,231562253903;
б) после столкновения v12xк / vxкр2= 3,121532492927 , М12к
= 0,152541393617, Р12к / vxкр2 = 0,476162916693 , Ек12к /
vxкр22 = 0,347458606383;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М11н + М12н) = 0,63409011852 ,
импульс (Р11н +
Р12н) / vxкр2 = 1,352582237306 , кинетическую энергию (Ек11н + Ек12н)
/ vxкр22 = 0,86590988148;
б) после столкновения
массу (М11к + М12к) = 0,63409011852 ,
импульс (Р11к + Р12к)
/ vxкр2 = 1,352582237306 , кинетическую энергию (Ек11к + Ек12к) / vxкр22 = 0,86590988148.
Для
примера № 2 числовые расчеты дают следующие результаты:
1) тело 1 имело:
а) до столкновения
скорость v21yн / vxкр2 = 0,9 , массу М21н
= 0,743294146247, импульс Р21н / vxкр2 = 0,668964731622 , кинетическую
энергию Ек21н /
vxкр22 = 0,256705853753;
б) после столкновения v21yк / vxкр2 = 0,691099932748, М21к
= 0,822656908881, Р21к / vxкр2 = 0,568538134403, Ек21к /
vxкр22 = 0,177343091119;
2) тело 2 имело:
а) до столкновения v22yн / vxкр2 = 0,6 , М22н =
0,428746462856 , Р22н
/ vxкр2 = 0,257247877714, Ек22н / vxкр22 = 0,071253537144;
б) после столкновения v22yк / vxкр2= 1,023729712365, М22к
= 0,349383700222 , Р22к / vxкр2 = 0,357674474934 , Ек22к /
vxкр22 = 0,150616299778 ;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М21н + М22н) = 1,172040609103 ,
импульс (Р21н + Р22н)
/ vxкр2 = 0,926212609336 , кинетическую энергию (Ек21н + Ек22н) / vxкр22 = 0,327959390897;
б) после столкновения
массу (М21к + М22к) = 1,172040609103,
импульс (Р21к+ Р22к) / vxкр2 = 0,926212609336 , кинетическую энергию (Ек21к + Ек22к)
/ vxкр22 = 0,327959390897;
II. В неподвижной системе отсчета O1x1y1z1 :
1) тело 1 имело:
а) до столкновения проекции
скорости v11xн / vxкр2 = 0,5 и v11yн / vxкр2 = 1,006230589875 , массу М11н
= 0,664822495315 , проекции импульса Р11xн / vxкр2 = 0,332411247657 и Р11yн / vxкр2 = 0,668964731622, кинетическую
энергию Ек11н / vxкр22 = 0,335177504685;
б) после столкновения проекции
скорости v11xк / vx кр2 = 0,5 и v11yк / vx кр2 = 0,772673214435 , М11к = 0,735806708167
, Р11xк / vxкр2 = 0,367903354084 , Р11yк / vxкр2 = 0,568538134403 , Ек11к /
vxкр22 = 0,264193291833;
2) тело 2 имело:
а) до столкновения v12xн / vxкр2 = 0,5 , v12yн / vxкр2 = 0,67082039325 , М12н =
0,383482494424 , Р12xн / vxкр2 = 0,191741247212 , Р12yн / vxкр2 = 0,257247877714 , Ек12н / vxкр22 = 0,116517505576;
б) после столкновения v12xк / vxкр2= 0,5, v12yк / vxкр2= 1,144564613718, М12к =
0,312498281571 , Р12xк / vxкр2 = 0,156249140785 , Р12yк / vxкр2 = 0,357674474934 , Ек12к /
vxкр22 = 0,187501718429;
3) система тел 1 и 2 имела:
а) до столкновения массу
(М11н + М12н) = 1,048304989738 , проекции
импульса (Р11xн + Р12xн) / vxкр2 = 0,524152494869 и (Р11yн + Р12yн) / vxкр2 = 0,926212609336 , кинетическую энергию (Ек11н + Ек12н)
/ vxкр22 = 0,451695010262;
б) после столкновения
массу (М11к + М12к) = 1,048304989738 , проекции импульса (Р11xк + Р12xк) / vxкр2 = 0,524152494869 и (Р11yк + Р12yк) / vxкр2 = 0,926212609336 , кинетическую энергию (Ек11к + Ек12к)
/ vxкр22 = 0,451695010262.
По результатам расчета можно сделать следующий вывод: в
примерах № 1 и № 2 в системах отсчета подвижной O2x2y2z2 и неподвижной O1x1y1z1 до и после столкновения масса,
импульс и кинетическая энергия механической системы тел 1 и 2 остаются
неизменными.
Следовательно, формулы (175)÷(178) в случае, когда
коэффициент перехода 0 < β < 1 , удовлетворяют требованиям
системы уравнений (133)÷(141).
3.1.6. Сравнение формул (155)÷(157)
с формулами (176)÷(178).
О
зависимостях (155)÷(157):
М(V)> =
Мо / [1 – (V2 / vxкр12)]1/2 ( 155 )
Р(V)> =
( Мо · V ) / [1 –
(V2 / vxкр12)]1/2 ( 156 )
Ек(V)> = Мо · vxкр12 ·
{{1 / [1 – (V2 / vxкр12)]1/2}
– 1} ( 157
)
для
массы М(V)> ,
импульса Р(V)> и кинетической энергии Ек(V)> движущегося тела со скоростью V в случае, когда коэффициент
перехода β > 1, можно сказать следующее:
- при
значениях скорости V, несоизмеримо малых по сравнению со скоростью vxкр1 :
М(V)> =
Мо , Р(V)> = Мо · V ,
Ек(V)> = (Мо
· V2)
/2 ;
- при
V = vxкр1
: М(V)> = ∞ , Р(V)> =
∞ , Ек(V)> =
∞ ;
- при
V < vxкр1 : М(V)> , Р(V)> и Ек(V)> - имеют
действительные значения;
- при
V > vxкр1 :
М(V)> , Р(V)> и Ек(V)> - действительных значений не имеют.
Аналогично
о зависимостях (176)÷(178):
М(V)< =
Мо / [1 + (V2 / vxкр22)]1/2 ( 176 )
Р(V)< =
( Мо · V ) / [1 +
(V2 / vxкр22)]1/2 ( 177 )
Ек(V)< = Мо · vxкр22 · { 1 – {1 / [1
+ (V2 / vxкр22)]1/2}} ( 178 )
для
массы М(V)<, импульса Р(V)< и кинетической энергии Ек(V)< движущегося тела со скоростью V в случае, когда коэффициент
перехода 0 < β < 1 , можно сказать следующее:
- при
значениях скорости V, несоизмеримо малых по сравнению со скоростью vxкр2 :
М(V)< =
Мо , Р(V)< =
Мо · V,
Ек(V)< = (Мо
· V2)
/2;
- при
V = vxкр2
: М(V)< =
Мо · (2)-1/2 , Р(V)< =
Мо· vxкр2 · (2)-1/2 и Ек(V)< = Мо·
vxкр22 · [1 – (2)-1/2] ;
- при
V < vxкр2 : М(V) Ек(V)< ,
Р(V)<
и Ек(V)< - принимают действительные
значения;
- при
V > vxкр2 :
М(V)< , Р(V)< и
Ек(V)< - принимают действительные значения;
- при
V = ∞
: М(V)< стремится к нулю, Р(V)< =
Мо · vxкр2
, Ек(V)< = Мо· vxкр22 .
Как
видно из сравнения, оба диапазона возможного значения коэффициента перехода β > 1 и
0 < β < 1 являются
равноценными (оба удовлетворяют граничному условию).
3.2. Определение
значения коэффициента перехода β
С помощью полученных зависимостей (155) и (176) массы
тела от скорости V постараемся установить, в каком именно диапазоне в
действительности находятся значения коэффициента перехода β
-
в β > 1 или в 0 < β < 1 , т.к. эти диапазоны являются взаимоисключающими
в связи с однозначностью зависимости коэффициента перехода β
от величины скорости V.
Попробуем решить эту задачу, рассматривая закон
сохранения импульса (закон сохранения механической энергии) в случае, если все
или часть тел (материальных точек), составляющих замкнутую механическую
систему, движутся нелинейно.
С этой целью обратимся к простейшему примеру.
3.2.1. Пример №
3
Допустим,
что имеются две инерциальные системы отсчета, аналогичные системам отсчета,
изображенным на рис. 1 - неподвижная O1x1y1z1 и подвижная O2x2y2z2, которая движется со скоростью V параллельно оси O1x1 относительно системы O1x1y1z1.
Предположим,
что имеется замкнутая механическая система тел, показанная на рис. 5 и
состоящая из точечных тел 1 и 2, имеющих равные массы Мо в
состоянии покоя, и нити 3.
Тела
1 и 2 соединены абсолютно жесткой (недеформируемой) нитью 3, не имеющей массы.
ω ω 3 1 2 R О Рис.
5
![]()
![]()
![]()

R
![]()
![]()
![]()

Тела
1 и 2 вращаются с угловой скоростью ω вокруг общего центра масс - точки
О. Расстояние от точечного тела 1 (тела 2) до точки О равно R.
Поместим
рассматриваемую замкнутую механическую систему тел 1 и 2 с нитью 3 в подвижную
систему отсчета O2x2y2z2 таким образом, чтобы точка О
была бы неподвижна в этой системе отсчета и совпадала с началом координат O2, а вращение тел 1 и 2 вокруг нее
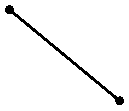
происходило бы по часовой стрелке в плоскости O2x2y2, как показано на рис. 6.
Рис.
6 ωּt22 υ22x υ22y ωּt21 υ22 y2 x2 2 О≡О2 υ21 υ21x 1 υ21y
![]()

![]()

![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()

Также
допустим, что в момент начала отсчета времени (t2=0) в системе отсчета O2x2y2z2
тела 1 и 2 находились на оси O2x2 , причем, тело 1 имело положительную
координату, а тело 2 – отрицательную.
Опираясь
на вышесказанное, можно отметить, что в подвижной системе отсчета O2x2y2z2 в любой момент времени t2 тела 1 и 2 будут иметь скорости υ21
и υ22,соответственно равные:
υ21 = υ22
= υ = ω · R ( 196
)
При
этом проекции υ21x и υ21y скорости тела 1 и проекции υ22x и υ22y скорости тела 2 на оси O2x2 и O2y2, соответственно для моментов времени
t21 и t22, будут равны:
υ21x
= – [υ · Sin (ω · t21)] ( 197 )
υ21y
= – [υ · Cos (ω · t21)] ( 198 )
υ22x
= υ · Sin (ω · t22) ( 199 )
υ22y
= υ · Cos (ω · t22) ( 200 )
Связь
между координатами x21 и y21 тела 1 в зависимости от времени t21 и связь между координатами x22 и y22 тела 2 в зависимости от времени t22 в подвижной системе отсчета O2x2y2z2 можно записать в виде:
x21 = R · Cos
(ω · t21) ( 201 )
y21 = – [R · Sin (ω
· t21)] ( 202 )
x22 = – [R · Cos (ω
· t22)] ( 203 )
y22 = R
· Sin (ω · t21) ( 204
)
Опираясь
на уравнения (34) и (36), можно написать связь между координатами x11 и y11 тела 1 в момент времени t11 в неподвижной системе отсчета O1x1y1z1 и координатами x21 и y21 тела 1 в момент времени t21 в подвижной системе отсчета O2x2y2z2 :
x11 =
β · [ x21
+ (V · t21)] ( 205 )
y11 =
y21 ( 206 )
Аналогично,
используя уравнения (34) и (36), можно записать связь между координатами x12 и y12 тела 2 в момент времени t12 в неподвижной системе отсчета O1x1y1z1 и координатами x22 и y22 тела 2 в момент времени t22 в подвижной системе отсчета O2x2y2z2 :
x12 =
β · [ x22
+ (V · t22)] ( 207 )
y12 =
y22
( 208 )
С
помощью формулы (38) можно написать связь между значениями времен t11 , t21 и t12 , t22 :
t11 =
{[(β2 –
1) · x21] / (β
· V)} + (β · t21) ( 209 )
t12 =
{[(β2 –
1) · x22] / (β
· V)} + (β · t22) ( 210 )
В
рассматриваемом примере нас будет интересовать положение тел 1 и 2 в
неподвижной системе отсчета O1x1y1z1 в один и тот же момент времени, т.е.
когда:
t11
= t12 ( 211
)
Тогда
уравнение (211) с учетом формул (201), (203), (205), (207), (209) и (210)
примет вид:
{[(β2–1)·R·Cos(ω·t21)]/(β·V)}+(β·t21)={[(1–β2)·R·Cos(ω·t22)]/(β·V)}+(β·t22) (212)
В
подвижной системе отсчета O2x2y2z2 при выполнении условия (211)
представляет интерес положение тел 1 и 2, когда:
t21 =
t22 =
t2р (
213 )
Подставив
условие (213) в уравнение (212) для случая, когда (ω · t2р) < π , получим:
(ω
· t2р)
= π / 2 ( 214 )
Т.е.
для выполнения условий (211) и (213) тела 1 и 2 в рассматриваемые моменты
времени должны находиться на линии, параллельной оси O2y2 (O1y1).
Также
в подвижной системе отсчета O2x2y2z2 при выполнении условия (211)
представляет интерес положение тел 1 и 2, когда:
t21 =
0 (
215 )
Значение
времени t22 при выполнении условий (211) и (215) обозначим t22т , для которого уравнение (212)
примет вид:
t22т = [1 – ( 1/ β2)] · [1 +
или:
ω · t22т
= [1 – ( 1/ β2)] · [1 + Cos (ω · t22т)] · (υ / V) ( 217 )
Как
видно из уравнения (217), значение времени t22т в зависимости от значения
коэффициента перехода β может быть:
-
t22т > 0 при β > 1 ;
( 218 )
-
t22т < 0 при 0 < β < 1 ; ( 219
)
-
t22т = 0 при β = 1 . ( 220 )
Теперь
можем приступить к проверке выполнения закона сохранения импульса (закона
сохранения кинетической энергии).
Рассмотрим
два момента времени в неподвижной системе отсчета O1x1y1z1 .
3.2.1.1. Момент времени
t1р
Согласно
условиям (211) и (213) для тел 1 и 2, моменту времени t1р в неподвижной системе отсчета O1x1y1z1 будет соответствовать момент времени
t2р в подвижной системе отсчета O2x2y2z2 .
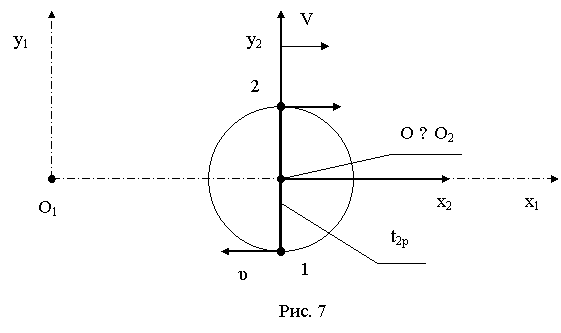
Как
показано на рис. 7, согласно уравнениям (214), (197)÷(200) в подвижной
системе отсчета O2x2y2z2 в момент времени t2р тела 1 и 2 соответственно имеют
следующие значения проекций υ21xр , υ21yр
и υ22xр , υ22yр скоростей своего движения на оси O2x2 и O2y2:
υ21xр
= – υ
( 221 )
υ21yр
= 0
( 222 )
υ22xр
= υ
( 223 )
υ22yр
= 0 ( 224
)
Тогда,
исходя из формул (40), (42) и равенств (221)÷(224), в неподвижной
системе отсчета O1x1y1z1 в момент времени t1р тело 1 и тело 2 соответственно будут
иметь следующие значения проекций υ11xр , υ11yр
и υ12xр , υ12yр скоростей своего движения на оси O1x1 и O1y1:
υ11xр = (V – υ) / {1
– {[(β2 –
1) · υ] / (β2
· V)}} ( 225 )
υ11yр = 0
( 226 )
υ12xр = (V +
υ) / {{[(β2
– 1) · υ] / (β2
· V)} + 1} ( 227 )
υ12yр
= 0
( 228 )
υ
3.2.1.2. Момент времени
t1т
Согласно
условиям (211) и (215) моменту времени t1т в неподвижной системе отсчета O1x1y1z1 будет соответствовать момент времени
t21 = 0
для тела 1 и момент времени t22т
для
тела 2 в подвижной системе отсчета O2x2y2z2.
Как
показано на рис. 8, в подвижной системе отсчета O2x2y2z2 в момент времени t21 = 0 тело 1 и в момент времени t22т тело 2 соответственно имеют следующие значения
проекций υ21xт , υ21yт
и υ22xт , υ22yт скоростей своего движения на оси O2x2 и O2y2, причем:
υ21xт
= 0
( 229 )
υ21yт
= – υ
( 230
)
Тогда,
исходя из формул (40), (42) и равенств (229), (230) в неподвижной системе
отсчета O1x1y1z1 в момент времени t1т тело 1 и тело 2 соответственно будут
иметь значения проекций υ11xт , υ11yт
и υ12xт , υ12yт скоростей своего движения на оси O1x1 и O1y1, причем
:
υ11xт = V
( 231 )
υ11yт = – (
υ /
β )
( 232 )
υ12xт = (V +
υ22xт) / {{[(β2
– 1) · υ22xт] / (β2
· V)} + 1} ( 233 )
υ12yт =
υ22yт / {{[(β2
– 1) · υ22xт] / (β
· V)} + β} ( 234 )
Рис.
8

Учитывая
условие (218), что при коэффициенте перехода β > 1 время t22т > 0, можно отметить, что при коэффициенте
перехода β > 1 проекция
скорости υ22yт будет направлена по направлению оси O2y2.
Также,
исходя из условия (219), утверждающего, что при коэффициенте перехода 0 <
β < 1 время t22т < 0, можно отметить, что при коэффициенте
перехода 0 < β < 1 проекция
скорости υ22yт будет иметь направление,
противоположное направлению оси O2y2.
Из
уравнений (199) и (200) можно получить:
υ22xт2
+ υ22yт2
= υ2
(
235 )
3.2.1.3.
Уравнения закона сохранения импульса и закона сохранения механической энергии
для примера № 3
В
неподвижной системе отсчета O1x1y1z1 в момент времени t1р тело 1 и тело 2 соответственно будут
иметь следующие значения кинетических энергий Ек11р и Ек12р и проекций Р11xр , Р11yр
и Р12xр , Р12yр импульсов на оси O1x1 и O1y1 :
Р11xр =
[Мо · f (V = υ11xр) · υ11xр] (
236 )
Р12xр =
[Мо · f (V = υ12xр) · υ12xр]
( 237 )
Р11ур
= 0
( 238 )
Р12ур
= 0
(
239 )
υ11xр
Ек11р = { Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} ( 240 )
0
υ12xр
Ек12р = { Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} ( 241 )
0
В
неподвижной системе отсчета O1x1y1z1 в момент времени t1т тело 1 и тело 2 соответственно будут
иметь следующие значения кинетических энергий Ек11т и Ек12т и проекций Р11xт , Р11yт
и Р12xт , Р12yт импульсов на оси O1x1 и O1y1:
Р11xт =
{Мо · f [V = (υ11xт2+υ11yт2)1/2] · υ11xт} (
242 )
Р12xт =
{Мо · f [V = (υ12xт2+υ12yт2)1/2] · υ12xт} (
243 )
Р11ут = {Мо · f [V=(υ11xт2+υ11yт2)1/2] ·υ11yт} ( 244
)
Р12ут
= {Мо ·
f [V=(υ12xт2+υ12yт2)1/2] · υ12yт} (
245 )
(υ11xт2+υ11yт2)1/2
Ек11т = { Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} ( 246 )
0
(υ12xт2+υ12yт2)1/2
Ек12т = { Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} ( 247 )
0
В
связи с тем, что механическая система тел 1 и 2 (и нити 3) является замкнутой,
закон сохранения импульса позволяет записать для моментов времени t1р и t1т следующие уравнения:
Р11xр + Р12xр =
Р11xт
+ Р12xт или
[Мо · f (V = υ11xр) · υ11xр] + [Мо · f (V = υ12xр) · υ12xр] = {Мо ·
f [V = (υ11xт2+υ11yт2)1/2] · υ11xт} + {Мо · f [V = (υ12xт2+υ12yт2)1/2] · υ12xт} (248)
Р11ур + Р12ур
= Р11ут + Р12ут
или
0 ={Мо · f [V=(υ11xт2+υ11yт2)1/2] ·υ11yт} + {Мо · f [V=(υ12xт2+υ12yт2)1/2] · υ12yт} (249)
Также
в связи с тем, что механическая система тел 1 и 2 (и нити 3) является замкнутой
и потенциальные энергии тел 1 и 2 не изменяются и являются постоянными
величинами, закон сохранения механической энергии позволяет записать для
моментов времени t1р и t1т следующее уравнение:
Ек11р + Ек12р = Ек11т + Ек12т или
υ11xр υ12xр
{ Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} + {
Мо · ∫ {[f (V) ·V] + [f′ (V) ·V2]}·dV} =
0
0
(υ11xт2+υ11yт2)1/2 (υ12xт2+υ12yт2)1/2
{ Мо
· ∫ {[f (V) ·V]+[f′ (V) ·V2]}·dV} +
{ Мо · ∫ {[f (V) ·V]+[f′ (V) ·V2]}·dV} (250)
0
0
3.2.1.4. Определение условий
выполнения закона сохранения импульса для примера № 3 при коэффициенте перехода
β ≥ 1
В
случае, если коэффициент перехода β ≥ 1 , то значения коэффициента перехода β и функции f (V) определяются:
β> 2 = 1 / [1 –
(V2 / vxкр12)] ( 64 )
f (V)> = 1 / [1
– (V2 / vxкр12)]1/2 ( 154 )
Тогда
с учетом формулы (154) уравнения (245) и (246) примут вид:
{(Мо·υ11xр)/[1–(υ11xр2/vxкр12)]1/2} + {(Мо·υ12xр)/[1–(υ12xр2/vxкр12)]1/2]} = {(Мо·υ11xт) / {1–[(υ11xт2+υ11yт2)/vxкр12]}1/2} + {(Мо
· υ12xт)/{1 – [ (υ12xт2+υ12yт2)/vxкр12]}1/2} (251)
0 = {(Мо
· υ11yт) / {1 – [(υ11xт2 + υ11yт2) / vxкр12]}1/2} + {(Мо
· υ12yт) / {1 – [(υ12xт2 + υ12yт2) / vxкр12 ]}1/2} (
252 )
Формулы
(225)÷(228) и (231)÷(234) с учетом формулы (64) можно записать:
υ11xр = (V – υ) / {1 – [(V · υ )/vxкр12]} ( 253 )
υ12xр = (V
+ υ) / {1 + [(V · υ )/ vxкр12]} ( 254 )
υ11xт = V
( 231 )
υ11yт = –
{υ · [1 – (V2/ vxкр12)]1/2} ( 255 )
υ12xт = (V +
υ22xт) / {1 + [(V · υ22xт)/ vxкр12]}
( 256 )
υ12yт =
{υ22yт · [1 – (V2/ vxкр12)]1/2} / {1 + [(V · υ22xт) / vxкр12]} ( 257
)
Вставив
проекции скоростей υ11xр , υ12xр , υ11xт , υ11yт , υ12xт и
υ12yт
из формул (231), (253)÷(257) в уравнения (251) и (252) и
используя формулу (235), получим:
{[Мо · (V – υ)] / {[1 – (υ2/vxкр12)]1/2 · [1 – (V2/vxкр12)]1/2}} + {[Мо
· (V +
υ) )] / {[1 – (υ2/vxкр12)]1/2 · [1 – (V2/vxкр12)]1/2}} = {(Мо
· V) / {[1 – (υ2/vxкр12)]1/2 · [1 – (V2/vxкр12)]1/2}} +{[Мо
· (V +
υ22xт)]/{[1 – (υ2/vxкр12)]1/2· [1 – (V2/vxкр12)]1/2}} (258)
0 = – {(Мо ·
υ) / [1 – (υ2/vxкр12)]1/2} + {(Мо · υ22yт) / [1 – (υ2/vxкр12)]1/2}
( 259 )
или:
V –
υ + V + υ = V
+ V + υ22xт
0 =
– υ
+ υ22ут
Из уравнений (258) и (259) получаем необходимые условия
(значения проекций скоростей υ22xт и υ22yт), при которых в примере № 3 при
коэффициенте перехода β ≥ 1 будет выполняться закон сохранения
импульса в неподвижной инерциальной системе отсчета O1x1y1z1:
υ22xт = 0
( 260 )
υ22yт =
υ
( 261 )
Из
равенств (260) и (261) следует, что величины проекций скоростей υ22xт и υ22yт не зависят от величины скорости V (и, следовательно, не зависят от
величины коэффициента перехода β).
Подставив
условия (260) и (261) в уравнения (199) и (200), получим:
t22т = t21т = 0
( 262 )
А
подставив уравнение (262) в формулу (217):
ω
· 0 = [1 – ( 1/ β2)] · ( 1 + 1 )
· (υ / V) ( 263 )
будем иметь еще одно
условие выполнения закона сохранения импульса в неподвижной инерциальной
системе отсчета O1x1y1z1 для примера № 3:
β = 1
( 264 )
Таким
образом, можно сделать вывод, что в замкнутой механической системе тел,
рассматриваемой в примере № 3, для значений коэффициента перехода β>1 закон сохранения импульса не
выполняется.
3.2.1.5. Определение условий
выполнения закона сохранения механической энергии для примера № 3 при
коэффициенте
перехода β ≥ 1
В
дополнение к условиям выполнения закона сохранения импульса постараемся
определить условия выполнения закона сохранения механической энергии.
С
учетом формулы (154) уравнение (250) примет вид:
[(Мо·vxкр12)·{{1/[1–(υ11xр2/vxкр12)]1/2}–1}] + [(Мо·vxкр12)·{{1/[1–(υ12xр2/vxкр12)]1/2}
–1}] = [(Мо·vxкр12)·{{1/[1–((υ11xт2+υ11yт2)/vxкр12)]1/2}–1}] + [(Мо·vxкр12)·{{1/[1–((υ12xт2+υ12yт2)/vxкр12)]1/2}–1}] (265)
Вставив
проекции скоростей υ11xр , υ12xр , υ11xт , υ11yт , υ12xт и
υ12yт
из формул (231), (252)÷(256) в уравнение (265), с учетом формулы
(235) получим:
{ [1 – (υ · V)/vxкр12)] · vxкр1 / {[1 – ( V2/vxкр12)] · [( vxкр12 – υ2)]}1/2}
+ { [1+
(υ · V)/vxкр12)]
· vxкр1 / {[1 – ( V2/vxкр12)] · [( vxкр12 – υ2)]}1/2} = { vxкр1 / {[1 – (V2/vxкр12)] · [( vxкр12 – υ2)]}1/2} +
{ [1 + (υ22xт · V)/vxкр12)]
· vxкр1 / {[1 – (V2/vxкр12)] · [[ (vxкр12 – υ2)]}1/2} (266)
Или:
1 – [(υ · V)/vxкр12 ] + 1+ [(υ · V)/vxкр12] = 1
+ 1 + [(υ22xт · V)/vxкр12]
Из
уравнения (266) получаем необходимое условие (значение проекции скорости υ22xт), при котором в примере № 3 при
коэффициенте перехода β ≥ 1 в неподвижной инерциальной системе
отсчета O1x1y1z1 будет выполняться закон сохранения механической
энергии, предполагая, что потенциальная энергия системы тел 1 и 2 не меняется:
υ22xт = 0
( 260 )
Тогда,
исходя из формулы (232), получим:
υ22yт =
υ
( 261 )
Это позволяет сделать вывод: условием для выполнения
закона сохранения механической энергии (как и условием для выполнения закона
сохранения импульса) в неподвижной инерциальной системе отсчета O1x1y1z1 для примера № 3 является:
β = 1
( 264 )
Таким
образом, получается, что в замкнутой механической системе тел, рассматриваемой
в примере № 3, для значений коэффициента перехода β>1 закон сохранения механической энергии
не выполняется.
Аналогично
может быть доказано, что в замкнутой механической системе тел, рассматриваемой
в примере № 3, для значений коэффициента перехода β>1 закон сохранения момента импульса не
будет выполняться.
Подтвердим вышесказанное числовыми расчетами.
3.2.1.6. Цифровой расчет для примера
№ 3 при коэффициенте перехода β > 1
Предположим,
что:
V / vxкр1 = 0,9, υ / vxкр1 = 0,6 .
Уравнение
(217) с учетом формулы (64) можно записать в виде:
ω · t22т
= [(υ · V)/ vxкр12] · [1 + Cos (ω · t22т)] ( 267 )
Тогда
получим:
ω
· t22т = 0,8828669738, проекции υ22xт / vxкр1 = 0,4635374427 и υ22yт / vxкр1 =
0,3809633042 скорости движения тела 2 в подвижной системе отсчета O2x2y2z2 .
В
неподвижной инерциальной системе отсчета O1x1y1z1:
а) в
момент времени t1р тела 1 и 2, соответственно, имели проекции К11xр / (Мо·vxкр1) =
0,860309002 и К12xр / (Мо·vxкр1) = 4,30154501
импульса на ось O1x1 , кинетические энергии Ек11р / (Мо·vxкр12) = 0,31914047 и Ек12р / (Мо·vxкр12) = 3,416252877;
б) в
момент времени t1т тело 1 имело проекции К11xт / (Мо·vxкр1) =
2,580927006 и К11yт /(Мо·vxкр1) = – 0,75
импульса на оси O1x1 и O1y1, соответственно, кинетическую
энергию Ек11т / (Мо·vxкр12) = 1,092373316;
в) в
момент времени t1т тело 2 имело проекции К12xт / (Мо·vxкр1) =
3,9102117884 и К12yт / (Мо·vxкр1) =
0,4762041303 импульса на оси O1x1 и O1y1, кинетическую энергию Ек12т / (Мо·vxкр12) = 3,064052977;
г) в
момент времени t1р система тел 1 и 2 имела проекции К11xΣр / (Мо·vxкр1) =
5,161854012 и К12yΣр / (Мо·vxкр1) = 0 импульса на оси O1x1 и O1y1, кинетическую энергию Екр / (Мо·vxкр12) = 3,735393347;
д) в
момент времени t1т система тел 1 и 2 имела проекции К11xΣт / (Мо·vxкр1) = 6,491138794 и К12yΣт /(Мо·vxкр1) = – 0,2737958696 импульса на оси O1x1 и O1y1, кинетическую энергию Ект / (Мо·vxкр12) = 4,931749651.
Закон
сохранения импульса не выполняется, т.к.: 5,161854012 #
6,491138794 и –
0,2737958696 # 0 .
Закон
сохранения кинетической энергии не выполняется, т.к.: 3,735393347 #
4,931749651.
3.2.1.7. Определение условий
выполнения закона сохранения импульса для примера № 3 при коэффициенте перехода
0 < β ≤ 1
В
случае, если коэффициент перехода 0 < β ≤ 1, то значения коэффициента перехода β и функции f (V) определяются:
β< 2 =
1 / [1 + (V2 / vxкр22)] ( 65 )
f (V)< = 1 / [1
+ (V2 / vxкр22)]1/2 ( 175 )
Тогда, с учетом формулы (175) уравнения (248)
и (249) примут вид:
{(Мо·υ11xр)/ [1+(υ11xр2/vxкр22)]1/2} + {(Мо·υ12xр)/[1+(υ12xр2/vxкр22) ]1/2}= {(Мо·υ11xт) / {1+[(υ11xт2+υ11yт2)/vxкр22]}1/2} + {(Мо
υ12xт)/{1+[ (υ12xт2+υ12yт2)/vxкр22]}1/2} (268)
0 = {(Мо
· υ11yт) / {1 + [(υ11xт2 + υ11yт2) / vxкр22]}1/2} + {(Мо
· υ12yт) / {1 + [(υ12xт2 + υ12yт2) / vxкр22 ]}1/2} (269)
Формулы
(225)÷(228) и (231)÷(234) с учетом формулы (65) можно записать:
υ11xр = (V – υ) / {1 + [(V · υ )/vxкр22]} ( 270 )
υ12xр = (V
+ υ) / {1 – [(V · υ )/ vxкр22]} ( 271 )
υ11xт = V
( 231 )
υ11yт = –
{υ · [1 + (V2/ vxкр22)] 1/2} ( 272 )
υ12xт = (V +
υ22xт) / {1 – [(V · υ22xт)/ vxкр22]}
( 273 )
υ12yт =
{υ22yт · [1 + (V2/ vxкр22)]1/2} / {1 – [(V · υ22xт) / vxкр22]} ( 274 )
Вставив проекции скоростей υ11xр , υ12xр , υ11xт , υ11yт , υ12xт и
υ12yт
из формул (231), (270)÷(274) в уравнения (268) и (269) и
используя формулу (235), получим:
{[Мо · (V – υ)] / {[1 + (υ2/vxкр22)]1/2 · [1 + (V2/vxкр22)]1/2}} + {[Мо
· (V +
υ) )] / {[1 + (υ2/vxкр22)]1/2 · [1 + (V2/vxкр22)]1/2}} = {(Мо
· V) / {[1 + (υ2/vxкр22)]1/2 · [1 + (V2/vxкр22)]1/2}} +{[Мо
· (V +
υ22xт)]/{[1 + (υ2/vxкр22)]1/2· [1 + (V2/vxкр22)]1/2}} (275)
0 = – {(Мо · υ) / [1 + (υ2/vxкр22)]1/2} + {(Мо · υ22yт) / [1 + (υ2/vxкр22)]1/2}
( 276 )
или:
V –
υ + V + υ = V
+ V + υ22xт
0 =
– υ
+ υ22ут
Из
уравнений (275) и (276) получаем необходимые условия (значения υ22xт и υ22yт), при которых в примере № 3 при
коэффициенте перехода 0 <
β ≤ 1 будет выполняться закон сохранения
импульса в неподвижной инерциальной системе отсчета O1x1y1z1:
υ22xт = 0
( 260 )
υ22yт =
υ
( 261 )
Из
равенств (260) и (261) следует, что величины проекций скоростей υ22xт и υ22yт не зависят от величины скорости V (и, следовательно, не зависят от
величины коэффициента перехода β).
Подставив
условия (260) и (261) в уравнения (199) и (200), получим:
t22т = t21т = 0
( 262 )
А
подставив уравнение (262) в формулу (217):
ω
· 0 = [1 – ( 1/ β2)] · ( 1 + 1 )
· (υ / V) ( 263 )
будем иметь еще одно
условие выполнения закона сохранения импульса в неподвижной инерциальной
системе отсчета O1x1y1z1 для примера № 3:
β = 1
( 264 )
Таким
образом, можно сделать вывод, что в замкнутой механической системе тел,
рассматриваемой в примере № 3, для значений коэффициента перехода 0 < β < 1 закон сохранения импульса не выполняется.
3.2.1.8. Определение условий
выполнения закона сохранения механической энергии для примера № 3 при
коэффициенте
перехода 0 <
β < 1
В
дополнение к условиям выполнения закона сохранения импульса постараемся
определить условия выполнения закона сохранения механической энергии.
С
учетом формулы (175) уравнение (250) примет вид:
[(Мо · vxкр22) · { 1 – {1/[1 + (υ11xр2/vxкр22)]1/2}}] + [(Мо·vxкр22)·{ 1 – {1/[1 + (υ12xр2/ vxкр22)]1/2}}] = [(Мо·vxкр22)·{ 1 – {1/[1+((υ11xт2+υ11yт2)/vxкр22)]1/2}}] + [(Мо·vxкр22)·{ 1 – {1/[1+((υ12xт2+υ12yт2)/vxкр22)]1/2}}] (277)
Вставив проекции
скоростей υ11xр , υ12xр , υ11xт , υ11yт , υ12xт и
υ12yт
из формул (231), (270)÷(274) в уравнение (277), с учетом формулы
(235), получим:
{ [1 + (υ · V)/vxкр22)] · vxкр1 / {[1 + ( V2/vxкр22)] · [( vxкр22 + υ2)]}1/2}
+ { [1– (υ · V)/vxкр22)] · vxкр2 / {[1 + ( V2/vxкр22)] · [( vxкр22 + υ2)]}1/2} = { vxкр2 / {[1 + (V2/vxкр22)] · [( vxкр22 + υ2)]}1/2} +
{ [1 – (υ22xт · V)/vxкр22)]
· vxкр2 / {[1 + (V2/vxкр22)] · [(vxкр22 + υ2)]}1/2} (278)
Или:
1 + [(υ · V)/vxкр12] + 1 – [(υ
· V)/vxкр12 ] =
1 + 1 – [(υ22xт · V)/vxкр12]
Из уравнения (278) получаем необходимое
условие (значение проекции скорости υ22xт), при котором в примере № 3 при
коэффициенте перехода 0 < β < 1
в неподвижной инерциальной системе отсчета O1x1y1z1 будет выполняться закон сохранения механической
энергии, предполагая, что потенциальная энергия системы тел 1 и 2 не меняется:
υ22xт = 0
( 260 )
Тогда,
исходя из формулы (232), получим:
υ22yт =
υ
( 261 )
Это позволяет сделать вывод: условием для выполнения
закона сохранения механической энергии (как и условием для выполнения закона
сохранения импульса) в неподвижной инерциальной системе отсчета O1x1y1z1 для примера № 3 является:
β = 1
( 264 )
Таким
образом, получается, что в замкнутой механической системе тел, рассматриваемой
в примере № 3, для значений коэффициента перехода 0 < β < 1 закон сохранения механической
энергии не выполняется.
Аналогично
может быть доказано, что в замкнутой механической системе тел, рассматриваемой
в примере № 3, для значений коэффициента перехода 0 < β < 1 закон сохранения момента импульса не
будет выполняться.
Подтвердим вышесказанное числовыми
расчетами.
3.2.1.9. Цифровой расчет для примера
№ 3 при коэффициенте
перехода 0 < β < 1
Предположим,
что V / vxкр2 = 0,9, υ / vxкр2 = 0,6 .
Уравнение
(217) с учетом формулы (65) можно записать в виде:
ω · t22т
= –
[(υ · V)/ vxкр22]
· [1 + Cos (ω · t22т)] ( 279 )
Тогда
получим:
ω
· t22т =
– 0,8828669738, проекции υ22xт / vxкр2 = – 0,4635374427 и υ22yт / vxкр2 =
0,3809633042 скорости движения тела 2 в подвижной системе отсчета O2x2y2z2 .
В
неподвижной инерциальной системе отсчета O1x1y1z1:
а) в
момент времени t1р тела 1 и 2, соответственно, имели проекции К11xр/(Мо·vxкр2) =
0,1912108416 и К12xр/(Мо·vxкр2) =
0,9560542082 импульса на ось O1x1, кинетические энергии Ек11р / (Мо·vxкр22) = 0,018451013 и Ек12р / (Мо·vxкр22) = 0,706810043;
б) в
момент времени t1т тело 1 имело проекции К11xт / (Мо·vxкр2) =
0,5736325249 и К11yт / (Мо·vxкр2) = –
0,5144957554 импульса на оси O1x1 и O1y1, соответственно, кинетическую
энергию Ек11т / (Мо·vxкр22) = 0,362630528;
в) в
момент времени t1т тело 2 имело проекции К12xт / (Мо·vxкр2) =
0,2781879097 и К12yт / (Мо·vxкр2) =
0,3266733383 импульса на оси O1x1 и O1y1, кинетическую энергию Ек12т / (Мо·vxкр22) = 0,628530682;
г) в
момент времени t1р система тел 1 и 2 имела проекции К11xΣр / (Мо·vxкр2) =
1,1472650498 и К12yΣр / (Мо·vxкр2) = 0 импульса на оси O1x1 и O1y1, кинетическую энергию Екр / (Мо·vxкр22) = 0,725261056;
д) в
момент времени t1т система тел 1 и 2 имела проекции К11xΣт / (Мо·vxкр2) =
0,8518204346 и К12yΣт / (Мо·vxкр2) = – 0,187822417 импульса на оси O1x1 и O1y1, кинетическую энергию Ект / (Мо·vxкр22) = 0,991161209.
Закон
сохранения импульса не выполняется, т.к.: 1,1472650498 #
0,8518204346 и –
0,187822417 # 0 .
Закон
сохранения кинетической энергии не выполняется, т.к.: 0,725261056 #
0,991161209.
К
результатам, полученным при рассмотрении примера № 3, приведет и рассмотрение
системы тел, изображенной на рис. 9, в которой тела 1 и 2, описанные в примере
№ 3, удерживаются не жесткой нитью, а силой притяжения тела 3 (точечного),
которое будет находиться в центре О.
1 2 R О ω ω 3
![]()
R
![]()
![]()
![]()

![]()
![]()
![]()
Рис.
9
3.2.1.10. Выводы
В
результате рассмотрения примера № 3 было получено, что при значениях
коэффициента перехода β, находящихся
в диапазонах β > 1 и
0 < β < 1, в неподвижной системе отсчета O1x1y1z1 :
- импульс
замкнутой механической системы тел 1 и 2 (и нити 3) в момент времени, когда
тела 1 и 2 находятся на линии, параллельной оси O1y1, не равен импульсу этой системы тел
1 и 2 (и нити 3) в любой другой момент времени, когда тела 1 и 2 не находятся
на линии, параллельной оси O1y1, т.е. в неподвижной
(инерциальной) системе отсчета O1x1y1z1 замкнутая механическая система тел 1
и 2 (и нити 3) будет иметь меняющийся во времени импульс, что является
нарушением закона сохранения импульса замкнутой механической системы тел;
- кинетическая
энергия (при неизменности потенциальной энергии системы тел 1 и 2) замкнутой
механической системы тел 1 и 2 (и нити 3) в момент времени, когда тела 1 и 2
находятся на линии, параллельной оси O1y1, не равна кинетической энергии этой
системы тел 1 и 2 (и нити 3) в любой другой момент времени, когда тела 1 и 2 не
находятся на линии, параллельной оси O1y1, т.е. в неподвижной
(инерциальной) системе отсчета O1x1y1z1 замкнутая механическая система тел 1
и 2 (и нити 3) будет иметь меняющуюся во времени кинетическую энергию,
что при неизменности величины потенциальной
энергии системы тел 1 и 2 является
нарушением закона сохранения механической энергии замкнутой механической
системы тел.
Аналогично может быть доказано, что при рассмотрении
примера № 3 получим, что при
значениях коэффициента перехода β, находящихся в диапазонах β > 1 и 0 < β < 1, в неподвижной системе отсчета O1x1y1z1 момент импульса замкнутой механической системы
тел 1 и 2 (и нити 3) в момент времени, когда тела 1 и 2 находятся на линии,
параллельной оси O1y1, не равен моменту импульса этой
системы тел 1 и 2 (и нити 3) в любой другой момент времени, когда тела 1 и 2 не
находятся на линии, параллельной оси O1y1, т.е. в неподвижной
(инерциальной) системе отсчета O1x1y1z1 замкнутая механическая система тел 1
и 2 (и нити 3) будет иметь меняющийся во времени момент импульса, что
является нарушением закона сохранения момента импульса замкнутой механической
системы тел.
Изменение во времени значений импульса, кинетической энергии (при
неизменности потенциальной энергии системы тел 1 и 2 (и нити 3)), момента импульса
замкнутой механической системы тел 1 и 2 (и нити 3) в примере № 3 свидетельствует о том, что при
значениях коэффициента перехода β, находящихся в диапазонах β > 1 и
0 < β < 1, имеет
место невыполнение законов сохранения импульса, механической энергии и момента импульса.
Исходя из того, что законы сохранения импульса, механической энергии (при
неизменности потенциальной энергии системы) и момента импульса замкнутой
механической системы связаны с симметрией пространства и времени (однородностью
и изотропностью пространства и однородностью времени), можно отметить, что при
значениях коэффициента перехода β, находящихся в диапазонах β > 1 и 0 < β < 1, нарушается
условие симметрии
пространства и времени.
Если
по определению (исходному предположению) симметричное пространство и время
являются областью, в которой должна действовать специальная теория
относительности, а при использовании специальной теории относительности для
рассмотрении отдельного примера № 3 было отмечено нарушение условия симметрии пространства и времени при значениях
коэффициента перехода β, находящихся в диапазонах β > 1 и 0 < β < 1, то
мы имеем случай, когда есть теория, но нет области ее применения.
Т.е.,
в случае симметрии пространства и времени связь между координатами и временем в
инерциальных системах отсчета не может
быть записана с помощью специальной теории относительности при значениях
коэффициента перехода β, находящихся в диапазонах β > 1 и 0 < β < 1.
Одним словом, при симметрии пространства и времени
для инерциальных систем отсчета специальная теория относительности (при коэффициенте перехода β ≠ 1) не
применима.
Как показано при рассмотрении примера № 3, законы
сохранения импульса, механической
энергии (при неизменности потенциальной энергии системы) и момента импульса
замкнутой механической системы, а, следовательно, и условие симметрии
пространства и времени выполняются только при коэффициенте перехода β = 1 (когда vxкр1 = ∞ или vxкр2 = ∞), т.е.
когда коэффициент
перехода β не является функцией скорости V движения инерциальной системы
отсчета.
А это
позволяет сделать вывод, что при симметрии пространства и времени соотношения
между координатами и временем одного и того же события в двух инерциальных
системах отсчета - неподвижной O1x1y1z1 и подвижной O2x2y2z2 , изображенных на рис. 1, исходя из формул (34)÷(38) и (260),
должны иметь следующий вид:
x1 = ( x2
+ V · t )
( 280 )
x2 = ( x1
+ V · t )
( 281 )
y1 = y2
( 35 )
z1
= z2
( 36 )
t1 = t2
= t ( 282 )
т.е., преобразования Галилея (система уравнений (35), (36) и (280)÷(282))
верны для любых значений скорости V движения инерциальной системы
отсчета.
3.3. Пример №
4, подтверждающий выводы, сделанные при рассмотрении примера № 3
Попробуем
рассмотреть следующий пример, позволяющий также прийти к выводам, полученным
при рассмотрении примера № 3.
В
примере № 4 в отличие от примера № 3 будут рассматриваться не криволинейные, а
прямолинейные движения тел, составляющих замкнутую механическую систему.
Допустим,
что имеются две инерциальные системы отсчета, аналогичные системам отсчета,
изображенным на рис.1, неподвижная O1x1y1z1 и подвижная O2x2y2z2 , которая движется со скоростью V параллельно оси O1x1 относительно системы O1x1y1z1.
Предположим,
что имеется замкнутая механическая система тел, показанная на рис. 10 и
состоящая из тела 1 и тела 2, имеющих равные массы Мо в
состоянии покоя, и пружины 3.
Тела
1 и 2 соединены с абсолютно упругой пружиной 3, не имеющей массы (масса которой
ничтожно мала по сравнению с массами тел 1 и 2).
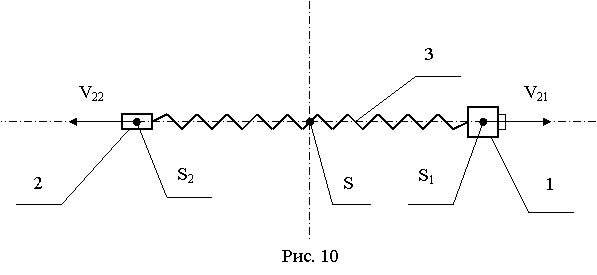
Под
действием пружины 3 тела 1 и 2 совершают симметричные возвратно-поступательные
движения относительно общего центра масс системы тел 1 и 2 - точки S.
Центр
масс тела 1 - точка S1 и
центр масс тела 2 - точка S2 постоянно находятся на одной прямой линии, проходящей
через точки S, S1 и S2.
Поместим
рассматриваемую замкнутую механическую систему тел 1 и 2 с пружиной 3 в подвижную
систему отсчета O2x2y2z2 таким образом, чтобы точка S была бы неподвижна в этой системе отсчета и совпадала
с началом координат O2, а точки S1 и S2 находились бы на оси O2x2, как показано на рис. 11÷13.
В
подвижной системе отсчета O2x2y2z2 тела
1 и 2 совершают симметричные периодически повторяющиеся через время T2 (период колебания системы тел 1 и 2)
движения.
Предположим,
как показано на рис. 11, что в момент начала отсчета времени (t2=0) в системе отсчета O2x2y2z2
пружина 3 полностью сжата (пружина 3 имеет максимальное значение
потенциальной энергии сжатия), тела 1 и 2 находятся в состоянии покоя, причем
точка S1 совпадает с точкой S2, точкой S и началом координат O2 (допустим, что добились этого
конструктивно).
Рис.
11

После
момента времени t2=0 пружина 3 начинает расжиматься и расталкивать тела 1 и 2 в разные
стороны, т.е. потенциальная энергия сжатия пружины 3 начинает переходить в
кинетические энергии тел 1 и 2 (скорость V21 и V22 движения тел 1 и 2 соответственно будет
постепенно возрастать).
В
системе отсчета O2x2y2z2
в какой-то момент времени t2 равный t2мо пружина 3 будет полностью расжата
(потенциальная энергия пружины 3 будет равна нулю), тела 1 и 2 будут иметь
максимальные величины V21м и V22м скорости своего движения и максимальные значения кинетических энергий (как
показано на рис. 12).
Рис.
12
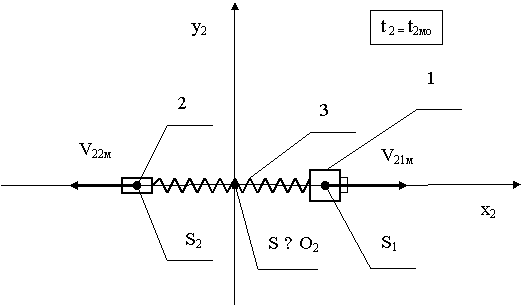
После
момента времени t2мо пружина 3 начинает растягиваться, а тела 1 и 2 начинают замедляться,
т.к. кинетические энергии тел 1 и 2 начинают переходить в потенциальную энергию
растяжения пружины 3.
В
системе отсчета O2x2y2z2
в какой-то момент времени t2 равный t2то тела 1 и 2 остановятся (кинетические
энергии тел 1 и 2 будут равны нулю), а
пружина 3 полностью растянется (кинетическая энергия тел 1 и 2 перейдет
полностью в потенциальную энергию растяжения пружины 3, которая в момент
времени t2то достигнет своего максимального значения), как показано на
рис. 13.
Рис.
13
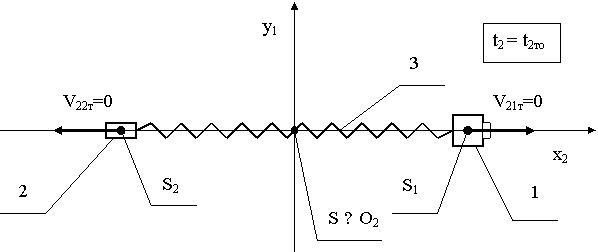
Далее
от момента времени t2то до момента времени t2, равного периоду T2 колебания, процесс взаимодействия тел
1 и 2 с пружиной 3 будет происходить обратным образом (т.е. пружина 3 будет
вначале сжиматься сама, передавая свою потенциальную энергию растяжения в
кинетические энергии тел 1 и 2, а затем будет сжиматься под воздействием тел 1
и 2, которые будут передавать свои кинетические энергии в энергию сжатия
пружины 3).
Учитывая
периодичность движения тел 1 и 2 (и пружины 3), можно отметить, что:
-
положение и состояние тел 1 и 2 и пружины 3, соответствующее моменту времени t2 = 0, будет
иметь место и для моментов времени t2р, равных:
t2р = t2 · n
(
283 )
где: n = 0, 1, 2, 3, 4 …;
-
положение и состояние тел 1 и 2 и пружины 3, соответствующее моменту времени t2мо, будет иметь место и для моментов
времени t2м, равных:
t2м = t2мо + (t2 · n) ;
( 284 )
-
положение и состояние тел 1 и 2 и пружины 3, соответствующее моменту времени t2то, будет иметь место и для моментов
времени t2т, равных:
t2т = t2то + (t2 · n) ;
( 285 )
Для
упрощения дальнейшего рассмотрения предположим, что тела 1 и 2 являются
точечными.
В
подвижной системе отсчета O2x2y2z2, исходя из симметрии (в любой момент
времени t2 массы тел 1 и 2 одинаковы, центр S масс тел 1 и 2 совпадает с началом координат O2), для любого момента времени t2 связь между координатой x21 тела 1 и координатой x22 тела 2 запишется следующим образом:
x21 = – x22 ( 286 )
а связь между скоростью V21 движения тела 1 и скоростью V22 движения тела 2 будет иметь вид:
V21 = – V22 ( 287 )
Если рассматривать движение системы тел 1 и 2 и пружины 3
в неподвижной системе отсчета O1x1y1z1 и подвижной инерциальной системе
отсчета O2x2y2z2, как показано на рис. 14, то опираясь
на уравнения (34) и (35), можно написать связь между координатой x11 тела 1 в момент времени t11 в неподвижной системе отсчета O1x1y1z1 и координатой x21 тела 1 в момент времени t21 в подвижной системе отсчета O2x2y2z2 :
x11 = β · [ x21 + (V · t21)] ( 288 )
x21 =
β · [ x11 – (V · t11)] ( 289 )
Аналогично,
используя уравнения (34) и (35), можно записать связь между координатой x12 тела 2 в момент времени t12 в неподвижной системе отсчета O1x1y1z1 и координатой x22 тела 2 в момент времени t22 в подвижной системе отсчета O2x2y2z2 :
x12 = β · [ x22 + (V · t22)] ( 290 )
x22 = β · [ x12 + (V · t12)] ( 291 )
Рис.
14

С
помощью формулы (38) можно написать связь между значениями времен t11 , t21 и t12 , t22 :
t11 =
{[(β2 –
1) · x21] / (β
· V)} + (β · t21) ( 292 )
t12 =
{[(β2 –
1) · x22] / (β
· V)} + (β · t22) ( 293 )
В
рассматриваемом примере нас будет интересовать положение тел 1 и 2 в
неподвижной системе отсчета O1x1y1z1 в один и тот же момент времени, т.е.
когда:
t11
= t12 ( 294
)
Тогда
уравнение (294) с учетом формул (292) и (293) примет вид:
{[(β2
– 1) · ( x21 – x22)] / (β2 · V)}
= ( t22 – t21) ( 295 )
В
подвижной системе отсчета O2x2y2z2 при выполнении условия (294)
представляет интерес положение тел 1 и 2, когда:
t21 =
t22 =
t2р ( 296 )
Подставив
условие (296) в уравнение (295), получим:
x21 = x22 =
0
( 297 )
Т.е.
для выполнения условий (294) и (296) тела 1 и 2 (их центры масс) в
рассматриваемый момент времени должны находиться в точке, совпадающей с центром
масс S тел 1 и 2 и
началом координат O2 .
Отсюда:
t2р = t2 · n
(
283 )
где: n = 0, 1, 2, 3, 4 …
Учитывая,
что x21 ≥ 0 и x22 ≤ 0 (исходное условие), для случая, когда t21 ≠ t2р и t22
≠ t2р,
из формулы (295) видно, что величина времени t22 в зависимости от значения
коэффициента перехода β может быть:
-
t22 > t21 при β > 1 ; ( 298 )
-
t22 < t21 при 0 < β < 1 ; ( 299 )
-
t22 = t21 при β = 1 . ( 300 )
Теперь
можем приступить к проверке выполнения закона сохранения импульса.
Рассмотрим
два момента времени в неподвижной системе отсчета O1x1y1z1 .
3.3.1.1. Момент времени
t1р
Как
показано на рис. 15, в подвижной системе отсчета O2x2y2z2 в момент времени t2, равный
t2р, тела 1 и 2 находятся в одной точке,
совпадающей с центром координат O2 (исходное условие), и их скорости V21р и V22р движения соответственно равны:
V21р = 0 ( 301 )
V22р = 0 ( 302 )
Исходя
из того, что в подвижной системе отсчета O2x2y2z2 в момент времени t2р тела 1 и 2 находятся в одной точке
(т.е. координаты x21р и x22р тел 1 и 2 равны), в неподвижной системе отсчета O1x1y1z1 тела 1 и 2 в момент времени t1р, соответствующий моменту времени t2р в подвижной системе отсчета O2x2y2z2, также будут находиться в одной
точке (т.е. координаты x11р и x12р тел 1 и 2 равны).
Таким
образом, в неподвижной системе отсчета O1x1y1z1 в момент времени t1р тела 1 и 2 находятся в одной точке и
их скорости V11р и V12р движения соответственно с учетом формулы (40) и равенств (301) и (302)
равны:
V11р = V ( 303 )
V12р = V ( 304 )
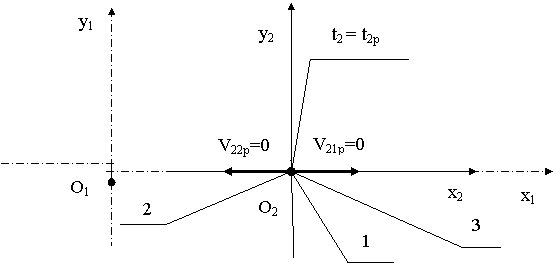
Рис.
15
Следовательно,
в неподвижной системе отсчета O1x1y1z1 импульс Р1р замкнутой
механической системы тел 1 и 2 (и пружины 3) в момент времени t1р с учетом формулы (152) и равенств (303)
и (304) равен:
Р11р + Р12р = Р1р = 2 · ( Мо · V ) / [1 – (V2 / Vxкр2)]1/2 ( 305 )
3.3.1.2. Момент времени
t1т
Как
уже рассматривалось ранее, в подвижной системе отсчета O2x2y2z2 в момент времени t2 равный t2т, который для тела 1 запишем, как t21т , тело 1 имеет скорость V21т движения равную нулю:
V21т = 0 ( 306 )
т.к. пружина 3 в момент
времени t2 равный t21т имеет максимальную потенциальную энергию растяжения.
Положению тела 1 в подвижной системе отсчета O2x2y2z2 в момент времени t21т будет соответствовать положение тела 1 в неподвижной
системе отсчета O1x1y1z1 в момент времени t1т.
В неподвижной системе отсчета O1x1y1z1 в момент времени t1т тело 1, согласно уравнению (40),
будет иметь скорость V11т своего движения равную:
V11т = V ( 307 )
В неподвижной
системе отсчета O1x1y1z1 в момент времени t1 равный t1т
тело 2 будет
иметь скорость движения равную V12т.
Положению
тела 2 в неподвижной системе отсчета O1x1y1z1 в момент времени t1т будет соответствовать положение тела
2 в подвижной системе отсчета O2x2y2z2 в момент времени t2, равный t22т .
Как
показано на рис. 16, предположим, что в подвижной системе отсчета O2x2y2z2 в момент времени t2 равный t22т тело 2 имеет скорость движения равную
V22т.
Рис.
16

Учитывая
условие (298), что при коэффициенте перехода β > 1 время t22 > t21
, можно отметить, что при коэффициенте перехода β > 1 скорость
V22т тела 2 будет направлена по направлению оси O2x2.
Кроме
этого, исходя из условия (299), утверждающего, что при коэффициенте перехода 0
< β < 1 время t22 < t21 , можно отметить, что при коэффициенте
перехода 0 < β < 1
скорость V22т тела 2 будет иметь направление, противоположное
направлению оси O2x2.
Используя
формулу (40), можно записать связь между скоростями V12т и
V22т тела 2:
V12т =
(V22т +
V) / {{[(β2
– 1) · V22т] / (β2
· V)} + 1} ( 308 )
Следовательно,
в неподвижной системе отсчета O1x1y1z1 импульс Р1т замкнутой
механической системы тел 1 и 2 (и пружины 3) в момент времени t1т
с
учетом формулы (152) и равенства (307) равен:
Р11т + Р12т =
Р1т = {( Мо · V ) / [1 –
(V2 / Vxкр2)]1/2} + {( Мо · V12т ) / [1 –
(V12т 2 / Vxкр2)]1/2} ( 309 )
3.3.1.3. Определение
условий выполнения закона сохранения импульса для примера № 4
В
связи с тем, что механическая система тел 1 и 2 (и пружины 3) является
замкнутой, закон сохранения импульса позволяет записать для моментов времени t1р и t1т в неподвижной системе отсчета O1x1y1z1 следующее уравнение:
Р1т
= Р1р
Или, исходя из формул (305) и (309):
{( Мо · V ) / [1 –
(V2 / Vxкр2)]1/2} + {( Мо · V12т ) / [1 –
(V12т 2 / Vxкр2)]1/2} =
2 · ( Мо · V ) / [1 – (V2 / Vxкр2)]1/2 (
310 )
Из
уравнения (310) следует, что необходимым условием (значением скорости V12т), при котором в примере № 4 будет
выполняться закон сохранения импульса в неподвижной инерциальной системе
отсчета O1x1y1z1 , является:
V12т =
V
( 311 )
или с учетом формулы (308):
V22т =
0
( 312 )
Из равенств (311) и (312) следует, что
величины скоростей V12т и V22т не
зависят от величины скорости V (и,
следовательно, не зависят от величины коэффициента перехода β).
Но в
подвижной системе отсчета O2x2y2z2 при значениях координат x21т тела 1 и x22т
тела 2,
не равных нулю, равенство нулю скорости V22т
тела 2
возможно только, когда:
t22т =
t21т ( 313 )
Вставив
равенство (313) в формулу (295), получим:
{[(β2
– 1) · ( x21 – x22)] / (β2 · V)}
= 0 ( 314 )
Но т.к. величина (
x21 – x22) > 0 , то из
уравнения (314) будем иметь еще одно условие выполнения закона сохранения
импульса в неподвижной инерциальной системе отсчета O1x1y1z1 для примера № 4:
β = 1
( 261 )
Таким
образом, можно сделать вывод, что в замкнутой механической системе тел,
рассматриваемой в примере № 4, для значений коэффициента перехода, находящихся
в диапазонах β > 1 и 0 < β < 1 , закон сохранения импульса не
выполняется.
IV. Заключение
В
заключение можно обобщить вышенаписанное.
Кинематика
Использование
принципа относительности и симметрии пространства и времени позволило:
1. Перейти
от системы уравнений связи инерциальных систем отсчета - неподвижной O1x1y1z1 и подвижной O2x2y2z2:
x1 = β1 · ( x2 + V1 · t2 )
( 24 )
x2 =
β2 · ( x1 +
V2 · t1 )
( 25 )
y1 = β3 · y2
( 26 )
y2 = β4 · y1
( 27 )
z1 = β5 · z2
( 28 )
z2 = β6 · z1
( 29 )
к
системе уравнений:
x1 = β · ( x2 + V · t2 ) ( 34 )
x2 = β · ( x1 –
V · t1 )
( 35 )
y1 =
y2
( 36 )
z1
= z2
( 37 )
2. Установить,
что значения коэффициента перехода β для инерциальных систем отсчета могут
находиться в двух взаимоисключающих диапазонах:
- β > 1 ,
- 0 < β < 1
3. Получить
формулу для коэффициента перехода β для инерциальных систем отсчета для
случая β > 1:
β> 2 = 1 / [1 –
(V2 / vxкр12)] ( 64 )
где: vxкр1
-
постоянная действительная величина;
4. Получить
формулу для коэффициента перехода β для инерциальных систем отсчета для
случая 0 < β < 1:
β< 2 =
1 / [1 + (V2 / vxкр22)] ( 65 )
где: vxкр2
- постоянная
действительная величина;
5.
Установить, что при
коэффициенте перехода β > 1 существует такое действительное
значение скорости Vxкр (равное vxкр1) движения точки, которая будет
инвариантна во всех направлениях и во всех инерциальных системах отсчета:
vxкр1 =
Const
( 76 )
6.
Установить, что при
коэффициенте перехода 0 < β < 1 имеет место только мнимое значение
скорости Vxкр (равное (ί · vxкр2)) движения точки, которая будет инвариантна во всех
направлениях и во всех инерциальных системах отсчета:
vxкр2 =
Const
( 77 )
Динамика
1.
Используя обязательность выполнения в инерциальных системах отсчета закона
сохранения импульса и закона сохранения механической энергии (а точнее, его
частного случая при постоянстве потенциальной энергии - постоянства
кинетической энергии) для замкнутой механической системы тел, двигающихся
прямолинейно и испытывающих только абсолютно упругие взаимодействия, были
получены зависимости массы, импульса и кинетической энергии тела от скорости
его движения:
- при
β
> 1 :
М(V)> =
Мо / [1 – (V2 / vxкр12)]1/2 ( 155 )
Р(V)> =
( Мо · V ) / [1 –
(V2 / vxкр12)]1/2
( 156 )
Ек(V)> = Мо · vxкр12 ·
{{1 / [1 – (V2 / vxкр12)]1/2}
– 1} ( 157
)
- при
0 < β < 1 :
М(V)< =
Мо / [1 + (V2 / vxкр22)]1/2 ( 176 )
Р(V)< =
( Мо · V ) / [1 +
(V2 / vxкр22)]1/2 ( 177 )
Ек(V)< = Мо · vxкр22 · { 1 – {1 / [1
+ (V2 / vxкр22)]1/2}} ( 178 )
2. На
отдельном примере (пример № 3), в котором рассматривалась замкнутая
механическая система тел, движущихся нелинейно, было показано, что при
значениях коэффициента перехода β, находящихся в диапазонах β > 1 и
0 < β < 1, имеет место нарушение законов сохранения
импульса, момента импульса и механической энергии (при неизменности потенциальной
энергии системы), т.е., импульс, момент
импульса и кинетическая энергия замкнутой механической системы оказались
переменными во времени величинами.
Связь между законами сохранения импульса, механической энергии и момента
импульса замкнутой механической системы и симметрией пространства и времени
(однородностью и изотропностью пространства и однородностью времени) позволила отметить,
что при значениях коэффициента перехода β, находящихся в диапазонах β > 1 и 0 < β < 1, нарушается
условие симметрии
пространства и времени.
При рассмотрении примера № 3 было показано, что
законы сохранения импульса, механической энергии и момента импульса замкнутой механической системы,
а, следовательно, и условие симметрии пространства и времени выполняются только
при коэффициенте перехода β = 1.
А
учитывая, что условие симметрии
пространства и времени является требованием (исходным условием) специальной
теории относительности к пространству и времени, то вступление выводов
специальной теории относительности в противоречие с условием симметрии пространства
и времени, заложенным при ее создании, позволяет предположить следующее:
- связь между координатами и временем в
инерциальных системах отсчета не может
быть записана с помощью специальной теории относительности, если
значения коэффициента перехода β будут находиться в диапазонах β > 1 или 0 < β < 1;
-
в однонаправленных инерциальных системах отсчета коэффициент перехода β не может быть больше или меньше 1, а
может быть только равен 1;
- в
инерциальных системах отсчета коэффициент перехода β не зависит от величины скорости V движения инерциальных систем отсчета;
-
преобразования Галилея верны для инерциальных систем
отсчета при любых значениях скорости V их движения:
x1 =
( x2 + V · t )
( 280 )
x2 =
( x1 + V · t
)
( 281 )
y1 = y2
( 35 )
z1
= z2 ( 36 )
t1
= t2 = t
( 282 )
Здесь
также следует отметить, что выводы, сделанные в главе «Динамика», верны лишь
при выполнении принятого предположения о том, что величина потенциальной
энергии тела не зависит от величины скорости его перемещения (т.е. от величины
его кинетической энергии).
P.S.: Основные идеи изложены в статье "Специальная теория
относительности без постулата о постоянстве скорости света", напечатанной
в журнале "Актуальные проблемы современной науки" (ISSN 1680-2721) № 1 (34) за 2007 год и
размещенной на сайтах "Новые идеи и гипотезы" http://new-idea.kulichki.net/?mode=physics и "Математическая
физика. Теория относительности" http://www.matphysics.ru/ .
Автор
В.Н. Кочетков