Другие статьи



 

ПАРАДОКС ЛЖЕЦА И ТЕОРИЯ ИСТИНЫ В КОМПЛЕКСНОЙ ЛОГИКЕ

А.С.Ионов, Г.А.Петров Новгородский государственный университет им. Ярослава Мудрого

 

Основным недостатком действительной (булевской) алгебры логики с точки зрения идентификации и управления объектами, обладающими сознанием (интеллектом), является то, что данная логика одномерна, то есть описывает лишь действительные логические состояния и не учитывает мнимых. На практике это приводит к тому, что материя и сознание (объект и субъект, мысль и слово) рассматриваются и описываются отдельно друг от друга и с использованием одной и той же (действительной) логики, что не дает возможности описать диалектику и взаимосвязь процессов мышления и поведения человека, приводит к неразрешимым в рамках действительной логики противоречиям (парадоксам). В статье рассматривается один из таких парадоксов – парадокс лжеца и его решение средствами комплексной логики и ее теории истины.

Парадокс лжеца заключается в утверждении, приписываемом Эпимениду – легендарному греческому поэту, жившему на Крите в 6 веке до нашей эры. По преданию Эпименид утверждал, что все критяне лжецы. Верно ли это утверждение, равнозначное высказыванию “Я лжец”, если учесть, что сам Эпименид родом с острова Крит?

Приписываемое ему утверждение логически противоречиво, если предположить детерминированность ситуации, то есть то, что лжецы всегда лгут, а нелжецы всегда говорят правду. При данном предположении утверждение “Я лжец” не может быть истинным, ибо тогда он был бы лжецом и лгал, утверждая в действительности “Я нелжец”. Но утверждение “Я лжец” не может быть и ложным, так как Эпименид был бы нелжецом и говорил истину. Другими словами, налицо неразличимость (логическая неопределенность) ситуации: если Эпименид лжец, то он нелжец, и наоборот: если он нелжец, то он лжец, то есть его утверждение и истинно и ложно одновременно, что противоречит действительной бинарной логике.

Многочисленные попытки разрешения парадокса лжеца, имеющие столь же давнюю историю, как и сам парадокс, к настоящему времени трансформировались в задачу построения непротиворечивой и адекватной логической теории истины. Основные попытки в этом направлении до сих пор связаны с созданием метаязыков и предприняты в работах Тарского. Построение теории истины и решение парадокса лжеца в комплексной логике основывается на корректировке логического закона тождества с учетом мнимой составляющей материи и рассматривается ниже.

1. Теория истины для 4-значной комплексной логики.

Булевская или действительная логика основана на традиционном понятии истины как безошибочности. Это нашло отражение в формулировке действительного логического закона тождества в виде

А = А , (1)

(всякий объект есть то, что он есть). При таком рассмотрении субъект В, заданный его ощущениями, также является отдельным объектом, и так как В = В, должен рассматриваться отдельно, что может приводить к неразличимости А и В, то есть субъекта и объекта, материи и сознания.

Комплексный закон тождества вытекает из ленинского определения материи как философской категории для обозначения объективной реальности, данной нам в ощущениях и не зависящей от них [1] и сформулирован в [2] следующим образом:

A = A + iВ, (2)

Где А – модель объекта (материи); В – модель субъекта (сознания как восприятия материи). Формула (2) означает: объект А есть то, что он есть, плюс мнимая ошибка iВ его восприятия субъектом, получающаяся путем умножения ощущения (восприятия) В на i, где i – чисто мнимое множество, мнимая логическая единица, являющаяся моделью истины в комплексной логике.

Заметим, что Ленин особое внимание обращает на недопустимость смешивания материи и сознания (А и В). Из (2) следует, что комплексная модель объекта как раз и представляет из себя пару упорядоченных действительных множеств и это упорядочение достигается существованием комплексной истины i.

Кроме того, определение (2) означает, во первых то, что субъект, заданный его ощущениями, являются частью объекта, но в то же время существует отдельно от него. Во-вторых, из (2) и (1) следует, что действительная истина (true) в комплексной логике является пределом (2) при ошибке iВ, стремящейся к нулю. В третьих, комплексный закон тождества утверждает бесконечность процесса познания во времени.

Итак, истина и ложь в действительной булевской логике выражаются следующим образом:

T= истина = true - отсутствие ошибки iВ ( достоверное событие);

F = ложь = false - присутствие ошибки iВ (невозможное событие) . (3)

Таким образом, теория действительной истины отрицает истинность комплексной логики, но не наоборот, как будет видно из дальнейшего изложения. С учетом (2), объектом изучения в комплексной логике является комплексное логическое событие В восприятия объективной реальности субъектом, для которого выполняется соотношение

. В = + i, (4)

где – действительная составляющая, а i – мнимая составляющая. Здесь и - действительные логические события, при этом из (4) следует, что событие воспринимается субъектом как . Рассмотрим их на примере рис. 1. Пусть для действительной логики означает событие, заключающееся в утверждении “Я нелжец” и = true = T. Тогда противоположное событие = false = F означает утверждение “Я лжец”.

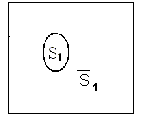
Рис.1. События действительной логики.

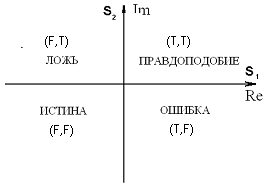
Как уже было отмечено при постановке задачи, парадокс лжеца заключается в неразличимости противоположных событий ( и ). Но при комплексном подходе существует второе измерение, задаваемое событием - восприятием события . В соответствии с этим и четырьмя вариантами логических событий и их восприятия, в 4-значной комплексной логике вводятся четыре комплексных события, представленные на комплексной плоскости (Re, Im) рис.2 и записанные в принятом порядке следования квадрантов прописными буквами в отличие от действительных терминов:

Рис.2. События 4-значной комплексной логики.

На рис.2 приняты следующие обозначения комплексных логических событий:

П = ПРАВДОПОДОБИЕ = (T,T) = T + iT ( T принимается за T);

Л = ЛОЖЬ = (F,T) = F + iT (F принимается за T);

И = ИСТИНА = (F,F) = F + iF = i (F принимается за F);

О = ОШИБКА = (T,F) = T + iF (T принимается за F). (5)

Как видим из (5), комплексная ИСТИНА определяется как мнимая логическая единица i. При этом здесь она определяется в соответствии с (2) через саму себя как i = F + iF. Таким образом, в 4-значной комплексной логике i = ИСТИНА - это ложь, воспринимаемая как ложь. Ниже будет дано и другое определение комплексной истины.

2. Теория истины для 9-значной комплексной логики.

Для получения 9-значной комплексной логики введем и интерпретируем в моделируемой гипотетической ситуации расчета продавца с покупателем следующие новые значения традиционных логических символов 1 и 0 как комплексных событий и символ –1 для комплексного отрицательного множества (при этом вербальной интерпретацией событий F и T являются утверждения “Я лжец” и “Я нелжец”):

1 = (F,T) = (F + iT) = ЛОЖЬ - положительное множество, присутствие в событии положительной ошибки ( продавец при расчете обсчитывает покупателя в свою пользу, выдает F за T – положительный обсчет ) – достоверное событие;

0 = (T,T) + (F,F) = (T,T) = (T + iT) = ПРАВДОПОДОБИЕ – пустое множество, отсутствие ошибки в событии ( продавец точно рассчитывается с покупателем, выдает T за T или F за F – обсчета нет ) – пустое событие;

-1 = (T,F) = (T + iF) = ОШИБКА – отрицательное множество, присутствие в событии отрицательной ошибки ( продавец обсчитывается в пользу покупателя, выдает T за F – отрицательный обсчет ) – антидостоверное событие.

Истина i в 9-значной комплексной логике задается (по аналогии с комплексными числами) как мнимое множество (мнимая логическая единица), которая, будучи умноженной на саму себя, дает отрицательное множество:

i i= -1, (6)

что с учетом (5) означает: (F,F)(F,F) = (T,F).

Комплексная 9 - значная логика получается из преобразования комплексной плоскости рис.2 таким образом, что составляющие и реальной, и мнимой оси могут принимать не по два, а по три значения: 1, 0,-1. Тогда возможны 9 гиперкомплексных логических событий.

Поясним их практический смысл с помощью таблицы 1, в которой коэффициент В при мнимой части комплексного события (А,В) отражает восприятие обсчета (реальной части А события) субъектом - в нашем примере покупателем, с которым рассчитывается продавец. При этом следует помнить, что, например, событие (1,1) = 1 + i1 и так далее, а произведение ii = -1.

Таблица 1.

№ события

Формула события

Реальная часть А события (А + iВ)

Коэф. В при мнимой части события (А+ iВ)

1

(1, 1)

Положительный обсчет (F,T)

Положительный обсчет (F,T)

2

(1, 0)

Положительный обсчет (F,T)

Обсчета нет (T,T)

3

(1,-1)

Положительный обсчет (F,T)

Отрицательный обсчет (T,F)

4

(0, 1)

Обсчета нет (T,T)

Положительный обсчет (F,T)

5

(0, 0)

Обсчета нет (T,T)

Обсчета нет (T,T)

6

(0,-1)

Обсчета нет (T,T)

Отрицательный обсчет (T,F)

7

(-1,1)

Отрицательный обсчет (T,F)

Положительный обсчет (F,T)

8

(-1,0)

Отрицательный обсчет (T,F)

Обсчета нет (T,T)

9

(-1,-1)

Отрицательный обсчет (T,F)

Отрицательный обсчет (T,F)

Алгебра 9-значной комплексной логики, включающая операции логического отрицания, обращения и сопряжения, а также логического сложения, умножения, вычитания и деления, описана в [3].

Возвратимся снова к действительной логике (3) с учетом данных выше определений комплексных событий. Получаемую в результате этого возврата логику назовем гипердействительной, а получаемые значения истины и лжи пометим апострофом. Связь событий действительной и 9-значной комплексной логики можно найти из решения системы уравнений (7), полученной из приведенных выше определений событий 1 и -1:

1 = F’ + iT’

-1 = T’+ iF’ (7)

Из (7) получим значение гипердействительной истины ГДИ

ГДИ = T‘= true’ = -1 –i = (-1,-1), (8)

что соответствует тому, что отрицательное множество (событие) принимается за отрицательное. Соответственно гипердействительная ложь ГДЛ определится как

ГДЛ = F’ = false’ = i = (0,1), (9)

что соответствует тому, что пустое событие принимается за положительное. Таким образом, гипердействительная истина и ложь являются событиями (частными случаями) 9-значной комплексной логики.

Значение гиперкомплексной истины в 9-значной комплексной логике найдем из значения ИСТИНЫ i, заданной (5), подставив в него значение гипердействительной лжи F’ из (9). Получим значение гиперкомплексной истины (ГКИ)

ГКИ = ИСТИНА’ = i = (F’ + iF’) = i + ii = -1 + i = (-1,1) (10)

Также из (5), подставив туда (8) и (9), получим значения остальных трех гиперкомплексных событий:

ГКП = ПРАВДОПОДОБИЕ’ = (T’,T’) = -i = (0,-1)

ГКЛ = ЛОЖЬ’ = ( F’,T’) = 1 = (1,0)

ГКО = ОШИБКА’ = (T’,F’) = -1 –i = (-1,-1) (11)

Сформулируем теперь физический и этический смысл введенных комплексных истинностных определений, исходя из того, что положительную ошибку 1 можно интерпретировать так: брать энергии больше, чем отдавать (эгоизм); отсутствие ошибки 0 – брать энергии столько, сколько отдавать (равновесие); отрицательную ошибку -1 - отдавать энергии больше, чем брать (альтруизм).

Тогда в соответствии с (8) и (9) гипердействительная истина – это альтруизм, воспринимаемый как альтруизм, а гипердействительная ложь – это равновесие, воспринимаемое как эгоизм. Гиперкомплексная истина (10) – это альтруизм, воспринимаемый как эгоизм. Аналогично могут быть интерпретированы события (11).

Отметим также наличие действительной ошибки в событии T’ и отсутствие в нем ошибки восприятия; и наоборот, отсутствие действительной ошибки в событии F’ и присутствие в нем ошибки восприятия.

3. Управление истиной в комплексных логических пространствах.

Довербальная логическая модель системы с интеллектом определяется формулой (2), где А – логическая модель объекта; В – логическая модель субъекта (задается его восприятием объекта); i – логическая модель среды взаимодействия субъекта и объекта (комплексного логического пространства).

Комплексная истина i (мнимая логическая единица ) имеет двоякую природу: с одной стороны, i = const, что вытекает из ii = -1. С другой стороны, i может изменяться как модель среды логического взаимодействия в процессе управления системой и, таким образом, i одновременно может являться переменной величиной, что позволяет ею управлять. Принципы управления истиной в довербальной логической модели рассмотрены в [4].

Схема управления истиной в поствербальном логическом пространстве приведена на рис 3. Будем искать соответствующую комплексную логическую модель системы в виде:

А = (A + iB) +i(C + iD), (12)

где объект А – собеседники Эпименида. Субъект В – Эпименид, заданный его восприятием собеседников. С – вербальная реакция субъекта (Эпименида) на рассогласование io – ic (рис.3). D – вербальное восприятие субъекта (Эпименида) объектом (собеседниками).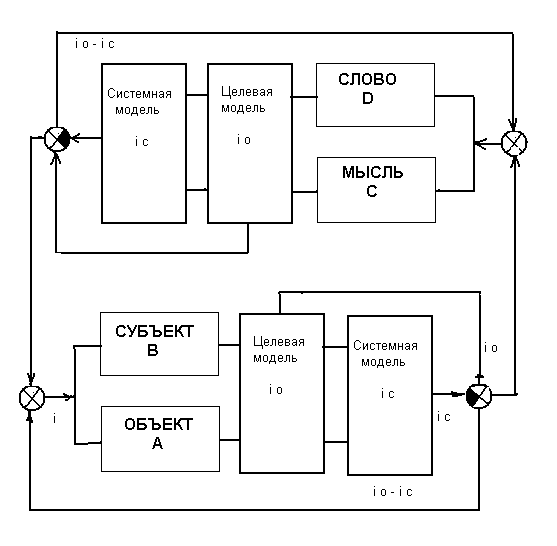

Рис.3. Схема комплексного поствербального логического управления.

В целом процессы, описанные для довербального управления истиной будут действовать и в условиях поствербального управления. Ниже проанализируем особенности данного случая, рассмотрев компоненту D, (СЛОВО) рис.3 для решения парадокса лжеца.

4. Применение теории комплексной истины к парадоксу лжеца.

Рассмотрим комплексное вербальное восприятие субъекта D из (12) в виде (4), где - мысль субъекта; - слово субъекта – в нашем случае это утверждение “я лжец”. В соответствии с действительной логикой, = (я лжец) может означать как истину Т, так и ложь F.

Назовем случай, когда = (я лжец) = F (противоположное событие Т = (я нелжец)) мужской ипостасью мышления, а обратный гипотетический случай, когда = (я лжица) = Т (противоположное событие F = (я нелжица)) – женской ипостасью мышления. Тогда в соответствии с (5) будет справедлива следующая таблица 2 для логических событий с мужской и женской ипостасями мышления:

 

 

Таблица 2

Комплексное логич. событие

Мужская ипостась

Женская ипостась

Номер

Наимен.

Мысль

Слово

Мысль

Слово

1

ПРАВДОПОДОБИЕ

Я нелжец

Я нелжец

Я лжица

Я лжица

2

ЛОЖЬ

Я лжец

Я нелжец

Я нелжица

Я лжица

3

ИСТИНА

Я лжец

Я лжец

Я нелжица

Я нелжица

4

ОШИБКА

Я нелжец

Я лжец

Я лжица

Я нелжица

Будем считать, что термин комплексный ЛЖЕЦ соответствует событию из таблицы 2, описываемому комплексной ЛОЖЬЮ, а термин НЕЛЖЕЦ – событию, описываемому комплексной ИСТИНОЙ. Тогда парадокс лжеца решится в 4-значной комплексной логике следующим образом:

Эпименид НЕЛЖЕЦ, если он использует мужскую ипостась мышления и говоря “Я лжец”, мыслит так же. Если Эпименид использует женскую ипостась мышления и говорит “Я лжица”, а мыслит “Я нелжица”, то он ЛЖИЦА. Как следует из табл.2, возможны еще две комплексные ситуации ПРАВДОПОДОБИЕ и ОШИБКА.

В 9-значной комплексной логике событие D из (11) может принимать 9 логических состояний, собранных в табл.3. для мужской ипостаси мышления и в табл. 4 - для женской. При этом объектами выступают не только мысль и слово, но и их восприятие самим субъектом.

Будем считать, что термин гипердействительный ЛЖЕЦ’ (ЛЖИЦА’) соответствует событиям таблиц 3 и 4, описываемым гипердействительной ложью ГДЛ, а термин гипердействительный НЕЛЖЕЦ’ (НЕЛЖИЦА’) соответствует гипердействительной истине ГДИ. Тогда парадокс лжеца для мужской ипостаси мышления разрешится следующим образом:

Эпименид НЕЛЖЕЦ’ (событие 9 табл.3), если он, говоря “Я лжец”, мыслит “Я нелжец”, думает, что он мыслит, что он нелжец и думает, что он говорит, что он лжец.

Таблица 3.

Комплексное логическое событие

Мужская ипостась мышления

№

Наимен.

Формула

Мысль

Слово

Восприятие мысли

Восприятие слова

1

(1, 1)

Я лжец

Я нелжец

Я лжец

Я нелжец

2

Л, ГКЛ

(1, 0)

Я лжец

Я нелжец

Я нелжец

Я нелжец

3

(1, -1)

Я лжец

Я нелжец

Я нелжец

Я лжец

4

И, ГДЛ

(0, 1)

Я нелжец

Я нелжец

Я лжец

Я нелжец

5

П

(0, 0)

Я нелжец

Я нелжец

Я нелжец

Я нелжец

6

ГКП

(0, -1)

Я нелжец

Я нелжец

Я нелжец

Я лжец

7

ГКИ

(-1, 1)

Я нелжец

Я лжец

Я лжец

Я нелжец

8

О

(-1, 0)

Я нелжец

Я лжец

Я нелжец

Я нелжец

9

ГДИ, ГКО

(-1, -1)

Я нелжец

Я лжец

Я нелжец

Я лжец

 

 

 

 

Таблица 4.

Комплексное логическое событие

Женская ипостась мышления

№

Наимен.

Формула

Мысль

Слово

Восприятие мысли

Восприятие слова

1

(1, 1)

Я нелжица

Я лжица

Я нелжица

Я лжица

2

Л, ГКЛ

(1, 0)

Я нелжица

Я лжица

Я лжица

Я лжица

3

(1, -1)

Я нелжица

Я лжица

Я лжица

Я нелжица

4

И, ГДЛ

(0, 1)

Я лжица

Я лжица

Я нелжица

Я лжица

5

П

(0, 0)

Я лжица

Я лжица

Я лжица

Я лжица

6

ГКП

(0, -1)

Я лжица

Я лжица

Я лжица

Я нелжица

7

ГКИ

(-1, 1)

Я лжица

Я нелжица

Я нелжица

Я лжица

8

О

(-1, 0)

Я лжица

Я нелжица

Я лжица

Я лжица

9

ГДИ, ГКО

(-1, -1)

Я лжица

Я нелжица

Я лжица

Я нелжица

Исходя из табл.4 (событие 4), для женской ипостаси мышления парадокс лжеца решается следующим образом: Эпименид – ЛЖИЦА’, если он, говоря “Я лжица”, мыслит так же, однако думает, что он мыслит “Я нелжица” и думает, что говорит “Я лжица”.

Заметим, что, как в этом случае, когда ГДЛ соответствует комплексной ИСТИНЕ, интерпретация одного и того же события зависит от принятой логики его анализа, что подтверждает гипотезу о двойственном характере истины. Интерпретация остальных событий описанной выше комплексной теории истины также вытекает табл.3 и 4.

В завершении раздела, возвращаясь к изложенной выше теории истины, отметим, что система (7) имеет еще одну (вторую) пару решений ГДИ = (0, -1); ГДЛ = (1,1), которую следует отбросить, так как ее значения противоречат, как нетрудно убедиться, таблицам 3 и 4 ( в этом случае для мужской ипостаси мышления решение парадокса лжеца отсутствует, а для женской ипостаси оно не имеет однозначности).

5. Заключение.

Приведенное комплексное решение парадокса лжеца на первый взгляд может показаться моделью расслоения личности Эпименида на реальные и мнимые состояния (мысль, слово и их самовосприятие). Однако такой взгляд не учитывает наличия и свойств описанной в статье комплексной модели истины – мнимой логической единицы i, связывающей казалось бы несовместимые события на основе принципа двойственности.

Изложенная выше комплексная теория истины содержит в себе все три закона диалектического познания: единства и борьбы противоположностей (действительная и комплексная истина); перехода количества в качество ( переход от 4-значной к 9-значной комплексной логике); отрицания отрицания ( взаимоотношения действительной и гипердействительной, комплексной и гиперкомплексной истины).

Что касается применения комплексной логики для моделирования, то она вполне пригодна для этой цели как новая математико-философская основа систем искусственного интеллекта. Особый интерес представляет приведенная мужская и женская логическая интерпретация, обобщая которую можно поставить в соответствие многозначной комплексной логике женский тип, а гипердействительной бинарной логике – мужской тип человеческого мышления.

Список литературы.

1. В.И. Ленин Материализм и эмпириокритицизм. Критические заметки об одной реакционной философии. М., Политиздат, 1969, 392 с.

2. Ионов А.С., Петров Г.А. Интерпретация логических законов комплексной логикой / Вестник Новг. гос. ун-та., Сер. Технические науки, №17, 2001 г

3. .Ионов А.С., Петров Г.А. Основы алгебры 9-значной комплексной логики / Вестник Новг. гос. ун-та, Сер. Технические науки, 2004, № 28.

4. Ионов А.С., Петров Г.А. К вопросу о логическом управлении системами с интеллектом / Вестник Новг. гос. ун-та, Сер. Технические науки, 2005, № 30.

5. Список публикаций авторов по комплексной логике и тексты статей до 2004 года – в разделе НАУКА сайта www.polg2.narod.ru