АЛГЕБРА
9-ЗНАЧНОЙ КОМПЛЕКСНОЙ ЛОГИКИ И ЕЕ
ПРИМЕНЕНИЕ
А.С.Ионов, Г.А.Петров Новгородский государственный университет им.
Ярослава Мудрого
(Скопировано с сайта: psi-logic.shadanakar.org с разрешения админа.)
Основным недостатком
булевской алгебры логики с точки зрения идентификации и управления объектами, обладающими
сознанием (интеллектом), является то, что данная логика одномерна, то есть
описывает лишь действительные логические состояния и не учитывает мнимых.
Словосочетание «комплексная логика» встречается с 70-х годов
XX века, в частности, в работах логика А. Зиновьева [1] для обозначения связи лексики с формальным
логическим аппаратом в рамках традиционной булевской (действительной) логики.
Авторы данной статьи вкладывают в указанный термин принципиально иное
содержание. Ранее занимаясь вопросами
идентификации сложных технических систем, начиная с середины 80-х годов [2] они
приступили к разработке основ комплексной логики, названной по аналогии с
комплексными числами и связывающей воедино действительные и мнимые части
логических состояний объектов. Авторами была
сформулирована соответствующая комплексная интерпретация логических
законов [3] и намечены подходы к описанию комплексной теории вероятностей для
4-значной комплексной логики [4].
Введение в [5] понятий
положительных, отрицательных и мнимых множеств позволило перейти к формированию
основ алгебры 9-значной комплексной логики и ее применению к управлению
системами с интеллектом. Данным вопросам и посвящена настоящая статья.
1.
Связь комплексной логики с традиционной действительной логикой.
Булевская (действительная)
логика основана на традиционном ( и принятом
большинством до сих пор в качестве единственного) понятии истины как
безошибочности. Это нашло отражение в формулировке логического закона тождества
в виде
А = А
, (1)
т. е. объект есть то, что он
есть. Комплексный логический закон тождества выглядит так [3]
:
A = A + iВ, (2)
что означает: объект есть то, что он есть, плюс
ошибка В его восприятия субъектом, умноженная на i, где i – чисто мнимое множество,
мнимая логическая единица.
Истина и ложь в
действительной булевской логике выражаются следующим образом:
T=
истина = true -
отсутствие ошибки В ( достоверное событие);
F = ложь =
false - присутствие
ошибки В (невозможное событие) . (3)
С
учетом (2), объектом изучения в
комплексной логике является ошибка B восприятия объективной
реальности субъектом, для которой выполняется соотношение
. В = ![]() + i
+ i![]() , (4)
, (4)
где
![]() – действительная
составляющая ошибки, а i
– действительная
составляющая ошибки, а i![]() – мнимая составляющая ошибки. Рассмотрим их на примере рис.
1.
– мнимая составляющая ошибки. Рассмотрим их на примере рис.
1.
Пусть
для действительной логики ![]() означает событие,
заключающееся в отсутствии ошибки, тогда в соответствии с (3),
означает событие,
заключающееся в отсутствии ошибки, тогда в соответствии с (3), ![]() = true = T. Противоположное событие
= true = T. Противоположное событие ![]() = false
= F означает наличие ошибки. Такие же значения может принимать событие
= false
= F означает наличие ошибки. Такие же значения может принимать событие ![]() .
.
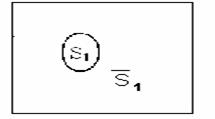
Рис.1. Действительные
логические события
Теперь
в соответствии с аксиоматикой 4-значной комплексной логики введем четыре
комплексных события, представленные на комплексной плоскости (Re, Im)
рис.2 и записанные в принятом порядке
следования квадрантов прописными буквами в отличие от действительных
терминов:
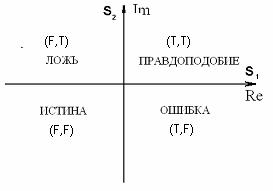
Рис.2.
Комплексная плоскость с
логическими событиями.
П = ПРАВДОПОДОБИЕ = (T,T) = T + iT
( T принимается за T);
Л = ЛОЖЬ = (F,T) = F + iT (F
принимается за T);
И = ИСТИНА = (F,F) = F + iF (F принимается за F);
О = ОШИБКА = (T,F) = T + iF (T принимается за F). (5)
.
Для получения 9-значной
комплексной логики введем и
интерпретируем следующие новые значения традиционных логических символов 1 и 0
как комплексных событий и символ –1 для комплексного
отрицательного множества:
1 = (F,T) =
ЛОЖЬ - положительное множество,
присутствие в событии положительной ошибки (например, продавец при расчете
обсчитывает покупателя в свою пользу) – достоверное событие;
0 = (T,T) + (F,F) =
ПРАВДОПОДОБИЕ + ИСТИНА = (T,T) – пустое множество, отсутствие ошибки в
событии (продавец точно рассчитывается с покупателем) – пустое событие;
-1 = (T,F) =
ОШИБКА – отрицательное множество, присутствие в событии отрицательной ошибки
(например, продавец обсчитывается в пользу покупателя) – антидостоверное
событие.
i - мнимая ошибка, чисто мнимое множество, задаваемое
формулой ii= -1, что подробно анализируется в [6].
Комплексная 9 - значная логика получается из
преобразования комплексной плоскости рис.2 таким образом, что составляющие и реальной, и мнимой оси могут принимать не
по два, а по три значения: 1, 0,-1. Тогда связь событий действительной и 9-значной комплексной логики
можно найти из решения системы уравнений (6):
1 = F + iT
-1 = T + iF, (6)
Из (6) получим T = true =
-1 –i = (-1,-1), что соответствует тому, что
отрицательное множество (событие)
принимается за отрицательное. Соответственно F = false = i = (0,1), что соответствует тому, что пустое событие
принимается за положительное.
В заключении раздела заметим, что целью комплексной логики является
нахождение значений мнимой логической
единицы i, обращающих ошибку
восприятия в выражении (2) в 0, что
соответствует выполнению закона тождества (1) для действительной логики. Таким
образом, действительная логика является частным случаем комплексной логики.
2.
Операции над комплексными событиями.
Вначале зададим операции логического сложения, вычитания,
умножения и отрицания над введенными тремя событиями действительной оси (1, 0,
-1) с помощью таблицы 1.
Таблица 1.
|
Сл.
|
0 |
1 |
-1 |
Выч.
|
0 |
1 |
-1 |
Умн. |
0 |
1 |
-1 |
Отр. |
|
|
0 |
0 |
1 |
-1 |
0 |
0 |
-1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
-1 |
1 |
-1 |
|
-1 |
-1 |
0 |
-1 |
-1 |
-1 |
-1 |
0 |
-1 |
0 |
-1 |
1 |
-1 |
1 |
Поясним практический смысл получаемых в результате добавления мнимой
составляющей 9 комплексных событий с
помощью таблицы 2, в которой мнимая часть В комплексного события (А,В) отражает
восприятие обсчета (реальной части А события)
субъектом - в нашем примере покупателем, с которым рассчитывается продавец. При
этом следует помнить, что, например, событие (1,1) = 1 + i1 и так далее, а произведение ii = -1.
Таблица
2.
|
№
события |
Формула события |
Реальная
часть события (А,В) |
Мнимая
часть события (А.В) |
|
1 |
(1, 1) |
Положительный обсчет |
Положительный обсчет |
|
2 |
(1, 0) |
Положительный обсчет |
Обсчета нет |
|
3 |
(1,-1) |
Положительный обсчет |
Отрицательный обсчет |
|
4 |
(0, 1) |
Обсчета нет |
Положительный обсчет |
|
5 |
(0,
0) |
Обсчета нет |
Обсчета нет |
|
6 |
(0,-1) |
Обсчета нет |
Отрицательный обсчет |
|
7 |
(-1,1) |
Отрицательный обсчет |
Положительный обсчет |
|
8 |
(-1,0) |
Отрицательный обсчет |
Обсчета нет |
|
9 |
(-1,-1) |
Отрицательный обсчет |
Отрицательный обсчет |
Определим теперь логические операции над событиями 9-значной комплексной логики с помощью формул и таблиц. Операцию логического сложения зададим формулой
(А,В) + (С,D) = ((A+C), (B+D))
,
(7)
где события А,В,С,D могут
принимать значения из множества {1,0,-1}, операции над которыми введены в таблице 1. Формуле (7)
соответствует таблица 3, в которой, как и в последующих таблицах 4,6 и 7, (А,В) записывается в 1 столбце, (С,D) – в первой строке.
Таблица 3.
|
+ |
( 1, 1) |
( 1, 0) |
( 1,-1) |
( 0, 1) |
( 0, 0) |
( 0,-1) |
(-1, 1) |
(-1, 0) |
(-1,-1) |
|
(1,1) |
(1,1) |
(1,1) |
(1,0) |
(1,1) |
(1,1) |
(1,0) |
(0,1) |
(0,1) |
(0,0) |
|
(1,0) |
(1,1) |
(1,0) |
(1,-1) |
(1,1) |
(1,0) |
(1,-1) |
(0,1) |
(0,0) |
(0,-1) |
|
(1,-1) |
(1,0) |
(1,-1) |
(1,-1) |
(1,0) |
(1,-1) |
(1,-1) |
(0,0) |
(0,-1) |
(0,-1) |
|
(0,1) |
(1,1) |
(1,1) |
(1,0) |
(0,1) |
(0,1) |
(0,0) |
(-1,1) |
(-1,1) |
(-1,0) |
|
(0,0) |
(1,1) |
(1,0) |
(1,-1) |
(0,1) |
(0,0) |
(0,-1) |
(-1,1) |
(-1,0) |
(-1,-1) |
|
(0,-1) |
(1,0) |
(1,-1) |
(1,-1) |
(0,0) |
(0,-1) |
(0,-1) |
(-1,0) |
(-1,-1) |
(-1,-1) |
|
(-1,1) |
(0,1) |
(0,1) |
(0,0) |
(-1,1) |
(-1,1) |
(-1,0) |
(-1,1) |
(-1,1) |
(-1,0) |
|
(-1,0) |
(0,1) |
(0,0) |
(0,-1) |
(-1,1) |
(-1,0) |
(-1,-1) |
(-1,1) |
(-1,0) |
(-1,-1) |
|
(-1,-1) |
(0,0) |
(0,-1) |
(0,-1) |
(-1,0) |
(-1,-1) |
(-1,-1) |
(-1,0) |
(-1,-1) |
(-1,-1) |
Операция комплексного
логического вычитания задается формулой
(А,В) – (С,D) = ((А-С), (В-D)) (8)
и соответствующей ей
таблицей 4.
Таблица
4.
|
- |
( 1, 1) |
( 1, 0) |
( 1,-1) |
( 0, 1) |
( 0, 0) |
( 0,-1) |
(-1, 1) |
(-1, 0) |
(-1,-1) |
|
(1,1) |
(0,0) |
(0,1) |
(0,1) |
(1,0) |
(1,1) |
(1,1) |
(1,0) |
(1,1) |
(1,1) |
|
(1,0) |
(0,-1) |
(0,0) |
(0,1) |
(1,-1) |
(1,0) |
(1,1) |
(1,-1) |
(1,0) |
(1,1) |
|
(1,-1) |
(0,-1) |
(0,-1) |
(0,0) |
(1,-1) |
(1,-1) |
(1,0) |
(1,-1) |
(1,-1) |
(1,0) |
|
(0,1) |
(-1,0) |
(-1,1) |
(-1,1) |
(0,0) |
(0,1) |
(0,1) |
(1,0) |
(1,1) |
(1,1) |
|
(0,0) |
(-1,-1) |
(-1,0) |
(-1,1) |
(0,-1) |
(0,0) |
(0,1) |
(1,-1) |
(1,0) |
(1,1) |
|
(0,-1) |
(-1,-1) |
(-1,-1) |
(-1,0) |
(0,-1) |
(0,-1) |
(0,0) |
(1,-1) |
(1,-1) |
(1,0) |
|
(-1,1) |
(-1,0) |
(-1,1) |
(-1,1) |
(-1,0) |
(-1,1) |
(-1,1) |
(0,0) |
(0,1) |
(0,1) |
|
(-1,0) |
(-1,-1) |
(-1,0) |
(-1,1) |
(-1,-1) |
(-1,0) |
(-1,1) |
(0,-1) |
(0,0) |
(0,1) |
|
(-1,-1) |
(-1,-1) |
(-1,-1) |
(-1,0) |
(-1,-1) |
(-1,-1) |
(-1,0) |
(0,-1) |
(0,-1) |
(0,0) |
Операции логического отрицания - (Отр.), логического обращения ‘ (Обр.) и логического сопряжения * (Сопр.) заданы в таблице 5.
Таблица 5.
|
|
(1,1) |
(1,0) |
(1,-1) |
(0,1) |
(0,0) |
(0,-1) |
(-1,1) |
(-1,0) |
(-1,-1) |
|
Отр.- |
(-1,-1) |
(-1,0) |
(-1,1) |
(0,-1) |
(0,0) |
(0,1) |
(1,-1) |
(1,0) |
(1,1) |
|
Обр.’ |
(1,1) |
(0,1) |
(-1,1) |
(1,0) |
(0,0) |
(-1,0) |
(1,-1) |
(0,-1) |
(-1,-1) |
|
Сопр.* |
(1,-1) |
(1,0) |
(1,1) |
(0,-1) |
(0,0) |
(0,1) |
(-1,-1) |
(-1,0) |
(-1,1) |
Соответствующие формулы для логического отрицания:
-(А,В) = (-А, -В), (9)
логического обращения
(А,В)’ = (В,А) (10)
и логического сопряжения
(А,В)* = (А, -В). (11)
Операция логического умножения
(Умн.) задается формулой (без знака операции):
(A,B)(C,D) = ((AC –
BD), (AD + BC)) (12)
и соответствующей таблицей
6.
Таблица
6.
|
Умн. |
( 1, 1) |
( 1, 0) |
( 1,-1) |
( 0, 1) |
( 0, 0) |
( 0,-1) |
(-1, 1) |
(-1, 0) |
(-1,-1) |
|
(1,1) |
(0,1) |
(1,1) |
(1,0) |
(-1,1) |
(0,0) |
(1,-1) |
(-1,0) |
(-1,-1) |
(0,-1) |
|
(1,0) |
(1,1) |
(1,0) |
(1,-1) |
(0,1) |
(0,0) |
(0,-1) |
(-1,1) |
(-1,0) |
(-1,-1) |
|
(1,-1) |
(1,0) |
(1,-1) |
(0,-1) |
(1,1) |
(0,0) |
(-1,-1) |
(0,1) |
(-1,1) |
(-1,0) |
|
(0,1) |
(-1,1) |
(0,1) |
(1,1) |
(-1,0) |
(0,0) |
(1,0) |
(-1,-1) |
(0,-1) |
(1,-1) |
|
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
|
(0,-1) |
(1,-1) |
(0,-1) |
(-1,-1) |
(1,0) |
(0,0) |
(-1,0) |
(1,1) |
(0,1) |
(-1,1) |
|
(-1,1) |
(-1,0) |
(-1,1) |
(0,1) |
(-1,-1) |
(0,0) |
(1,1) |
(0,-1) |
(1,-1) |
(1,0) |
|
(-1,0) |
(-1,-1) |
(-1,0) |
(-1,1) |
(0,-1) |
(0,0) |
(0,1) |
(1,-1) |
(1,0) |
(1,1) |
|
(-1,-1) |
(0,-1) |
(-1,-1) |
(-1,0) |
(1,-1) |
(0,0) |
(-1,1) |
(1,0) |
(1,1) |
(0,1) |
Введем, наконец, операцию логического деления / с помощью формулы (13) и соответствующей ей таблицы 7.
(А,В)/(С,D) = (A,B)(C,D)* = (А,В)(C,-D) (13)
В соответствии с таблицей 7,
заданное в ней логическое деление
совместимо с логическим умножением, то есть из АВ = С
следует C/A = B и C/B = A за
исключением случая, когда делитель – пустое (нулевое) множество (0,0). Поэтому
будем считать, что логическое деление на нулевое множество невозможно (по
аналогии с тем, как это принято в отношении нуля в математике чисел), что и отражено в таблице
7 постановкой знаков пробелов в
соответствующем столбце.
Таблица 7.
|
/ |
( 1, 1) |
( 1, 0) |
( 1,-1) |
( 0, 1) |
( 0, 0) |
( 0,-1) |
(-1, 1) |
(-1, 0) |
(-1,-1) |
|
(1,1) |
(1,0) |
(1,1) |
(0,1) |
(1,-1) |
- |
(-1,1) |
(0,-1) |
(-1,-1) |
(-1,0) |
|
(1,0) |
(1,-1) |
(1,0) |
(1,1) |
(0,-1) |
- |
(0,1) |
(-1,-1) |
(-1,0) |
(-1,1) |
|
(1,-1) |
(0,-1) |
(1,-1) |
(1,0) |
(-1,-1) |
- |
(1,1) |
(-1,0) |
(-1,1) |
(0,1) |
|
(0,1) |
(1,1) |
(0,1) |
(-1,1) |
(1,0) |
- |
(-1,0) |
(1,-1) |
(0,-1) |
(-1,-1) |
|
(0,0) |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
- |
(0,0) |
(0,0) |
(0,0) |
(0,0) |
|
(0,-1) |
(-1,-1) |
(0,-1) |
(1,-1) |
(-1,0) |
- |
(1,0) |
(-1,1) |
(0,1) |
(1,1) |
|
(-1,1) |
(0,1) |
(-1,1) |
(-1,0) |
(1,1) |
- |
(-1,-1) |
(1,0) |
(1,-1) |
(0,-1) |
|
(-1,0) |
(-1,1) |
(-1,0) |
(-1,-1) |
(0,1) |
- |
(0,-1) |
(1,1) |
(1,0) |
(1,-1) |
|
(-1,-1) |
(-1,0) |
(-1,-1) |
(0,-1) |
(-1,1) |
- |
(1,-1) |
(0,1) |
(1,1) |
(1,0) |
Из таблицы 7 следует также,
что деление комплексного логического события на само себя (за исключением нулевого
события) дает в результате логическую единицу 1.
3.
К определению алгебры комплексной логики.
Современная алгебра имеет дело с математическими моделями, определяемыми в терминах бинарных операций. Введенные выше четыре операции 9-значной комплексной логики позволяют перейти к рассмотрению вопросов соответствующей алгебры.
Назовем алгеброй комплексной
логики (комплексной алгеброй) класс S комплексных объектов А, В,
С,… , в котором определены четыре 9-значные операции,
обозначаемые как логическое сложение, вычитание, умножение и деление со следующими свойствами:
Для всех А,В,С
из S выполняется следующее:
1.
S содержит А+В, А-В, АВ и А/В
(свойство замкнутости).
2.
А+В = В+А;
АВ = ВА (коммутативные законы относительно
сложения и умножения).
3.
А(ВС) = (АВ)С
(ассоциативный закон относительно умножения).
4.
А + А = А
(свойство идемподентности относительно
сложения).
5.
S содержит элементы (1,1),
(1,0), (1,-1), (0,1), (0,0), (0,-1), (-1,1), (-1,0), (-1,-1) такие, что для
всякого элемента из S ( при том, что (1,0) = 1; (0,0) = 0 и (-1,0) =
-1) А+0 = А; А0 = 0; А1 = А; А(-1) = -А;
А/А = 1. Последнее – за исключением случая, когда А =
(0,0) = 0. При этом же из АВ =С следует С/А = В и С/В = А.
6.
Для каждого элемента А класс S
содержит:
а). Элемент –А, то есть отрицание элемента А такое, что А-А = 0. При этом если АВ = С, то (-А)В = -С и А(-В) = -С;
б) Элемент
А’ – обращение элемента А.
в) Элемент А* -
сопряжение элемента А.
В заключении дадим
определение комплексной логической функции. Если заданы n
комплексных логических переменных X1,X2,…,Xn, каждое из которых может быть равно любому элементу
данной алгебры комплексной логики, то комплексной логической функцией Y = F(X1,X2,…,Xn) называется выражение, получаемое из X1,X2,…,Xn путем логического сложения, вычитания, умножения,
деления и взятия отрицания, обращения и сопряжения.
4.
Применение полученных результатов к вопросам управления.
Разработка основ алгебры 9-значной комплексной логики позволяет перейти к
комплексной идентификации и управлению системами «субъект-среда-объект». При
традиционном подходе к идентификации объекта по его «входу-выходу» модель
восприятия (субъект) часто не включается в контур идентификации, хотя в
действительности модель может существенно влиять на объект и даже меняться с
ним местами, как это бывает в рассматриваемом случае, когда и субъект и
объект обладают интеллектом (логикой).
Разработанная для таких систем комплексная логика
позволяет их описывать и одновременно управлять ими с помощью мнимой логической единицы i, которая входит в описание
как модели (субъекта), так и объекта и вместе с тем является средой их
логического взаимодействия.
Будем искать комплексную логическую модель системы в
виде (2), где А
– логическая модель объекта; В – логическая модель субъекта (задается его
восприятием объекта); i – логическая модель среды взаимодействия субъекта и
объекта (рис.3).
Выскажем гипотезу о том, что i (мнимая логическая единица, невозможное событие)
имеет двоякую природу: с одной стороны, i = const, что вытекает из
ii = -1. С другой стороны, i может изменяться как модель среды логического
взаимодействия в процессе управления системой и, таким образом, i одновременно может
являться переменной величиной, что позволяет ею управлять.
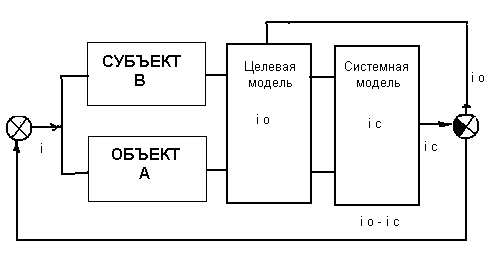
Рис.3. Схема комплексного
логического управления
В
качестве реального примера системы возьмем расчет продавца (объекта А) с
покупателем (субъектом В) в рамках 9-значной комплексной логики, для которой А и В могут
принимать любое из 9 логических состояний
(1,1), (1,0),…, (-1,-1) таблицы 2.
Целевая модель рис.3 служит для вычисления текущего
целевого значения среды взаимодействия io, соответственно являющегося целью управления. С
помощью системной модели вычисляется текущее выходное значение системы ic. Рассогласование между указанными моделями и является
управляющим воздействием среды, подаваемым на вход системы с помощью обратной
связи.
Логические уравнения, описывающие систему рис.3.,
вытекают из (2), откуда следует А’ = В + iА и В = А’ - i А (где ‘ – операция обращения), а также из возможных
психологических стратегий поведения системы, некоторые из которых собранны в
табл. 8.
. Таблица
8.
|
Номер |
Формула |
Подробная
формула |
Содержание
стратегии модели |
|
1 |
А = -А |
А
+ iВ = -А - iВ |
Модель
отрицания объекта |
|
2 |
А = А’ |
A + iB
= B + iA |
Модель
обращения объекта |
|
3 |
В = - В |
A’ – iA
= -A’ + iA |
Модель
отрицания субъекта |
|
4 |
B = B’ |
A’ – iA
= A – iA’ |
Модель
обращения субъекта |
|
5 |
А = А* |
A + iB
= A - iB |
Модель
сопряжения объекта |
|
6 |
В = В* |
A’ – iA
= A’ + iA |
Модель
сопряжения субъекта |
Проиллюстрируем работу схемы рис.3 на конкретном примере.
Пусть модель продавца А = (-1,1), то есть в реальности
продавца существует отрицательный обсчет, который им
воспринимается как положительный. Модель восприятия поведения продавца
покупателем зададим в виде В = (0,-1).
Выберем из таблицы 8 в качестве целевой модели модель 1 (отрицание объекта),
а в качестве системной модели – модель 2 (обращение объекта). Подставляя
выбранные значения А и В в
соответствующие формулы таблицы 8 и решая получаемые уравнения относительно iо и iс, можно найти рассогласование iс – iо и значения А и В
для следующего шага управления – и так до достижения нулевого
рассогласования. В результате получим:
Первый шаг управления: i = i; io = 0; iс
= -1; А=(-1,1); В = (0,-1);
Второй шаг управления: i = i + io – ic = i + 1; iо =0, iс = 1; А = -1 +
(i + 1) = (0,1); В = 0– (i + 1) = (-1,-1);
Третий шаг управления: i = i – 1; iо = 0; iс = 0; А = (-1,1); В = (0,-1);
Таким образом, за три шага управления достигнуто нулевое рассогласование, что и является заданной
целью управления средой логического взаимодействия.
Подводя итог, отметим, что в реальности рассмотренное
управление мнимой логической единицей i протекает в
условиях
1.
Изменения во
времени А и В
(моделей объекта и субъекта) в принятом 9-значном множестве значений (таблица
2).
2.
Изменения во
времени целевых и системных моделей управления (табл.8).
3.
Логической
неопределенности, возникающей из-за преднамеренного или случайного искажения
комплексной действительности.
4.
Динамического
характера процессов в системе рис.3.
Все это будет предметом дальнейших
исследований, направленных на поиск практического использования разработок
авторов в области комплексной логики.
Выводы.
Данное выше определение
алгебры 9-значной комплексной логики (комплексной алгебры) является предварительным
и сделано по аналогии с определением булевской алгебры. При этом заметим, что
по сравнению с последней, в описанной
комплексной алгебре не выполняются в общем случае многие закономерности,
такие как ассоциативный закон для сложения, дистрибутивные законы, свойство идемподентности относительно умножения, свойство
совместимости и т.д..
С другой стороны, наличие
новых операций логического вычитания и деления позволяет выявить целый ряд
новых свойств комплексной алгебры, подробное изучение которых является
предметом дальнейшей разработки и выходит за пределы данной статьи. Отметим
также, что введенное в статье расширение набора объектов и операций над ними
позволяет не только расширить класс функций комплексной алгебры, но и
составлять и решать соответствующие логические уравнения.
Приведенное в статье
использование алгебры 9-значной комплексной логики для управления средой
логического взаимодействия систем с интеллектом позволяет наметить пути
дальнейшего исследования системы рис.3, методами теории автоматического
управления. Полученные результаты могут быть использованы также в целях решения
проблем в области искусственного интеллекта и построения соответствующих
компьютеров.
Список литературы.
1.
Зиновьев А.А. Комплексная логика. М., «Наука», 1970г.
2. Ионов А.С. Комплексная логика для идентификации
систем, учитывающих возможные ошибки // Деп. рук.
ВИНИТИ, №7018-В88 от 16.09.88,13с.
3. Ионов А.С., Петров Г.А. Интерпретация логических
законов комплексной логикой / Вестник Новг. гос. ун-та., Сер. Технические
науки, №17, 2001 г
4. Ионов А.С., Петров Г.А. К построению основ теории
вероятности комплексных логических событий /
Вестник Новг. гос.
ун-та, Сер. Технические науки, 2004, № 26.
5. Ионов А.С., Петров Г.А. Построение основ алгебры комплексной логики на базе расширения теории множеств./ Вестник Новг. гос. ун-та. Сер.: Математика и информатика №22, 2002г
6. Ионов А.С., Петров Г.А. Принципы построения
гиперкомплексной логики / В сб. трудов Межд. научн. конференции « Искусственный
интеллект 2004» Таганрог-Донецк, т.1,
2004 г
7. .Ионов А.С., Петров Г.А.
Основы алгебры 9-значной комплексной логики /
Вестник Новг. гос.
ун-та, Сер. Технические науки, 2004, № 28.