Числа в троичном представлении Стахова

Класс HHT    (выполнение преобразования Гильберта-Хуанга на C++)

---

ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА-ХУАНГА

( сайт автора данного текста, Давыдова А.В. – geoin.org )

Судьба новой истины такова: в начале своего существования она всегда кажется ересью.

Томас Генри Гексли.

Эту стадию Хуанг уже прошел. Вытирать об него ноги математики прекратили и скопом ринулись обосновывать новый метод. А практикам понравилось: работает хорошо, интеграл всего один, и тот позаимствован у Гильберта. Наши, правда, опять лопухнулись, мир вопит от восторга, а мы интересуемся – о чем галдеж?

Игорь Бреднев. Уральский геофизик.

Содержание

Введение.

1. Преобразование Гильберта и аналитический сигнал. Определение и формула. Мгновенная амплитуда, фаза и частота сигнала. Симметрия огибающих сигнала.

2. Эмпирический метод декомпозиции (EMD) сигналов. Огибающие сигналов. Функции внутренних мод сигналов. Процесс отсеивания функций IMF. Критерии останова процесса декомпозиции. Ортогональность базиса декомпозиции. Примеры практического применения EMD.

3. Спектральный анализ Гильберта (HSA). Спектр мгновенных частот Гильберта.

4. EMD шумовых сигналов. EMD «белого шума». Частотная избирательность EMD.

Введение

Под преобразованием Гильберта-Хуанга (Hilbert-Huang transform – HHT) понимается метод эмпирической модовой декомпозиции (EMD) нелинейных и нестационарных процессов и Гильбертов спектральный анализ (HSA). HHT представляет собой частотно-временной анализ данных (сигналов) и не требует априорного функционального базиса преобразования. Функции базиса получаются адаптивно непосредственно из данных процедурами отсеивания функций «эмпирических мод». Мгновенные частоты вычисляются от производных фазовых функций Гильбертовым преобразованием функций базиса. Заключительный результат представляется в частотно-временном пространстве /1/.

EMD-HSA был предложен Норденом Хуангом в 1995 в США (NASA) для изучения поверхностных волн тайфунов, с обобщением на анализ произвольных временных рядов коллективом соавторов в 1998 г. /2/. В последующие годы, по мере расширения применения EMD-HSA для других отраслей науки и техники, вместо термина EMD-HSA был принят более короткий термин преобразования HHT.

Традиционные методы анализа данных предназначены, как правило, для линейных и стационарных сигналов и систем, и только в последние десятилетия начали активно развиваться методы анализа нелинейных, но стационарных и детерминированных систем, и линейных, но нестационарных данных (вейвлетный анализ, распределение Wagner-Ville и др.). Между тем, большинство естественных материальных процессов, реальных физических систем и соответствующих этим процессам и системам данных в той или иной мере являются нелинейными и нестационарными, и при анализе данных используются определенные упрощения, особенно в отношении априорно устанавливаемого базиса преобразования данных в новые, удобные для обработки и анализа метрические пространства.

Необходимое условие корректного представления нелинейных и нестационарных данных заключается в том, чтобы иметь возможность формирования адаптивного базиса, функционально зависимого от содержания самих данных. Такой подход и реализуется в методе HHT, хотя на данный момент без достаточно строгих математических обоснований. Хорошие результаты применения метода для решения многих практических задач позволяют надеяться, что за разработкой строгой теории метода дело не станет.

24.1. ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА И АНАЛИТИЧЕСКИЙ СИГНАЛ

Определение и формула. Преобразование Гильберта TH[x(t)] действительной функции x(t), -∞ < t < ∞, - есть действительная функция, определенная как

(t) = ТН[x(t)] = x(t) _* (1/pt),

(t) = . (24.1.1)

Функция 1/(t-t) называется ядром преобразования Гильберта. Преобразование имеет особую точку при t-t Þ 0, в которой при вычислении используется главное значение интеграла по Коши. Функции x(t) и (t) обычно называют сопряженными по Гильберту.

Физически, преобразование Гильберта может быть интерпретировано как естественный p/2 фазовращатель, который при прохождении через систему сигнала x(t) изменяет фазу всех частотных составляющих сигнала на p/2, и тем самым делает сигнал (t) ортогональным сигналу x(t). Это позволяет сформировать из сигналов x(t) и (t) комплексный аналитический сигнал z(t), как

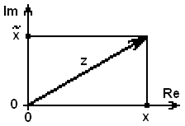
Рис. 24.1.1.

z(t) = x(t) + j(t), (24.1.2)

где z(t) представлен вектором на комплексной плоскости с проекциями на действительной и мнимой оси соответственно x(t) и (t) (рис. 24.1.1). Преимущество этого представления состоит в том, что возникает возможность однозначно определять текущие временные параметры сигнала z(t), а именно – мгновенные значения его амплитуды и фазы.

Допустим, что имеем зарегистрированный радиосигнал x(t) с несущей частотой w_o, который содержит определенную информацию, заключенную в огибающей сигнала u(t) и его фазе j(t):

x(t) = u(t) cos (w_ot+j(t)).

В другой форме:

x(t) = a(t)×cos(w_ot) + b(t)×sin(w_ot),

a(t) = u(t) cos wt, b(t) = u(t) sin wt, u(t) =, tg j(t) = b(t)/a(t).

Мгновенная амплитуда, фаза и частота сигнала. С использованием преобразования Гильберта из сигнала x(t) сформируем аналитически сопряженный сигнал (t). С учетом сдвига фазы на p/2:

(t) = a(t)×sin(w_оt) – b(t)×cos(w_ot).

z(t) = x(t) + j×(t).

Квадрат модуля сигнала z(t):

|z(t)|²= x²(t)+²(t)= a²(t)[cos²(w_ot)+sin²(w_ot)]+b²(t)[cos²(w_ot)+sin²(w_ot)]= u²(t).

Отсюда, огибающая u(t) и мгновенная фаза w(t) сигнала x(t):

u(t) =. (24.1.3)

f(t) = w_ot+j(t) = arctg[(t)/x(t)]. (24.1.4)

j(t) = f(t) - w_ot.

Мгновенная частота сигнала определяется по скорости изменения мгновенной фазы:

dj(t)/dt = [’(t)x(t) - x’(t)(t)] / (²(t)+x²(t)). (24.1.5)

Определения (24.1.3) и (24.1.5) подразумевают, что в каждый текущий момент времени в сигнале существует единственное значение амплитуды и частоты. Однако физическая интерпретация понятия «мгновенности» неоднозначна и требует определенных ограничений.

Действительно, в стационарных моногармонических сигналах и в сигналах с непрерывным гладким изменением частоты понятие «мгновенности» имеет вполне определенный физический смысл, поскольку точно фиксирует положение каждой текущей точки в частотно-временном пространстве, что можно наглядно видеть на рис. 24.1.2 и 24.1.3.

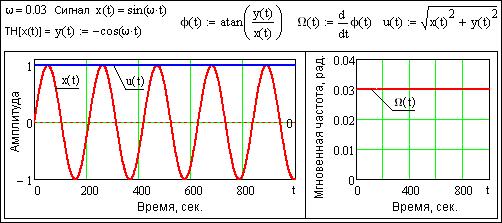
Рис. 24.1.2. Мгновенная амплитуда и частота гармонического сигнала.

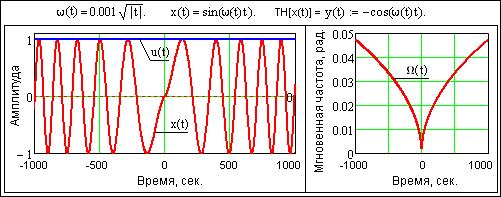
Рис. 24.1.3. Мгновенная амплитуда и частота гладкого непрерывного сигнала.

Однако уже для суммы двух гармонических сигналов, приведенных на рис. 24.1.4, положение усложняется. Физически в каждой текущей точке сигнала постоянно присутствуют две частоты с определенной амплитудой колебаний. Мгновенная амплитуда преобразования Гильберта в этом случае отображает не сумму значений гармоник в каждый текущий момент времени, а огибающую интерференции этих гармоник, при этом максимальные мгновенные значения огибающей, равные сумме амплитуд гармоник, фиксируются в точках максимумов по модулю суммы первых производных гармоник, а минимальные значения, равные разности амплитуд гармоник, в точках минимума суммы модулей первых производных гармоник. Это обеспечивает симметричность верхней и нижней огибающих относительно временной оси. Все вышеизложенное действительно и для любых многотональных сигналов.

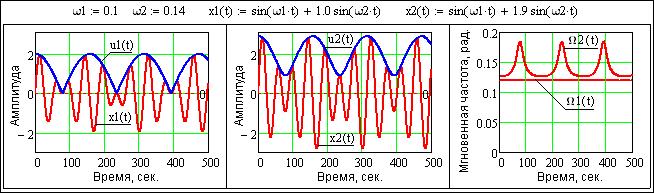
Рис. 24.1.4. Мгновенные амплитуды и частоты двутональных сигналов.

Что касается мгновенных значений частоты, то при равной амплитуде гармоник мгновенная частота во всех точках сигнала равна среднему значению частот гармоник. При неравной амплитуде гармоник функция мгновенной частоты сдвигается в сторону частоты гармоники с большей амплитудой и приобретает пульсирующий характер, при этом пики экстремумов частотных пульсаций соответствуют минимумам огибающих пульсаций и также направлены в сторону частоты гармоники с большей амплитудой.

Симметрия огибающих сигнала имеет существенное значение и ее нарушение, например, в случае наличия в сигнале постоянной составляющей или тренда, существенно изменяет результаты преобразования.

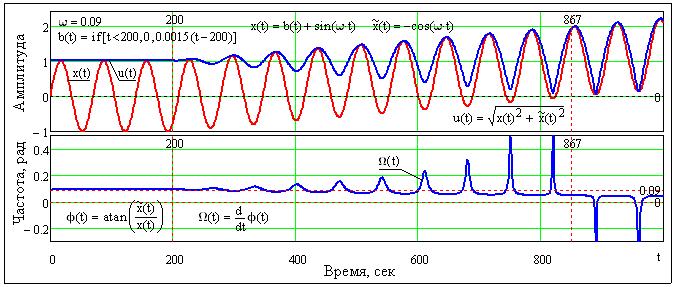
Рис. 24.1.5. Преобразование Гильберта сигнала с трендом.

На рис. 24.1.5 приведен сигнал, представленный монотонной гармоникой с амплитудой a=1 в сумме с трендом b(t), значения которого изменяются линейно от нуля до 1.2 в интервале 200 < t < 1000.

При отсутствии тренда (0<t<200) значения мгновенной амплитуды и частоты соответствуют амплитуде и частоте гармоники. При появлении в сигнале тренда и его значениях b(t)<a в значениях мгновенной амплитуды появляются пульсации, синхронные с гармоникой сигнала, полный размах которых (от максимума до минимума) нарастает пропорционально b(t)/(2a), и становится практически постоянным порядка 2а при b(t)>a.

Отношение a = b(t)/a в интервале 0≤a≤1 в первом приближении может считаться коэффициентом локальной асимметрии формы сигнала относительно временной оси. Асимметрия формы сигнала существенно влияет на вычисления мгновенных частот, что наглядно видно на частотно-временном графике рис. 24.1.5 в интервале 200<t<867. В интервалах минимумов мгновенных амплитуд появляются частотные пики максимумов, амплитуда которых пропорциональна a. При a>1 колебания становятся стоячими и частотные пики меняют знак, уходя в область отрицательных частот, а, следовательно, мгновенные частоты в этом случае вообще не имеют смысла.

Таким образом, можно констатировать, что для простых гармонических сигналов физически значимая мгновенная частота может быть определена только для функций локально симметричных относительно нулевого среднего уровня. Аналогичное заключение может быть распространено и на многокомпонентные сигналы, при условии, что каждый из таких сигналов симметричен относительно нулевого уровня.

В принципе, любой произвольный сигнал можно рассматривать в виде суммы колебательных процессов, удовлетворяющих условию симметричности и наложенных на тренд произвольной формы. В этом случае правомочна и обратная задача разложения произвольного сигнала на эти составляющие компоненты и остаточный тренд. Метод решения этой задачи был предложен Н.Хуангом и получил название эмпирической модовой декомпозиции (EMD) сигналов.

24.2. МЕТОД ЭМПИРИЧЕСКОЙ МОДОВОЙ ДЕКОМПОЗИЦИИ СИГНАЛОВ /1,2,3/

EMD (Empirical Mode Decomposition) - метод разложения сигналов на функции, которые получили название внутренних или «эмпирических мод». Метод представляет собой адаптивную итерационную вычислительную процедуру разложения исходных данных (непрерывных или дискретных сигналов) на эмпирические моды или внутренние колебания.

Огибающие сигналов. У каждого сигнала имеются локальные экстремумы: чередующиеся локальные максимумы и локальные минимумы с произвольным расположением по координатам (независимым переменным) сигналов. По этим экстремумам с использованием методов аппроксимации можно построить две огибающие сигналов: нижнюю - построенную по точкам локальных минимумов, и верхнюю - построенную по точкам локальных максимумов, а также функцию «среднего значения огибающих», которой отвечает срединная линия, расположенная в точности между нижней и верхней огибающими.

Функции внутренних мод сигналов. Модовая декомпозиция сигналов основана на предположении, что любые данные состоят из различных внутренних колебаний (intrinsic mode functions, IMF). В любой момент времени данные могут иметь множество сосуществующих внутренних колебаний - IMFs. Каждое колебание, линейное или нелинейное, представляет собой модовую функцию, которая имеет экстремумы и нулевые пересечения. Кроме того, колебания в определенной степени «симметричны» относительно локального среднего значения. Конечные сложные данные образуются суммой модовых функций, наложенных на региональный тренд сигнала.

Эмпирическая мода - это такая функция, которая обладает следующими свойствами:

1. Количество экстремумов функции (максимумов и минимумов) и количество пересечений нуля не должны отличаться более чем на единицу.

2. В любой точке функции среднее значение огибающих, определенных локальными максимумами и локальными минимумами, должно быть нулевым.

IMF представляет собой колебательный режим, но вместо постоянной амплитуды и частоты, как в простой гармонике, у IMF могут быть переменная амплитуда и частота, как функции независимой переменной (времени, координаты, и пр.). Первое свойство гарантирует, что локальные максимумы функции всегда положительны, локальные минимумы соответственно отрицательны, а между ними всегда имеют место пересечения нулевой линии. Второе свойство гарантирует, что мгновенные частоты функции не будут иметь нежелательных флуктуаций, являющихся результатом асимметричной формы волны.

Любую функцию и любой произвольный сигнал, изначально содержащие произвольную последовательность локальных экстремумов (минимум 2), можно разделить на семейство функций IMFs и остаточный тренд. Если данные лишены экстремумов, но содержат точки перегиба («скрытые» экстремумы наложения модовых функций и крутых трендов), то для открытия экстремумов может использоваться дифференцирование сигнала.

Допустим, что имеется произвольный сигнал y(t). Сущность метода EMD заключается в последовательном вычислении функций эмпирических мод c_j(t) и остатков r_j(t) = r_j-1(t) - c_j(t), где j = 1, 2, 3, …, n при r₀ = y(t). Результатом разложения будет представление сигнала в виде суммы модовых функций и конечного остатка:

x(t) = c_j(t) + r_n(t),

где n — количество эмпирических мод, которое устанавливается в ходе вычислений.

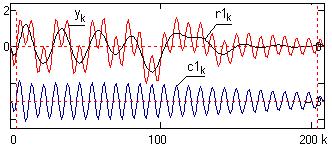
Для наглядности методику реализации EMD рассмотрим на примере разложения цифрового массива модельного сигнала y(k), представленного на рис. 24.2.1. Сигнал смоделирован суммой трех нестационарных по амплитуде гармоник различной частоты на интервале отсчетов по k от 0 до 200, и продлен на начальном и конечном участках на интервалы tp=4 для задания начальных и конечных условий преобразования и устранения ошибок преобразования на концевых интервалах обрабатываемого массива данных.

Рис. 24.2.1.

Процесс отсеивания функций IMF. Алгоритм эмпирической декомпозиции сигнала складывается из следующих операций его преобразования.

Рис. 24.2.2.

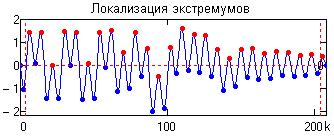
Операция 1. Находим в сигнале y(k) положение всех локальных экстремумов, максимумов и минимумов процесса (номера точек k_i.ext экстремумов), и значения y(k_i.ext) в этих точках (рис. 24.2.2). Между этими экстремумами сосредоточена вся информация сигнала. Группируем раздельно для максимумов и для минимумов массивы координат k_i.ext и соответствующих им амплитудных значений у(k_i.ext). Число строк в массивах максимумов и минимумов не должно отличаться более чем на 1.

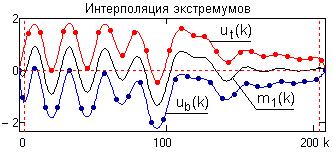
Рис. 24.2.3.

Операция 2. Кубическим сплайном (или каким либо другим методом) вычисляем верхнюю u_t(k) и нижнюю u_b(k) огибающие процесса соответственно, по максимумам и минимумам, как это показано на рис. 24.2.3 (красный и синий цвет). Определяем функцию средних значений m₁(k) между огибающими (черный цвет).

m₁(k) = (u_t(k)+u_b(k))/2.

Разность между сигналом y(k) и функцией m₁(k) дает нам первую компоненту отсеивания (Sifting) – функцию h₁(k), которая является первым приближением к первой функции IMF:

h₁(k) = y(k) – m₁(k). (24.2.1)

Операция 3. Повторяем операции 1 и 2, принимая вместо y(k) функцию h₁(k), и находим второе приближение к первой функции IMF – функцию h₂(k).

h₂(k) = h₁(k) – m₂(k).

Последующие итерации выполняются аналогично. Алгоритм итераций нахождения первой функции IMF:

h_i(k) = h_i-1(k) – m_i(k), (24.2.2)

По мере увеличения количества итераций функция m_i(k) стремится к нулевому значению, а функция h_i(k) - к неизменяемой форме. С учетом этого, естественным критерием останова итераций является задание определенного предела по нормализованной квадратичной разности между двумя последовательными операциями приближения, определяемой как

d = S_k [|h_i-1(k) - h_i(k)|² /h_i-1²(k)]. (24.2.3)

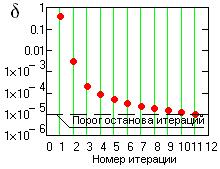
Рис. 24.2.4.

Как правило, для выполнения качественного отсеивания модовых функций достаточно 6-8 итераций. Слишком строгий критерий останова может завышать количество IMF и создавать компоненты, не несущие какой-либо полезной информации. С другой стороны, при слабом критерии возможно отсеивание IMF, не полностью удовлетворяющих свойствам модовых функций, что может приводить к появлению в этих IMF отрицательных мгновенных частот.

Останов итераций по нормализованной квадратичной разности (24.2.3) исторически был первым по применению. В 2003 г. Quek [4] предложил другой, более эффективный критерий переменной меры, определенной как

d = S_k |h_i-1(k) - h_i(k)|² / S_k h_i-1²(k). (24.2.3)

Пример изменения значений d в процессе итераций приведен на рис. 24.2.4.

Однако для сложных и объемных (по количеству отсчетов) сигналов в процессе итераций может изменяться количество выделяемых экстремумов (появление ранее «скрытых» экстремумов), при этом наблюдаются скачки значения d в большую сторону, начиная с которых снова начинается процесс уменьшения d, а общее количество итераций может увеличиваться до 20-30 без существенного повышения качества отсеивания. Опыт показывает, что для оптимальных отсеиваний число итераций порядка 6-8 является вполне достаточным. Все большее применение находит и другие критерии останова процесса отсеивания, ориентированные на характер и особенности обрабатываемых данных, и останов по нескольким критериям с заданием определенных логических условий по их соотношению (например, по порогу d, но не более J-итераций, и т.п.).

Рис. 24.2.5.

Последнее значение h_i(k) итераций принимается за наиболее высокочастотную функцию с₁(k) = h_i(k) семейства IMF, которая непосредственно входит в состав исходного сигнала y(k). Это позволяет вычесть с₁(k) из состава сигнала и оставить в нем более низкочастотные составляющие (показано на рис. 24.2.5):

r₁(k) = y(k) – c₁(k). (24.2.4)

Функция r₁(k) обрабатывается как новые данные по аналогичной методике с нахождением второй функции IMF – c₂(k), после чего процесс продолжается:

r₂(k) = r₁(k) – c₂(k), и т.д. (24.2.5)

Таким образом, достигается декомпозиция сигнала в n – эмпирическом приближении:

y(k) = c_n(k)+r_n(k). (24.2.6)

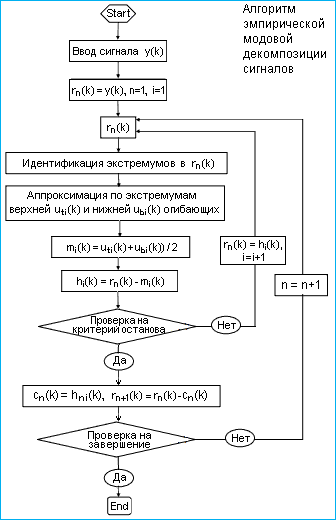
Рис. 24.2.6.

Полный алгоритм EMD приведен на рис. 24.2.6.

Критерии останова процесса декомпозиции сигнала могут быть следующими:

1. Остаток r_n(k) не содержит экстремальных точек, т.е. становится либо константой, либо монотонной функцией, из которой больше не может быть извлечено функций IMF.

2. Остаток r_n(k) во всем интервале задания сигнала становится несущественным по своим значениям по сравнению с сигналом и не представляет интереса для анализа.

3. Так как суммирование всех функций IMF (реконструкция сигнала) должно давать исходный сигнал, то можно останавливать разложение заданием относительной погрешности среднеквадратической реконструкции (без учета остатка r_n(k)) .

4. По мере увеличения количества функций IMF относительная среднеквадратическая погрешность реконструкции достаточно сложных и протяженных сигналов уменьшается, но, как правило, имеет определенный минимум. По-видимому, это определяется попытками алгоритма разложить остаток на функции, частично компенсирующие друг друга. Соответственно, останов программы может выполняться, если следующая выделенная функция IMF увеличивает погрешность реконструкции.

Другими словами, остановка декомпозиции сигнала должна происходить при максимальном «выпрямлении» остатка, т.е. превращения его в тренд сигнала по интервалу задания с числом экстремумов не более 2-3. Даже для данных с нулевым средним значением конечный остаток может отличаться от нуля. Чтобы применять метод EMD, центрирования данных не требуется, метод нуждается только в локализациях экстремумов. Нулевая линия для каждого компонента декомпозиции будет сформирована процессом отсеивания. Извлеченные IMFs локально симметричны, имеют физически значимые функции мгновенных частот, различные IMFs не показывают ту же самую частоту в то же самое время. Каждая IMF содержит более низкие частотные составляющие, чем извлеченная перед ней.

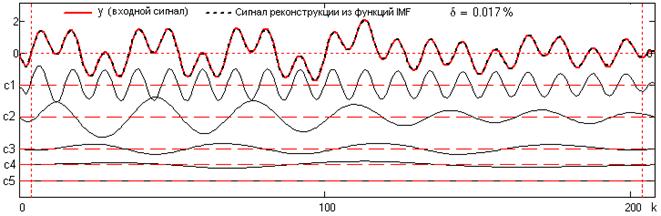
На рис. 24.2.7 приведен пример полной декомпозиции сигнала с остановом по критерию 1. На верхнем графике рисунка приведен входной сигнал преобразования (красным) и сигнал обратной реконструкции (пунктиром) суммированием функций разложения c_i (c1-c5).

Рис. 24.2.7.

Компоненты EMD обычно физически значимы, поскольку характеристические параметры функций IMF определяются материальными данными.

Ортогональность базиса декомпозиции. Таким образом, входной сигнал y(k) в соответствии с выражением (24.2.6) раскладывается по базису, который, не определен аналитически, но удовлетворяет всем традиционным требованиям базиса. На основании проверки на модельных и опытных данных он является:

- законченным и сходящимся (сумма всех функций IMF и остатка равна исходному сигналу и не зависит от критериев останова итераций),

- ортогональным (все IMF и остаток ортогональны друг другу),

- единственным.

И, что самое главное – он является адаптивным, так как получен непосредственно из анализируемых данных эмпирическим методом.

Ортогональность базиса может быть проверена скалярным произведением любых пар компонентов IMF. Сумма (24.2.6) всех компонентов IMF, включая остаток, должна реконструировать входной сигнал и может использоваться для определения ошибки декомпозиции. Как правило, наибольшие локальные ошибки декомпозиции наблюдаются на концевых участках входного массива данных. Для исключения ошибок рекомендуется задавать интервалы начальных и конечных условий, а сигнал на этих интервалах формировать какой-либо функцией прогнозирования, или продлевать (четно или нечетно) функцией самого сигнала.

Н. Хуанг утверждает также, что базис разложения является единственным. Но это утверждение можно считать спорным. Эмпирический процесс разложения сигнала в силу своей адаптивности неуправляем, по крайней мере, в настоящей форме. Даже монотональные составляющие многокомпонентного сигнала при определенном влиянии дестабилизирующих факторов (шумов, импульсных помех и т.п.) и близких по частоте соседних компонент могут при декомпозиции «перетекать» на отдельных временных интервалах в модовые функции соседних IMF.

Примеры практического применения EMD. В качестве примера в работе /3/ приводится EMD-анализ данных девиации периода вращения Земли. В результате исследований всем выделенным функциям IMF сопоставлены определенные физические процессы, которыми и вызвано их формирование (влияние штормов и тайфунов, месячных вариаций мощности приливов, явления Эль-Ниньо и прочие факторы). Ниже, без комментариев, приводятся выборки из результатов данного анализа, демонстрирующие свойства базиса.

Рис. 24.2.8. Данные.

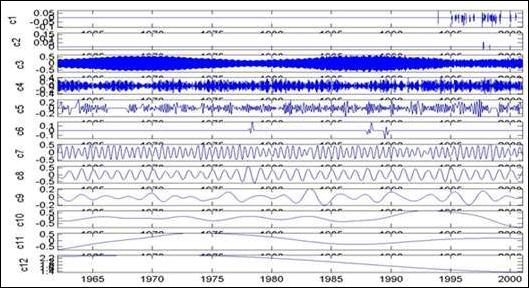
Рис. 24.2.9. Семейство IMF.

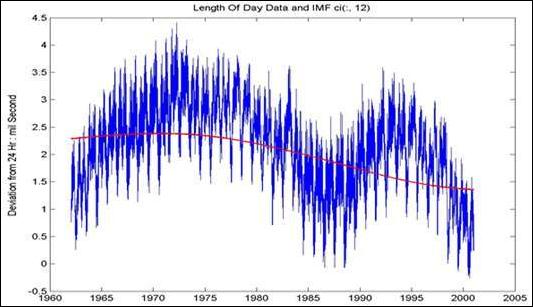
Рис. 24.2.10. Данные и с12 IMF.

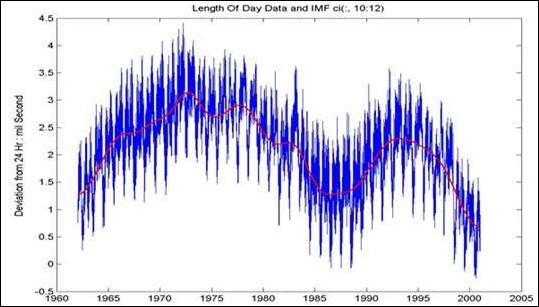
Рис. 24.2.11. Данные и сумма с10+с11+с12.

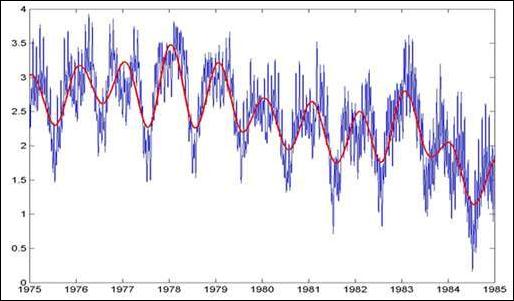
Рис. 24.2.12. Детализация данных и сумма с8+с9+с10+с11+с12.

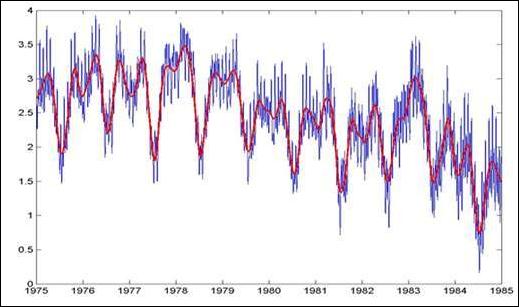
Рис. 24.2.13. Детализация данных и сумма с7+с8+с9+с10+с11+с12

Еще один пример из этой же работы /3/.

Рис. 24.2.14. Глобальная температурная аномалия. Ежегодные данные с 1856 до 2003.

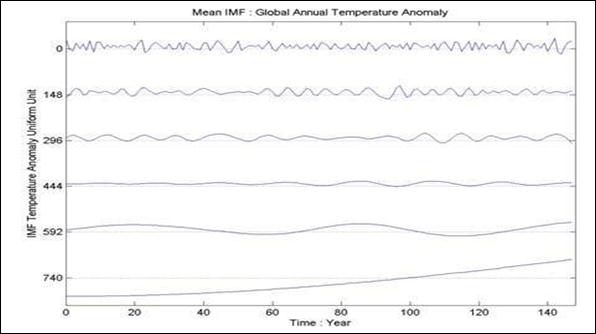
Рис. 24.2.15. Средние значения IMF за 10 просеиваний: СС(1000, I)

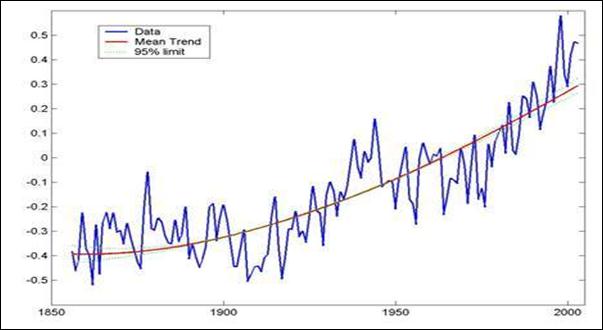
Рис. 24.2.16. Данные и тренд C6.

24.3. СПЕКТРАЛЬНЫЙ АНАЛИЗ ГИЛЬБЕРТА (HSA) /1,2/

IMF, определенные вышеприведенным способом, допускают вычисление физически значимых мгновенных частот, что дает возможность создать частотно-временное представление сигнала на основе преобразования Гильберта.

Спектр мгновенных частот Гильберта. После выполнения преобразования Гильберта на каждой компоненте IMF первоначальные данные x(t) могут быть выражены как вещественная часть комплексной формы в следующем виде:

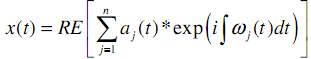(24.3.1)

Здесь, остаток r_n не учтен, поскольку это постоянная или монотонная функция. В отличие от преобразования Фурье, здесь и амплитуда a_j(t), и мгновенная частота w_j(t) являются функцией от времени. На рис. 24.3.1 приведено сопоставление частотно-временного представления модельного сигнала в трех представлениях.

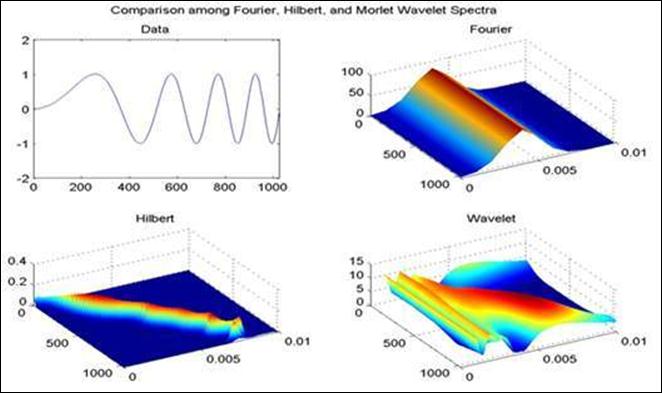
Рис. 24.3.1.

Разрешающая способность по времени спектра Гильберта определяется частотой дискретизации данных, в то время как частотная разрешающая способность произвольна. Самая низкая извлекаемая частота равна 1/Т, где Т – интервал задания сигнала, а самая высокая частота 1/(nDt), где Dt – интервал дискретизации данных, а n = 5 минимальное число отсчетов для точного определения частоты.

Выбор сплайна - основной шаг в генерации модовых функций, как базиса для спектрального анализа Гильберта. Обычно используются кубические сплайны, но при их применении могут возникать серьезные проблемы на концевых участках сигналов, где у кубического сплайна могут быть большие колебания. На качество выделения модовых функций влияет также четкость выделения всех экстремумов, которая зависит от частоты дискретизации данных. Для повышения качества процесса EMD и частотной разрешающей способности анализа можно использовать сплайны более высокого порядка, но это связано с увеличением трудоемкости вычислений.

Кроме типа сплайна на точность преобразования Гильберта на концевых интервалах сигналов конечной длины оказывает влияние явление Гиббса в области концевых разрывов сигналов. Чтобы уменьшить оба типа концевых эффектов можно рекомендовать задание начальных условий в начале и в конце сигнала в виде двух волн. Другой эффективный метод - выбирать сигнал так, чтобы концевые эффекты находились вне окна анализа.

24.4. EMD ШУМОВЫХ СИГНАЛОВ /5/

Шумы, сопровождающие полезную информацию в сигнале, в принципе, не относятся к типу колебательных в прямом смысле этого понятия. Но они полностью удовлетворяют приведенным выше определениям функций IMF. При распределении во всем частотном диапазоне входного сигнала и выполнении EMD, они распределяются по всем функциям IMF. Так как информация в главном частотном диапазоне дискретных сигналов обычно является низкочастотной, то шумы «отсеиваются», в основном, в высокочастотные функции IMF. Но в эти функции могут "просачиваться" и высокочастотные спектральные составляющие информационной части сигнала в зависимости от их положения в главном частотном диапазоне. Соответственно, на первый план выдвигается задача формирования определенных критериев отбора только шумовых функций IMF (для исключения их при последующей реконструкции сигнала) и влияния на этот отбор как статистических и спектральных характеристик самих шумов, так и спектрального состава полезной информации в сигнале.

EMD «белого шума». Белый шум является стационарным случайным процессом q(t), автокорреляционная функция которого описывается дельта - функцией Дирака и, соответственно, спектральная плотность мощности шумов не зависит от частоты и имеет постоянное значение Wq(f) = s², равное дисперсии значений q(t). По существу, это идеализированный случайный процесс с бесконечной энергией. Но в случае постоянства спектральной плотности мощности случайного процесса в конечном диапазоне частот это существенно упрощает анализ сигналов. Многие помехи в радиотехнике, в технике связи и в других отраслях техники рассматривают как белый шум, если эффективная ширина спектра сигналов много меньше эффективной ширины спектра шумов и спектральная плотность мощности шумов слабо изменяется в интервале спектра сигнала.

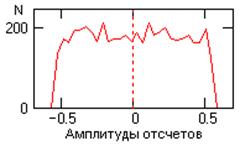
Рис. 24.4.1. Гистограмма шумов

Понятие "белый шум" определяет только спектральную характеристику случайного процесса, а, следовательно, под это понятие подпадают любые случайные процессы, имеющие равномерный энергетический спектр и различные законы распределения. На рис. 24.4.1. Приведена гистограмма единичной реализации модельного «белого шума» y(k) в системе Mathcad (5000 отсчетов) с равномерным распределением отсчетов от -0.55 до +0.55 и дисперсией 0.1. Спектральную плотность мощности модельной реализации шума можно посмотреть на рис. 24.4.5.

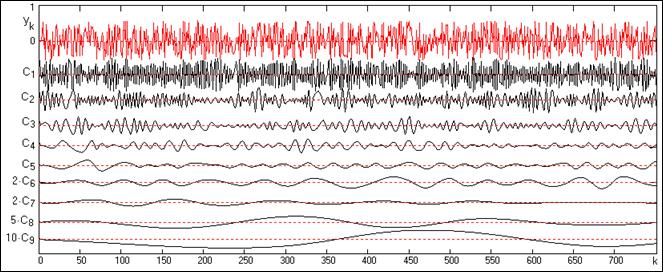
Рис. 24.4.2.

Рис. 24.4.3.

На рис. 24.4.2 приведен результат EMD модели y(k) шума на первых 750 отсчетах. Шумовой сигнал данной реализации был разложен на 12 функций IMF, первые девять из которых приведены на рисунке (4 последних функции в увеличенном масштабе). Останов процесса декомпозиции выполнен по минимуму погрешности реконструкции без учета остатка, процесс снижения погрешности при увеличении количества функций IMF приведен на рис. 24.4.3. Количество функций IMF в различных реализациях случайного сигнала изменяется от 8 до 14. Останов итераций при вычислении каждой функции IMF был установлен по относительному расхождению между последовательными итерациями с порогом 0.01%, при этом количество итераций для первых функций IMF достигает 30 и, как правило, постепенно снижается. Погрешность реконструкции с учетом остатка практически равна нулю. Вычислением скалярного произведения любых двух функций IMF можно убедиться в их взаимной ортогональности.

На рис. 24.4.4-А приведены гистограммы первых четырех IMF в сопоставлении с гистограммой входного сигнала y(k). Как следует из этих графиков, EMD существенно изменяет плотности распределения выходных функций. Распределение первой IMF становится двумодальным с прогибом вниз на малых (близких к нулевым) амплитудах. Это объясняется тем, что для рядом расположенных однополярных импульсов при EMD выделяются экстремумы импульсов большей амплитуды, которые и отсеиваются в первую функцию IMF. При вычитании этой функции из входного сигнала распределение оставшейся части шумов становится близким к гауссовому с нулевым средним значением и резким сокращением рядом расположенных однополярных импульсов. На отборе всех последующих IMF этот фактор уже не сказывается, и они имеют распределение, близкое к гауссовому, а рядом расположенные однополярные импульсы воспринимаются, как более низкочастотные составляющие шума. Статистика последовательной реконструкции шумового сигнала частично показана на рис. 24.4.4-В.

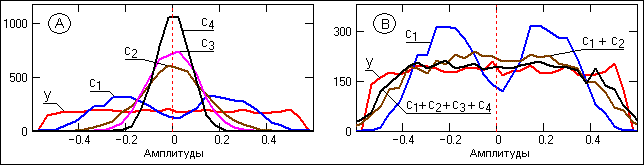
Рис. 24.4.4.

Проверка процесса EMD на шумовых сигналах с другими законами распределения (Гаусса, Пуассона и пр.) показала, что качественный характер процесса остается практически неизменным.

На рис. 24.4.5 приведены спектры плотности мощности сигнала y(k) и первых семи функций IMF в главном частотном диапазоне сигнала 0-p (5000 отсчетов шума с Dk = 1, отсчеты по спектру 0-2500 с шагом Dw = p/2500).

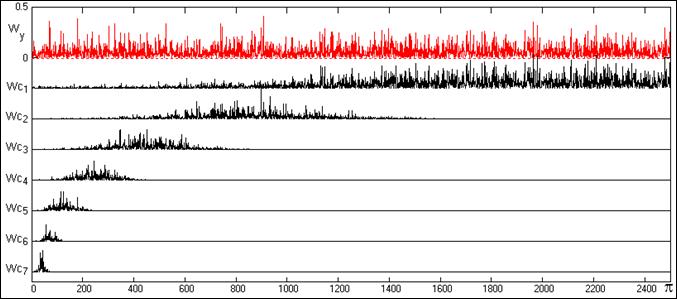
Рис. 24.4.5.

Частотная избирательность EMD. По рис. 24.4.5 видно, что процесс EMD обладает вполне определенной частотной избирательностью на каждом уровне EMD. Но говорить о каких-либо частотных передаточных функциях EMD, по-видимому, будет некорректным, так как любая частотная составляющая w_i исходного сигнала в процессе EMD может быть расщеплена по амплитуде и фазе на составляющие разных уровней функций IMF. Это можно видеть на рис. 24.4.6, где приведены графики модулей «эквивалентных» частотных передаточных характеристик разложения для первых пяти функций IMF, полученные осреднением отношения спектров функций к спектру исходного сигнала. Для получения достаточно гладких «эквивалентных» передаточных функций входной белый шум реализовался массивом из 30000 отсчетов, а сглаживание отношения спектров выполнялось в скользящем временном окне 2000 отсчетов.

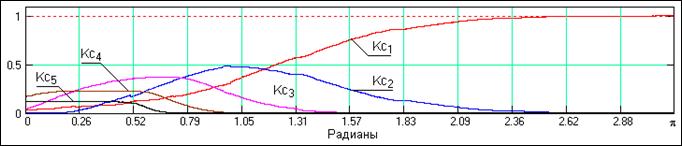
Рис. 24.4.6.

На рис. 24.4.7 приведены графики последовательного суммирования коэффициентов «эквивалентных» передаточных функций, которые показывают процесс последовательного перекрытия всего частотного диапазона входного сигнала.

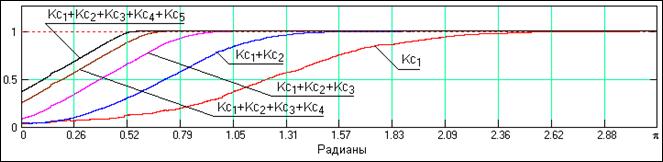
Рис. 24.4.7.

Обратным преобразованием Фурье по спектрам мощности могут быть вычислены нормированные автокорреляционные функции семейства IMF, первые 5 из которых приведены на рис. 24.4.8. Как следует из графиков, статистическая независимость отсчетов в какой-то мере сохраняется только для первой IMF. Но даже в ней появляется отрицательная (знакопеременная) корреляция между последовательными отсчетами. Во всех остальных функциях четко прослеживается появление затухающей косинусоидальной зависимости между отсчетами с последовательным увеличением интервала корреляции по мере увеличения номера IMF.

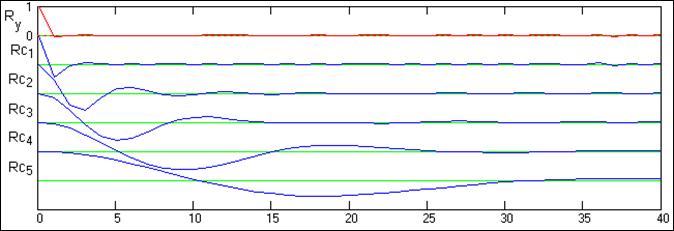
Рис. 24.4.8.

Литература.

1. The Hilbert-Huang transform and its applications / editors, Norden E. Huang, Samuel S.P. Shen. - World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck. Link, Singapore 596224

2. Huang N. E. Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q., Yen N.-C., Tung С. C., and Liu H. H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of R. Soc. London, Ser. A, 454, pp. 903-995, 1998.

3. An Introduction to Hilbert-Huang Transform: A Plea for Adaptive Data Analysis. Norden E. Huang. Research Center for Adaptive Data Analysis. National Central University.

4. Quek, S., Tua, P., and Wang, Q. Detecting anomalies in beams and plate based on the Hilbert–Huang transform of real signals. Smart Materials and Structures 12, 2003, pp. 447-460.

5. Давыдов В.А., Давыдов А.В. Очистка геофизических данных от шумов с использованием преобразования Гильберта-Хуанга.// Электронное научное издание "Актуальные инновационные исследования: наука и практика", 2010, № 1. http://www.actualresearch.ru.