Circulia lilium

 

Халиков Э.Г., Лопаткин Ю. А.

 

         Окружность с центром О и радиусом r_on , разделенная точками 1,2,… п (рис. 1) на п равных частей, есть основная окружность п-лепестковой циркульной лилии.

 

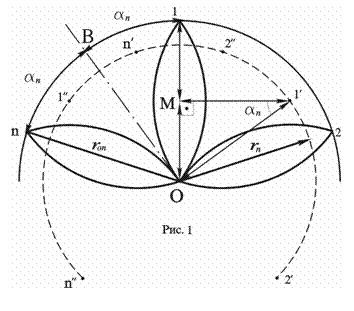Определим местоположение точек 1 и 1’ – центров окружностей, пересекающиеся дуги которых образуют 1-й лепесток циркульной лилии. Полагаем, что :

точка 1’ находится на перпендикуляре к оси 01  1-го лепестка, проходящем через его центр М;

точка 1’ расположена на перпендикуляре к прямой ОВ, которая в точке О касается левой дуги 1-го лепестка.

Точка 1’  является точкой пересечения указанных перпендикуляров. Заметим, что ОВ – биссектриса угла, образованная осями 01 и On  1-го  и смежного с ним п-го лепестков. Расстояние точки 1’ от центра О равно расстоянию точки 1’ от вершины 1 1-го лепестка лилии. Это расстояние есть радиус r_n  кривизны левой дуги 1-го лепестка.  Вследствие симметричности, тождественности и кругового расположения лепестков, центры кривизны их дуг находятся на окружности. Эта окружность  с центром О и радиусом r_n  есть центриса п-лепестковой циркульной линии.

На рис. 1 показана штриховая дуга центрисы, проходящая через центры п”, 1”, n’, 1’, 2” и 2’  кривизны дуг п-го, 1-го и 2-го лепестков, соответственно. Для геометрического построения (вычерчивания) i-го (i = 1, 2, …, п ) лепестка п-лепестковой циркульной лилии необходимо выполнить  следующие действия:

1) установить иглу циркуля в i-ю точку (вершину i-го  лепестка) основной окружности и отметить на центрисе точки i' , i" ;

2) установить иглу циркуля  в точку i'  центрисы и соединить точки О и i левой дугой i-го лепестка;

3) установить иглу циркуля в точку i" центрисы и соединить точки О и        i правой  дугой i-го лепестка.

Указанные действия выполняются при постоянном расстоянии  r_n  между концами «ног» циркуля. В изложенном способе не применялись вычисления по уравнениям. Уравнения для вычисления значений радиуса r_n  центрисы через значения радиуса r_on основной окружности «дает» прямоугольный треугольник с вершинами О,1’, М (рис. 1), углом a_п  при вершине 1’ , гипотенузой r_n  и катетом r_on / 2:

r_n  = r_on / 2 (sin a_п );  a_п  = 180^о / п,  п = 2, 3, … .

Результаты вычислений по этим уравнениям значений радиуса r_n центрисы в зависимости от количества п лепестков, в предположении, что радиусы окружностей соответствующих лилий одинаковы: r₀₂  = r₀₃  = … = r₁₀  = 1, приведены в следующей таблице

 

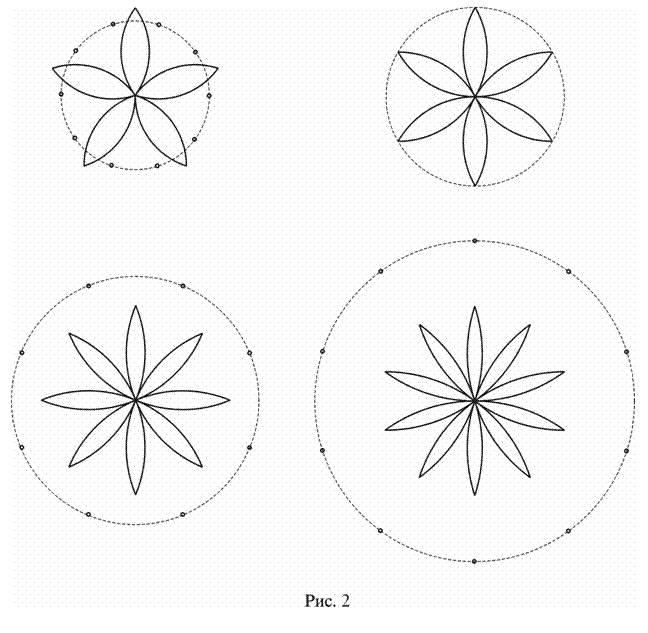
На рис. 2 показаны 5-лепестковая, 6-лепестковая, 8-лепестковая и 10-лепестковая циркульные лилии. точки - метки указывают центры кривизны дуг и лепестков. Заметим, что при n < 6 лепестки пересекаются центрисами. При n > 6 справедливо неравенство r_n  >  r_on и, следовательно, и центры кривизны дуг лепестков располагаются «дальше» вершин лепестков. Особый случай – 6-лепестковая линия, когда r₆ = r₀₆ ,  a₆  = 30^о. Следовательно (и это всем известно), вычерчивание основной окружности, деление ее на 6 равных частей и вычерчивание дуг лепестков выполняется при постоянном расстоянии r₀₆ между концами «ног» циркуля, а центры кривизны дуг располагаются в вершинах лепестков. В общем случае при нечетном количестве п лепестков требуется 2п центров кривизны для вычерчивания 2п дуг . В случае четного п  следует указать только п центров кривизны, поскольку каждый из этих центров используется дважды :  при вычерчивании левой дуги i-го и правой дуги k-го (i ¹ k) лепестков.

Указанные дуги есть половины одной большой дуги, проводимой через три точки: вершину i , центр О и вершину k, определяемую уравнениями

k = i – 1 + n / 2    для 1 < = i  < = 1 + n / 2,

k = i – (1 + n / 2)  для 2 + п / 2 < = i  < =   n.

Заметим еще, что расстояние между точками пересечения осей смежных лепестков с центрисой циркульной лилии равно r_on (рис. 1). Другими словами: длина радиуса основной окружности равна длине стороны правильного п-угольника, вписанного в центрису п-лепестковой циркульной лилии.

В заключение рассмотрим 10-лепестковую циркульную лилию.

Согласно уравнениям (1) для этой лилии a_п  = a₁₀  = 18^о; sin 18^o = 1/ (2Ф), r₁₀ = Ф r₀₁₀ , где Ф = (sqrt(5) + 1) /2 есть ,так называемое, «золотое число» [1, 2]. Известно, что для правильного 10-угольника, сторона которого a₁₀ , вписанного в окружность радиуса r₀₁₀ , справедливо уравнение Ф a₀₁₀ =  r₀₁₀ . Вследствие этих уравнений и тождества Ф² = Ф + 1, получим

r₁₀ = Ф r₀₁₀  = Ф² a₁₀ = Фa₁₀ + a₁₀ =  r₀₁₀  + a₁₀ .

Это уравнение выявляет еще одно замечательное геометрическое свойство «золотого числа» Ф: радиус центрисы 10 – лепестковой циркульной лилии равен сумме радиуса основной окружности и расстояния между вершинами смежных лепестков .

Любознательный читатель может самостоятельно выявить другие общие и частные замечательные свойства циркульных лилий, в чем желают ему успехов авторы.

 

Литература

 

1.     Энциклопедический словарь юного математика. – М.: 1989.

2.     Азевич А.И. Двадцать уроков гармонии. Гуманитарно-математический курс. – М.: 1998.