Численное моделирование возникновения 3D торнадо в теории мезомасштабных вихрей по Николаевскому.

( Тезисы для ICMAR - 2007 )

А.Ю. Губарь ¹, А.И. Аветисян, Бабкова В.В. ²

¹Институт физики Земли РАН, 123995, ГСП-5, Москва Д-242, Б.Грузинская, 10

²Институт системного программирования РАН, 109004, Москва, Б.Коммунистическая, 25

Введение

В основу мезомасштабной теории турбулентности по Николаевскому (МТН) «положена простая идея, что малый вихрь – элемент турбулентной мезо-структуры – подчиняется собственной динамике как объект, вращающийся со своей спиновой скоростью в соответствии с законом Ньютона для конечного тела. … Далее, осреднение по пространству приводит к континуальным уравнениям» [1].

Под мезовихрями в МТН подразумеваются вихри характерного масштаба L ~  << L, где L – характерный масштаб явления (макровихря), J – момент инерции мезовихрей [1], [2]. Такие мезовихри, часто наблюдаемые при образовании и лабораторном моделировании интенсивных атмосферных вихрей (ИАВ), играют существенную, но малоизученную роль в их динамике [3]-[7]. Заметим, что в метеорологии мезовихри определяются как вихри характерного масштаба L ~ 100 км, например, ураганы, в то время как масштаб мезовихря в МТН может меняться в зависимости от задачи. Так для торнадо (L ~ 1 – 10 км) масштаб мезовихрей L ~ 10 – 100 м, а для урагана (L ~ 100 км) типичный мезомасштаб – километры.

Взаимодействие турбулентных движений воздуха разных масштабов приводит к периодической перекачке энергии между масштабами. При определенном соотношении энергии мезовихрей к энергии макровихрей E_mes/E_mac [2] происходит лавинообразный рост ИАВ; когда энергия мезовихрей иссякает, начинается медленный обратный процесс накопления энергии в мезомасштабе. Механизмы этого процесса могут быть весьма различны: образование когерентных структур масштаба 50-500 м в поверхностном слое атмосфере [8]; вихри в плавучих турбулентных струях, вызванные как естественными, так и антропогенными факторами [9]; геоэлектромагнитные эффекты [10]; кратковре­менные аномалии среднемесячной температуры [11]; и, конечно же, разрушение глобальных вихрей, например, тропических циклонов [12].

Возможность развития ИАВ (торнадо, ураганов) за счет начальной энергии мезо­вихрей впервые была показана в [2], где представлены результаты численного моделиро­вания осесимметричного вихря в одномерной несжимаемой нестратифицированной атмосфере. В данной работе реализована численная модель развития торнадо в трехмер­ной сжимаемой сухоадиабатической атмосфере. Колоссальный объем вычислений для получения численного решения задач подобного типа требует выполнения программы на высокопроизводительных вычислительных системах. Кластеры являются одним из распространенных типов таких систем. Численная модель была реализована в среде разработки параллельных программ для кластерных систем ParJava [13]. Инструментальные средства, входящие в состав этой среды, позволили в короткие сроки разработать эффек­тивную параллельную версию численной модели ИАВ.

Математическая модель и вычислительная реализация

Принимая гипотезу сухоадиабатической атмосферы [14], из общей теории мезо­масштабной турбулентности [1] можно получить следующую систему уравнений движе­ния воздуха, представляющих собой законы сохранения массы, импульса, а также их первых моментов:

                                                                                                                 (1)

,  (2)

,                                                                                                           (3)

,                   (4)

где i, j = 1, 2, 3, ось z=X₃ направлена вертикально вверх; U_i – скорость ветра, ;  – возмущение логарифма плотности, , , Дж/(кг К) – удельная теплоемкость воздуха при постоянном давлении [14], T₀, ρ₀ – температура и плотность воздуха при t = 0, z = 0,  – ускорение свободного падения; , ω₀ – начальный модуль мезовихря,  – его фоновое значение; A_j – модули коэффициентов турбулентной вязкости в начальный момент [2];  – суммарная завихренность,  – макрозавихренность, ω_k – мезозавихренность;  – квадрат скорости звука, , , . В (1)-(4) опущены члены o(a²).

В системе координат () с центром в r = 0 (x,y = L/2) начальные условия имеют вид: , , где R₀ < L/2 – радиус «облака» мезовихрей, ,, - амплитуды в начальный момент, σ(r) – функция Хевисайда, , , , H – высота области; все остальные компоненты равны нулю.

Задача ставится в прямоугольной области D = {|x|, |y| < L; 0 < z < H}. Граничные условия для скорости и давления соответствуют обычной модели [15]; МТН позволяет задать турбонапряжения, из которых все нулевые, за исключением тангенциальных напряжений у Земли, где они задаются по формуле Шифринсона [16].

Задача (1-4) решалась численно по модифицированной схеме Рунге-Кутта-Адамсона с реализацией конечно-разностного аналога (1) по схеме «чехарда» с осреднением во времени на трех полуслоях [17]: назовем ее схемой МРКАч. Это условно-устойчивая схема второго порядка точности по времени и пространству; критерии ее устойчивости оказались близкими к явной схеме Маккормака [17].

Вычислительная реализация выполнялась по схеме параллельных кластерных расчетов в среде ParJava [13]. Распараллеливание производилось двумя способами: с одномерным и двумерным разбиением массивов. Тестирование производилось на Myrinet-кластере ИСП РАН, на 8 узлах (16 AMD Athlon XP 1500+). При этом на 16 процессорах достигалось ускорение в 11.5 раз. При тестировании производительности использовалась кубическая матрица размерности N = 100 (число точек сетки в каждом направлении). Более подробно вопросы оптимизации параллельного счета в зависимости от разбиения, размерности матрицы и числа процессоров описаны в [18].

Результаты численного моделирования 3D торнадо

Задача (1)-(4) решалась в кубе со стороной L = H = 1500 м; N менялось от 70 до 200; U₀ = 1.5 м/с, R₀ = 300 м, z_rgh = 0.1 м, A₁ = 1000 м2/с; безразмерные параметры взаимодействия с мезомасштабом, выбирались близкими к использованным в [2]: S_v = 0.5A₂/A₁= 0.01, M_v = A₃/A₁ = 1, I_v = A₄/A₁ = 1, П_m = 0.25(I_v+M_v)(1+ω_rel)J_rel = 750 ÷ 3000, П_v = S_v(1+ω_rel) = 100 ÷ 300 (ω_rel = ω₀R₀/U₀; J_rel = J_rel /R₀²); J_bk/J₀ = 0.05, w_bk/w₀ = 0.01, термодинамические параметры у земли – «стандартная атмосфера» [14]. Как и в [2], при этих значениях параметров отношение энергий (E_mes/E_mac)₀ ~ П_mП_v больше критического, и образуется торнадо: энергия ветра E_mac резко возрастает (за счет убыли энергии мезовихрей E_mes), достигая некоторого пикового значения (~ П_mП_v), после чего медленно убывает. Суммарная энергия E = E_mac + E_mes + E_in (внутренняя энергия) всегда убывает, т.к. система в целом замкнута (при этом подсистема макродвижений ветра – открытая, так как взаимодействует с подсистемой мезомасштабных движений, за счет чего, собственно, и возможно возникновение ИАВ, как явление самоорганизации в диссипативных системах [19]).

Специфические черты трехмерной сжимаемой модели рассмотрим на конкретном примере расчета с П_m = 750, П_v = 120.

В начальный момент (t₀ = 0 с) вертикальных и радиальных составляющих скорости ветра не было; был задан лишь почти штилевой местный циклонический ветер с амплитудой 1.5 м/с. В течение минуты формируется характерная для торнадо вертикально-радиальная циркуляция. При t₅ = 51.7 с восходящая скорость достигает 31 м/с на высоте около 600 м, максимальная скорость притока (+U_r ) -- около 7 м/с на высоте 500 м и расстоянии 230 м от центра (оттока, +U_r  , соответственно, 5 м/с на высоте 1200 м и радиусе 330 м). В целом характерная «грибовидная» структура торнадо формируется примерно за минуту.

На рис.1 показан результат 3D визуализации скорости ветра (в пакете VisAD) при t₁₆=165.4 с. Такая структура сохраняется в течение нескольких минут; скорость ветра за это время меняется в пределах 25 ÷ 35 м/с, затем плавно угасает до 12 м/с в течение получаса.

Такое поведение вообще характерно для малых и средних торнадо (интенсивности Т2 ÷ T4): быстрое (порядка минуты) возрастание энергии ветра до 80% от максимальной и затем плавное угасание.

На рис. 2 показан снимок местного урагана (торнадо интенсивности Т3), наблюдавшегося в течение нескольких минут в Монтане (США) в августе 2005 г.

По временным и масштабным параметрам сходство с моделью МТН практически идентичное. Заметим, что такие явления редко фиксируются. В работе [20] описан малый ураган («приводнившийся» смерчь) с аналогичными параметрами вблизи городка Госпорт, гр.  Гэмпшир, Англия 5.11.1999. Достигнув берега, он быстро переместился на 750 м внутрь деревни Хилл-Хед, вблизи городка, затем, «подняв несколько свиней в воздух, затух в течение получаса».

На рис. 3 приведена эволюция нормированных среднеквадратичных значений: абсолютной скорости ветра U/U_max; термодинамического параметра возмущения сухо-адиабатической атмосферы a/a_max и суммарной энергии Е/E_max. Интересно поведение термодинамического параметра  a/a_max. Явно прослеживаются инфразвуковые колебания, вызванные как геометрическими факторами (около 0.2  Гц), так и самим вихрем (около 1÷7 Гц). Вообще говоря, инфразвук от торнадо наблюдался в этом диапазоне [21],  но это явление заслуживает отдельного рассмотрения, как в прогностических, так и в эвристических целях.

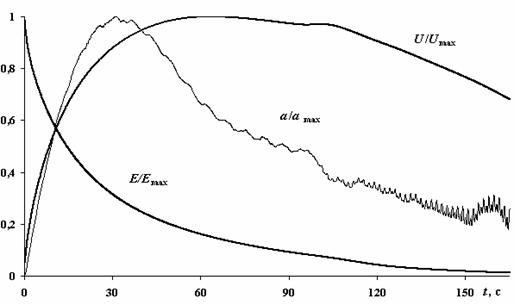
Рис. 3.  Эволюция во времени интегральных параметров торнадо.

 

Выводы

В целом, полученные результаты численного моделирования процесса рождения 3D торнадо в теории мезовихревой турбулентности по Николаевскому (МТН) [1] описывают реальный процесс рождения торнадо или местного урагана за счет накопленной в атмосфере энергии мезовихрей уже при гипотезе сухоадиабатической атмосферы (1)-(4). Как и в [2], наличие избыточной мезовихревой активности (E_mes/E_mac)₀ ~ П_mП_v > (E_mes/E_mac)_cr ~ 10000 большего некоторого критического уровня приводит к возникновению ИАВ. Избыточную мезовихревую активность можно измерять на станциях метеонаблюдения при достаточном количестве распределенных датчиков скорости ветра и соответствующей обработке результатов измерений, что в принципе дает возможность прогнозирования вероятности рождения торнадо или других ИАВ в данном регионе.

Разумеется, гипотеза сухоадиабатической атмосферы (1)-(4) не может моделировать медленные процессы накопления мезовихревой активности, приводящие к рождению ИАВ. Для этого следует учесть приток энергии извне, главным образом от солнечной радиации (например, подогрев подстилающей поверхности), термических процессов, связанных с влажностью или загрязненностью воздуха, а также иных факторов: вращение Земли и передача энергии от глобальных вихрей (ураганов и тропических циклонов); факторов изменения климата; электромагнитной активности атмосферы [8]-[12].

При учете этих факторов, реальная счетная задача естественно усложнится. Реализованные в данной задаче [18] кластерные вычисления с использованием инструментов ParJava [13], показали свою вычислительную эффективность (в предложенной схеме МРКАч  численного решения задачи (1)-(4) рассчитывалось около 10⁴ временных слоев, с обработкой порядка 300 математических операций с массивами в 300 Мб на каждом слое). Главными проблемами вычислительной реализации остаются вопросы оптимального распределения обрабатываемых данных между узлами, их промежуточной пересылки, сохранения значимых массивов и, разумеется, их конечной обработки для графического 1D ÷ 3D представления результатов счета.

Работа выполнена при поддержке <<# темы Пр.РАН>> и РФФИ, проекты № 05-01-00995 и 05-07-90308, а также проекты по программе фундаментальных исследований Президиума РАН.

Авторы выражают благодарность Калугину М.Д. за разработку программ по 3D визуализации результатов счета, Николаевскому В.Н.,  Гайсаряну С.С. и Арсеньеву С.А. – за неоценимые критику, обсуждения и поддержку.

ЛИТЕРАТУРА

1.   Nikolaevskiy V.N. Angular Momentum in Geophysical Turbulence: Continuum. Spatial Averaging Method. Dordrecht: Kluwer (Springer). 2003. P. 245.

2.   Арсеньев С.А., Губарь А.Ю., Николаевский В.Н. Самоорганизация торнадо и ураганов в атмосферных тече­ниях с мезомасштабными вихрями. // ДАН, 2004, т.396, № 4, с.541-546.

3.   Bluestein H. Synoptic-dynamic meteorology in mid-latitudes. Volume 2.Observations and theory of weather sys­tems. Oxford University Press: 1992. 594 pp.

4.   Churilov S.M., Shuchman I.G. // J. Fluid Mech. 1992. V.243. P.155-169.

5.   Kossin J.P., Shubert W.H. // J. Atmos. Sci. 2001. V. 58. P.2196 – 2209.

6.   Montgomery M.T., Vladimirov V.A.,Denissenko P.V. // J.Fluid Mech.2002.V.471.P.1-32.

7.   Wilczak J.M. and others // Monthly Weather Review. 1992. V.120. P.497-520.

8.   Korpov B.M., Korpov V.M., Makarova T.I. and G.S.Golitsyn. Coherent structures in the atmospheric surface layer under stable conditions // Bound-Layer Meteorology.2004.V.111.No.1.P.19-32.

9.   Голицын Г.С., Гостинцев Ю.А., Солодовник А.Ф. Плавучая турбулентная струя в стратифицированной атмосфере. // ЖПМТФ.1989.№4.С.61-72.

10.Berson F.A, Power H. On the geo-electromagnetic aspects of tornado initiation // J. Pure Appl. Geoph. 1972, V.101, No.1, P.221-230.  

11.Etkin D.A. Beyond the year 2000, more tornadoes in western Canada? Implications from the historical record// Natural Hazards, Nat. Hazards. 1995. V.12. No.1. P.19-27.

12.Голицын Г.С. Статистика и энергетика тропических циклонов//ДАН. 1997. Т.354. №4. С.535-538.

13.Ivannikov V., Gaissaryan S., Avetisyan A., Padaryan V. Improving properties of a parallel program in ParJava Environment // The 10th EuroPVM/MPI conference. LNCS 2840. Sept. 2003, Venice. pp. 491-494.

14.Хргиан А.Х. Физика атмосферы. М: Изд-во Московского Университета, 1986. С.240.

15.Хаин А.П., Сутырин Г.Г. Тропические циклоны и их взаимодействие с океаном. Л.: Гидрометеоиздат, 1983. C.272.

16.Емцев Б.Т. Техническая гидромеханика. М.: Машиностроение, 1978. С.463.

17.Флетчер К. Вычислительные методы в динамике жидкостей (2т). М.: Мир, 1991.

18.Аветисян А.И., Бабкова В.В., Гайсарян С.С., Губарь А.Ю. "Моделирование интенсивных атмосферных вихрей в среде ParJava."// Шестая международная конференция "Перспективы систем информатики", рабочий семинар "Наукоемкое программное обеспечение" Новосибирск, 2006, стр. 28-30.

19.Васильев В.А, Романовский Ю.М, Яхно В.Г. Автоволновые процессы. М.: Наука, 1987. С.240.

20.Gilbert Anthony. Tornado With a Measured Intensity of T3 at Hill Head, Hampshire, 5, November 1999. // J.Meteorol. 2000. 25, N254. c.361-367.

21.E. S. Posmentier//Geophys. J. R.astr. Soc. (1967), 13, pp.487 - 501.