Гринбаум О.Н.
Динамические модели ритмики пушкинского стиха
Статья опубликована в Материалах XXХIII международной филологической конф. Вып.25. Т.2 - СПб.: СПбГУ, 2004. С.10-23.
Проблема, на которой фокусируется наш исследовательский интерес, в общем виде может быть сформулирована как поиск единства ритма и содержания поэтического текста. Эта проблема — центральная в стиховедческой науке, ибо по словам А. Белого “лишь у плохих поэтов аллегоризируется смысл, насильственно отрываясь от ритма” (Белый 1929: 67).
Позволим себе кратко перечислить базовые положения эстетико-формального метода исследования русского классического стиха (Гринбаум 2001a: 13-15) с тем, чтобы представленные ниже эстетико-формальные основания изучения крупных поэтических форм стиха не оказались малопонятными и малопригодными алгебраическими построениями, а воспринимались в контексте воззрений Б.В. Томашевского: “Числа должны переживаться как качество... В стихах Пушкина наиболее совершенным образом осуществились какие-то строгие законы речевого ритма” (Томашевский 1929: 56; 1990: 63).
(1) “Ритм делает ощутимой гармонию” (Е.Г. Эткинд). Гармонию измерить нельзя, но ощущения, вызываемые в нас ритмом, и их соотнесенность с гармонической, божественной пропорцией “золотого сечения” дают возможность “поверять алгеброй гармонию” без разрушения природы и материи стихотворного текста.
(2) Применительно к стихосложению “божественная” пропорция ритма позволяет соотнести реальные ритмико-гармонические параметры текста с единичным уровнем РГТ
t = 1 (обозначим его через t 0), который был определен нами по результатам анализа строфического ритма эталонного текста русской поэзии — романа А.С. Пушкина “Евгений Онегин” (Гринбаум 2000, 54-57). Композиционно-ритмическое золотое сечение, речь о котором пойдет ниже, вычисляется по трем силлабо-тоническим параметрам стиха, а именно по общему числу слогов S в строфе (“целое”), числу безударных слогов B (“большее”) и числу ударных слогов T (“меньшее”):|
τ = 0,087 / Dзс = 0,087 / ( S / B – B / T ), |
(1) |
где коэффициент 0,087 соответствует единичному уровню РГТ τ
0 = 1.(3) Для эстетико-формального стиховедения сущностным является тот факт, что принцип “золотого сечения”, сформулированный Леонардо да Винчи для геометрических фигур, в самом общем случае выражает соотношение между целыми числами — членами так называемого “ряда Фибоначчи”, в котором каждый последующий его член (начиная с третьего) равен сумме двух предыдущих (0+1=1; 1+1=2; 1+2=3; 2+3=5; 3+5=8; 5+8=13 и т.д.):
|
{ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...} |
(2) |
Коэффициент
Φ “золотого сечения” получает в этом алгебраическом представлении новое толкование, связанное с делением n-го члена ряда Фибоначчи на его (n – 1)-й член при n® Ґ . Ряд (2) — простейший, но не единственный ряд Фибоначчи; ряд Фибоначчи — это динамический ряд, векторной геометрической интерпретацией которого является спираль Фибоначчи, а “золотое сечение” есть асимптотическое равенство двух отношений для тройки чисел (kn – 1; kn; kn + 1) этого ряда при n® Ґ .“В каждой науке, имеющей тенденцию к точности,— писал А. Белый,— по своему отражается ширящаяся диалектическая спираль, размыкающая всюду (от неба до электрона) неподвижные круги форм, в спиральном расширении метаморфозы
; в таблицу Менделеева, расположение листьев растения, в небесную механику ввинчена та же диалектическая спираль…”. И далее: “…принцип метаморфозы называю я принципом ритма” (Белый 1929: 15, 16, 19).. Приведем здесь же слова Гете, который говорил, что “кривой жизни является спираль”.Принцип формирования ряда Фибоначчи, отражая принцип саморазвития в его самом общем философском и естественнонаучном смысле, кодирует числовой последовательностью симметричность (1, 1) и асимметричность (1, 2, 3, 5…) движения, основанную на едином универсальном алгоритме:
|
kn + 1 = kn + kn – 1 , |
(3) |
где
n — номер элемента k ряда (1) для nі 3. В самом общем случае тот же алгоритм (2) порождает “золотые” р-ряды Фибоначчи, а динамический ряд Фибоначчи 1-го уровня иерархии (kn + 1 = kn + kn ) кодирует математическими символами принцип симметрии (см., напр.: Гринбаум 2002: 23-26).(4) Три основных параметра силлабо-тонического стиха S, B и T могут вычисляться для самых разных поэтических структур (4-стиший, 5-стиший, 8-стиший, 14-стиший и т.п.), и в этом случае мы получаем возможность оценивать как теоретические качественно-количественные характеристики многочисленных строфических форм стиха, так и степень их реализации в конкретных художественных текстах (Гринбаум 2000).
(5) Анализ единого “ритмо-смысла” крупных форм поэтического текста базируется на темпоральном подходе к рассматриваемой проблеме, предполагающем изучение динамических параметров развития ритмики словесного уровня от начала и до конца стихотворного текста, от его первой строчки и до последней. При этом последовательно измеряются величины S, B и T для постоянно нарастающего объема поэтического текста, а величины РГТ τ представляют собой ритмодинамические оценки процесса саморазвития поэтической мысли (точнее, читательского восприятия этого процесса).
Рассмотрим последнее концептуальное положение более обстоятельно.
1. Основания ритмодинамических моделей крупных поэтических форм стиха
Последовательное измерение величин S, B и T для постоянно нарастающего объема поэтического текста позволяет вычислять величину ритмико-гармонической точности РГТ τ в структурных, узловых точках поэтического текста, положение которых в тексте определяется строфическими, рифмическими, а в ряде случаев и содержательными факторами. Такой способ измерения реальных величин отклонения параметра РГТ от идеальных, “золотых” соотношений между S, B и T позволяет строить модели изменения во времени параметра РГТ τ, представляя в графической (наиболее наглядной) форме ритмодинамические оценки процесса восприятия поэтического текста.
Разное поведение параметра τ, которое обнаруживается при анализе ритмики стиха Пушкина в двух (первой и пятой) “наиболее красочных”, по мнению В.В. Набокова, главах романа “Евгений Онегин” и в поэме “Гавриилиада” (речь об этом пойдет ниже) безусловно свидетельствуют в пользу способности данного исследовательского инструмента привносить новые данные в копилку знаний о динамической организации пушкинского стиха.
Более того, адекватное поведение ритмодинамического параметра τ в разных эмоционально-содержательных фрагментах поэтического текста и явная соотнесенность этого параметра с наиболее выразительными центрами поэтического повествования дают нам все основания для поиска новых эстетико-формальных средств анализа экспрессивно-смысловых характеристик стиха, для поиска более тонких аналитических процедур, способных расширить возможности эстетической математики “поверять алгеброй гармонию”.
Новым параметром, способным усилить методический базис эстетико-формального стиховедения, является показатель экспрессивности гармонических ритмоощущений КЭ, введение и обоснование которого требует особого и обстоятельного разговора.
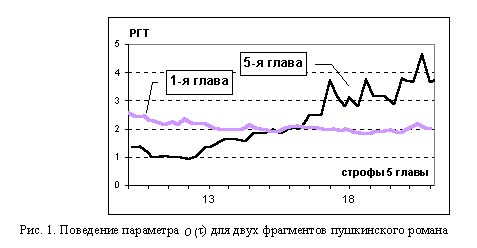
Наши рассуждения основаны на том факте, что разные в эмоционально-содержательном плане фрагменты пушкинского стиха характеризуются разным — и по своей амплитуде, и плотности пульсаций (колебаний) — поведением параметра ритмико-гармонической точности РГТ τ. Для иллюстрации приведем пример (см. рис. 1) поведения параметра РГТ для двух фрагментов из ЕО — текст “хандры” Онегина (глава 1, строфы XXXVII – ILVIII) на фоне строф Сна Татьяны (глава 5, строфы XI – XXI). На этом рисунке по горизонтали отложены номера строф 5-й главы ЕО, а по вертикали — значения РГТ вида O(τ) = 1 + ln(τ) δλя узловых точек каждой строфы стиха.
Не требуется особо изощренной наблюдательности, чтобы сопоставить спокойное в содержательном плане течение 1-й главы пушкинского повествования на протяжении ряда строф, показывающего читателю Онегина, возвратившегося с бала домой и описывающего в деталях хандру главного героя, с таким же спокойным поведением параметра РГТ на этом участке поэтического повествования Пушкина.

С другой стороны, Сон Татьяны, который следует за сценами Гадания (строфы VII – IX), характеризуется совсем иной эмоционально-динамической темпоральностью — развитие событий и ритмика пушкинского стиха в строфах Сна Татьяны демонстрируют переход от более или менее плавного движения ко все более и более выразительному и драматическому по своему характеру повествованию. Сон Татьяны — это и сказочный сюжет с фольклорно-мифологическими фигурами, и реальные герои романа (Ольга, Ленский, Онегин), помещенные в контекст святочных гаданий, и вовсе не сказочный, трагический финал сновидения. Но более всего Сон Татьяны — это судьбоносный Рубикон, включающий в себя метафорически представленное прошлое главной героини романа и провидческое предсказание будущих событий. Предсказание, как мы помним, неполное (в нем нет даже намека на будущее замужество Татьяны и на метаморфозу чувств Онегина), но тем не менее, сбывшееся в главном — в смерти Ленского.
Различия в ритмике этих фрагментов подтверждают и средние величины Тср тонических объемов (ударности) строф: для текста “хандры” Онегина Тср = 44,1 в противовес Тср = 46,0 ударных слогов в тексте Сна Татьяны. Напомним, что тот же параметр для всех строф 1-й главы ЕО имеет значение Тср = 44,7 (средняя величина для 54 полных строф этой главы), тогда как для 5-й главы в целом Тср = 45,2 ударных слога (42 строфы).
Еще раз сопоставив эти данные с графиками на рис. 1, мы не можем не сделать вывода о том, что кривая РГТ, полученная на основе измерения динамических значений величин ритмико-гармонической точности τ, явным образом соотносится с эмоционально-содержательной динамикой пушкинских фрагментов ЕО.
Итак, вопрос заключается о том, чтобы найти способ измерения степени размаха и плотности пульсаций параметра РГТ τ : с этой целью мы вводим в исследовательский оборот показатель экспрессивности ритмоощущений КЭ. Второй и важнейшей задачей явится затем необходимость определить степень соответствия этого параметра КЭ реальным, качественным, литературоведческим оценкам соответствующих поэтических фрагментов и произведений в целом.
2. Формальные аспекты расчета динамических показателей ритмики стиха
Прежде чем представить формальный способ вычисления величины КЭ, уточним некоторые известные в теории статистики положения, связанные с методами анализа временных рядов, а также возможности использования существующих в этом разделе математики параметров для решения стоящих перед нами задач.
В статистике анализ временных рядов (изучение изменения значений некоторого параметра во времени) проводится на базе двух показателей: коэффициента “роста” К
р и коэффициента “прироста” Кпр (см., напр.: Дайитбегов 1984, 154-155). Коэффициент роста Кр показывает, во сколько раз данный уровень ряда yi больше (или меньше) уровня ряда yi-k, отстоящего от данного на k единиц времени; величина Кр вычисляется по формуле:К
р = yi / yi-k .Второй показатель стандартных статистических измерений (коэффициент прироста К
пр), показывает абсолютное изменение коэффициента роста и вычисляется по формуле:|
Кпр = (yi – yi-k) / yi-k . |
(4) |
В том случае, если точки измерения не равноудалены друг от друга, т.е. если значение k ≠ const, вместо параметра К
пр используется приведенное к единичному расстоянию значение Кприв = Кпр / k.Прежде всего отметим, что параметр К
р фактически напрямую соотносится с используемым нами способом динамического измерения параметра ритмико-гармонической точности τ, поскольку мы в каждой узловой точке стиха мы вычисляем т.н. обратный “базисный” коэффициент роста, когда k = 1, а в качестве величины yi-1 выступает значение Dзс = 0,087 (определяющее величину единичного уровня РГТ τ0 = 1 — см.: Гринбаум 2000, 54-57).Далее, при изучении любого динамического процесса изменения его параметров могут и должны описываться не только последовательностью собственных значений величин (в нашем случае — значений τ
i) в каждой i-ой точке измерений (узловой строке стиха), но и скоростью изменения этих величин. Именно с этой целью в стандартных статистических измерениях временных рядов используется коэффициент прироста Кпр, а в наших исследованиях — динамический показатель экспрессивности ритмоощущений КЭ.Формула (4) была принята за основу при выборе способа вычисления вводимого нами показателя экспрессивности ритмоощущений КЭ
:|
КЭ(i) = [ABS(Oi – O i-1) / (xi – xi-1)] * [(Oi-1) / СРЗНАЧ(Oi-1)], |
(5) |
или, что то же:
|
КЭ(i) = [ABS(Oi – Oi-1) / СРЗНАЧ(O i-1)] * [(O i-1) / (xi – xi-1)], |
(5а) |
где
i — номер строки от начала текста; Oi = 1+ln(τi) — уровень ритмико-гармонических ощущений в i-ой узловой точке стиха, т.е. в конце i-ой строки текста; СРЗНАЧ(Oi-1) — стандартное среднее значение параметра O(τ), βϋчисленное для всех значений O i в интервале от 1 до ( i-1); разность (xi – xi-1) — это расстояние (число строк) между двумя соседними узловыми точками стиха; ABS — абсолютное значение разности (O i – O i-1). Число “1” в выражении Oi = 1+ln(τi) используется с тем, чтобы исключить появление отрицательных чисел в качестве значений O(τ) θ ςем самым обеспечить размещение кривой КЭ в первом квадранте ее графического представления.Первый сомножитель в записи (5), т.е. [ABS(
O i – O i-1) / (xi – xi-1)] явным образом показывает, что эта формула действительно позволяет вычислять скорость изменения величины Oi как отношение разности двух соседних значений (O i – O i-1) к расстоянию между этими точками измерений, равному (xi – xi-1).Второй множитель в формуле (5), а именно [(
O i-1) / (xi – xi-1)] позволяет формальными средствами усилить чувствительность показателя экспрессивности ритмоощущений КЭ. Действительно, величина O i-1 указывает на тот уровень РГТ, относительно которого мы оцениваем изменение величины Oi в очередной i-ой точке динамического процесса ритмовосприятия стиха: чем больше величина Oi-1, относительно среднего значения СРЗНАЧ(Oi-1), тем ощутимее разность значений (Oi – Oi-1) для читательского восприятия. Очевидно, что здесь требуется особые пояснения, которые мы представим ниже.Формула (5а) показывает, что первый множитель [(
Oi – O i-1) / СРЗНАЧ(O i-1)] введен нами в полном соответствии со стандартным способом вычисления коэффициента прироста Кпр (см. выше). Отличие состоит лишь в том, что мы оцениваем величину изменения двух соседних значений (Oi – Oi-1) относительно среднего значения этого параметра, вычисленного для предыдущих (i–1) шагов. Использование среднего значения СРЗНАЧ(Oi-1) диктуется самим характером процесса восприятия стиха, а именно интегрирующей способностью органов чувств демпфировать (сглаживать) величины внешний раздражителей, т.е. формировать общее впечатление путем усреднения его контрастных значений.Если сравнивать между собой формулы (5) и (5а), то второй сомножитель в формуле (5), а именно [
Oi-1 / СРЗНАЧ(Oi-1)] несколько в ином виде представляет коэффициент чувствительности для выбранного способа измерений, отражая отношение текущего значения величины Oi-1 к ее среднему значению для всех предшествующих точек измерения.Уточнение 1. Оно связано с тем обстоятельством, что мы проводили сопоставительный анализ эффективности формальных способов измерения показателя экспрессивности ритмоощущений КЭ, сравнивая результаты, полученные по формуле (5), с результатами вычислений по двум другим формулам (6) и (7).
Формула (6)
|
КЭ(i) = ABS(O i – O i-1) / (xi – xi-1), |
(6) |
отличается от формулы (5) тем, что в ней отсутствует второй сомножитель, т.е. коэффициент чувствительности измерений [(
O i-1) / СРЗНАЧ(O i-1)].В формуле (7)
|
КЭ(i) = [ABS(O i – O i-1) / (xi – xi-1)] * [(O i + O i-1)/2], |
(7) |
использован коэффициент чувствительности измерений (
Oi + Oi-1)/2, равный среднему значению параметра O для двух соседних точек измерения.Уточнение 2. Величины КЭ
(i) сами по себе мало информативны, таковыми они могут стать лишь в сопоставлении с аналогичными значениями для некоторого базового фрагмента стихотворного текста. Поэтому мы используем относительные значения КЭО, приведенные к средней величине КЭ для всей 1-й главы романа “Евгений Онегин” (эту среднюю величину обозначим через К0). Отметим (несколько забегая вперед), что среднее значение параметра КЭ для всей 1-й главы пушкинского романа КЭ равно КЭ = К0 = 0,054 и что текущее значение КЭО(i) для i-ой узловой позиции стиха определяется как:|
КЭО(i) = КЭ(i) / К0 = КЭ(i) / 0,054. |
(8) |
Таким образом, параметр КЭО
(i) показывает относительное превышение текущего значения показателя экспрессивности ритмоощущений над единичным уровнем К0 среднего значения для 1-й главы ЕО, принятого нами за единицу аналогично тому, что было сделано при расчетах параметра РГТ τ.3. Содержательные аспекты расчета динамических показателей ритмики стиха
Напомним, что психофизиологический закон Вебера-Фехнера позволяет переходить от уровня ритмико-гармонической точности τ, вычисленный в некоторой i-ой точке стиха, к уровню ритмико-гармонических ощущений Oi посредством простой операции — взятия логарифма от величины τi, т.е. полагая Oi =1+ln(τi). Поскольку расчеты ведутся для последовательности узловых точек стиха, т.е. для i = (1, 2, 3,… n), то результаты подобного рода вычислений формируют динамическую модель гармонических ритмоощущений М(Oi), представляемую в виде графика изменения параметра Oi во времени: Oi = 1+ln(τ i) = 1+ln(0,087 / Dзс i) =1+ ln(0,087 / ( S i / B i – B i / T i )).
Теперь вспомним, что для вычисления значений τ
i и, следовательно, Oi в каждой узловой точке стиха используются накопленные значения силлабо-тонических параметров S, B и Т — это обстоятельство дает нам все основания считать, что модель М(Oi) математически представляет реальную картину изменения гармонических ритмоощущений при чтении стиха от его начала. Еще один принципиальный момент заключается в том, что величины τi — относительные, а не абсолютные, т.е. они определяются по отношению к уровню ритмико-гармонической точности τ0, принятой за единицу на основании изучения соотношений между параметрами S, B и Т для каждой из Онегинских строф романа Пушкина “Евгений Онегин” (τ0 = 1 при Dзс = 0,087).Предположим, что вид развертывающегося во времени (при чтении стиха от его начала) процесса изменения гармонических ритмоощущений можно схематично изобразить как некоторую кривую (см. рис.2), а текущее состояние — как положение шарика на вершине этой кривой, т.е. в позиции ее некоторого локального максимума.
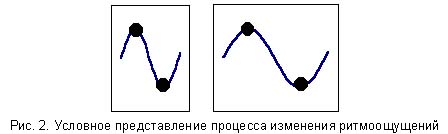
Пусть в этой первой (
i-1)-й позиции стиха величина локального максимума определяется значением Oi-1, а следующая i-я позиция измерений расположена в точке локального минимума кривой. Не требуется особых доказательств для того, чтобы (учитывая характер самого параметра O) утверждать, что чем выше значение Oi-1 и чем ближе друг к другу по оси абсцисс (оси времени) расположены соседние узловые точки стиха, тем ощутимее будет переход от одного состояния к другому. Поэтому второй множитель в формуле (5а) состоит из знаменателя Oi-1 и числителя (xi – xi-1). Числитель (xi – xi-1) позволяет вычислять значение КЭ(i) как импульсную величину, т.е. как значение КЭ, приведенное к единичному расстоянию между двумя соседними узловыми точками стиха.Подобный импульсный характер измерений делает возможным использование параметра КЭ для исследования и сопоставительного анализа поэтических текстов любой строфической организации: и для строгих форм с однородной строфикой (напр., стихов, написанных только 4-стишиями), и для текстов с разнородной строфикой (с разными объемами строф в пределах одного произведения), и для астрофических текстов. Наиболее простым примером является Онегинская строфа, 14 строк которой в наибольшей степени соответствуют структуре 14 = (4+4+4+2). Внутренняя структура Онегинской строфы предопределяет равное расстояние между ее тремя узловыми точками (1-м, 2-м и 3-м катренами, т.е. для строк 4, 8 и 12) — оно равно четырем (
xi – xi-1) = 4, тогда как для последнего узла (для 14-й строки) это значение равно двум: 14 – 12 = 2.Напомним еще раз, что параметр ритмико-гармонической точности τ
i позволяет оценивать степень приближенности силлабо-тонических параметров стиха S, B и Т к гармонической пропорции “золотого сечения”. Отсюда следует, что чем больше перепад значений τi для двух соседних узловых точек стиха, с одной стороны, и чем меньше расстояние между этими точками измерения — с другой, тем сильнее ощущается беспокойство из-за резких колебаний ритма, нарушающих, а в ряде случаев и разрушающих гармоническую плавность восприятия стиха. Подобное явление хорошо известно представителям психологической науки: “У беспокойства обычно быстрый неровный ритм дыхания и скачущие мысли” (Похилько, Федотова 2003, 155).Именно эти особенности восприятия мы стремились учесть в формуле (5) как формальном показателе пульсации ритмоощущений.
4. Замечания к выбору способа измерения динамических показателей ритмики стиха
1. Рассмотрим вопросы, связанные с выбором и обоснованием способа вычисления параметра КЭ. Сопоставительный анализ эффективности вычислений по формулам (5), (6) и (7) проводился на материале 1-й и 5-й глав романа Пушкина “Евгений Онегин” и поэмы “Гавриилиада”, включая не только их полные тексты, но и отдельные части повествования, напр., фрагменты Сна Татьяны из 5-й главы ЕО и строки Сна Марии из “Гавриилиады”. Напомним, что процедура вычисления параметра КЭ(i) — накопительная, соотносимая с реальными явлениями при непрерывном чтения стиха от его начала. Следовательно, измерение этого параметра для отдельных фрагментов текста происходит не для изолированного варианта прочтения каждого отрывка, а как части единого процесса восприятия стиха.
Ниже в табл. 2 приведены сравнительные данные, связанные с чувствительностью параметра КЭ при его вычислении по формулам (5), (6) и (7).
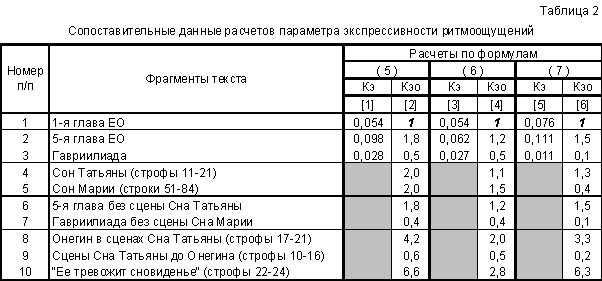
Прежде чем дать краткий комментарий к числовым значениям параметра КЭ, приведенным в табл. 2, отметим, что отсутствие данных в строках 4–10 этой таблицы (столбцы [1], [3], [5]) продиктовано нашим стремлением не перегружать таблицу теми значениями, которые легко восстанавливаются на основании данных, приведенных в столбцах [2], [4] и [6]. Отметим также, что в столбцах [2], [4] и
[6] находятся значения параметра КЭО, вычисленные как отношение соответствующих абсолютных величин КЭ к значению К0, определенному по формуле (5), (6) и (7) соответственно. Эти абсолютные значения приведены в ячейках [1, 1], [1, 3] и [1, 5], что предопределяет значения КЭО = 1 в ячейках [1, 2], [1, 4] и [1, 6].Анализ числовых значений КЭ для трех вариантов его вычисления показывает следующее. Если величины КЭ для 1-й главы ЕО весьма близки друг к другу (см. значения в ячейках [1, 1], [1, 3] и [1, 5] таблицы 2), то для 5-й главы ЕО и “Гавриилиады” значения параметра КЭ характеризуются значительно большим разбросом и рассогласованием его абсолютных и, следовательно, относительных величин. Еще сильнее эти различия проявляются при вычислении средних значений КЭО для “контрастных” в художественном плане фрагментов пушкинских текстов, например, для сцен Сна Татьяны до и после появления в сновидении Онегина (табл.2, ячейки [9, 2] и [8, 2], [8, 4] и [9, 4], [9, 6] и [8, 6]).
Привлечение разных в эмоционально-содержательном плане фрагментов поэтического текста становится, таким образом, не только необходимым, но и обязательным условием для обоснования методики вычисления показателя экспрессивности ритмоощущений КЭ, поскольку расширение и углубление чисто формального аспекта анализа данных, полученных по формулам (5), (6) и (7), грозит выродиться в бесперспективный разбор незначительных деталей, разбор затруднительный и малопродуктивный.
Итак, сопоставительный анализ данных из табл. 2 позволяет сделать вывод о том, что с точки зрения сбалансированности и контрастности полученных результатов, а также с учетом тех доводов, которые были представлены в предыдущем разделе, предпочтение при выборе одной из формул (5), (6) и (7) следует отдать формуле (5).
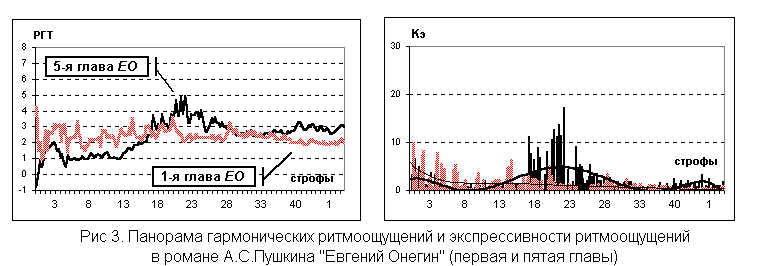
В качестве примера на рис. 3 показаны графики изменения величин РГТ и КЭ для 1-й и 5-й глав романа “Евгений Онегин”; величины КЭ вычислены здесь по формуле (5).
2. Второе замечание касается вопроса о связи между единичным уровнем ритмико-гармонической точности стиха РГТ τ
0 = 1 и единичным значением показателя экспрессивности ритмоощущений К0 = 0,054. Чтобы убедиться в неординарности приводимой ниже формулы (9), напомним еще раз, как определяются оба этих параметра.Единичный уровень РГТ τ
0 = 1 при Dзс = 0,087 выбран исходя из того обстоятельства, что величина Dзс = 0,087 определяется по формуле (1) тройкой чисел Фибоначчи (44–74–118). Последняя характеризует силлабо-тонические параметры Онегинской строфы с числом ударений в строфе T = 44 — для двух других вариантов “гармонических” строф с T = 45 и T = 46 величина Dзс < 0,087. Это означает, что из трех наиболее часто встречающихся у Пушкина значений тонических объемов Онегинской строфы T = 44, 45 и 46 ударных слогов нами для единичного значения величины τ был выбран наихудший в отношении ритмико-гармонической точности вариант с T = 44. Следовательно, выбор единичного уровня РГТ был обусловлен анализом дистрибуции силлабо-тонических параметров Онегинской строфы Пушкина, одной из самых крупных по своему объему и самой гармоничной (“гениальной”, по мнению Б.В. Томашевского) структурной единицей русского классического стиха.С другой стороны, единичный уровень показателя экспрессивности ритмоощущений К
0 = 1 при среднем значении КЭ = 0,054 был получен чисто эмпирическим путем как результат наблюдений над ритмикой 1-й главы ЕО — одной из самых “спокойных” в эмоциональном плане и красочных глав пушкинского романа.Итак, связь между величинами τ
0 и К0 определяется с точностью до третьего знака после запятой следующим образом:|
τ0 = Ф * К0 , |
(9) |
где Ф есть коэффициент “золотого сечения”
Φ = 1,618. Для приверженцев точных значений укажем, что ошибка вычислений по формуле (9) составляет 0,5% и что стандартное представление чисел в табличном процессоре “Excel” включает 15 знаков после запятой.Более того, соотношение (9), связывающее величины τ
0 и К0, справедливо как для вычислений по формуле (5), так и по формуле (6) — самой простой из всех возможных формул для измерения скорости изменения параметра РГТ τ.Данные из табл. 2 показывают, что для поэмы “Гавриилиада” в целом величины КЭ, вычисленные по тем же формулам (5) и (6), практически одинаковы (0,028 и 0,027), тогда как использование формулы (7) не только для этого текста, но и для 1-й главы ЕО предопределяет совсем другие результаты (см. табл.2). Это дает нам дополнительные основания отказаться от формулы (7) как наименее эффективной в области исследования ритмики русского классического стиха.
Итак, неординарность эмпирического соотношения (9) заключается в том, что оно демонстрирует гармоническую связь между двумя формальными параметрами поэтического текста, которые были выбраны нами на основе качественных оценок пушкинского стиха. Поэтому (1) учитывая изложенные выше обстоятельства и, в первую очередь, разные основания для выбора единичных значений τ
0 и К0 и (2) принимая во внимание особые гармонические свойства коэффициента “золотого сечения” (см., напр.: Стахов 2003; Смирнов 2002), результат исследований, математически выражаемый в виде соотношения (9) представляется нам не только не случайным, но симптоматичным и закономерным. Повторим еще раз и вывод о том, что формула (5) позволяет получать более сбалансированные и, вместе с тем, контрастные значения параметра экспрессивности ритмоощущений в сравнении с формулой (6) и что формула (7) в дальнейшем использоваться не будет. Отметим в заключение, что наши ближайшие исследования будут связаны с анализом поведения ритмико-гармонических параметров в других главах романа “Евгений Онегин”, полученных при использовании бинарной и тернарной моделей градации ударных слогов.Литература
Белый А. Ритм как диалектика и “Медный всадник”. М., 1929.
Белый А. О ритмическом жесте // Структура и семиотика художественного текста / Учен. записки Тартусского ун-та. Вып. 515. Тарту. 1981.
Гринбаум. О.Н. Гармония строфического ритма в эстетико-формальном измерении. СПб., 2000.
Гринбаум О.Н. Эстетико-формальное стиховедение: Методология. Аксиоматика. Результаты. Гипотезы. СПб., 2001a.
Гринбаум. О.Н. Гармония ритма в стихотворении А.А. Фета “Шопот, робкое дыханье…” / Язык и речевая деятельность. Т.4., ч.I. 2001b.
Гринбаум О.Н. Строка, строфа и стих как ритмическая система // Матер. XXXI межвуз. науч.-методич. конф. препод. и асп. филологич. ф-та СПбГУ. Вып.4., Ч.2. СПб., 2002.
Набоков В.В. Комментарий к роману А.А. Пушкина “Евгений Онегин”. СПб., 1998.
Похилько В. И., Федотова Е. О. Техника репертуарных решеток в экспериментальной психологии личности / Вопросы психологии, № 3, 1984, с.151-157.
Розенов Э.К. Закон золотого сечения в поэзии и музыке // Э.К. Розенов. Статьи о музыке. М., 1982.
Смирнов В.С. Золотое сечение – основа математики и физики будущего. СПб, 2002.
Стахов А. П. Новая математика для живой природы. Винница, 2003.
Томашевский Б.В. О стихе. Л., 1929.
Томашевский Б.В. Пушкин. Работы разных лет. М., 1990.
Холшевников В.Е. Основы стиховедения. СПб., 1996.
Шенгели Г. Техника стиха. М., 1960. С.111.
Эткинд Е.Г. Ритм поэтического произведения как фактор содержания // Ритм, пространство и время в литературе и искусстве. М., 1974.