ОБЪЯСНЕНИЕ
ОТРИЦАТЕЛЬНОГО РЕЗУЛЬТАТА
ОПТИЧЕСКОГО
ЭКСПЕРИМЕНТА МАЙКЕЛЬСОНА-МОРЛИ
Galina-2001
Введение
Отрицательный результат эксперимента Майкельсона-Морли
[1] послужил доказательством постулата Эйнштейна об инвариантности скорости
света и стал основой для создания теории относительности.
После проведения Саньяком опыта с вращением интерферометра Саньяка [2] и
получения им положительных результатов, доказывающих, что скорость света и
скорость приемника света складываются по классическому принципу сложения
скоростей, возникла необходимость проверки эксперимента Майкельсона-Морли на
предмет выявления допущенных в интерпретации результатов опыта ошибок.
Теория - два принципа, релятивистский и классический,
определения угла отражения луча от движущегося зеркала
При изображении траекторий хода лучей Майкельсон
руководствовался релятивистским принципом зависимости угла отражения
луча от зеркала от скорости зеркала в ИСО наблюдателя. Согласно релятивистским
идеям, при нулевой скорости зеркала в ИСО наблюдателя, то есть в ИСО самого
зеркала, угол отражения луча равен углу падения луча.
ИСО зеркала:
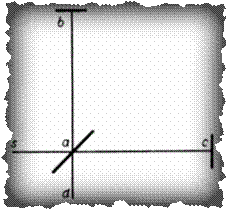
Рис. 1. В ИСО зеркала углы отражений лучей равны углам
падений лучей
Во всех других системах отсчета
зеркало движется и, согласно релятивистскому мировоззрению, углы отражения
лучей не равны углам падений лучей. Траектория отраженного луча в ИСО
наблюдателя изображается с таким расчетом, чтобы в ИСО зеркала угол отражения
луча был равен углу падения.
Абсолютная система отсчета АСО:.
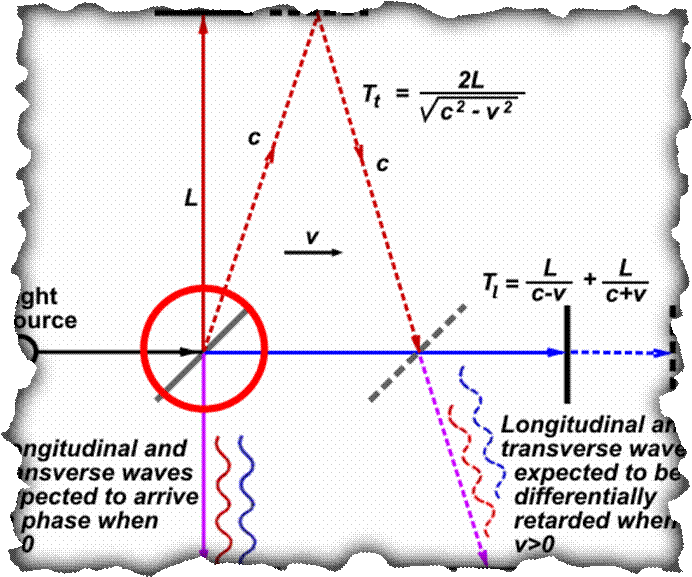
Рис.
2. Релятивистский принцип определения угла отражения луча от движущегося
зеркала. Абсолютная система отсчета АСО. В красном круге угол отражения луча не
равен углу падения луча, отличаясь от угла падения луча на угол абберрации.
Траектория отраженного луча изображается с таким расчетом, чтобы в ИСО зеркала
угол отражения луча был равен углу падения луча.
Так как у нас нет никаких оснований считать верным релятивистский принцип определения
углов отражений лучей от движущегося зеркала, мы вправе изображать отраженные
лучи, руководствуясь совершенно другим, классическим, принципом
определения углов отражений лучей от движущегося зеркала.
Итак, каким же же должен быть
классический, не релятивистский принцип определения углов отражений лучей от
движущегося зеркала?
Твердо установлен экспериментально факт
независимости скорости света от скорости источника света.Раз скорость света
никак не может зависеть от скорости источника света (включая и такой источник
света, как зеркало), то вполне логично предположить, что в АСОугол отражения
луча света не может зависеть от скорости зеркала. Трудно вообразить, что
изменение скорости зеркала в АСО меняет направление вектора скорости
отраженного луча, оставляя неизменным длину этого вектора. Логичнее
предположить, что скорость зеркала никак не влияет на вектор скорости
отраженного луча света, ни на его длину, ни на его направление. Тогда
классическй принцип определения углов отражений лучей от движущегося зеркала
должен выглядеть так:
Классический
принцип определения угла отражения луча от движущегося зеркала
В абсолютной системе отсчета АСО угол отражения луча будет равен углу падения
луча при ЛЮБОЙ скорости зеркала в АСО.
В ИСО любого наблюдателя, чье
ИСО движется в АСО (включая наблюдателя, в чьем ИСО зеркало неподвижно) угол
отражения луча зависит от скорости наблюдателя в АСО и отличается от угла
падения луча на угол абберрации.
У нас есть все основания считать, что классический
принцип определения углов отражений лучей от движущегося зеркала верен, потому
что зависимость углов отражений лучей в ИСО зеркала от скорости зеркала в АСО
обнаружена экспериментально рядом исследователей. Наиболее впечатляющи
результаты исследований директора Берлинской/Бабельсбергской обсерватории
Леопольда Курвуазье (LeopoldCourvoiser) [3].
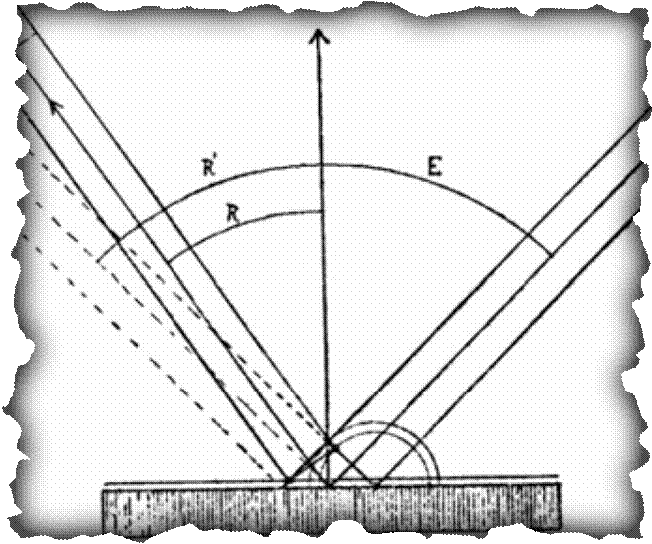
Рис. 3. Отражение лучей звезд от ртутного зеркала
Берлинской/Бабельсбергской обсерватории в экспериментах Леопольда Курвуазье
(LeopoldCourvoiser) [3].ИСО зеркала, движущегося в АСО. Угол отражения луча не
равен углу падения луча в ИСО зеркала.
Изображение траектории хода поперечного луча при
руководствовании классическим принципом зависимости угла отражения луча от
зеркала от скорости зеркала в ИСО наблюдателя
Руководствуясь принципом равенства угла отражения луча
углу падения луча в АСО, мы должны исправить траекторию перпендикулярного луча
на схеме опыта Майкельсона.
Для упрощения расчетов Майкельсон максимально упростил схему эсперимента,
условно изобразив прямыми не прямые на установке углы..
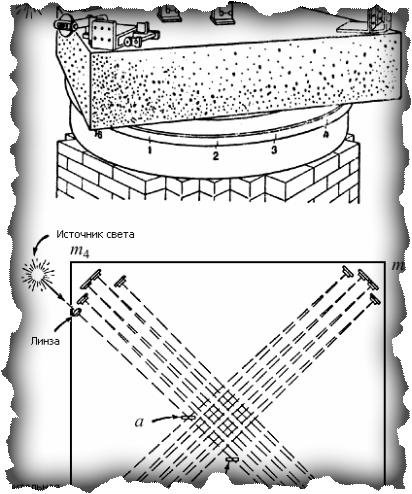
Рис. 4. Реальная установка. Углы падений и отражений лучей в ИСО установки не
равны 90 градусов.
Мы воспользуемся тем же самым приемом и максимально упростим схему, направив
горизонтальный и вертикальный лучи строго перпендикулярно друг другу в ИСО
установки. Чтобы вертикальный луч имел возможность попасть в телескоп, верхнее
зеркало придется немного развернуть на угол, равный половине угла аберрации,
вот так:
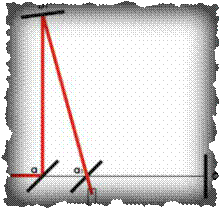
Рис. 5. Упрощенная условная схема установки Майкельсона-Морли.
АСО. Верхнее зеркало немного развернуто на небольшой угол, равный половине угла
аберрации, с целью направить отраженный луч в телескоп движущейся установки.
Угол отражения в точности равен углу падения. Угол между падающим и отраженным лучом
равен углу аберрации. В ИСО зеркала траектория падающего и отраженного луча
совпадают, при том как угол отражения не равен углу падения (так как зеркало не
перпендикулярно лучам).
Расчет длин оптических путей обоих лучей
Продольный луч
t’=d/(c-v) (1)
t’’=d/(c+v) (2)
t=t’+t’’=d/(c-v)+d/(c+v)=2cd/(c2-v2) (3)
Итак, t= 2cd/(c2-v2) (4)
Длина оптического пути будет:
S=tc=2c2d/(c2-v2) (5)
Поперечный луч
Путь s, пройденный полупрозрачным зеркалом:
s=Tv (6)
где T – время, за которое луч света проходит расстояние ab1a1, v –скорость
Земли.
Путь, пройденный лучом:
d+l=Тc (7)
где d – расстояние ab1, l – расстояние b1a1, с – скорость света.
l=Tc-d (8)
Согласно теореме Пифагора:
l2=s2+d2 (9)
Подставляем здачения l и s:
(Tc-d)2=(Tv)2+d2 (10)
Преобразовываем:
T2c2-2Tcd+d2=T2v2+d2 (11)
T2c2- T2v2=2Tcd (12)
T2(c2-v2)=2Tcd (13)
T(c2-v2)=2cd (14)
И в итоге получаем:
T=2cd/(c2-v2) (15)
S=Tc=2c2d/(c2-v2) (16)
Мы получили идентичные формулы (5) и (16). Следовательно, длины оптических
путей обоих лучей одинаковы. Разность длин оптических путей равна 0 при любой
скорости системы.
Выводы
1. Как мы видим, отрицательный результат опыта
Майкельсона-Морли легко объясним без привлечения теории относительности, в
рамках классического принципа определения угла отражения луча от движущегося
зеркала.
2. Интерферометр Майкельсона не является
подходящим прибором для выявления эфирного ветра.
Примечание
Многие читатели пишут мне, что при развороте
интерферометра на 90 градусов лучи не попадут в телескоп.
Лучи не попадут в телескоп только на упрощенной условной схеме. В реальной
установке (см. рис.4):
1. Лучи идут под непрямыми углами, поэтому вертикальный луч попадает в телескоп
без разворота верхнего зеркала.
2. Лучи в реальной установке представляют собой не линии точечной толщины, а
пучки лучей ощутимой толщины. Поэтому при любых разворотах интерферометра
каждый раз какая-то часть лучей обязательно попадает в телескоп. В каждую точку
мишени при разных положениях установки попадают разные лучи. Но
интерференционная картина не меняется, поскольку длина лучей всегда одна и та
же.
Литература
1.Об
относительном движении Земли и светоносном эфире Альберт А.Майкельсон, Эдвард
В.Морли.
2.КВАНТОВАЯ ОПТИКА М.О. Скалли, М.С. Зубайри.
3. Searching
for the Ether: Leopold Courvoiser’s Attempts to Measure the Absolute Velocity
of the Solar System ROBERTO DE ANDRADE MARTINS Physics Department, State
University of Paraiba (UEPB), Brazil