Другие статьи

В.Гагин "Системный синтез ("Лезвие жизни")"

Глава VII

"Природа - не сырье для цивилизации, а прекрасный солнечный дворец, в который человек должен своим трудом, волей, разумом вносить усовершенствования и изменения. Нет большего преступления, чем насиловать, уродовать, извращать природу. Природа, неповторимая во Вселенной колыбель жизни, - это мать, родившая, вскормившая, воспитавшая нас, и поэтому относиться к ней нужно, как к своей матери, - с высшей степенью нравственной любви".

7. Выборы эволюции. Модели.

"Вселенную нельзя низводить до уровня человеческого разумения, как это делалось до сих пор, но следует расширять и развивать человеческое разумение, дабы воспринимать образ Вселенной по мере ее открытия".

7.1.Проблема выбора.

"Те, что веруют слепо, - пути не найдут.

Тех, кто мыслит, - сомнения вечно гнетут.

Опасаюсь, что голос раздастся однажды:

"О невежды! Дорога не там и не тут!".

Современной физикой доказано: материя подвержена самопроизвольным, и непредсказуемым /стохастическим/ изменениям, и не только на микроуровне. На макроуровне, например, недавно,открыты явления названные "странным аттрактором" - когда дальнейший ход какого-то процесса перестает определяться прошлыми состояниями. Т. е., в таких ситуациях, крайне малые воздействия /причины/,могут иметь, сколь угодно значительные, последствия. Но, ведь термодинамика утверждает: мир,полный стохастических, самопроизвольных движений, совершающихся или возможных, должен, очень скоро, превратиться в равномерный хаос.

А наш мир, вопреки второму закону термодинамики, довольно сильно, упорядочен и продолжает развиваться и усложняться. Т.о., у всех природных процессов, существует определенная направленность. Какие же свойства и механизмыобеспечивают эту направленность? Ответ на этот вопрос содержится в дарвиновском, фундаментальном исследовании эволюционных процессов. Любой такой процесс, состоит из трех составляющих: наследственность, изменчивость и отбор. Эти понятия для эволюции универсальны и, сегодня, наполнились более глубоким содержанием, чем во времена Дарвина.

Прошлые состояния материальной системы, в той или иной степени, предопределяют ее будущее, воздействуют на него. Какие-то особенности, характеристики,сохраняются при любых изменениях. Сами изменения, раз совершившись, тоже, могут закрепиться и сохраниться. Все это,в общем виде, и называется наследственностью.

Об изменчивости, уже говорилась в общем виде, когда речь шла о стохастических движениях материи. Взаимодействие наследственности и изменчивости сложно. Законы делают одни изменения невозможными, другие маловероятными, третьи - непродолжительными, а какие-то, ихменьшинство, сохраняются и закрепляются. Какие законы создают телеологичностъ, сказать, пока трудно. Но, не будь их, мы жили бы,в совершенно неупорядоченном и, абсолютно непредсказуемом, мире. Действие этих законов, реализуется в последнем элементе триады - в отборе. И, логично предположить, что среди механизмов отбора, существуют такие, под действием которых, с большей вероятностью, закрепляются те изменения, которые повышают организованность.

И направленность эволюции, должна получить объяснение, как результат определенных "предпочтительных выборов", постоянно осуществляемых Природой. А может быть, воспользоваться "бритвой Оккама" и привлечь на помощь энтелехию?

Рассмотрим подробнее, систему принципов и механизмов отбора, действующих в Природе и обществе. Действия всех природных и социальных законов, можно представить, как постоянный отбор: из мыслимого выбирается возможное. Этот отбор осуществляют и законы Ньютона, и внутренняя конкуренция /внутривидовая/, и основные балансовые соотношения экономики. Все динамические системы, постоянно, делают выбор. Далеко не в каждом случае, конкретный результат выбора, может быть предсказан заранее. Наши представления, о сфере действия "странного аттрактора", постоянно расширяются. Работа по детальной классификации механизмов, определяющих выбор, еще предстоит. Но два типа таких механизмов, можно уже выделить.

Первый, можно назвать: механизмы адаптационного типа - к их числу относятся и дарвиновские принципы естественного отбора. Их характерная особенность - предсказуемость. Под действием этого механизма, система не обретает, никаких неожиданных и, существенно новых, свойств.

Второй тип, принципиально другой. Под его действием происходит не медленное накопление изменений, а стремительная перестройка.

Такие перестройки, система претерпевает, когда нагрузки на нее, превышают какой-то критический предел. Тогда, она теряет устойчивость (спонтанное нарушение симметрии?), и выходит на пересечение нескольких возможных каналов (направлений) эволюции.В математике, такие точки ветвления, называются точками бифуркации, а сами механизмы такого рода, будут называться бифуркационными. Какое направление, какой канал, выберет система, по такому направлению и пойдет ее развитие, после точки бифуркации. Можно утверждать, что какой бы вариант ни выбрала система, но ей придется подчиняться некоему, "своду законов" Природы, выстроенному в жесткой иерархический последовательности.

Приоритет, среди этих "сводов законов" принадлежит, конечно, законам сохранения вещества, энергии, импульса, информации. Оставшиеся возможные состояния, должны пройти через фильтр, чрезвычайно примечательных, законов, о которых говорилось выше, и которые, называются вариационными: при любом перемещении физической точки в пространстве, и любом изменении физической величины во времени, эти законы, как бы, выбирают наиболее экономную траекторию. В этом их суть, это - экстремальные принципы.

Суть экстремальных принципов, для эволюции, в том, что из бесчисленного количества вариантов состояния системы, информация (вернее ее тезаурус - знание), выбирает оптимальный, по отношению к Цели. Это и будет, минимум или максимум, или экстремум.

Например, как уже говорилось выше, луч света идет по кратчайшему пути. Время движения вдоль истинного светового луча - минимально. А минимально время - минимальна и энтропия. Ключ, к нахождению траектории истинного светового луча, дает информация.

Законы Ньютона, также допускают вариационную формулировку.

7.2. Принцип экономии энтропии.

"Оставьте трудиться напрасно, стараясь извлечь из разума всю мудрость; спрашивайте природу, она хранит все истины и на вопросы ваши будет отвечать вам непременно и удовлетворительно".

Сложные системы, созданные Природой, должны иметь преимущество перед простыми, иначе, они не имели бы права, на существование. В чем это преимущество? Оно выражаетсяэмпирическим принципом: "принципом минимума диссипации".

Суть его в том, что из множества состояний системы, равно соответствующих фундаментальным законам Природы, реализуется тот, при котором рассеивание энергии системы (или рост энтропии), минимально. Похожий принцип, был сформулирован, в 1931 г.,Л. Онсагером, применительно к задачам неравновесной термодинамики. Примеров противоречащих ему не обнаружено.

Можно предположить, что он частный случай другого, более общего принципа, который можно назвать принципом экономии энтропии. Если, в каких-то условиях, возможны несколько типов организации материи, не противоречащих законам сохранения, и другим принципам, то реализуется и сохранит наибольшие шансы на стабильность и последующее развитие, именно тот, который позволит утилизировать внешнюю энергию, в наибольших количествах, наиболее эффективно.

Системы, которые способны поглощать энергию эффективнее, получают преимущество. И это, как правило, более сложные и организованные системы. Поэтому, постоянное повышение организованности - важнейший элемент, важнейший критерий, при выборе у Природы. Принцип экономии энтропии, замыкает "свод законов" yпpaвляющих отбором. Он выбирает, из всех возможных, состояний траекторий движения и развития, те, которые удовлетворяют, всем остальным законам Природы. Он несет ответственность, за направленность эволюции.

Суть другого важнейшего принципа выбора, в обратных связях. Во все более усложняющихся условиях, для поддержания гомеостаза, живым системам все более необходима, отражающая информация. Она дает возможность, оперативно менять свое состояние, под давлением каких-то физико-химических процессов, при опасных изменениях окружающей среды, прогнозируя приближение бифуркационных состояний.

Подытоживая, можно заключить, что критерии, по которым происходит отбор в живой природе - это движение, по лезвию бритвы. С одной стороны, законы эволюции заставляют живые системы, постоянно стремиться, к более эффективному использованию внешней энергии и усложняться, а с другой стороны, чем сложнее система, тем больше у нее параметров. Тем больше шансов, неверно просчитать приоритеты, больше вероятность ошибки и больше шансов оказаться в зоне бифуркации. А бифуркация - огромный риск. Отсюда, потрясающая драматичность, всех процессов эволюции жизни.

7.3. Эволюция - информационный выбор.

"Разве то,что человек может знать, и есть именно то, что он должен знать?".

Механизмы обратной связи, информационные механизмы отбора, дав невиданные возможности развития, помогли перейти, на принципиально новый уровень адаптации, но обрекли живые системы на вечную неустойчивость.

Когда выяснилось, что обычных, рефлекторных, обратных связейнедостаточно для дальнейшего развития, когда, даже животные,научились просматривать сразу несколько путей адаптации, перебирать варианты, прогнозировать, тогда положение осложнилось еще больше. Появившаяся способность предвидеть результаты действий, строить поведение, не как цепочку однозначных реакций, на внешние раздражители, а как определенную программу, вероятность ошибки, возросла многократно.

Развиваясь, системы обрели способность соотносить, друг с другом, фрагменты информации, сопоставлять разные типы ситуаций, переносить представления и ожидания, с одного класса объектов, на другие. Информация, потеряв жесткую, как в случае условного рефлекса, связь с конкретным действием и став, казалось бы, бесцельной, начала заготавливаться впрок. Это открыло колоссальные возможности, качественно повысить эффективность использование информации.

Умение накапливать информацию, оторванную от конкретной ситуации, конкретного действия, открыло грандиозную возможность: создавать нечто,несуществующее в Природе, реализовывать такие варианты и формы организации материи, которые, сами по себе, из-за малой вероятности, не просочилась бы, через фильтр отборов, хотя, в принципе, не противоречат законам Природы. Это всевозможные искусственные системы, становящиеся все более мощными, и повышающие, таким образом, как подсистемы, мощность систем их создавших.

Мощность подсистем (человека и сообществ) геосистемы (Земли),настолько возросла, что это, позволило перейти, на новый уровень самоорганизации, такой, что свертывать рост, переходить в стационарное состояние, уже невозможно. Но и расширять поле гомеостаза, за счет окружающей среды и ее ресурсов,тоже нельзя. По многим параметрам,человечество, и так привело биосферу, вплотную, к критическим состояниям. А перегрузка, как известно, приводит к бифуркации.

7.4. Моделирование эволюционных процессов.

"Мир покоится на закономерностях и в своих проявлениях представляется как продукт разума - это указание на его Творца".

Сегодня, уже назрела необходимость, радикальной смены критериев выбора. Ими должны стать критические параметры, нарастающие в окружающей среде. Необходим всесторонний анализ: насколько способны те,или иные, варианты развития приближать к нам, или отдалять, от точек бифуркации. Для этого нужны глобальные модели. Они должны стать для человечества тем, чем когда-то стали для живых систем, механизмы обратной связи: источником сигналов о приближении к границам, области гомеостаза. Например, моральный запрет на ядерную войну - это, не просто современное воплощение древней заповеди "Не убий", но и безусловное предвидение, последствий перехода, за точку бифуркации.

Создавая модели эволюционных процессов, необходимо использовать принцип дополнительности. Создать полную модель, пока, практически невозможно. А создание математической, физической, биологической, кибернетической, энергетической, социальной и т. д., моделей, вполне, уже по силам. Объединение их позволит приблизиться к модели реальной, проявить неявные тенденции и векторно-тензорные особенности.

Попробуем создать первичную, математическую модель эволюции, в самом общем виде, вернее ее геометрическое воплощение, в режиме ручного управления. Основными определяющими категориями, управляющими эволюцией, являются информация, и ее антагонист - энтропия.

Как уже говорилось ранее, для определения их значений необходимо логарифмирование величин. Т. е., информационные и энтропийные процессы описываются логарифмическими зависимостями.

Динамические эволюционные процессы описываются спиральными кривыми. Поэтому, представим информационно-энтропийные, динамические процессы эволюции, в виде логарифмических спиралей.

При создании модели необходимо учитывать, что в реальности, при создании систем и их зависимостей, Природа использовала критерии пропорционирования (Золотой пропорции), ряд чисел Фибоначчи, принцип резонансного изоморфизма, топологические принципы организации пространства и материи, в форме Замечательных многогранников и дискретные операторы.

Для определенности и конкретизации задачи, выберем геометрическую модель эволюции геосистемы (Земли). Самоорганизация, самосинхронизация, резонансный отбор,принципиально соотносятся с этими общими критериями моделирования.

В модели, должные быть отражены, такие составляющие естественной эволюции, как наследственность, изменчивость и отбор. Предполагая, что геосистема, не только живая, но и разумная, при построении модели, необходимо использовать дискретные операторы 5 и √5.

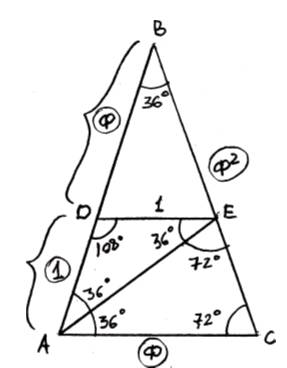
Из математики известно, что логарифмическая спираль, описывается двумя чудесными фигурами, тесно связанными с Золотой пропорцией. Один способ, - с помощью совершенного, квадрируемого прямоугольника, бесконечного порядка, путем вращения, образующихся в нем квадратов. Он называется, способом вращающихся квадратов. Другой способ, - с помощью равнобедренного треугольника, стороны которого, находятся в золотом отношении к основанию. Углы при основании такого треугольника равны 72⁰, что вдвое больше угла при вершине, равного 36⁰.

Треугольник АВС, разбивается на 3 треугольника Золотой пропорции. В них стороны равны:

В треугольнике АВС, точка пересечения биссектрисы угла при основании, с противолежащей стороной, делит эту сторону в среднем и крайнем отношении. При этом, весь треугольник разбивается на два меньших треугольника, один из которыхподобен исходному. В свою очередь, его можно разбить, на два, еще меньших треугольника, проведя в нем биссектрису утла, при основании. Продолжая процесс, получим бесконечную последовательность треугольников, чьи вершины описывают логарифмическую спираль.

АД = 1

ДВ = Ф

ВС = АВ = Ф + 1 = Ф²

АС = АЕ = Ф

Характерно, что отношение углов, отвечает отношению целых чисел, а отношения сторон несоизмеримы.

Стороны равны Ф и Ф².

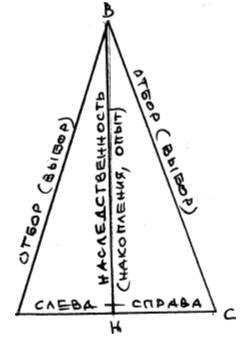
Стороны треугольника АВС отражают триадуэволюционных категорий: наследственность, изменчивость, отбор.

В основание, положена изменчивость, стремящаяся слева и справа, по алгоритму ряда чисел Фибоначчи, к Золотому отношению, пределу Ф. Высота треугольника - наследственность: то что система накопила, прошлый опыт и прогнозируемые ситуации /прогноз - функция опыта/. Большие стороны треугольника - это отбор /слева и справа/, в процессе осциллирующих процессов изменчивости, согласно набора критериев - законов Природы.

Логарифмическая спираль образованная "вращающимися треугольниками":

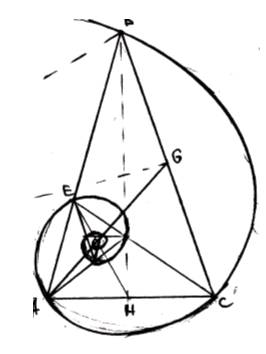
Логарифмическая спираль, выбрана моделью эволюционных процессов системы. Вернее, мы рассматриваем ее проекцию на плоскость.

Трехмерную модель рассмотрим ниже.

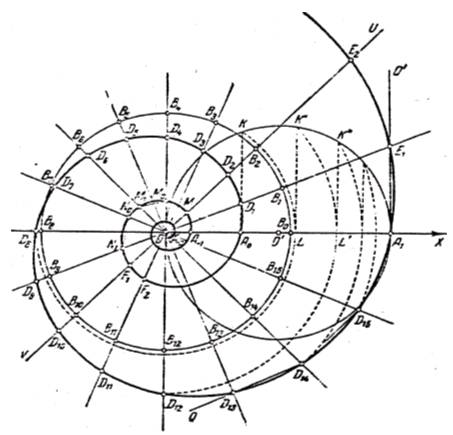
Классическая логарифмическая спираль.

Прямая UV,равномерно вращается вокруг неподвижной точки О /полюс/, а точка М, движется вдоль UV,удаляясь от О, со скоростью, пропорциональной расстоянию ОМ. Линия,описываемая точкой М - логарифмическая кривая.

Отношение q, конечного полярного радиуса (ОА₁), к начальному (ОАо), при повороте прямой UV, на угол+2π,будем называть, коэффициентом роста спирали.

Вращение UV, против часовой стрелки, создает правую спираль, по часовой- левую спираль. Для правой спирали коэффициент роста q - больше единицы,а для левой - меньше единицы. При q = 1, спираль вырождается в окружность.

Рассматриваемый эволюционный процесс не статичен, а динамичен. При вращении плоской модели - треугольника АВС, его высота (наследственность, накопленная информация),неуклонно растет. Основание АС,в какой-то период, вращаясь, занимает место стороны ВС, включая в себя и изменчивость критериев отбора и выбора Природы. А сторона ВС (или AВ) занимает новое, более высокое положение, определяя, вместе с возросшей наследственностью (накоплениями, опытом), с высотойВН - новую точку кривой, олицетворяющей эволюцию.

Точки В и С (или А и В), находятся на кривой (спирали). Прямая, их соединяющая, это отобранные фундаментальные законы, явления, характеристики, величины (из наследственного и измененного, привнесенного), а точки на кривой, это, построенные на этих базовых понятиях, следствия, выводы, настройка эволюции, на каком-то этапе развития

Далее. Рассмотрим энтропию системы. В какой-то начальный момент,в каком-тообъеме(в декартовой системе координат), ее величинастремится к нулю.

Возьмем, какой-то объем пространства,ограниченный кубом (для определенности). В этом пространстве, все точки равноправны, имеют одинаковую энергию, система равновесна (или почти). Проекция этого куба на плоскость - квадрат. Используем для построения логарифмической спирали, метод вращения квадратов.

Процесс энтропийного изменения, подчиняется, также, логарифмической зависимости.

Построим Золотой прямоугольник /т. е. прямоугольник стороны которого находятся в золотом отношении/. Отрезав от прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим Золотой прямоугольник меньших размеров.

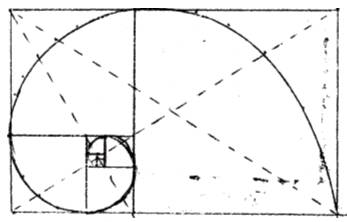
Логарифмическая спираль - образованная вращающимися квадратами

Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие прямоугольники. Точки, делящие стороны прямоугольника, в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь. Полюс лежит на пересечении пунктирных диагоналей. Мы получили закручивающуюся спираль.

Предыдущая спираль была правой, данная является левой. Идет процесс противоположный предыдущему: с ростом, накоплением информации, энтропия убывает.

Мы рассматриваем модель в проекции на плоскость. Рассмотрим ее в пространстве. Известно, что при стереографической проекции полушария в логарифмическую спираль,проектируется локсодрома. Т.е., это линия на сфере, которая пересекает все меридианы под одним и тем же углом, как и логарифмическая спираль, которая пересекает под одним и тем же углом радиус-векторы.

Свойства логарифмической спирали универсальны и обладают рядом замечательных свойств. Их широко используют, например, в технике. Лезвия вращающихся ножей в резальных машинах, имеют форму логарифмической спирали, благодаря чему угол резания остается постоянным. В гидротехнике: по логарифмический спирали закручивают трубу, подводящую воду к лопастям. Логарифмическую спираль, применяют при проектировании специальных зубчатых передач. На земном шаре, локсодрома определяет самый удобный куре судна в открытом океане: угол между его курсом и магнитной стрелкой, остается неизменным. Как уже говорилось, по логарифмической спирали, свернуты многие ракушки, семена подсолнечника в корзинке и т. д.

Много внимания, изучению логарифмической спирали, уделили такие математики, как Р. Декарт, Торричелли, Бернулли. Последний, открыв свойство спирали, оставаться неизменной при различных геометрических преобразованиях плоскости, былнастолько поражен этим свойством, что завещал, после его смерти, написать на могиле: "Измененная, не изменяюсь" Название этой замечательной кривой дал П. Вариньон, в начале 18 ст.

Это, действительно, замечательная кривая. Она описывает многие естественные процессы в Природе, явления, отвечающие экстремальным принципам, асимметрии живого, экономии энтропии и т.д. Поэтому, выбор, в качестве модели движения эволюции системы, логарифмической спирали и локсодромы, вполне оправдан. Ее свойства так же универсальны, как у Золотого сечения и ряда Фибоначчи.

Таким образом, моделью эволюции, выбираем сферу с развивающейся локсодромой на ее поверхности. Модель обратного процесса - снижения энтропии, отражает локсодрома завивающаяся в обратном порядке.

Ноосфера привязана к конкретной геосистеме. А как уже говорилась ранее, геосистема моделируется додекаэдром, вписанном в структуру икосаэдра. Полагая, что биосфера развивается по такой же модели, как и геосистема (учитывая их соразмерность), принимаем, пространственную модель эволюции биосферы, аналогичной.

Известно, что додекаэдр двойствен (дуален) икосаэдру - центры граней правильного икосаэдра, являются вершинами правильного додекаэдра. Т.е.,описанная вокруг додекаэдра сфера, является вписанной в икосаэдр. Кроме этой сферы, в состав модели, войдут еще две: вписанная в додекаэдр и описанная вокруг икосаэдра.

Процесс эволюции системы, описывают локсодромы на средней сфере. Каждой точке на локсодроме, соответствует определенное время. Динамика процессов эволюции ритмична и выражается пульсацией средней сферы. Ее радиус изменяется от меньшей (вписанной) сферы,до большей (описанной).

Свойства системы, протекание процессов, зависят от того поля влияния (додекаэдра или икосаэдра), в котором находится сфера моделирования, и зависит от отраженных свойств этих тел.

Учитывая, что локсодромы описываются, различными по конструкции фигурами, они имеют различный коэффициент роста, зависящий, так же, и от других причин. Информационная локсодрома влияет на энтропийную, но это влияние, не прямо. На энтропию влияют и другие подсистемы и факторы.

Данная модель схематична и крайне упрощена. Тем не менее, даже такую, изобразить на плоскости - ненаглядно и сложно для восприятия. Для наглядности проверки достоверности модели и прогнозирования, в первом приближении, необходимо, как минимум, использовать компьютерную графику и анализ. Чем больше других моделей будет наложено на эту, тем реальнее будет модель, и точнее прогнозирование.