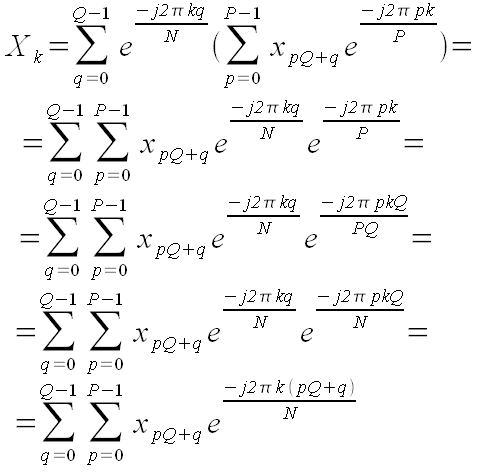Пусть N = PQ. Этот представляет собой более общий случай, чем рассмотренный в предыдущей главе. Теперь не требуется, чтобы
P или Q были степенями двойки.
Напомним основную формулу:
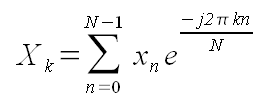 (1).
(1).
Рассмотрим формулу:
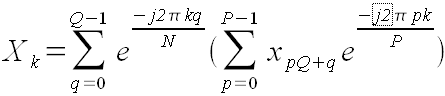 (41).
(41).
Эта формула эквивалентна формуле (1). В самом деле:
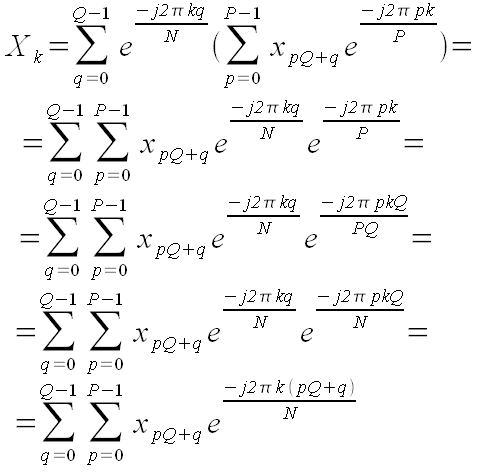
Двойная сумма по pQ + q - это все равно, что одинарная сумма по n, просто
порядок слагаемых другой.
Вернемся к формуле (41). В скобках там стоит обычное прямое БПФ, только не для всех xn,
а для последовательности из P штук, взятых с шагом Q. Количество последовательностей равно Q.
Элементы последовательности выбираются формулой xpQ + q, где p - номер элемента,
q - номер последовательности.
Пусть мы умеем вычислять БПФ для P элементов за время Z(P). Нам понадобится вычислить Q
таких БПФ, на что потратим время O(QZ(P)). Тем самым мы получим все множители в скобках из формулы (41).
После этого надо будет вычислить N элементов Xk, каждый из которых
потребует O(Q) действий, итого потребуется еще O(NQ) действий, а в сумме -
O(QZ(P) + QN) действий.
В предыдущем алгоритме P - было степенью двойки, а для такого числа элементов мы умеем вычислять
БПФ за O(Plog2P) шагов, т.е. Z(P) = Plog2P, и получится
O(QZ(P) + QN) = O(QPlog2P + QN) = O(Nlog2P + N2/P) действий.
Тем самым, мы несколько более простым путем получим ту же оценку сложности алгоритма.
Если P - не степень двойки, мы умеем вычислять ПФ за O(P2) шагов,
т.е. Z(P) = P2, и получится
O(QZ(P) + QN) = O(QP2 + QN) = O(N2/Q + N2/P) действий.
Если P и Q достаточно велики, это лучше, чем O(N2).
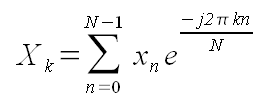 (1).
(1).
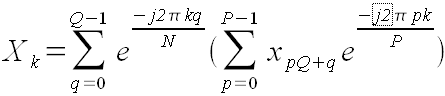 (41).
(41).