Длина береговой
линии. Фрактальная размерность.
(
По материалам сайта
programmersclub.ru )
При изучении географии вы,
конечно, помните, что каждая из стран имеет свою площадь территории и длину границы,
в частности, если страна омывается каким-либо морем или океаном, то она имеет
морскую границу определенной длины. Задумывались ли вы когда-либо, как эту
длину границы определяют? В 1977 г. американский математик Бенуа Мандельброт
поставил перед собой следующий вопрос: чему равна длина береговой линии
Великобритании? Оказалось, что корректно ответить на этот "детский
вопрос" не удается. В 1988 г. норвежский ученый Енс
Федер решил выяснить, чему равна длина береговой
линии Норвегии. Обратите внимание на то, что побережье Норвегии сильно изрезано
фиордами. Другие ученые задавали себе аналогичные вопросы о длинах береговых
линий побережий Австралии, Южной Африки, Германии, Португалии и других стран.
Мы можем измерить длину береговой линии
только приблизительно. По мере того как мы уменьшаем масштаб, нам приходится
измерять все больше маленьких мысов и бухт - длина береговой линии
увеличивается, и объективного предела уменьшению масштаба (и, тем самым,
увеличению длины береговой линии) просто не существует; мы вынуждены признать,
что эта линия имеет бесконечную длину. Мы знаем, что размерность прямой линии
равна одному, размерность квадрата - двум, а размерность куба - трем.
Мандельброт предложил использовать для измерения "чудовищных" кривых
дробные размерности - размерности Хаусдорфа - Безиковича. Бесконечно изломанные кривые, подобные
береговой линии - не вполне линии. Они как бы "заметают" часть
плоскости, подобно поверхности. Но они и не поверхности. Значит, резонно
предположить, что их размерность больше одного, но и меньше двух, то есть это
дробно-размерные объекты.
Норвежский ученый Е. Федер,
предложили другой способ измерения длины береговой линии. Карту покрыли
квадратной сеткой, ячейки которой имеют размеры е ? е.
Видно, что число N(e) таких ячеек, которые покрывают береговую линию на карте,
приближенно равно числу шагов, за которое можно обойти по карте береговую линию
циркулем с раствором e. Если е уменьшать, то число N(e) будет возрастать. Если
бы длина береговой линии Великобритании имела определенную длину L, то число
шагов циркуля с раствором (или число квадратных ячеек N(e), покрывающих
береговую линию на карте) было бы обратно пропорционально e, а величина Ln(e)=N(e) ? e при уменьшении к
стремилась бы к постоянной L. К сожалению, расчеты, проведенные многими
учеными, показали, что это не совсем так. При уменьшении шага измеренная длина
возрастает. Оказалось, что взаимосвязь измеренной длины L(e) и шага e может
быть описана приближенным соотношением
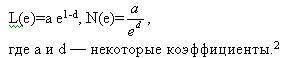
Коэффициент D называется фрактальной
размерностью. Слово фрактал происходит от латинского слова fractal
- дробный, нецелый. Множество называется фрактальным, если оно имеет нецелую
размерность. Для Норвегии D=1,52, а для Великобритании D=1,3. Таким образом,
береговая линия Норвегии и Великобритании - фрактал с фрактальной размерностью
D. Расчеты были также проведены и для окружности, и фрактальная размерность
окружности D=1, что и следовало ожидать. Таким образом, фрактальная размерность
- обобщение обычной размерности.
Как это понимать и что бы это могло
означать? Математики стали вспоминать, было ли что-либо подобное раньше в
математике или нет? И вспомнили! Рассмотрим часть некоторой линии АВ на плоскости
(рис. 3). Возьмем квадрат с ребром e и спросим себя: сколько нужно квадратиков
N(е) с ребром длиной е, чтобы покрыть линию АВ такими квадратиками? Видно, что
N(e) пропорционально
![]()
Аналогично, если замкнутую ограниченную
область на плоскости (рис. 4) покрыть квадратной сеткой со стороной e, то
минимальное число квадратиков со стороной е, покрывающих область, будет равно
![]()
Если мы рассмотрим замкнутую ограниченную
область в трехмерном пространстве и возьмем кубик с ребром e, то количество
кубиков, заполняющих эту область,
![]()
Определим фрактальную размерность исходя из
выше изложенного в общем случае следующим образом:
![]()
Возьмем логарифм от левой и правой частей
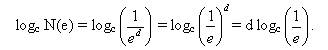
Переходя к пределу при e, стремящемся к нулю (N, стремящемся к бесконечности), получим
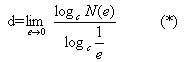
Это равенство является определением размерности которая обозначается d.
Вернемся к нашей исходной задаче.
Рассмотрим длину береговой линии L(е) = аoe1-d и сделаем следующие
преобразования:
![]()
т.е. N(e) пропорционально
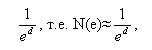
и переходя к пределу, имеем
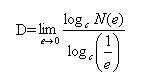
Таким образом, d - размерность.
Расчеты показывают, что
![]()
Таким образом, береговые линии
Великобритании и Норвегии являются фракталами и имеют фрактальную размерность
1,3 и 1,52, соответственно.