Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
(Продолжение; начало см. в [1])
4.2.
Преобразование «поворот»
4.2.1
Рассмотрим множество векторов ![]() , где
, где ![]() принимает все
целочисленные значения,
принимает все
целочисленные значения, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (т.е. первый отличный
от нуля член
(т.е. первый отличный
от нуля член ![]() положителен),
положителен), ![]() – произвольный вектор.
Таблицу,
– произвольный вектор.
Таблицу, ![]() -й строкой которой является
-й строкой которой является ![]() ,обозначим
,обозначим ![]() :
:
![]() :
:
 ,
,
где ![]() . Каждую строку таблицы заменим восходящей диагональю,
имеющей со строкой общий нулевой член. Полученную таблицу обозначим
. Каждую строку таблицы заменим восходящей диагональю,
имеющей со строкой общий нулевой член. Полученную таблицу обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, результат обозначим
проделаем ту же
операцию, результат обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т. д. Например:
проделаем ту же
операцию, и т. д. Например:
![]() :
: ![]() :
:
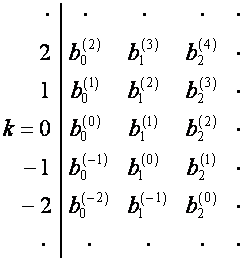 ,
,  .
.
Каждую строку таблицы ![]() заменим нисходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим
заменим нисходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим
![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т. д. Например:
проделаем ту же
операцию, и т. д. Например:
![]() :
:
![]() :
:
 ,
, 
Преобразование, отображающее каждую строку
таблицы ![]() на одноименную строку
таблицы
на одноименную строку
таблицы ![]() , назовем
, назовем ![]() -м поворотом таблицы
-м поворотом таблицы ![]() и обозначим
и обозначим ![]() , имея в виду, что для
всех
, имея в виду, что для
всех ![]() преобразование одно и
то же.
преобразование одно и
то же.
Во введении было показано, что
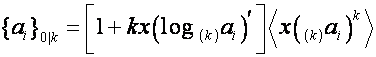 ,
,
где ![]() определяется
уравнениями
определяется
уравнениями
![]() ,
, ![]() .
.
Доказательство опиралось на ряды Лагранжа. Чтобы
подчеркнуть элементарность рассматриваемой конструкции, опишем ее, не ссылаясь
на ряды Лагранжа.
Представим таблицу, нулевая строка которой
совпадает с вектором ![]() , все члены нулевого столбца равны
, все члены нулевого столбца равны ![]() . Остальные элементы не определены. Отталкиваясь от этих
начальных условий, составим таблицу
. Остальные элементы не определены. Отталкиваясь от этих
начальных условий, составим таблицу ![]() , где
, где ![]() –
– ![]() -я нисходящая диагональ составляемой таблицы,
-я нисходящая диагональ составляемой таблицы, ![]() – определенный вектор
(по определению
– определенный вектор
(по определению ![]() ).
).
Умножая вектор ![]() , два первых члена которого известны, на
, два первых члена которого известны, на ![]() , где
, где ![]() последовательно принимает
все значения, получаем первый столбец составляемой таблицы. Умножая
последовательно принимает
все значения, получаем первый столбец составляемой таблицы. Умножая ![]() , три первых члена которого известны, на
, три первых члена которого известны, на ![]() , получаем второй столбец составляемой таблицы, и т. д. Таким
образом действительно получаем таблицу, нисходящие диагонали которой связаны
равенством
, получаем второй столбец составляемой таблицы, и т. д. Таким
образом действительно получаем таблицу, нисходящие диагонали которой связаны
равенством
![]() .
.
Аналогичным образом, отталкиваясь от тех
же начальных условий, можно составить таблицу ![]() , где
, где ![]() –
– ![]() -я восходящая диагональ составляемой таблицы. Например, при
-я восходящая диагональ составляемой таблицы. Например, при ![]() :
:
![]() :
:

![]() :
:
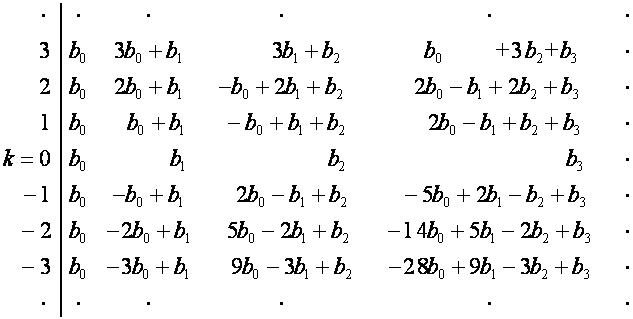
При замене нулевой строки таблицы ![]() на
на ![]() , должна получиться таблица,
, должна получиться таблица, ![]() -й столбец которой совпадает с
-й столбец которой совпадает с ![]() -м столбцом таблицы
-м столбцом таблицы ![]() . Тем самым доказывается, что коэффициент при
. Тем самым доказывается, что коэффициент при ![]() в разложении
в разложении ![]() -го члена
-го члена ![]() -й строки таблицы
-й строки таблицы ![]() по членам нулевой
строки равен коэффициенту при
по членам нулевой
строки равен коэффициенту при ![]() в разложении
в разложении ![]() -го члена. Следовательно,
-го члена. Следовательно, ![]() -я строка таблицы имеет вид
-я строка таблицы имеет вид ![]() , где
, где ![]() – определенный вектор.
При замене нулевой строки на
– определенный вектор.
При замене нулевой строки на 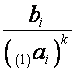 должна получиться
таблица,
должна получиться
таблица, ![]() -я строка которой (
-я строка которой (![]() – целое число)
совпадает с
– целое число)
совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() . Тем самым доказывается, что
. Тем самым доказывается, что ![]() – это
– это ![]() -я степень
-я степень ![]() .
.
Аналогичные рассуждения применимы и к
таблице ![]() .
.
Таким образом,
![]() ,
, ![]() .
.
Другими словами, если строки таблицы связаны
равенством ![]() , то ее восходящие диагонали связаны равенством
, то ее восходящие диагонали связаны равенством ![]() , нисходящие диагонали связаны равенством
, нисходящие диагонали связаны равенством ![]() .
.
Обобщая, выводим:
![]() ,
,
где
![]() ,
, ![]() – определенные
векторы.
– определенные
векторы.
Обозначим: ![]() .
. ![]() -й член
-й член ![]() -й строки таблицы
-й строки таблицы ![]() обозначим
обозначим ![]() . Тогда
. Тогда ![]() . Если
. Если ![]() , то
, то ![]() ,
, ![]() .
. ![]() -й член
-й член ![]() -й строки таблицы
-й строки таблицы ![]() обозначим
обозначим ![]() . Так как нулевая строка и нулевой столбец таблицы
. Так как нулевая строка и нулевой столбец таблицы ![]() известны, остальные
элементы таблицы находим по правилам:
известны, остальные
элементы таблицы находим по правилам:
![]() ,
,
![]() .
.
Например,
![]() :
:
 ,
,
![]() :
: ![]() :
:
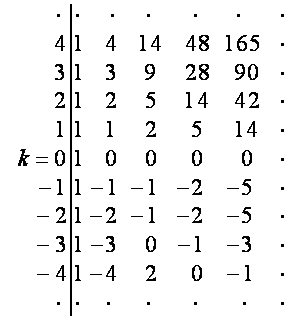 ,
, .
.
Так как при ![]()
![]() ,
,
то
![]() .
.
Например,
![]() :
: ![]() :
:
 ,
, 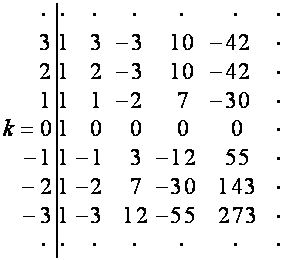 .
.
Преобразование ![]() отображает
отображает ![]() -ю строку таблицы
-ю строку таблицы ![]() на
на ![]() -ю восходящую диагональ,
-ю восходящую диагональ, ![]() -й член которой равен
-й член которой равен ![]() . Следовательно,
. Следовательно, ![]() -я строка матрицы
-я строка матрицы ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы ![]() , и, как видно из таблицы
, и, как видно из таблицы ![]() ,
, ![]() -й столбец матрицы
-й столбец матрицы ![]() совпадает с умноженной
на
совпадает с умноженной
на ![]()
![]() -й восходящей диагональю таблицы
-й восходящей диагональю таблицы ![]() .
.
Таким образом,
![]() ,
,
где ![]() – нулевая восходящая
диагональ таблицы
– нулевая восходящая
диагональ таблицы ![]() . Например,
. Например,
![]()
 ,
,
![]()
 ,
,
![]()

Аналогично, ![]() -я строка матрицы
-я строка матрицы ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы ![]() ,
, ![]() -й столбец совпадает с умноженной на
-й столбец совпадает с умноженной на ![]()
минус
![]() -й нисходящей диагональю таблицы
-й нисходящей диагональю таблицы ![]() :
:
![]() ,
,
где ![]() – нулевая нисходящая
диагональ таблицы
– нулевая нисходящая
диагональ таблицы ![]() . Например,
. Например,
![]()
 ,
,
![]()
 ,
,
![]()

Так как ![]() является матрицей
поворота таблицы
является матрицей
поворота таблицы ![]() :
:
![]() ,
,
где ![]() – нулевая восходящая
диагональ таблицы
– нулевая восходящая
диагональ таблицы ![]() , она также является матрицей поворота таблицы
, она также является матрицей поворота таблицы ![]() , где
, где ![]() – произвольный вектор.
То же относится к матрице
– произвольный вектор.
То же относится к матрице ![]() .
.
По определению ![]() -я строка таблицы
-я строка таблицы ![]() совпадает с
совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() , так что
, так что
![]() ,
,
![]() ,
,
![]() .
.
Так
как
![]() ,
,
то
![]() ,
,
т.е
![]() .
.
Аналогично, ![]() -я строка таблицы
-я строка таблицы ![]() совпадает с
совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() , так что
, так что
![]() ,
,
![]() ,
,
![]() .
.
Переобозначим:
![]() .
.
Обозначим:
![]() .
.
Тогда
![]() ,
,
![]() .
.
Вектор ![]() находим из уравнения
находим из уравнения
![]() .
.
Пусть
![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
Тогда
![]() ,
,
![]() ,
,
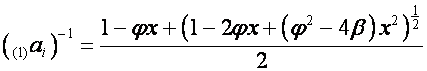 .
.
Пусть
![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
Тогда
 ,
,
![]() ,
,
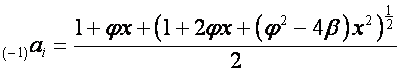 .
.
Пусть
![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
Тогда
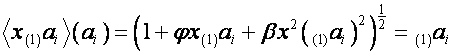 ,
,
 ,
,
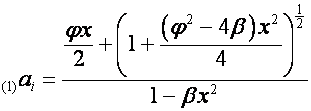 .
.
Пусть
![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
Тогда
 ,
,
![]() ,
,
 .
.
4.2.2
Пусть ![]() ,
, ![]() – векторы, связанные
первым поворотом таблицы
– векторы, связанные
первым поворотом таблицы ![]() и минус первым поворотом
таблицы
и минус первым поворотом
таблицы ![]() :
:
![]() ,
,
![]() .
.
![]() -ю строку таблицы
-ю строку таблицы ![]() ,
, ![]() , умножим на
, умножим на ![]() , нулевую восходящую диагональ умножим на
, нулевую восходящую диагональ умножим на ![]() . Полученную таблицу обозначим
. Полученную таблицу обозначим ![]() ;
; ![]() -ю строку таблицы
-ю строку таблицы ![]() ,
, ![]() , умножим на
, умножим на ![]() , нулевую нисходящую диагональ умножим на
, нулевую нисходящую диагональ умножим на ![]() . Полученную таблицу обозначим
. Полученную таблицу обозначим ![]() . Сформулируем основное свойство изучаемой структуры в виде
утверждения:
. Сформулируем основное свойство изучаемой структуры в виде
утверждения: ![]() -я восходящая диагональ таблицы
-я восходящая диагональ таблицы ![]() совпадает с
совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() ,
, ![]() -я строка таблицы
-я строка таблицы ![]() совпадает с
совпадает с ![]() -й нисходящей диагональю таблицы
-й нисходящей диагональю таблицы ![]() . Например:
. Например:
![]() :
: ![]() :
:


![]() :
: ![]() :
:


Рассмотрим вектор
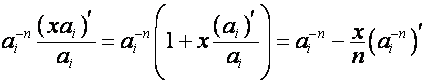 .
.
Если вектор имеет вид 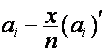 , его
, его ![]() -й член равен нулю. Умножая каждую строку таблицы
-й член равен нулю. Умножая каждую строку таблицы ![]() на
на 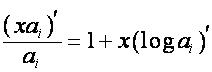 , получаем таблицу, нулевой нисходящей диагональю которой является
, получаем таблицу, нулевой нисходящей диагональю которой является
![]() :
:
![]() .
.
Аналогично,
![]() .
.
Так
как
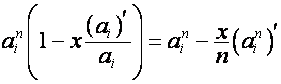 ,
,
то
![]() ,
,
![]() .
.
Таким образом,
![]() ,
,
![]() .
.
Так как
![]() ,
,
![]() ,
,
то
![]() .
.
![]() -й член
-й член ![]() -й строки таблицы
-й строки таблицы ![]() обозначим
обозначим ![]() ,
, ![]() -й член
-й член ![]() -й строки таблицы
-й строки таблицы ![]() обозначим
обозначим ![]() ,
, ![]() . Так как
. Так как
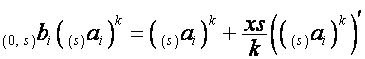 ,
,
то
![]() .
.
Так
как
![]() ,
,
то
![]() ,
, ![]() .
.
При ![]() получаем
доказательство утверждения о таблицах
получаем
доказательство утверждения о таблицах ![]() и
и ![]() .
.
4.2.3
По определению логарифма
и экспоненты
![]() .
.
Отсюда вытекает, что если
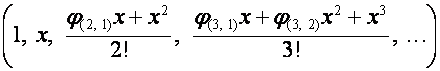
– последовательность строк матрицы ![]() , то
, то
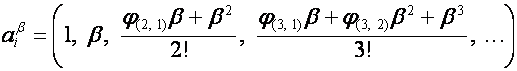 .
.
Соответствие
![]() между строками матрицы
между строками матрицы
![]()
![]() ,
, ![]() , и значениями вектора
, и значениями вектора ![]() , обобщая биномиальный ряд, назовем биномиальной формой
записи вектора
, обобщая биномиальный ряд, назовем биномиальной формой
записи вектора ![]() и обозначим
и обозначим
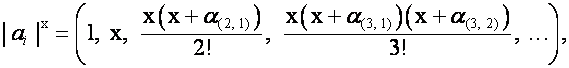
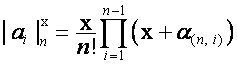 .
.
В формуле общего члена
подразумевается, что ![]() ,
, ![]() . Коэффициенты
. Коэффициенты ![]() могут быть
комплексными числами, необходимыми для представления вектора
могут быть
комплексными числами, необходимыми для представления вектора ![]() в виде
в виде
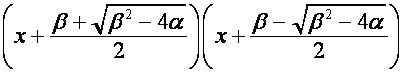 .
.
Используя
биномиальную форму записи вектора ![]() , составим таблицу
, составим таблицу ![]() (по определению
(по определению ![]() ). Первый член
). Первый член ![]() -ой строки таблицы равен
-ой строки таблицы равен ![]() ,
, ![]() -й член
-й член ![]() -ой строки равен
-ой строки равен 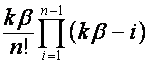 :
:
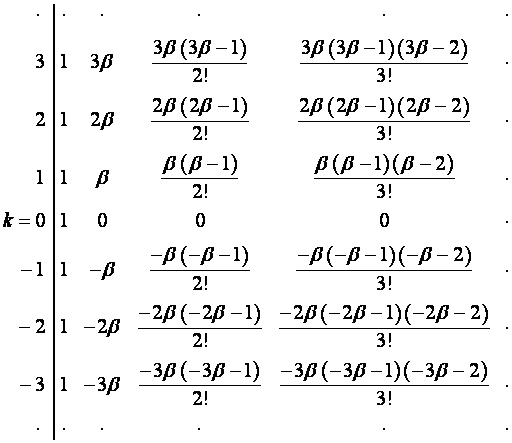
Множество
строк с положительными номерами назовем верхней половиной таблицы, множество
строк с отрицательными номерами – нижней половиной таблицы. Пользуясь
равенством ![]() и подстановкой
и подстановкой ![]() , выводим, что
, выводим, что ![]() -й член
-й член ![]() -ой строки верхней половины таблицы
-ой строки верхней половины таблицы ![]() ,
, ![]() , равен
, равен  :
:
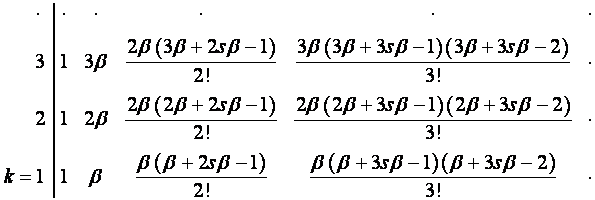 ,
,
![]() -й член
-й член ![]() -ой строки нижней половины таблицы
-ой строки нижней половины таблицы ![]() ,
, ![]() , равен
, равен  :
:

Обозначим:
![]()
![]() ,
, ![]() – матрица, нулевая и
первая строка которой соответственно
– матрица, нулевая и
первая строка которой соответственно ![]() и
и ![]() , а
, а ![]() -я строка имеет вид
-я строка имеет вид 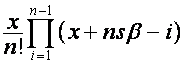 . Тогда
. Тогда
![]() ,
,
![]() ,
,
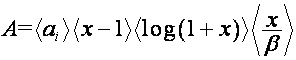 ,
,
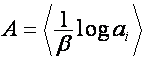 .
.
Обозначим:
![]()
![]() ,
, ![]() – матрица, нулевая и
первая строка которой соответственно
– матрица, нулевая и
первая строка которой соответственно ![]() и
и ![]() , а
, а ![]() -я строка имеет вид
-я строка имеет вид 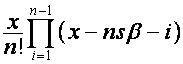 . Тогда
. Тогда
![]() ,
,
![]() ,
,
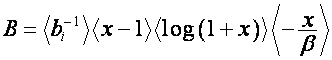 ,
,
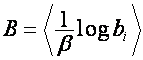 .
.
Таким
образом,
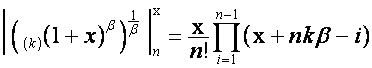 .
.
Например:
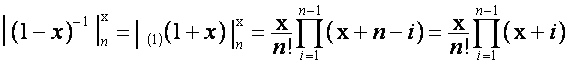 ;
;
 ;
;
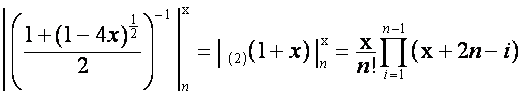 ,
,
или
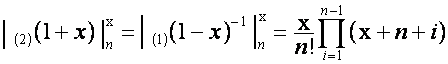 ;
;
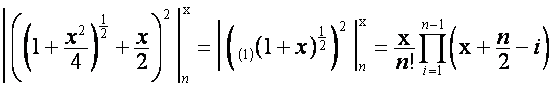 .
.
Обобщая, выводим: если
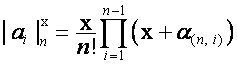 ,
,
то
 .
.
1.
Е. В. Бурлаченко. Алгебраические заметки.
2. Риордан Д. Введение в
комбинаторный анализ. – М.: ИЛ, 1963.
3. Сачков В. Н.
Комбинаторные методы дискретной математики. – М.: Наука, 1977.