Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
(Продолжение; начало см. в [1])
4.
Обобщенное преобразование Эйлера и оператор сдвига
4.1.
Собственные базисы
4.1.1
Обобщенным преобразованием Эйлера
называется преобразование, матрица которого транспонирована к матрице оператора
сдвига на ![]() :
:
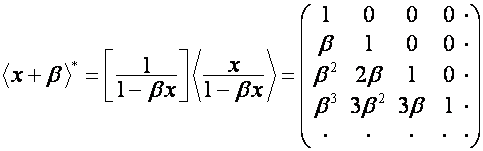 .
.
Обозначим:
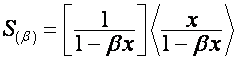 ,
, ![]() ,
,
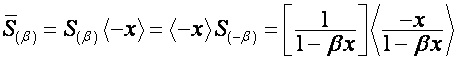 :
:
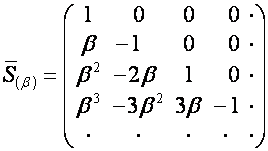 ,
,
![]() .
.
Тогда
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Преобразования ![]() и
и ![]() являются отражениями:
являются отражениями:
![]() ,
, ![]() .
.
Пространство векторов, отображаемых преобразованием ![]() на себя, назовем тождественным
подпространством преобразования
на себя, назовем тождественным
подпространством преобразования ![]() и обозначим
и обозначим ![]() ; пространство векторов, отображаемых на противоположные,
назовем антитождественным подпространством преобразования
; пространство векторов, отображаемых на противоположные,
назовем антитождественным подпространством преобразования ![]() и обозначим
и обозначим ![]() . Аналогичные подпространства преобразования
. Аналогичные подпространства преобразования ![]() обозначим
обозначим ![]() и
и ![]() .
.
Векторы ![]() и
и 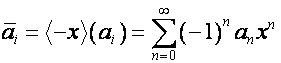 назовем спаренными.
назовем спаренными.
Преобразования ![]() и
и ![]() не имеют собственных
векторов, кроме
не имеют собственных
векторов, кроме ![]() и
и ![]() ,
, ![]() соответственно,
поэтому их удобно представлять в виде композиции отражений:
соответственно,
поэтому их удобно представлять в виде композиции отражений:
![]() ,
, ![]() .
.
Таким образом, преобразование ![]() векторы пространства
векторы пространства ![]() отображает на
спаренные, векторы пространства
отображает на
спаренные, векторы пространства ![]() – на противоположные
спаренным. Преобразование
– на противоположные
спаренным. Преобразование ![]() векторы пространства
векторы пространства ![]() отображает на спаренные, векторы пространства
отображает на спаренные, векторы пространства ![]() – на противоположные спаренным.
– на противоположные спаренным.
Поскольку мы не затрагиваем вопроса о
сходимости рядов, в область определения преобразований ![]() и
и ![]() входят только конечные
векторы, иначе говоря – полиномы. Хотя, казалось бы, если
входят только конечные
векторы, иначе говоря – полиномы. Хотя, казалось бы, если
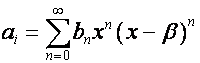 ,
,
то
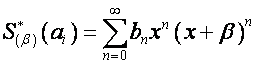
безотносительно к вопросу о сходимости рядов.
Например, так как
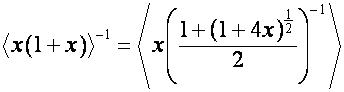 ,
,
то
справедливо равенство
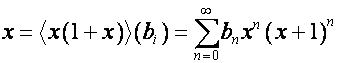 ,
,
где
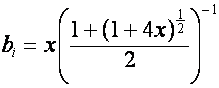 .
.
Но
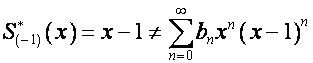 ,
,
так
как
![]() .
.
Дело в том, что произведение бесконечных матриц ![]() ассоциативно, только
если все строки или все столбцы матриц
ассоциативно, только
если все строки или все столбцы матриц ![]() ,
, ![]() ,
, ![]() конечны [2, стр.21].
Все строки и столбцы матрицы
конечны [2, стр.21].
Все строки и столбцы матрицы ![]() конечны, но строки
матрицы
конечны, но строки
матрицы ![]() бесконечны. Поэтому,
если
бесконечны. Поэтому,
если ![]() – бесконечный вектор,
то
– бесконечный вектор,
то
![]() .
.
Последовательность векторов, четные члены
которой образуют базис пространства ![]() , а нечетные – базис пространства
, а нечетные – базис пространства ![]() , назовем собственным базисом преобразования
, назовем собственным базисом преобразования ![]() . Аналогичным образом определим собственный базис
преобразования
. Аналогичным образом определим собственный базис
преобразования ![]() .
.
Равенство
![]()
означает, что преобразование ![]() четные столбцы матрицы
четные столбцы матрицы
![]() умножает на
умножает на ![]() , а нечетные столбцы умножает на
, а нечетные столбцы умножает на ![]() . Следовательно, последовательность столбцов матрицы
. Следовательно, последовательность столбцов матрицы ![]() образует собственный
базис преобразования
образует собственный
базис преобразования ![]() .
.
Равенство
![]()
означает, что последовательность столбцов матрицы ![]() образует собственный
базис преобразования
образует собственный
базис преобразования ![]() .
.
Отметим характерные свойства
преобразований ![]() ,
, ![]() :
:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Составляющие вектора ![]() в пространствах
в пространствах ![]() и
и ![]() соответственно равны
соответственно равны
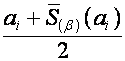 ,
, 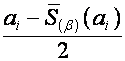 ,
,
так
что
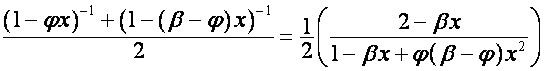 ,
,
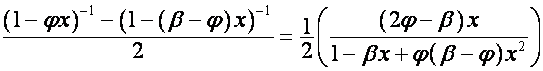 .
.
Между преобразованиями ![]() ,
, ![]() и векторами вида
и векторами вида ![]() существует
определенная связь, изучению которой посвящены статья [3] и разделы 4 – 6
статьи [4]. Отметим, например, равенства:
существует
определенная связь, изучению которой посвящены статья [3] и разделы 4 – 6
статьи [4]. Отметим, например, равенства:

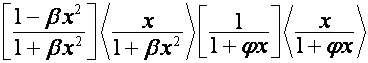 ,
,

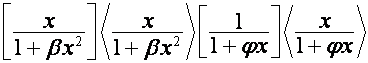 ,
,

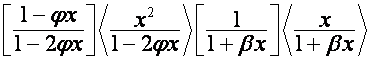 ,
,

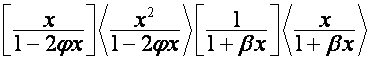 ,
,
которые при транспонировании выражают: корни строк
матрицы 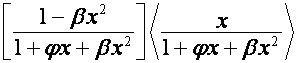 через корни строк
матрицы
через корни строк
матрицы 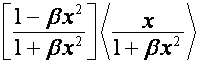 ,
, ![]() -я строка которой,
-я строка которой, ![]() , имеет вид
, имеет вид
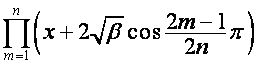 ;
;
корни сторок матрицы 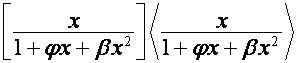 через корни строк
матрицы
через корни строк
матрицы 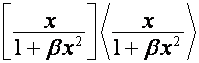 ,
, ![]() -я строка которой,
-я строка которой, ![]() , имеет вид
, имеет вид
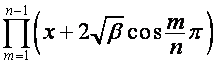 ;
;
корни строк матрицы 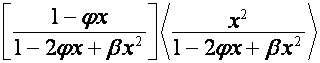 через корни строк
матрицы
через корни строк
матрицы 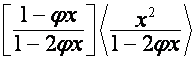 ,
, ![]() -я строка которой,
-я строка которой, ![]() , имеет вид
, имеет вид
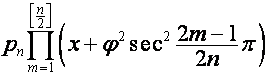 ,
, ![]() ,
, ![]() ,
,
где ![]() – целая часть от
– целая часть от ![]() ; корни строк матрицы
; корни строк матрицы 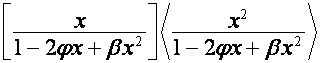 через корни строк матрицы
через корни строк матрицы
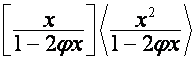 ,
, ![]() -я строка которой,
-я строка которой, ![]() , имеет вид
, имеет вид
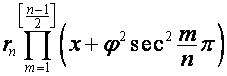 ,
, ![]() ,
, ![]() .
.
Матрицу и базис, образованный ее столбцами,
будем обозначать одним и тем же символом. Отметим трансформации
транспонированных матриц умножения в базисах ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Так как
. Так как
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() – конечный вектор, то
– конечный вектор, то
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
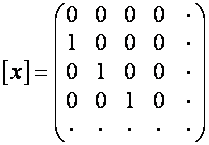
4.2
Рассмотрим преобразования
 ,
, 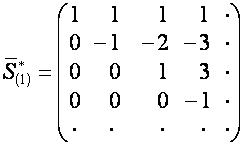 .
.
Отметим равенства:
 ;
;
![]()
![]() ;
;
![]() ,
,  ,
,
![]() ,
,  .
.
Так как
 ,
,
то
столбцы матрицы

образуют
базис пространства ![]() .
.
Так как
![]() ,
,
то
столбцы матрицы

образуют
базис пространства ![]() .
.
Если ![]() – произвольный вектор,
– произвольный вектор,
![]() – конечный вектор,
скалярным произведением
– конечный вектор,
скалярным произведением ![]() и
и ![]() назовем число
назовем число
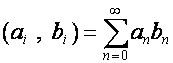 .
.
Если скалярное произведение равно нулю, будем называть
векторы ортогональными. Пусть матрица ![]() – двусторонняя
обратная к матрице
– двусторонняя
обратная к матрице ![]() . Каждый столбец матрицы
. Каждый столбец матрицы ![]() ортогонален каждому
столбцу матрицы
ортогонален каждому
столбцу матрицы ![]() , за исключением одноименного, скалярное произведение с
которым равно единице. То же самое касается столбцов матриц
, за исключением одноименного, скалярное произведение с
которым равно единице. То же самое касается столбцов матриц ![]() и
и ![]() . Базисы
. Базисы ![]() и
и ![]() назовем биортогональными. Для бесконечных треугольных матриц
биортогональные базисы можно рассматривать как естественную замену
ортогональному базису, для которого
назовем биортогональными. Для бесконечных треугольных матриц
биортогональные базисы можно рассматривать как естественную замену
ортогональному базису, для которого ![]() (среди бесконечных
треугольных матриц этим свойством обладают только диагональные матрицы с
диагональными элементами, равными
(среди бесконечных
треугольных матриц этим свойством обладают только диагональные матрицы с
диагональными элементами, равными ![]() ). Если
). Если ![]() – последовательность координат вектора
– последовательность координат вектора ![]() в базисе
в базисе ![]() ,
, ![]() – последовательность
координат вектора
– последовательность
координат вектора ![]() в базисе
в базисе ![]() , то
, то
![]() .
.
Таким образом, ![]() -я координата вектора
-я координата вектора ![]() в базисе
в базисе ![]() равна скалярному
произведению
равна скалярному
произведению ![]() с
с ![]() -м столбцом матрицы
-м столбцом матрицы ![]() ,
, ![]() -я координата вектора
-я координата вектора ![]() в базисе
в базисе ![]() равна скалярному произведению
равна скалярному произведению ![]() с
с ![]() -м столбцом матрицы
-м столбцом матрицы ![]() .
.
Понятие биортогональности обычно вводится
при объединении пары взаимодополнительных векторных пространств в единую конструкцию.
Взаимодополнительными в определенном смысле [2, стр.310] являются пространство
всех последовательностей и пространство всех конечных последовательностей.
Можно иметь это в виду, рассматривая нижние треугольные матрицы как базисы
пространства всех последовательностей, а верхние треугольные – как базисы
пространства всех конечных последовательностей.
Базисы ![]() и
и ![]() являются
биортогональными.
являются
биортогональными.
Так как ![]() и
и ![]() – сопряженные
преобразования, то
– сопряженные
преобразования, то
![]() .
.
Если
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() ,
,
![]() .
.
Таким образом,каждый вектор пространства ![]() ортогонален каждому конечному вектору пространства
ортогонален каждому конечному вектору пространства ![]() .
.
Так как
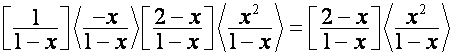 ,
,
то
столбцы матрицы
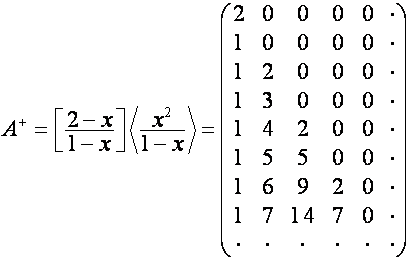
образуют
базис пространства ![]() .
.
Так как
![]() ,
,
то
столбцы матрицы

образуют
базис пространства ![]() .
.
Рассуждая так же, как в отношении матриц ![]() и
и ![]() , выводим, что каждый столбец матрицы
, выводим, что каждый столбец матрицы ![]() ортогонален каждому столбцу матрицы
ортогонален каждому столбцу матрицы ![]() .
.
Сопоставим столбцы матрицы ![]() со столбцами матрицы
со столбцами матрицы ![]() .
. ![]() -й столбец матрицы
-й столбец матрицы ![]() ортогонален
ортогонален ![]() первым столбцам
матрицы
первым столбцам
матрицы ![]() . Его скалярное произведение с
. Его скалярное произведение с ![]() -м столбцом матрицы
-м столбцом матрицы ![]() равно
равно ![]() . Его скалярное произведение с
. Его скалярное произведение с ![]() -м столбцом равно
-м столбцом равно ![]() -му члену вектора
-му члену вектора
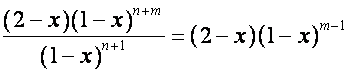 ,
,
т.е. нулю.
Подобным образом доказывается, что каждый
столбец матрицы ![]() ортогонален каждому столбцу матрицы
ортогонален каждому столбцу матрицы ![]() , за исключением одноименного, скалярное произведение с
которым равно
, за исключением одноименного, скалярное произведение с
которым равно ![]() .
.
Таким образом,
![]() ,
,
![]() .
.
Отметим характерную деталь. Сумма столбцов
матрицы ![]() – это последовательность
чисел Фибоначчи:
– это последовательность
чисел Фибоначчи:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
сумма столбцов матрицы ![]() – последовательность
чисел Фибоначчи, «продолженная в другую сторону»:
– последовательность
чисел Фибоначчи, «продолженная в другую сторону»:
![]() ,
, ![]() ;
;
сумма
столбцов матрицы ![]() – последовательность
чисел Люка:
– последовательность
чисел Люка:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
сумма столбцов матрицы ![]() – последовательность
чисел Люка, «продолженная в другую сторону»:
– последовательность
чисел Люка, «продолженная в другую сторону»:
![]() ,
, ![]() .
.
Иначе говоря,
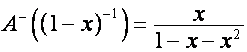 ,
,  ,
,
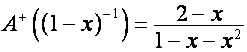 ,
, 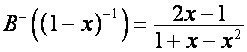 .
.
В [4] показано, что
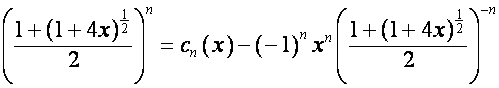 ,
,
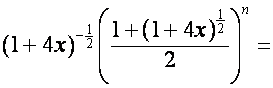
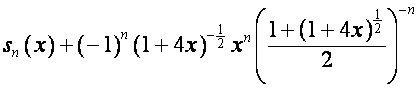 ,
,
где
![]() ,
, ![]() ,
,
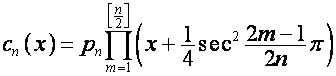 ,
,
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
,
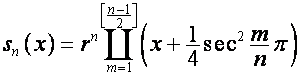 ,
,
![]() ,
, ![]() .
.
Так как
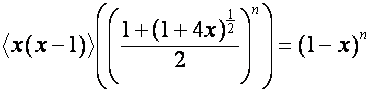 ,
,
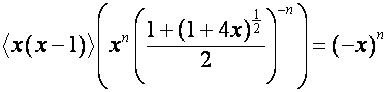 ,
,
то
![]() .
.
Так
как
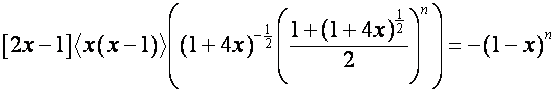 ,
,
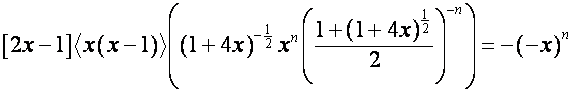 ,
,
то
![]() .
.
В [4] также показано, что ![]() -я строка матрицы
-я строка матрицы 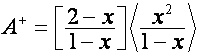 совпадает с полиномом
совпадает с полиномом ![]() ,
, ![]() -я строка матрицы
-я строка матрицы 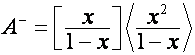 совпадает с полиномом
совпадает с полиномом
![]() . Отсюда получаем равенства:
. Отсюда получаем равенства:
![]() ,
, ![]() ,
,
![]() ,
,
![]() ;
;
Аналогичные равенства получаем для транспонированных
матриц.
Отметим, что ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , совпадает с полиномом
, совпадает с полиномом
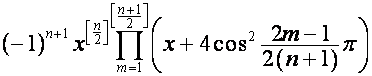 ,
,
![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , совпадает с полиномом
, совпадает с полиномом
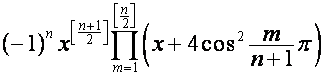 .
.
Собственный базис преобразования ![]() , четные члены которого совпадают с последовательностью столбцов
матрицы
, четные члены которого совпадают с последовательностью столбцов
матрицы ![]() , а нечетные – с последовательностью столбцов матрицы
, а нечетные – с последовательностью столбцов матрицы ![]() , обозначим
, обозначим ![]() ; собственный базис преобразования
; собственный базис преобразования ![]() , четные члены которого совпадают с последовательностью
столбцов матрицы
, четные члены которого совпадают с последовательностью
столбцов матрицы ![]() , а нечетные – с последовательностью столбцов матрицы
, а нечетные – с последовательностью столбцов матрицы ![]() , обозначим
, обозначим ![]() :
:
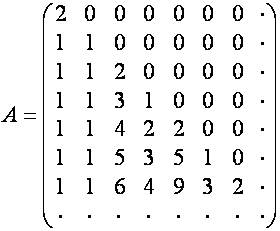 ,
,  .
.
Каждый столбец матрицы ![]() ортогонален каждому
столбцу матрицы
ортогонален каждому
столбцу матрицы ![]() , за исключением одноименного, скалярное произведение с
которым равно
, за исключением одноименного, скалярное произведение с
которым равно ![]() . Следовательно, если четные столбцы матрицы
. Следовательно, если четные столбцы матрицы ![]() и нечетные столбцы
матрицы
и нечетные столбцы
матрицы ![]() умножить на
умножить на ![]() , получится пара биортогональных базисов.
, получится пара биортогональных базисов.
По сравнению с другими собственными
базисами преобразования ![]() , базис
, базис ![]() интересен тем, что в
интересен тем, что в ![]() -мерном пространстве, образованном
-мерном пространстве, образованном ![]() первыми столбцами
матрицы
первыми столбцами
матрицы ![]() , содержится пространство полиномов степени
, содержится пространство полиномов степени ![]() . Любой вектор вида
. Любой вектор вида ![]() , где
, где ![]() – полином, выражается
конечной комбинацией столбцов матрицы
– полином, выражается
конечной комбинацией столбцов матрицы ![]() . Другими словами, преобразование
. Другими словами, преобразование ![]() взаимно однозначно
отображает пространство всех конечных последовательностей на пространство
векторов вида
взаимно однозначно
отображает пространство всех конечных последовательностей на пространство
векторов вида ![]() , подпространством которого является пространство всех
конечных последовательностей. Чтобы в этом убедиться, достаточно представить
матрицу
, подпространством которого является пространство всех
конечных последовательностей. Чтобы в этом убедиться, достаточно представить
матрицу ![]() в виде суммы:
в виде суммы:
 .
.
Отметим, что
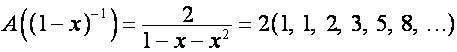 ,
,
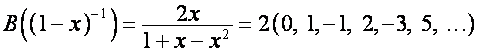 .
.
4.3
Рассмотрим общий метод построения
собственных базисов преобразований ![]() и
и ![]() с помощью матриц
степеней.
с помощью матриц
степеней.
Если
![]() ,
,
то
![]() ,
, ![]() .
.
Пусть
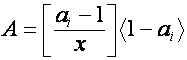 ,
, ![]() ,
, ![]() ,
,
где,
символ ![]() означает умножение на
означает умножение на ![]() :
:
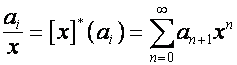 .
.
Тогда
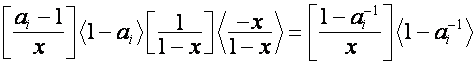 .
.
Равенство
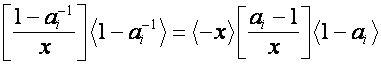
означает,
что
![]() ,
,
или
![]() ,
, ![]() ,
, ![]() .
.
Очевидно,
этим свойством обладают векторы ![]() и
и ![]() . Так как
. Так как
![]() ,
,
то 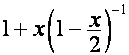 является вектором того же типа. Действительно, пусть
является вектором того же типа. Действительно, пусть
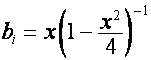 ,
, 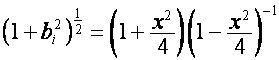 .
.
Тогда
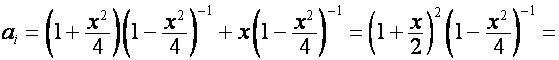
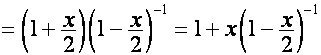 .
.
Пусть
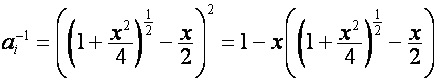 .
.
В
разделе 1.2 мы выяснили, что для вектора
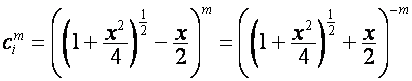 :
:
![]() ,
, ![]() ,
, 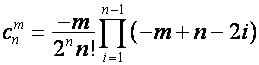 ,
,
так
что
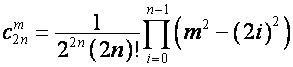 ,
,
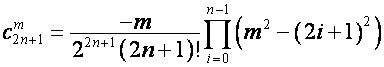 .
.
Так
как
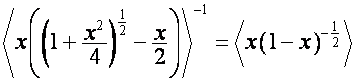 ,
,
то
cтолбцы матрицы
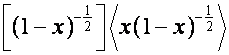

образуют
собственный базис преобразования ![]() ; столбцы матрицы
; столбцы матрицы
 ,
,
где 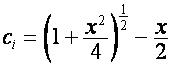 , образуют собственный базис преобразования
, образуют собственный базис преобразования ![]() . Так как
. Так как ![]() -я восходящая диагональ таблицы
-я восходящая диагональ таблицы
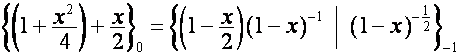 :
:

совпадает с вектором
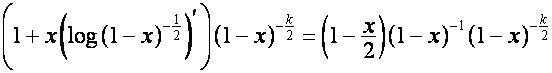 ,
,
то
![]() -я строка матрицы
-я строка матрицы ![]() совпадает с вектором
совпадает с вектором
![]() .
.
Так как (см. введение)
 ,
,
то
![]() .
.
Пусть
![]() .
.
Тогда
![]() ,
,
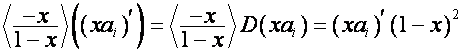 ,
,
![]() ,
,
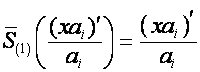 .
.
Так
как
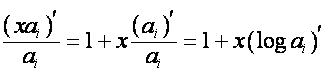 ,
,
то
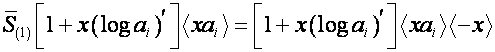 .
.
Если
![]() ,
,
то
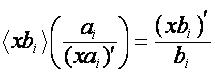 ,
,
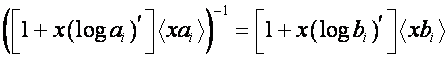 .
.
Таким образом, если ![]() и
и ![]() – собственные базисы
преобразований соответственно
– собственные базисы
преобразований соответственно ![]() и
и ![]() , то
, то 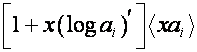 и
и 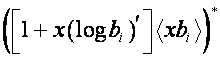 также являются собственными базисами преобразований
также являются собственными базисами преобразований ![]() и
и ![]() .
.
Следовательно, столбцы матрицы

образуют
собственный базис преобразования ![]() ; столбцы матрицы
; столбцы матрицы
 ,
,
где
 ,
,
образуют собственный базис преобразования ![]() . Так как
. Так как ![]() -я восходящая диагональ таблицы
-я восходящая диагональ таблицы
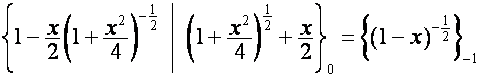 :
:

совпадает с вектором
![]() , то
, то ![]() -я строка матрицы
-я строка матрицы 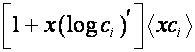 совпадает с вектором
совпадает с вектором ![]() .
.
4.1.4
Выделим общую схему.
Пусть
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Так как
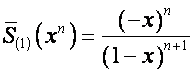 ,
,
то
![]() .
.
Если также
![]() ,
,
то
![]() .
.
Таким образом, столбцы матрицы ![]() ,
, ![]() ,
, ![]() , образуют собственный базис преобразования
, образуют собственный базис преобразования ![]() .
.
Как мы выяснили в предыдущем разделе, если
![]() , то и
, то и ![]() .
.
Строки матрицы ![]() образуют собственный
базис преобразования
образуют собственный
базис преобразования ![]() . Мы выяснили, что
. Мы выяснили, что
![]() .
.
Пусть ![]() ,
, ![]() – собственные базисы
преобразования
– собственные базисы
преобразования ![]() ;
; ![]() ,
, ![]() – собственные базисы
преобразования
– собственные базисы
преобразования ![]() . Так как каждый вектор пространства
. Так как каждый вектор пространства ![]() ортогонален каждому конечному вектору пространства
ортогонален каждому конечному вектору пространства ![]() , а каждый вектор пространства
, а каждый вектор пространства ![]() ортогонален каждому конечному вектору пространства
ортогонален каждому конечному вектору пространства ![]() , то объединив четные столбцы матрицы
, то объединив четные столбцы матрицы ![]() с нечетными столбцами
матрицы
с нечетными столбцами
матрицы ![]() , а четные столбцы матрицы
, а четные столбцы матрицы ![]() с нечетными столбцами матрицы
с нечетными столбцами матрицы ![]() , мы получим пару биортогональных базисов.
, мы получим пару биортогональных базисов.
Пусть
![]() .
.
Тогда
![]() .
.
Обозначим: ![]() ,
, ![]() – базисы, образованные
соответственно последовательностью четных столбцов и последовательностью
нечетных столбцов матрицы
– базисы, образованные
соответственно последовательностью четных столбцов и последовательностью
нечетных столбцов матрицы ![]() ;
; ![]() ,
, ![]() – базисы, образованные
соответственно последовательностью четных столбцов и последовательностью
нечетных столбцов матрицы
– базисы, образованные
соответственно последовательностью четных столбцов и последовательностью
нечетных столбцов матрицы ![]() . Тогда
. Тогда
![]() ;
; ![]() .
.
![]() -й столбец матрицы
-й столбец матрицы ![]() и
и ![]() -й столбец матрицы
-й столбец матрицы ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и ![]() . Из равенств
. Из равенств
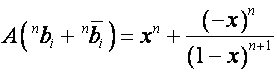 ,
,
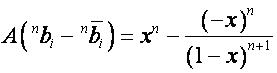
вытекают
равенства
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Проиллюстрируем сказанное одним ярким примером.
Так как:
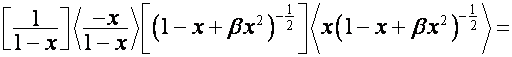
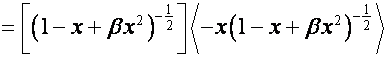 ,
,
 ,
,
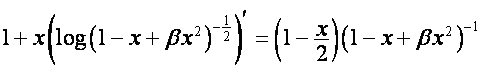 ,
,
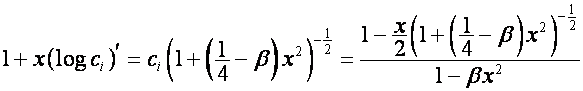 ,
,
где
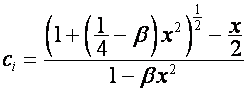 ,
,
то
столбцы матриц
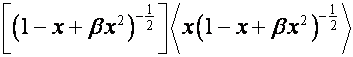 ,
,
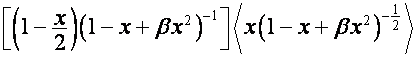
образуют
собственные базисы преобразования ![]() , столбцы матриц
, столбцы матриц
![]() ,
, 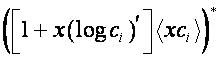
образуют
собственные базисы преобразования ![]() .
.
Так как ![]() -я восходящая диагональ таблицы
-я восходящая диагональ таблицы
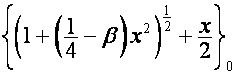 ,
,
где
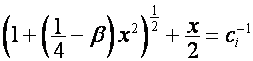 ,
,
совпадает
с вектором
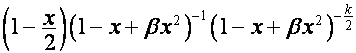 ,
,
то
![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
![]() .
.
Так
как ![]() -я восходящая диагональ таблицы
-я восходящая диагональ таблицы
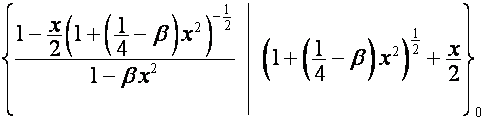
совпадает с вектором
![]() , то
, то ![]() -я строка матрицы
-я строка матрицы 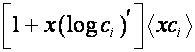 имеет вид
имеет вид ![]() .
.
Отметим, что при ![]()
 ,
,
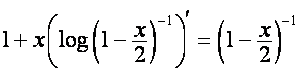 ,
,
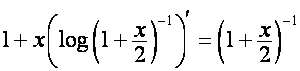 .
.
Так как
![]() ,
,
![]() ,
,
 ,
,
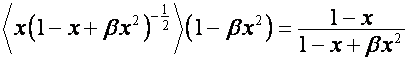 ,
,
то
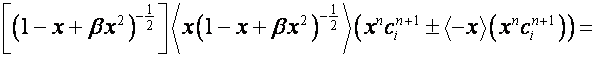
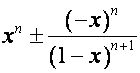 .
.
Обозначим:
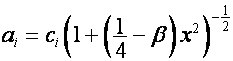 .
.
Тогда
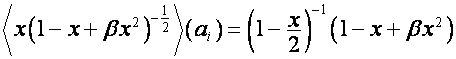 ,
,
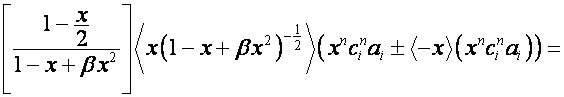
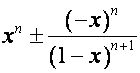 .
.
Например:
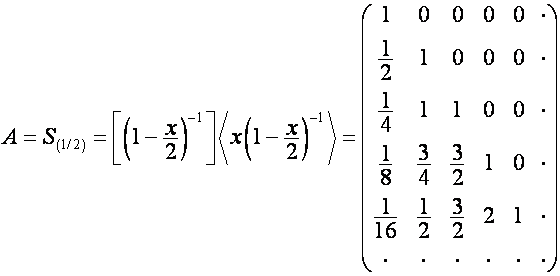 ,
,
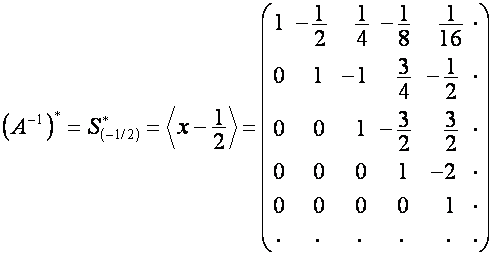 ,
,
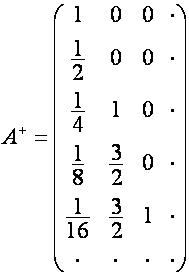 ,
, 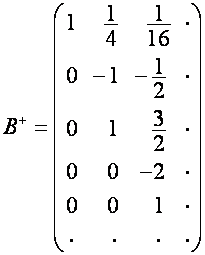 ,
,
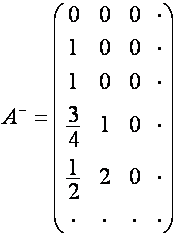 ,
,  ,
,
![]() ,
, ![]() .
.
1.
Е. В. Бурлаченко. Алгебраические заметки.
2. Кук Р. Бесконечные матрицы и пространства
последовательностей. М.: ФМ, 1960.
3. Е. В. Бурлаченко. О чем говорят «металлические
пропорции»?
4. Е. В. Бурлаченко. Биномиальная форма записи
степенного ряда.