Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
Настоящие заметки
посвящены изучению алгебры формальных степенных рядов. Формальный степенной ряд
отождествляется с вектором в бесконечномерном пространстве. Оказывается, что
представление векторов в виде степенных рядов находит отклик со стороны
структуры векторного пространства. Базисы, образованные степенными рядами, в
бесконечномерном пространстве играют такую же конструктивную роль, какую
ортогональные базисы играют в конечномерном пространстве. Алгебра формальных
степенных рядов как бы погружается в свою естественную среду обитания.
Освободившись от смысловых нагрузок, связанных с комбинаторикой и другими
математическими дисциплинами, она демонстрирует свойства, присущие ей как
организатору структуры бесконечномерного векторного пространства. Одним из
организующих начал является аналогичная вращению операция, знакомая нам по
разложению функции в ряд Лагранжа и образующая неразрывное единство с
операциями логарифмирования и возведения в степень. Благодаря пониманию этого
единства, факты, казавшиеся ранее разрозненными, начинают складываться в общую
схему.
Введение
Будем рассматривать
формальный степенной ряд с действительными коэффициентами как
последовательность этих коэффициентов, т.е. как элемент векторного
пространства. Обозначим:
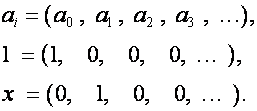
Базис
пространства, в котором координаты каждой последовательности (т.е. коэффициенты
разложения по базисным векторам) совпадают с ее значениями, назовем основным.
Каждой матрице ![]() поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы
поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы
![]() . Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Транспонированную к
. Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Транспонированную к
![]() матрицу обозначим
матрицу обозначим ![]() . Образ вектора
. Образ вектора ![]() при
преобразовании
при
преобразовании ![]() обозначим
обозначим ![]() .
.
Целые
неотрицательные числа будем обозначать буквами ![]() ,
, ![]() ,
, ![]() ,
, ![]() , целые числа – буквами
, целые числа – буквами
![]() ,
, ![]() , действительные числа
– буквами
, действительные числа
– буквами ![]() ,
, ![]() ,
, ![]() .
.
Произведением ![]() назовем вектор
назовем вектор ![]() , где
, где
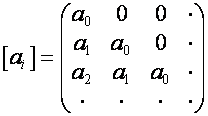 ,
,
или, что то же самое, –
вектор ![]() , где
, где
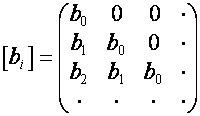 .
.
Матрицу
вида ![]() (
( ![]() -й член
-й член ![]() -го столбца матрицы равен
-го столбца матрицы равен ![]() и нулю при
и нулю при ![]() ) назовем матрицей умножения на вектор
) назовем матрицей умножения на вектор ![]() .
.
Обратным
к ![]() назовем вектор
назовем вектор 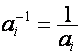 , определяемый уравнением
, определяемый уравнением
![]() .
.
Вектор
![]()
назовем ![]() -й степенью
-й степенью ![]() .
. ![]() -й вектор основного базиса представим как
-й вектор основного базиса представим как ![]() -ю степень
-ю степень ![]() . Каждый вектор запишется в виде
. Каждый вектор запишется в виде
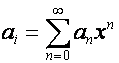 .
.
Матрицу,
![]() -й столбец которой является
-й столбец которой является ![]() -й степенью
-й степенью ![]() , назовем матрицей
степеней вектора
, назовем матрицей
степеней вектора ![]() и обозначим
и обозначим ![]() . Матрица степеней отображает произведение векторов на
произведение их образов:
. Матрица степеней отображает произведение векторов на
произведение их образов:
![]() ,
,
так что
![]() ,
, ![]() .
.
Если рассматривать ![]() и
и ![]() как функции
как функции ![]() и
и ![]() , то выражению
, то выражению ![]() соответствует
подстановка
соответствует
подстановка ![]() .
.
Обозначим:
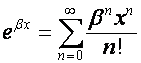 .
.
Убедимся, что векторы данного вида умножаются по
правилу
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Обозначим:
![]() ,
,
так что
![]() .
.
Пусть ![]() – элемент
матрицы
– элемент
матрицы ![]() , где
, где ![]() – номер строки,
– номер строки, ![]() – номер столбца. Тогда
– номер столбца. Тогда
![]()
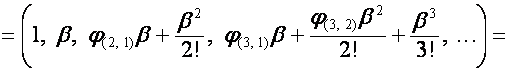
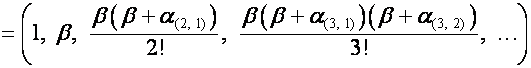 ,
,
где ![]() – комплексные числа.
Так как все члены вектора
– комплексные числа.
Так как все члены вектора ![]() , начиная с
, начиная с ![]() -го, равны нулю, то
-го, равны нулю, то ![]() . Таким образом,
. Таким образом,
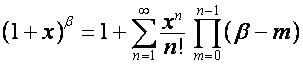 .
.
Вектор
![]() ,
, ![]() ,
,
назовем ![]() -й степенью
-й степенью ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Пусть
![]() .
.
Так как
![]()
![]() ,
, ![]() ,
,
то
![]() .
.
Получаем правило: если
![]() ,
,
то
![]() .
.
![]() Среди матриц степеней особое место занимает матрица
Среди матриц степеней особое место занимает матрица ![]() : транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
: транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
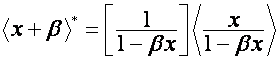 ,
,
![]() ,
,![]()
где ![]() – диагональная
матрица, диагональные элементы которой равны значениям вектора
– диагональная
матрица, диагональные элементы которой равны значениям вектора ![]() :
:
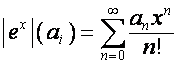 .
.
Например,
![]()

![]()
 .
.
Первый
столбец матрицы ![]() обозначим
обозначим ![]() . Вектор
. Вектор ![]() ,
, ![]() , назовем логарифмом вектора
, назовем логарифмом вектора ![]() и обозначим
и обозначим ![]() ; вектор
; вектор ![]() , где
, где ![]() произвольно, назовем
экспонентой вектора
произвольно, назовем
экспонентой вектора ![]() и обозначим
и обозначим ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Пусть ![]() и
и ![]() – преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
– преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
![]() ,
, ![]() .
.
Обозначим:
![]() ,
, ![]() .
.
Убедимся, что
![]() ,
,
или
![]() .
.
Следовательно,
![]() ,
,
![]() ,
,
или
![]() .
.
Так как
![]() ,
,
то
![]() ,
,
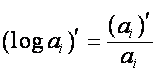 .
.
Отсюда находим:
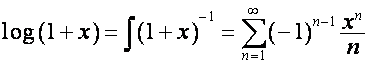 .
.
Таблицу, ![]() -й строкой которой является вектор
-й строкой которой является вектор ![]() , обозначим
, обозначим ![]() . Рассмотрим таблицу
. Рассмотрим таблицу ![]() , например, при
, например, при ![]() :
:
![]()

Каждую
строку таблицы ![]() заменим восходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим
заменим восходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, результат обозначим
проделаем ту же
операцию, результат обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т.д. Например:
проделаем ту же
операцию, и т.д. Например:
![]()
![]()
![]()
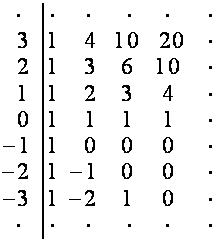
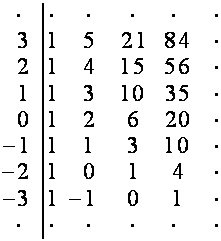
Каждую
строку таблицы ![]() заменим нисходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим
заменим нисходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу обозначим
![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т.д. Например:
проделаем ту же
операцию, и т.д. Например:
![]()
![]()
![]()
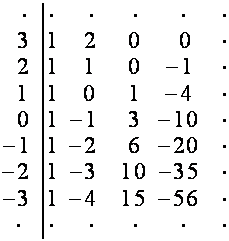

Найдем
преобразование ![]() , отображающее каждую строку таблицы
, отображающее каждую строку таблицы ![]() на одноименную строку
таблицы
на одноименную строку
таблицы ![]() .
.
Пусть ![]() и
и ![]() – формальные степенные
ряды,
– формальные степенные
ряды, ![]() ,
, ![]() , где
, где ![]() – коэффициенты
ряда
– коэффициенты
ряда ![]() .
. ![]() раскладывается в ряд
Лагранжа по правилам [1, с.147]:
раскладывается в ряд
Лагранжа по правилам [1, с.147]:
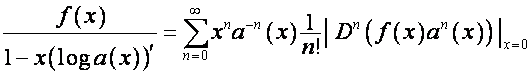 ,
,
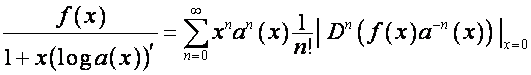 .
.
Если ![]() – нулевая строка
таблицы
– нулевая строка
таблицы ![]() , то выражения
, то выражения ![]() и
и ![]() означают
соответственно
означают
соответственно ![]() -й член нулевой восходящей диагонали и
-й член нулевой восходящей диагонали и ![]() -й член нулевой нисходящей диагонали таблицы
-й член нулевой нисходящей диагонали таблицы ![]() . Пусть
. Пусть ![]() .
. ![]() -ю восходящую и
-ю восходящую и ![]() -ю нисходящую диагонали таблицы
-ю нисходящую диагонали таблицы ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и ![]() . Так как
. Так как
![]() ,
, ![]() ,
,
то
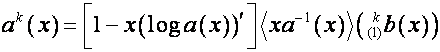 ,
,
![]()
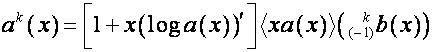 .
.
Отсюда видно, что
![]() ,
,
![]() ,
,
где ![]() и
и ![]() – определенные
векторы,
– определенные
векторы,
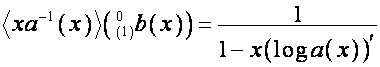 ,
,
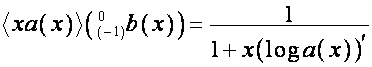 .
.
Следовательно,
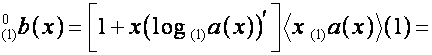
![]() ,
,
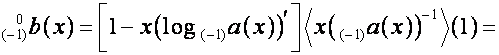
![]() .
.
Вернемся к прежним
обозначениям:
![]() .
.
Мы выяснили, что
![]() ,
,
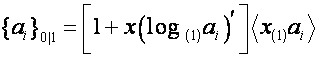 ,
,
![]() ,
,
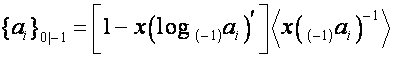 .
.
Нулевая строка
таблицы ![]() совпадает с нулевой
строкой таблицы
совпадает с нулевой
строкой таблицы ![]() , нулевая строка таблицы
, нулевая строка таблицы
![]() совпадает с нулевой строкой
таблицы
совпадает с нулевой строкой
таблицы ![]() . Следовательно,
. Следовательно,
![]() ,
, ![]() ,
,
где ![]() означает
означает ![]() -ю степень
-ю степень ![]() ,
,
![]() ,
,
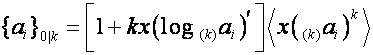
Таким образом, ![]() является решением
уравнения
является решением
уравнения
![]() .
.
Так как
![]()
то
![]()
Обозначим: ![]() . Тогда
. Тогда
![]() .
.
Решая уравнение
![]() ,
,
находим:
![]() .
.
Таким же образом находим ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
 .
.
![]() ,
,
![]() ,
,
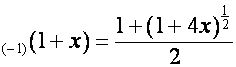 .
.
Обозначим: ![]() . Тогда
. Тогда
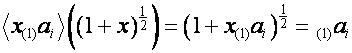 ,
,
![]() ,
,
![]()
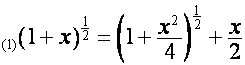 .
.
Применительно к ![]() : так как
: так как
![]() ,
,
то
![]() .
.
Пусть
![]() .
.
Так как
![]() ,
,
![]() ,
,
то
![]() .
.
Например,
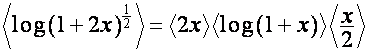 ,
,
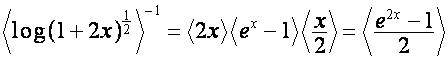 ,
,
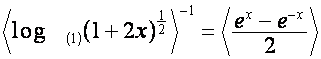 .
.
![]() -ю строку матрицы
-ю строку матрицы
![]()
обозначим ![]() . Так как
. Так как
![]() ,
,
то
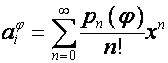 .
.
В [2] показано, что если
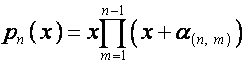 ,
, ![]() ,
,
где ![]() – корни полинома
– корни полинома ![]() , то
, то ![]() -я строка матрицы
-я строка матрицы
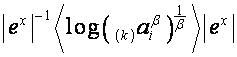
имеет вид
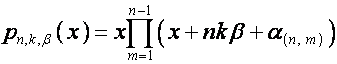 .
.
Например, если ![]() , то
, то
![]() ,
, ![]() .
.
1. Теория биномиальных последовательностей
1.1
В математической литературе последовательности строк
матриц
![]() ,
, ![]()
называются соответственно аппелевой и биномиальной последовательностями.
Оператор
![]()
называется оператором сдвига на ![]() (или просто оператором
сдвига, если
(или просто оператором
сдвига, если ![]() ) и обозначается
) и обозначается ![]() . Операторы
. Операторы
![]() ,
,
где
![]() – тождественный
оператор, и
– тождественный
оператор, и

называются соответственно разностным оператором и оператором
центральных разностей. Оператор
![]()
называется оператором дифференцирования и обозначается
![]() .
.
Отсюда видно, что изучение биномиальных
последовательностей сводится к изучению свойств матриц ![]() ,
, ![]() и применению к
полученным результатам операций трансформирования и транспонирования по правилу
умножения транспонированных матриц: если
и применению к
полученным результатам операций трансформирования и транспонирования по правилу
умножения транспонированных матриц: если ![]() , то
, то ![]() .
.
Основные свойства матриц ![]() и
и ![]() :
:
![]() ,
,
![]() ,
, ![]() ,
,
где
левая формула имеет смысл всегда, правая – при
![]() ,
,
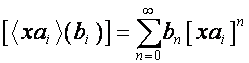 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
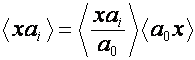 ,
,
![]() ,
,
где
![]() ,
, ![]() ,
, ![]() .
.
Классическое определение [3, стр.124]:
последовательность полиномов ![]() называется
биномиальной, если
называется
биномиальной, если
![]() ,
, 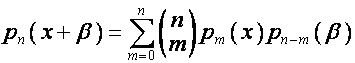 ,
,
что
в наших обозначениях соответствует равенству
![]() .
.
Наше определение биномиальной последовательности
совпадает с другим традиционным определением: последовательность полиномов ![]() называется
биномиальной, если
называется
биномиальной, если
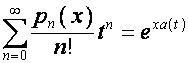
для некоторого формального степенного ряда 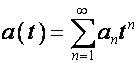 .
.
Оператор ![]() , удовлетворяющий условиям
, удовлетворяющий условиям
![]() ,
, ![]() ,
, ![]() ,
,
называется базисным оператором последовательности
полиномов ![]() , которая, в свою очередь, называется базисной
последовательностью оператора
, которая, в свою очередь, называется базисной
последовательностью оператора ![]() .
.
Пусть
![]() .
.
Так
как
![]() ,
,
то ![]() – базисный оператор последовательности строк матрицы
– базисный оператор последовательности строк матрицы ![]() . Например
. Например ![]() – базисный оператор
последовательности полиномов
– базисный оператор
последовательности полиномов ![]() ,
, ![]() – базисный оператор
последовательности строк матрицы
– базисный оператор
последовательности строк матрицы ![]() , т.е. последовательности полиномов
, т.е. последовательности полиномов 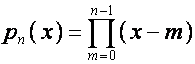 .
.
По определению преобразование ![]() является оператором,
перестановочным со сдвигами. Так как
является оператором,
перестановочным со сдвигами. Так как
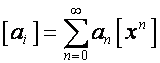 ,
,
то
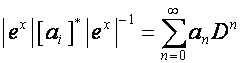 .
.
Так
как
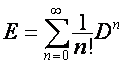 ,
,
то элементы матрицы
![]() равны произведению одноименных элементов матриц
равны произведению одноименных элементов матриц ![]() и
и 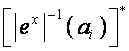 :
:
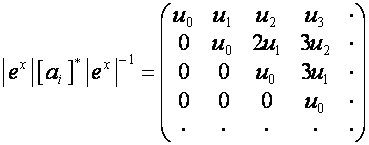 ,
,
где
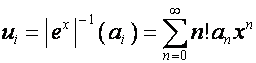 .
.
Обозначим ![]() . Пусть
. Пусть
![]() .
.
Тогда
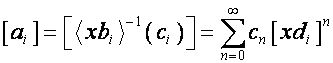 ,
,
где
![]() .
.
Таким
образом,
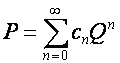 ,
,
где ![]() – базисный оператор
последовательности строк матрицы
– базисный оператор
последовательности строк матрицы ![]() . Это тривиальное утверждение в теории биномиальных
последовательностей считается одним из основных результатов, что демонстрирует
преимущество наших обозначений по сравнению с традиционными. В классической
теории много энергии уходит на доказательство того, что заложено в наших
обозначениях.
. Это тривиальное утверждение в теории биномиальных
последовательностей считается одним из основных результатов, что демонстрирует
преимущество наших обозначений по сравнению с традиционными. В классической
теории много энергии уходит на доказательство того, что заложено в наших
обозначениях.
Обозначим ![]() . Так как
. Так как
![]() ,
,
то
![]() .
.
Из равенства
![]()
вытекает,
что если
![]() ,
,
то
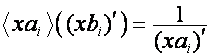 .
.
Следовательно,
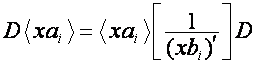 ,
,
что
равнозначно формуле Родригеса
![]() ,
, ![]() ,
,
где ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, 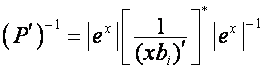 .
.
Если
![]() – формальный степенной
ряд, то по правилу разложения в ряд Лагранжа
– формальный степенной
ряд, то по правилу разложения в ряд Лагранжа
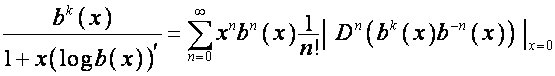 ,
,
где выражение ![]() означает
означает ![]() -й коэффициент ряда
-й коэффициент ряда ![]() . В наших обозначениях:
. В наших обозначениях:
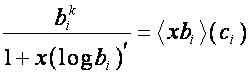 ,
,
где
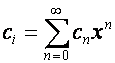 . Так как
. Так как
![]() ,
,
то
![]() ,
,
![]() ,
,
где
![]() ,
, 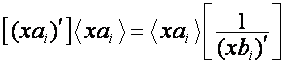 .
.
Так как ![]() -й член вектора
-й член вектора ![]() равен
равен ![]() -му члену вектора
-му члену вектора ![]() , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы ![]() .
.
Таким образом, равенство
![]()
равнозначно
формуле Стеффенсена
![]() ,
, ![]() ,
,
где ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() .
.
1.2
Рассмотрим два класса биномиальных
последовательностей, связанных с векторами
![]() и
и ![]() .
.
Обозначим ![]() ,
, ![]() .
. ![]() -ю строку матрицы
-ю строку матрицы 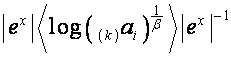 обозначим
обозначим ![]() . Тогда
. Тогда
![]() ,
, ![]() ,
, 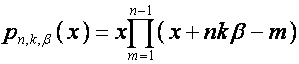 ,
,
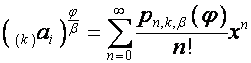 .
.
Например,
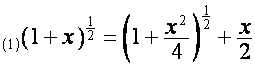 ,
,
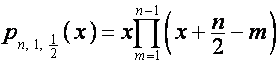 ,
,
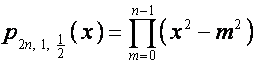 ,
,
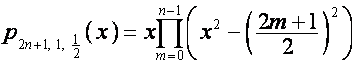 .
.
Так
как
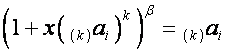 ,
,
![]() ,
,
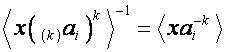 ,
,
то
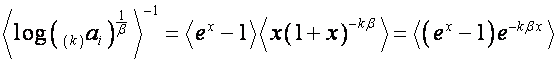 .
.
Так
как
![]() ,
,
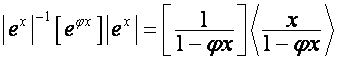 ,
,
то
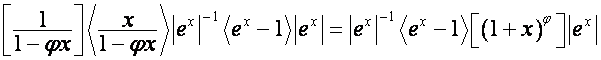 .
.
Так как ![]() -й столбец матрицы
-й столбец матрицы ![]() , элементами которой являются числа Стирлинга второго рода,
имеет вид
, элементами которой являются числа Стирлинга второго рода,
имеет вид 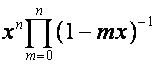 ,
, ![]() -й столбец матрицы
-й столбец матрицы ![]() имеет вид
имеет вид ![]() ,
, ![]() -й столбец матрицы
-й столбец матрицы ![]() имеет вид
имеет вид ![]() , то
, то ![]() -й столбец матрицы
-й столбец матрицы
![]()
имеет
вид
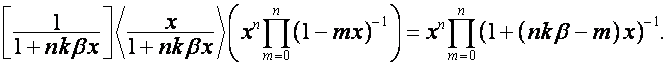
Например,
![]() -й столбец матрицы
-й столбец матрицы
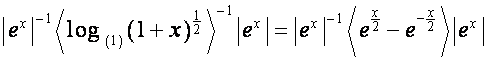
имеет
вид
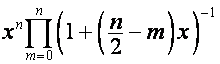 ,
,
так
что четные и нечетные столбцы имеют вид
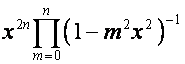 ,
, 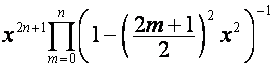 .
.
Обозначим ![]() ,
, ![]() .
. ![]() -ю строку матрицы
-ю строку матрицы 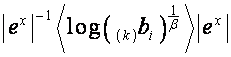 обозначим
обозначим ![]() . Тогда
. Тогда
![]() ,
, ![]() ,
, ![]() ,
,
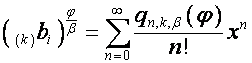 .
.
Так как
![]() ,
,
то
![]() ,
,
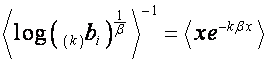 .
.
Так как элементы матрицы ![]() равны произведению
одноименных элементов матриц
равны произведению
одноименных элементов матриц ![]() ,
, ![]() и
и ![]() , то
, то ![]() -й столбец матрицы имеет вид
-й столбец матрицы имеет вид
![]() .
.
Полиномы
![]() называются полиномами
Абеля, базисный оператор
называются полиномами
Абеля, базисный оператор ![]() называется оператором
Абеля.
называется оператором
Абеля.
1.3
Введем в рассмотрение векторы нового вида.
Обозначим
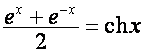 ,
, 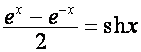 ,
,
![]() ,
,
![]() ,
,
так
что
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
Так как
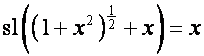 ,
,
то
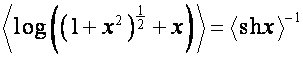 ,
,
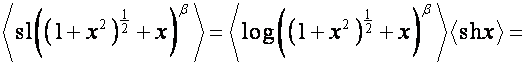
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Таким образом, получаем равенство
![]()
![]()
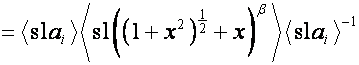 .
.
Покажем, что преобразование, собственным
вектором которого является ![]() ,
, ![]() ,
, ![]() , с собственным значением
, с собственным значением ![]() , является трансформацией оператора
, является трансформацией оператора ![]() . Так как
. Так как
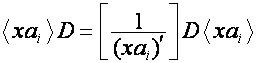 ,
,
то
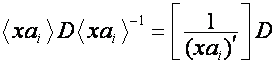 .
.
Следовательно,
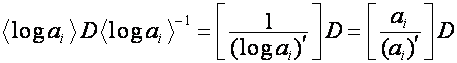 ,
,
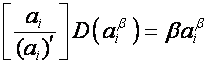 .
.
Пусть ![]() – полином степени
– полином степени ![]() , т.е. вектор, все члены которого, начиная с
, т.е. вектор, все члены которого, начиная с ![]() -го номера, равны нулю. Тогда
-го номера, равны нулю. Тогда ![]() является собственным
вектором преобразования
является собственным
вектором преобразования
![]()
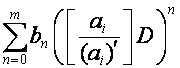
с собственным значением 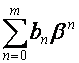 .
.
Так как
![]() ,
, ![]() ,
,
то
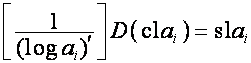 ,
, 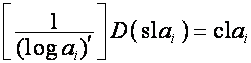 ,
,
или
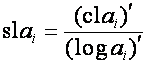 ,
, 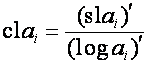 .
.
Отметим также равенство
![]()
![]()
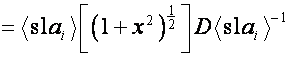 .
.
1.4
Выявим одну интересную особенность строк
матрицы ![]() .
.
Представим таблицу, строки которой
образуются последовательным умножение различных векторов:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , …
, …
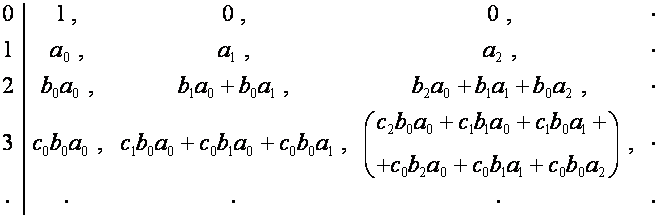
Алгоритм операции умножения приводит к тому, что
множеству слагаемых в разложении ![]() -го члена
-го члена ![]() -й строки таблицы соответствует множество размещений
-й строки таблицы соответствует множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() различным ячейкам:
различным векторам соответствуют различные ячейки, номеру члена соответствует
число предметов в ячейке.
различным ячейкам:
различным векторам соответствуют различные ячейки, номеру члена соответствует
число предметов в ячейке.
Если ![]() … , таблица принимает вид
… , таблица принимает вид
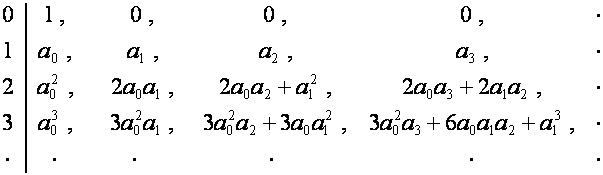
Множеству слагаемых в разложении ![]() -го члена
-го члена ![]() -й строки таблицы соответствует множество размещений
-й строки таблицы соответствует множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() неразличимым ячейкам:
выражение
неразличимым ячейкам:
выражение ![]() означает, что в
соответствующем слагаемому размещении
означает, что в
соответствующем слагаемому размещении ![]() ячеек содержат
одинаковое число предметов, равное
ячеек содержат
одинаковое число предметов, равное ![]() . Коэффициент при
. Коэффициент при ![]() равен
равен 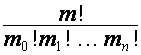 .
.
Множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() неразличимым ячейкам можно разбить на подмножества размещений
с одинаковым числом пустых ячеек, равным
неразличимым ячейкам можно разбить на подмножества размещений
с одинаковым числом пустых ячеек, равным ![]() . Каждому такому подмножеству соответствует множество разбиений
числа
. Каждому такому подмножеству соответствует множество разбиений
числа ![]() на
на ![]() слагаемых. При
слагаемых. При ![]() число подмножеств
равно
число подмножеств
равно ![]() , при
, при ![]() число подмножеств
равно
число подмножеств
равно ![]() .
.
Таким образом, ![]() -й столбец таблицы можно представить в виде
-й столбец таблицы можно представить в виде
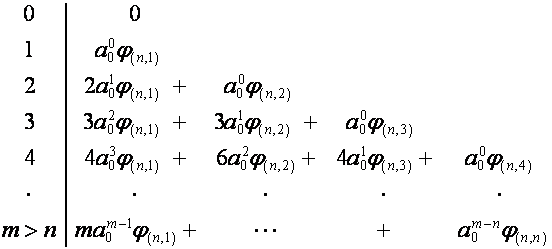
![]() ,
,
где
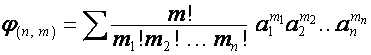 ,
, ![]() ,
,
и суммирование ведется по всем разбиениям числа ![]() на
на ![]() слагаемых. Коэффициент при
слагаемых. Коэффициент при ![]() в
в ![]() -й строке таблицы равен вынесенному за знак суммы произведению
величины
-й строке таблицы равен вынесенному за знак суммы произведению
величины ![]() с ее долей
комбинаторного коэффициента, т.е.
с ее долей
комбинаторного коэффициента, т.е. 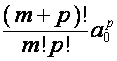 .
.
Матрицу, ![]() -й строкой которой является полином
-й строкой которой является полином
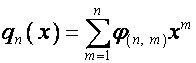 ,
, ![]() ,
,
обозначим
![]() . Тогда, как видно из таблицы,
. Тогда, как видно из таблицы,
![]() ,
,
и,
следовательно,
![]() .
.
Отсюда, при ![]() , получаем выражение значений
, получаем выражение значений ![]() через значения
через значения ![]() :
: ![]() -й член
-й член ![]() равен
равен
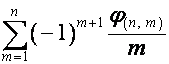 .
.
1.5
Найдем преобразование, отображающее ![]() -ю строку матрицы
-ю строку матрицы ![]() на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() .
.
Рассмотрим равенства
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() .Так как
.Так как ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , – вектор
, – вектор 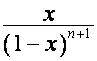 ,
, ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , – вектор
, – вектор 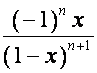 , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 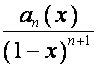 , где
, где ![]() – полином степени
– полином степени ![]() ,
, ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 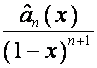 , где
, где ![]() – полином степени
– полином степени ![]() .
.
Матрицу, которая получается из единичной
матрицы размерности ![]() перестоновкой столбцов
в обратном порядке, обозначим
перестоновкой столбцов
в обратном порядке, обозначим ![]() . Например,
. Например,
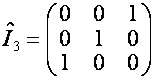 .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() . Обозначим также
. Обозначим также ![]() , где
, где ![]() – произвольный вектор.
Тогда, как показано в [2],
– произвольный вектор.
Тогда, как показано в [2],
![]() ,
,
![]() ,
,
так что
![]() .
.
Например,
если ![]() , то
, то ![]() ,
, ![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() . Тогда
. Тогда
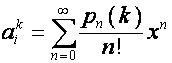 ,
,
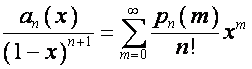 ,
, 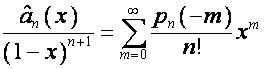 .
.
Найдем корни полинома ![]() в разложении
в разложении
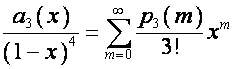
при
![]() ,
, ![]() ,
, ![]() .
.
Так
как, соответственно
![]() ,
, ![]() ,
, ![]() ,
,
то
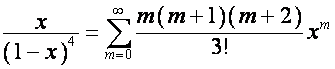 ,
,
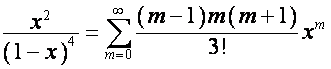 ,
,
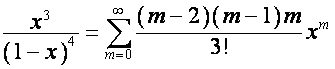 .
.
Обобщая,
выводим
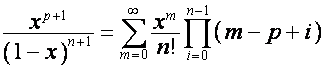 ,
, ![]() .
.
Матрицу, ![]() -м столбцом которой является полином
-м столбцом которой является полином
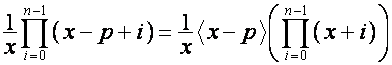 ,
, ![]() ,
,
обозначим
![]() . Например
. Например
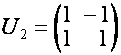 ,
, 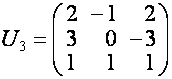 ,
, 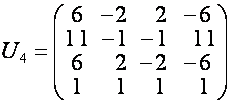 .
.
По определению преобразования ![]() , если
, если
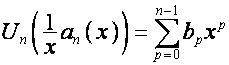 ,
,
то
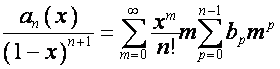 .
.
Таким
образом, если 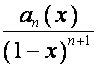 –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() , то
, то
![]() .
.
Так как
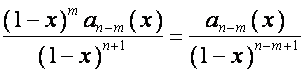 ,
,
![]() , то
, то
![]() .
.
Если ![]() , то
, то ![]() ,
, ![]() , где
, где ![]() – полином Эйлера [4,
стр.253], [5, стр.139]:
– полином Эйлера [4,
стр.253], [5, стр.139]:
![]() ,
, ![]() ,
, ![]() ,
,
![]() , …
, …
Так как
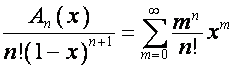 ,
,
то
![]() ,
, ![]() .
.
Таким
образом, ![]() -м столбцом матрицы
-м столбцом матрицы ![]() является полином
является полином ![]() :
:
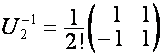 ,
, 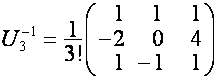 ,
,  .
.
Итак, если ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() ,
, ![]() ,
, ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() , то
, то
![]() ,
,
![]() .
.
2. Обобщенные биномиальные коэффициенты
Рассмотрим известное обобщение
биномиальных коэффициентов [6, с.106].
Для последовательности ![]() ,
, ![]() ,
, ![]() при
при ![]() , обозначим:
, обозначим:
![]() ,
, 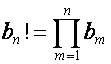 ,
,
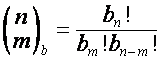 ;
; 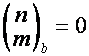 ,
, ![]() .
.
Тогда
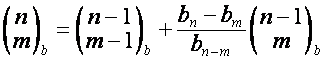 .
.
Диагональную матрицу, диагональные
элементы которой равны значениям вектора ![]() , обозначим
, обозначим ![]() :
:
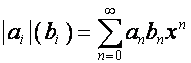 .
.
Вектор,
![]() -й член которого является обратной величиной
-й член которого является обратной величиной ![]() -го члена вектора
-го члена вектора ![]() ,
, ![]() , обозначим
, обозначим ![]() :
:
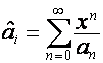 ,
, ![]() .
.
Рассмотрим
трансформацию
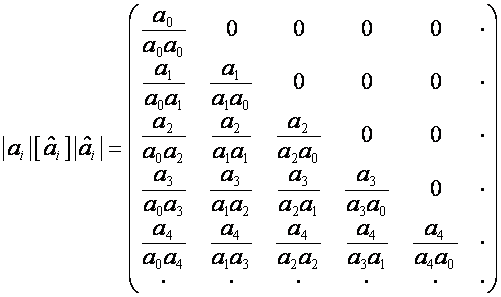 .
.
Первый столбец матрицы обозначим ![]() . Элемент матрицы, стоящий на пересечении
. Элемент матрицы, стоящий на пересечении ![]() -й строки и
-й строки и ![]() -го столбца обозначим
-го столбца обозначим ![]() . Если
. Если ![]() , то
, то
![]() ,
, 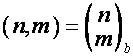 .
.
Если ![]() – произвольная матрица
умножения, то элементы матрицы
– произвольная матрица
умножения, то элементы матрицы ![]() равны произведению
одноименных элементов матриц
равны произведению
одноименных элементов матриц ![]() и
и ![]() .
.
Особый интерес представляет случай
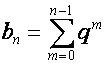 ,
, ![]() ,
,
который
при ![]() принимает вид
принимает вид
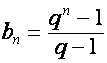 .
.
Обозначим
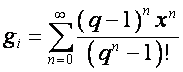 ,
, ![]() ,
, ![]() ,
, ![]() ,
,
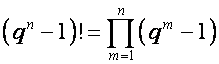 ,
, ![]() .
.
Элементы
матрицы ![]() равны коэффициентам Гаусса:
равны коэффициентам Гаусса:
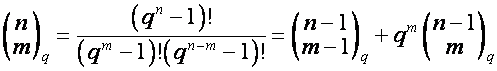 .
.
Пусть ![]() ,
, ![]() – соседние столбцы
бесконечной матрицы. Если
– соседние столбцы
бесконечной матрицы. Если
![]() ,
, ![]() ,
,
то
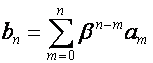 ,
, ![]() .
.
Следовательно,
![]() -й столбец матрицы
-й столбец матрицы ![]() имеет вид
имеет вид
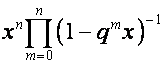 .
.
В [6] показано, что если последовательность столбцов
матрицы имеет вид
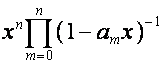 ,
,
где ![]() – произвольная последовательность чисел, то
последовательность строк обратной матрицы имеет вид
– произвольная последовательность чисел, то
последовательность строк обратной матрицы имеет вид
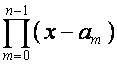 .
.
Например, при ![]() получаем матрицы
получаем матрицы ![]() и
и ![]() ; при
; при ![]() получаем матрицы
получаем матрицы ![]() и
и ![]() ; при
; при ![]() получаем матрицы
получаем матрицы ![]() и
и ![]() ; при
; при ![]() получаем матрицы
получаем матрицы ![]() и
и ![]() .
.
Таким образом, ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
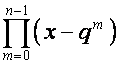 .
.
Гаусс показал, что
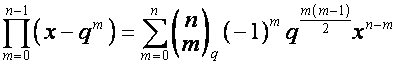 .
.
Следовательно,
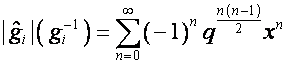 ,
,
где
 ,
, ![]() ,
,
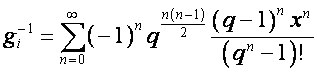 .
.
Обозначим
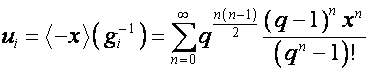 .
.
Первый столбец матрицы ![]() обозначим
обозначим ![]() , элемент, стоящий на пересечении
, элемент, стоящий на пересечении ![]() -й строки и
-й строки и ![]() -го столбца обозначим
-го столбца обозначим 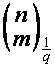 . Тогда
. Тогда
 ,
,
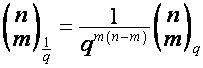 .
.
Таким образом,
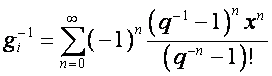 .
.
Представим ![]() как функцию от
как функцию от ![]() и
и ![]() . Тогда
. Тогда
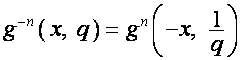 .
.
(Продолжение
следует)
1.
Риордан Д. Комбинаторные тождества. М.: Наука, 1982.
2. Бурлаченко Е. В. Биномиальная форма записи
степенного ряда.
3.
Айгнер М. Комбинаторная теория. М.: Мир, 1982.
4.
Риордан Д. Введение в комбинаторный анализ. М.: ИЛ, 1963.
5. Сачков В. Н. Комбинаторные методы дискретной
математики. М.: Наука, 1977.
6. Платонов М. Л. Комбинаторные числа класса
отображений и их приложения. М.: Наука, 1979.