Е. В.
Бурлаченко
ОБОБЩЕНИЕ
ОДНОЙ КЛАССИЧЕСКОЙ ПАРЫ ПОЛИНОМОВ
1
Рассмотрим последовательность преобразований,
связывающую корни полиномов деления круга с корнями полиномов
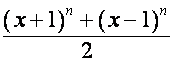 ,
, 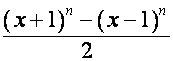 .
.
Обозначим:
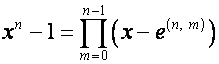 ,
,
![]() ,
, ![]() .
.
Тогда
 .
.
Заменим
![]() на
на ![]() :
:
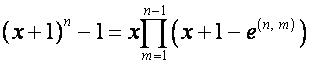 ,
,
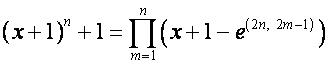 .
.
Переставим
коэффициенты в обратном порядке:
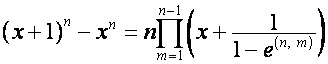 ,
,
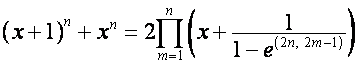 ,
,
где
 ,
,  .
.
Заменим
![]() на
на ![]() :
:
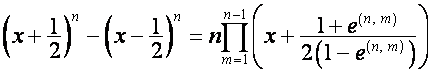 .
.
Следовательно,
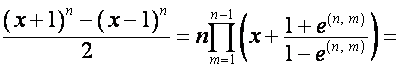
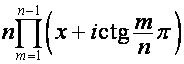 .
.
Аналогично

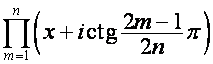 .
.
Отметим аналогию с
полиномами Чебышева первого и второго рода
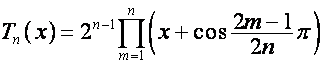 ,
,
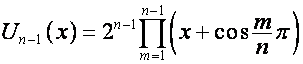 .
.
Обозначим
![]() ,
,  ,
,
![]() ,
, ![]() ,
, 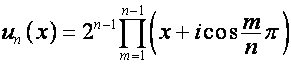 .
.
Так как
 ,
,
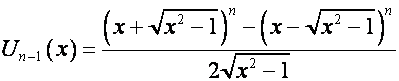 ,
,
то
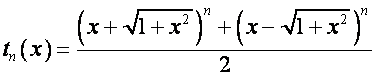 ,
,
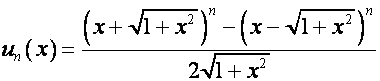 .
.
Обозначим
![]() .
.
Так как
![]() ,
, ![]()
то
![]() ,
,
![]() .
.
Раскладывая
![]() в бином Ньютона и
группируя члены, можно представить его в виде
в бином Ньютона и
группируя члены, можно представить его в виде
![]() ,
,
где

– полином степени ![]() , четные члены которого равны нулю, если
, четные члены которого равны нулю, если ![]() нечетно, нечетные члены
равны нулю, если
нечетно, нечетные члены
равны нулю, если ![]() четно,
четно,
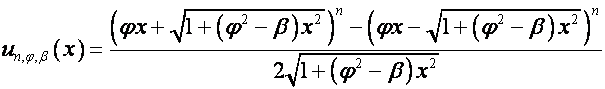
– полином
степени ![]() , четные члены которого равны нулю, если
, четные члены которого равны нулю, если ![]() четно, нечетные члены
равны нулю, если
четно, нечетные члены
равны нулю, если ![]() нечетно. Например:
нечетно. Например:
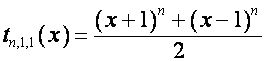 ,
, 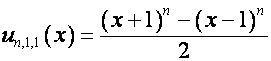 ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Докажем, что
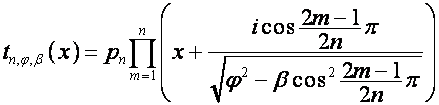 ,
, ![]()
 ,
,
 ,
, ![]()
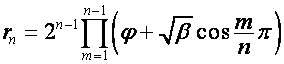 ,
,
где условие ![]() означает, что степень
означает, что степень ![]() равна
равна ![]() , условие
, условие ![]() означает, что степень
означает, что степень ![]() равна
равна ![]() .
.
Убедимся, что
![]()
при 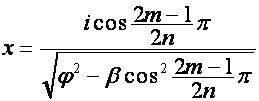 ,
,
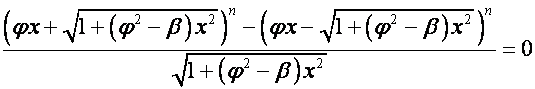
при  ,
, ![]() .
.
Если ![]() ,
, ![]() – формальные степенные
ряды,
– формальные степенные
ряды, ![]() раскладывается в ряд
Лагранжа по правилу [1, с.147]:
раскладывается в ряд
Лагранжа по правилу [1, с.147]:
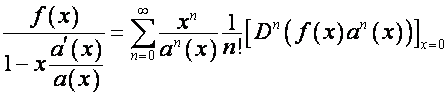 ,
, ![]()
где выражение ![]() означает
означает ![]() -й коэффициент ряда
-й коэффициент ряда ![]() . Обозначим
. Обозначим 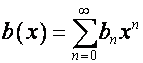 . Пусть
. Пусть ![]() ,
, ![]() . Тогда
. Тогда
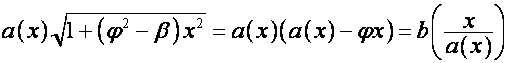 ,
,
откуда, пользуясь уравнением ![]() , находим
, находим
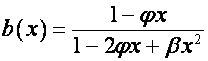 .
.
Так как [2, с.172]
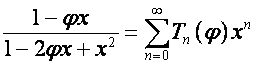 ,
,
где
![]() ,
, 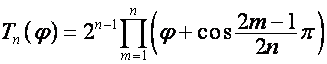 ,
,
то
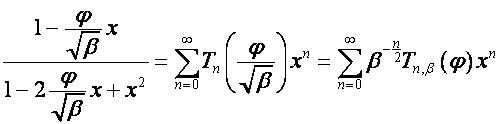 ,
,
где
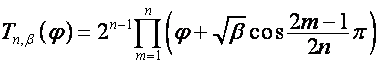 ,
,
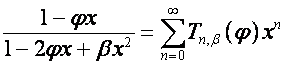 .
.
![]() -й коэффициент ряда
-й коэффициент ряда ![]() равен
равен ![]() -му коэффициенту полинома
-му коэффициенту полинома ![]() , обозначенному нами
, обозначенному нами ![]() . Следовательно,
. Следовательно,
![]() .
.
Пусть в
формуле ![]()
![]() ,
, 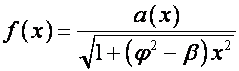 . Тогда
. Тогда
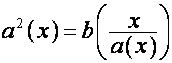 ,
,
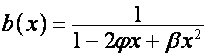 .
.
Так как
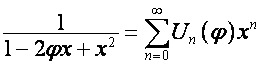 ,
,
где
![]() ,
, 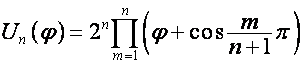 ,
,
то
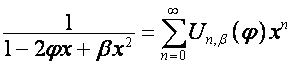 ,
,
где
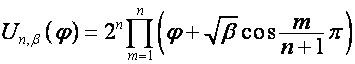 .
.
![]() -й коэффициент ряда
-й коэффициент ряда

равен ![]() -му коэффициенту полинома
-му коэффициенту полинома ![]() , обозначенному нами
, обозначенному нами ![]() .Следовательно,
.Следовательно,
![]() .
.
Подставляя в формулы ![]() ,
, ![]()
![]() ,
, ![]() , получаем равенства
, получаем равенства
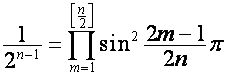 ,
, 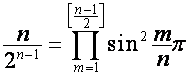 ,
,
где ![]() – целая часть от
– целая часть от ![]() .
.
Отметим также равенство
![]() ,
,
вытекающее из уравнения ![]() .
.
2
Рассмотрим аналогичный случай.
Обозначим
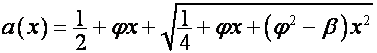 .
.
Так как
![]() ,
, ![]()
то
![]() ,
,
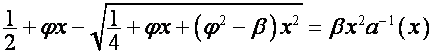 .
.
Раскладывая
![]() в бином Ньютона и
группируя члены, можно представить его в виде
в бином Ньютона и
группируя члены, можно представить его в виде
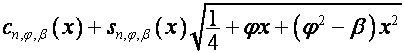 ,
,
где
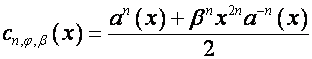
– полином степени![]() ,
,
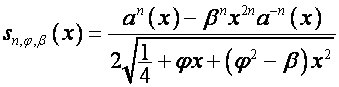
– полином степени ![]() . Например
. Например
![]() ,
, ![]() ,
,
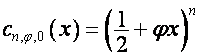 ,
, 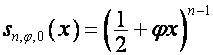 ,
,
![]() ,
, ![]() .
.
Докажем, что
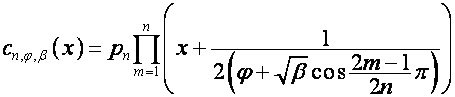 ,
,
 ,
,
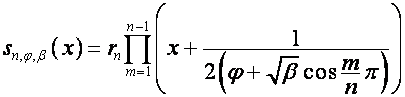 ,
,
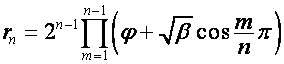 ,
,
где условие ![]() означает, что степень
означает, что степень ![]() равна
равна ![]() , условие
, условие ![]() означает, что степень
означает, что степень ![]() равна
равна ![]() .
.
Убедимся,
что
![]()
при 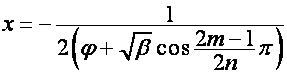 ,
,
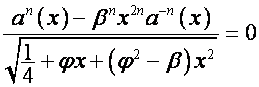
при 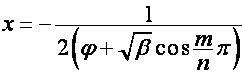 ,
, ![]() .
.
Пусть в
формуле ![]()
![]() ,
, 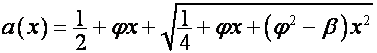 . Тогда
. Тогда
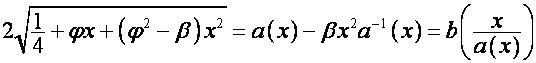 ,
,
откуда, пользуясь уравнением ![]() , находим
, находим
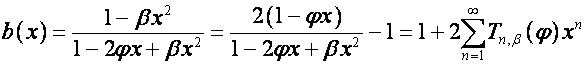 .
.
Так как
![]() ,
,
то ![]() ,
, ![]() , равен
, равен ![]() -му коэффициенту полинома
-му коэффициенту полинома ![]() .
.
Пусть в
формуле ![]()
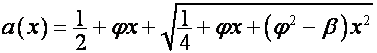 ,
, 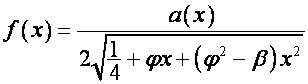 . Тогда
. Тогда
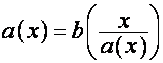 ,
,
 .
.
Так как
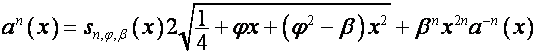 ,
,
то ![]() равен
равен ![]() -му коэффициенту полинома
-му коэффициенту полинома ![]() .
.
Отметим
также равенство
![]() ,
,
вытекающее из уравнения ![]() .
.
1. Риордан Д. Комбинаторные тождества. – М.: Наука,
1982.
2. Справочная математическая библиотека.
Математический анализ. Вычисление элементарных функций. – М.: Физматгиз, 1963.