Е. В.
Бурлаченко
БИНОМИАЛЬНАЯ ФОРМА ЗАПИСИ СТЕПЕННОГО
РЯДА
ПРЕДИСЛОВИЕ
Для
формального степенного ряда

выражение
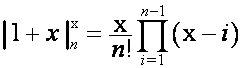
назовем биномиальной формой записи полинома ![]() . Любой ряд
. Любой ряд ![]() , два первых коэффициента которого равны единице, имеет
биномиальную форму записи
, два первых коэффициента которого равны единице, имеет
биномиальную форму записи
 ,
,
но коэффициенты ![]() выражаются общей
формулой только в особых случаях.
выражаются общей
формулой только в особых случаях.
В статье рассматривается связь
биномиальной формы записи с рядами Лагранжа. Выводится формула, объединяющая
биномиальные формы записи рядов
![]() ,
, 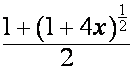 и
и 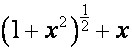 .
.
Ставится задача найти более общую формулу для
коэффициентов ![]() в биноминальной форме
записи ряда
в биноминальной форме
записи ряда 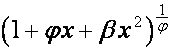 .
.
Рассматривается связь полиномов деления
круга с рядами
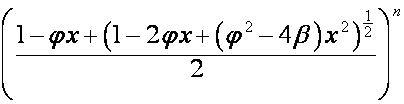 ,
,
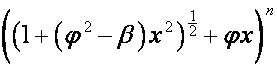 .
.
При
этом в новой роли выступают полиномы Чебышева
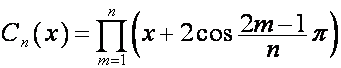 ,
,  ,
,
 ,
, 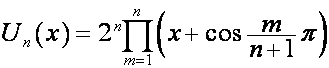 .
.
Рассматриваются связанные с биномиальной
формой записи преобразования. При этом в новой роли выступают полиномы Эйлера
![]()
 .
.
1
Будем рассматривать формальный степенной
ряд с действительными коэффициентами как последовательность этих коэффициентов,
т.е. как элемент векторного пространства. Обозначим:

Базис пространства, в
котором координаты каждой последовательности (т.е. коэффициенты разложения по
базисным векторам) совпадают с ее значениями, назовем основным. Каждой матрице ![]() поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы
поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы
![]() . Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Транспонированную к
. Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Транспонированную к
![]() матрицу обозначим
матрицу обозначим ![]() . Образ вектора
. Образ вектора ![]() при
преобразовании
при
преобразовании ![]() обозначим
обозначим ![]() .
.
Целые неотрицательные
числа будем обозначать буквами ![]() целые числа –
буквами
целые числа –
буквами ![]() действительные числа –
буквами
действительные числа –
буквами ![]() .
.
Произведением ![]() назовем вектор
назовем вектор ![]() , где
, где
 ,
,
или, что то же самое, – вектор ![]() , где
, где
 .
.
Матрицу вида ![]() (
( ![]() -й член
-й член ![]() -го столбца матрицы равен
-го столбца матрицы равен ![]() и нулю при
и нулю при ![]() ) назовем матрицей умножения на вектор
) назовем матрицей умножения на вектор ![]() .
.
Обратным к ![]() назовем вектор
назовем вектор  , определяемый уравнением
, определяемый уравнением
![]() .
.
Вектор
![]()
назовем ![]() -й степенью
-й степенью ![]() .
. ![]() -й вектор основного базиса представим как
-й вектор основного базиса представим как ![]() -ю степень
-ю степень ![]() . Каждый вектор запишется в виде
. Каждый вектор запишется в виде
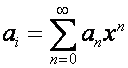 .
.
Матрицу, ![]() -й столбец которой является
-й столбец которой является ![]() -й степенью
-й степенью ![]() , назовем матрицей
степеней вектора
, назовем матрицей
степеней вектора ![]() и обозначим
и обозначим ![]() . Матрица степеней отображает произведение векторов на произведение
их образов:
. Матрица степеней отображает произведение векторов на произведение
их образов:
![]() ,
,
так что
![]() ,
, ![]() .
.
Если рассматривать ![]() и
и ![]() как функции
как функции ![]() и
и ![]() , то выражению
, то выражению ![]() соответствует
подстановка
соответствует
подстановка ![]() .
.
Обозначим:
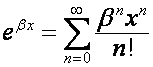 .
.
Убедимся, что векторы данного вида умножаются по
правилу
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Обозначим:
![]() ,
,
так что
![]() .
.
Пусть ![]() – элемент
матрицы
– элемент
матрицы ![]() , где
, где ![]() – номер строки,
– номер строки, ![]() – номер столбца. Тогда
– номер столбца. Тогда
![]()

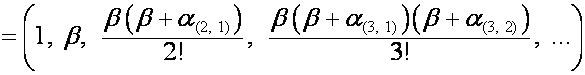 ,
,
где ![]() – комплексные числа.
Так как все члены вектора
– комплексные числа.
Так как все члены вектора ![]() , начиная с
, начиная с ![]() -го, равны нулю, то
-го, равны нулю, то ![]() . Таким образом,
. Таким образом,
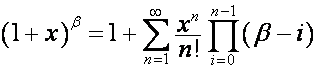 .
.
Вектор
![]() ,
, ![]() ,
,
назовем ![]() -й степенью
-й степенью ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Пусть
![]() .
.
Так как
![]()
![]() ,
, ![]() ,
,
то
![]() .
.
Получаем правило: если
![]() ,
,
то
![]() .
.
![]() Среди матриц степеней особое место занимает матрица
Среди матриц степеней особое место занимает матрица ![]() : транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
: транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
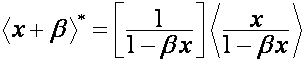 ,
,
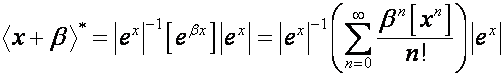 ,
,![]()
где ![]() – диагональная
матрица, диагональные элементы которой равны значениям вектора
– диагональная
матрица, диагональные элементы которой равны значениям вектора ![]() :
:
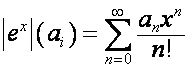 .
.
Например,
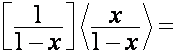
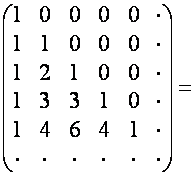
 .
.
Преобразование ![]() принято называть
оператором сдвига. Также последовательности строк матриц
принято называть
оператором сдвига. Также последовательности строк матриц ![]() и
и ![]() принято называть
соответственно аппелевой и биномиальной последовательностями.
принято называть
соответственно аппелевой и биномиальной последовательностями.
Первый столбец
матрицы ![]() обозначим
обозначим ![]() . Вектор
. Вектор ![]() ,
, ![]() , назовем логарифмом вектора
, назовем логарифмом вектора ![]() и обозначим
и обозначим ![]() ; вектор
; вектор ![]() , где
, где ![]() произвольно, назовем
экспонентой вектора
произвольно, назовем
экспонентой вектора ![]() и обозначим
и обозначим ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Пусть ![]() и
и ![]() – преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
– преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
![]() ,
, ![]() .
.
Обозначим:
![]() ,
, ![]() .
.
Убедимся, что
![]() ,
,
или
![]() .
.
Следовательно,
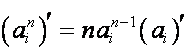 ,
,
![]() ,
,
или
![]() .
.
Так как
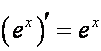 ,
,
то
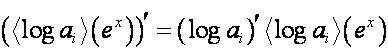 ,
,
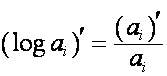 .
.
Отсюда находим:
 .
.
2
Предметом дальнейшего изучения будет множество
векторов
![]() ,
, ![]() ,
, ![]() .
.
Таблицу, ![]() -й строкой которой является вектор
-й строкой которой является вектор ![]() , обозначим
, обозначим ![]() . Множество строк с положительными номерами назовем верхней
половиной таблицы, множество строк с отрицательными номерами – нижней половиной
таблицы.
. Множество строк с положительными номерами назовем верхней
половиной таблицы, множество строк с отрицательными номерами – нижней половиной
таблицы.
Рассмотрим таблицу ![]() , например, при
, например, при ![]() :
:
![]()
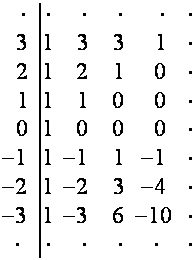
Каждую строку таблицы ![]() заменим восходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу
обозначим
заменим восходящей
диагональю, имеющей со строкой общий нулевой член. Полученную таблицу
обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, результат обозначим
проделаем ту же
операцию, результат обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т.д. Например:
проделаем ту же
операцию, и т.д. Например:
![]()
![]()
![]()

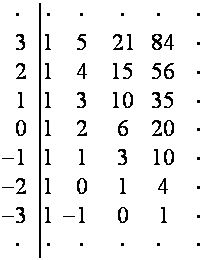
Каждую строку
таблицы ![]() заменим нисходящей диагональю,
имеющей со строкой общий нулевой член. Полученную таблицу обозначим
заменим нисходящей диагональю,
имеющей со строкой общий нулевой член. Полученную таблицу обозначим ![]() . С таблицей
. С таблицей ![]() проделаем ту же
операцию, и т.д. Например:
проделаем ту же
операцию, и т.д. Например:
![]()
![]()
![]()

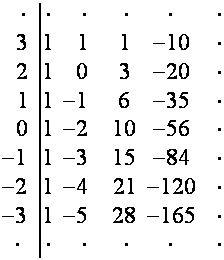
Найдем преобразование ![]() , отображающее каждую строку таблицы
, отображающее каждую строку таблицы ![]() на одноименную строку
таблицы
на одноименную строку
таблицы ![]() .
.
Пусть ![]() и
и ![]() – формальные степенные
ряды,
– формальные степенные
ряды, ![]() ,
, ![]() , где
, где ![]() – коэффициенты
ряда
– коэффициенты
ряда ![]() .
. ![]() раскладывается в ряд
Лагранжа по правилам [1, с.147]:
раскладывается в ряд
Лагранжа по правилам [1, с.147]:
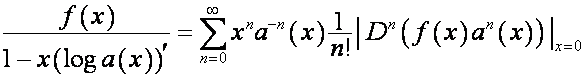 ,
,
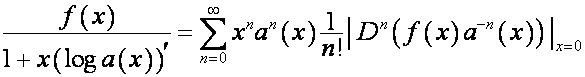 .
.
Если ![]() – нулевая строка
таблицы
– нулевая строка
таблицы ![]() , то выражения
, то выражения  и
и 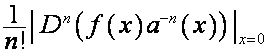 означают
соответственно
означают
соответственно ![]() -й член нулевой восходящей диагонали и
-й член нулевой восходящей диагонали и ![]() -й член нулевой нисходящей диагонали таблицы
-й член нулевой нисходящей диагонали таблицы ![]() . Пусть
. Пусть ![]() .
. ![]() -ю восходящую и
-ю восходящую и ![]() -ю нисходящую диагонали таблицы
-ю нисходящую диагонали таблицы ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и ![]() . Тогда
. Тогда
 ,
,
![]()
 .
.
Отсюда видно, что![]()
![]() ,
,
![]() ,
,
где ![]() и
и ![]() – определенные
векторы. Следовательно,
– определенные
векторы. Следовательно,
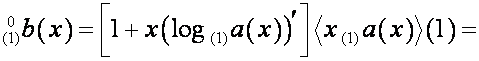
![]() ,
,
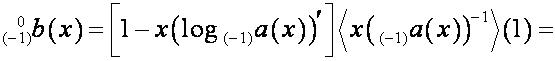
![]() .
.
Вернемся к прежним
обозначениям:
![]() .
.
Мы выяснили, что
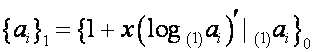 ,
, 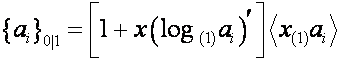 ,
,
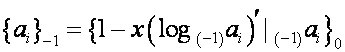 ,
, 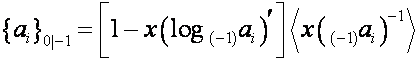 .
.
Нулевая строка
таблицы ![]() совпадает с нулевой
строкой таблицы
совпадает с нулевой
строкой таблицы ![]() , нулевая строка таблицы
, нулевая строка таблицы
![]() совпадает с нулевой
строкой таблицы
совпадает с нулевой
строкой таблицы ![]() . Следовательно,
. Следовательно,
![]() ,
, ![]() ,
,
где ![]() означает
означает ![]() -ю степень
-ю степень ![]() ,
,
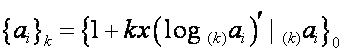 ,
, 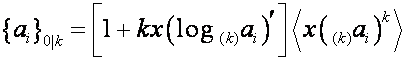 .
.
Так как
![]() ,
,
то
 .
.
Таким образом, ![]() является решением
уравнения
является решением
уравнения
![]() .
.
Обозначим: ![]() . Тогда
. Тогда
![]() .
.
Решая уравнение
![]() ,
,
находим:
![]() .
.
Таким же образом находим ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
 .
.
![]() ,
,
![]() ,
,
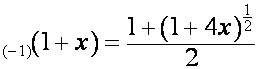 .
.
Обозначим: ![]() . Тогда
. Тогда
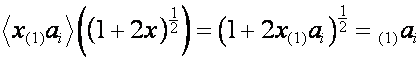 ,
,
![]() ,
,
![]()
 .
.
Так как
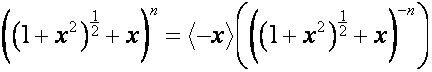 ,
,
то
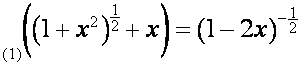 ,
,
 .
.
Применительно к ![]() : так как
: так как
 ,
,
то
![]() .
.
Пусть
![]() .
.
Так как
![]() ,
,
 ,
,
то
![]() .
.
Например,
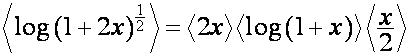 ,
,
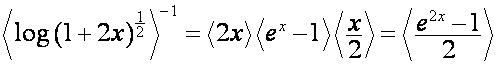 ,
,
 .
.
![]() -й член вектора
-й член вектора ![]() обозначим
обозначим ![]() ,
, ![]() ,
, ![]() -й член вектора
-й член вектора 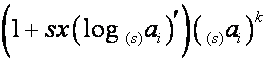 (т.е.
(т.е. ![]() -й член
-й член ![]() -ой строки таблицы
-ой строки таблицы ![]() ) обозначим
) обозначим ![]() .Так как
.Так как
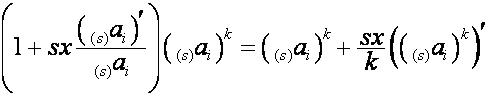 ,
,
то
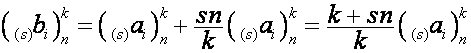 .
.
Так как
![]() ,
,
то
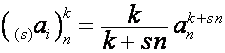 ,
, 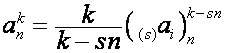 .
.
3
По определению логарифма
и экспоненты
![]() .
.
Отсюда вытекает, что если
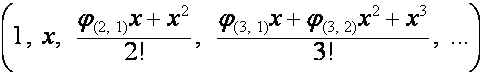
– последовательность строк матрицы ![]() , то
, то
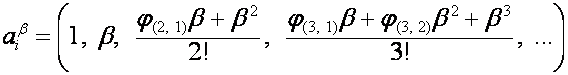 .
.
Соответствие
![]() между строками матрицы
между строками матрицы
![]()
![]() ,
, ![]() , и значениями вектора
, и значениями вектора ![]() , обобщая биномиальный ряд, назовем биномиальной формой
записи вектора
, обобщая биномиальный ряд, назовем биномиальной формой
записи вектора ![]() и обозначим
и обозначим
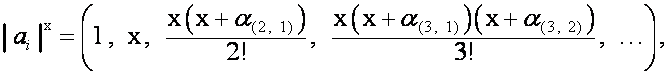
 .
.
В формуле общего члена
подразумевается, что ![]() ,
, ![]() . Коэффициенты
. Коэффициенты ![]() могут быть
комплексными числами, необходимыми для представления вектора
могут быть
комплексными числами, необходимыми для представления вектора ![]() в виде
в виде
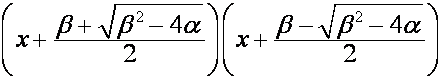 .
.
Используя
биномиальную форму записи вектора ![]() , мысленно составим
таблицу
, мысленно составим
таблицу ![]() (по определению
(по определению ![]() ). Первый член
). Первый член ![]() -ой строки таблицы равен
-ой строки таблицы равен ![]() ,
, ![]() -й член
-й член ![]() -ой строки равен
-ой строки равен 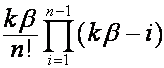 . Пользуясь
равенством
. Пользуясь
равенством 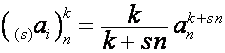 и подстановкой
и подстановкой ![]() , выводим, что
, выводим, что ![]() -й член
-й член ![]() -ой строки верхней половины таблицы
-ой строки верхней половины таблицы ![]() ,
, ![]() , равен
, равен 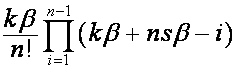 ,
, ![]() ,
, ![]() -й член
-й член ![]() -ой строки нижней половины таблицы
-ой строки нижней половины таблицы ![]() ,
, ![]() , равен
, равен 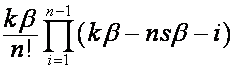 ,
, ![]() .
.
Обозначим:
![]()
![]() ,
, ![]() , где
, где ![]() – матрица, нулевая и
первая строка которой соответственно
– матрица, нулевая и
первая строка которой соответственно ![]() и
и ![]() , а
, а ![]() -я строка имеет вид
-я строка имеет вид 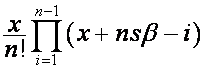 . Тогда
. Тогда
![]() ,
,
![]() ,
,
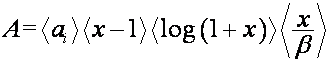 ,
,
 .
.
Обозначим:
![]()
![]() ,
, ![]() , где
, где ![]() – матрица, нулевая и
первая строка которой соответственно
– матрица, нулевая и
первая строка которой соответственно ![]() и
и ![]() , а
, а ![]() -я строка имеет вид
-я строка имеет вид 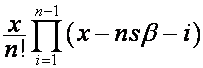 . Тогда
. Тогда
![]() ,
,
![]() ,
,
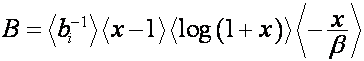 ,
,
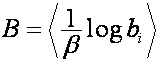 .
.
Таким
образом,
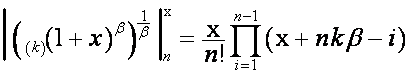 .
.
Например,
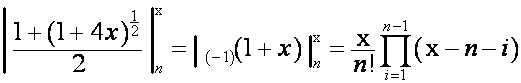 ,
,
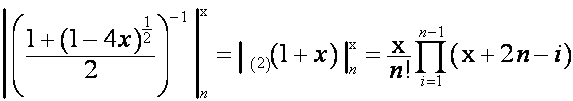 ,
,
или
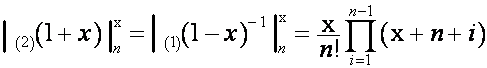 ,
,
 .
.
Обобщая, выводим: если
 ,
,
то
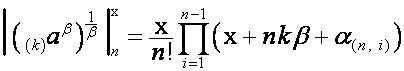 .
.
В биномиальной форме
записи вектора ![]() все коэффициенты
все коэффициенты ![]() равны нулю,
следовательно
равны нулю,
следовательно
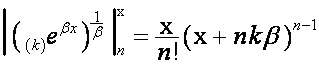 .
.
Например,
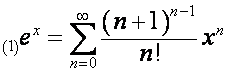 ,
, 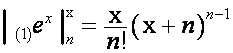 .
.
Равенство
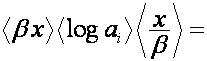
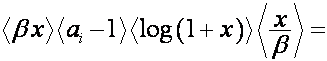
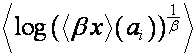 ,
,
где  , означает, что если
, означает, что если
 ,
,
то
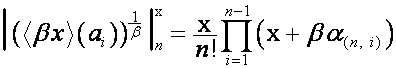 .
.
Применительно к
![]() , выводим:
, выводим:
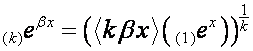 .
.
Так как
 ,
,
то
 ,
,
 ,
,
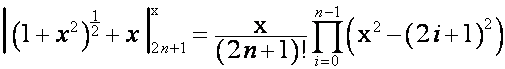 .
.
4
Биномиальная форма записи определена для ![]() с условиями:
с условиями: ![]() ,
, ![]() . Формулы же
. Формулы же
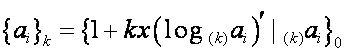 ,
,
![]()
справедливы для ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В частности, если
. В частности, если
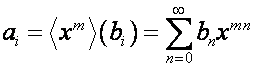 ,
,
то
![]() ,
, ![]() .
.
Обозначим:
 ,
, ![]() ;
; ![]() , если
, если ![]() .
.
Тогда
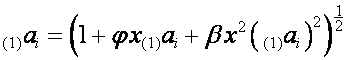 ,
,
![]()
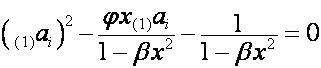 ,
,
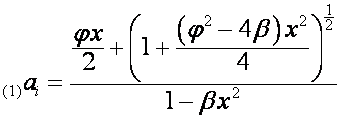 .
.
Обозначим:
![]() .
.
Тогда
![]() ,
,
![]() ,
,
 .
.
Предположив, что в биномиальной форме
записи вектора  коэффициенты
коэффициенты ![]() выражаются общей
формулой, как в случае
выражаются общей
формулой, как в случае ![]() ,
, ![]() ,
, ![]() , попробуем очертить ее контуры.
, попробуем очертить ее контуры.
Пусть ![]() . Составим фрагменты таблиц
. Составим фрагменты таблиц ![]() и
и ![]() , например, при
, например, при ![]() :
:
![]()
![]()
![]()
![]()
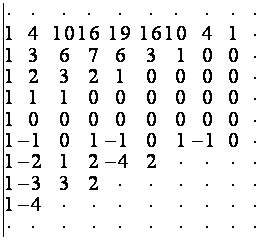

Для
верхней половины таблицы ![]() справедливо
равенство
справедливо
равенство ![]() ,
, ![]() . Учитывая, что
. Учитывая, что 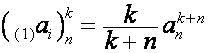 , выводим:
, выводим:
![]() ,
,
где ![]() – полином степени
– полином степени ![]() (т.е. вектор, все члены
которого, начиная с номера
(т.е. вектор, все члены
которого, начиная с номера ![]() , равны нулю),
, равны нулю), ![]() .
.
Таким образом, если
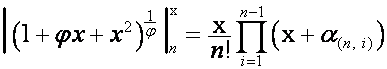 ,
,
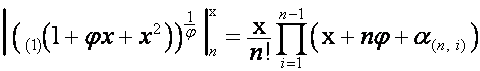 ,
,
то
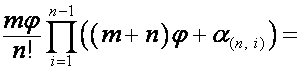
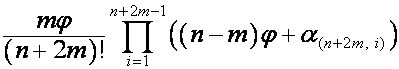 .
.
![]() -й член нулевой нисходящей диагонали таблицы
-й член нулевой нисходящей диагонали таблицы ![]() , т.е.
, т.е. ![]() -й член вектора
-й член вектора 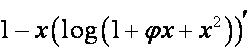 , равен
, равен 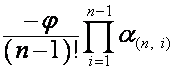 . Эйлер нашел, что [2, с.16]:
. Эйлер нашел, что [2, с.16]:
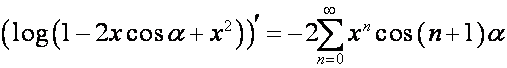 .
.
Следовательно, если ![]() , то
, то
 .
.
Кроме
того, [2, с.15]:
 .
.
Следовательно,
 .
.
Матрицу, которая получается из
единичной матрицы рамерности ![]() перестановкой в
обратном порядке строк или столбцов, обозначим
перестановкой в
обратном порядке строк или столбцов, обозначим ![]() . Например
. Например
 .
.
Преобразование
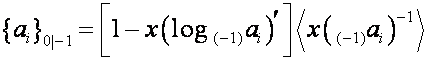
отображает ![]() -ю строку таблицы
-ю строку таблицы ![]() на
на ![]() -ю нисходящую диагональ. Отсюда вытекает, что
-ю нисходящую диагональ. Отсюда вытекает, что ![]() -я строка матрицы
-я строка матрицы ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы ![]() .
.
Таким образом, полином ![]() ,
, ![]() , совпадает с
, совпадает с ![]() -й строкой матрицы
-й строкой матрицы
 .
.
Так
как
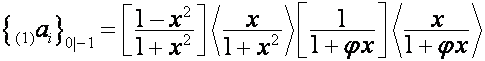 ,
,
 ,
,
то
![]() ,
,
где ![]() ,
, ![]() , –
, – ![]() -я строка матрицы
-я строка матрицы
 .
.
Из таблицы ![]() видно, что для таблицы
видно, что для таблицы
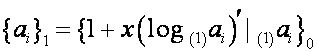 , где
, где
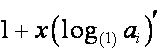
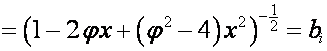 ,
,
справедливо
равенство
![]() ,
,
где ![]() – полином степени
– полином степени ![]() ;
; ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы

 ,
,
так
что
![]() ,
,
где
![]() –
– ![]() -я строка матрицы
-я строка матрицы
 .
.
Таким образом,
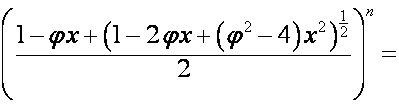
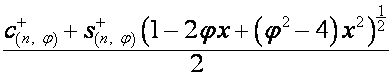 ,
,
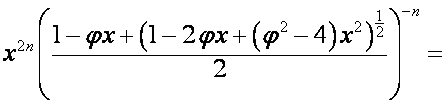
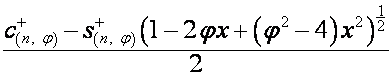 ;
;
Пусть ![]() . Составим фрагменты таблиц
. Составим фрагменты таблиц ![]() и
и ![]() , например, при
, например, при ![]() :
:
![]()
![]()

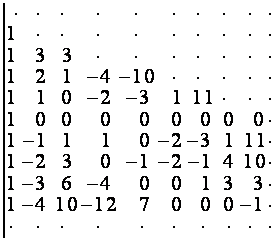
Легко доказать, что если ![]() – полином степени
– полином степени ![]() , то
, то
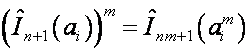 .
.
Поэтому,
если
![]() ,
,
как
в случае с полиномом ![]() , то
, то
![]() .
.
Таким образом, для верхней половины таблицы ![]() справедливо равенство
справедливо равенство
![]() ,
, ![]() .
.
Следовательно,
![]() ,
,
где ![]() ,
, ![]() совпадает
с
совпадает
с ![]() -й строкой матрицы
-й строкой матрицы![]()

 ,
,
![]() ,
,
где
![]() ,
, ![]() , –
, – ![]() -я строка матрицы
-я строка матрицы
 .
.
Из таблицы ![]() видно, что для таблицы
видно, что для таблицы
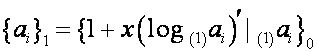 , где
, где
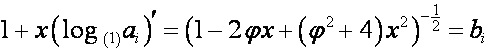 ,
,
справедливо
равенство
![]() ,
,
где
![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы

 ,
,
![]() ,
,
где ![]() –
– ![]() -я строка матрицы
-я строка матрицы
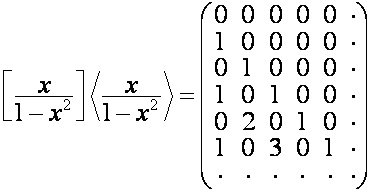 .
.
Таким образом,
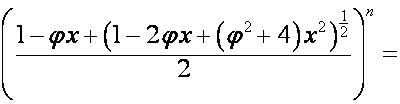
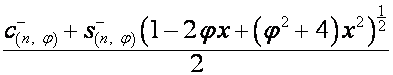 ,
,

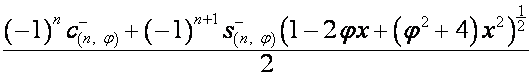 .
.
Перейдем к общему случаю. Пусть ![]() ,
, ![]() . Тогда
. Тогда
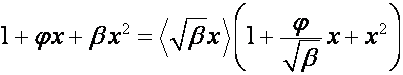 ,
,
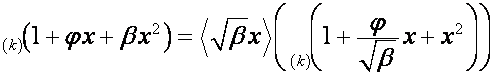 ,
,
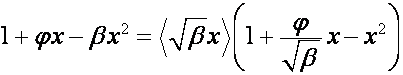 ,
,
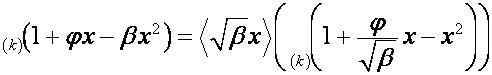 ,
,
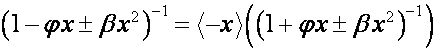 ,
,
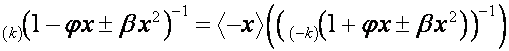 .
.
Пусть теперь ![]() ,
, ![]() – любые действительные
числа.
– любые действительные
числа. ![]() -ю строку матрицы
-ю строку матрицы

 ,
,
![]() , обозначим
, обозначим ![]() ;
; ![]() -ю строку матрицы
-ю строку матрицы

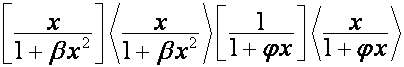
обозначим
![]() . Тогда
. Тогда
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() –
– ![]() -я строка матрицы
-я строка матрицы
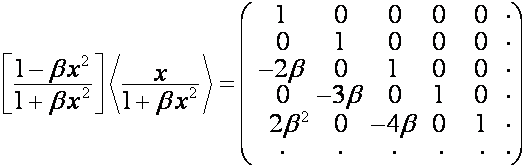 ,
,
![]() –
– ![]() -я строка матрицы
-я строка матрицы
 ,
,

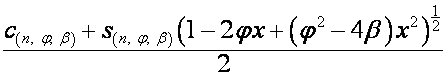 ,
,

 .
.
Отметим,
что
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Отметим
также равенство
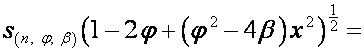
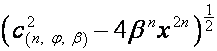 .
.
5
Рассмотрим метод, позволяющий выражать
корни некоторых полиномов через корни полиномов
![]() .
.
Обозначим:
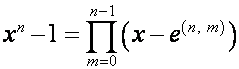 ,
,
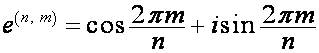 ,
, ![]() .
.
Тогда:
 ,
,
 ,
,
 .
.
Запомним правила: если
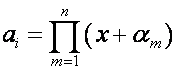 ,
, ![]() ,
,
то
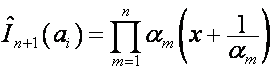 ,
,
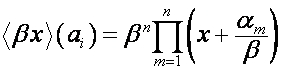 ,
,
 ,
,
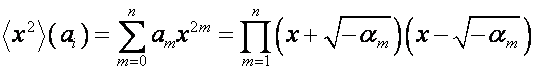 .
.
Следовательно,
 ,
,
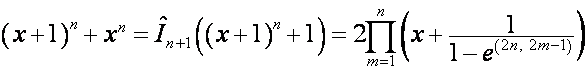 ,
,
где
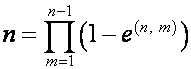 ,
, 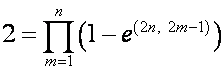 .
.
Так
как
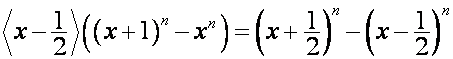 ,
,
то
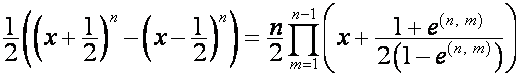 ,
,
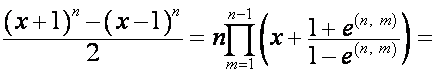
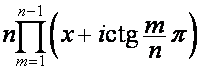 .
.
Аналогично
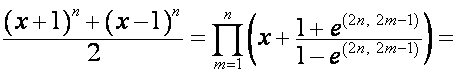
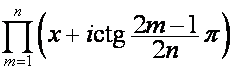 .
.
Найдем корни полиномов
![]() и
и ![]() ,
,
где
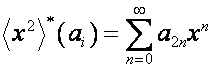 .
.
Обозначим:
![]() .
.
Так
как
 ,
,
то
 .
.
Из
таблицы
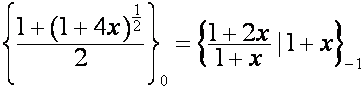 :
:
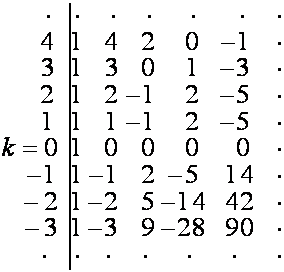
видно,
что ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы
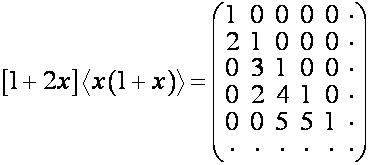 .
.
Так
как
 ,
,
 ,
,
то
![]()
![]()
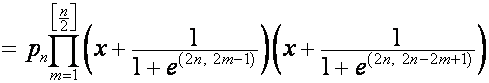 ,
,
где ![]() – целая часть от
– целая часть от ![]() ,
, ![]() ,
, ![]() . Обозначим:
. Обозначим:
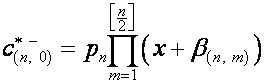 .
.
Тогда
![]()
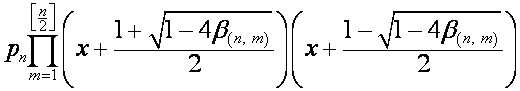 ,
,
 ,
,
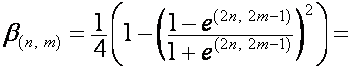
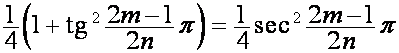 .
.
Таким образом,
![]()
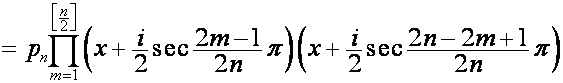 ,
,
 ,
,
![]()
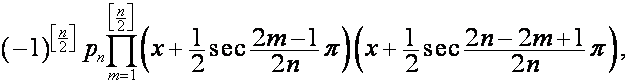
 .
.
Найдем корни полиномов
![]() и
и ![]() .
.
Обозначим:
![]() .
.
Из
таблицы
![]()
![]()
 :
:
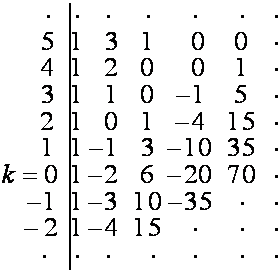
видно,
что
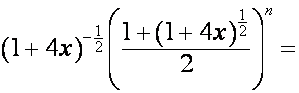
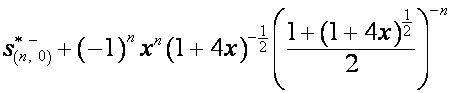 ,
,
где ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы
 .
.
Так
как
 ,
,
то
![]()
![]()
 ,
,
где
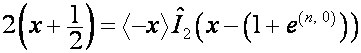 ,
, ![]() ,
, ![]() .
.
Обозначим:
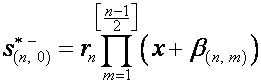 .
.
Тогда
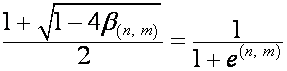 ,
,
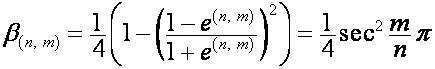 .
.
Таким образом,
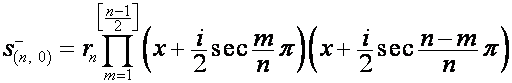 ,
,
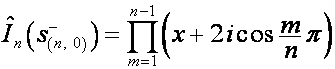 ,
,
![]()
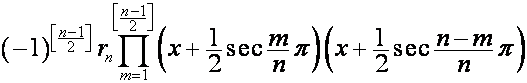 ,
,
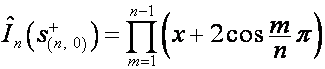 .
.
В общем случае:
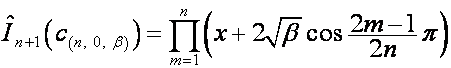 ,
,
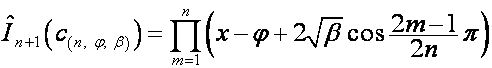 ,
,

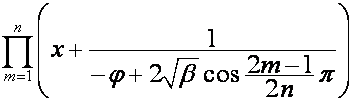 ,
,
где ![]() ,
, ![]() ,
, ![]() . Если один из сомножителей множетеля
. Если один из сомножителей множетеля 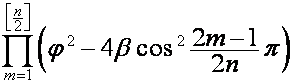 равен нулю (в этом
случае
равен нулю (в этом
случае ![]() , поскольку
, поскольку ![]() – действительное
число) он заменяется на
– действительное
число) он заменяется на  , соответствующий ему полином
, соответствующий ему полином 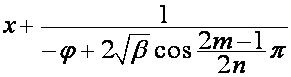 заменяется на
заменяется на ![]() .
.
Аналогично
 ,
,
 ,
,
![]()

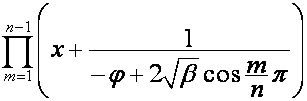 ,
,
где
![]() ,
, ![]() ,
, ![]() .
.
6
Обозначим:
![]()
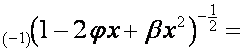
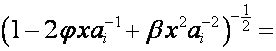
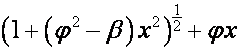 ,
,
где
по определению ![]() . Тогда
. Тогда
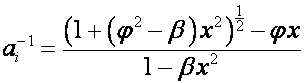 ,
, ![]() .
.
Раскладывая ![]() в бином Ньютона и
группируя члены, можно представить его в виде
в бином Ньютона и
группируя члены, можно представить его в виде
 ,
,
где ![]() – полином степени
– полином степени ![]() , четные члены которого равны нулю, если
, четные члены которого равны нулю, если ![]() нечетно, нечетные
члены равны нулю, если
нечетно, нечетные
члены равны нулю, если ![]() четно;
четно; ![]() – полином степени
– полином степени ![]() , четные члены которого равны нулю, если
, четные члены которого равны нулю, если ![]() четно, нечетные члены
равны нулю, если
четно, нечетные члены
равны нулю, если ![]() нечетно. Например:
нечетно. Например:
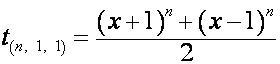 ,
,  ;
;
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Так
как
![]() ,
,
то
![]() ,
,
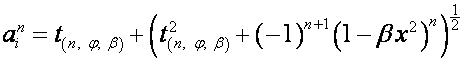 .
.
![]() -й член
-й член ![]() -й восходящей диагонали таблицы
-й восходящей диагонали таблицы ![]() , т.е.
, т.е. ![]() -й член вектора
-й член вектора
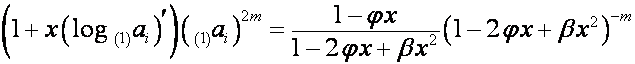
равен ![]() -му члену полинома
-му члену полинома ![]() . Отсюда вытекает, что
. Отсюда вытекает, что ![]() совпадает с
совпадает с ![]() -й строкой матрицы
-й строкой матрицы
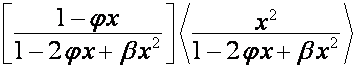 .
.
Например:
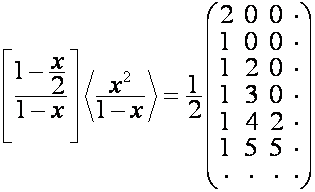 ,
,
 ,
,
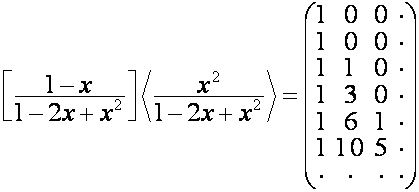 .
.
Обозначим:
![]() .
.
Так
как

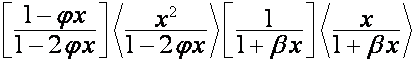 ,
,
то
![]() .
.
Так
как
![]() ,
,
то
![]() .
.
Так
как
 ,
,
то
 ,
, ![]() ,
, ![]() ,
,
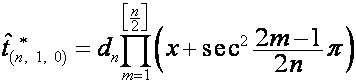 ,
,
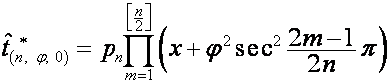 ,
,
где
![]() ,
, ![]() ,
,
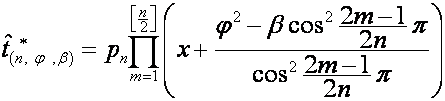 ,
,
![]()
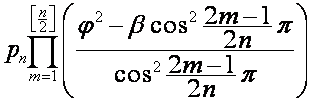
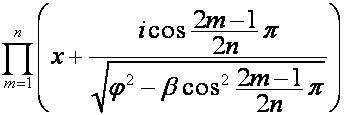 ,
,
где множитель 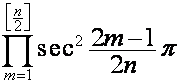 равен
равен ![]() , если
, если ![]() четно, и
четно, и ![]() , если
, если ![]() нечетно (проверяется
подстановкой
нечетно (проверяется
подстановкой ![]() ,
, ![]() ); если один из сомножителей (в случае
); если один из сомножителей (в случае ![]() – любой из
сомножителей) множителя
– любой из
сомножителей) множителя  равен нулю, он
заменяется на
равен нулю, он
заменяется на 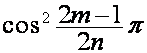 , соответствующая ему пара полиномов заменятся на
, соответствующая ему пара полиномов заменятся на ![]() . Отметим также, что
. Отметим также, что ![]() .
.
![]() -й член вектора
-й член вектора 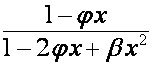 равен
равен ![]() -му члену полинома
-му члену полинома ![]() и нулю, если степень
и нулю, если степень ![]() меньше
меньше ![]() . Следовательно,
. Следовательно,
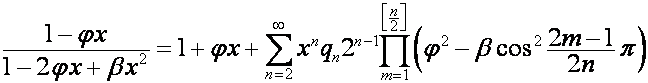
где ![]() ,
, ![]() , множитель
, множитель 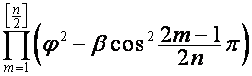 равен нулю, если один
из сомножителей равен нулю.
равен нулю, если один
из сомножителей равен нулю.
Обозначим:
![]() ,
, 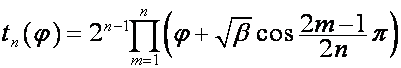 .
.
Тогда
![]()
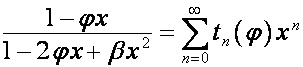 .
.
Так
как
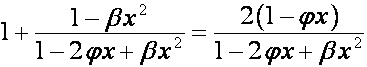 ,
,
то
 .
.
Убедимся, что
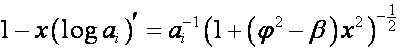 .
.
Следовательно,
![]() -я строка верхней половины таблицы
-я строка верхней половины таблицы
![]()
имеет
вид
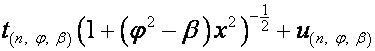 .
.
![]() -й член
-й член ![]() -й восходящей диагонали таблицы
-й восходящей диагонали таблицы ![]() ,
, ![]() , т.е.
, т.е. ![]() -й член вектора
-й член вектора ![]() , равен
, равен ![]() -му члену полинома
-му члену полинома ![]() . Отсюда вытекает, что
. Отсюда вытекает, что ![]() совпадпнт с
совпадпнт с ![]() -й строкой матрицы
-й строкой матрицы
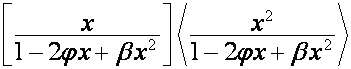 .
.
Например:
 ,
,
 ,
,
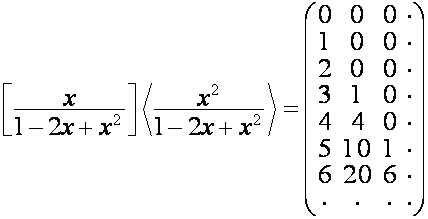 .
.
Обозначим:
![]() .
.
Так
как
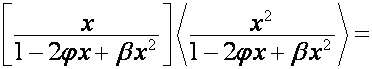
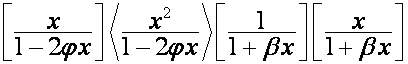 ,
,
то
![]() .
.
Так
как
![]() ,
,
то
![]() .
.
Так
как
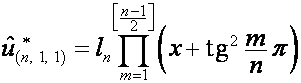 ,
, ![]() ,
, ![]() ,
,
то
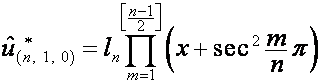 ,
,
 ,
,
где
![]() ,
, ![]() ,
,
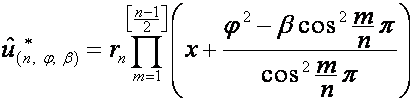 ,
,
![]()
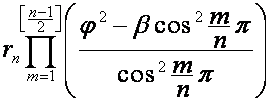
 ,
,
где множитель 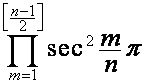 равен
равен 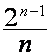 , если
, если ![]() четно, и
четно, и ![]() , если
, если ![]() нечетно; если один из
сомножителей (в случае
нечетно; если один из
сомножителей (в случае ![]() – любой из
сомножителей) множителя
– любой из
сомножителей) множителя 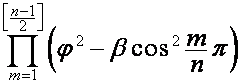 равен нулю, он
заменяется на
равен нулю, он
заменяется на 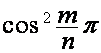 , соответствующая ему пара полиномов заменяется на
, соответствующая ему пара полиномов заменяется на ![]() . Отметим, что
. Отметим, что ![]() .
.
![]() -й член вектора
-й член вектора ![]() равен
равен ![]() -му члену полинома
-му члену полинома ![]() и нулю, если степень
и нулю, если степень ![]() меньше
меньше ![]() . Следовательно,
. Следовательно,
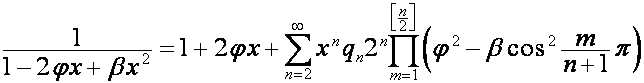 ,
,
где ![]() ,
, ![]() , множитель
, множитель 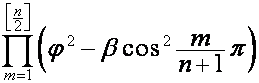 равен нулю, если один
из сомножителей равен нулю.
равен нулю, если один
из сомножителей равен нулю.
Обозначим:
![]() ,
,  .
.
Тогда
 .
.
7
Последовательности
столбцов матриц ![]() и
и ![]() ,
, ![]() ,
, ![]() , совпадают с последовательностями строк верхней и нижней половин
таблицы
, совпадают с последовательностями строк верхней и нижней половин
таблицы ![]() . Формулы
. Формулы
![]() ,
,
![]()
позволяют изучать
таблицу ![]() , рассматривая в качестве ее элементов не строки, а столбцы.
, рассматривая в качестве ее элементов не строки, а столбцы.
Единичную
матрицу размерности ![]() обозначим
обозначим ![]() . Матрицу, которая получается из
. Матрицу, которая получается из ![]() перестановкой столбцов
в обратном порядке , как и прежде, будем обозначать
перестановкой столбцов
в обратном порядке , как и прежде, будем обозначать ![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() ,
, ![]() , обозначим
, обозначим
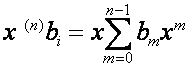 .
.
Так как ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , – вектор
, – вектор 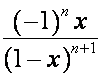 , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
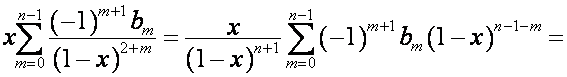
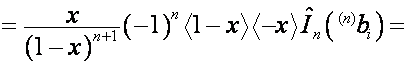
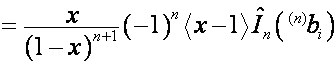 .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() ,
, ![]() , обозначим
, обозначим
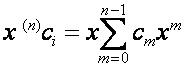 .
.
Так как ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , – вектор
, – вектор  , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
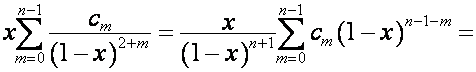
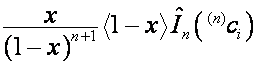 .
.
Так как
![]() ,
,
![]() ,
,
то
![]() .
.
Таким образом, ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
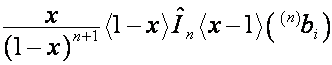 .
.
Так как
![]()
![]() ,
, ![]() ,
,
то
![]() .
.
Например,
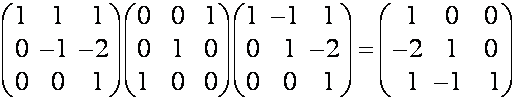 .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим 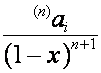 ,
, ![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим 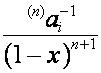 . Мы выяснили, что
. Мы выяснили, что
![]() ,
,
где ![]() –
– ![]() -я строка матрицы
-я строка матрицы ![]() , умноженная на
, умноженная на ![]()
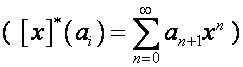 , и, что самое
интересное,
, и, что самое
интересное,
![]() .
.
Например, если ![]() , то
, то ![]() ,
, ![]() .
.
Пусть ![]() . Тогда
. Тогда
 .
.
Преобразование ![]()
![]() -ю строку матрицы
-ю строку матрицы ![]() отображает на
отображает на ![]() -ю строку матрицы
-ю строку матрицы
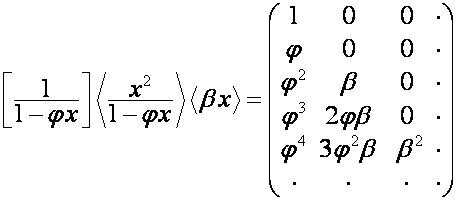 ,
,
т.е., при ![]() , на полином
, на полином
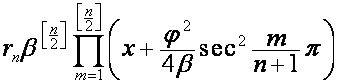 ,
, ![]() ,
, ![]() .
.
Следовательно,
 ,
,
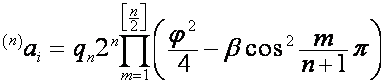
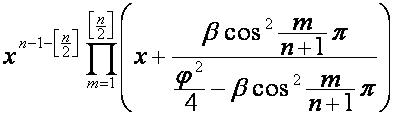 ,
,
где ![]() ,
, 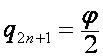 ; если один из сомножителей множителя
; если один из сомножителей множителя  равен нулю, он
заменяется на
равен нулю, он
заменяется на  , соответствующий полином заменяется на
, соответствующий полином заменяется на ![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() , где
, где ![]() , обозначим
, обозначим 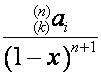 ,
, ![]() . Найдем преобразование
. Найдем преобразование
![]() , такое, что
, такое, что
![]() .
.
Воспользуемся
биномиальной формой записи.
Для формулы общего члена
последовательности введем обозначение
![]() ,
, ![]()
Если  –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() ,
, 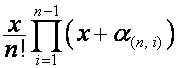 –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , то
, то
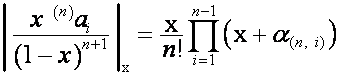 .
.
Рассмотрим выражение
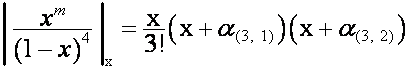 ,
, ![]()
Так как
![]() ,
, ![]() ,
, ![]() ,
,
то
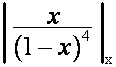 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
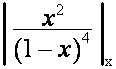 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
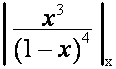 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
Следовательно,
![]()
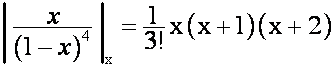 ,
,
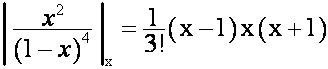 ,
,
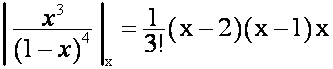 .
.
Обобщая, выводим:
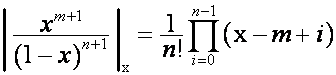 ,
, ![]() .
.
Матрицу, ![]() -м столбцом которой является полином
-м столбцом которой является полином
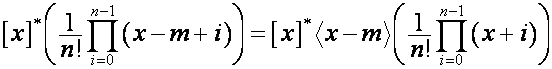 ,
,
![]() , обозначим
, обозначим ![]() . Например:
. Например:
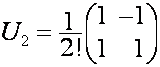 ,
, 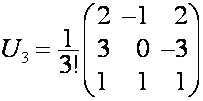 ,
, 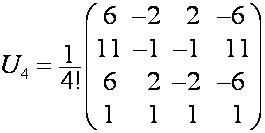 .
.
По определению преобразования ![]() , если
, если
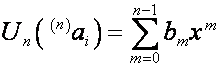 ,
,
то
 .
.
Таким
образом, преобразование ![]() отображает
отображает ![]() на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() , умноженную на
, умноженную на ![]() . Так как
. Так как
 ,
,
то
![]() ,
,
![]() .
.
Обозначим:
![]() . Тогда полином
. Тогда полином ![]() совпадает с
совпадает с ![]() . Так как
. Так как
![]() ,
,
то из определения преобразования ![]() вытекает, что
вытекает, что
![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() ,
, ![]() , в порядке исключения выделив множитель, обозначим
, в порядке исключения выделив множитель, обозначим  , где
, где ![]() совпадает с полиномом
Эйлера
совпадает с полиномом
Эйлера ![]() [3, с.254], [4, c.139]:
[3, с.254], [4, c.139]:
![]() ,
, ![]() ,
, ![]() ,
,
![]() , …
, …
Так как
 ,
,
то
![]() ,
, ![]() .
.
Таким
образом, ![]() -м столбцом матрицы
-м столбцом матрицы ![]() является вектор
является вектор ![]() :
:
 ,
, 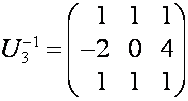 ,
,  .
.
Мы знаем,
что если ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 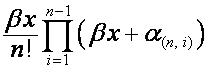 , где
, где ![]() , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид  . Окончательно получаем:
. Окончательно получаем:
![]() .
.
Например:
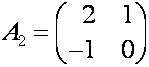 ,
,  ,
, 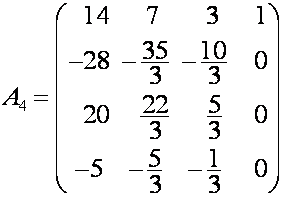 .
.
Из
определения преобразования ![]() вытекает, что
если
вытекает, что
если ![]() , то
, то ![]() . Действительно, так как
. Действительно, так как
![]() ,
,
![]() ,
,
то
![]() .
.
Таким
образом, матрица ![]() получается из
получается из ![]() перестановкой в
обратном порядке строк и столбцов.
перестановкой в
обратном порядке строк и столбцов.
Обозначим:
![]() ,
,
![]() .
.
Так как
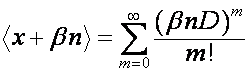 ,
,
то
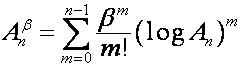 .
.
Например:
 ,
,
 ,
,
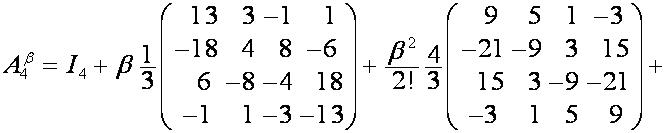
 .
.
Так как
каждый столбец матрицы ![]() , кроме последнего, содержит множитель
, кроме последнего, содержит множитель ![]() , то каждый столбец матрицы
, то каждый столбец матрицы
![]() ,
, ![]() , также содержит множитель
, также содержит множитель ![]() и сумма его членов
равна нулю. Следовательно, сумма членов каждого столбца матрицы
и сумма его членов
равна нулю. Следовательно, сумма членов каждого столбца матрицы ![]() равна единице.
равна единице.
Таким
образом, преобразование ![]() сохраняет сумму
значений вектора.
сохраняет сумму
значений вектора.
![]() -ю строку матрицы
-ю строку матрицы  ,
, ![]() , обозначим
, обозначим  . Тогда
. Тогда![]()
![]()
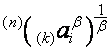 .
.
Так как
![]() ,
,
![]() ,
,
то
 .
.
Обозначим:
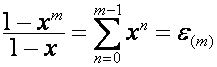 .
.
Диагональную матрицу,
диагональные элементы которой равны значениям вектора ![]() , обозначим
, обозначим ![]() :
:
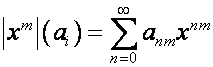 .
.
Вектор 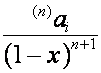 раскладывается на
составляющие по правилу
раскладывается на
составляющие по правилу
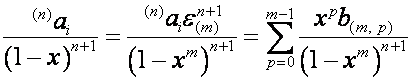 ,
,
где
![]() ,
,
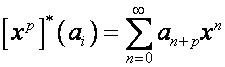 .
.
Например,
 .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим 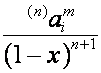 . Так как
. Так как ![]() -й член вектора
-й член вектора 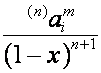 равен
равен ![]() -му члену вектора
-му члену вектора 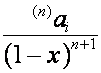 , т.е.
, т.е.
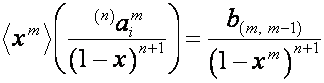 ,
,
то
![]() ,
,
где
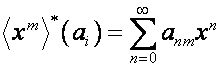 .
.
Обозначим:
![]() .
.
Например,
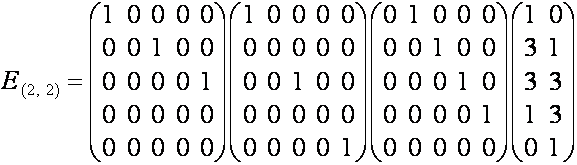 .
.
Убедимся, что ![]() – квадратная матрица
размерности
– квадратная матрица
размерности ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, 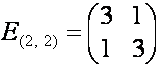 ,
, 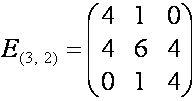 .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, 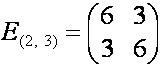 ,
,  .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,  ,
, 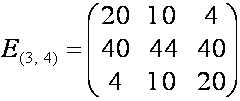 .
.
![]() ,
,
![]() .
.
 ,
, 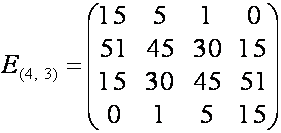 .
.
Преобразование ![]() отображает
отображает ![]() на
на ![]() . Отсюда вытекает, что, во-первых,
. Отсюда вытекает, что, во-первых,
![]() ,
,
во-вторых,
![]() ,
,
так как преобразование ![]() отображает
отображает ![]() -ю строку матрицы
-ю строку матрицы ![]() на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() .
.
Таким
образом, ![]() является собственным
вектором преобразования
является собственным
вектором преобразования ![]() с собственным
значением
с собственным
значением ![]() .
.
Рассмотрим
равенство
![]() .
.
Каждый член вектора ![]() , начиная с
, начиная с ![]() -го, равен сумме членов вектора
-го, равен сумме членов вектора ![]() , т.е.
, т.е. ![]() . Следовательно, сумма членов вектора
. Следовательно, сумма членов вектора ![]() ,
, ![]() , также равна
, также равна ![]() .
.
Таким
образом, сумма членов каждого столбца матрицы
![]() равна
равна ![]() и на эту величину
преобразование
и на эту величину
преобразование ![]() умножает сумму
значений вектора.
умножает сумму
значений вектора.
Отметим
также, что
![]() ,
,
![]() .
.
1. Риордан Д. Комбинаторные тождества. – М.: Наука,
1982.
2. Паплаускас А. Б.
Тригонометрические ряды от Эйлера до Лебега. – М.: Наука, 1966.
3. Риордан Д. Введение в
комбинаторный анализ. – М.: ИЛ, 1963.
4. Сачков В. Н.
Комбинаторные методы дискретной математики. – М.: Наука, 1977.